Spiediens šķidrumos un gāzēs

Nodaļā ''Cieta ķermeņa spiediens uz virsmu'' aplūkojām cieta ķermeņa spiedienu uz virsmu.

Spiediens (\(p\)) ir fizikāls lielums, kas raksturo, cik liels spēks darbojas uz virsmas laukuma vienību perpendikulāri virsmai: \(p=\frac{F_\mathrm{sp}}{S}\),
kur \(F_\mathrm{sp}\) – spiediena spēks, kas darbojas uz virsmu, bet \(S\) – tās laukums.

Spiediena mērvienība ir paskāls: \([p]=\frac{N}{m^2}=Pa\).

Spiediena rašānās mehānisms šķidrumos un gāzēs

Gāzes (un arī šķidruma) spiedienu uz trauka sienām rada gāzes molekulu triecieni.

Lūk, vienkāršots spiediena rašanās mehānisma apraksts. Iztēlosimies, ka gāze atrodas slēgtā nemainīga tilpuma traukā. Gāzes molekulas nepārtraukti un haotiski kustas, tādēļ tās  triecas pret trauka sienām un atlec no tām. Katrai molekulai pirms sadursmes piemīt impulss \(mv\) kur \(m\) — molekulas masa, bet \(v\) — tās ātrums. Atlecot no trauka sienas, molekulas impulss mainās par \(\Delta (mv)\), un, atbilstoši impulsa nezūdamības likumam, šādu impulsu saņem trauka siena.

Līdz ar to, atbilstoši otrajam Ņūtona likumam, šī molekula uz trauka sienau iedarbojas ar spēku \(F_\mathrm{i} =\frac{\Delta (mv)}{\Delta t}\)

kur \(\Delta t\) — trieciena ilgums.

Tā kā molekulu ir ļoti daudz un tās kustas pilnīgi haotiski (visi kustības virzieni molekulām, kas kustas ar vienādu ātrumu, ir vienlīdz iespējami), molekulu triecienu spēkiem \(F_\mathrm{i}\) summējoties, to rezultējošais spēks \(F\), kas pielikts trauka sienai, ir vērsts perpendikulāri tai. Ja sienas laukums ir \(S\), tad uz to darbojas spiediens \(p = \frac{F}{S}\). (tuvāk gāzes spiediens aplūkots nodaļā ''Gāzes spiediens'').

Saskaņā ar Paskāla likumu, ko formulēsim šajā nodaļā, tāds pats gāzes spiediens darbojas arī visā gāzes tilpumā.

Protams, šādā sistēmā, kas sastāv no daudzām daļiņām, ir iespējamas spiediena fluktuācijas — neregulāras izmaiņas, kas ir jo jūtamākas, jo mazāks ir daļiņu skaits tilpuma vienībā. Ja gāze ir ļoti retināta, vai arī objekts, kas izjūt spiedienu ir mikroskopiski mazs, Paskāla likums lokāli var nebūt spēkā (skatīt nodaļu par Brauna kustību ''Vielas atomārā uzbūve'').

Šajā nodaļā aplūkosim, kā līdzsvarā esošs (būtībā nekustīgs) šķidrums vai gāze iedarbojas uz tajā iegremdētiem ķermeņiem, radot spiedienu uz tiem. 

Gāzes no šķidrumiem būtiski atšķiras ar to dažādo saspiežamību. Gāzu saspiežamība ir liela, bet šķidrumus var uzskatīt par nesaspiežamiem - šķidruma blīvums (\(\rho=\frac{m}{V}\)) ārējas iedarbības rezultātā nemainās. Neraugoties uz šo atšķirību, līdzsvara stāvoklī gāzes un šķidrumi pakļaujas vieniem un tiem pašiem likumiem.

Ja uz šķidrumu vai gāzi, kas atrodas līdzsvarā (miera stāvoklī) cilindriskā traukā (1. attēls), spiež virzulis, tad, atbilstoši trešajam Ņūtona likumam, šķidrums darbojas uz virzuli ar skaitliski tik pat lielu, bet pretēji vērstu spēku.

Tieši uz virzuli darbojas tam tuvākais šķidruma slānis, bet uz to savukārt spiež dziļākie slāņi. Tāpēc virzuļa iedarbībā šķidrumā, līdzīgi kā cietā vielā, ārējā slodze rada spriegumu (skatīt nodaļu ''Mehāniskais spriegums''), kas pastāv visā šķidruma tilpumā. Statiskais spriegums šķidrumā būtiski atšķiras no tā sprieguma, ko ārējā iedarbība rada cietā vielā.

Šķidruma un gāzes slāņi, kā arī to molekulas, atšķirībā no cietu ķermeņu molekulām, var brīvi pārvietoties cita attiecībā pret citu visos virzienos.

Spiediena spēks šķidrumos un gāzēs

Varam iztēloties arī šķidrumā (vai gāzē) iegremdētu plānu plāksnīti vai vienkārši tilpuma elementu (1. attēls). Tā kā šķidrums atrodas līdzsvarā, šāds tilpuma elements nepārvietojas. Tātad - uz šādu ''plāksnīti'' šķidrumam no abām pusēm jādarbojas uz laukumu \(\Delta S\) ar spēkiem \(\Delta F\), kas, neatkarīgi no plāksnītes orientācijas, ir pretēji vērsti un skaitliski vienādi.

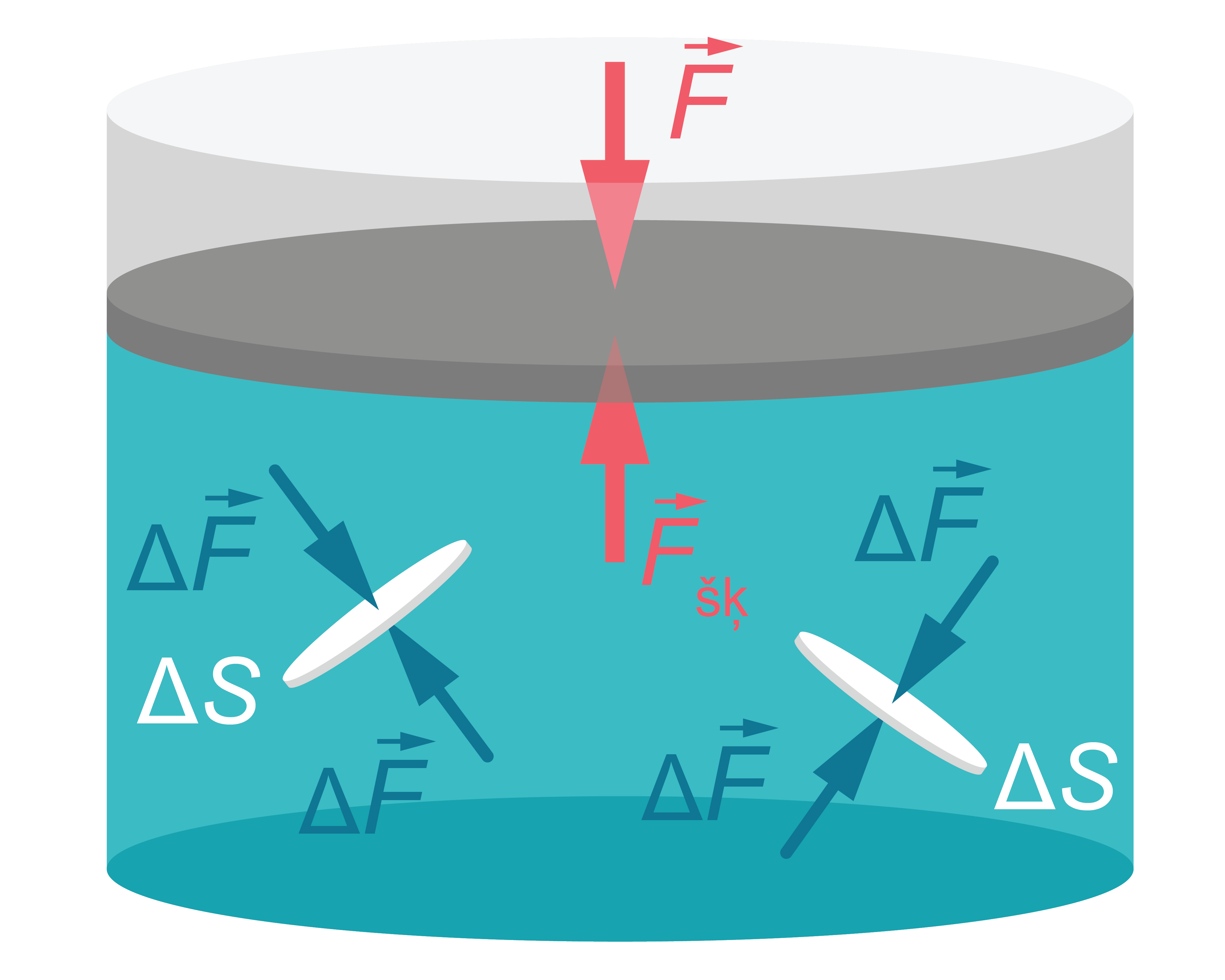
Secinājums – arī spriegums, kas darbojas uz ''plāksnītes'' virsmu, katrā punktā vienmēr ir vērsts tai perpendikulāri (pa normāli). Tas nozīmē, ka šķidrumā un gāzē nepastāv tangenciāli spriegumi.

Lai uzsvērtu atšķirību no mehāniskā sprieguma cietā vielā, spriegumu šķidrumā (vai gāzē) sauc par spiedienu \(p\). 
Līdz ar to, spiediens ir spēks, kas šķidrumā vai gāzē darbojas uz jebkuru virsmas laukuma vienību un ir vērsts perpendikulāri šim laukumam.
Protams, tāpat, kā cieta ķermeņa spiedienam uz virsmu, spiediena SI mērvienība ir paskāls: \([p]=\frac{N}{m^2}=Pa\).

Saistībā ar spiedienu šķidrumos vai gāzēs  nereti izmanto arī citas spiediena mērvienības:

• bārs (bar) - 100000 Pa
• tehniskā atmosfēra (at) - 1 kg/cm² - 98066 Pa
• fizikālā atmosfēra (atm) - 101325 Pa (parasti ar ''atmosfēru'' saprot šo vērtību)
• tors (milimetr dzīvsudraba stabiņa) (mm Hg) - 133,322 Pa (izmanto atmosfēras spiediena raksturošanai meteoroloģijā).

Paskāla likums

Fakts, ka šķidrumā vai gāzē spiediens (tātad arī spiediena spēks) vienmēr darbojas uz jebkuru laukuma elementu perpendikulāri, ir noformulēts Paskāla likumā:

1. Mierā esoša šķidruma vai gāzes jebkurā punktā spiediens visos virzienos ir vienāds. Ja tā nebūtu, tad šķidrumā vienmēr varētu atrast tilpuma elementu, uz kuru darbojošies spēki nav līdzsvaroti un notiktu šķidruma kustība.

2. Šķidrumam vai gāzei pieliktais ārējais spiediens izplatās bez pārmaiņām visā šķidruma vai gāzes tilpumā un ir vienāds visos tā punktos.

Pēdējo apgalvojumu var pamatot, aplūkojot ar virzuli hermētiski noslēgtu trauku, kurā atrodas gāze (2. attēls). 

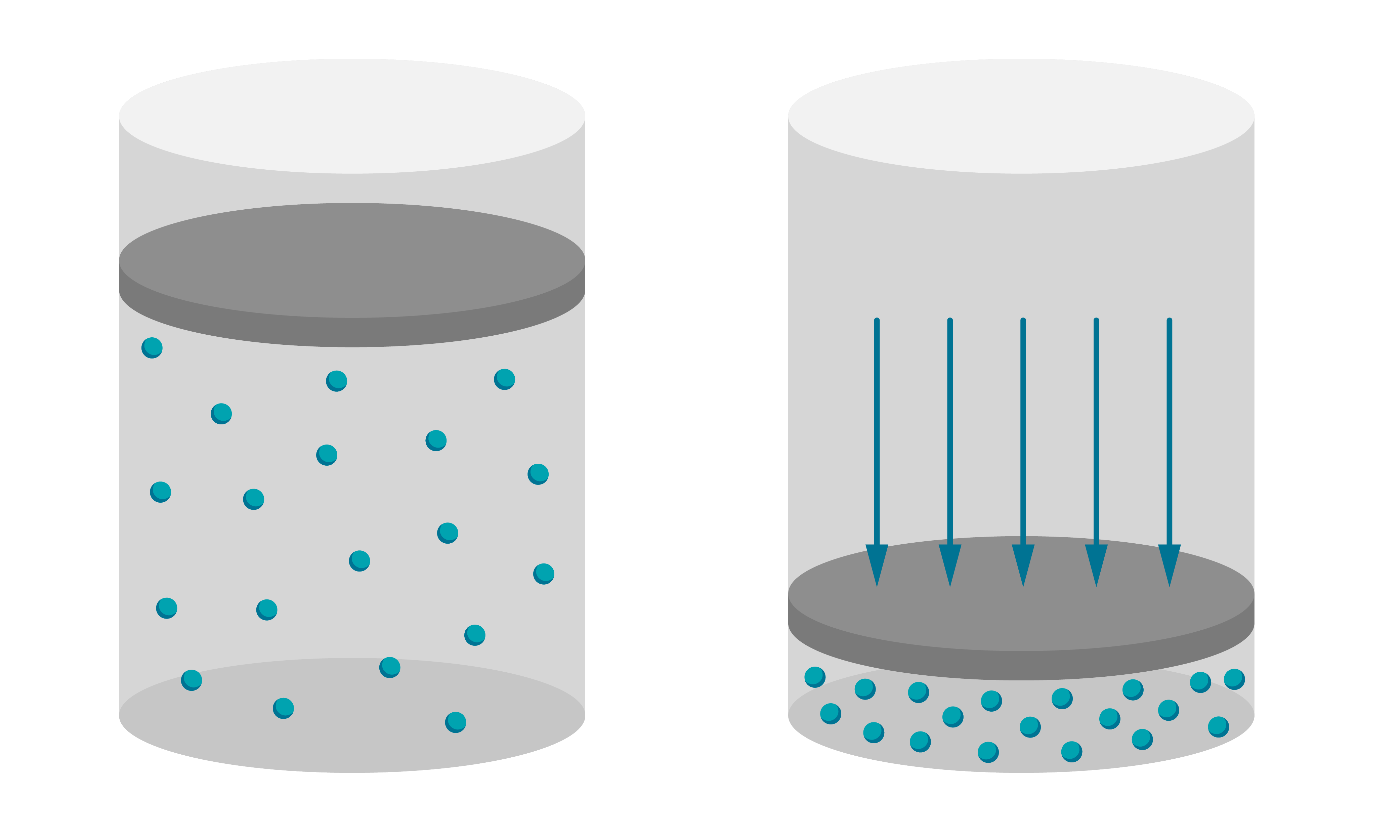
Gāzes molekulas ir vienmērīgi sadalītas visā trauka tilpumā. Gāzi saspiež -  ārējā spēka iedarbībā tā ieņem jaunu, mazāku tilpumu, taču molekulu skaits paliek nemainīgs. Molekulas atkal izvietojas vienmērīgi visā trauka tilpumā.

Tā kā spiedienu gāzē rada molekulu triecieni, tad ārējā spēka darbības rezultātā spiediens ir vienādi palielinājies visos trauka punktos vienādi, jo vienādi ir palielinājusies molekulu koncentrācija - molekulu skaits tilpuma vienībā.

Pamatojoties uz Paskāla likumu, var izskaidrot dažādas parādības, izveidot hidrauliskas ierīces. Tās aplūkosim nodaļā ''Hidrostatiskais spiediens''.

Hidrostatiskais spiediens

Hidrostatiskais spiediens ir šķidruma spiediens uz trauka, kurā tas atrodas, sienām un dibenu.
Vērojot klasisku demonstrējumu (1. attēls) var pārliecināties, ka dziļākos šķidruma slāņos spiediens ir lielāks, nekā augšējos slāņos, kā rezultātā ūdens izplūst no traukā esošā cauruma ar lielāku ātrumu. 

Tas ir tādēļ, ka uz šķidrumu vaļējā traukā darbojas atmosfēras spiediens, kā arī šķidruma augšējie slāņi smaguma spēka darbības rezultātā spiež uz dziļākajiem šķidruma slāņiem. 
Neievērojot atmosfēras spiedienu, šķidruma ar blīvumu \(\rho\) stabs, kura augstums \(h\) un šķērsgriezuma laukumu \(S\), spiež uz laukumu ar savu svaru \(m g=\rho V g=\rho g h \cdot S\) (2. attēls a)

\(p_{\mathrm{šķ}}=\frac{\rho g h \cdot S}{S}=\rho g h \)

Ja ievēro arī atmosfēras spiedienu \(p_{a t m}\) un virzuļa radīto papildus spiedienu \(p_0=\frac{F_\mathrm{ā r}}{S}\), tad hidrostatiskais spiediens \(p=p_0+p_\mathrm{a t m}+\rho g h\)

Redzams, ka spiediens šķidrumā ir atkarīgs tikai no ārējā spiediena \(p_\mathrm{ ār}=p_0+p_\mathrm{a t m}\) un šķidruma staba augstuma \(h\). Līdz ar to, dažādas formas traukos, kuros vienādā līmenī ieliets viens un tas pats šķidrums, spiediens uz trauka dibenu un spiediens uz trauka sienām vienādā augstumā būs vienāds.

Ja ielejam šķidrumu traukos ar vienādiem pamata laukumiem, kuru pašu masu var neievērot, spēks ar kādu šķidrums spiež uz trauka dibenu, var būt gan lielāks, gan mazāks par trauka svaru – šo pretrunīgo faktu sauc par hidrostatisko paradoksu. Skaidrojums varētu būt šāds: saskaņā ar trešo Ņūtona likumu – ja šķidrums, atbilstoši Paskāla likumam, spiež uz trauka sienām perpendikulāri tām, tad trauka sienas spiež uz šķidrumu, ''palīdzot'' to noturēt vai arī iedarbojoties ar papildus spēku.

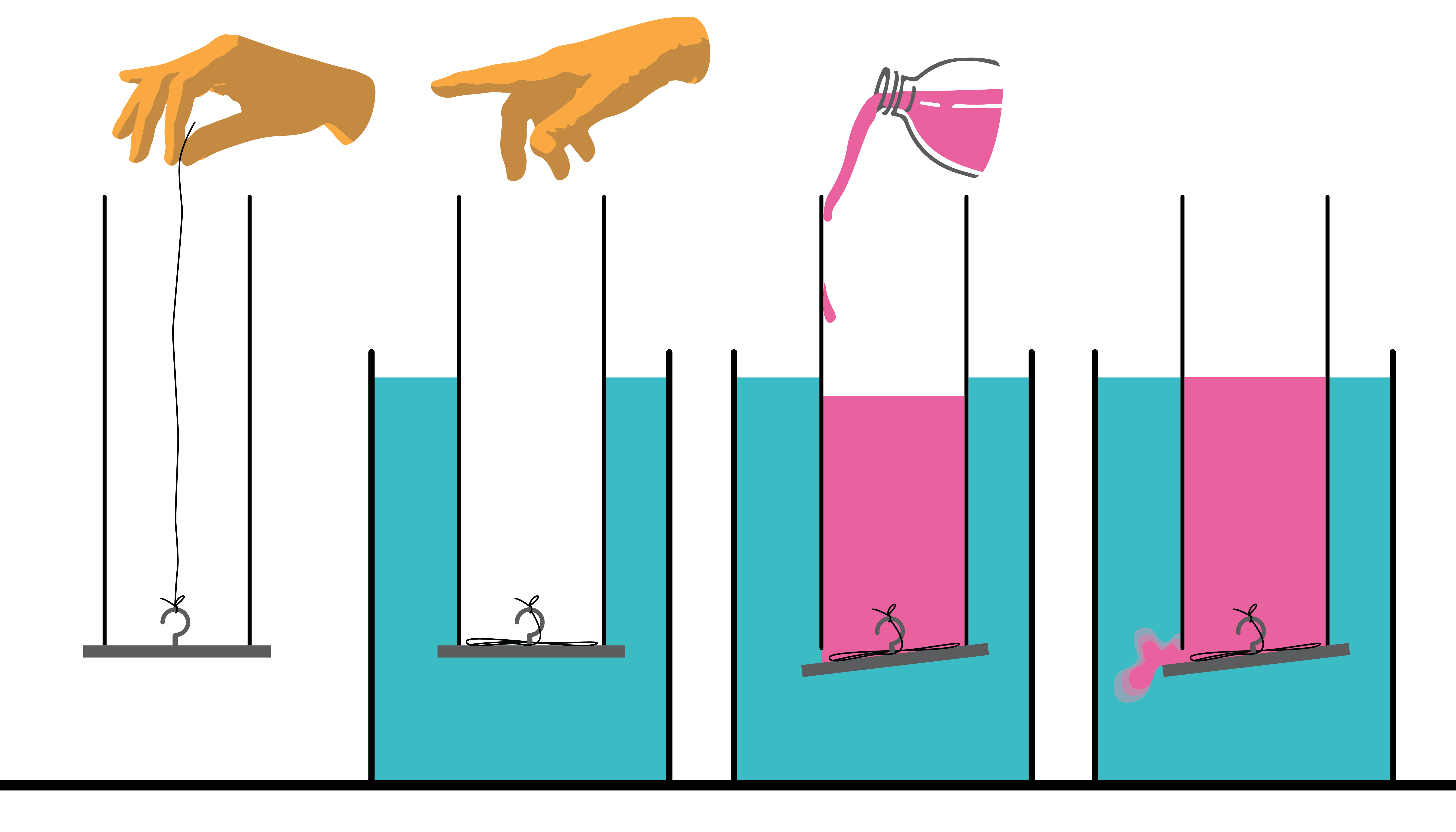
Hidrostatiskais spiediens ļauj izprast klasisko demonstrējumu, kurā izpaužas Paskāla likums: iegremdējot ūdenī stikla caurulīti, kurai viens gals aizverams ar plānu plāksnīti, to pieturot (3. attēls). Ūdenī plāksnīte turas pie cilindra, jo, atbilstoši Paskāla likumam, uz to no apakšas spiež ūdens. Tā nenokrīt arī tad, ja caurulīti ūdenī ievieto slīpi vai tajā ielej nedaudz iekrāsota ūdens. Plāksnīte atkrīt tikai tad, kad ūdens līmenis cilindrā ir vienāds ar ūdens līmeni traukā – ūdens spiediens no abām pusēm kļūst vienāds un plāksnīte nokrīt smaguma spēka darbības dēļ.

Izpratni par hidrostatisko spiedienu izmanto dažādos tehniskos risinājumos un ierīcēs.

Piemēram, būvējot aizsprostus, to apakšējo daļu veido biezāku, jo jāiztur lielāku ūdens spiedienu (4. attēls).

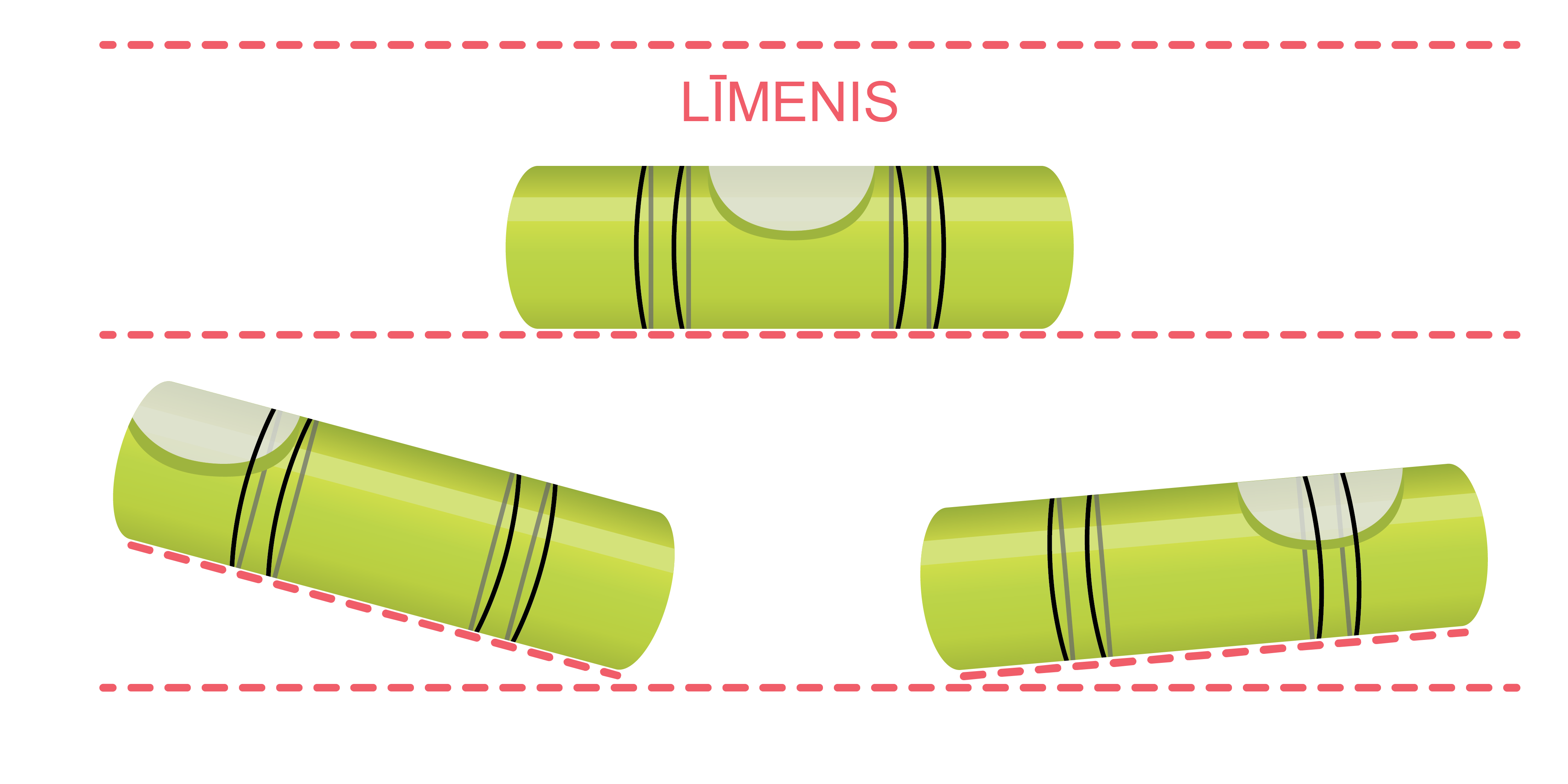
Jebkura līdzsvarā esoša (nekustīga) šķidruma virsma vienmēr būs horizontāla – smaguma spēka iedarbībā šķidruma daļiņas pārvietosies no augstākas vietas uz zemāku, līdz tās visas atradīsies vienlīdz zemu – cik tas būs iespējams. Šādu horizontālu virsmu sauc par šķidruma līmeni. 
Fakts, ka šķidruma virsma vienmēr ir horizontāla, ir, piemēram, līmeņrāža darbības principa pamatā (5 .attēls) – gaisa burbulītis atradīsies caurulītes vidū tikai tad, ja tā būs novietota horizontāli:

Savienotie trauki

Paskāla likums un hidrostatiskais spiediens ļauj izskaidrot šķidruma līmeni savienotajos traukos.

Jebkurus divus vai vairākus savā starpā savienotus traukus, kuros šķidrums var brīvi pārplūst no viena trauka otrā, sauc par savienotajiem traukiem. Kādi ir šķidruma līdzsvara nosacījumi?

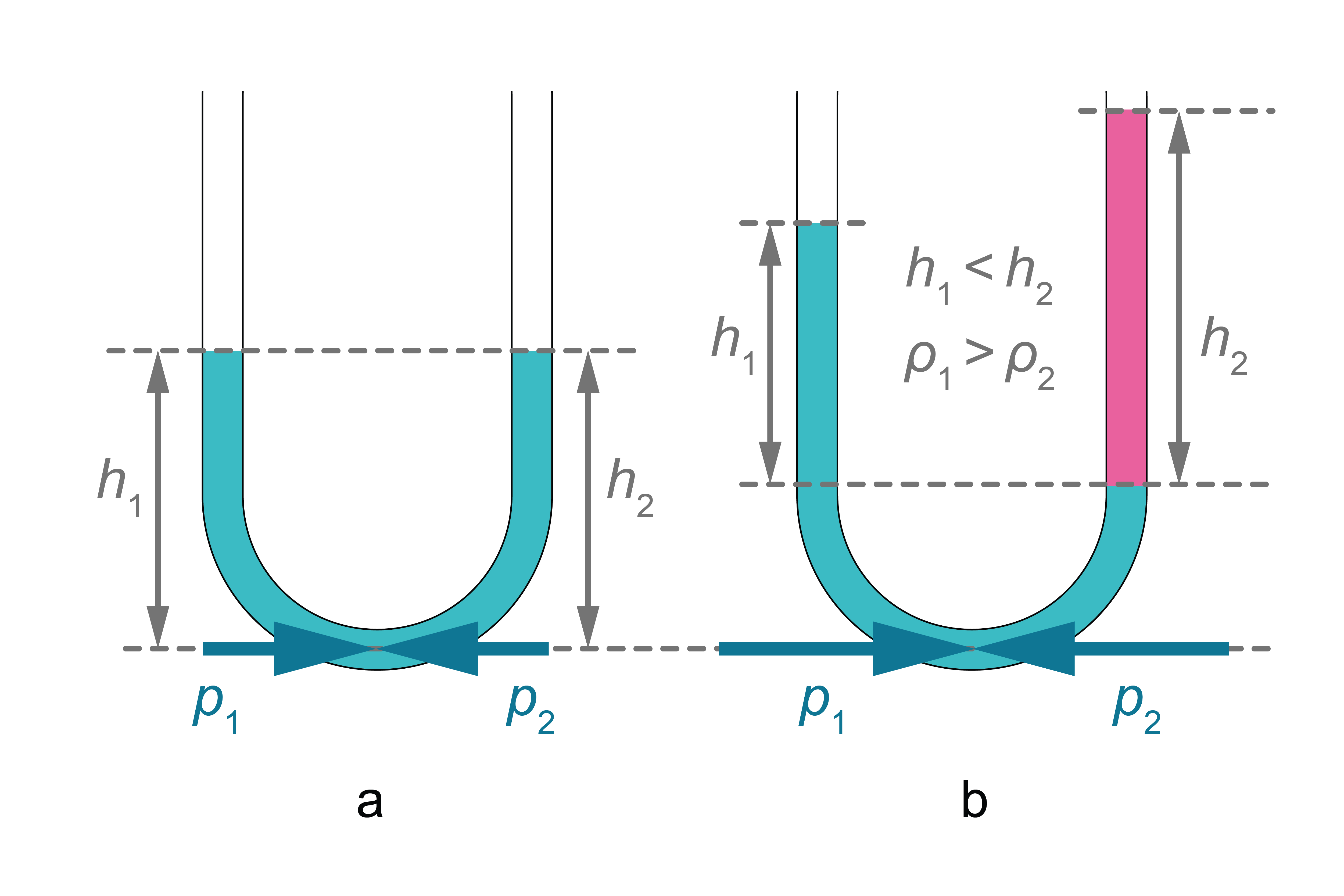
Aplūkosim šķidrumu U veida caurulītē. Šķidrums atrodas līdzsvarā, ja abu šķidruma stabu spiediens no abām pusēm uz jebkuru šķērsgriezuma laukumu ir vienāds. t. i., \(p_\mathrm{1}=p_\mathrm{2}\) (6. attēls).

Tas iespējams tikai tad, ja šķidruma līmeņi abos traukos ir vienādi: \(h_1=h_2\). Tad \(p_1=\rho g h_1\) un \(p_2=\rho g h_2\). (6. attēls a). Ja šķidruma stabu augstumi atšķirtos, šķidrums, spiediena spēku atšķirības dēļ, pārvietotos no trauka, kur līmenis ir augstāks, uz trauku, kur šķidruma līmenis ir zemāks, līdz spiedieni kļūtu vienādi.

Tātad - jebkuras formas savienotajos traukos līdzsvarā esošā šķidruma līmeņi ir vienādā augstumā (7. attēls.).

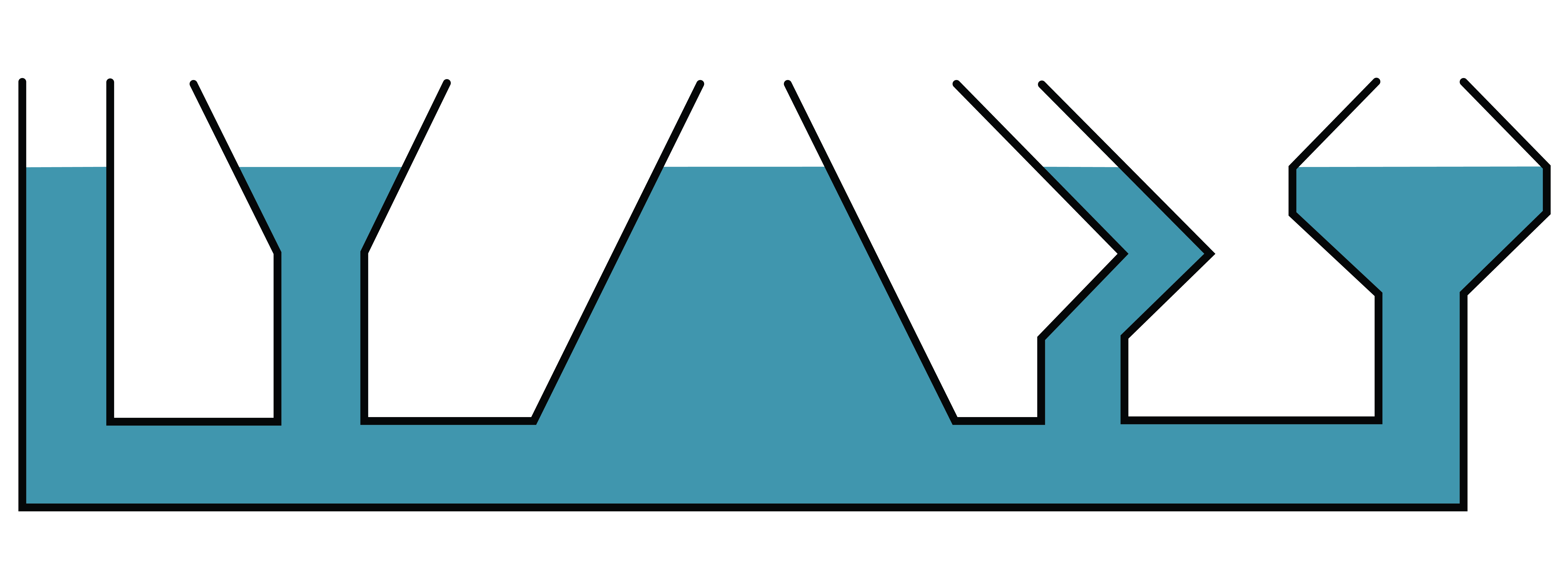
Ja savienotajos traukos atrodas atšķirīgi šķidrumi, kuri nesajaucas, šķidruma stabu augstumi atšķiras (6. attēls b).

\(\rho_1 g h_1=\rho_2 g h_2\), tātad \(\rho_1 h_1=\rho_2 h_2\):  tā šķidruma līmenis, kura blīvums ir mazāks, ir augstāks - šķidrumu līmeņu augstumi ir apgriezti proporcionāli šķidrumu blīvumiem.

Savienoto trauku principa pielietojumi

Savienoto trauku darbības princips ir pamatā daudzu sadzīvē lietojamo ierīču uzbūvei, arī ēku ūdensapgādei. Ūdeni uzsūknē ūdenstornī, kurš ir augstāks par visaugstāko namu (tvertne var atrasties ēkas bēniņos). No tvertnes pa caurulēm ūdens nokļūst namu ūdensvados, kur tas tiecas pacelties tikpat augstu kā tvertnē (8. attēls).

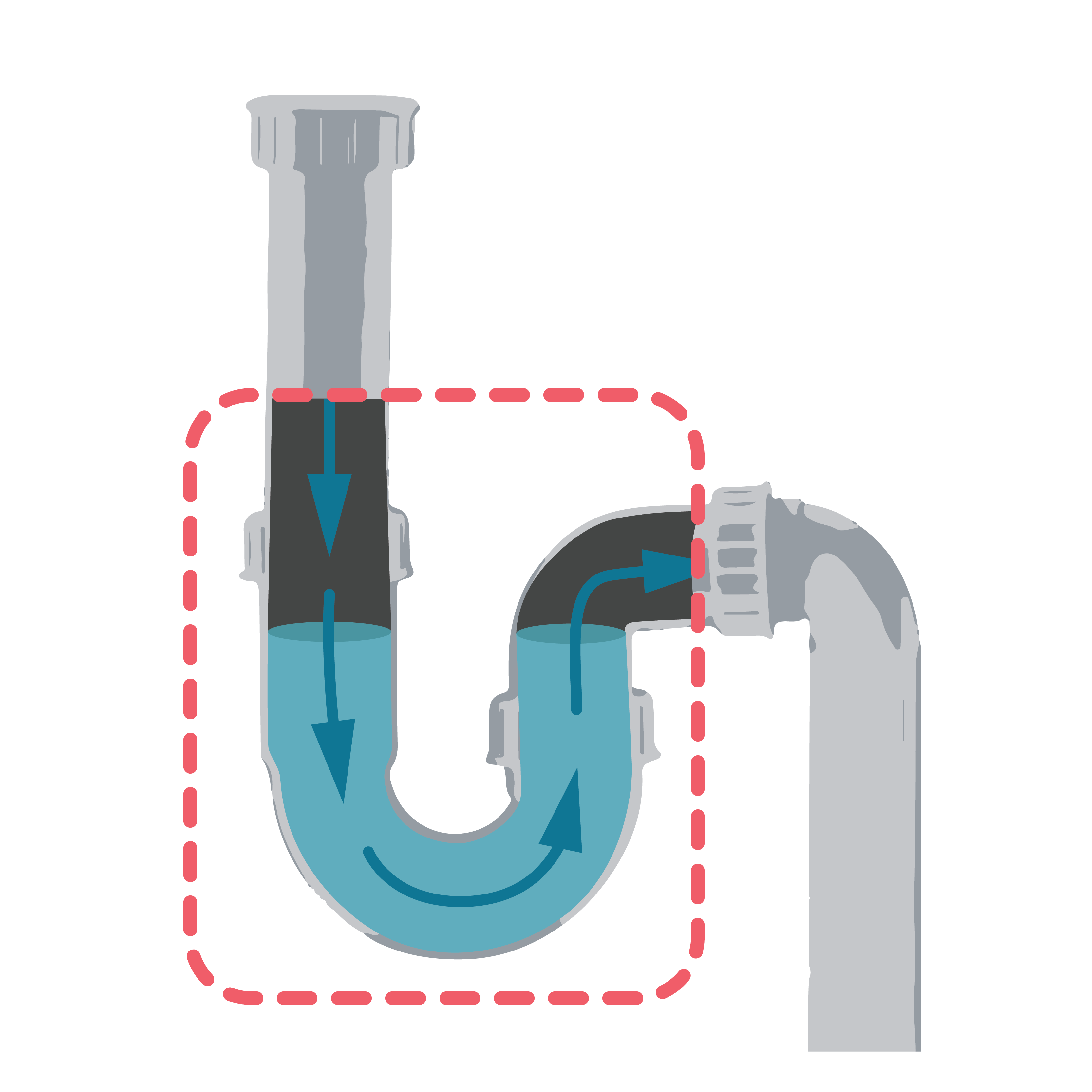
Šo principu izmanto arī, lai novērstu kanalizācijas smaku: zem izlietnes atrodas sifons - izliekta caurule. Sifonā palikušais tīrais ūdens neļauj smakai nokļūt telpā (9. attēls).

Arī upju un kanālu slūžu darbības pamatā ir savienoto trauku princips.

Paskāla likums un hidrostatiskā spiediena rašanās ir arī dažādu hidraulisku ierīču darbības pamatā.

Ja divi vertikāli cilindri noslēgti ar virzuļiem, ar ārēja spēka palīdzību šķidrumā var radīt spiedienu, kas daudzas reizes pārsniedz hidrostatisko spiedienu. Var uzskatīt, ka spiediens \(p\) visā sistēmā ir vienāds. Ja virzuļu laukumi ir \(S_1\) un \(S_2\), šķidrums uz virzuļiem darbojas ar spēkiem: \(F_1=p S_1\) un \(F_2=p S_2\) (10. attēls).

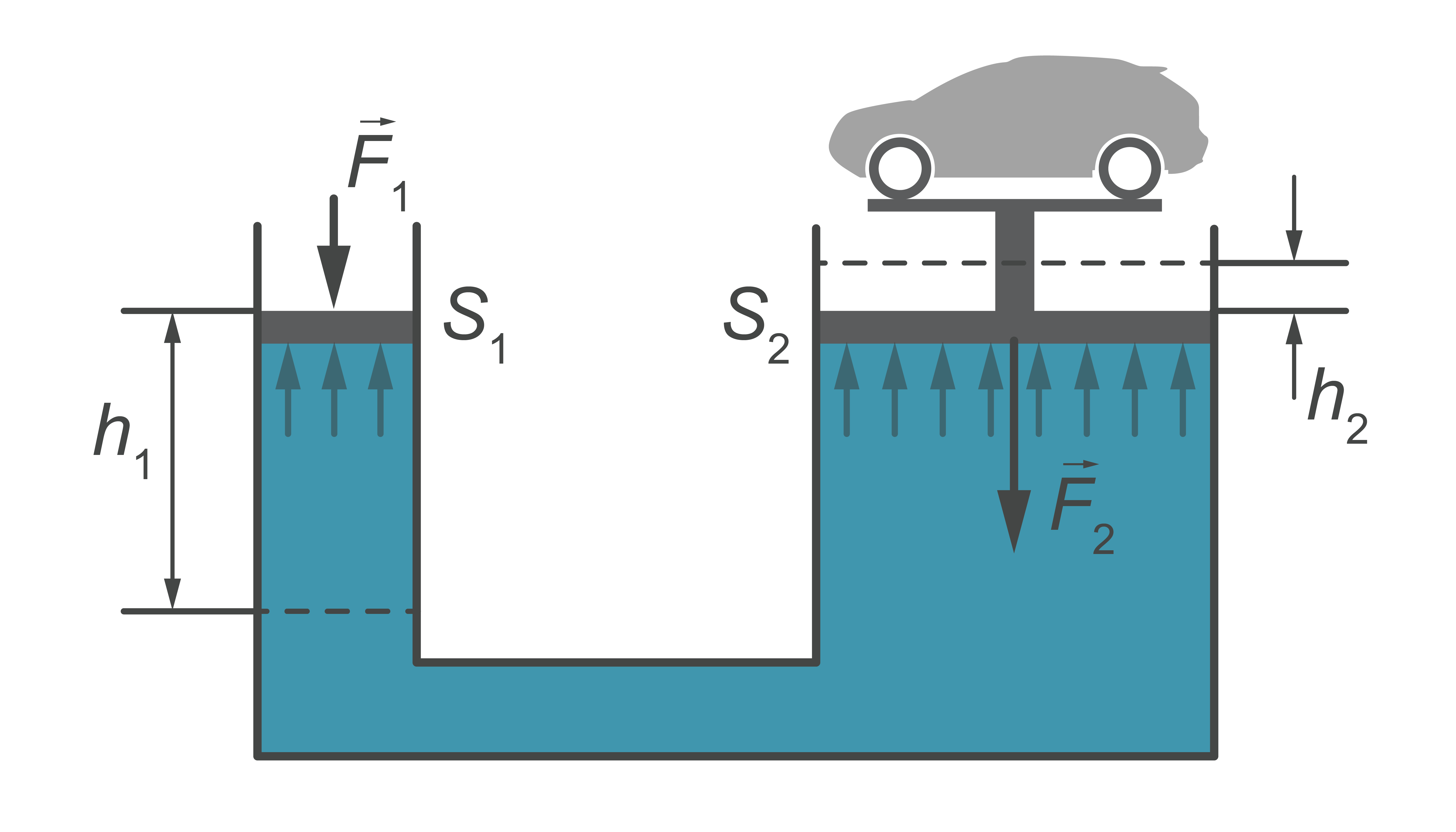
Tātad – hidrauliskā iekārta ļauj lielu spēku līdzsvarot ar mazu spēku. 
Protams, darba ietaupījums nav iespējams – ja mazākais virzulis pārvietojas par attālumu \(h_1\), lielākais pārvietojas tikai par attālumu \(h_2\), jo šķidrums praktiski nav saspiežams un tā tilpums nemainās.

\(\begin{gathered} F_1 h_1=F_2 h_2 \\ h_2=h_1 \frac{S_1}{S_2} F_2=F_1 \frac{S_2}{S_1} \end{gathered}\)

Reālās situācijas, ievērojot to, ka šķidrums ir nedaudz saspiežams un darbojas berzes spēki, iegūtais spēka ietaupījums būs mazāks.

Uz šķidrumā vai gāzē iegremdētu ķermeni darbojas Arhimēda spēks, kas rodas hidrostatiskā spiediena atšķirības dēļ dažādā dziļumā zem šķidruma virsmas, to aplūkojam nodaļā ''Arhimēda spēks''.

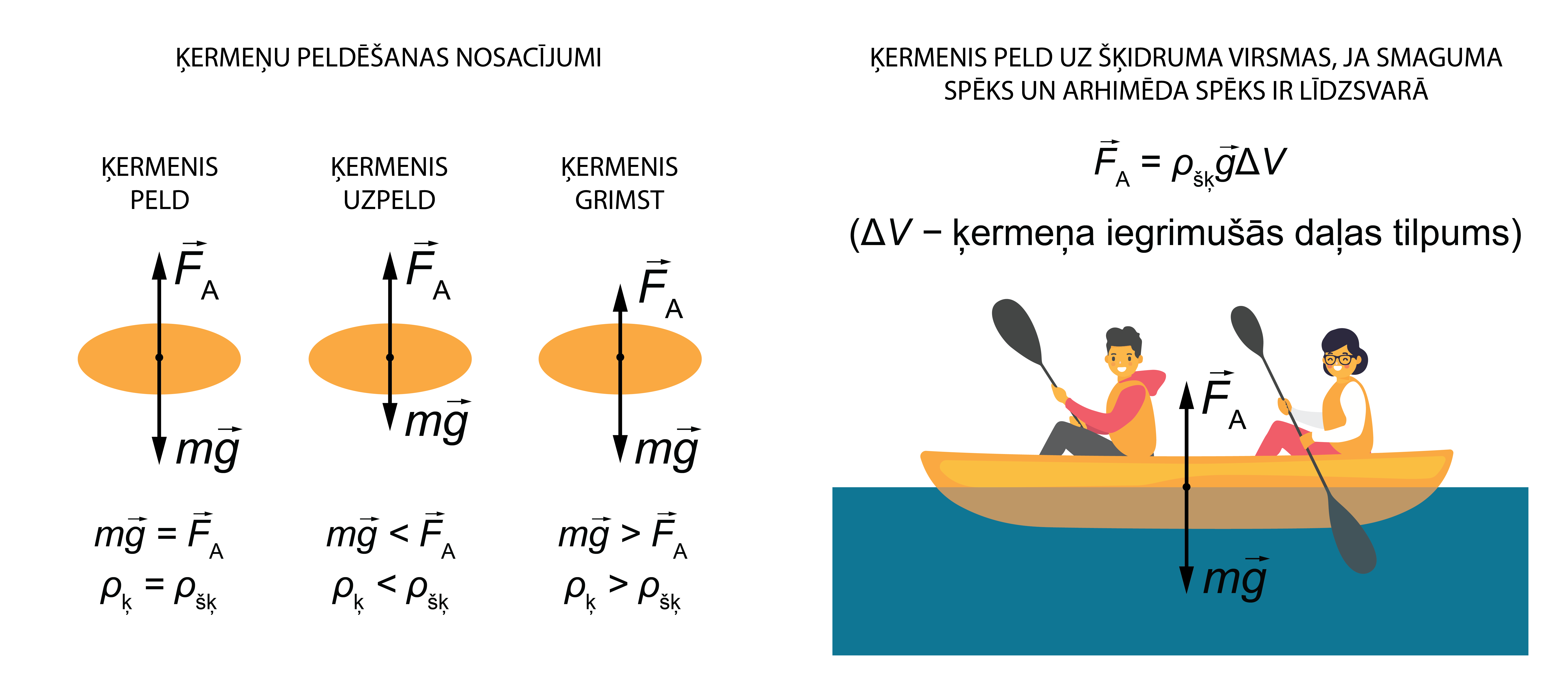
Ķermeņu peldēšana

Uz šķidrumā vai gāzē pilnīgi vai daļēji iegremdētu ķermeni darbojas vismaz divi spēki – smaguma spēks \(F_\mathrm{g}\), un spēks, kas rodas hidrostatiskā spiediena atšķirības dēļ dažādā dziļumā zem šķidruma virsmas – Arhimēda vai ''hidrostatiskais cēlējspēks'' \(F_\mathrm{A}\) (skatīt nodaļu ''Arhimēda spēks'').

\(F_\mathrm{g} = mg = \rho_\mathrm{Ķ}Vg\), kur \(\rho_\mathrm{Ķ}\) ir ķermeņa vielas blīvums, ja tas ir homogēns, vai arī ķermeņa vidējais blīvums, ja tas nav homogēns (viendabīgs).

\(F_\mathrm{A} = \rho_{ŠĶ}Vg\), kur \(\rho_{ŠĶ}\) ir ķermeņa vielas blīvums.

Redzams, ka abus šos spēkus aprakstošo formulu vienīgā atšķirība ir blīvums (1.attēls a).

Tātad:
Ja ķermeņa blīvums ir lielāks par šķidruma vai gāzes blīvumu, kurā tas iegremdēts, smaguma spēks ir lielāks par Arhimēda spēku un ķermenis grimst (turklāt šī kustība sākumā ir paātrināta, līdz vides pretestības spēki līdz ar ātrumu pieaug un, kopā ar Arhimēda spēku, līdzsvaro smaguma spēku).

Ja ķermeņa blīvums ir lielāks par šķidruma vai gāzes blīvumu, kurā tas iegremdēts, smaguma spēks ir vienāds ar Arhimēda spēku un ķermenis peld šķidrumā, nemainot savu atrašanās vietu tajā.

Ja ķermeņa blīvums ir mazāks par šķidruma vai gāzes blīvumu, kurā tas iegremdēts, smaguma spēks ir mazāks par Arhimēda spēku un ķermenis uzpeld (turklāt šī kustība sākumā ir paātrināta, līdz vides pretestības spēki līdz ar ātrumu pieaug un, kopā ar smaguma spēku, līdzsvaro Arhimēda spēku). 
Kad ķermenis sasniedz šķidruma virsmu, tas paceļas virs virsmas tik daudz, lai Arhimēda spēks kļūtu vienāds ar smaguma spēku (1. attēls b). Pēc tam ķermenis vairs neceļas uz augšu, bet peld, daļēji iegrimis šķidrumā. Tātad peldoša ķermeņa svars gaisā ir vienāds ar šī ķermeņa izspiestā šķidruma svaru.

Peldēšanas nosacījumi

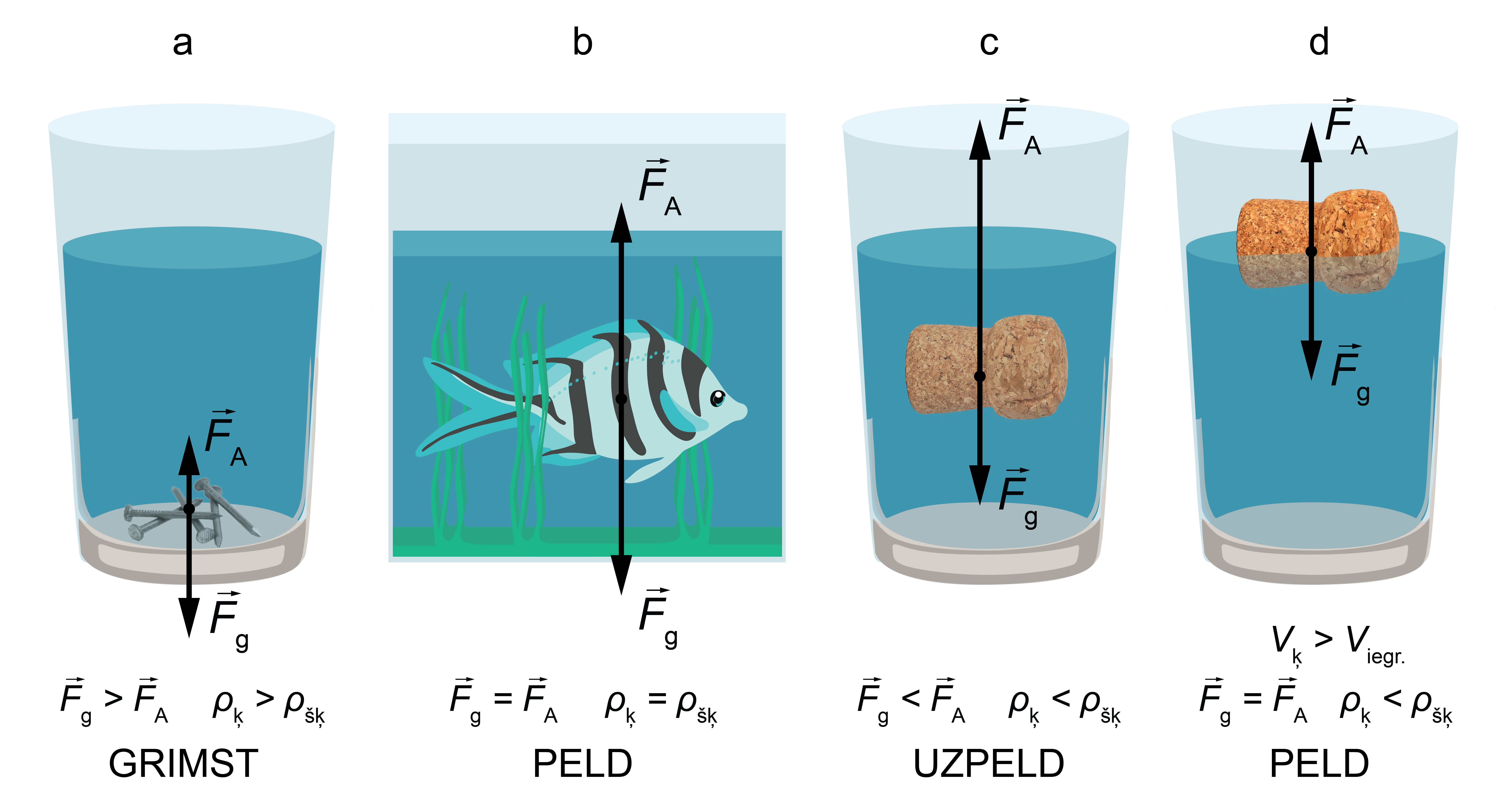
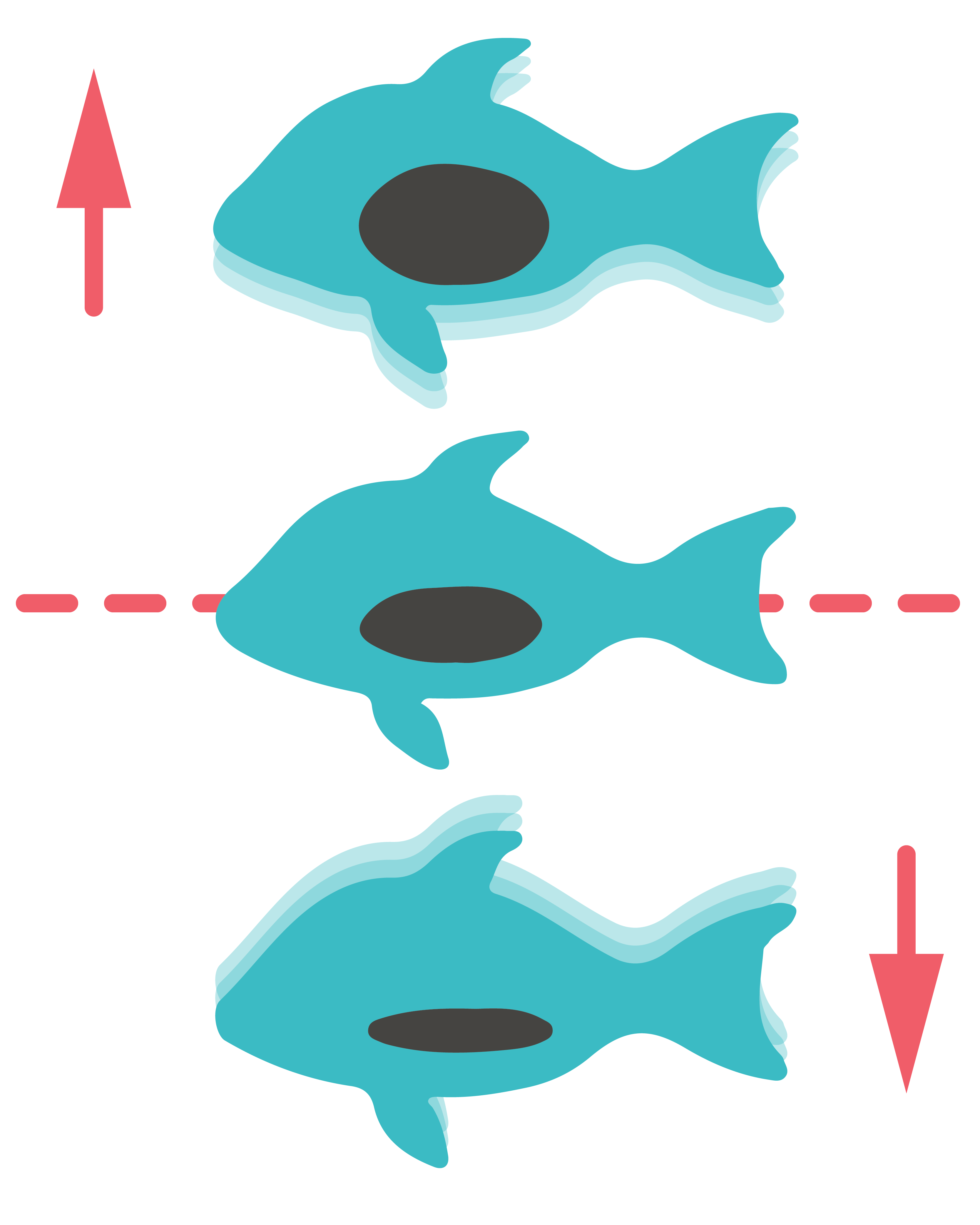
Tātad, ja ķermenis grimst, varam secināt, ka tā blīvums ir lielāks par šķidruma blīvumu, kurā tas atrodas, ja uzpeld – ka tā blīvums mazāks.

Lūk, piemēri:
Ūdenī iemesta nagla grims, jo naglas materiāls ir blīvāks par ūdeni (2. att. a). Ja šķidruma blīvums ir vienāds ar ķermeņa blīvumu, tad \(F_\mathrm{A} = F_\mathrm{g}\) un ķermenis, piemēram, zivs, var peldēt noteiktā dziļumā (2. att. b). Savukārt, korķa gabaliņš, kura blīvums ir mazāks par ūdens blīvumu, uzpeldēs (2. att. c) un atradīsies šķidruma virspusē daļēji iegrimis.

Zinot, kāda daļa no peldoša ķermeņa tilpuma atrodas zem ūdens, viegli noteikt tā (vidējo) blīvumu.

Klucītis, kura tilpums ir \(V\) un tā vielas (vidējais) blīvums \(\rho_K\) peld daļēji iegrimis šķidrumā, kura blīvums ir  \(\rho_{ŠĶ}\). Iegrimušās daļas tilpums vienāds ar \(V_\mathrm{i}\) (3. attēls a)

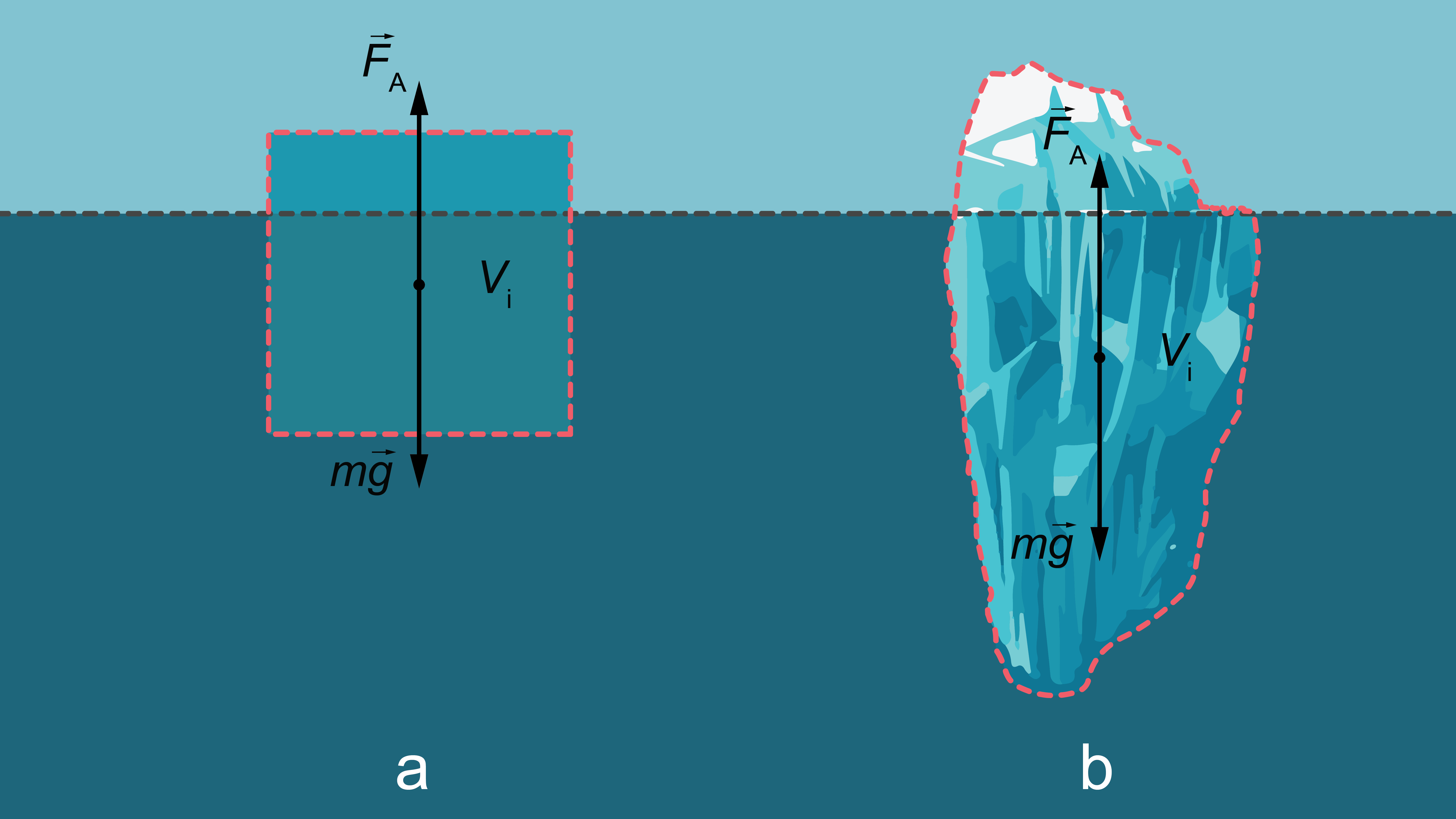
Arhimēda spēks līdzsvaro smaguma spēku: \(F_\mathrm{A} = \rho_{ŠĶ}V_\mathrm{i}g = mg = \rho_ķVg\) 

Tātad:  \(V/V_\mathrm{i} = \rho_{ŠĶ}/\rho_Ķ\)
Ja zinām, ka zem šķidruma līmeņa atrodas, piemēram, puse ķermeņa tilpuma, tad zinām arī, ka tā blīvums ir divas reizes mazāks kā šķidrumam, kurā ķermenis peld.

Aisbergu zemūdens daļa veido aptuveni 9/10 no to kopējā tilpuma, jo ledus blīvums ir aptuveni 900 kg/m³ (3. attēls b).

Peldošu ķermeņu stabilitāte

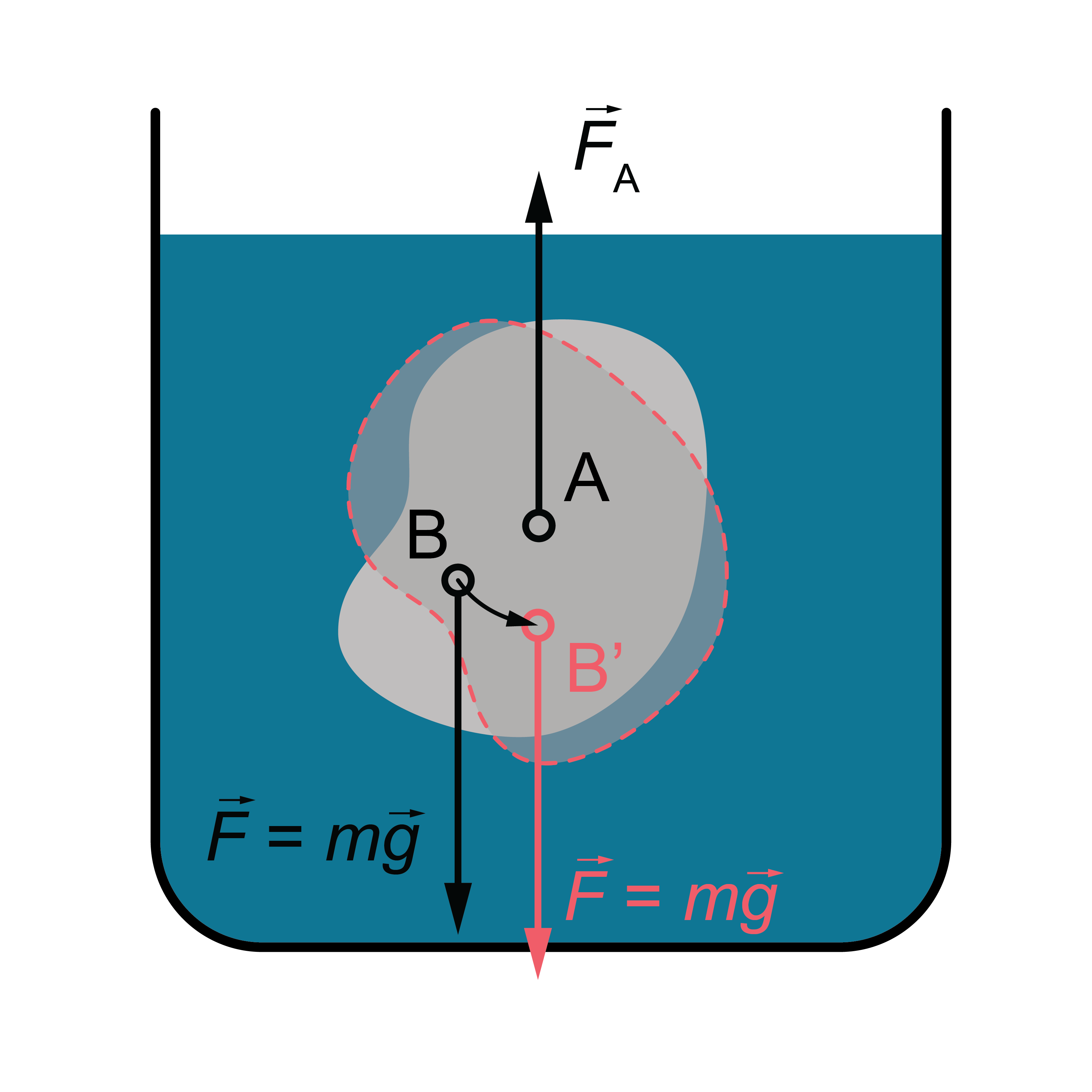
Lai šķidrumā iegremdēts peldošs ķermenis atrastos līdzsvarā, nekustētos,  ar to, ka smaguma spēks un Arhimēda spēks ir vienādi, nepietiek. Jābūt spēkā vēl vienam nosacījumam:  ķermeņa un tā izspiestā šķidruma masas centriem jāatrodas uz vienas vertikāles. Pretējā gadījumā ķermenim ir pielikts spēka moments, kas to pagriež (4. attēls).

Šķidrumā peldoša ķermeņa līdzsvars var būt stabils vai nestabils. Iespējamas vairākas situācijas:

1. Šķidrumā pilnīgi iegrimuša ķermeņa masas centrs B atrodas zemāk par izspiestā šķidruma masas centru centru A un, ķermeni šķidrumā pārvietojot, šie abi masas centri nemaina savu savstarpējo novietojumu. Pilnīgi iegrimis peldošs ķermenis parasti atrodas stabilā līdzsvarā, jo, izvirzot to no līdzsvara, rodas spēka moments, kas ķermeni atgriež līdzsvara stāvoklī (4. attēls).

2. Ja šķidrumā daļēji iegrimuša ķermeņa masas centrs atrodas zem izspiestā šķidruma masas centra, tad stabils līdzsvars iestājas vienmēr.

   

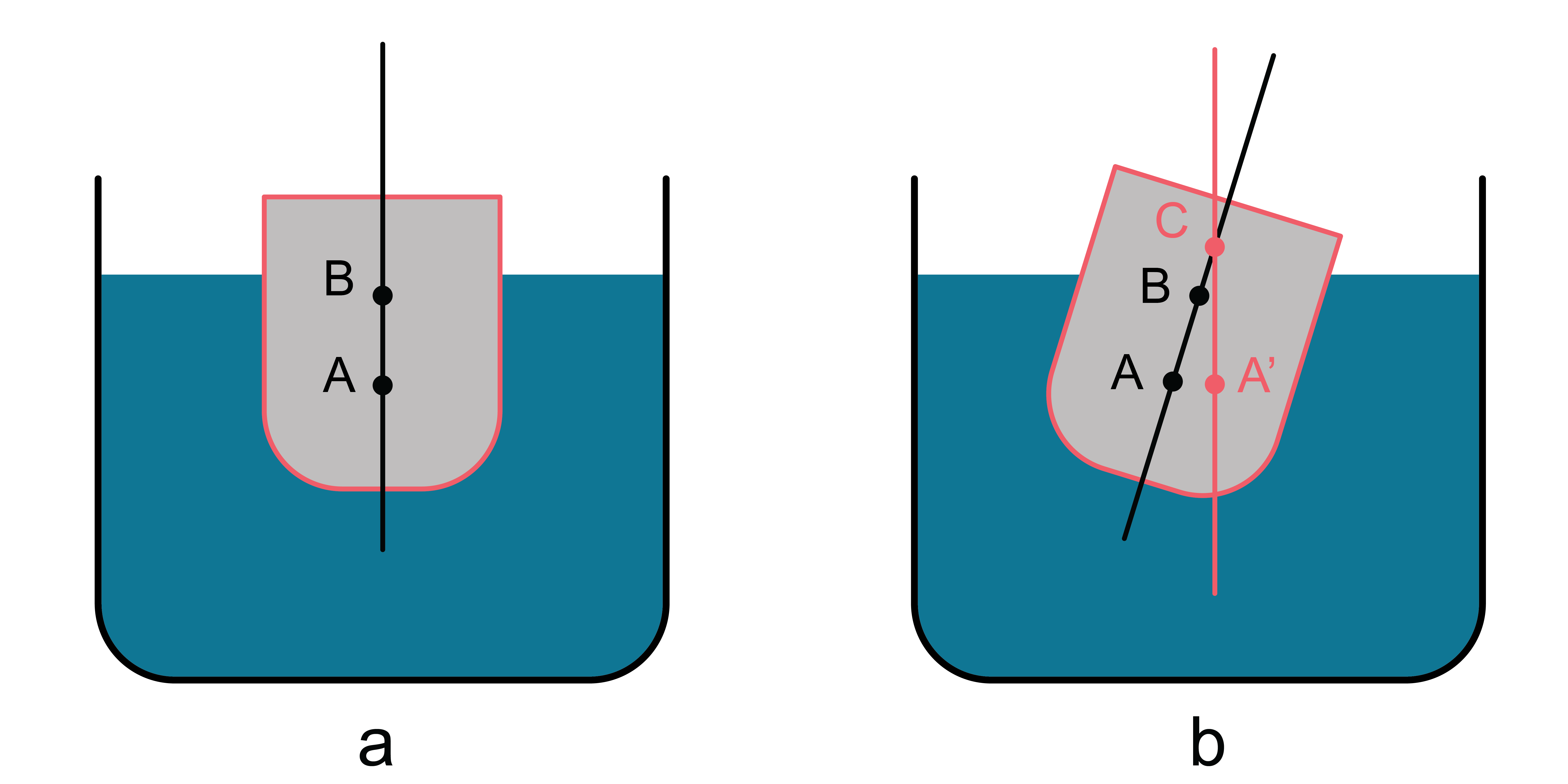
3. Daļēji iegrimuša ķermeņa masas centrs ir virs izspiestā šķidruma masas centra. Ar šādu situāciju jāsastopas kuģu būvē. Peldoša kuģa izspiestā ūdens masas centrs A atrodas zem paša kuģa masas centra B, un abi centri ir uz vienas vertikāles (5. att. a). Kuģim sasveroties, izspiestā ūdens masas centrs centrs atvirzās punktā A, paliekot gandrīz tajā pašā augstumā (5. att. b), turklāt Arhimēda spēka darbības līnija šķērso kuģa vertikālo simetrijas asi AB punktā C. Ja punkts C atrodas virs masas centra, kuģis neapgāžas, tā līdzsvars ir stabils. Jo lielāks ir attālums BC, jo kuģis ir stabilāks un pieļaujama lielāka kuģa sānsvere. Ja Punkts C ir zem masas centra, līdzsvars ir nestabils un kuģis var apgāzties.

Zivis, zemūdenes un dirižabļi

Zemūdenes var ienirt ūdenī, peldēt tajā un uzpeldēt ūdens virspusē. Tātad ir jābūt kādai īpašai sistēmai, kas tai ļauj mainīt zemūdenes vidējo blīvumu. Tā sastāv no balasta kamerām un sūkņiem, kuri var iesūknēt vai izsūknēt no šīm kamerām ūdeni, lai iegrimtu vai paceltos.

Savukārt ūdens dzīvnieku blīvums maz atšķiras no ūdens blīvuma, Arhimēda spēks praktiski līdzsvaro smaguma spēku. Tā zivis viegli maina sava ķermeņa tilpumu un līdz ar to arī ķermeņa vidējo blīvumu, izmantojot speciālu orgānu — peldpūsli, kas ļauj tām regulēt iegrimšanas dziļumu (6. attēls).

Aerostati ir lidaparāti, kuru vidējais blīvums var būt mazāks vai vienāds ar gaisa blīvumu, tādēļ tie var ''uzpeldēt'' gaisā. Aerostats sastāv no čaulas, kas ir pildīta ar gāzi (ūdeņradi, hēliju vai sakarsētu gaisu), kuras blīvums ir mazāks par gaisa blīvumu. Aerostatus iedala vadāmajos (dirižablis – 7. attēls), nevadāmajos (gaisa baloni, stratostati) un piesietajos jeb pūķa aerostatos.

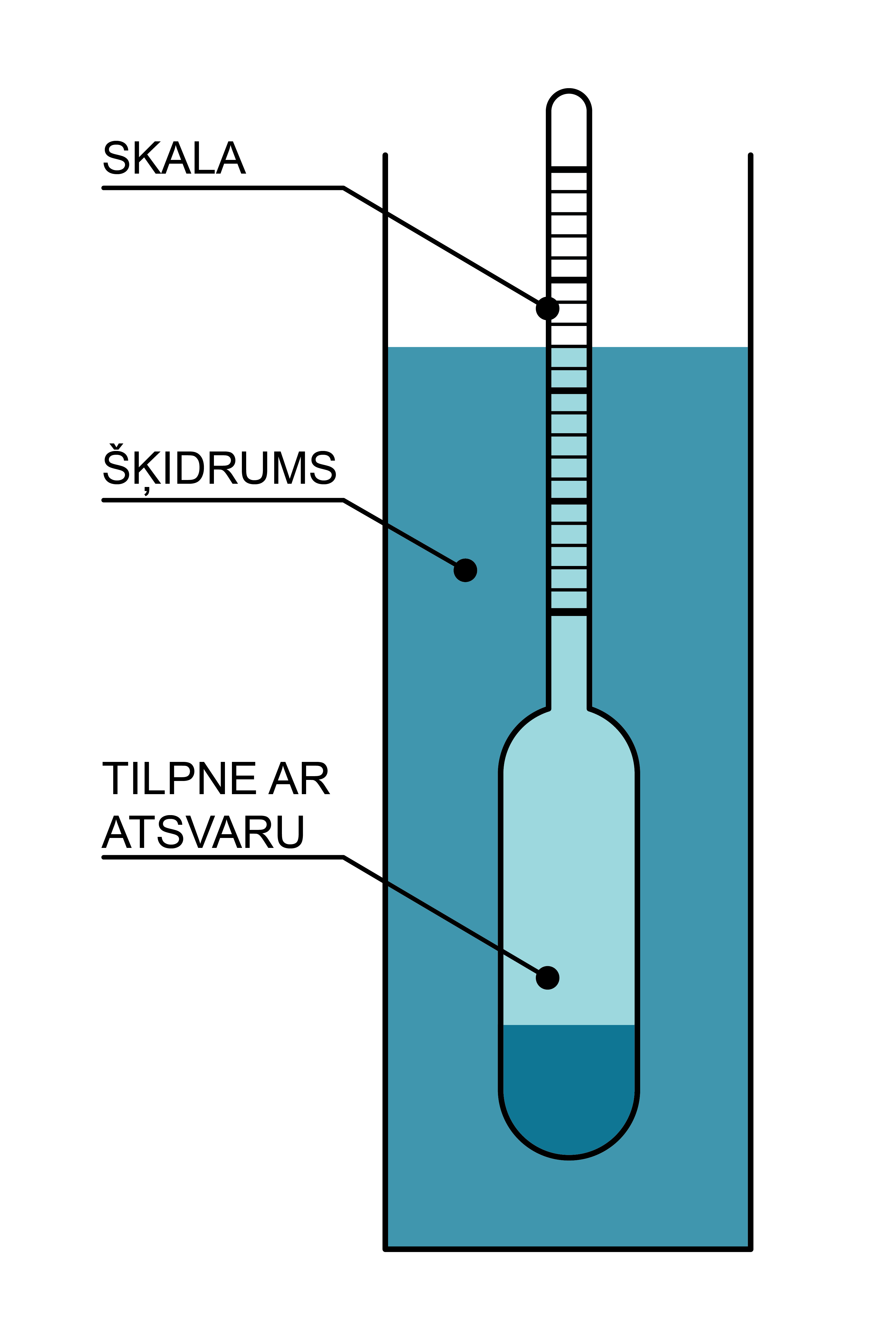
Aerometrs

Ķermeņu peldēšanas nosacījumu izmanto arī, lai noteiktu šķidruma blīvumu. Šādas ierīces sauc par aerometriem (hidrometriem) (8. attēls). Aerometrs ir aizkausēta stikla caurulīte, kuras apakšējā, platākajā daļā atrodas smagums - atsvars, kas nodrošina aerometra peldēšanu vertikālā stāvoklī. Ierīci iegremdē pētāmajā šķidrumā. Aerometra iegrimes dziļums atkarīgs no šķidruma blīvuma, kurā tas peld. Jo blīvāks ir šķidrums, jo mazāka iegrime. Līdz ar to iespējams izveidot atbilstošu skalu blīvuma vienībās.

Atmosfēra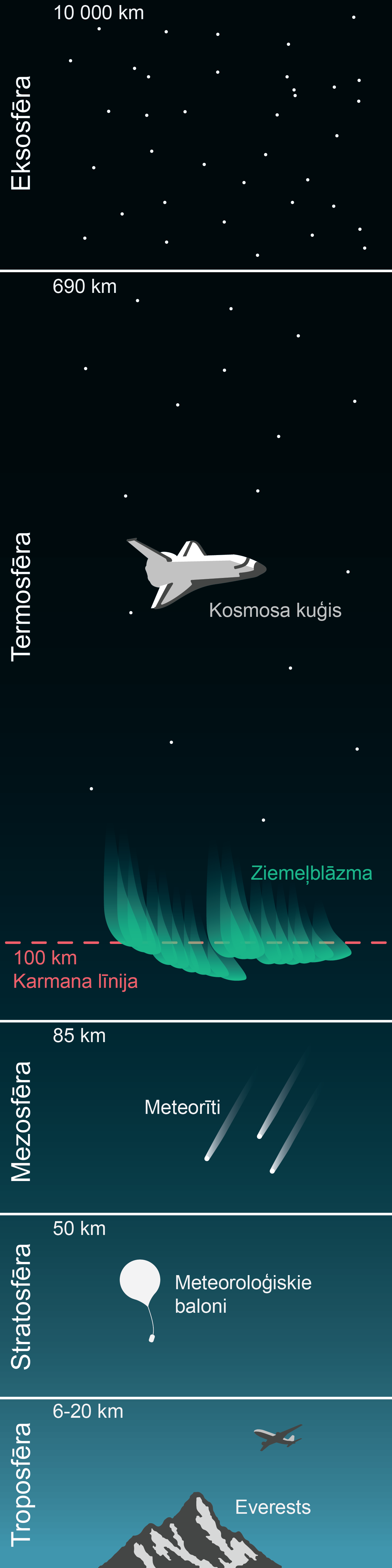

Nodaļā ''Spiediens šķidrumos un gāzēs'' iepazināmies ar Paskāla likumu, nodaļā ''Hidrostatiskais spiediens'' aplūkojām, kā šķidruma vai gāzes ''stabs'' rada spiedienu uz ķermeņiem, kas šajā šķidrumā vai gāzē atrodas.

Atmosfēra ir gaisa slānis, kas aptver Zemi, un tā sniedzas aptuveni līdz 2000 km augstumam (atmosfēras biezums faktiski ir ''norunas lieta'', literatūrā atrodami arī citi dati).

Gaisa molekulas atrodas Zemes smaguma spēka laukā - uz katru molekulu darbojas smaguma spēks, kura ietekmē gaisa molekulas ''krīt'' tuvāk Zemes virsmai. Taču, molekulu haotiskās kustības dēļ, tās arī pārvietojas pretējā virzienā. Rezultātā gaisa blīvums atmosfērā ir atkarīgs no augstuma virs Zemes (2. attēls a). Mēs dzīvojam šā «gaisa okeāna» dibenā.

Atmosfēru atkarībā no augstuma virs Zemes mēdz iedalīt vairākos slāņos: troposfērā, stratosfērā, mezosfērā, termosfērā utt (1. attēls). 

Ja paņemtu vienu kvadrāmetru lielu laukumu un saskaitītu kopā masu visām gaisā esošajām molekulām, kas virs tā atrodas, kopā iznāktu ap 10000 kg (2. att. b). Uz šādu masu darbojas aptuveni 100000 N liels gravitācijas spēks, kas, izdalot ar laukumu, uz vienu kvadrātmetru dod 100000 Pa lielu spiedienu - atmosfēras spiedienu.

1.att. Atmosfēras slāņi
 

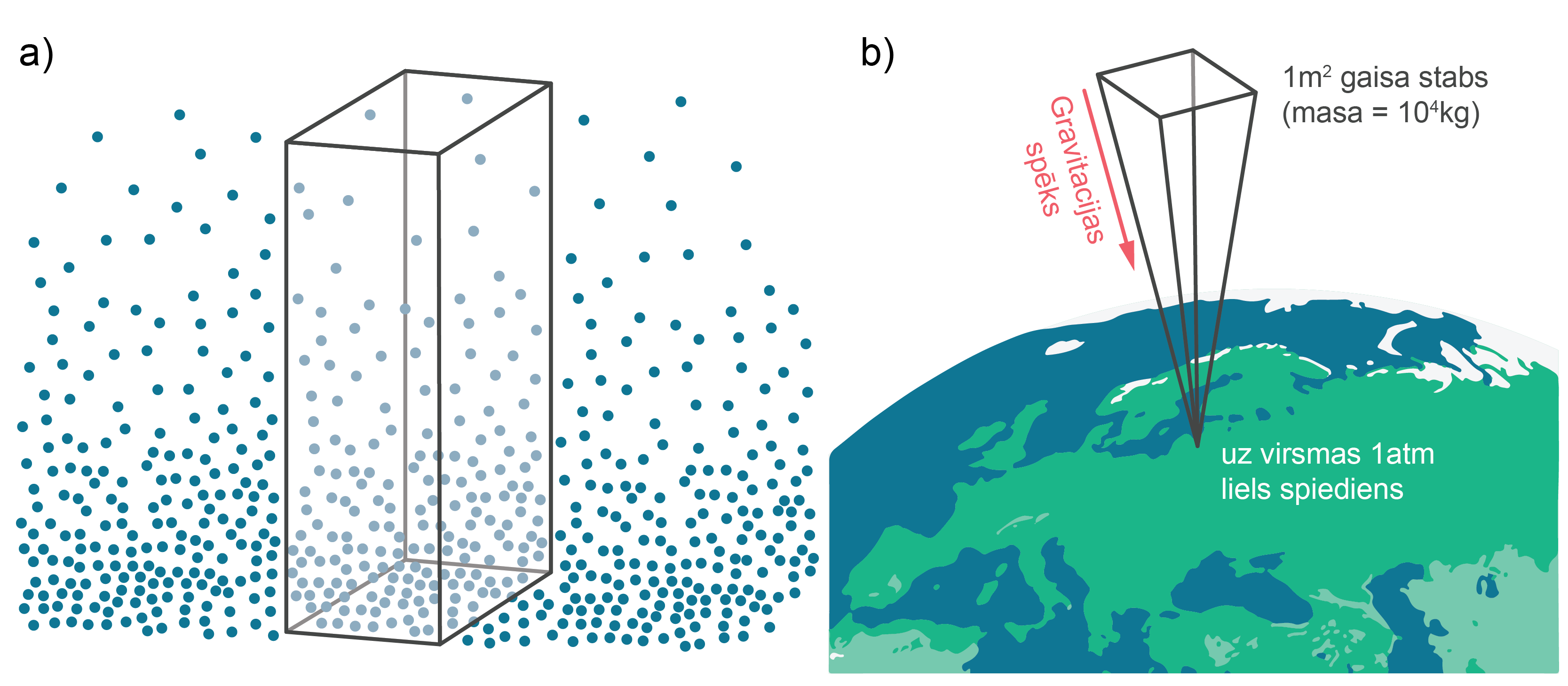
Savukārt, ja atmosfēra būtu homogēna un tās blīvums būtu 1,3 kg/m³, tā būtu tikai 8 km bieza.

78% kopējā atmosfēras tilpuma ir slāpeklis, 21% skābeklis, argons ir 0,9%, oglekļa(IV) oksīds 0,03% un neons, hēlijs, amonjaks, kriptons, slāpekļa oksīds, ūdeņradis, ozons kopā 0,07%.

Šo gāzu koncentrācijas un molmasas ir atšķirīgas, taču gaisa mehānisko īpašību un procesu analīzē gaisu var uzskatīt par viendabīgu gāzi, kuras molmasa ir 0,029 kg/mol.

Sausa gaisa blīvums 0 °C temperatūrā un vienas atmosfēras (101,308 kPa) spiedienā ir 1,293 kg/m³. Atmosfēras kopējā masa ir aptuveni 5,3∙10¹⁸ kg.

Augšējie gaisa slāņi spiež uz zemākajiem, atbilstoši Paskāla likumam radot spiedienu uz katru virsmu, kas atrodas gaisā. Gaisa smaguma spēka radīto hidrostatisko (aerostatisko) spiedienu sauc par atmosfēras spiedienu.

Tomēr atmosfēras spiedienu nevar rēķināt kā šķidruma hidrostatisko spiedienu uz trauka pamatu un sienām (\(p=\)p\(gh\)) – nepastāv konkrēta atmosfēras augstuma vērtība un gaisa blīvums mainās atkarībā no augstuma virs Zemes. Tādēļ atmosfēras spiedienu nosaka, to izmērot ar barometriem.

Toričelli eksperiments

Pirmoreiz atmosfēras spiedienu izmērīja E. Toričelli 1643. gadā (4. attēls). Metru garu stikla cauruli, kuras viens gals aizkausēts, piepildīja ar dzīvsudrabu, caurules vaļējo galu aizspieda, lai neizlītu, cauruli apvērsa ar aizkausēto galu uz augšu un vaļējo galu iegremdēja traukā ar dzīvsudrabu. Atbrīvojot caurules vaļējo galu, daļa dzīvsudraba izlija traukā, tomēr caurulē palika 760 mm augsts dzīvsudraba stabiņš virs dzīvsudraba līmeņa traukā. Caurules galā virs dzīvsudraba staba ir tikai dzīvsudraba tvaiki - Toričelli tukšums. E. Toričelli eksperimentu izskaidroja būtībā ar savienoto trauku principu – no vienas puses spiedienu rada atmosfēra, no otras puses – tikai dzīvsudraba stabiņš, un, atbilstoši Paskāla likumam, šiem spiedieniem jābūt vienādiem.

Tātad - uz dzīvsudraba virsmas atmosfēras spiediens ir vienāds ar dzīvsudraba staba spiedienu caurulē:  p \(= \rho_\mathrm{Hg}gh\)

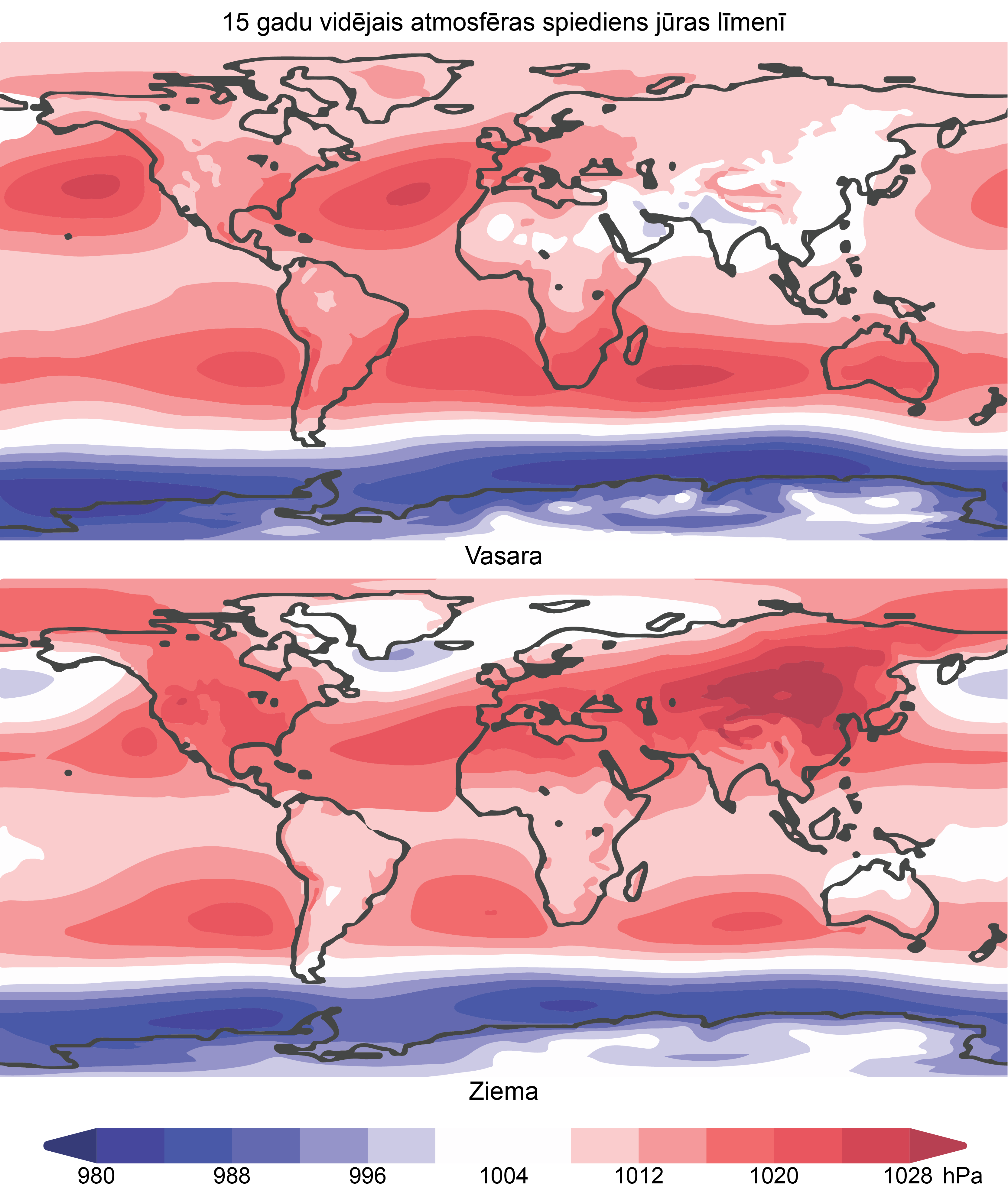
Atmosfēras spiediens mainās - tas nedaudz paaugstinās (anticiklons) vai pazeminās (ciklons) atkarībā no procesiem, kas notiek atmosfērā. 3. attēlā skatāms vidējais atmosfēras spiediens (hektopaskālos) jūras līmenī 15 gadu laikā vasarā un ziemā.

Par ''normālo'' atmosfēras spiedienu pieņem spiedienu, ko līdzsvaro 760 mm augsts dzīvsudraba stabiņš. Šis spiediens ir 101 325 Pa, jo dzīvsudraba blīvums ir 13 600 kg/m³.

Meteoroloģijā lieto arī spiediena vienību ''dzīvsudraba staba milimetrs'' (mm Hg) (1 mm augsta dzīvsudraba stabiņa radītais spiediens - 1 mm Hg=133 Pa) (4. attēls). Lieto arī mērvienības ''bārs'', ''atmosfēra'' un ''tehniskā atmosfēra''.

Barometri

Atmosfēras spiedienu mēra ar barometriem. Dzīvsudraba barometrs būtībā ir ''savienotie trauki'', vienam no kuriem gals ir aizkausēts (5. attēls a). Aizkausēto caurulīti piepilda ar dzīvsudrabu un novieto vertikāli un atmosfēras spiediens uz dzīvsudraba brīvo virsmu līdzsvaro dzīvsudraba staba spiedienu caurulītē. Uz skalas var nolasīt dzīvsudraba (Hg) staba augstumu milimetros. Šie barometri ir ļoti precīzi, bet neērti praktiskajai lietošanai, tādēļ tos izmanto tikai meteoroloģiskajos mērījumos. 

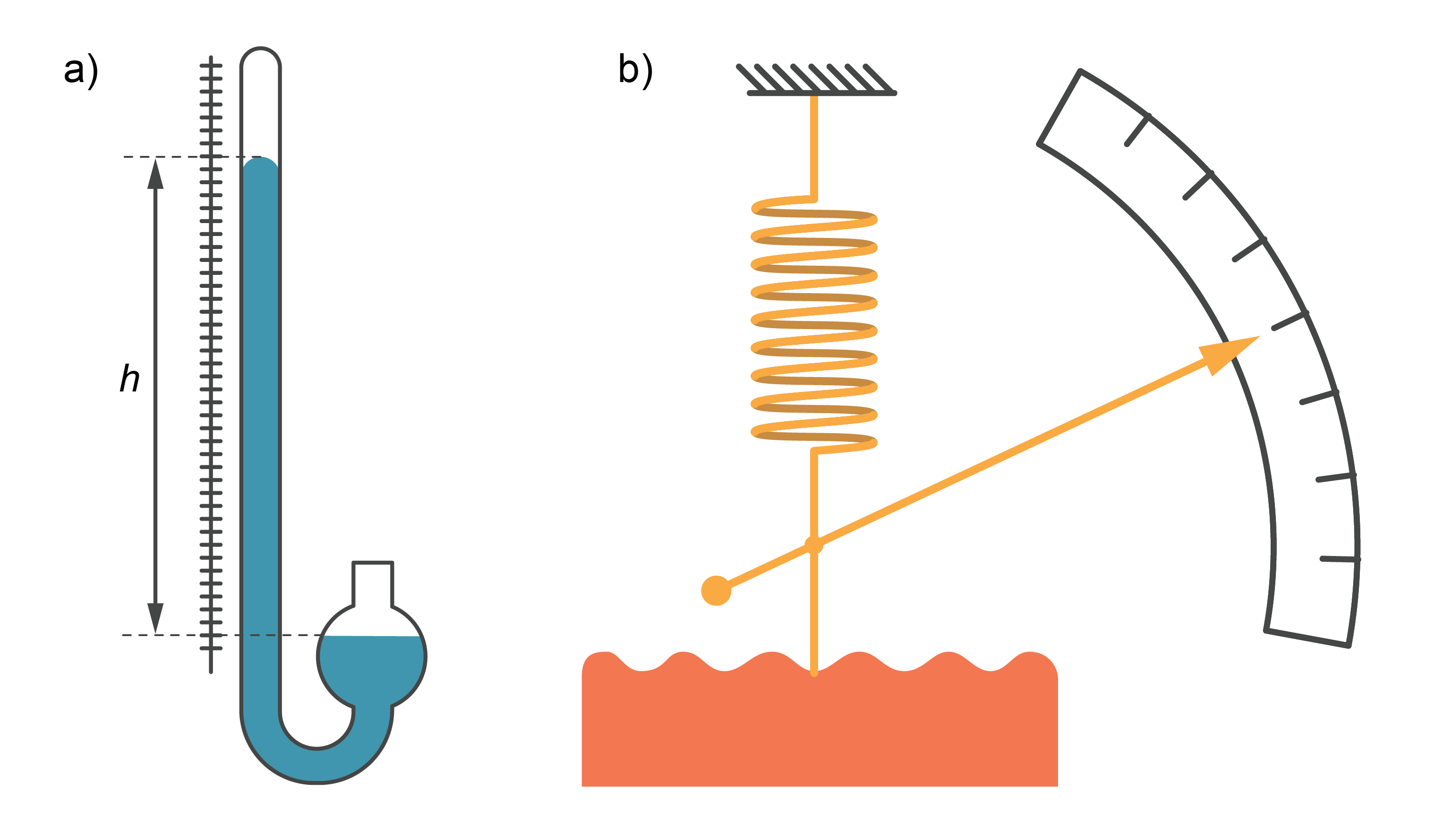
Metāla barometra - aneroīda galvenā sastāvdaļa ir slēgta metāla kārbiņa ar viļņotu virsmu (5. attēls b). No kārbiņas ir izsūknēts gaiss. Atspere neļauj kārbiņu saspiest. Mainoties atmosfēras spiedienam, mainās arī atsperes sastiepums. Ar atsperi savienotā rādītāja ''bultiņa'' pārvietojas gar skalu, kas graduēta spiediena vienībās. Tā kā atsperes elastība ir atkarīga no dažādiem faktoriem, aneroīds var būt neprecīzs.

Atmosfēras spiediena līdzsvarošana ar ūdens stabu

Atmosfēras spiediena mērīšanai varētu izmantot arī ūdeni, bet ūdens stabs, kas līdzsvaro atmosfēru, būtu pārāk augsts praktiskai lietošanai (10 metri). 

Lūk piemērs (6. attēls):

Kad 2014. gadā FIZMIX aicināja piedalīties Ginesa rekorda uzstādīšanā, tapa video, kurā basketbola kluba VEF puiši centās pēc iespējas augstāk uzsūkt šķidrumu caur garu salmiņu. Video apgalvo, ka, balstoties uz fizikas likumiem, nebūs iespējams šķidrumu uzsūkt augstāk par aptuveni 10 m. Arī eksperiments apliecina, ka nevienam neizdodas uzsūkt šķidrumu augstāk par 8 m. Šī 10 m robeža ir tādēļ, ka šķidruma celšanos salmiņā nodrošina starpība starp ārējo spiedienu (atmosfēras spiedienu) un spiedienu salmiņā. Ideālā gadījumā salmiņā varētu rādīt vakuumu jeb spiediens būtu 0, tādā gadījumā spiedienu starpība būtu 1 atmosēra jeb aptuveni 100000 Pa. Ja aprēķina kādu hidrostatisko spiedienu rada 10 m augsts ūdens stabs, tad iznāk tie paši 100000 Pa. Līdz ar to atmosfēras spiediens darbojas pretī šķidruma hidrostatiskajam spiedienam.

Dažkārt tomēr arī dažādās iekārtās spiediens tiek mērīts šķidruma stabiņa milimetros. Piemēram, 7. attēlā redzams gāzes skaitītājs, kuram darba spiediens tiek mērīts ūdens stabiņa milimetros.

Atmosfēras spiediens dažādos augstumos virs jūras līmeņa

Jo tālāk no Zemes virsmas (jūras līmeņa), jo atmosfēras spiediens ir mazāks.
Tā kā gāzes ir stipri saspiežamas, atmosfēras spiediens pieaugot augstumam virs Zemes virsmas samazinās nevis lineāri (kā šķidrumos), bet gan eksponenciāli (8. attēls):

\(p \approx p_0 \cdot \exp \left(-\frac{g \cdot h \cdot M}{T_0 \cdot R_0}\right)\)

kur:
\(h\) – augstums virs jūras līmeņa
\(p_0\) – spiediens jūras līmenī 101325 Pa
\(M\) – gaisa vidējā molmasa 0.02896968 kg/mol
\(T_0\) – gaisa absolūtā temperatūra jūras līmenī (288.16 K)
\(g\) – brīvās krišanas paātrinājums jūras līmenī 9.80665 m/s²
\(R_0\) – universālā gāzu konstante 8.314462618 J/(mol·K)

Tomēr līdz apmēram 600 m augstumam spiediens samazinās vidēji par 1 mm Hg uz katriem 12 metriem.

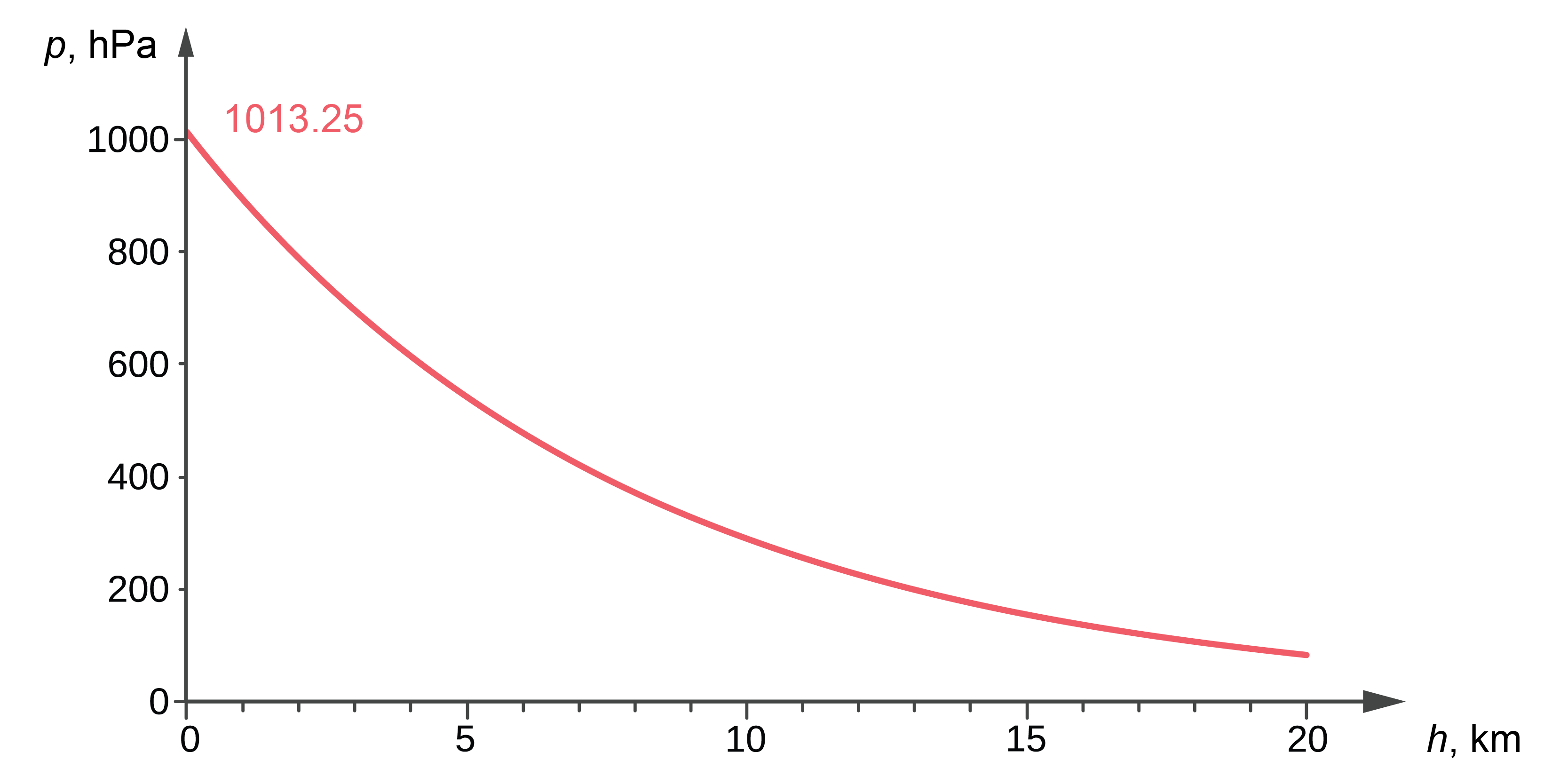
Sakarību starp spiedienu un augstumu virs Zemes var izmantot, lai noteiktu augstumu virs Zemes, izmantojot atmosfēras spiediena mērījumus. Aneroīdus, kuru skala ir graduēta augstuma vienībās (metros virs jūras līmeņa), sauc par altimetriem.

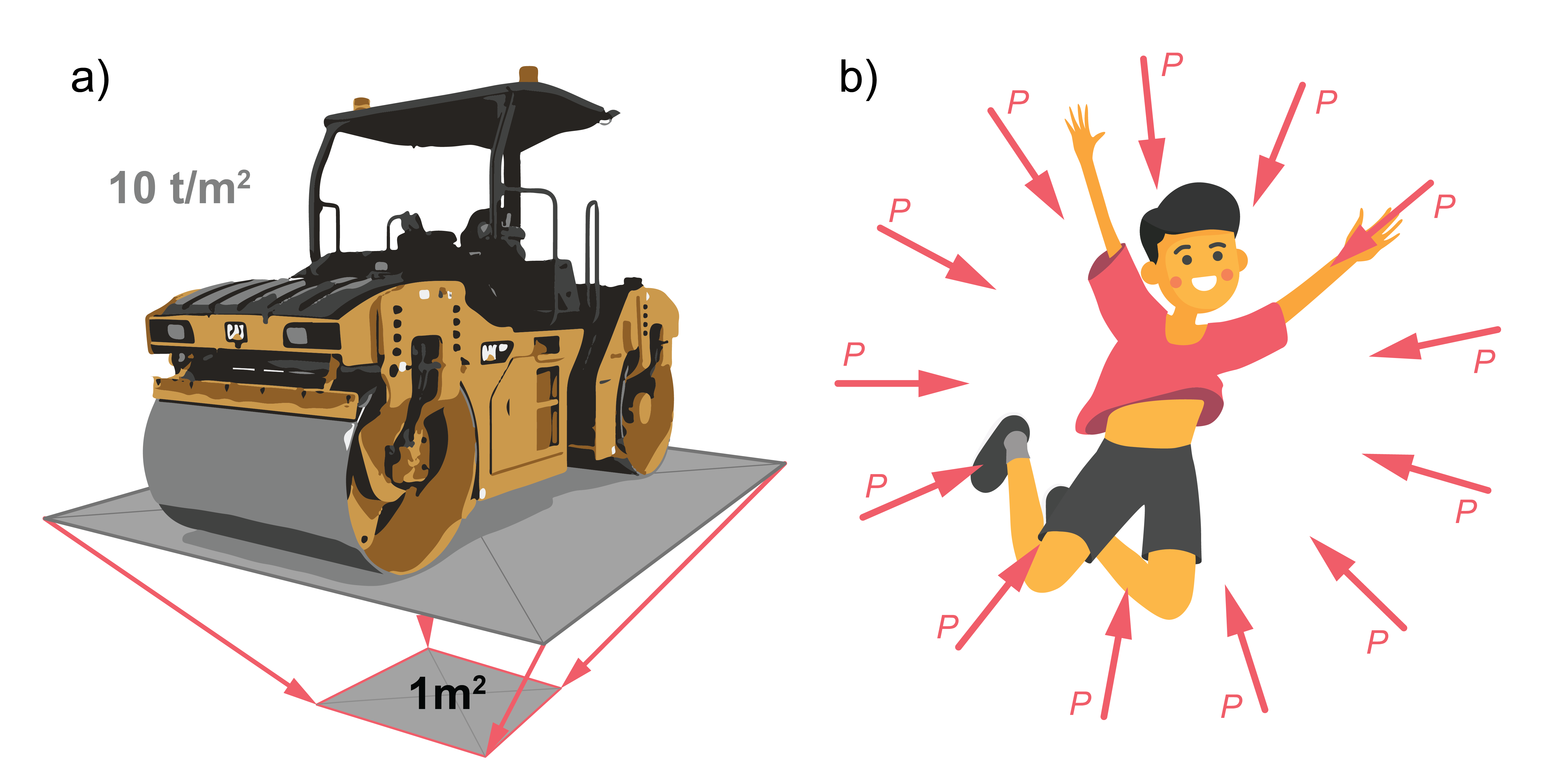
Jūras līmenī atmosfēras spiediens ir vienāds ar spiedienu, ko uz 1 m² lielu laukumu radītu 10 t smags veltnis (9. attēls a). Mēs nejūtam apkārtējās atmosfēras spiedienu, jo spiediens mūsu ķermenī (audos, orgānos) ir aptuveni tāds pats kā atmosfēras spiediens ārpusē un spiediena spēki, kas darbojas uz mūsu ķermeni, ir līdzsvarā.