Cietu vielu modelēšana

Daļiņu mijiedarbība cietā vielā

Vielai (ķermeņiem) cietā agregātstāvoklī piemīt noteikta forma un tilpums. Cietas vielas raksturojums, salīdzinājumā ar šķidrumiem un gāzēm, atrodams nodaļā ''Cietas vielas, šķidrumi un gāzes''.

Lai izveidotu vienkāršotu cietas vielas modeli, atcerēsimies molekulu savstarpējo mijiedarbību vielā Molekulas ir lādētu daļiņu — atomu kodolu un elektronu sistēmas, un molekulu mijiedarbības spēki galvenokārt ir elektromagnētiskas dabas (skatīt nodaļas ''Vielas atomārā uzbūve'' un ''Cietas vielas, šķidrumi un gāzes'').

1. attēlā molekulu mijiedarbības spēki attēloti grafiski. Redzams, ka rezultējošais spēks maina zīmi, kad \(r=r_0\) (attālums, kurā pievilkšanās un atgrūšanās spēki līdzsvarojas). Ja \(r>r_0\), mijiedarbības spēks ir negatīvs. Tas nozīmē, ka lielos attālumos pārsvarā ir pievilkšanās spēks.

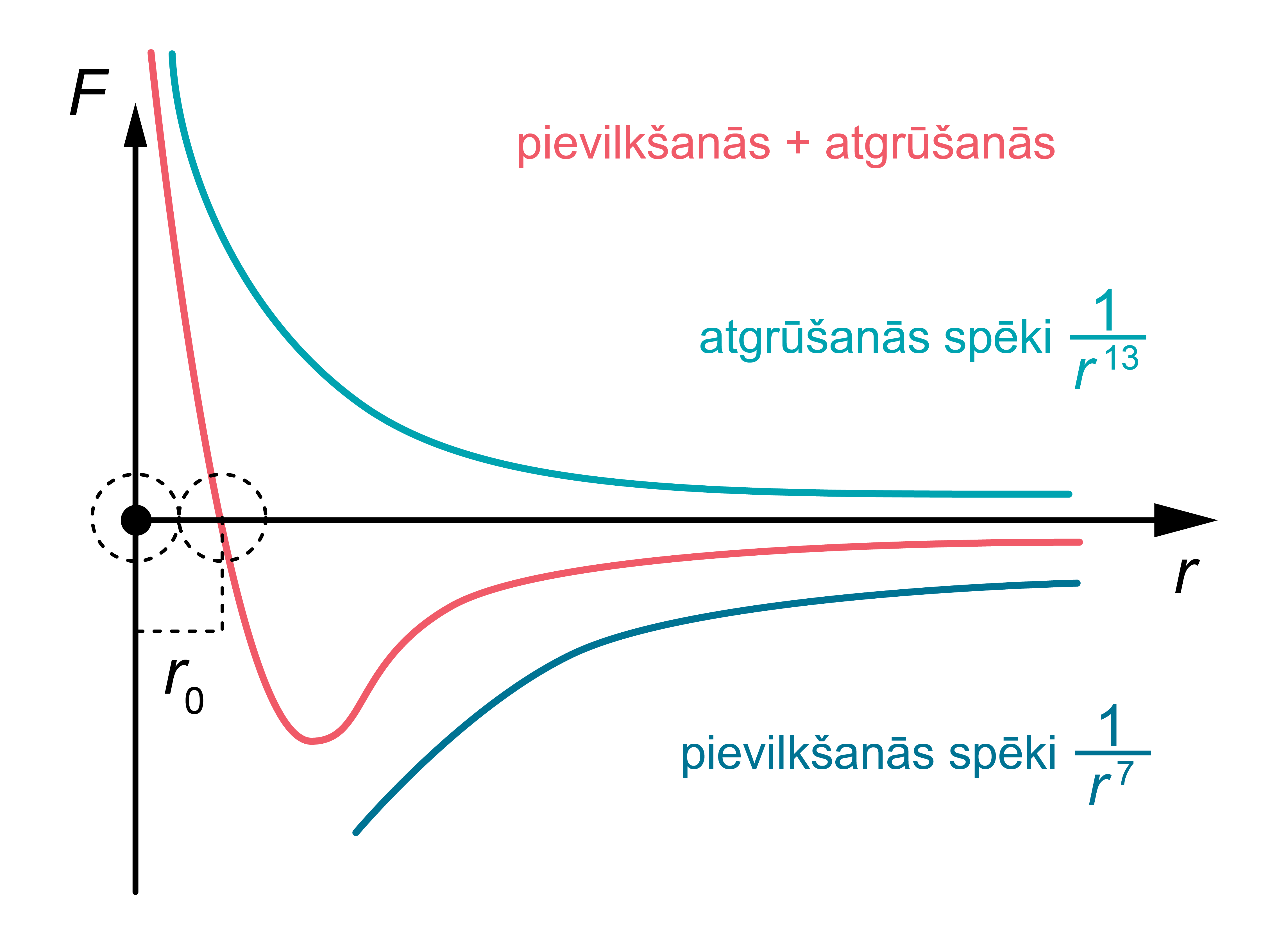
1.att. Molekulu mijiedarbības spēki

Cietas vielas modeļi

Vielas modelī to veidojošās daļiņas (atomus vai molekulas) nosacīti varam attēlot kā apaļas cietas bumbiņas.

Cietā vielā, izmantojot šādu modeli, attālumu \(r_0\) nosacīti var uzskatīt par atoma vai molekulas diametru. Mijiedarbības potenciālā enerģija pie \(r=r_0\) ir minimāla – daļiņas atrodas ‘’potenciāla bedrē’’, un to atdalīšanai ir nepieciešama enerģija (skatīt 1. attēlu tematā ''Cietas vielas, šķidrumi un gāzes'').

Tātad, visvienkāršākajā cietas vielas modelī varam uzskatīt, ka molekulas – bumbiņas atrodas viena otrai tik tuvu, cik vien tas iespējams, un  ''saskaras ar sāniem''.

Izmantojot šo modeli un mola jēdzienu (skatīt tematu ''Vielas atomārā uzbūve'') varam veikt aptuvenu atoma izmēru aprēķinu.

Ja atomus modelē kā apaļas bumbiņas ar diametru \(r_0=d\), kas sabērtas kastē (nosakot ''cietajai vielai'' formu un tilpumu) (1. attēls), tad katra bumbiņa (atoms vai molekula) aizņem kubveida tilpumu \(d^3\) (2. attēls).

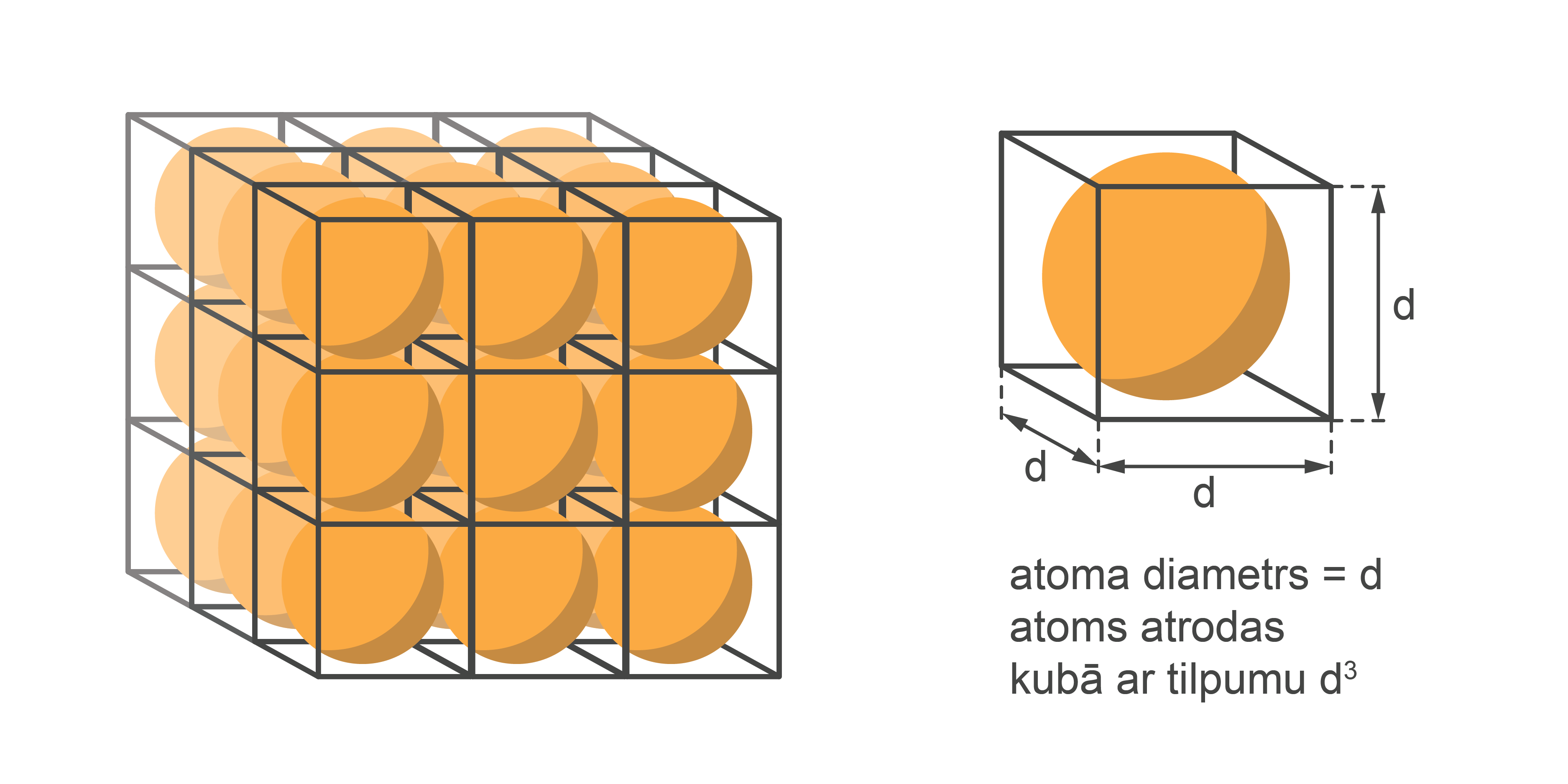
Tā, piemēram, dzelzs molmasa ir 0,056 kg/mol, bet blīvums ρ = 7800 kg/m³.

Atbilstoši blīvuma definīcijai, tilpumu var izteikt kā V = m : ρ. Tas nozīmē, ka viens mols dzelzs aizņem tilpumu \(V = 0,056 : 7800 = 7,18 · 10^{-6} m^3\). Ja viens dzelzs atoms aizņem tilpumu \(d^3\), tad viena mola tilpums ir  \(d^3 · N_\mathrm{A} = d^3 · 6,02 · 10^{23}\). Līdz ar to \(d^3  =  7,18 ·10^{-6} : 6,02 · 10^{23} = 11,93 · 10^{-30}\) m³. Izvelkot trešās pakāpes sakni, iegūst \(d ≈ 2,28·10^{-10}\) m.

Eksperimentāli noteiktā vērtība ir \(1,40 · 10^{-10}\) m. Redzams, ka lieluma kārta sakrīt, bet šādi iegūtais dzelzs atoma  diametrs ir lielāks par eksperimentāli iegūto.

Acīmredzot, cietas vielas modelī, attēlojot daļiņas kā bumbiņas, jāparedz ''brīva vieta'' starp tām – daļiņām jābūt iespējai svārstīties ap līdzsvara stāvokļiem, jābūt arī iespējai kādām citām daļiņām iekļūt starp cietās vielas atomiem vai molekulām (zināms, ka difūzija notiek arī cietā vielā). Turklāt zināms arī, ka ūdens cietā stāvoklī ir mazāk blīvs, salīdzinot ar šķidru ūdeni, kas nozīmē – molekulas nav novietojušās maksimāli tuvu viena otrai.

Modelī jāparedz arī starp daļiņām pastāvošās mijiedarbības – saišu attēlojums. Atkarībā no tā, kādu parādību vai īpašību skaidrošanai modelis paredzēts, tajā var būt attēlotas tikai ''saites'', lai parādītu vielas struktūru, atbilstoši neparādot atomu vai molekulu izmērus (3. attēls).

Savukārt, ja cieto vielu veido daudzatomu molekulas, modelī, lai skaidrotu vielas īpašības, ietver arī informāciju par molekulas uzbūvi. Tādā gadījumā vielas daļiņu vairs neattēlo kā bumbiņu, bet parāda arī molekulas (piemēram, ūdens molekulas) struktūru (3. attēls).

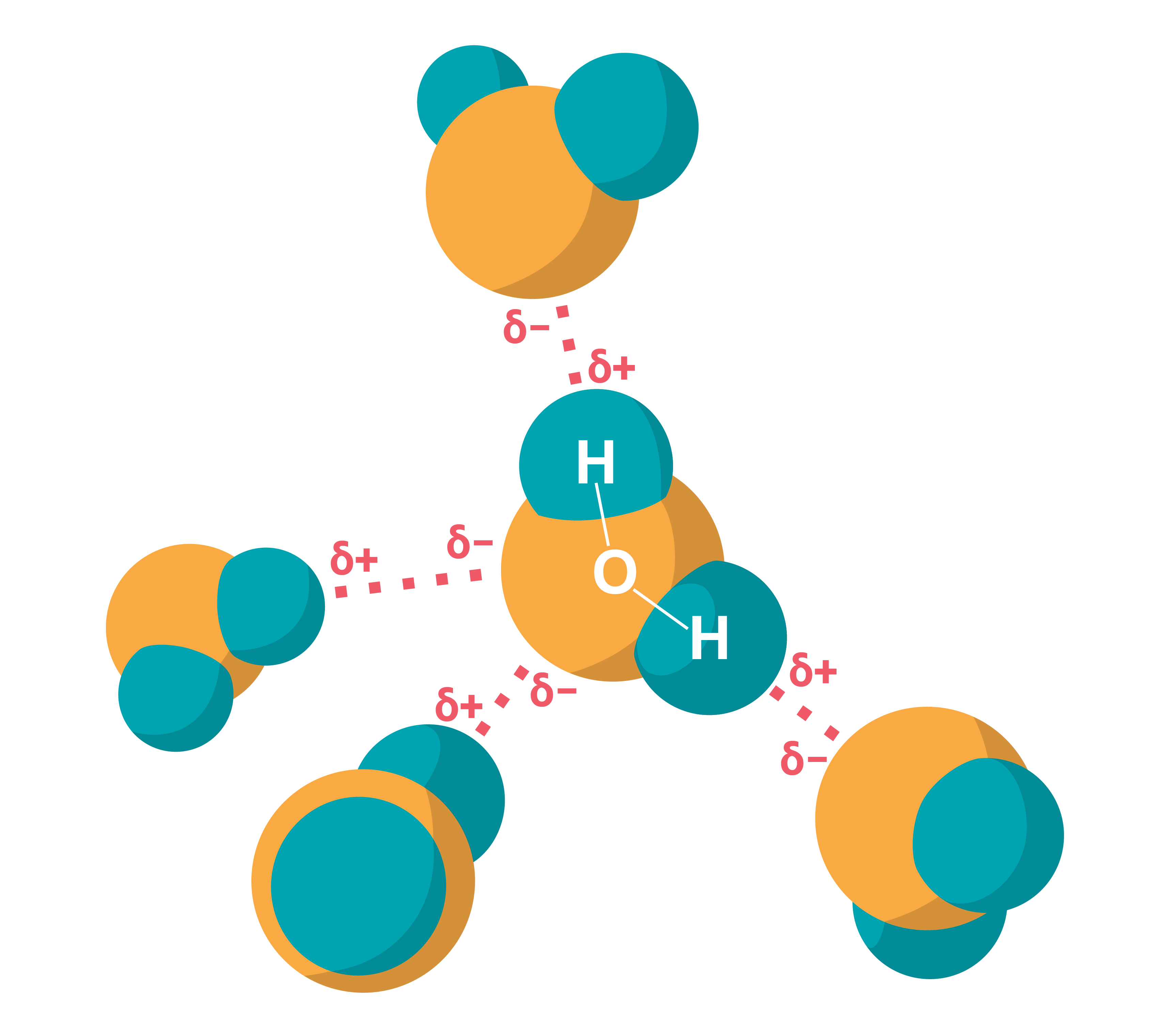
Kristāliskas un amorfas vielas

Cietas vielas iedala kristāliskās un amorfās vielās, savukārt kristāliskās vielas tālāk iedalās monokristālos un polikristālos (4. attēls). Kristāliskas vielas tuvāk aplūkosim nodaļā ''Kristāliskas vielas'', bet amorfas - nodaļā ''Amorfas vielas''.

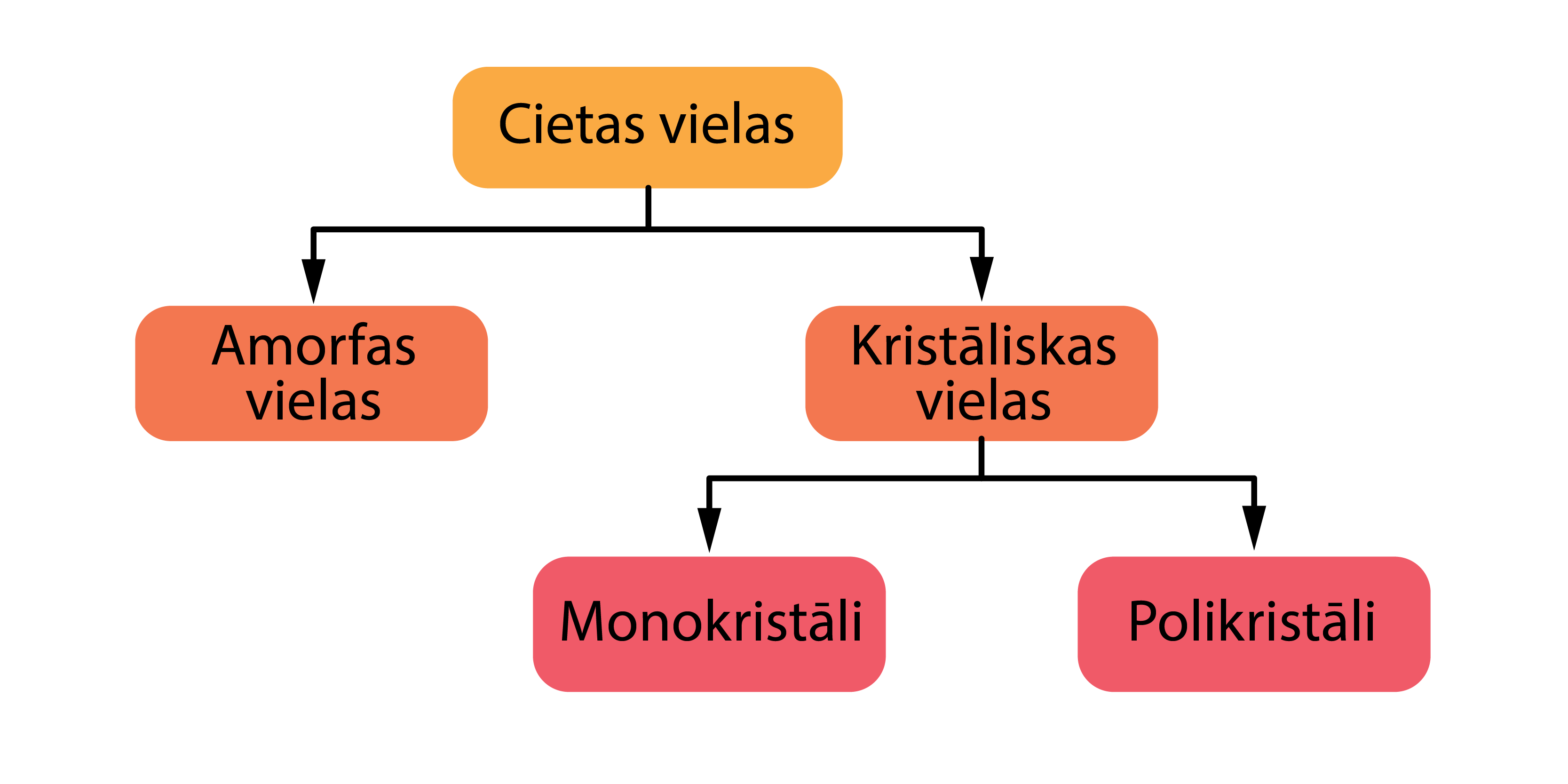
Daļiņu izkārtojums kristāliskās vielās, piemēram, vārāmajā sālī NaCl vai kvarcā, ir regulārs pat lielā attālumā (5. att. a). Šo kārtību sauc par tālo kārtību. Monokristālos daļiņas ir regulāri sakārtotas visā ķermeņa tilpumā (5. att. a), bet polikristāliskas vielas veido haotiski izvietoti monokristāliņi (5. att. b). Kristālā pastāv arī tuvā kārtība - sakārtotība atomu vai molekulu savstarpējā izkārtojumā vielā, kas (atšķirībā no tālās kārtības) atkārtojas tikai attālumos, kas ir samērojami ar attālumiem starp atomiem, tātad - blakus esošo atomu vai molekulu izkārtojumā. 

Atšķirībā no kristālisku vielu tālās kārtības, amorfās vielās ir sastopama tikai tuvā kārtība (5. att. c).  Amorfa viela ir, piemēram, stikls.

Ir vielas, kas var būt kā amorfas, tā kristāliskas. Tādā gadījumā atsevišķas šo vielu fizikālās īpašības atšķiras. Piemēram, kristāliskām vielām ir noteikta kušanas temperatūra, bet amorfām vielām tādas nav - amorfu vielu kušanas temperatūru raksturo temperatūru diapazons, kurā tās pamazām kļūst šķidras. Jebkurai amorfai vielai, piemēram, arī stiklam piemīt plūstamība. Ar laiku amorfā stāvoklī esoša viela var kristalizēties.

Parasti tālā kārtība ir novērojama tikai cietām vielām, bet šķidrumiem ir raksturīga tikai tuvā kārtība. Tomēr pastāv arī izņēmumi. Šķidrajos kristālos pastāv arī tālā kārtība (6. attēls), tomēr tiem piemīt šķidrumiem raksturīgās īpašības. Šķidrie kristāli ir, piemēram, parafīni un fenilbenzonāti.

Kristāliskās vielas

Cietas vielas stāvokli, kad daļiņu (atomu vai molekulu) izvietojums telpā ir regulārs (periodisks), sauc par kristālisku stāvokli. 
Tas, kā daļiņas ir izvietotas kristālrežģī, nosaka vielas fizikālās īpašības - mehāniskās īpašības, elektromagnētiskā starojuma (gaismas) caurlaidību, siltumvadītspēju, elektrovadītspēju u.c.

Monokristāli

Ja kārtība, kas raksturīga daļiņu savstarpējam novietojumam kādā virzienā ir periodiski atkārtojas un ir nemainīga visā kristāla tilpumā, tad saka, ka kristālā pastāv ''tālā kārtība'' un šādu kristālu sauc par monokristālu (skatīt nodaļu "Cietu vielu modelēšana"). Monokristāla ārējā forma var būt kā regulāra (tā, piemēram, varamās sāls NaCl kristāliem ir taisnstūra paralēlskaldņu forma, ledum – sešstūra forma (1. attēls), bet dimantam – oktaedra forma), tā arī neregulāra. 

Monokristāli viegli skaldās pa noteiktām plaknēm, kuras sauc par skaldāmības plaknēm, tad veidojas tās pašas formai mazāki kristāli. Piemēram, drupinot vārāmās sāls kristālu, veidojas sīki kubi un taisnstūra paralēlskaldņi. Šis fakts noveda pie domas, ka kristālisks ķermenis sastāv no elementāršūnām (kubiem, sešstūra prizmām vai oktaedriem u. tml.), kuras cieši pieguļ viena otrai. Bet tas, savukārt, nozīmē, ka cietā ķermeni daļiņas (molekulas, atomi vai joni) novietotas stingri simetriskā kārtībā cita attiecībā pret citu, veidojot telpisku režģi – kristālrežģi. 

Kristālrežģis

Kristālrežģa simetrijai jābūt tādai, lai ar šādām elementāršūnām varētu vienmērīgi aizpildīt visu telpu. Daļiņu novietojuma vietas sauc par režģa mezgliem. Šo hipotēzi 1848. gadā izteica Bravē, pierādot, ka kristāliem iespējami 14 telpisko režģu tipi (Braves režģi) (2. attēls).

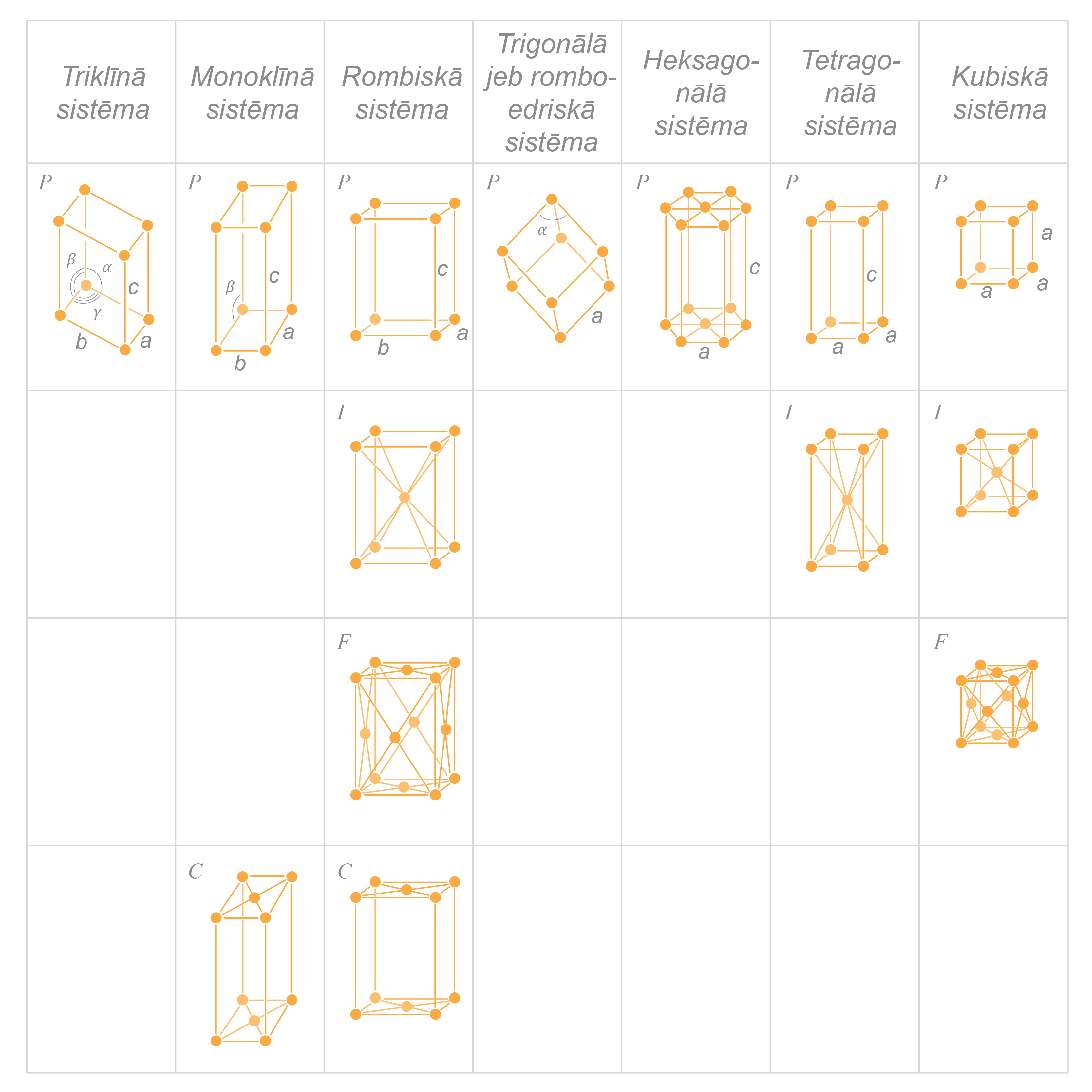
Tātad telpisko režģu formas var būt dažādas, bet ne jebkuras: nepieciešams, lai elementāršūnas, kas veido režģi, blīvi, bez atstarpēm saskartos cita ar citu - šāds sakārtojums atbilst režģa potenciālās enerģijas minimumam. Šādi var novietot, piemēram, kubiskas šūnas un sešstūra prizmu, bet nevar novietot piecstūra prizmu šūnas. Turklāt starp telpisko režģi un kristāla struktūru ir atšķirība – nozīme ir arī daļiņu izvietojumam elementāršūnā. Ir aprēķināts, ka dabā var eksistēt tikai 230 dažādi kristālrežģu tipi, kas veido 32 simetrijas klases, ko pierāda arī kristālu rentgenstruktūranalīze.

Daļiņu simetrisko novietojumu kristālrežģī nosaka tas, ka mijiedarbības spēki (pievilkšanās un atgrūšanās) starp daļiņām līdzsvarojas un daļiņu potenciālā enerģija ir minimālā. Daļiņas ap saviem līdzsvara stāvokļiem svārstās ar mazām amplitūdām (aptuveni 10^‒11 m).

Atomu izkārtojums monokristālā dažādos virzienos var atšķirties, tā rezultātā iespējama dažādu kristāla īpašību anizotropija – īpašību atkarība no virziena.
 

Polikristāli

Polikristālus veido ļoti daudzi, parasti mikroskopiski mazi, haotiski novietoti monokristālu graudi, līdz ar to notiek īpašību "vidējošanās" un  polikristāliem īpašību anizotropija nepiemīt, nav arī "regulāras" ārējās formas. Tomēr atsevišķu graudu robežās "tālā kārtība" pastāv. Polikristāliska struktūra parasti ir visiem metāliem. To, vai veidosies mono- vai poli- kristāls, nosaka kristalizācijas apstākļi. Piemēram, metālus var iegūt arī monokristāla veidā, ja nodrošina lēnu kausējuma atdzišanu.

Jonu, atomu, metālu un molekulārie kristāli

Kristālus var klasificēt arī pēc to kristālrežģi veidojošo daļiņu tipa un to mijiedarbības rakstura. Aplūko četras galvenās grupas: jonu, atomu, metālu un molekulāros kristālus (skatīt arī nodaļu "Ķīmiskās saites"). 

Jonu kristālu režģi veido ar pretējām zīmēm lādēti joni, kurus kristālrežģa mezglos notur elektriskie spēki. 

Atomāro režģi veido neitrāli atomi, kurus kristālrežģa mezglos notur kovalentās saites: blakus esošie atomi saistīti sava starpā ar kopējiem elektroniem, kuri riņķo ap šo atomu kodoliem. 

Metālu režģi veido pozitīvie joni, kurus savā starpā saista brīvie elek­troni. Šāds režģis raksturīgs metāliem. Metālā brīvie elektroni kļūst par visa kristāla "kopīpašumu". 

Molekulāro režģi var veidot atsevišķas, elektriski neitrālas polāras (dipolu) molekulas, kuras režģa mezglos no­tur elektriskie spēki. Tomēr polārām mole­kulām šie spēki ir izteikti vājāki, nekā joniem. 

Alloptropās modifikācijas

Vielas, kas veidojas no viena ķīmiskā elementa atomiem, sauc par šī elementa allotropajām modifikācijām. Terminu "allotropija" izmanto tikai attiecībā uz vienkāršām vielām, neatkarīgi no to agregātstāvokļa, bet attiecībā uz jebkuru cietu vielu, nenorādot, vai tā ir vienkārša vai sarežģīta, lieto terminu "polimorfisms". 

Polimorfās modifikācijas cita no citas atšķiras ar fizikālajām īpašībām. 
Lūk spilgts piemērs - oglekļa polimorfās modifikācijas: 

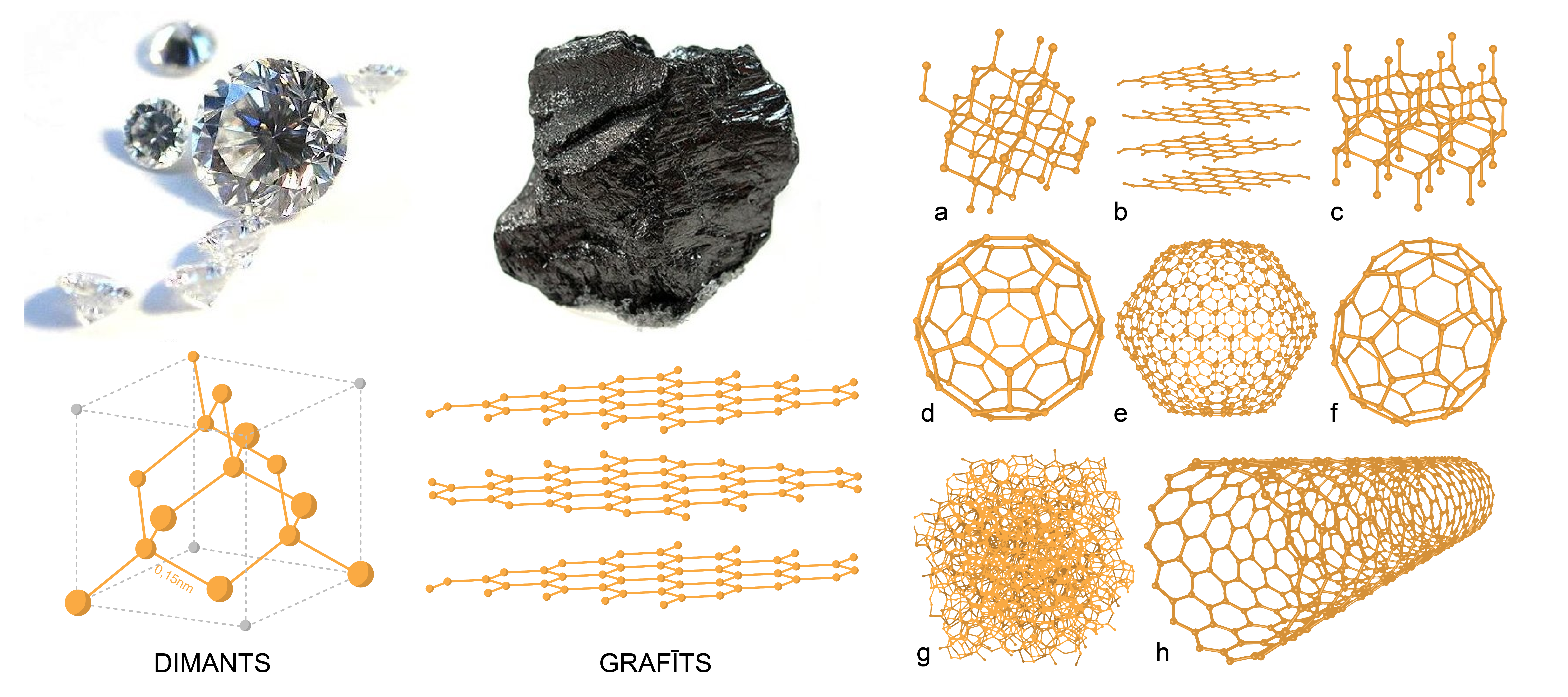
Ogleklis ir viela ar ļoti lielu allotropo (polimorfo) modifikāciju skaitu (3. attēls). Līdz šim atklātas vairāk nekā deviņas, lai gan ir avoti, kuros minēts mazāks skaits, amorfos allotropus ‘’pieskaitot’’ grafītam. Oglekļa allotropās modifikācijas pēc īpašībām ļoti atšķiras: no mīkstas līdz cietai, no melnas necaurspīdīgas līdz caurspīdīgai, no abrazīvas līdz eļļojošai un no lētas līdz dārgai. Tie ir gan amorfie oglekļa allotropi (ogles, sodrēji), gan kristāliskie allotropi – dimants, grafīts, lonsdeilīts, arī nanocaurulītes un fullerēni. 
 

Amorfas vielas

Materiālzinātnē un cietvielu fizikā amorfa (no grieķu a, "bez" un morphé, "forma") vai "nekristāliska" cieta viela ir cieta viela, kurā daļiņu (atomu vai molekulu) izvietojumā nav "tālās kārtības", bet pastāv tikai "tuvā kārtība".

• Tuvā kārtība - sakārtotība atomu vai molekulu savstarpējā izkārtojumā, kas atkārtojas tikai attālumos, kas ir salīdzināmi ar starpatomu attālumiem, tātad - blakus esošo atomu vai molekulu izkārtojumā. Tuvā kārtība raksturīga kā kristāliskām, tā amorfām vielām, tā šķidrumiem.
• Tālā kārtība - sakārtotība atomu vai molekulu savstarpējā izkārtojumā, kas atkārtojas lielos attālumos.

Tātad - amorfajiem materiāliem pastāv iekšējā struktūra, ko veido savstarpēji saistīti strukturālie bloki. Šo bloku uzbūve var būt līdzīga struktūrām, kas atrodamas konkrētā savienojuma kristāliskajā fāzē.

Agrāk terminu "amorfa viela" lietoja kā sinonīmu vārdam "stikls". Šobrīd kā vispārinošu terminu lieto "stiklveida cietviela" vai "amorfa cietviela", bet stikls tiek uzskatīts par speciālgadījumu: stikls ir amorfa cieta viela, kas tiek uzturēta zem tās ''stiklošanās temperatūras''. 

Stiklošanās temperatūra (Tg) raksturo temperatūru diapazonu, kurā amorfs materiāls pāriet no cieta trausla stāvokļa uz viskozu stāvokli. Ja vielas temperatūra ir zem Tg, tās daļiņām ir maz enerģijas, un molekulas nevar pārvietoties jaunās pozīcijās, ja ķermenim tiek pielikts spēks. Ja temperatūra ir virs Tg, molekulām ir lielāka kinētiskā enerģija, kas ļauj tām pārvietoties, lai mazinātu radušos mehāniskos spriegumus.

Fizikas literatūrā sastopams uzskats, par cietiem ķermeņiem sauc tieši kristāliskus ķermeņus, bet amorfus ķermeņus par pārdzesētiem šķidrumiem ar ļoti lielu viskozitāti.

Pastāv vairākas lielas amorfo vielu grupas: stikli (tiem pieder arī amorfi metālu sakausējumi), plastmasa (polimēri), gēli. Šo grupu robežas nav skaidri noteiktas, piemēram, ir organiskais stikls, kas ir arī plastmasa. Bieži amorfās vielas klasificē pēc to izgatavošanas metodēm. 

Vienas un tās pašas ķīmiskās vielas var būt kā kristāliskā tā amorfā stāvoklī.
Tipisks piemērs ir SiO₂ (1. attēls).

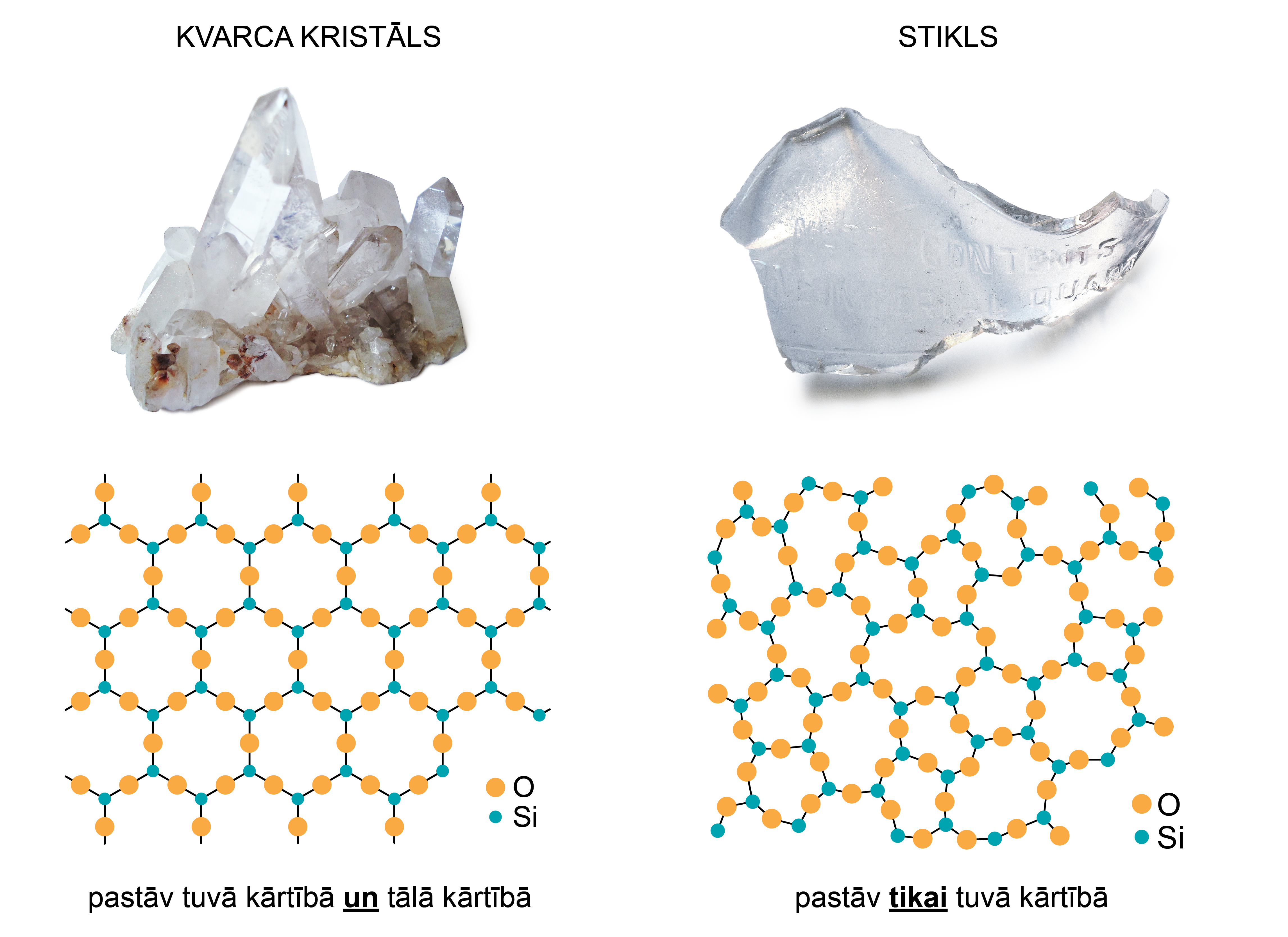
Amorfu un kristālisku vielu īpašību salīdzinājums

Amorfā stāvoklī vielu īpašības var būt atšķirīgas no tās pašas vielas īpašībām kristāliskā stāvoklī.
Atšķirībā no kristāliem, amorfas vielas nesacietē, veidojoties kristāliskām virsmām, un tās ir izotropas – nepastāv vielas īpašību atkarība no virziena. Amorfām vielām nav noteiktas kušanas temperatūras: temperatūrai paaugstinoties, stabili amorfās vielas pakāpeniski kļūst mīkstas un virs "stiklošanās temperatūras" nonāk šķidrā stāvoklī. 

Amorfu vielu siltumvadītspēja parasti ir zemāka nekā kristāliem. Amorfajiem metāliem ir zema cietība, bet augsta izturība.

Vienas un tās pašas vielas sacietē kristāliskā vai amorfā veidā atkarībā no dzesēšanas režīma. 

Vielas, kurām parasti ir (poli)kristāliska struktūra, bet kuras ir stipri pārdzesētas, var sacietēt amorfā stāvoklī, kas, pēc tam sekojošas karsēšanas rezultātā vai laika gaitā, kļūst kristāliskas (cietā stāvoklī ar nelielu siltuma izdalīšanos). Daudzu vielu amorfais stāvoklis tiek iegūts, šķidru kausējumu ļoti ātri dzesējot vai tad, kad tvaiki kondensējas uz virsmas, kas ir atdzisusi krietni zem kušanas temperatūras. 

Amorfā vielā daļiņas neatrodas potenciālās enerģijas minimuma situācijā, tādēļ amorfais stāvoklis ir metastabils un viela laika gaitā mēdz kristalizēties.

Tomēr šis kristalizācijas process istabas temperatūrā var ilgt daudzus gadus, gadsimtus vai pat tūkstošgades. Tā, piemēram, no parastajiem polimēriem (plastmasām) tikai polietilēnam ir ievērojams kristalizācijas ātrums istabas temperatūrā - apmēram divus gadus mīkstajam (LDPE) un vairākus gadus (pat ar kristalizāciju aizkavējošām piedevām) cietajam (ABPE) - jau apmēram puse ir kristalizējusies. Tas ir viens no polietilēna izstrādājumu trausluma iemesliem laikam ejot, īpaši paaugstinātā temperatūrā.

Šāda pāreja uz kristālisku formu nebūt nav obligāta visiem amorfajiem ķermeņiem: vecākais atrastais dzintars ir 320 000 000 gadus vecs un paliek amorfs. Obsidiāns (dabīgais stikls) reti pastāv ilgāk par dažiem miljoniem gadu, taču šajā laikā tam nav tendence kristalizēties (2. attēls). 
 

Konkrētos dzesēšanas režīmos var rasties ķermeņi ''jauktā stāvoklī'', kurā dažus nanometrus lielus kristālus atdala amorfas fāzes starpslāņi. Ir arī starpposma pusamorfie (puskristāliski) stāvokļi.

Tas, vai materiāls ir šķidrs vai ciets, galvenokārt ir atkarīgs no saitēm starp šādiem blokiem - cietā vielā ir tie ir cieši saistīti, bet šķidrumos vājāk. Pētījumi ir parādījuši, ka šķidrumu un amorfo ķermeņu struktūrām ir daudz kopīga. 

Deformācijas

Vielai (ķermeņiem) cietā agregātstāvoklī piemīt noteikta forma un tilpums.

Ķermenim pielikts spēks var deformēt ķermeni — pārvietot to veidojošās daļiņas citu attiecībā pret citu. Deformācija ir ķermeņa formas un/vai tilpuma izmaiņa ārējas iedarbības rezultātā.

Turklāt (saskaņā ar trešo Ņūtona likumu) deformētajā ķermenī rodas pretdarbības spēks, kas skaitliski vienāds ar deformējošo spēku - elastības spēks (\(F_\mathrm{el}\)).

Elastības spēks rodas tādēļ, ka (piemēram, kristālu stiepjot), attālumi starp vielas daļiņām spēka darbības virzienā palielinās un izzūd līdzsvars starp daļiņu pievilkšanās un atgrūšanās spēkiem. Tā rezultātā vielā rodas iekšējie spēki, kas cenšas jebkuru daļiņu pārvietot atpakaļ uz iepriekšējo stāvokli (elastīgas deformācijas mehānismu un elastības spēku rašanos aplūkosim nodaļa ''Elastības spēks'').

Izšķir elastīgu un plastisku deformāciju (piemēri 1. attēlā):

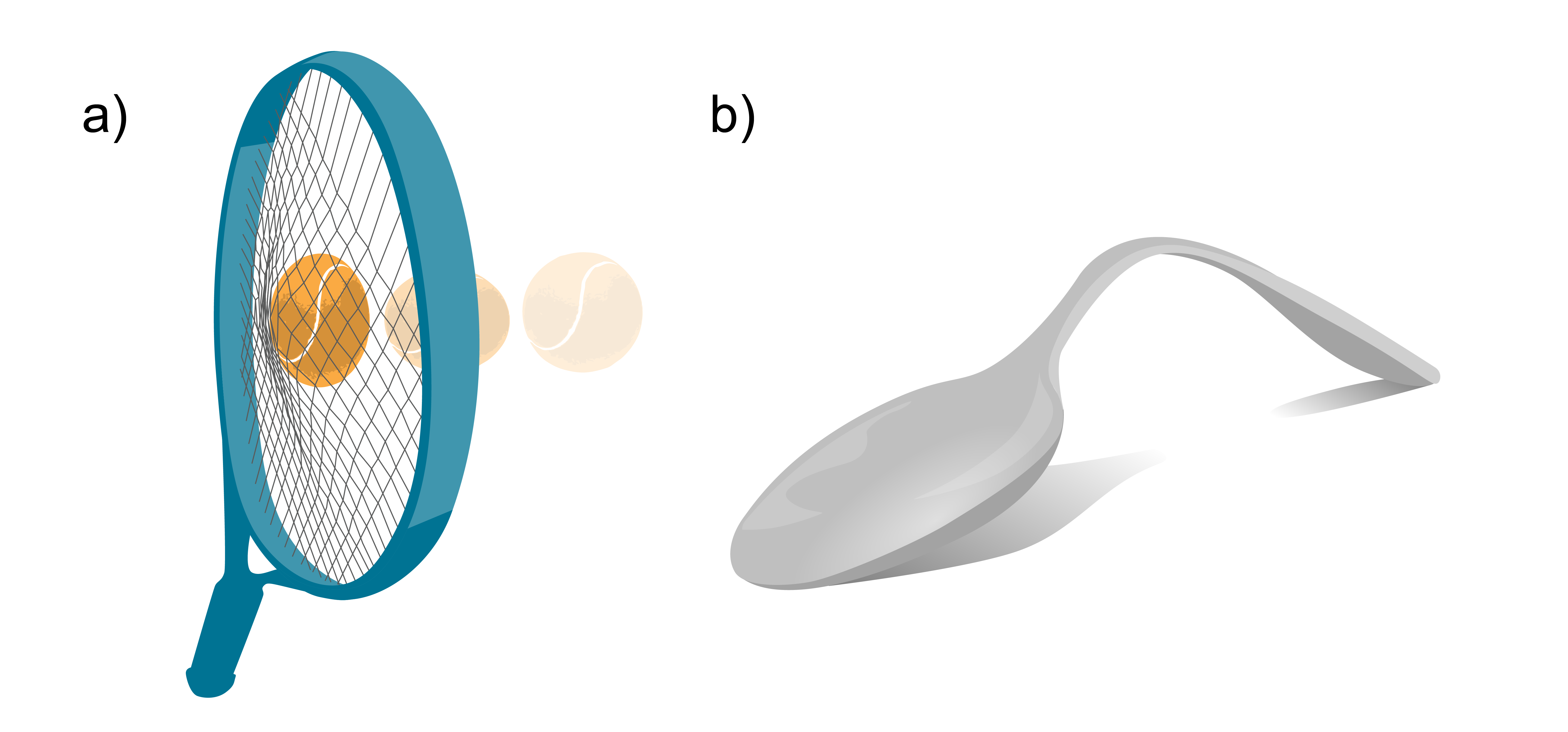
Ja ķermeņa izmēru relatīvā izmaiņa ir maza, tad reālu ķermeņu deformācija parasti ir praktiski elastīga. Lielāku izmaiņu gadījumā rodas paliekošā deformācija — ķermeņa forma un izmēri neatjaunojas pilnīgi. Vēl lielāku deformāciju gadījumā ķermenis var sagrūt (pārrāvums — pie stiepes, lūzums — pie lieces u. tml.)

Elastīgās un plastiskās deformācijas mehānismi ir ļoti atšķirīgi (plastisku deformāciju aplūkosim nodaļā ''Stiepes diagramma'').

Pastāv vairāki deformāciju veidi (skatīt 2. attēlu):

Stiepe-spiede (vienpusīga vai daudzpusīga stiepe, vienpusīga vai daudzpusīga spiede).

Stiepes un spiedes deformācija ir deformācijas veids, kad ārējo spēku iedarbībā mainās ķermeņa izmērs noteiktā virzienā. Ja ķermeņa izmērs palielinās, tā ir stiepes deformācija jeb stiepe, bet, ja samazinās — spiedes deformācija jeb spiede. Elastīgas deformācijas gadījumā pagarinājums (saīsinājums) \(\Delta l\) ir tieši proporcionāls pieliktajam spēkam. Stiepei ir pakļautas dažādas troses, ķēdes, mūzikas instrumentu stīgas vai, piemēram, griestu lampas iekare (3. att. a). Spiedei pakļautas dažādas virsmas, ēku sienas un pamati, galda kājas un ēku kolonas (3. att. b).

Stiepei ir pakļautas dažādas virves, troses, auklas, ķēdes, bet spiedei ir pakļauti, piemēram, ēku pamati un galdu kājas.

Bīde. Tas ir deformācijas veids, kas ķermenī rodas, ja spēks tiek pielikts pa tā virsmu (kamēr ķermeņa pretējā virsma ir fiksēta nekustīgi) - virsma tiek pārvietota paralēli pretējai virsmai. Bīdes deformācijā dažādi ķermeņa slāņi nobīdās cits attiecībā pret citu, un elastīgā bīdes deformācijā nobīdes leņķis \(y\) ir tieši proporcionāls pieliktajam spēkam \(F\). (4. att. a). Bīdes deformācijai ir pakļauts, piemēram materiāls, ja to zāģē (3. att. b). Bīde ir atbildīga arī par dažādu lietu, piemēram, apģērbu, apavu (2. att. c) un darbarīku nodilšanu. 

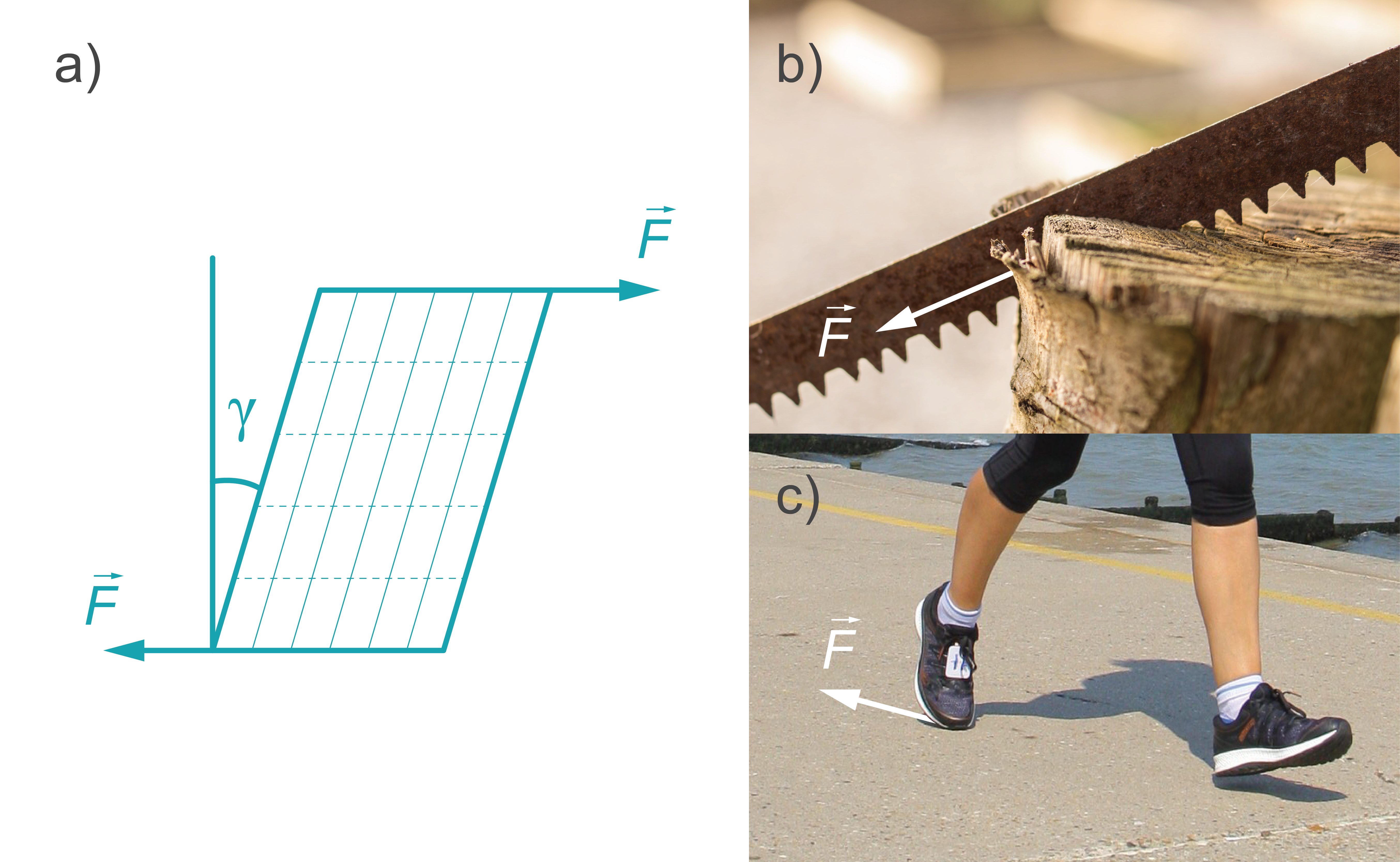
Liece. Lieces deformāciju var reducēt uz vienlaikus notiekošām stiepes un spiedes deformācijām, kas notiek dažādās ķermeņa daļās. To raksturo ielieces augstums \(h\) kas ir proporcionāls pieliktajam spēkam \(F\) (5. att. c). Šādam deformācijas veidam ir pakļautas sijas, plaukti un mūzikas instrumentu stīgas.

Ja ķermenis ir pakļauts liecei, tad vienā pusē ķermenim notiek spiedes deformācija, bet otrā stiepes. Līdz ar to sanāk, ka pa vidu ir deformācijai nepakļauts (neitrāls) slānītis (5. att. a). Šim neitrālajam slānītim ir maza nozīmē ķermeņa izturībā, tādēļ konstrukcijas, kas pakļautas lieces deformācijai, var veidot ar mazāk materiālu vidusslāni vai vispār tukšu vidu (5. att. b), tādā veidā ietaupot materiālu.

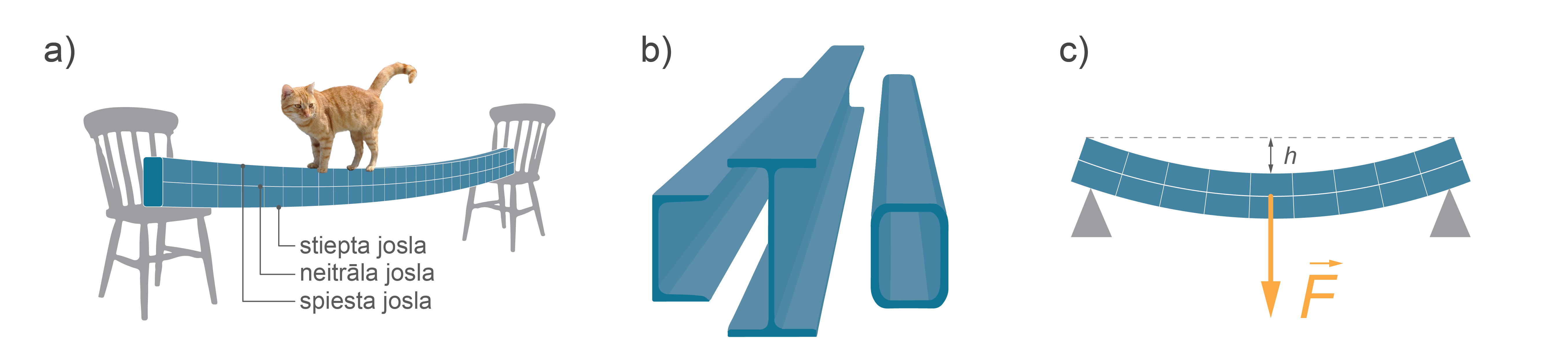
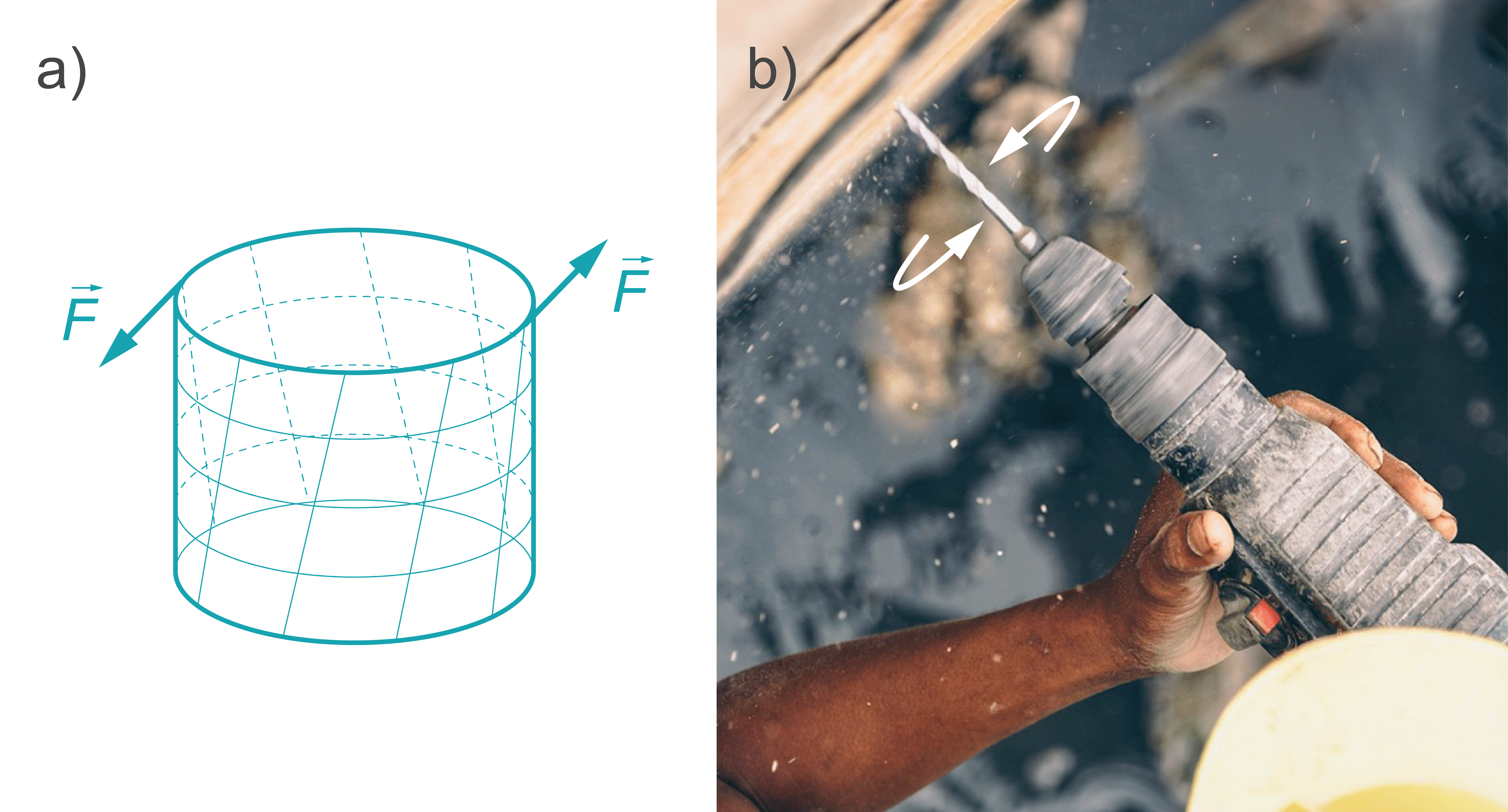
Vērpe. Vērpes deformācija ir neviendabīga bīde, kas rodas, ja uz ķermeni darbojas spēku pāris, kuru pielikšanas punkti atrodas noteiktā attālumā viens no otra (6. attēls a.) un kas darbojas vērpšanas asij perpendikulārā plaknē. Šādā deformācija sastopama vietās, kur notiek kāda rotācijas kustība, piemēram, izmantojot skrūvgriezi (5. attēls b), urbjot, pievelkot skrūves vai pagriežot aizdedzes atslēgu.

Elastības spēks

Ķermenim pieliekot spēku, tas var deformēties (skatīt nodaļu ''Deformācija''). 
Saskaņā ar trešo Ņūtona likumu, deformētajā ķermenī rodas elastības spēks (\(F _\mathrm{el}\)) - pretdarbības spēks, kas ir skaitliski vienāds ar deformējošo spēku, vērsts tam pretējā virzienā un darbojas uz ķermeni, kurš rada deformāciju \(\overrightarrow F_\mathrm{el} =-\overrightarrow F\) (1. attēls b)

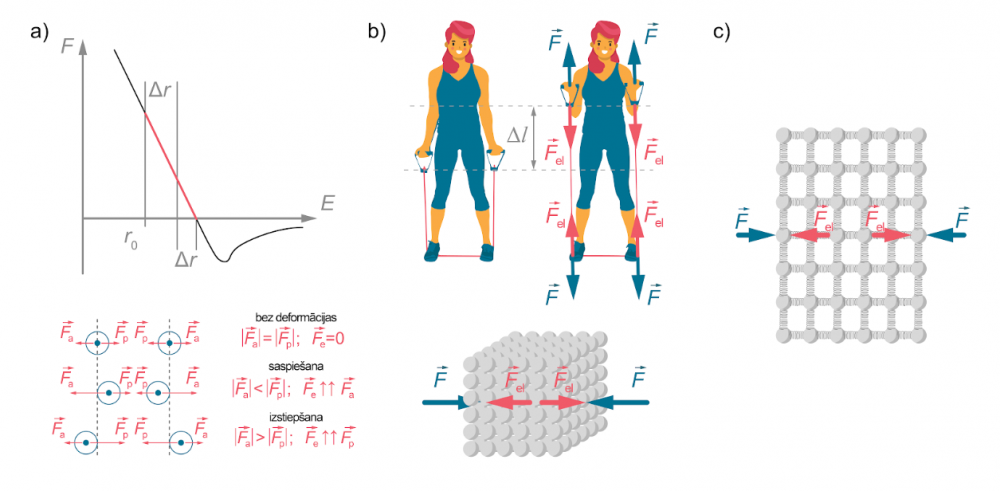
1.att. Daļiņu mijiedarbības spēki un to izmaiņa

Elastības spēks ir elektromagnētiskās mijiedarbības izraisīts spēks, kas darbojas starp ķermeni veidojošajām daļiņām (atomiem vai molekulām). Nedeformētā ķermenī elektromagnētiskie daļiņu pievilkšanās un atgrūšanās spēki, kas ir atkarīgi no attāluma starp daļiņām, ir līdzsvarā (skatīt nodaļu ''Cietu vielu modelēšana''). Kad mēs, pieliekot spēku, cenšamies ķermeni deformēt, līdzsvars starp šiem spēkiem zūd. Samazinot starpdaļiņu attālumus (piemēram, par \(\Delta r\)), virsroku gūst atgrūšanās spēki, bet palielinot tos – pievilkšanās spēki. Tā rezultātā rodas elastības spēks (1. attēls a). Tomēr saites starp vielas daļiņām elastīgās deformācijās izjauktas netiek. 
Situācija ir līdzīga, ja mēs mēģinātu deformēt cietas vielas modeli - ķermeni, kas sastāv no ar atsperēm savienotām bumbiņām. Saspiežot vai izstiepjot ķermeni tiek saspiestas vai izstieptas atsperes, kas pretojas deformācijai (1. attēls c)

Huka likums

Elastīgas stiepes un spiedes deformācijas pakļaujas eksperimentāli noteiktajam Huka likumam:
Elastības spēks \(F_\mathrm{el}\) ir tieši proporcionāls deformējamā ķermeņa pagarinājumam (saīsinājumam) (\(\Delta l\)) un vērsts pretēji ķermeņa daļu nobīdes virzienam šajā deformācijā (2. attēls, 1. attēls b):

2.att. Elastīga stiepes deformācija

\(\overrightarrow F_\mathrm{el}= -k\cdot \Delta l\)

kur 
\(k\) — ķermeni raksturojošs lielums, ko sauc par elastības koeficientu vai (atsperēm)stinguma koeficientu (mērvienība \(N/m\)).
\(\Delta l\)- pagarinājums (mērvienība \(m\)). 

Mīnusa zīme formulā rāda, ka elastības spēka virziens ir pretējs deformācijai.
Ja uzzīmē grafiku elastības spēka atkarībai no pagarinājuma, tad Huka likuma izpildīšanas gadījumā šis grafiks ir taisne (3. attēls a, b), kuras slīpuma koeficients ir elastības koeficients \(k \).

3.att. Huka likums

Arī elastīgu lieces, bīdes un vērpes deformāciju gadījumos to raksturlielumi (līdzīgi kā \(\Delta l \)) ir tieši proporcionāli pieliktajam spēkam.

Šādu proporcionalitāti var izskaidrot, ņemot vērā, ka pie nelielām starpdaļiņu attālumu izmaiņām   vielā molekulu rezultējošā mijiedarbības spēka atkarība no attāluma starp daļiņām arī ir lineāra (1. attēlā sarkani iekrāsotais posms (\(r_0\) ± \(\Delta r \))), bet elastības spēks veidojas kā visu ķermeni veidojošo daļiņu mijiedarbības kopīgs rezultāts.

Elastīgas deformācijas tuvāk aplūkosim nodaļā ''Mehāniskais spriegums. Elastības modulis''.
 

Cieta ķermeņa spiediens uz virsmu

Spiediena spēks un svars

Spēku, ar kuru ķermenis darbojas uz virsmu perpendikulāri tai, sauc par spiediena (normālspiediena) spēku (\(F_\mathrm{sp}\)).
Termins ''normāle'' nozīmē perpendikulu pret virsmu.
Jebkurš ciets ķermenis var spiest uz atbalstu – citu ķermeni – tādēļ, ka uz šo ķermeni darbojas smaguma spēks un/vai kāds cits spēks (1. attēlā grāmata darbojas ar spiediena spēku uz vertikālu sienu, jo grāmatu sienai klāt spiež, piemēram, cilvēka roka - faktiski attēlā parādīts rokas radītais spēks, kas vienāds ar grāmatas spiediena spēku uz sienu).

1.att. Spiediena spēks

Normālspiediena spēka speciālgadījums ir ķermeņa svars (\(P\)) - spēks, ar kādu ķermenis Zemes pievilkšanas spēka ietekmē (perpendikulāri) spiež uz atbalsta virsmu vai nostiepj piekari.

Ja uz ķermeni darbojas tikai smaguma spēks un atbalsts ir horizontāls, tad ķermenis ar savu smaguma spēku spiež uz atbalstu vertikāli lejup. Tādā gadījumā ķermeņa svars (tā radītais spiediena spēks) un smaguma spēks ir skaitliski vienādi (2. att. a). 
\(F_\mathrm{sm}=F_\mathrm{sp}=P=mg\)

Ja ķermenis atrodas uz slīpas virsmas, kur spiediena spēks nav vērsts smaguma spēka virzienā, to skaitliskā vērtība ir atšķirīga - mazāka.  Smaguma spēka virziens vairs nesakrīt ar virsmai perpendikulāro virzienu, kurā ir vērsts ķermeņa svars. Ja šādā gadījumā koordinātu sistēmu izvēlas tā, ka X-ass ir paralēla virsmai, uz kuras atrodas ķermenis, tad svars ir vienāds ar smaguma spēks \(F_\mathrm{g}\) projekciju uz Y-ass. Ja virsma ar horizontu veido leņķi α, tad \(P=F_\mathrm{gY}=mg\mathrm {cos\alpha}\) (2. att. b).  

2.att. Ķermeņa svars uz horizontālas un slīpas virsmas

Svara jēdzienu dažādās mācību grāmatās definē atšķirīgi - vairumā angļu vaōdā rakstītu mācību grāmatu ''svars'' tiek definēts vienāds ar smaguma spēku (weight = mg), bet situācijās, kad ķermenis spiež uz virsmu, kas nav horizontāla, runā par ''spiediena spēku''. Savukārt krieviski rakstītās mācību grāmatās runā par ''normālo svaru'', ja virsma, uz kuru ķermenis spiež smaguma spēka darbības dēļ, ir horizontāla. Jāmēģina neapjukt un saprast, kas katrā gadījumā ar ''svaru'' domāts.

Balsta reakcijas spēks

Ķermenis, balstoties uz virsmu, to deformē. Elastības spēku, ar kuru balsts darbojas uz ķermeni, sauc par balsta reakcijas spēku (\(\overrightarrow{F}_\mathrm{R}\)). Balsta reakcijas spēks vienmēr vērsts perpendikulāri ķermeņu saskares virsmām.

Savukārt, ja nostiprinātā auklā iekar ķermeni, tad aukla deformējas un tajā rodas elastības spēks, kuru sauc par auklas (iekares) elastības vai sastiepuma spēku (\(\overrightarrow{F}_\mathrm{el} \)) (skatīt nodaļu ''Elastības spēks'').

3.att. Svars un elastības spēks (balsta reakcijas vai sastiepuma spēks)

Spiediens

Tomēr spēka iedarbības rezultāts nav atkarīgs tikai no spēka lieluma, bet arī no virsmas laukuma, uz kuru tas darbojas.

Spiediens (\(p\)) ir fizikāls lielums, kas raksturo, cik liels spēks darbojas uz virsmas laukuma vienību perpendikulāri virsmai (4. att. a).

 \(p=\frac{F_\mathrm{{}sp}}{S}\)

kur \(F_\mathrm{sp}\) – spiediena spēks, kas darbojas uz atbalstu, bet \(S\) – atbalsta laukums.

Ja spēku izsaka ņūtonos (\(N\)) un laukumu kvadrātmetros (\(m^2\)), tad spiediena mērvienība ir paskāls (\(Pa\)).
\([p]=\frac{N}{m^2}=Pa\) (paskāls)

Piemēram, lai aprēķinātu, kādu spiedienu uz zemi rada cilvēks, jāzina smaguma spēks \(F_\mathrm{g}\) (tas skaitliski vienāds ar svaru) un apavu zoļu laukums \(S\), kas saskaras ar zemi (līdzīga situācija 4. att. b).

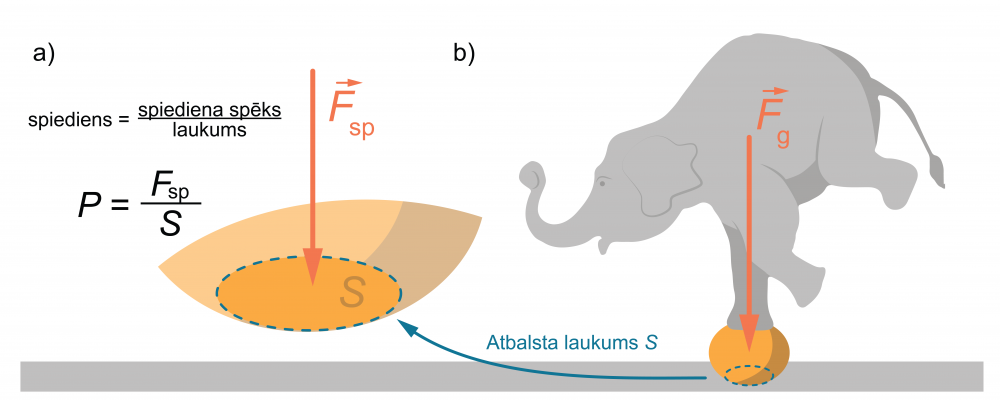
4.att. Spiediena definīcija un piemērs