Kosmiskie ātrumi

Kas ir Zemes mākslīgais pavadonis un neliela vēsturiskā izziņa

Par ZMP sauc cilvēku radītu ķermeni (kosmisko aparātu), kas pārvietojas pa orbītu apkārt Zemei. ZMP kustība apkārt Zemei notiek tikai viena spēka – gravitācijas spēka iedarbībā. Par ZMP var kļūt jebkuras masas ķermenis, ja tam Zemes virsmas tuvumā horizontālā virzienā piešķir ātrumu \(v_1=7,9\frac{km}{s}\). Šo ātrumu sauc par pirmo kosmisko ātrumu. Ar pirmo kosmisko ātrumu ZMP kustas apkārt Zemei pa riņķveida orbītu (trajektoriju).

1957. gada 4. oktobra vakarā ap pusastoņiem pēc vietējā laika no Baikonuras kosmodroma, kas atrodas Kazahstānas teritorijā, tika palaists pirmais mākslīgais zemes pavadonis "Sputnik -1" (1. attēls). Pēc 92 dienām, kuru laikā "Sputnik - 1" 1440 reizes aplidoja ap Zemi, pavadonis iegāja planētas atmosfērā un sadega. 

1.att.

Venta-1 ir Latvijas pirmais Zemes mākslīgais pavadonis (2. attēls), kas polārā orbītā (skatīt sadaļu "ZMP izmantošana'') palaists 2017. gada 23. jūnijā Indijā. Tas paredzēts kuģu satiksmes Automātiskās identifikācijas sistēmas (AIS) sakaru starp pavadoņiem un attēlu uzņemšanas kameras izmēģinājumiem. Projektu vada Ventspils Augstskola. Ventspils Augstskolas satelīts ''Venta-1'' griežas pa zemo piezemes orbītu, aptuveni 505 km augstumā. ''Venta-1'' aplido zemi 16 reizes diennaktī, bet ne vienmēr var noķert tā signālu. Labu signālu var uztvert tikai 2-3 reizes dienā aptuveni 10 minūtes. 

2017. gada oktobrī  Latvijas Pasts izdeva pastmarku un aploksni, uz kuras attēlots pavadonis Venta-1.

2.att.

Kosmiskie ātrumi

Shematiskajā attēlā ZMP atrodas augstumā \(h\) virs Zemes virsmas (3. attēls). Tādēļ rotācijas rādiuss \(r\) ap Zemes centru ir vienāds \(r=R+h\), kur \(R\) – Zemes rādiuss. Gravitācijas spēks \(F_\mathrm{gr}\), kas vērsts uz Zemes centru, piešķir pavadonim centrtieces paātrinājumu \(a_\mathrm{ct}\). Lai noteiktu ZMP ātrumu \(v\) augstumā \(h\), izmantosim gravitācijas spēku formulu \(F_\mathrm{gr}=G\frac{Mm}{r^2}\) (centrtieces spēks), otrā Ņūtona likuma formulu \(F_\mathrm{gr}=ma_\mathrm{ct}\) un centrtieces paātrinājuma formulu \(a_\mathrm{ct}=\frac{v^2}{r}\) kur \(M\) – Zemes masa, \(m\) – pavadoņa masa.

Iegūstam \(G\frac{Mm}{r^2}=m\frac{v^2}{r}\) vai \(G\frac{Mm}{(R+h)^2}=m\frac{v^2}{R+h}\). Nosakām kustības ātrumu pa orbītu \(v\) : \(v=\sqrt{\frac{GM}{R+h}}\).          

Ja \(h=0\), tad \(v_1=\sqrt{\frac{GM}{R}}\) vai \(v_1=\sqrt{\frac{GM}{R}}=\sqrt{\frac{GM}{R^2}R}=\sqrt{gR}\) – pirmā kosmiska ātruma formula. 

Formulu \(v_1=\sqrt{gR}\) var iegūt arī citādi. Jāatbild uz jautājumu – ar kādu ātrumu nepieciešams kustēties pa "ideālo" Zemes virsmu, lai centrtieces paātrinājums būtu vienāds ar brīvas krišanas paātrinājumu? Izsakot ar fprmulu, iegūstam: \(g=\frac{v^2}{R}\). Tādēļ \(v=\sqrt{gR}\). 

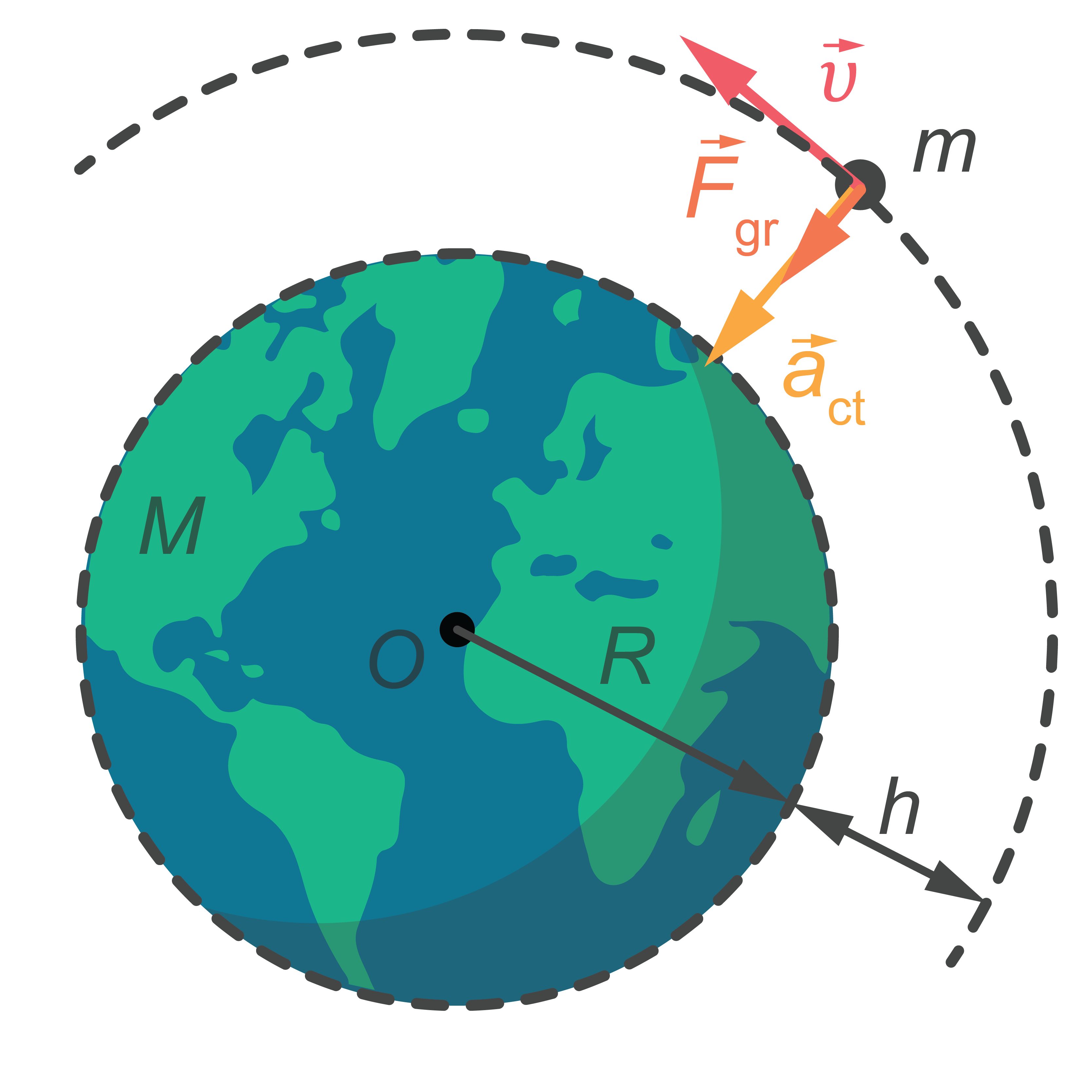
3.att.

Ja pavadoņa ātrums ir lielāks par pirmo kosmisko ātrumu, tad tā orbīta ir elipse, bet, sasniedzot otro kosmisko ātrumu \(v_2=\sqrt{2v_1}\approx{11,2}\) \(\frac{km}{s}\), pavadonis kustas pa parabolu un iziet ārpus Zemes gravitācijas spēka darbības zonas. Pavadonis kļūst par Saules mākslīgo pavadoni.

Lai ķermenis pārvarētu Saules gravitācijas spēka iedarbību un no Zemes aizlidotu ārpus Saules sistēmas, tam jāpiešķir trešais kosmiskais ātrums \(v_3\approx{16,7}\) \(\frac{km}{s}\). Tad ķermeņa kustības trajektorija ir hiperbola.

Trešā un otrā kosmisko ātrumu formulas izvedums

Lai izlidotu no Saules sistēmas no Zemes orbītas, ķermenim nepieciešams pārvarēt mijiedarbības potenciālo enerģiju starp ķermeni un Sauli: \(\frac{mv_S^2}{2}+(-G\frac{mM_\mathrm{S}}{r_\mathrm{S-Z}})=0\) un \(v_\mathrm{S}=\sqrt{\frac{2GM_\mathrm{S}}{r_\mathrm{S-Z}}}\), kur \(M_\mathrm{S}\) – Saules masa, \(r_\mathrm{S-Z}\) – attālums starp Zemi un Sauli. 

Raķete, kas kustas kopā ar Zemi ap Sauli, jau kustas ar Zemes ātrumu ap Sauli: pēc otrā Ņūtona likuma \(G\frac{M_\mathrm{S}M_\mathrm{Z}}{r^2_\mathrm{S-Z}}=M_\mathrm{Z}\frac{v^2_\mathrm{Z}}{r_\mathrm{S-Z}}\) un \(v_Z=\sqrt{\frac{GM_\mathrm{S}}{r_\mathrm{S-Z}}}\). \(M_\mathrm{Z}\) – Zemes masa.

Secinājums: ja raķete startē Zemes kustības ātrumā, tad raķetes kustības ātrums: \(v_\mathrm{RZ}=v_\mathrm{S}-v_\mathrm{Z}=v_\mathrm{Z}(\sqrt{2}-1)\).  

Lai pilnībā pārvarētu Zemes pievilkšanas spēku, raķetei nepieciešams piešķirt otro kosmisko ātrumu: \(\frac{mv_2^2}{2}+(-G\frac{mM_\mathrm{Z}}{r_\mathrm{Z}})=0\), kur \(r_\mathrm{Z}\) – Zemes rādiuss. Iegūstam otrā kosmiskā ātruma formulu:

\(v_2=\sqrt{\frac{2GM_\mathrm{Z}}{r_\mathrm{Z}}}=\sqrt{2}v_1\approx{11,2}\) \(\frac{km}{s}\), kur \(v_1\) – pirmais kosmiskais ātrums.

Saskaņā ar enerģijas nezūdamības likumu, raķetei nepieciešams piešķirt kinētisko enerģiju, lai pārvarētu gan Zemes gravitāciju, gan Saules gravitāciju no Zemes orbītas: \(\frac{mv_3^2}{2}=\frac{mv_2^2}{2}+\frac{mv^2_\mathrm{RZ}}{2}\).  

Iegūstam \(v_3=\sqrt{v_2^2+v^2_\mathrm{RZ}}\) ⇒  \(v_3=\sqrt{v_2^2+v^2_\mathrm{Z}(\sqrt{2}-1)^2}\) ⇒ \(v_3=\sqrt{11,2^2+30^2(\sqrt{2}-1)^2}\approx{16,7}\) \(\frac{km}{s}\).

Zemes mākslīgo pavadoņu (ZMP) izmantošana

Zemes mākslīgo pavadoņu tipi darbības sfēras

Ģeostacionāra orbīta – orbīta, kurā ievadītais ZMP nemaina stāvokli pret Zemes virsmu. Orbīta ir riņķveida un atrodas Zemes ekvatora plaknē. Orbītas augstums virs Zemes virsmas ap 36 000 km. 

Polāra orbīta  – orbīta, kurā ievadītais ZMP pārlido zemeslodes polu apgabalus. Atbilstoši izvēloties orbītas parametrus var panākt, ka pavadonis secīgi pārlūko visus Zemes virsmas apgabalus.

Starptautiskā kosmosa stacija

Starptautiskā kosmosa stacija (SKS), (angļu: International Space Station (ISS)) ir orbitālās stacijas starptautisks projekts, kurā piedalās piecas kosmiskās aģentūras no ASV (NASA), Kanādas (CSA), Krievijas (Roskosmos), Eiropas (ESA) un Japānas (JAXA) (1. attēls).

1.att.

SKS atrodas zemā Zemes orbītā aptuveni 400 km augstumā virs jūras līmeņa ar orbītas slīpumu pret ekvatoru ~ 51,6°, apriņķojot planētu apmēram 92 minūtēs. Stacija pastāvīgi zaudē augstumu termosfērā esošo retināto daļiņu berzes dēļ, tādēļ periodiski jāiedarbina pašas stacijas vai tai pievienoto kosmosa kuģu raķešdzinēji, lai ''paaugstinātu'' orbītu. 

Keplera likumi

Planētu kustība ap Sauli notiek Saules gravitācijas spēka dēļ. Planētu kustības likumsakarības atklāja matemātiķis Johanness Keplers (tās publicētas no 1609. līdz 1619. gadam). Viņš formulējis trīs likumus. 

Planētu orbītas ir elipses. Elipse ir noslēgta ovālveida plaknes līkne, kurai ir divi fokusi. Attālumu summa no katra elipses punkta līdz abiem fokusiem ir konstants lielums. 

Planētas orbītas izmērus raksturo lielā pusass \(a\) (1. attēls). Tās garums ir puse no lielās ass AP. Zemes orbītas lielās pusass garums (jeb Zemes vidējais attālums līdz Saulei) ir vienāds ar vienu astronomisko vienību (\(AU\)), \(1\) \(AU=1,5\cdot{10}^8\) \(km\) vai \(1,5\cdot{10}^{11}\) \(m\). Planētas rādiusvektors FB ir nogrieznis, kas vērsts no elipses viena fokusa uz patvaļīgu orbītas punktu.

Pirmais Keplera likums (elipses likums): katra planēta kustas ap Sauli pa elipsi, kuras vienā fokusā atrodas Saule (1. attēls). Likums nosaka, ka kustības laikā nepārtraukti mainās attālums starp planētu un Sauli.

Zeme atrodas Saulei vistuvāk ap 5. janvāri.

Otrais Keplera likums (vienādo laukumu likums): Planētas rādiusvektors vienādos laika sprīžos apraksta vienādus laukumus (1. attēls). Likums nosaka, ka dažādos orbītas punktos planēta kustas ar atšķirīgu ātrumu. Tuvāk Saulei ātrums ir lielāks. P punktu sauc par perihēliju, A punktu – par afēliju. 

1.att.

Trešais Keplera likums (harmonijas likums): Jebkuru divu planētu apriņķošanas ap Sauli periodu \(T_1\) un \(T_2\) kvadrātu attiecība vienāda ar to orbītu lielo pusasu \(a_1\) un \(a_2\) kubu attiecību:

\(\frac{T_1^2}{T_2^2}=\frac{a_1^3}{a_2^3}\) .

No šā likuma var secināt – jo tālāk no Saules atrodas planēta, jo lēnāk tā kustas.

Izmantojot trešo Keplera likumu var  "izmērīt" attālumus starp planētām un Sauli. Planētas rotācijas periodu ap Sauli nosaka, izmantojot Zemes kustības ap Sauli raksturlielumus. Formulā \(\frac{T_1^2}{T_2^2}=\frac{a_1^3}{a_2^3}\) indekss "1" attiecas uz Zemi. Zemes rotācijas periods \(T_1\) ap Sauli ir vienāds ar 1 gadu, vidējais attālums starp Zemi un Sauli \(a_1\) ir vienāds ar 1 \(AU\). Zinot planētas rotācijas periodu ap Sauli \(T_2\), var noteikt vidējo attālumu \(a_2\) starp planētu un Sauli.

Uzdevuma risināšanas piemērs

Jupiters veic vienu apriņķojumu ap Sauli 12 gados. Noteiksim attālumu starp Jupiteru un Sauli.
Indekss ''1'' – Zeme (\(T_1\) = 1 gads; \(a_1\)= 1 \(AU\)), indekss ''2'' – Jupiters (\(T_2\) = 12 gadi; \(a_1\) nav zināms).

Likuma \(\frac{T_1^2}{T_2^2}=\frac{a_1^3}{a_2^3}\) formulu var uzrakstīt šādi: \(\frac{1^2}{12^2}=\frac{1^3}{a_2^3}\). Nosakām, ka \(a_2=\sqrt[3]{144}\approx{5,2}\) \(AU\).

Citu planētu dabisko pavadoņu kustība arī pakļaujas Keplera likumiem. Mūsdienās atbilstoši  Keplera likumiem kustas arī mākslīgie pavadoņi ap Zemi.

Ne visu debess ķermeņu orbītas ap Sauli ir noslēgtas. Dažu komētu orbītas ir nenoslēgtas līknes. Tad tās mūsu redzeslokā parādās tikai vienu reizi.

Trešā Kiplera likums vispārigajā formā

Pastāv arī tāda trešā Keplera forma, kas dot iespēju noteikt planētu masas. 

Likuma formula: \(\frac{T_1^2}{T_2^2}\frac{M_1+m_1}{M_2+m_2}=\frac{a_1^3}{a_2^3}\), kur \(M_1\) un \(M_2\) – lielo ķermeņu masas, \(m_1\) un \(m_2\) – lielo ķermeņu pavadoņu masas. Piemēram, ja \(M_1=M_2=M_\mathrm{S}\) – Saules masa, tad \(m_1\) un \(m_2\) – planētu masas.

Tātad \(m_1\ll{M_\mathrm{S}}\) un \(m_2\ll{M_\mathrm{S}}\) un formula \(\frac{T_1^2}{T_2^2}\frac{M_1+m_1}{M_2+m_2}=\frac{a_1^3}{a_2^3}\) pāriet formulā \(\frac{T_1^2}{T_2^2}=\frac{a_1^3}{a_2^3}\).

Var piešķirt indeksus arī citādi: indekss ''1'' – Zeme un \(M_1\) – Saules masa, indekss ''2'' – Mēness un \(M_2\) – Zemes masa.

Tad iegūsim: \(\frac{T^2_\mathrm{Zeme}}{T^2_\mathrm{Mēness}}\frac{(M_\mathrm{Saule}+m_\mathrm{Zeme})}{(M_\mathrm{Zeme}+m_{Mēness})}=\frac{a^3_\mathrm{Zeme}}{a^3_\mathrm{Mēness}}\). 

Ir skaidrs, ka \(m_\mathrm{Zeme}\ll{M_\mathrm{Saule}}\) un \(m_\mathrm{Mēness}\ll{M_\mathrm{Zeme}}\). Tad \(\frac{T^2_\mathrm{Zeme}}{T^2_\mathrm{Mēness}}\frac{M_\mathrm{Saule}}{M_\mathrm{Zeme}}=\frac{a^3_\mathrm{Zeme}}{a^3_\mathrm{Mēness}}\), un no formulas var noteikt attiecību \(\frac{M_\mathrm{Saule}}{M_\mathrm{Zeme}} =\frac{a^3_\mathrm{Zeme}}{a^3_\mathrm{Mēness}}:\frac{T^2_\mathrm{Zeme}}{T^2_\mathrm{Mēness}}\). Tātad - var noteikt, cik reizes Saules masa ir lielākā, nekā Zemes masa.

Līdzīgi var rīkoties ar citiem objektiem Saules sistēmā: piemēram, indekss ''1'' – Mēness un \(M_1\) – Zemes masa, indekss ''2'' – Jupitera pavadonis un \(M_2\) – Jupitera masa.

Piezīme: lielai planētai jābūt vismaz vienam pavadonim.

Slavenāko komētu tops cilvēces vēsturē

Haleja komēta (2. attēls) ir visspožākā. Tā nosaukta angļu astronoma Edmonda Haleja (1656 - 1742) vārdā, kuram izdevies noteikt komētas atgriešanās Saules tuvumā periodisko raksturu – tā atgriežas ik pēc 70-75 gadiem –  un aprēķināts tās nākamās parādīšanās brīdi.

Pēdējās parādīšanās laikā 1986. gadā Haleja komēta kļuva par pirmo komētu, ko izpētīja, izmantojot kosmiskos aparātus ''Vega-1'' un ''Vega-2''. Tie sniedza informāciju par komētas kodola struktūru, kā arī komas un komētas astes veidošanās mehānismiem.

Šīs komētas pēdējais gājiens caur perihēliju  bija 1986. gada 9. februārī, nākamais gaidāms  2061. gada 28. jūlijā, bet pēc tam - 2134. gada 27. martā. 

2.att. Haleja komēta

Enkes komēta

Šo komētu neatkarīgi viens no otra ''atklāja'' Pjērs Mešēns (1786. g.) un Karolīna Geršele (1795. g.), bet pēc tam (1805. un 1818. g.) - Žans Luī Ponss. 1819. gadā Johans Enke pierādīja, ka visi šie novērojumi attiecas uz vienu un to pašu komētu, un izskaitļoja tās orbītu.

Enkes komēta tiek uzskatīta par komētu ar visīsāko apriņķošanas periodu ap Sauli - 3,3 gadi.

Heršela-Rigoles komēta

Heršela-Rigoles komēta tiek uzskatīta par komētu ar garāko riņķošanas periodu ap Sauli, kas ir 155 gadi.
Komēta tika atklāta 1788. gadā un nosaukta tās pirmatklājēju vārdā.

Tās pēdējais gājiens cauri perihēlijam bija 1939. gada 9. augustā, nākamais gaidāms 2092. gada 16. martā.

Švasmana-Vahmana komēta

Atklāta 1925. gadā un nosaukta par godu pirmatklājējiem. Tiek uzskatīta par komētu ar visapaļāko orbītu.

Tās pēdējie gājieni cauri perihēlijam – 2004. gada 10. jūlijā un 2019. gada 7. martā.

Brorzena-Metkalfa komēta

Šī komēta atklāta 1847. gadā un nosaukta par godu pirmatklājējiem. Tā tiek uzskatīta par komētu ar visizstieptāko orbītu – tās maksimālais attālums no Saules ir gandrīz 70 reizes lielāks par minimālo attālumu no Saules.

Pēdējais gājiens cauri perihēlijām bija- 1989. gada 11. septembrī, nākamais gaidāms 2059. gada 8. jūnijā.

Leksela komēta

Atklāta 1770. gadā, nosaukta astronoma Andreja Leksela vārdā, kurš izskaitļojis tās orbītu (3. attēls). Tiek uzskatīta par komētu, kas Zemei pietuvojas vismazākajā attālumā - nedaudz vairāk par 2 miljoniem kilometru. Komētu raksturoja kā komu, ko ieskauj sudrabota gaisma. Turklāt komētas spilgtākā daļa spīdēja spožāk, nekā Mēness disks. 

Domājams, ka tuvināšanās Jupiteram ir izvedusi Leksela komētu ārpus Saules sistēmas.

3.att. Leksela komēta