Termiskā izplešanās

Nodaļā "Vielas atomārā uzbūve" jau pieminēts, ka viena no parādībām, kas apliecina, ka viela veidota no daļiņām, starp kurām ir "spraugas", ir termiskā izplešanās.

Sasilstot izplešas gan cieti ķermeņi (vielas), gan šķidrumi gan arī gāzes. Jāpiebilst, ka iespējami arī izņēmumi – ir vielas, kuras kādā noteiktā temperatūru intervālā saraujas. Savukārt gāze vienmēr aizņem visu tai atvēlēto tilpumu, tādēļ par termisko izplešanos varam runāt tikai aptuveni nemainīga spiediena gadījumā (skatīt nodaļu "Gāzu termiskā izplešanās").

Cietiem ķermeņiem sasilstot mainās kā tilpums, tā arī virsmas laukums un lineārie izmēri. Šķidrumiem parasti aplūko tikai tilpuma izmaiņu.

Termiskās izplešanās skaidrojums

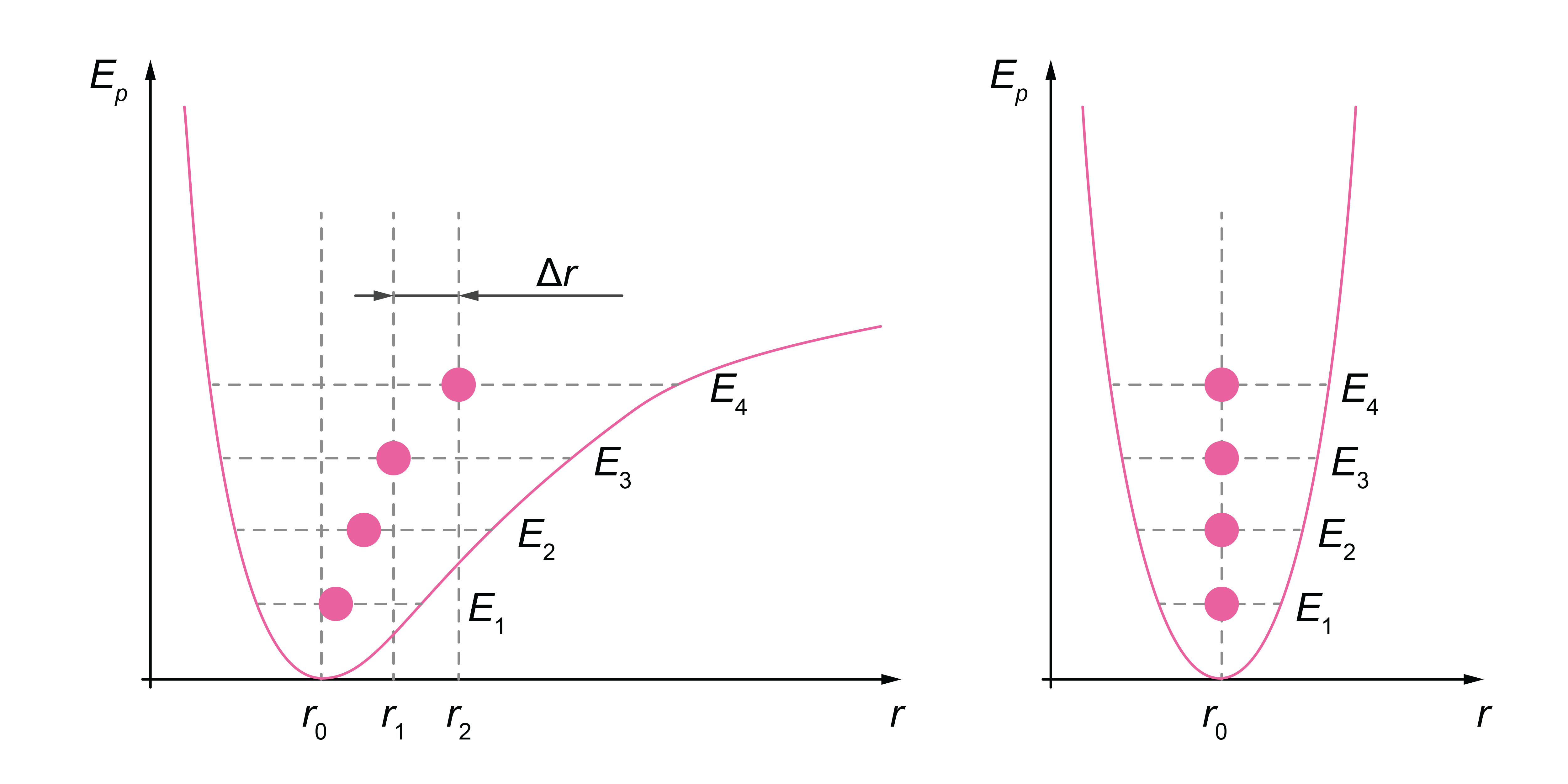
Ķermeņu termiskā izplešanās ir atkarīga no šķidruma vai cietvielas atomu (molekulu) mijiedarbības rakstura. Starp vielas atomiem darbojas pievilkšanās un atgrūšanās spēki. Atgrūšanās spēki, mainoties attālumam starp atomiem, mainās straujāk nekā pievilkšanās spēki (skatīt nodaļu "Cietas vielas, šķidrumi un gāzes"). Tādēļ atomu mijiedarbības potenciālās enerģijas \(E_\mathrm{P}\) atkarību no starpdaļiņu attāluma r attēlo asimetriska līkne (1. attēls a). Paaugstinoties šķidruma vai cietas vielas temperatūrai, pieaug ne tikai daļiņu svārstību amplitūda un palielinās to svārstību siltumkustības vidējā enerģija \(E\), bet būtiski pieaug arī vidējais starpatomu attālums \(r\). Sasilstot no kādas temperatūras \(T_1\) līdz temperatūrai \(T_2\) starpatomu attālumi pieaug par \(\Delta{r-}\) no \(r_1\) līdz \(r_2\) un, šiem pieaugumiem summējoties, ķermenis izplešas. Ja enerģijas līkne būtu simetriska, tad, pieaugot svārstību amplitūdai, līdzsvara stāvokļa attālumi r praktiski nemainītos. Zemās temperatūrās (tuvu \(E_\mathrm{P}\) līknes minimumam) potenciālās enerģijas līkne ir gandrīz simetriska (līdzīgi kā 1.attēlā b). Tādēļ, temperatūrai tiecoties uz absolūto nulli, termiskā izplešanās praktiski nenotiek.

Termiskās izplešanās koeficients

Ja aplūkojam ķermeņa lineāro izmēru izmaiņu sasilstot, pieredze liecina, ka ķermeņa pagarinājums \(\Delta{l}\) (lineārā izplešanās) pat visai plašā temperatūru diapazonā ir tieši proporcionāls tā temperatūras izmaiņai.

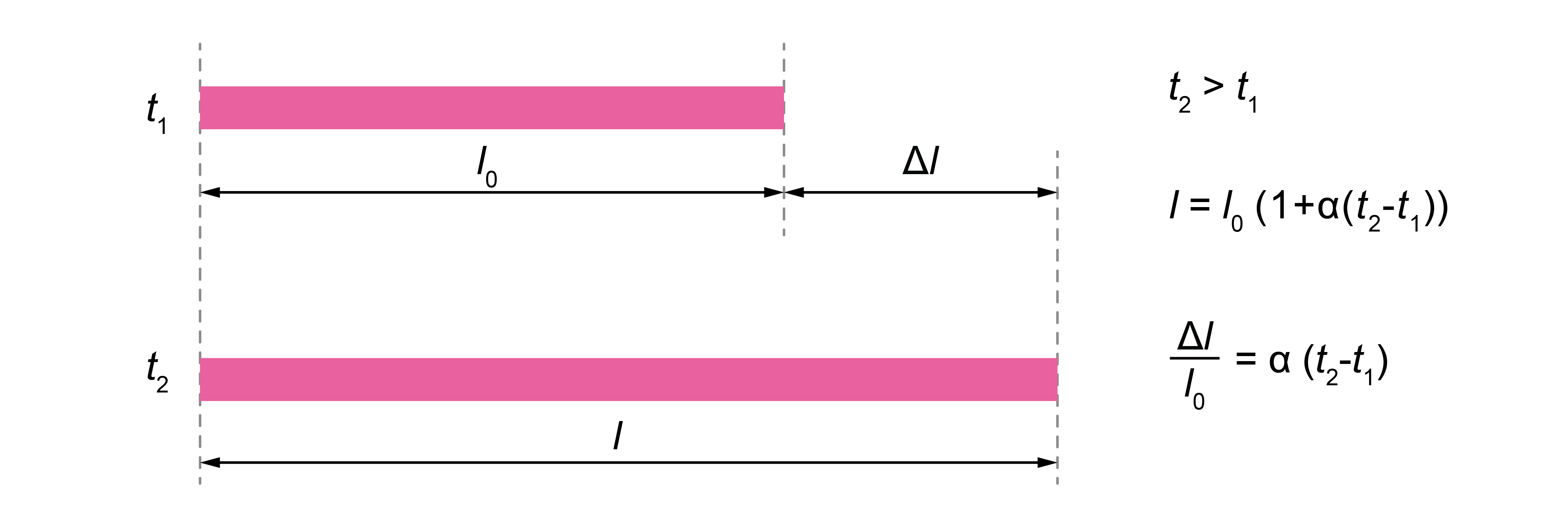
Ja temperatūrā t₁ stieņa garums ir \(l_0\), tad, temperatūrai pieaugot līdz \(t_2\), stienis pagarinās par \(\Delta{l}\)(2. att.) un 
\(\Delta{l} \thicksim (t_2-t_1)\)

Ķermeņa pagarinājums, protams, ir atkarīgs no ķermeņa sākotnēja garuma: \(\Delta{l} \thicksim l_0\).
Tātad pagarinājumu varam izteikt:
\(\Delta{l}=\alpha l_0 (t_2-t_1)\),
kur proporcionalitātes koeficients α ir lineārās izplešanās termiskais koeficients: \(\alpha=\frac{\Delta{l}}{l_0(t_2-t_1)}\)

Būtībā šis koeficients parāda to , par cik metriem palielināsies 1 m garš stienis, ja tā temperatūra pieaugs par 1 Celsija grādu vai Kelvinu.

Fizikālo lielumu ε, ko iegūst, pagarinājumu Δl izdalot ar sākotnējo garumu l0 un izsakot procentos, sauc par relatīvo pagarinājumu. 
\(\varepsilon=(\Delta{l}:l_0)\cdot{100}\)%

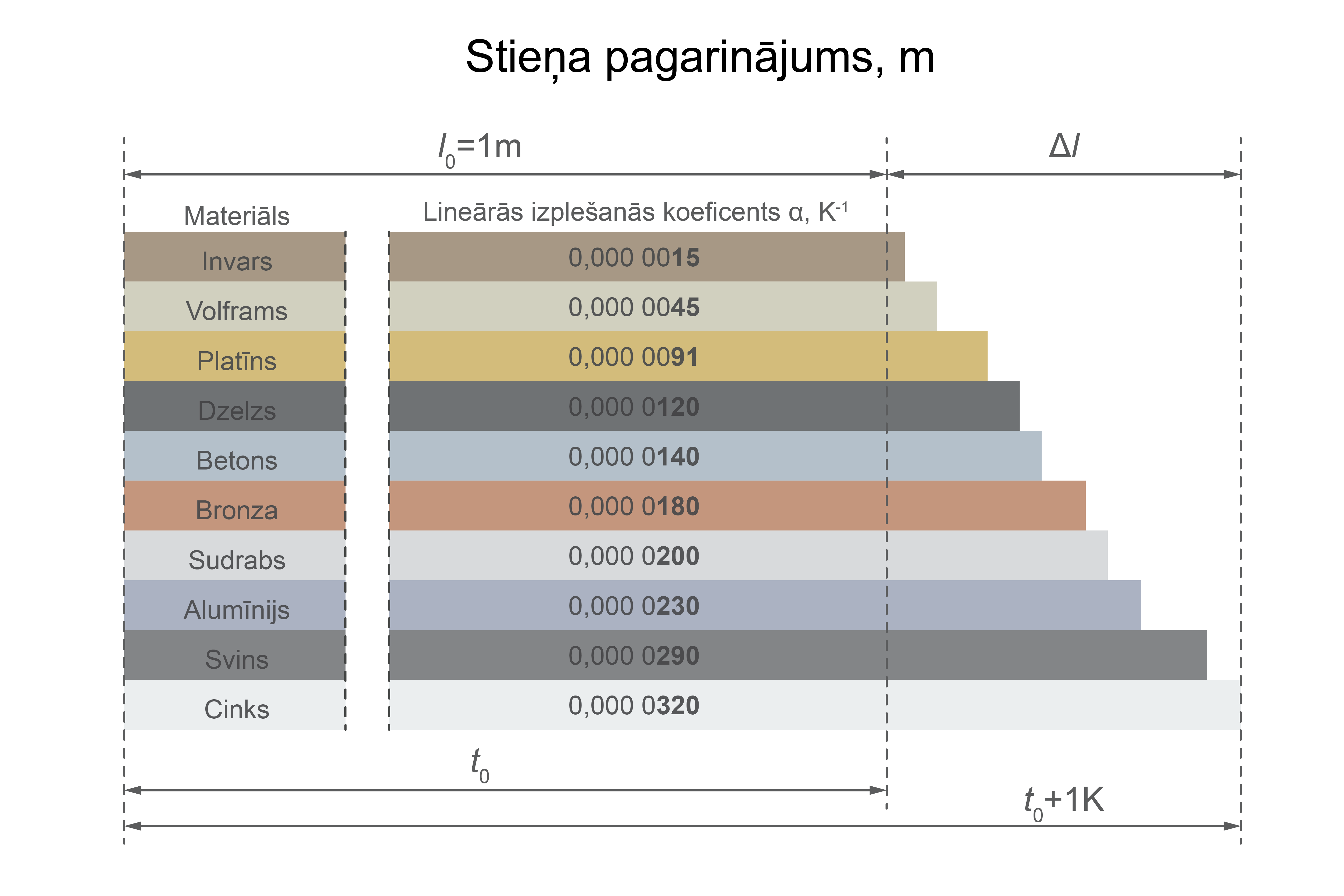
Lineārās izplešanās termiskais koeficients \(\alpha\) dažādām vielām ir atšķirīgs (3. attēls). 

Savā ziņā aplūkotā termiskā izplešanās ir "lineāra" divās nozīmēs – garuma izmaiņa ir tieši proporcionāla temperatūras izmaiņai un runa ir tikai par vienu dimensiju.

Tā kā izplešanos ietekmē tikai temperatūras izmaiņa, nevis sākuma un beigu temperatūras absolūtās vērtības, un temperatūras izmaiņa Celsija grādos un Kelvinos ir vienāda, varam formulā izmantot kā Celsija grādus, tā Kelvinus.

Tādiem ķermeņiem kā stieņi vai vadi garums krietni pārsniedz pārējos izmērus, tādēļ var aplūkot termisko izplešanos tikai vienā virzienā. Patiesībā ķermeņu izmēri temperatūras ietekmē mainās visos virzienos, tādēļ tiek apskatīta arī ķermeņu virsmas laukuma un tilpuma izplešanās. 

Ja ķermeņa sākotnējais virsmas laukums ir \(S_0\), tad, palielinot temperatūru par \(\Delta{t}\), ķermeņa tilpums izplešas līdz \(S=S_0(1+\beta\Delta{t})\), kur β ir virsmas izplešanās termiskais koeficients. Var pierādīt, ka, ja ķermenis ir veidots no izotropa materiāla, kura īpašības visos virzienos ir vienādas, tad var uzskatīt, ka β ≈ 2α.

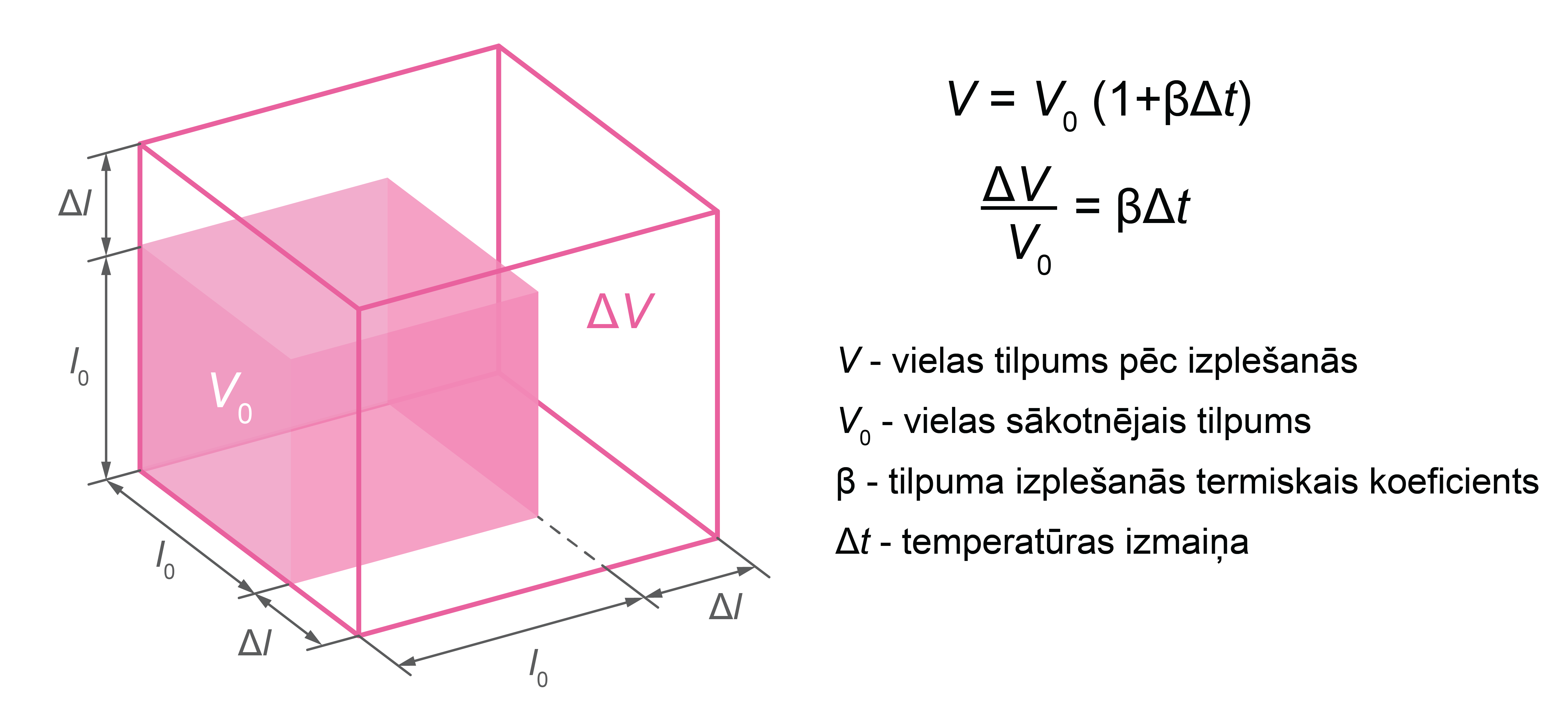
Savukārt, ja ķermeņa sākotnējais tilpums ir \(V_0\), tad, palielinot temperatūru par \(\Delta{t}\), ķermeņa tilpums izplešanās beigās ir \(V=V_0(1+\beta\Delta{t})\), kur β ir tilpuma izplešanās termiskais koeficients (4. attēls).  Ja ķermenis ir veidots no viena izotropa materiāla, tad var uzskatīt, ka β ≈ 3α.
Ja ķermenis ir veidots no dažādiem materiāliem, tad jārēķinās, ka tie temperatūras ietekmē izplešas atšķirīgi. 
Ķermeņu termisko izplešanos ir jāņem vērā ikdienā, arī veidojot dažādas konstrukcijas un ierīces. To tuvāk aplūkosim nodaļā "Cietu vielu termiskā izplešanās".

Cietu vielu termiskā izplešanās

Sasilstot cieti ķermeņi (vielas) izplešas - mainās kā tilpums, tā arī virsmas laukums un lineārie izmēri. Cieta ķermeņa izmēru izmaiņa ir tieši proporcionāla temperatūras izmaiņai, ja temperatūras maiņas intervāls nav liels.
Nodaļā "Termiskās izplešanās koeficients" aplūkots termiskās izplešanās mehānisms un definēts termiskās izplešanās koeficients – fizikāls lielums, kas ļauj ķermeņa izmēru maiņu raksturot skaitliski.
\(l=l_0(1+\alpha\Delta{t})\);
\(S=S_0(1+\beta\Delta{t})\), (izotropām vielām  β ≈ 2α);
\(V=V_0(1+\beta\Delta{t})\), (izotropām vielām  β ≈ 3α).

Pieņemot, ka viela ir izotropa – tās īpašības visos virzienos ir vienādas - tabulās parasti norāda tikai lineārās izplešanās termisko koeficientu α, kas dažādām vielām ir atšķirīgs. Tātad, ja ķermenis ir veidots no dažādiem materiāliem, tad jārēķinās, ka tie temperatūras ietekmē izplešas atšķirīgi. 

Termiskās izplešanās ietekmeuz būvēm un konstrukcijām

Tādēļ ķermeņu termisko izplešanos jāņem vērā celtniecībā un tehnikā, veidojot dažādas ierīces konstrukcijas, ja tās tiek pakļautas temperatūras maiņai.  Mehāniskie spriegumi, kas rodas termiskās izplešanās rezultātā, tuvāk aplūkoti nodaļā "Mehāniskais spriegums un termiskā izplešanās".

Elektrības vadus gaisa līnijās siltā laikā nedrīkst stingri nostiept starp stabiem, jo ziemā, atdziestot un saraujoties, tie var pārtrūkt. Termisko izplešanos jāņem vērā, ceļot tiltus un augstceltnes, ir jāparedz kompensācijas mehānismi, kas neļautu konstrukcijām deformēties (1. attēls). 

1.att. Kompensācijas mehānisms tiltos

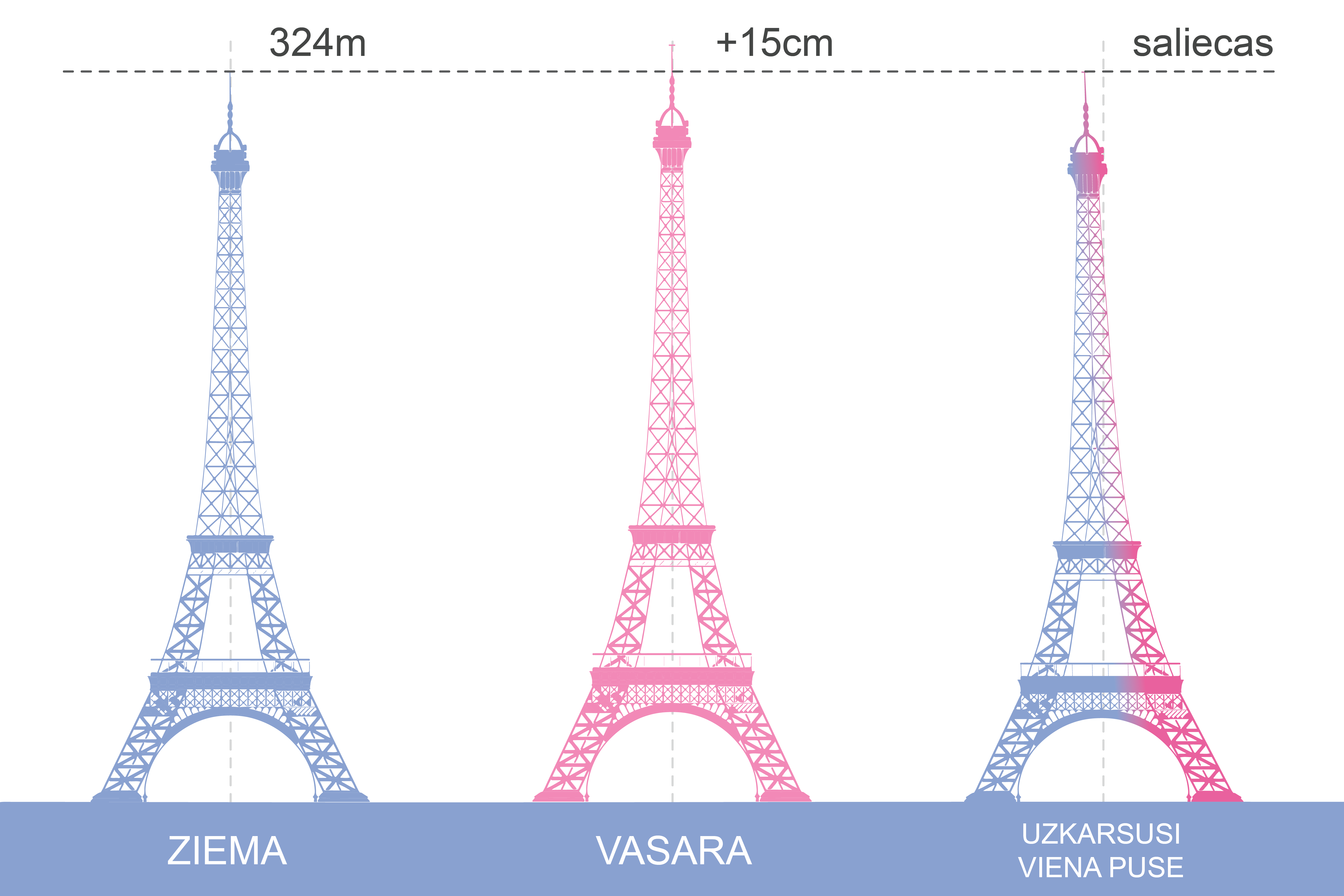
Tā, piemēram, 368 metru augstais Zaķusalas TV tornis, kas ir pilnībā būvēts no tērauda, karstuma ietekmē izplešas. Aprēķini liecina, ka karstā vasarā tornis kļūst par apmēram 4 centimetriem garāks nekā ziemā.  
Saulainā laikā, kad vairāk sasilst torņu viena puse, tie arī pavisam nedaudz saliecas (2. attēlā). 

Termisko izplešanos jāņem vērā un jāparedz iespēja to kompensēt arī būvējot sliežu ceļus (3. attēls a) un ierīkojot gāzes vai ūdens cauruļvadus (3. attēls b). 

Cieši savā starpā savienot var tikai tādus materiālus, kam ir vienādi izplešanās termiskie koeficienti, jo tad, mainoties temperatūrai, vienādi mainās arī to izmēri. Šāds celtniecības materiāls ir dzelzsbetons, kura komponentēm – dzelzij un betonam – ir vienādi lineārās izplešanās termiskie koeficienti.

Arī pašā ķermenī var rasties mehāniski spriegumi, ja tā daļas nevienādi sasilst un izplešas. Nereti saplīst, piemēram, stikla trauki, ja tajos strauji ielej karstu ūdeni. Tas tādēļ, ka trauka iekšējie slāņi sasilstot strauji izplešas, bet ārējie, kas nav paguvuši sasilt materiāla zemās siltumvadītspējas dēļ, izpletušies nav. Strauju temperatūras izmaiņu dēļ var plaisāt arī, piemēram, zobu emalja.

Bimetāla plāksnītes

Termisko izplešanos izmanto veidojot dažādas ierīces – piemēram, gludekļu un ledusskapju termoregulatorus un elektriskos drošinātājus. Šādās ierīcēs izmanto bimetāla plāksnītes,  ko izgatavo no diviem dažādiem metāliem, kuriem ir atšķirīgi lineārās izplešanās termiskie koeficienti un kas cieši savienotas savā starpā. Ja šādu plāksnīti silda vai dzesē, tad viena tās daļa pagarinās vairāk nekā otra, un plāksnīte izliecas (4. attēls a).

Sasilstot plāksnīte saliecas uz tā materiāla pusi, kuram ir mazāks izplešanās termiskais koeficients, atdziestot – otrādi.

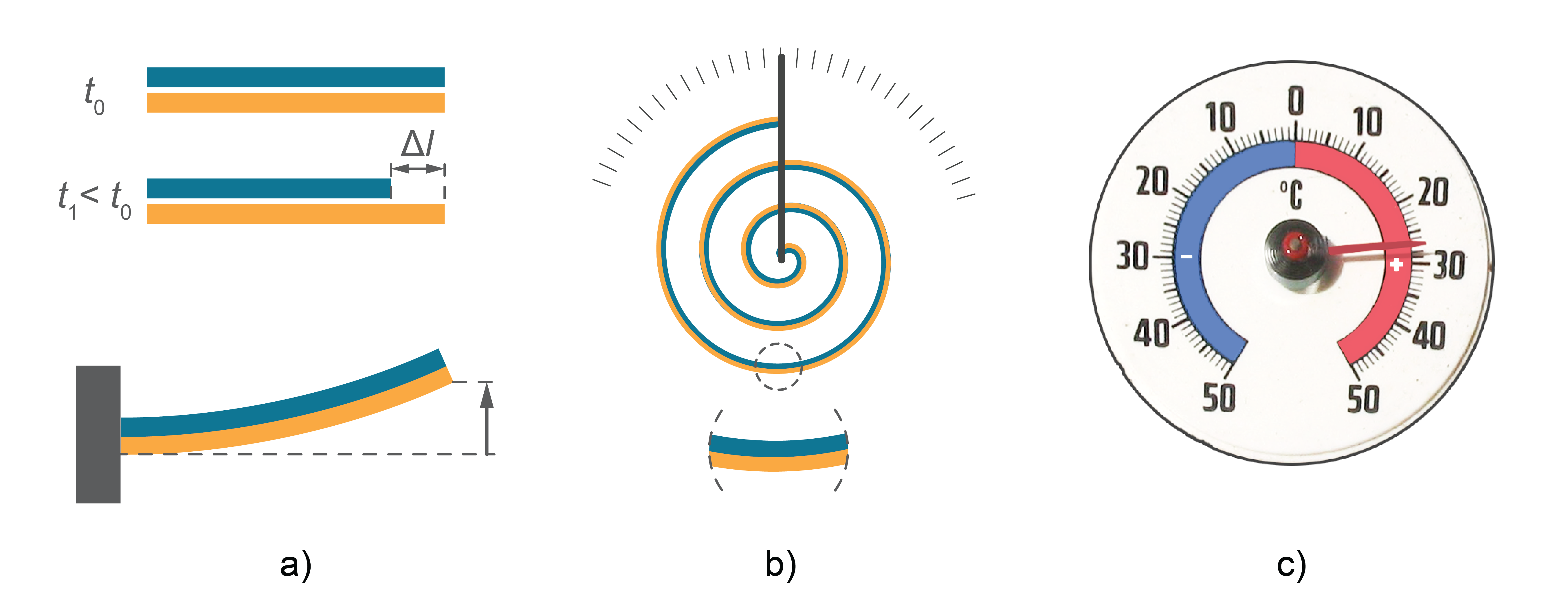
Bimetāla plāksnīte ir arī  labi pazīstama "āra" termometra darbības pamatā (4. attēls b un c).

Termiskās izplešanās kompensēšana

Materiālus ar atšķirīgiem izplešanās koeficientiem izmanto arī, lai termisko izplešanos kompensētu, ja tā ir nevēlama. Tā tas ir, piemēram, svārsta pulksteņiem, jo svārstību frekvence ir atkarīga no svārsta garuma. 5. attēlā redzams šādas kompensācijas piemērs.

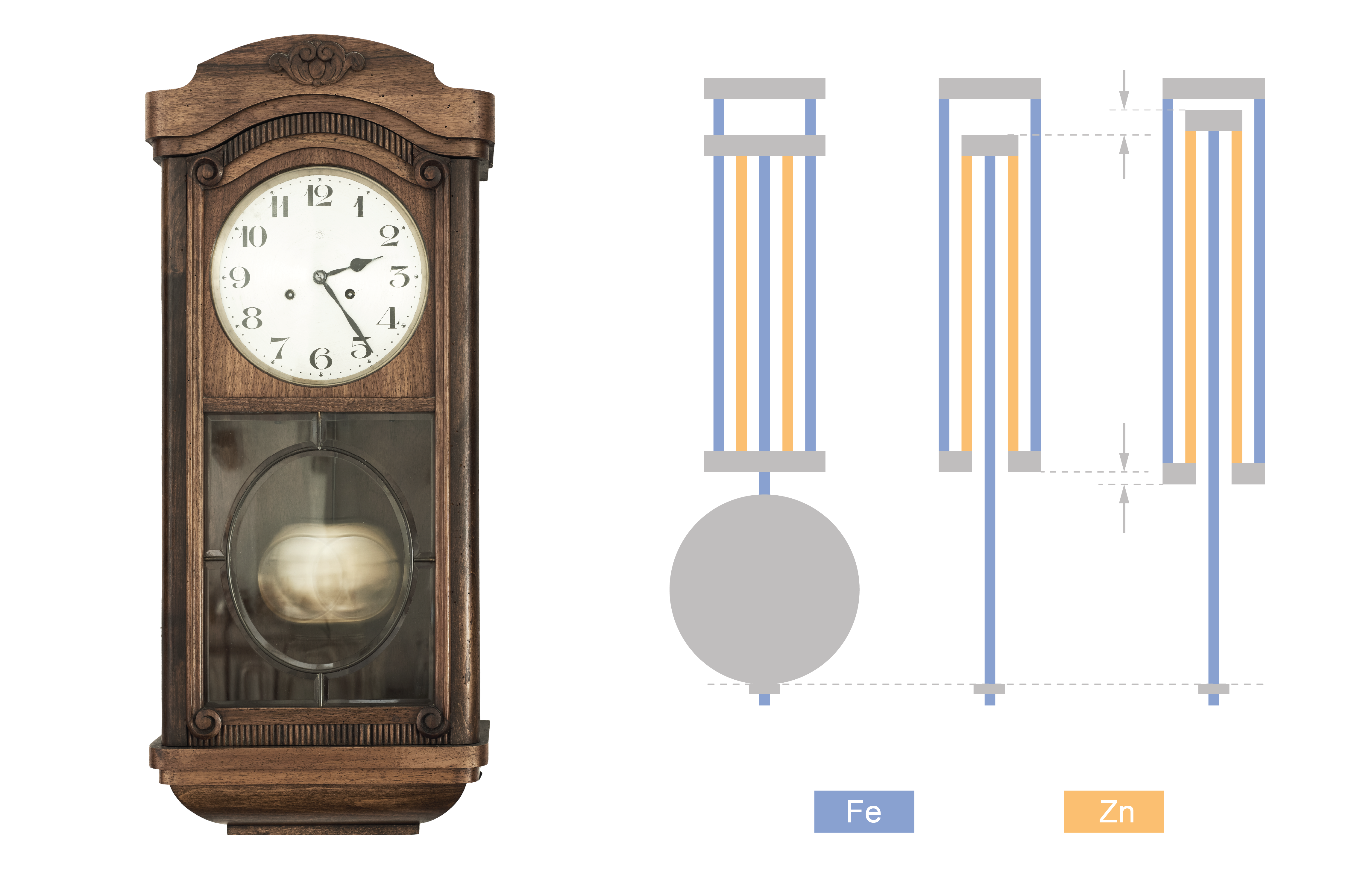
Pastāv arī materiāli, kuru termiskā izplešanās ir ļoti maza, piemēram, dzelzs-niķeļa sakausējums invars (FeNi36).

Tāpat ir izveidoti arī materiāli, kas sasilstot saraujas – tiem ir negatīvs lineārās izplešanās termiskais koeficients. Viens no šādas "termiskās saraušanās" mehānismiem ir, piemēram, materiāla kristāliskās struktūras izmaiņa sasilstot (vienkāršots piemērs 6. attēlā).

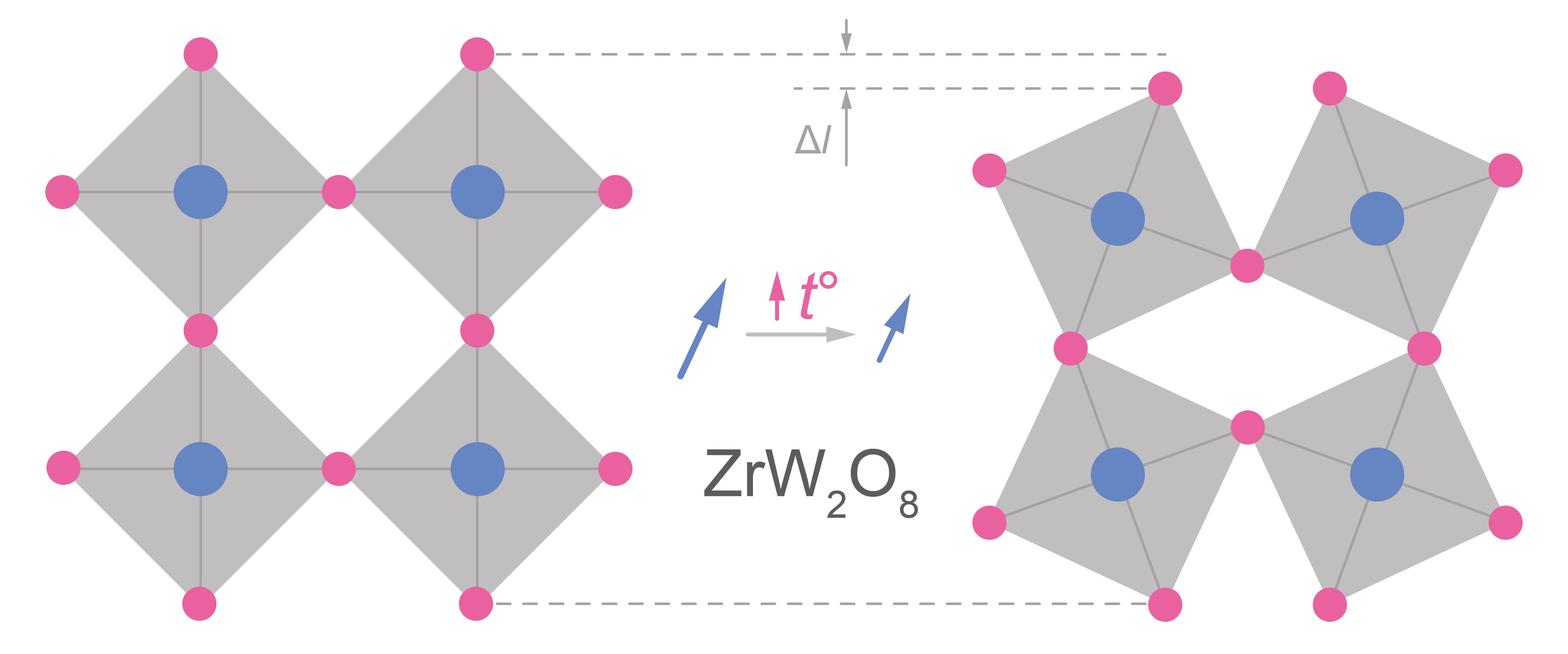
Šādus materiālus sauc par NTE ("negative thermal expansion") materiāliem. Tiem pieder arī dažādi kompozītmateriāli. 
 

Šķidrumu termiskā izplešanās

Šķidrumu tilpuma maiņa sasilstot

Sasilstot vielas izplešas. Cietiem ķermeņiem aplūko tilpuma, virsmas laukuma un lineāro izmēru maiņu, bet šķidrumiem parasti runa ir tikai par tilpuma izmaiņu. Vairumā gadījumu tilpuma izmaiņa ir tieši proporcionāla temperatūras izmaiņai, ja temperatūras maiņas intervāls nav liels. Tomēr šķidrumi sasilstot var izplesties nevienmērīgi – jo augstāka temperatūra, jo tie izplešas straujāk. Izņēmums ir dzīvsudrabs, ko izmanto termometros.

Saites starp daļiņām šķidrumā ir vājākas nekā starp tādām pašām daļiņām cietā vielā. Tādēļ sagaidāms, ka, pie vienādas temperatūras izmaiņas, šķidrumi izplešas lielākā mērā nekā cietās vielas. To patiešām apstiprina eksperimenti.

Nodaļā "Termiskās izplešanās koeficients" aplūkots termiskās izplešanās mehānisms un definēts tilpuma termiskās izplešanās koeficients β – fizikāls lielums, kas ļauj tilpuma maiņu raksturot skaitliski.
\(V=V_0(1+\beta\Delta{t})\)

Šķidrumu termiskās izplešanās koeficients β ir daudz lielāki nekā cietvielu tilpuma izplešanās koeficienti, tie var sasniegt vērtību β =  10^-3 K^-1. Šie koeficienti atrodams tabulās.

Tā kā šķidrumi ieņem trauka formu, runa ir tikai par šķidruma tilpuma, nevis izmēru izmaiņām. Šķidrumu nevar uzsildīt, nesildot trauku, kurā tas atrodas. Tāpēc mēs nevaram novērot patieso šķidruma izplešanos traukā, jo paša trauka izplešanās neļauj novērtēt šķidruma tilpuma pieaugumu. Tomēr stikla un citu cietu vielu tilpuma izplešanās koeficients parasti ir daudz mazāks nekā šķidruma tilpuma izplešanās koeficients, un, ar ne pārāk precīziem mērījumiem, trauka tilpuma palielināšanos var neņemt vērā.

Saprotams, ka šķidrumi ir izotropi – to īpašības visos virzienos ir vienādas.

Ūdens termiskā izplešanās
 

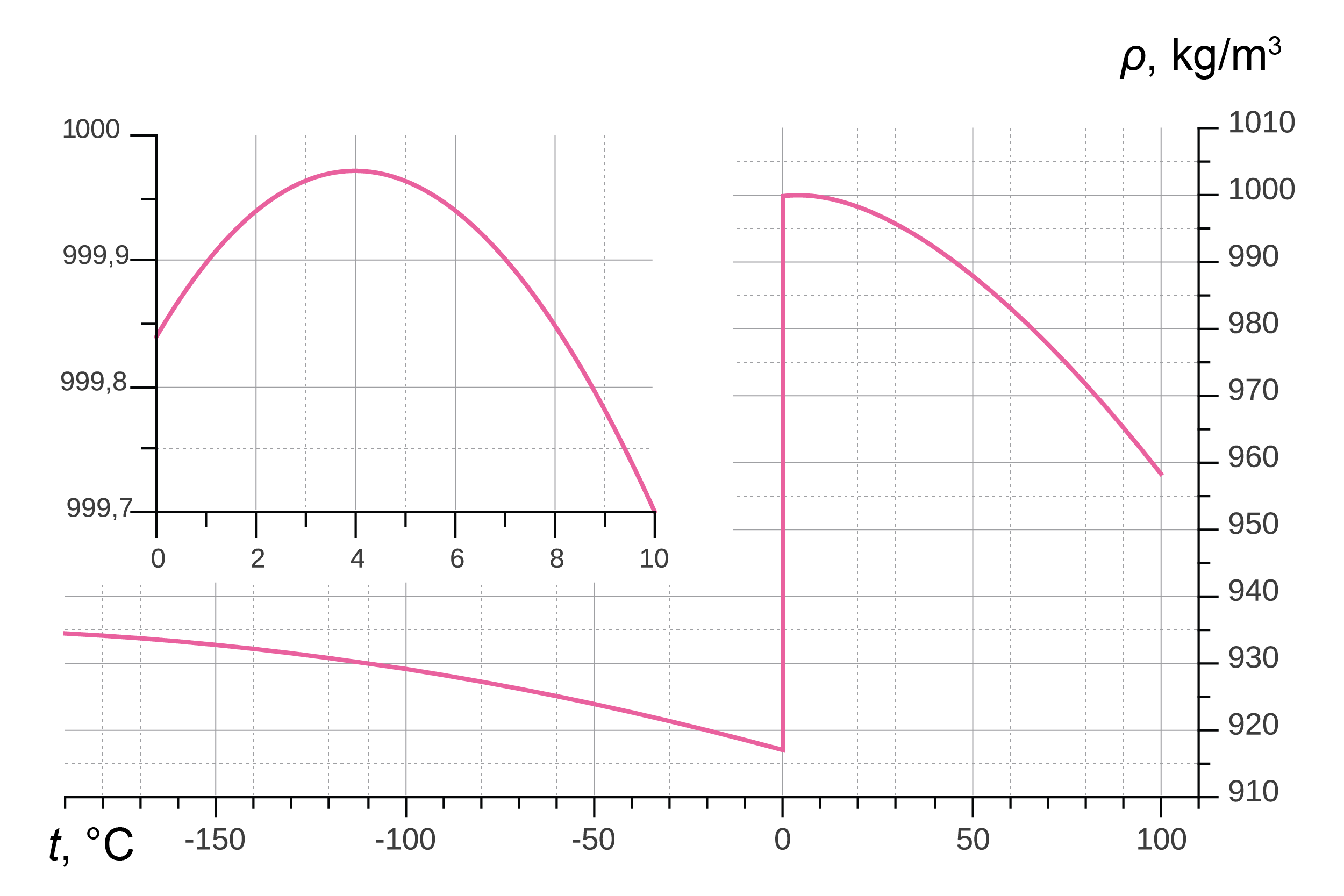
Uz Zemes visizplatītākajam šķidrumam – ūdenim – piemīt termiskās izplešanās anomālija, kas to atšķir no citiem šķidrumiem. Ūdenim, sasilstot no 0 °C līdz +4 °C, tilpums nepalielinās, bet gan samazinās. Tikai sākot no +4 °C sildot ūdens tilpums sāk palielināties. Tātad + 4 °C temperatūrā ūdens tilpums ir minimāls, bet blīvums ir maksimālais (1. attēls). Tas attiecas uz ķīmiski tīru ūdeni. Lielākais jūras ūdens blīvums ir pie aptuveni +3 °C.

Šī ūdens īpašība lielā mērā ietekmē siltuma pārnesi ūdenstilpēs. Kad, iestājoties aukstam gadalaikam, ūdens atdziest, augšējo slāņu blīvums vispirms palielinās, un tie nogrimst. Bet pēc tam, kad gaiss sasniedz +4 °C temperatūru, turpmāka dzesēšana jau samazina blīvumu, un aukstie ūdens slāņi paliek uz virsmas. Tā rezultātā dziļās ūdenskrātuvēs pat pie ļoti zemas gaisa temperatūras ūdens dziļāko slāņu temperatūra ir aptuveni +4 °C (2. attēls). Tāda pat temperatūra dziļākajos slāņos ir arī vasarā. Šai parādībai ir milzu nozīme dzīvības pastāvēšanā uz Zemes.

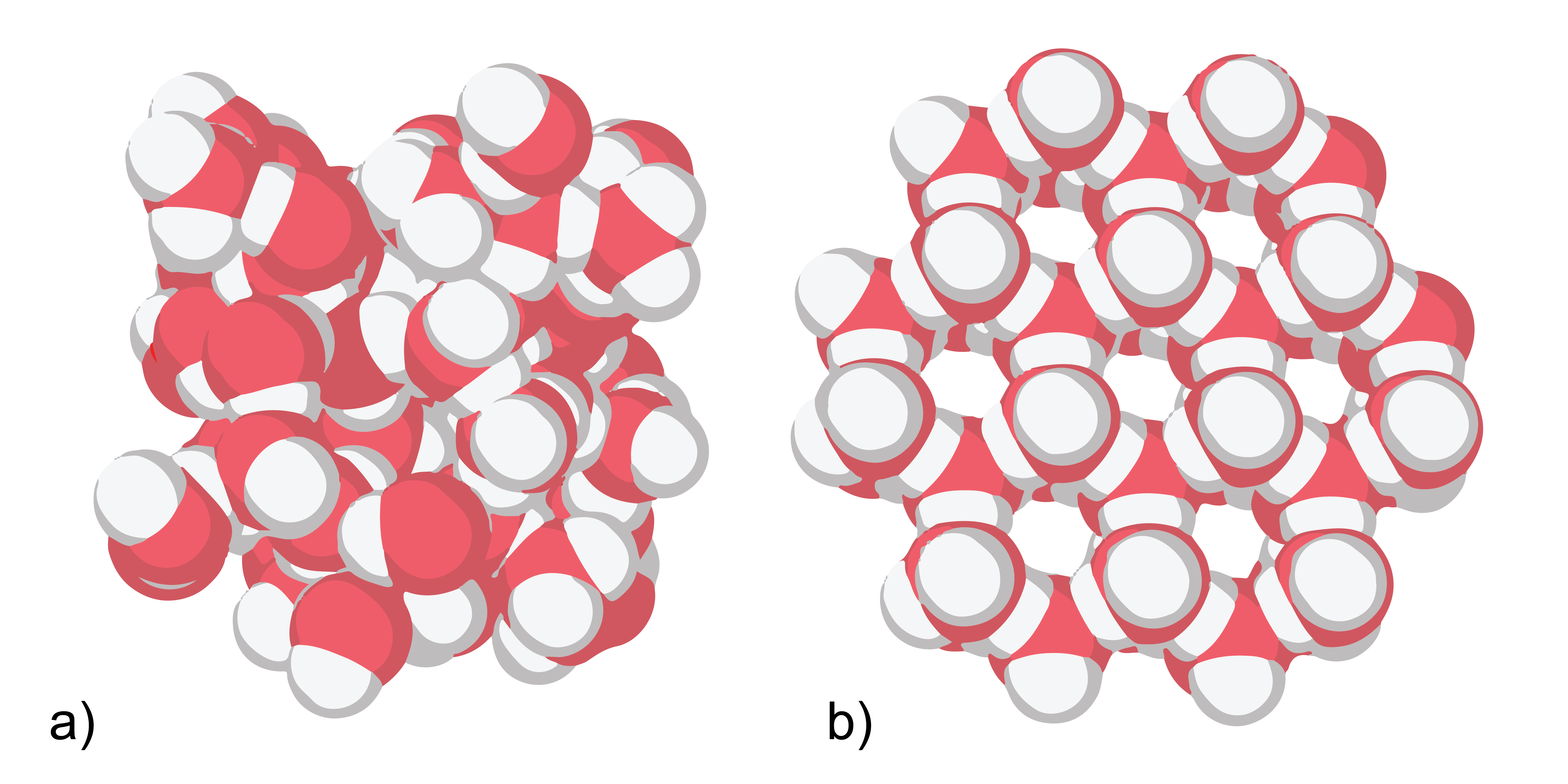
Šo ūdens anomāliju var izskaidrot ar ūdens molekulārās uzbūves un starpmolekulu saišu īpatnībām – šķidrā ūdenī molekulas var veidot blīvāku pakojumu (3. attēls a)un nokļūt vidēji tuvāk viena otrai, nekā kristāliskā stāvoklī (3. attēls b).

Fakts, ka šķidrumi izplešas desmitiem reižu vairāk, kā cietas vielas, izmantots arī veidojot Galileja termometru (4. attēls a, b). 

Galileja termometrā stikla cilindrā ielietā šķidrumā, parasti ūdenī, atrodas vairāki cieta materiāla pludiņi, kuru vidējais blīvums tuvs šķidruma blīvumam. Šķidrumam sasilstot, tā blīvums samazinās un pludiņš, kura blīvums kļuvis lielāks par šķidruma blīvumu, nogrimst. Sasilstot vairāk, nogrimst jau nākamais. No pludiņiem piestiprinātajiem žetoniņiem var nolasīt atbilstošo temperatūru (pieņemot, ka tā vienāda ar apakšējā nenogrimušā un augšējā nogrimušā  pludiņa rādījuma vidējo vērtību).

Mehāniskais spriegums un termiskā izplešanās

Zināms, ka cieti ķermeņi sasilstot izplešas (skatīt nodaļu "Termiskā izplešanās"). Ja kādi citi ķermeņi sakarsētajam ķermenim neļauj mainīt izmērus, tajos rodas lieli elastības spēki un mehāniskie spriegumi (aplūkoti nodaļā "Mehāniskais spriegums. Elastības modulis.").

Šie elastības spēki ir proporcionāli temperatūras izmaiņai.
Aplūkosim starp divām sienām nekustīgi nostiprinātu metāla stieni, kura garums ir \(l_0\) un šķērsgriezuma laukums \(S\) (1. attēls). Ja šis stienis sasilstot varētu izplesties, tad tā absolūtais pagarinājums varētu būt \(\Delta{l}=\alpha l_0(t_2-t_1)\),
kur \(\alpha\) — metāla lineārās izplešanās termiskais koeficients, \(\Delta{t}\) — temperatūras izmaiņa.

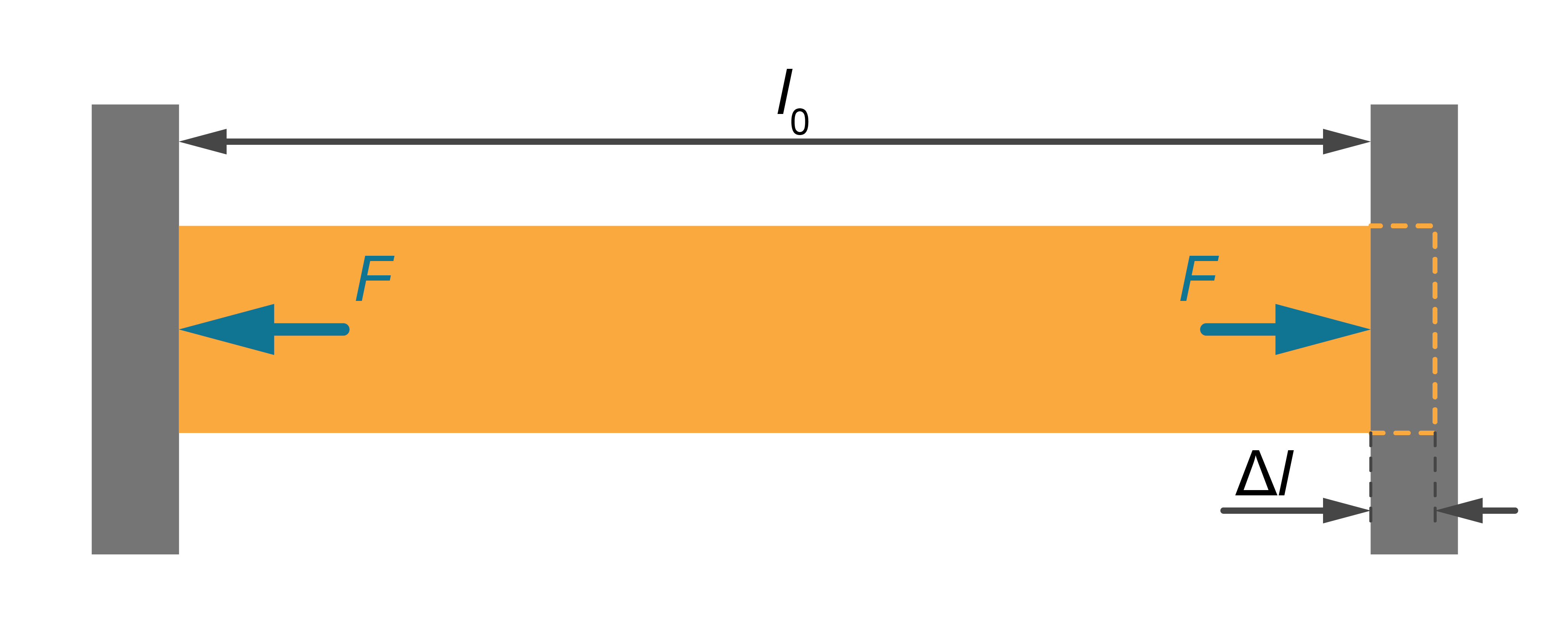
Tomēr, tā kā stienis ir nostiprināts starp divām sienām, tad pagarināties tas nevar. 
Tas nozīmē, ka sienas no abiem galiem spiež uz stieni ar spēku \(F\), kāds nepieciešams, lai to saīsinātu par šo \(\Delta{l}\). 

Šā spēka, kas darbojas uz stieni, skaitlisko vērtību var noteikt, zinot Huka likumu (skatīt nodaļu ''Mehāniskais spriegums. Elastības modulis.'').

Saskaņā ar Huka likumu: \(\sigma=E\cdot\varepsilon\)

Stieņa relatīvais pagarinājums ir \(\varepsilon=\frac{\Delta{l}}{l_0}\), bet mehāniskais spriegums, kas rodas stienī to saspiežot ir \(\sigma=\frac{F_\mathrm{el}}{S}\)  

Tātad \(F_\mathrm{el}=\alpha{ES}(\frac{\Delta{l}}{l_0})\) kur \(E \) — konkrētā materiāla Janga modulis. 

Apvienojot izteiksmes, varam iegūt stienim izplešoties radītā elastības spēka izteiksmi:
\(F_\mathrm{el}=\alpha{ES}\Delta{t}\).

Saskaņā ar trešo Ņūtona likumu, tērauda sija ar skaitliski tik pat lielu, bet pretēji vērstu spēku darbojas uz sienu. Tātad ķermeņu termisko izplešanos nedrīkst ignorēt, ja ierīces vai būvkonstrukcijas tiek pakļautas temperatūras maiņai.

Gāzu termiskā izplešanās

Sasilstot izplešas gan cieti ķermeņi, gan šķidrumi gan arī gāzes (skatīt nodaļu "Termiskā izplešanās"). 

Gāzu termiskā izplešanās ir noteikta gāzes daudzuma tilpuma palielināšanās temperatūras paaugstināšanās rezultātā. Ja gāzes spiediens nemainās, sasilstot tās tilpums mainās tūkstošiem reižu vairāk, kā šķidrumu tilpums – tas tādēļ, ka gāzes molekulas savā starpā vāji saistītas. Visas gāzes nemainīgā spiedienā sasilstot izplešas vienādi un vienmērīgi.

Gāze vienmēr aizņem visu tai atvēlēto tilpumu, tādēļ par termisko izplešanos varam runāt tikai aptuveni nemainīga spiediena gadījumā, ja tilpums var brīvi palielināties. Tomēr mainoties temperatūrai parasti mainās (arī) gāzes spiediens.

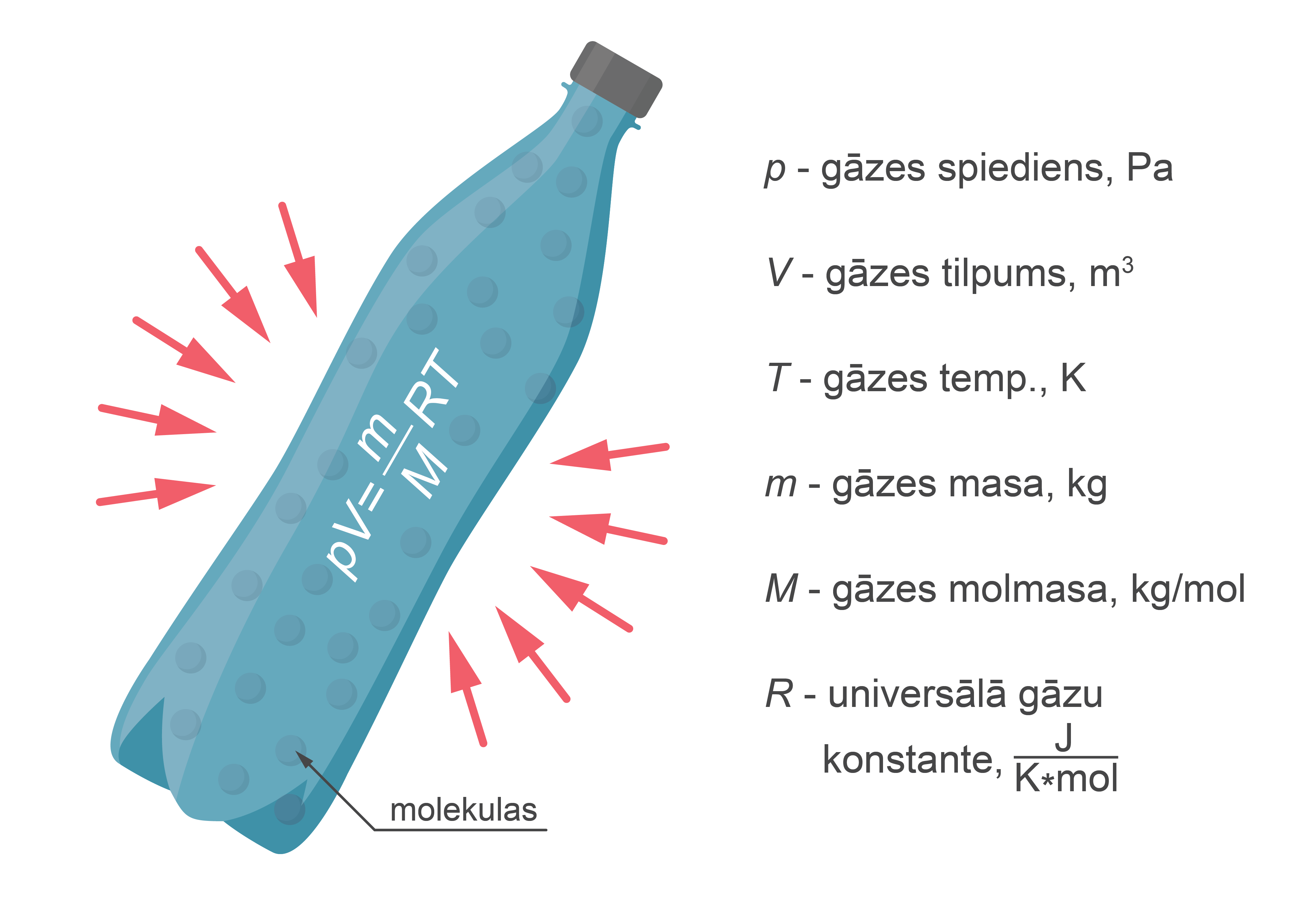
Nodaļā "Ideālās gāzes stāvokļa vienādojums" var iepazīties ar Mendeļejeva-Klapeirona vienādojumu. Šis vienādojums apraksta sakarību starp gāzes parametriem (makroskopiskajiem, izmērāmajiem raksturlielumiem \(p\), \(V\) un \(T\): 
 \(pV=nRT\), kur \(n=\frac{m}{M}\) – gāzes daudzums molos (1. attēls)

Izobārisks process

Procesu, kurā nemainās gāzes spiediens, sauc par izobārisku. Šādā procesā tilpums ir tieši proporcionāls temperatūrai, kas redzams arī procesa grafiskajā attēlojumā (2. attēls). Tātad – nemainīgā spiedienā ideāla gāze temperatūrai pieaugot izplešas lineāri.
 

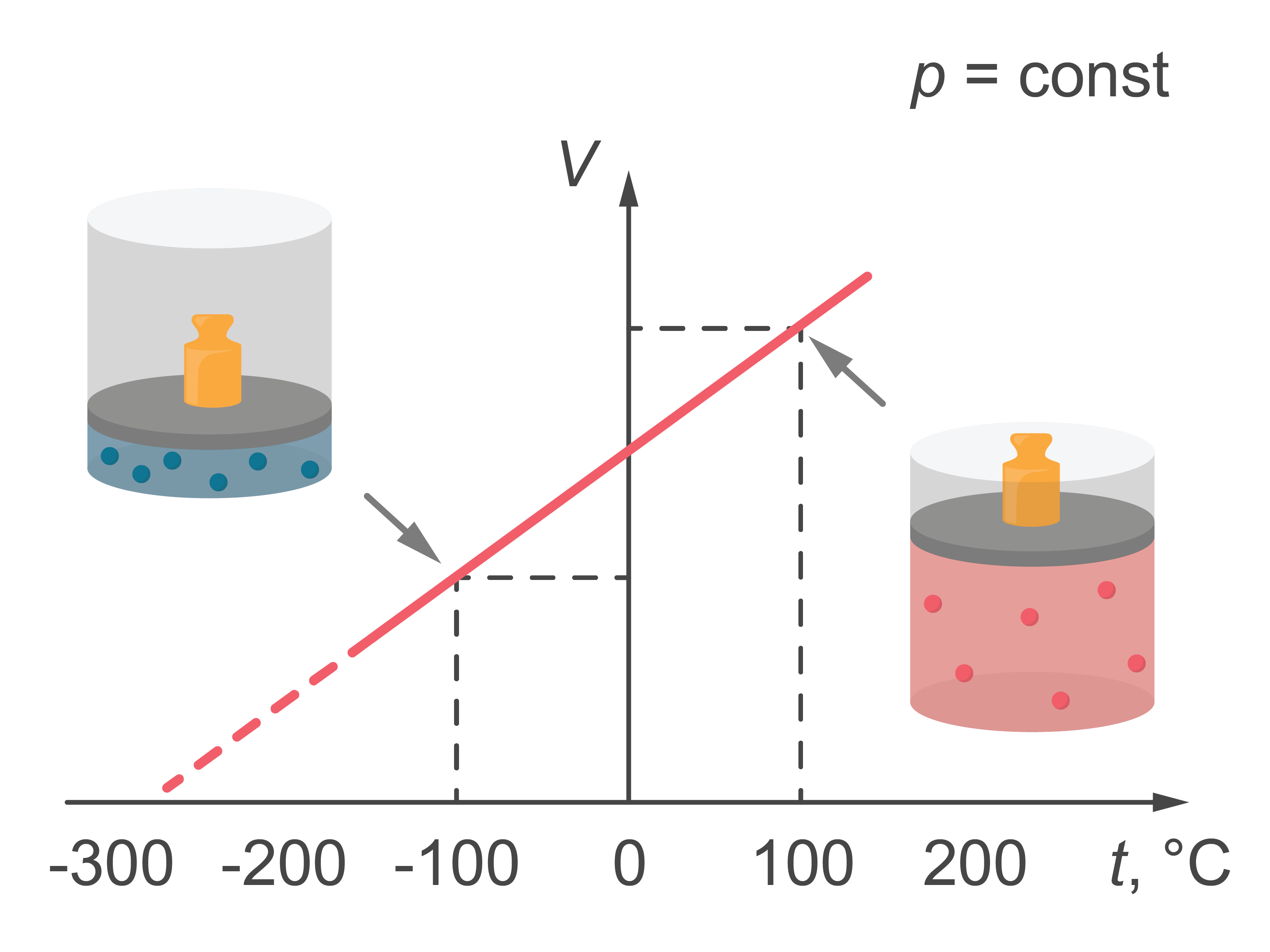
Tā kā \(pV=nRT\), tad izobāriskā procesā \(p\Delta{V}=nR\Delta{T}\) un \(\frac{\Delta{V}}{\Delta{T}}\) = \(\frac{nR}{p}\)

Savukārt (skatīt nodaļu "Termiskā izplešanās"), tilpuma izplešanās termisko koeficientu β definē kā fizikālu lielumu, kas parāda, par cik kubikmetriem palielināsies 1 m3 vielas tilpums, ja tā temperatūra pieaugs par 1 Celsija grādu vai Kelvinu:
\(\beta=\frac{\Delta{V}}{V_0\Delta{T}}\)

Apvienojot izteiksmes iegūstam:  \(\beta=\frac{nR}{pV}=\frac{1}{T}\).

Tātad, tilpuma izplešanās termiskais koeficients visām ideālām gāzēm ir vienāds un 0°C temperatūrā 
\(\beta=\frac{1}{T}=\) \(\frac{1}{273,15} = 0,00366 K^{-1}\)

Tilpuma izplešanās koeficientam ir aptuveni vienāda vērtība visām gāzēm. Labā tuvinājumā to var uzskatīt par vienādu ar ideālās gāzes tilpuma izplešanās koeficientu. 

Reālām gāzēm tas nedaudz atšķiras (3. attēlā). 

Demonstrējumi par gāzu izplešanos

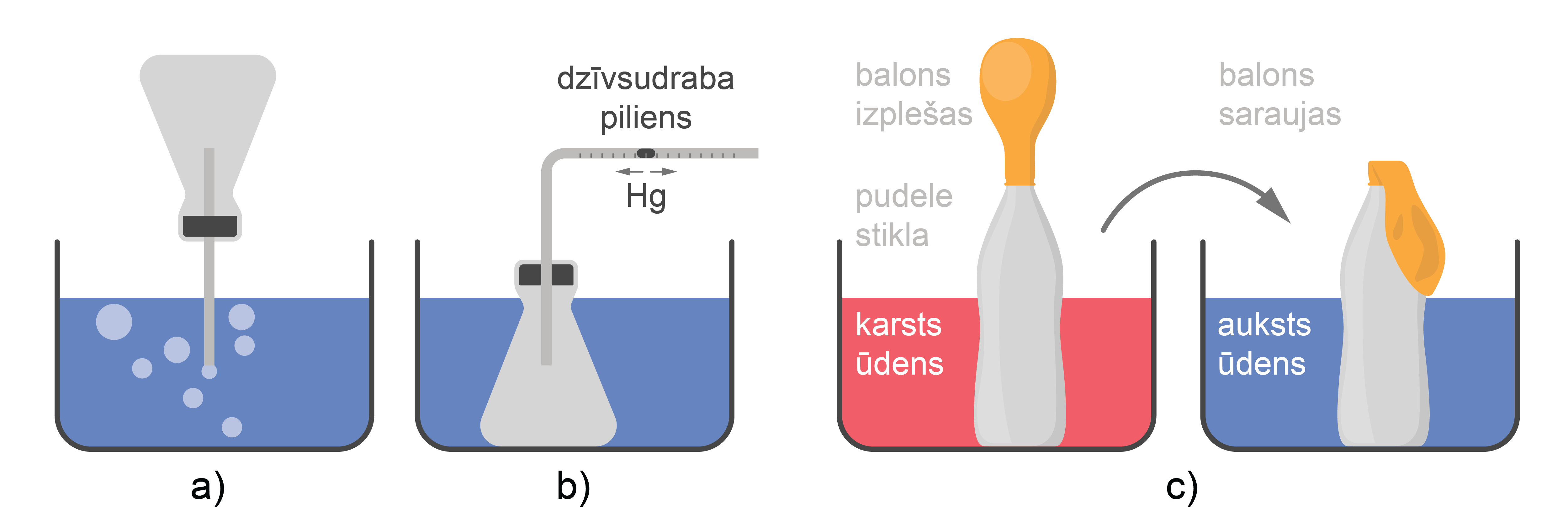
Gāzu izplešanos var novērot dažādos demonstrējumos (sasilstot nemainīgā tilpumā gāzes spiediens aug un daļa gāzes izplūst no kolbas, līdz spiediens kolbā atkal ir vienāds ar atmosfēras spiedienu (4. attēs a) un, gāzei sasilstot un izplešoties, stikla stobriņā pārvietojas dzīvsudraba pilieniņš, līdz spiediens kolbā atkal ir vienāds ar atmosfēras spiedienu (4. attēs b). Šādu ierīci var izmantot kā termometru, ja pieņem, ka atmosfēras spiediens tiešām nemainās. 

Ieskaties ''Fizmix'' eksperimentu sadaļā un izpēti gāzes termometra darbību.

Gāzu izplešanās uzskatāmi redzama arī demonstrējumā ar balonu, kas izplešas karstā ūdenī (4. attēls c). Šajā situācijā temperatūra, tilpums un spiediens visi ir mainīgi. Tādējādi neviens no gāzu izoparametrisko procesu likumiem nav spēkā. 
 

Vēl gaisa termisko izplešanos varētu novērot, ja karstā dienā piepūstu balonu atstātu ārā. Saulei lecot un dienai kļūstot karstākai, jūs pamanītu, ka balons izplešas, jo palielinās spiediens balona iekšpusē un līdz ar to palielinās arī tilpums (\(pV\thicksim{T}\)). Līdzīgi var novērot, kā aukstā ziemas dienā saplok gaisa balons, ja to piepūš siltā telpā un tad iznes ārā.