Kustības laikā ir svarīgi, kā pārvietojas visi ķermeņa punkti, tomēr, ja visi ķermeņa punkti kustas vienādi (nenotiek deformācijas un struktūras maiņas), tad to var uzskatīt par punktveida ķermeni, un tādējādi raksturot ķermeņa kustību ar matemātiskiem vienādojumiem ir vienkāršāk. Ja kustība tiek pētīta apstākļos, kad ķermeņa izmērus var neievērot, tad ķermeni modelē kā punktu, un to sauc par masas punktu. Lai novērtētu to, vai kustošu ķermeni var uzskatīt par masas punktu vai nē, ir jāsaprot, ko mēs par šo kustību vēlamies uzzināt un pret kādiem ķermeņiem kustība notiek. Piemēram, kad GPS tiek attēlota kāda objekta kustība, tā izmēriem nav nozīmes, tādēļ šajā gadījuma objekts tiek uzskatīts par masas punktu (1. att.) . Lasi par atskaites sistēmu DZM materiālā!

1.att. GPS uzrāda objekta kā masas punkta kustību
Masas punkts ir novietots ķermeņa masas centrā. Par masas centru sauc to ķermeņa punktu, kurā to atbalstot (ja vien tas ir iespējams) ķermenis atradīsies līdzsvarā. Piemēram, cilvēka masas centrs atrodas tā nabas rajonā (2. att. a). Masas punktā ir it kā koncentrēta visa ķermeņa masa. Var gadīties, ka masas centrs atrodas ārpus paša ķermeņa, piemēram, barankas gadījumā (2. att. b).

2.att. Ķermeņu masas centri
Lai mēs varētu aprakstīt kustību, ir nepieciešams ķermenis, attiecībā pret kuru mēs šo kustību aprakstām. To sauc par atskaites ķermeni. Piemēram, ja lietus lāse slīd pa loga rūti, tad par atskaites ķermeni var uzskatīt pašu loga rūti (3. att.), pret kuru var novērot lāses kustību, tomēr var arī par atskaites ķermeni izvēlēties kādu tālāku objektu, piemēram, ārpusē esošu koku vai automašīnu.

3.att. Lietus lāses kustība pa loga rūti
GPS esošās kartes ir saistītas ir atskaites ķermeni – Zemi. Līdz ar to, ja tiek novērota objekta kustība kartē, tad tā ir kustība pret Zemi. Veicot, piemēram, ar automašīnu kādu maršrutu, GPS iespējams redzēt, pa kādu līniju ir notikusi kustība (4. att.). Šo līniju sauc par kustības trajektoriju, bet tās garumu par veikto ceļu. Braukšanas trajektorija un veiktais ceļš ir viens no GPS pieejamajiem kustības parametriem.
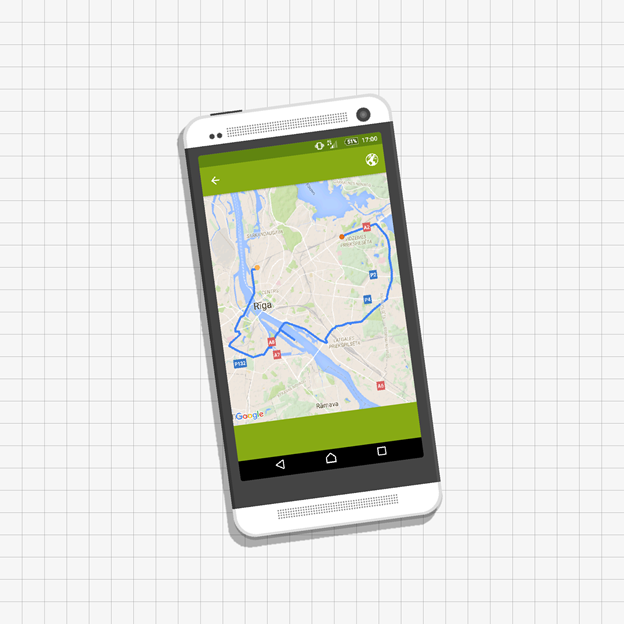
4.att. Automašīnas kustība kartē
GPS kartei ir piesaistīta ģeogrāfiskā koordinātu sistēma, tādēļ, zinot savas atrašanās vietas koordinātas, ir viegli noteikt, kurā zemeslodes rajonā atrodies. Taču dažkārt ir svarīgi kustību aprakstīt ne tik globālā līmenī. Šim nolūkam var ieviest „vietējo” koordinātu sistēmu (5. att.). Koordinātu sistēmas ieviešanai ir jāizvēlas atskaites punkts un pret to jānovelk koordinātu asis, kurās var apskatīt objekta kustību (5. att.). Bez iepriekš apskatītā ceļa un trajektorijas, ja no kustības sākuma punkta novelk vektoru, kas sniedzas līdz kustības beigu punktam, iegūst pārvietojumu s. Pārvietojuma noteikšanai svarīgs ir tikai kustības sākuma un beigu punkts, nav svarīgi, pa kādiem „neceļiem” objekts ir kustējies pa vidu. Pārvietojums, kā jau iepriekš noskaidrots, ir vektoriāls lielums. Vektorus ir iespējams projicēt uz koordinātu asīm. (5. att.) Tādā veidā var uzzināt, cik objekts ir pārvietojies attiecībā pret katru asi.
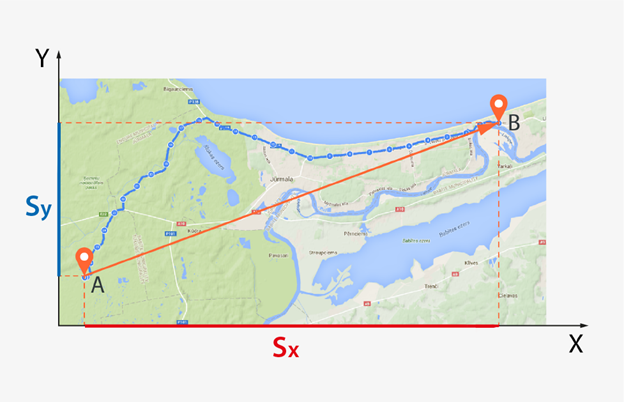
5.att. Pārvietojums un vektoru projekcijas
Iepriekšējā solī tika apskatīta kustība koordinātu sistēmā ar divām asīm X un Y, kas noteiktu kustību aprakstam ir pilnīgi pietiekami, piemēram, ja skeitbordista kustība triku laikā tiek vērota no „putna lidojuma” (1. att. b). Ja nepieciešams precīzāk kustības apraksts tuvplānā, jālieto trīs koordinātu asis X, Y un Z (1. att. c). Pastāv arī salīdzinoši vienkārša skeitbordista kustība, piemēram, kad tas slīd taisnā līnijā gar žogu, tad kustība aprakstāma ar vienu koordinātu asi, piemēram, X (1. att. a).
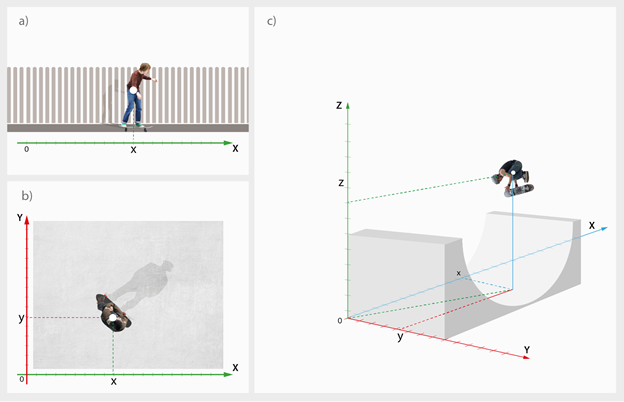
1.att. Skeitbordista kustība dažādās koordinātu sistēmās
Ja būtu jāraksturo ielu vingrotāja kustība, tad visticamāk būtu jālieto koordinātu sistēma ar trīs asīm, kura piesaistīta kādam apkārtnē esošam objektam, piemēram, kādam no ietvi veidojošiem elementiem vai ceļa malā esošam akmenim (2. att.).

2.att. Ielu vingrotājs un viņa kustības raksturošanai nepieciešamā koordinātu sistēma
Ja ķermeni var uzskatīt par masas punktu, tad koordinātu sistēma attēlo šo punktu, savukārt ja ķermeni nevar uzskatīt par masas punktu, tad grafikos parasti attēlo tā masas centru vai arī kādu no šī ķermeņa punktiem, piemēram, grafiski attēlojot, kā kustas ielu dejotāja labā plauksta (3. att.).
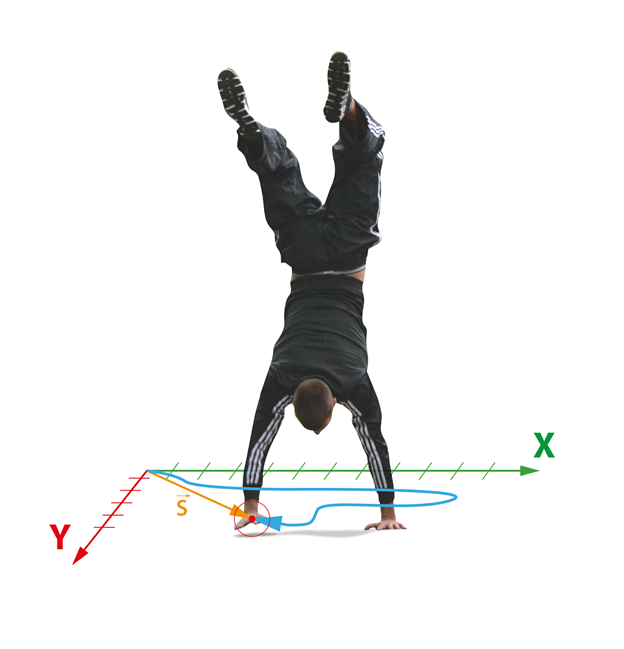
3.att. Vingrotāja labās plaukstas trajektorija, ceļš un pārvietojums
Aprakstot kāda ielu vingrotāja priekšnesumu, par atskaites ķermeni, kam piesaistīt koordinātu sistēmu, var izvēlēties citu vingrotāju. Tādā gadījumā jārēķinās ar to, ka citi dejotāji kustas attiecībā pret nevērotāju un novērojamo dejotāju, tādēļ kustības apraksts būs sarežģīts. Lielākajā daļā gadījumu visvienkāršāk ir lietot atskaites ķermeni, kas nekustas pret mums tik pierasto atskaites ķermeni – Zemi (4. att.).
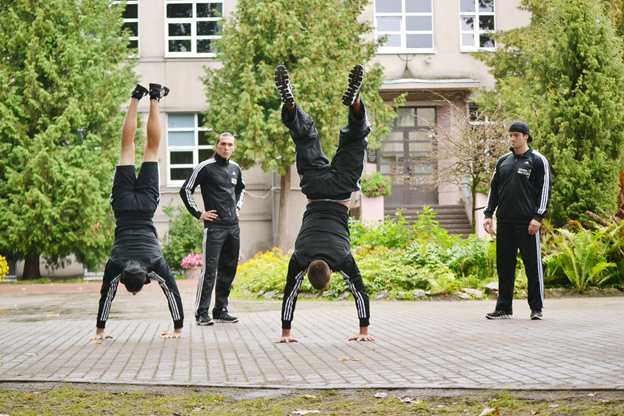
4.att. Ielu vingrotāji darbībā
Ja cilvēka kustības aprakstam lieto tā masas centru, tad jāuzmanās, jo dažādā ķermeņa daļu novietojumā masas centrs maina atrašanas vietu. Piemēram, ja ielu vingrotājs veic vingrojumu, kurā tiek izplestas kājas, tad masas centrs nobīdās tuvāk vingrotāja galvai (5. att.).

5.att. Masas punkts, kad cilvēks vingro uz stieņa
Cilvēka masas centrs var būt arī ārpus tā ķermeņa. Kā jau minēts iepriekš, stalti stāvot, cilvēkam masas centrs ir nabas rajonā (1. att.), bet ja cilvēks sākt liekties, tad masas centrs arvien vairāk virzās uz āru (1. att.).

1.att. Masas punkts, kad cilvēks vingro uz zemes
Masas punkts un no tā nosacītais masas centrs ir fizikāls modelis, lai aprakstītu kustības aprēķinu, bet tas nav vienīgais. Ja kustībā nozīmīgi kļūst ķermeņa izmēri, tad var lietot absolūti cieta ķermeņa modeli. Lai ķermeņa kustībai izmantotu šādu modeli, ir svarīgi, ka ķermenim nemainās attālums starp to veidojošajiem punktiem. Absolūti ciets ķermenis ir nozīmīgs, aprakstot rotācijas kustību, kurā dažādi ķermeņa punkti kustas ar dažādu ātrumu un paātrinājumu, piemēram, ielu vingrotājs, kas rotē ap stieni (2. att.).
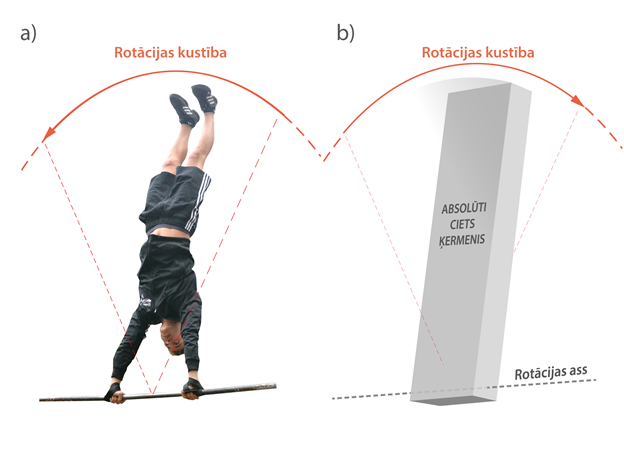
2.att. Vingrotājs kā absolūti ciets ķermenis
Sarežģītāku kustību aprakstam lieto koordinātu sistēmas, kuras var neveidot taisnas koordinātu asis ar koordinātām X, Y un Z. Piemēram, cilindriskajā koordinātu sistēmā objekta novietojumu raksturo koordinātes r, Θ un z, kur z ir taisna koordinātu ass, bet r ir attālums līdz šai asij, savukārt Θ ir pagrieziena leņķis. Cilindrisku koordinātu sistēmu var izmantot, piemēram, šķidruma kustības aprakstam cilindriskā caurulē. Vēl ir, piemēram, sfēriska koordinātu sistēma (3. att. b), kurā ķermeņu novietojumu apraksta ar diviem pagrieziena leņķiem Θ un φ, kā arī ar attālumu līdz centram r. Sfērisko koordinātu sistēmu izmanto, piemēram, zvaigžņu kustības aprakstam.
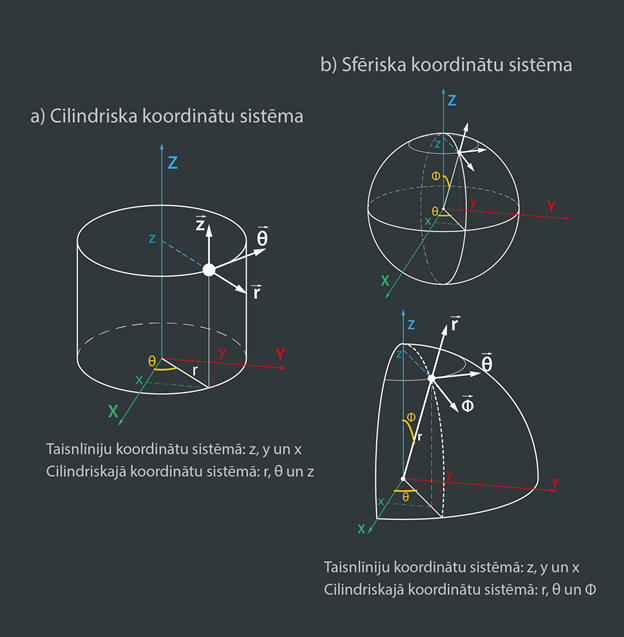
3.att. Cilindriska un sfēriska koordinātu sistēma