Ikdienā mēs saskaramies ar visdažādākajiem gaismas avotiem: Sauli, dienasgaismas spuldzēm, ekonomiskajām spuldzēm un, piemēram, zvaigznēm. Acīmredzami ir tas, ka zvaigznes spīd vājāk nekā Saule, līdz ar to avotus ir iespējams iedalīt pēc to radītā gaismas stipruma. Veicot gaismas avotu iedalījumu, rodas problēma ar to, ka cilvēka redze ir subjektīva. Piemēram, mobilajam telefonam ir iespējams mainīt ekrāna gaismas stiprumu jeb spilgtumu. Ja tumšā telpā tiek mainīts spilgtums, tad atšķirība starp mazu (1. att. a) un lielu (1. att. b) spilgtumu ir ļoti labi pamanāma. Tomēr, ja telefons tiek iznests labā apgaismojumā, saglabājot maksimālo spilgtumu, ir grūti ar aci noteikt, ka šis gaismas stiprums (1. att. c) ir tāds pats, kāds tas bija tumšā telpā (1. att. b). Tādēļ, nosakot avota gaismas stiprumu, tas ir jāsalīdzina ar kāda zināma avota gaismas stiprumu.
Apskaties DZM materiālu par fotometriju un gaismas avotiem.
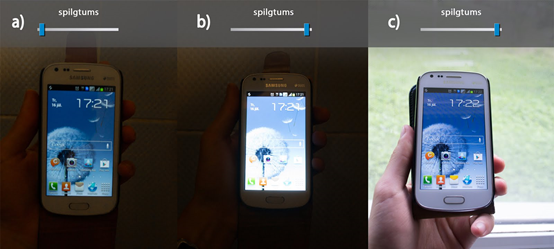
1.att. Mobilais telefons kā gaismas avots
Gaismas avots, atkarībā no stipruma, izstaro ap sevi vairāk vai mazāk enerģijas gan siltuma, gan arī gaismas veidā. Redzamās gaismas enerģiju, ko katrā laika vienībā izstaro gaismas avots, sauc par gaismas plūsmu Φ un mēra lūmenos (lm). Uzmetot aci ielu apgaismojuma lampām (4. att.) vai, piemēram, galda lampai (2. att.), redzams, ka šie gaismas avoti spēcīgi apgaismo noteiktu virsmas laukumu S. Jo lielāka gaismas plūsma no gaismas avota krīt uz šo laukumu, jo spēcīgāks ir gaismas avots. Lai aprakstītu to, cik spēcīgu gaismu avots izstaro, izmanto fizikālu lielumu – gaismas avota stiprumu I , ko aprēķina I=ΦR2:S, kur
Φ - gaismas plūsma, lm
R – attālums no gaismas avota līdz apgaismojamai virsmai, m
S – laukums, m2
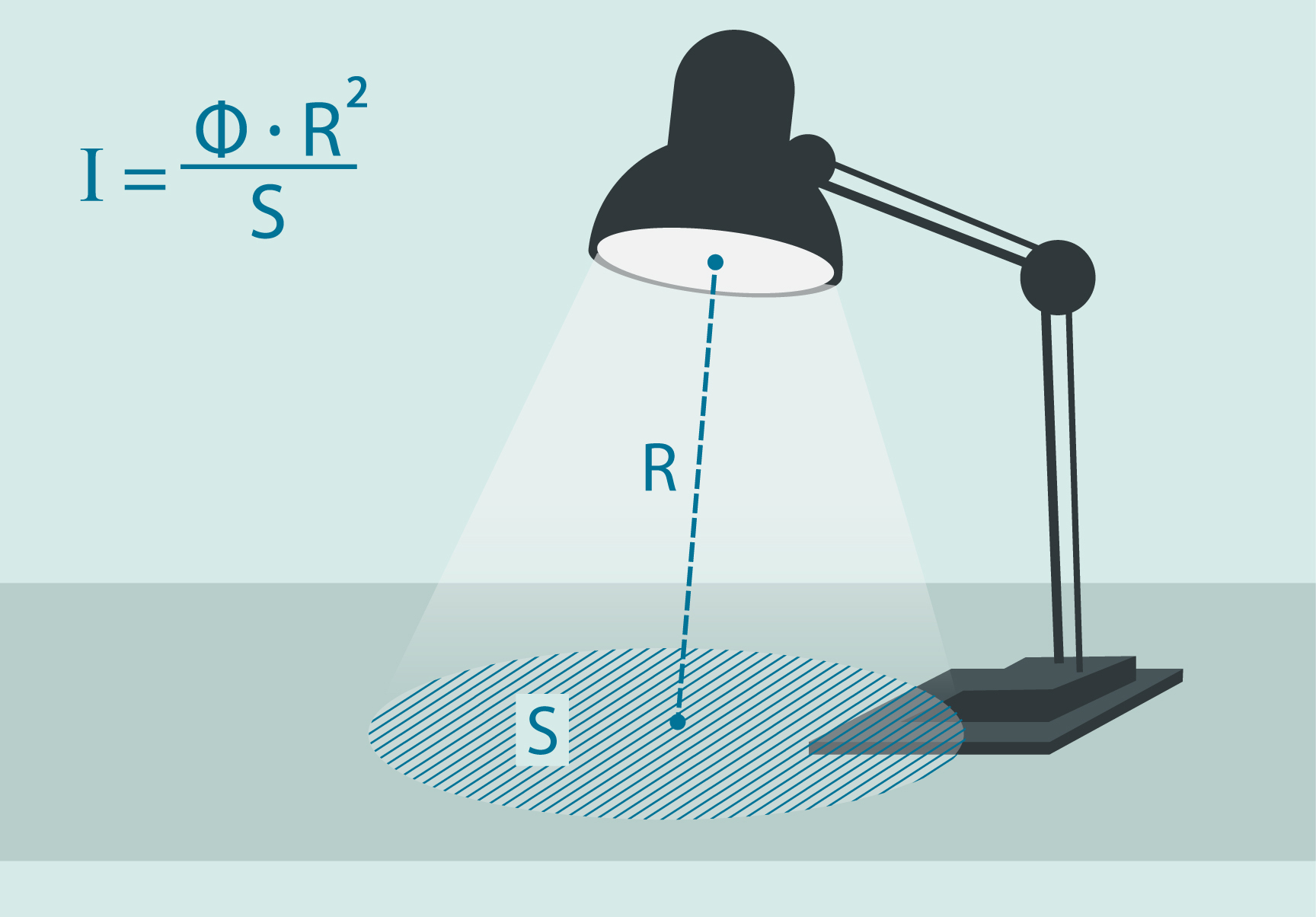
2.att. Gaismas avota stiprums
Ja gaismas avotu attālina no apgaismojamās virsmas, tad apgaismotais laukums palielinās, bet gaismas avota stiprums paliek tas pats. Tas nozīmē, ka apgaismotais laukums S un attālums līdz virsmai R ir savās starpā saistīti un šos abus lielumus saista telpiskais leņķis. Ja ap punktveida gaismas avotu apvelk sfēru ar rādiusu R (3 .att.), tad apgaismota tiek visa sfēra. Tomēr mums parasti ir svarīgs apgaismojums kādā noteiktā laukumā, teiksim riņķveida laukumā S uz šīs sfēras (2. att.), kas atbilstu laukumam, ko reāli apgaismo kāds apgaismes ķermenis. Uz šo laukumu krīt starojums, kas atrodas koniskā ķermenī. Šo telpas daļu sauc par telpas leņķi Ω. Telpas leņķi var aprēķināt, izmantojot izteiksmi Ω=S:R2, kur
S – apgaismotais virsmas laukums, m2
R – attālums no sfēras centra līdz apgaismotajam laukumam, m
Telpas leņķa mērvienība ir steradiāns (sr).
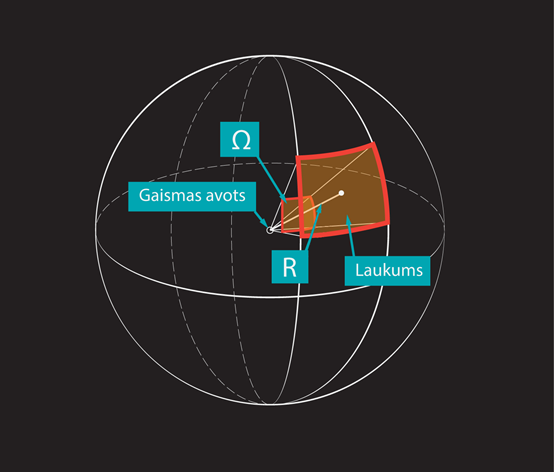
3.att. Telpas leņķis
Izmantojot telpas leņķi, gaismas avota stiprumu var izteikt I=Φ:Ω (4. att.), kur
Φ – gaismas plūsma, lm
Ω – telpas leņķis, sr.
Gaismas stipruma mērvienība ir kandela (cd). Ja gaismas avotam ir lielāks stiprums, tad tas izstaro lielāku gaismas plūsmu.
Jo lielāka gaismas plūsma krīt uz kādu ķermeni, jo ķermenis ir vairāk apgaismots un mums to ir vieglāk ieraudzīt. Apgaismojumu E var aprēķināt, izmantojot izteiksmi E=Φ:S, kur
Φ – gaismas plūsma, lm
S – laukums, m2
Apgaismojuma mērvienība ir lukss (lx).
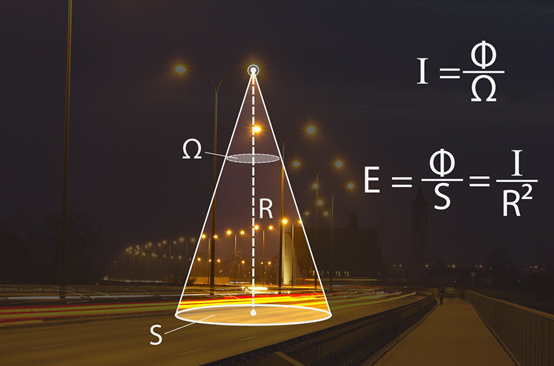
4.att. Dažādi gaismas avota parametri
Vēl viens veids, kā izteikt apgaismojumu, ir lietot gaismas avota stiprumu. Ja apskata virsmas apgaisojumu tieši zem gaismas avota (5. att. a), tad izteiksme izskatās šādi: E=I:R2,, kur
I – gaismas avota stiprums, cd
R – attālums līdz apgaismojamai virsmai.
Ja gaisma no avota uz virsmu krīt slīpi (5. att. b), tad apgaismojuma izteiksmē jāņem vērā nolieces leņķis: I:R2cosα, kur
α – staru krišanas leņķis, grādos.
Apskaties DZM materiālu par apgaismojumu un apgaismojuma likumiem!
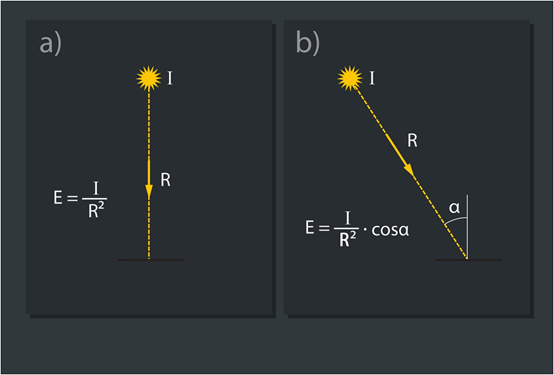
5.att. Virsmas apgaismojums dažādos leņkos
Apgaismojuma formulu E=I:R2var iegūt no apgaismojuma definīcijas. Apgaismojums ir gaismas plūsmas attiecība pret laukumu, uz kuru gaisma krīt: E=Φ:S. Gaismas plūsmu izsaka no gaismas stipruma izteiksmes I=Φ:Ω, no kurienes Φ=IΩ. Ievietojot šo apgaismojuma definīcijā, iznāk E=IΩ:S. Visbeidzot, telpas leņķi Ω izsaka kā Ω=S:R2un tad iegūst gala izteiksmi E=I:R2 (1. att.).
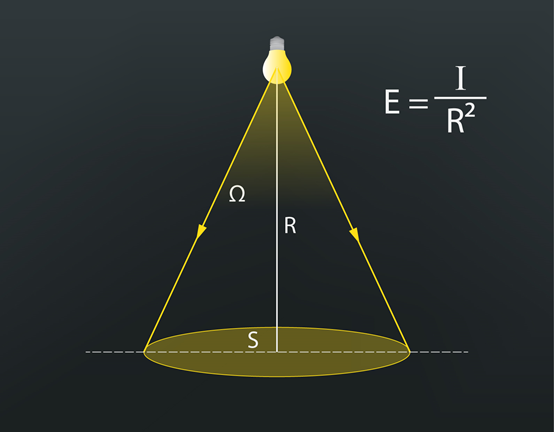
1.att. Apgaismojuma atkarība no avota gaismas stipruma
Iegūto likumu var vizualizēt, ja aplūko gaismas avotu ar stiprumu I, kas atrodas sfēras centrā un apgaismo laukumu S uz sfēras virsmas (2. att.). Laukuma S apgaismojums ir E0, bet sfēras rādiuss R. Ja pavēro, kas notiek šajā pašā telpiskajā leņķī, ja apgaismoju apskata attālumā 2R, tad var redzēt, ka tā pati gaismas plūsma sadalās uz četras reizes lielāku laukumu, līdz ar to apgaismojums ir E0:4. Ja paiet 3R attālumā, tad attiecīgi plūsma sadalās jau uz laukumu, kas ir 9 reizes lielāks kā sākotnējais, tādēļ apgaismojums ir E0:9. Šādā veidā atklājas, ka apgaismojums ir apgriezti proprocionāls attāluma kvadrātam, tieši tā, kā norāda izteiksme E=I:R2.
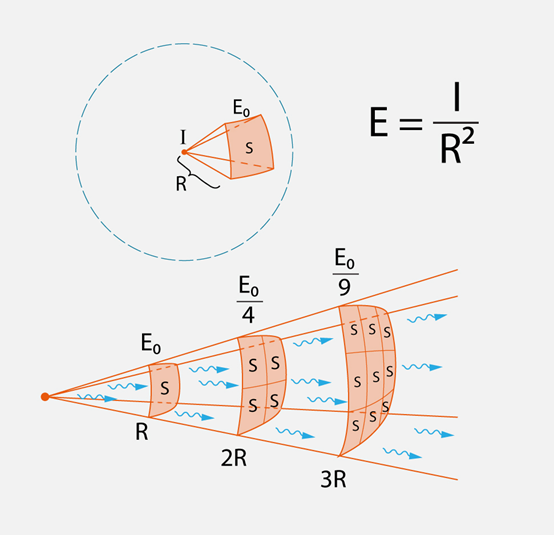
2.att. Apgaismojuma atkarība no avota gaismas stipruma
Šim apgaismojuma likumam ir arī grafitī zīmētāju analoģija. Ja krāsa no baloniņa tiek pūsta uz sienas no attāluma R, tad uz sienas izveidojas apaļš krāsas laukums S (3. att. a). Ja attālums tiek divas reizes palielināts līdz 2R, tad krāsas laukums pieaug četras reizes līdz 4S, līdz ar to krāsa uzkrājas četras reizes plānākā kārtā (3. att. b).
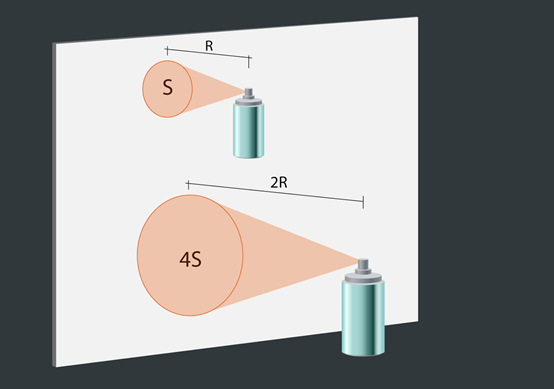
3.att. Grafiti zīmētāju analoģija
Lai komfortabli varētu veikt noteiktus darbus vai uzturēties noteiktās vietās, cilvēkam ir nepieciešams apgaismojums. Dažādās situācijās ir dažādas prasības pēc apgaismojuma stipruma, tādēļ ir izstrādātas speciālas apgaismojuma normas, kurās norādīts nepieciešamais apgaismojums dažādās situācijās (4. att.)

4.att. Apgaismojuma normas
Tā kā cilvēka acs ir subjektīvs gaismas stipruma mērītājs, tad, lai kontrolētu apgaismes normu ievērošanu, tiek lietota speciāla mērierīce – luksmetrs –, ar kuru var izmērīt apgaismojumu (5. att.).

5.att. Luksametrs
Viens no apgaismojuma nodrošinātājiem mūsu mājās ir elektriskās spuldzes. Agrāk plaši tika lietotas kvēlspuldzes, kuru spožuma rādītājs ir elektriskā jauda – jo lielāka jauda, jo spēcīgāk spīd spuldze. Turklāt katrai jaudas vērtībai atbilda aptuvena gaismas plūsma, ko šī spuldze izdala (1. att.). Šīs spuldzes nav ekonomiskas, jo gaismā pārvēršas tikai daži procenti no izlietotās enerģijas, pārējā pārvēršas siltumā. Attīstoties tehnoloģijām, tirgū ienāca arī ekonomiskākas spuldzes, piemēram, halogēnie un LED gaismekļi.
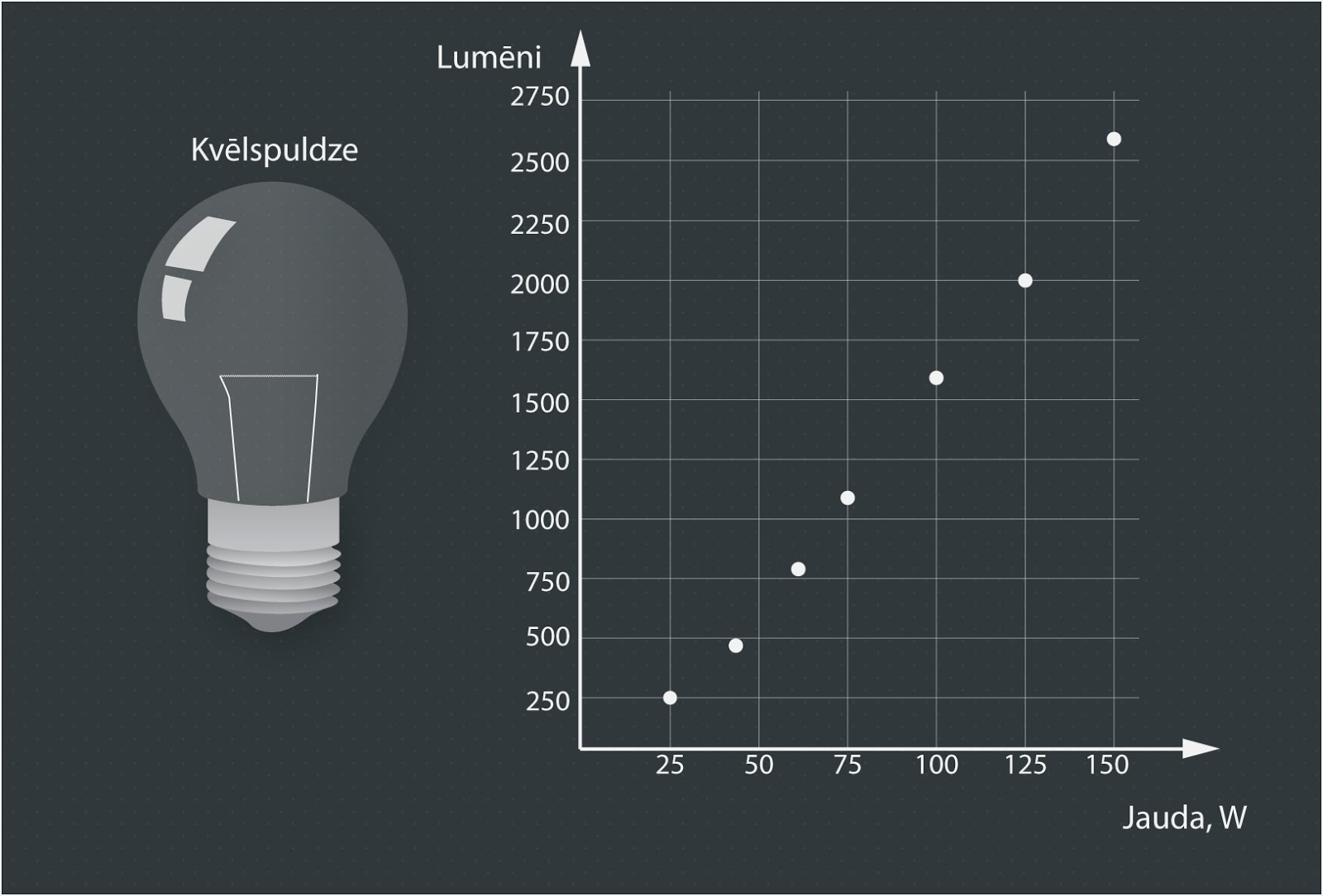
1.att. Kvēlspuldžu gaismas plūsmas un jaudas saistība
Līdz ar ekonomiskāku spuldžu parādīšanos, spuldzes jauda vairs nebija parametrs, pēc kura var noteikt to, cik spēcīgi spuldze spīdēs, jo ekonomiskās spuldzes ar mazāku enerģijas patēriņu (mazāku jaudu) panāk to pašu gaismas daudzumu ko kvēlspuldze. Tādēļ tagad uz spuldžu iepakojumiem norāda spuldzes gaismas plūsmu lūmenos (lm) (2. att.), kas ir daudz precīzāks spuldzes spožuma rādītājs. Lai uzsvērtu spuldzes ekonomiju, uz iepakojuma norāda spuldzes jaudu salīdzinājumā ar kvēlspuldzes jaudu, kas būtu nepieciešama, lai iegūtu to pašu gaismas daudzumu.

2.att. Elektriskās spuldzes iepakojums
Gaismas plūsma patiesībā ir enerģijas mērs, un lūmens ir enerģijas mērvienība. Jau Fizmix sadaļā par spēkiem un mijiedarbību noskaidrojām, ka enerģijas mērvienība ir džouls (J), tomēr gaismas plūsmas mērīšanā šo mērvienību nelieto. Tas ir tādēļ, ka cilvēka acs ir subjektīva EM starojuma uztvērēja. 3. attēlā redzama acs jutības līkne, kurā atklājas, ka acs uztver tikai EM starojumu, kura viļņu garums ir no aptuveni 400 nm līdz 700 nm. Turklāt jutība atšķiras arī dažādu krāsu gaismu uztverē (zaļo krāsu uztver vislabāk). Lūmens ir gaismas enerģijas mērvienība, kurā ir ņemta vērā acs jutības līkne. Tādēļ, piemēram, 1 vatam atbilst 603 lm zaļās gaismas plūsmas, bet tādai pašai jaudai atbilstošā sarkanās gaismas plūsma ir tikai 219 lm, jo cilvēka redze uz sarkano gaismu ir mazāk jutīga (3. att. b).
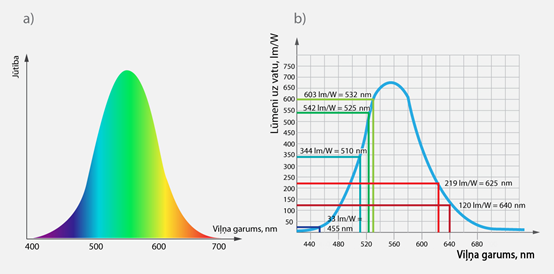
3.att. Acs redzamības līkne un dažādu krāsu gaismu plūsmas saistība ar jaudu
Ja ir nepieciešamība palielināt apgaismojumu, tad var izmantot vairākus gaismas avotus, jo kopējais apgaismojums veidosies no visu gaismekļu radītā apgaismojuma summas. Piemēram, ja lietojam divas spuldzes, kuras uz galda rada apgaismojumu E1 un E2, tad kopējais galda apgaismojums būs E=E1+E2 (4.att.).

4.att. Apgaismojuma summēšanās likums
Apgaismojumu var mainīt arī ar dažada veida spoguļiem un lēcām. Piemēram, ja aiz lampiņas noliek sfērisku spoguli, tad uz ekrāna nonāk ne tikai tiešie spuldzes stari, bet arī tie, kas atstarojas no spoguļa (5. att. a). Apgaismojumu iespējams palielināt, ja starp ekrānu un spuldzi novieto savācējlēcu. Šī lēca sakopo gaismas starus, tādā veidā samazinot telpas leņķi Ω. Rezultātā apgaismojums pieaug (5. att. b). Arī būvējot ēkas ir jāuzmanās, lai ieliekti konstrukcijas elementi neradītu nevēlamu gaismas sakopošanas efektu, kā, piemēram, vienam no Londonas debeskrāpjiem.
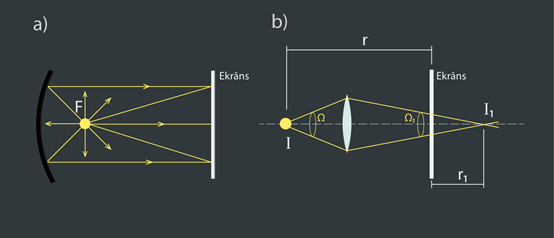
5.att. Metodes apgaismojuma palielināšanai