Sadaļās par gaismu un gaismas viļņiem šis EM starojums tika apskatīts kā viļņi, kas izplatās telpā. Tomēr gaismas daba ir grūti izprotama – to pierāda fakts, ka zinātniekiem bija nepieciešami simtiem gadu, lai atbildētu uz jautājumu, vai gaisma ir vilnis vai daļiņa. Šobrīd atbilde uz šo jautājumu ir stabili izkristalizējusies: gaismai piemīt gan viļņa, gan daļiņu īpašības, ka arī var izpausties abas īpašības reizē (1. att.).

1.att. Gaismas īpašību dualitāte
Lai izprastu gaismu kā daļiņu plūsmu, jāapskata tuvāk, kā gaisma tiek izstarota. Gaismu izstaro gaismas avotā esošie atomi, taču šī starošana notiek ar pārtraukumiem. Vienā reizē atoms izstaro vienu viļņu enerģijas porciju, ko sauc par gaismas kvantu. Tā kā atomu gaismas avotā ir daudz, tad šādas porcijas vienā laika momentā tiek izstarotas lielā daudzumā, kopumā veidojot kopēja avota starojumu (2. att.). Katru izstaroto enerģijas porciju var uzlūkot kā kustībā esošu daļiņu.

2.att. Gaismas kvanti
Ja gaismas izplatīšanās tiek uzlūkota kā daļiņu – kvantu plūsma, tad katram šādam kvantam ir jābūt ar savu enerģijas krājumu. Mehānikā (3. att.) kustībā esošam objektam enerģiju nosaka, izmantojot izteiksmi E = mv2 : 2, kur
m – objekta masa, kg
v – objekta ātrums, m/s
Savukārt gaismas kvantiem (3. att.) enerģija ir atkarīga no starojuma frekvences: E = hν, kur
ν – starojuma frekvence, Hz
h – Planka konstante, J·s
Planka konstante h ≈ 6,626·10-34J·s ir viena no mikropasaules fundamentālajām (pamata) konstantēm.

3.att. Fotona enerģija
Ja kāda daļiņa vai objekts, kuram piemīt enerģija, triecas pret kādu virsmu, tad šī trieciena rezultātā var iestāties manāmas sekas (4. att.). Tā kā gaismas kvantiem arī ir enerģija un šie kvanti milzīgā skaitā nemitīgi bombardē visapkārt esošos priekšmetus, tad varētu gaidīt, ka apkārtējiem priekšmetiem vajadzētu nemitīgi ciest no kvantu bombardēšanas. Par laimi, viena gaismas kvanta enerģija ir ļoti niecīga, līdz ar to redzamu seku šīm sadursmēm nav, tomēr ir situācijas, kad fotonu triecieni ir jāņem vērā. Ja ar fotoniem tiek apstarota metāla virsma, tad fotonam nav pietiekoši enerģijas, lai izsistu kādu metāla atomu, tomēr ap šiem metāla atomiem pārvietojas daudz vājāk piesaistītie elektroni, kurus fotonu plūsma var no metāla izsist (5. att.). Šo elektronu izsišanu fotonu triecienu rezultātā sauc par fotoefektu.

4.att. Fotoefekts
Fotoefektu pirmais izskaidroja un par to Nobela prēmiju saņēma slavenais zinātnieks Alberts Einšteins, tādēļ enerģijas nezūdamības likumu, kas uzrakstīts fotoefektam, sauc par Einšteina vienādojumu: hν = A + mv2 : 2, kur
A – elektronu izejas darbs, J
v – elektrona ātrums pēc izsišanas, m/s
Elektrona izejas darbs ir materiālu raksturojošs lielums, kas nosaka to, cik viegli ir atraut elektronu no materiāla.
Izpēti fotoefektu mazliet citādāk!
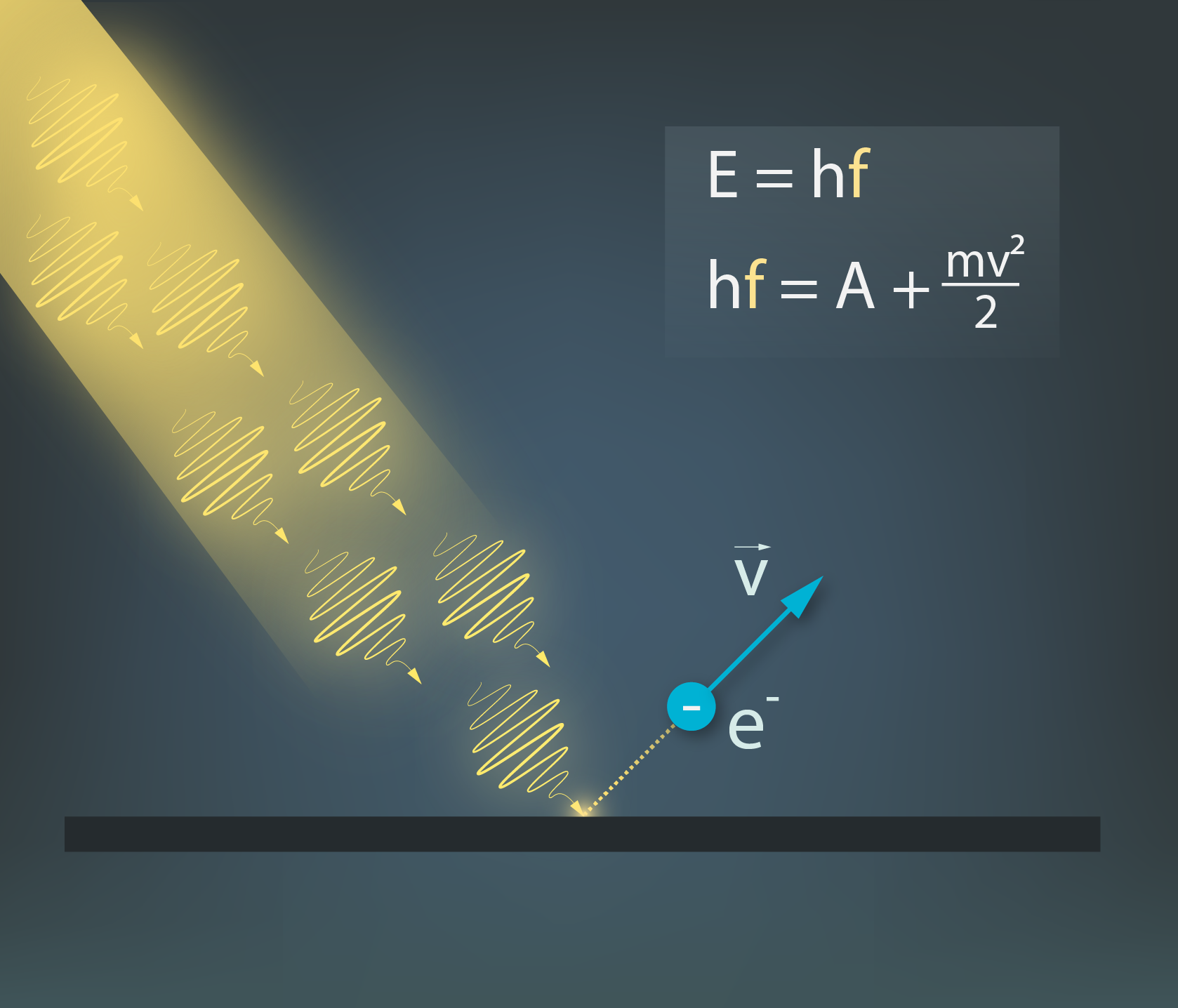
5.att. Einšteina vienādojums fotoefektam
Dažādu krāsu redzamās gaismas fotoniem ir atšķirīga enerģija, jo atšķiras dažādu krāsu gaismas starojuma svārstību frekvence. Tā kā sarkanajai gaismai svārstību frekvence ir mazāka nekā zilajai, tad, izmantojot enerģijas izteiksmi E = hν, var iegūt, ka sarkanās krāsas gaismas fotoniem ir mazāka enerģija nekā zilās krāsas gaismas fotoniem (1. att.). Tomēr, lai arī zilās krāsas fotonu enerģija ir lielāka, viena šāda fotona enerģija tik un tā ir niecīga. Viena zilās gaismas (≈ 460 nm) kvanta enerģija ir aptuveni 4,1·10-19J. Šādas enerģijas vērtības ir neērti lietot, tādēļ šādos gadījumos lieto enerģijas mērvienību elektronvolts (eV). Viens elektronvolts ir vienāds ar 1,6·10-19J. Izsakot elektronvoltos, viena zilās gaismas kvanta enerģija ir ≈2,56 eV.
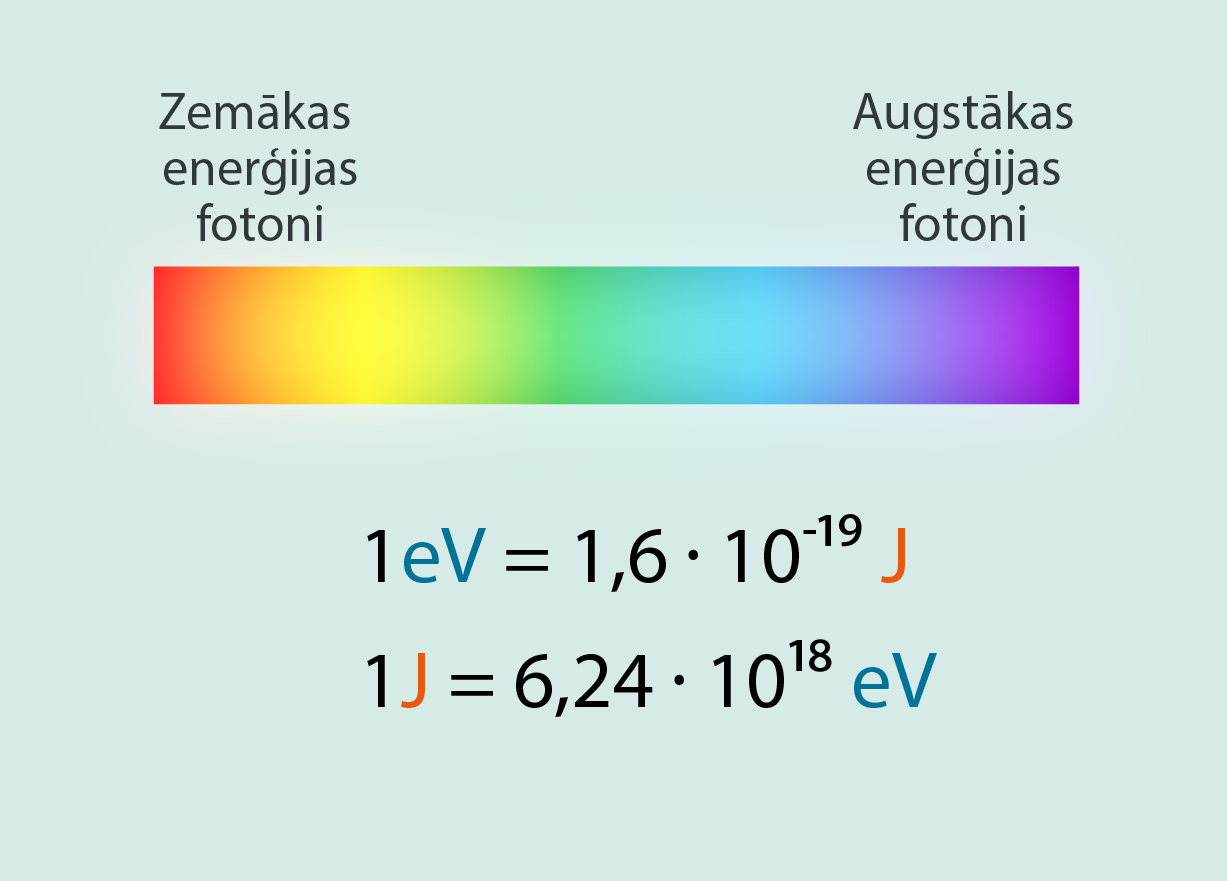
1.att. Redzamās gaismas fotonu enerģija
Enerģijas porcijas jeb kvanti raksturo ne tikai redzamo EM starojumu, tās ir īpašības, kas piemīt dažāda viļņu garuma EM starojumam, sākot no garajiem radioviļņiem un līdz pat gamma starojumam. Līdz ar krasi atšķirīgajiem viļņu garumiem stipri atšķiras dažādu EM starojumu kvantu enerģija (2. att.).
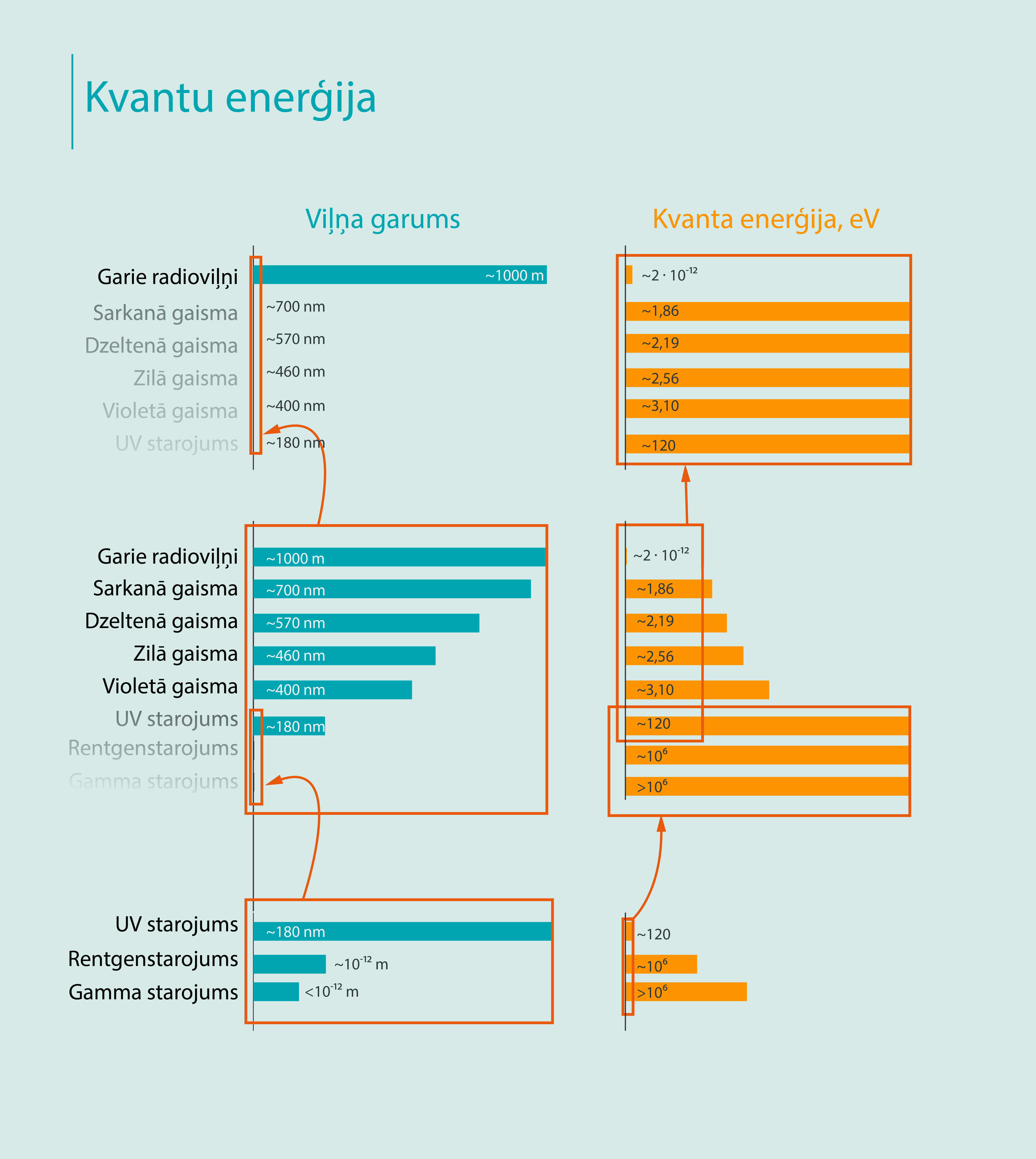
2.att. Kvantu enerģijas infografiks
Fotoefekts jau vienreiz tika pieminēts fiztēmā par elektrisko strāvu vakuumā un gāzēs. Šajā tēmā tika apskatīts stikla trauks, kurā ir vakuums un 2 elektrodi: katods un anods (3. att.). Ja elektrodus pieslēdz strāvas avotam, tad strāva starp elektrodiem neplūst. Situācija mainās tad, kad katodu apgaismo ar EM starojumu. Uz katoda norit fotoefekts un rodas brīvie elektroni, kas var pārvietoties no katoda uz anodu, tādā veidā vakuumā rodas lādētu daļiņu plūsma – elektriskā strāva. Tika minēts arī tas, ka to, cik viegli elektronu ir izsist no katoda, nosaka katoda materiāla elektronu izejas darbs.
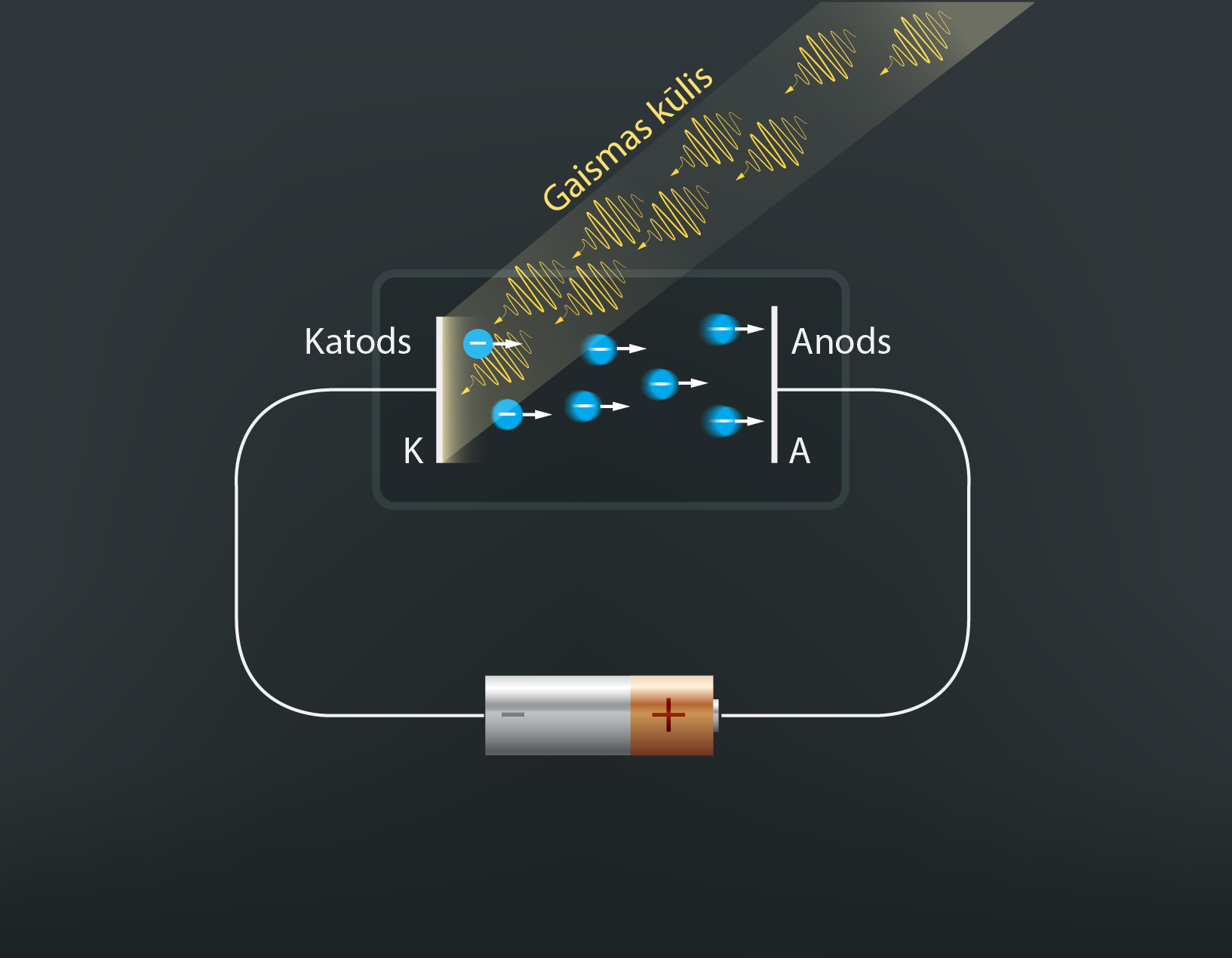
3.att. Fotoelektronu emisija vakuumā
Elektronu izejas darbu var salīdzināt ar elektrona potenciālo enerģiju, kas tam jāpiešķir, lai atrautu no metāla. Enerģētiski situācija ir tāda, ka metālā elektroni atrodas uz zemāka enerģijas pakāpiena (4. att.) un nokļūšana ārpus metāla nozīmē pārvarēt pakāpienu, kas ved uz šo ārpusi (4. att.). No mehānikas likumiem iznāk, ka šī pakāpiena pārvarēšanai elektrons ir jāpaceļ pakāpiena augstumā. Lai to izdarītu, ir nepieciešams paveikt darbu A, kas tad arī ir vienāds ar elektronu izejas darbu. Fotona enerģija hν, kas netiek patērēta elektrona izejas darba padarīšanai, pārvēršas lektrona kinētiskajā enerģijā mv2 : 2 (4. att.). Izmantojot enerģijas nezūdamības likumu, no šī arī iegūst Einšteina vienādojumu fotoefektam: hν = A + mv2 : 2.
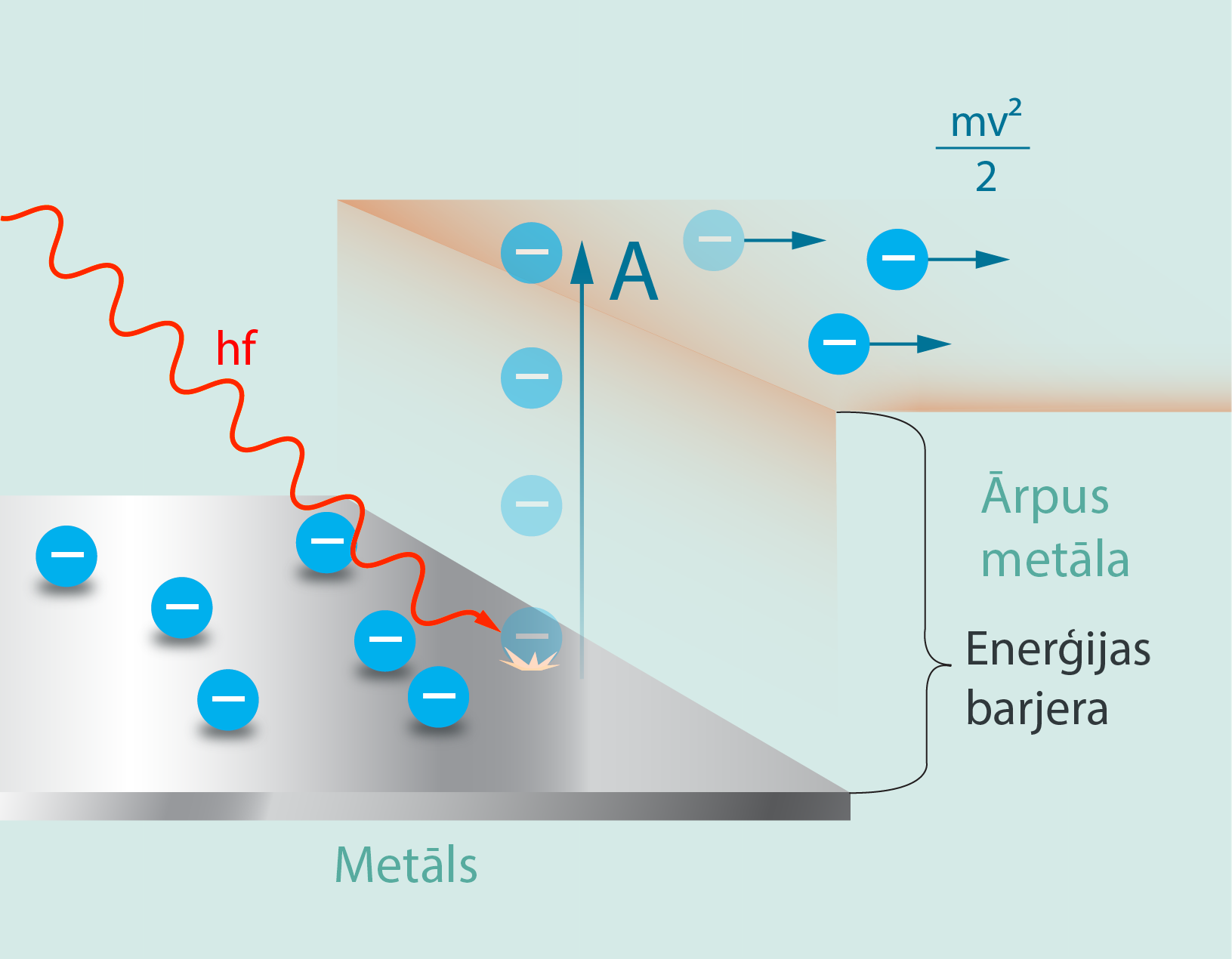
4.att. Elektronu izejas darbs
Jo mazāks ir elektrona izejas darbs, jo lielāku kinētisko enerģiju iegūst izsistais elektrons. Dažādu vielu elektronu izejas darbi apskatāmi 5. attēlā.

5.att. Elektronu izejas darbu infografiks
Fotoefektu spēcīgi ietekmē divas krītošās gaismas īpašības: gaismas kvanta enerģija un krītošās gaismas intensitāte. Tā kā gaisma šajā gadījumā tiek apskatīta kā daļiņu plūsma, tad gaismu ar mazu kvanta enerģiju varam iedomāties kā mazu daļiņu – bumbiņu plūsmu, bet lielai kvantu enerģijai tad atbilst lielākas bumbiņas. Piemēram, salīdzinot sarkanās un zilās gaismas enerģiju, sarkanai gaismai atbilst maza kvantu enerģija un līdz ar to mazāka “bumbiņa” nekā zilajai gaismai (6. att.). Lielāka bumbiņa, triecoties ar to pašu ātrumu (gaismas ātrumu) pret virsmu, izraisa lielāku efektu, tādēļ zilajā gaismā notiek spēcīgāks fotoefekts jeb tiek izsisti vairāk elektroni.
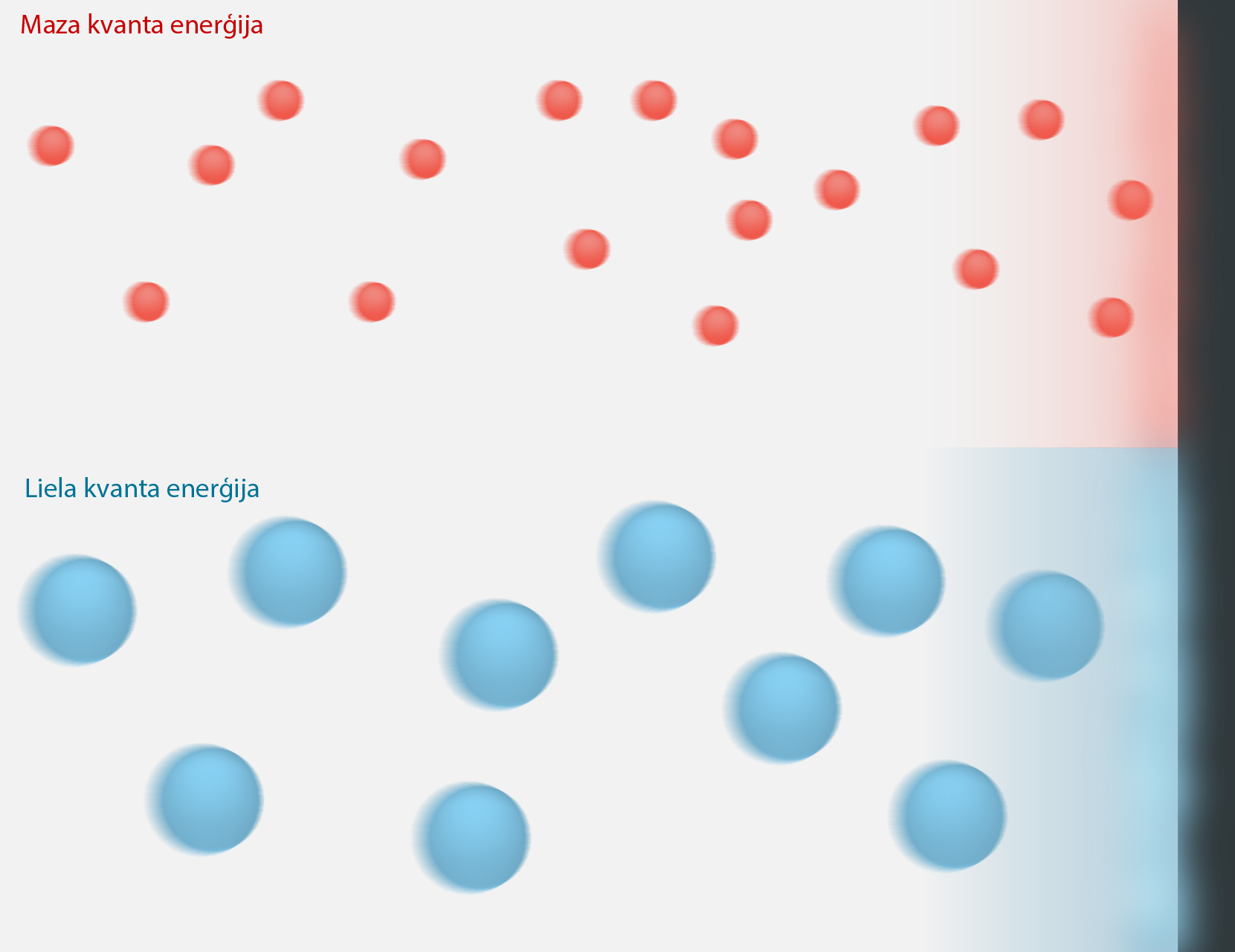
6.att. Mazas un lielas kvantu enerģijas attēlojums
Fiztēmā Fotometrijas pamati gaismas stiprums ir definēts kā I = Φ : Ω, kur
Φ – gaismas plūsma, lm
Ω – telpas leņķis, sr
Aplūkojot gaismu kā daļiņu plūsmu, mazākam gaismas stiprumam atbilst mazāks daļiņu skaits, kas laika vienībā triecas pret virsmu, bet stiprākai gaismai atbilst lielāks daļiņu skaits (7. att.). Vairāk daļiņu uz virsmu iedarbojas spēcīgāk, tādēļ, pieaugot gaismas stiprumam, pieaug arī fotoefekta apmēri.

7.att. Mazs un liels gaismas stiprums
Lielāka nozīme fotoefektā ir gaismas kvanta enerģijai jeb tam, cik lielu efektu spēj radīt viens gaismas kvants. Piemēram, ja uz litiju laiž spēcīgu zilo gaismu (liels apgaismojums), tad rodas spēcīgs fotoefekts (8. att. a). Ja laiž to pašu zilo gaismu, tikai mazāk intensīvu (mazs apgaismojums), tad fotoefekta apmēri samazinās (8. att. b). Taču, ja zilo gaismu nomaina pret sarkanu, tad vienalga, cik spēcīgu gaismu izmanto, fotoefekts netiks novērots. Tas ir tādēļ, ka sarkanās gaismas viena kvanta enerģija ir par mazu, lai izsistu kādu elektronu. No šī var secināt, ka, mainot gaismas viļņu garumu no mazāka uz lielāku (no lielākas frekvences uz mazāku), pie kāda viļņa garuma iestāsies situācija, ka fotoefekts vairs nenotiek. Maksimālo viļņa garumu λmax, pie kura vēl notiek fotoefekts, sauc par fotoefekta sarkano robežu.
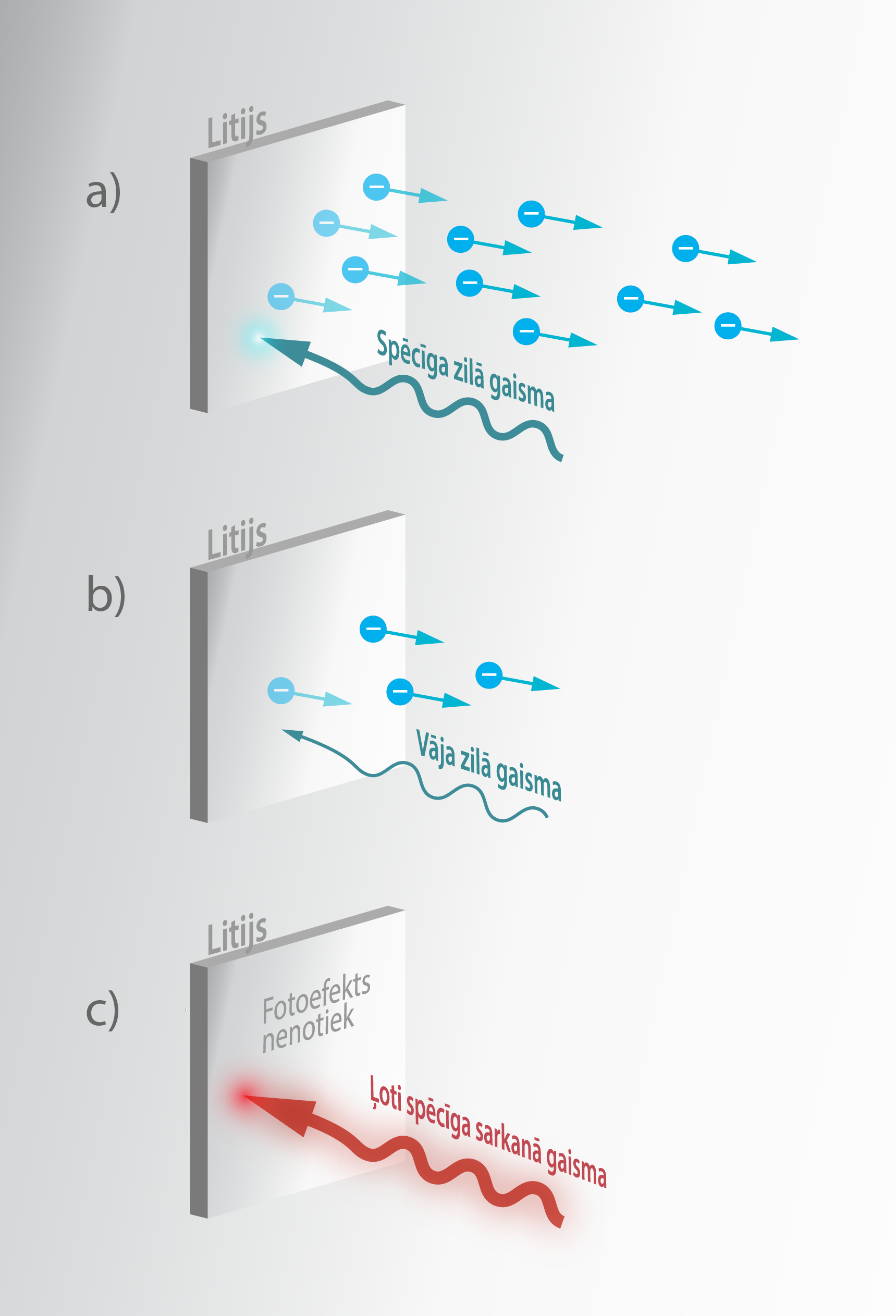
8.att. Fotoefekta atkarība no gaismas kvanta enerģijas un gaismas stipruma
Dažādu materiālu fotoefekta sarkanās robežas apskatāmas 9. attēlā.
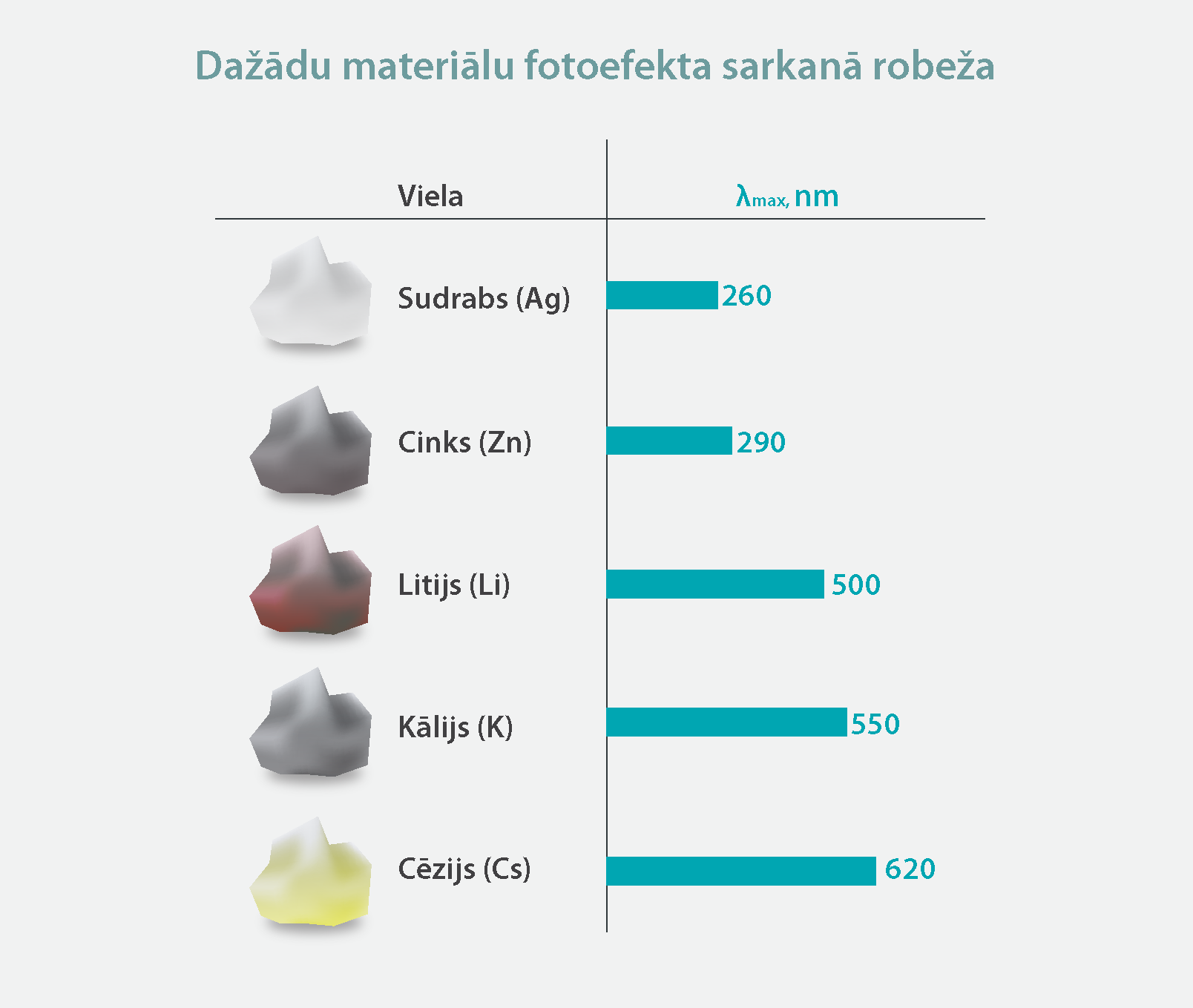
9.att. Dažādu materiālu fotoefekta sarkanā robeža
Fiziķi fotoefektu izmanto vāju signālu pastiprināšanai, piemēram, pētot EM starojumu, ko izstaro atomi un molekulas. Šāda signāla pastiprināšana tiek izmantota arī Geigera skaitītajos, kas mēra radiācijas līmeni. Vājais signāls tiek laists uz katodu (10. att.). Šī vājā signāla fotoni no katoda izsit elektronus. Tā kā signāls ir vājš, tad izsisto elektronu skaits nav liels, taču šie elektroni nonāk ārējā elektriskā laukā un paātrinās. Šādi paātrināti elektroni ietriecas citā katodā un izsit jau vairāk elektronu. Arī šie elektroni tiek paātrināti elektriskajā laukā un triecas nākamajā katodā (10. att.). Tādā veidā lavīnveidīgi tiek palielināts elektronu skaits, līdz beidzot tie nonāk uz anoda un tiek reģistrēta strāvas plūsma. Jo spēcīgāk signāls tiek pastiprināts, jo vairāk elektronu nonāk uz anoda un attiecīgi ir spēcīgāks plūstošās strāvas stiprums.

10.att. Fotoefekta pielietojums vāju signālu pastiprināšanā
Ja fotoefektu apskata vakuuma caurulē, kurā ievietoti divi strāvas avotam pieslēgti elektrodi (katods un anods), tad fotoefekta intensitāti var noteikt pēc strāvas stipruma, kas plūst ķēdē. Ja uz katodu spīd stipra zilā gaisma, tad ir izteiks fotoefekts un strāva ķēdē ir spēcīga (1. att. a). Ja tiek samazināta zilās gaismas intensitāte, tad samazinās arī ķēdē plūstošās strāvas stiprums (1. att. b). Ja zilo gaismu nomaina pret sarkanu, tad strāva ķēdē pārstāj plūst, jo pie šāda katoda materiāla fotoefekts sarkanajā gaismā nenotiek (1. att. c).
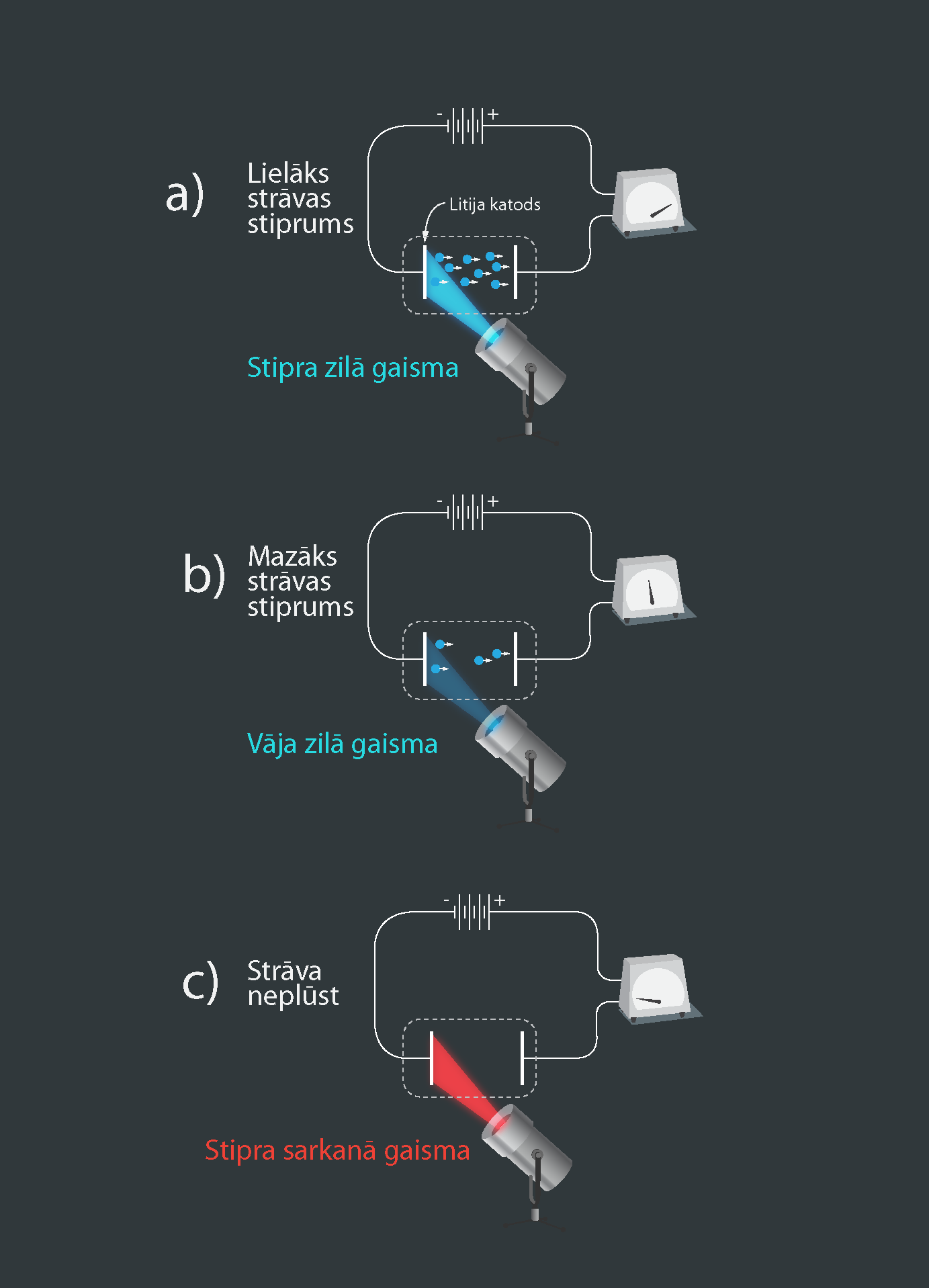
1.att. Fotoefekta novērošana vakuuma caurulē
Ķēdē plūstošās strāvas stiprums ir atkarīgs arī no sprieguma, kāds ir vakuumcaurulē starp katodu un anodu (2. att. a). Jo lielāks ir šis spriegums, jo vairāk no katoda izsisto elektronu nonāk līdz anodam, līdz ar to pieaug fotostrāvas stiprums. 2. attēla a gadījumā redzams, kā mainās fotostrāvas stiprums atkarībā no pieliktā sprieguma starp elektrodiem pie diviem gaismas stiprumiem I1un I2. Redzams, ka fotostrāva palielinās ne tikai pie lielāka sprieguma, bet arī pie lielākas gaismas intensitātes (2. att. b).
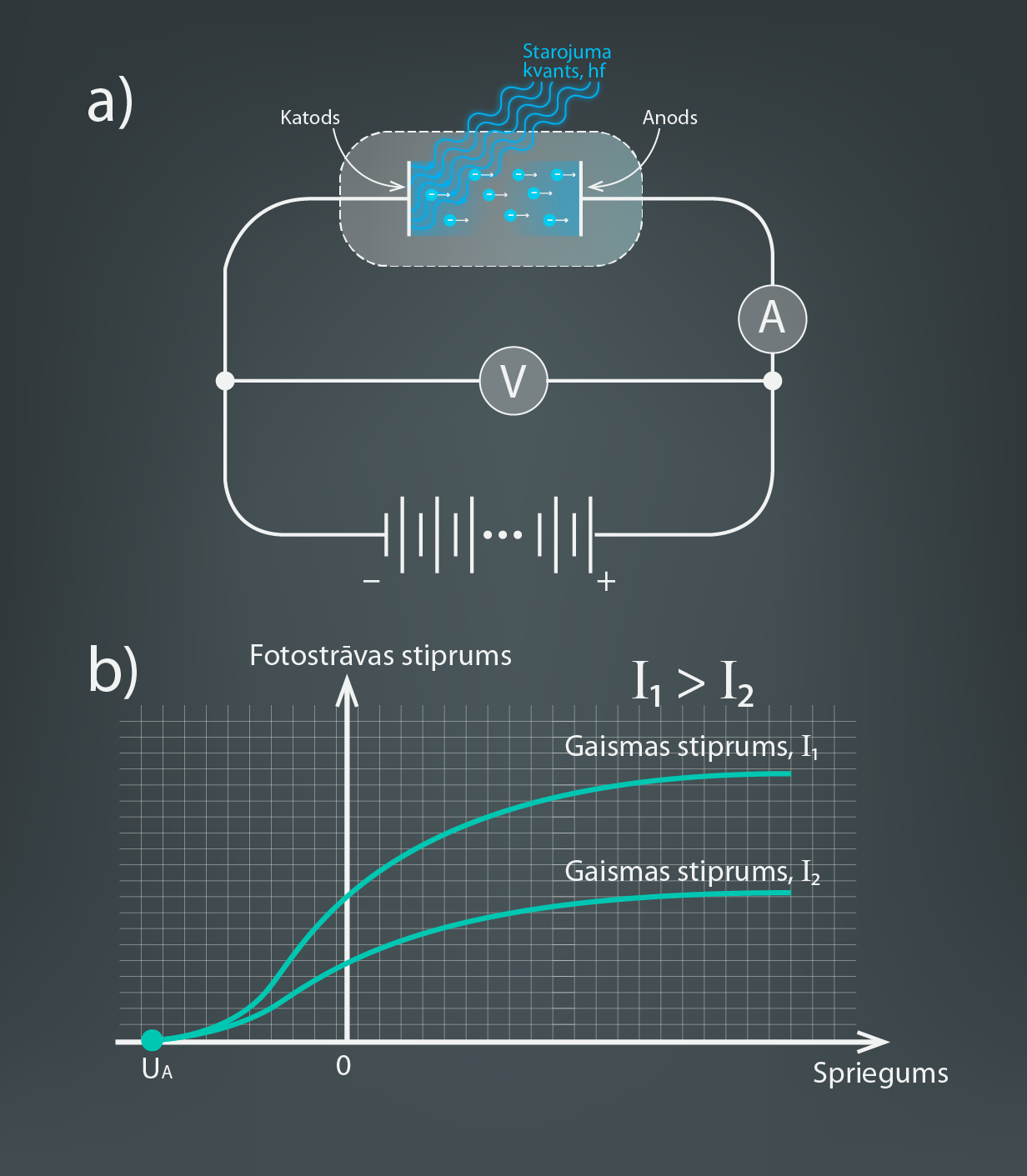
2.att. Sprieguma ietekme uz fotoefektu
Fotoefektu iedala divos veidos: iekšējais un ārējais. Līdz šim tika apskatīts ārējais fotoefekts. Šo fotoefektu sauc par ārējo tādēļ, ka rezultāts ir novērojams ārpus materiāla. Iekšējā fotoefekta rezultāta izmaiņas notiek pašā materiālā. Materiāls sastāv no atomiem, pie kuriem piesaistīti vairāk vai mazāk elektronu. Šie piesaistītie elektroni nevar piedalīties strāvas vadīšanā. Ja šo materiālu apstaro ar EM starojumu, tad fotoni šos piesaistītos elektronus var izsist no vietas, tādā veidā atsaistot tos no atoma (3. att.). Šādi atsaistīti elektroni var piedalīties strāvas vadīšanā, līdz ar to materiālam paaugstinās elektrovadītspēja.
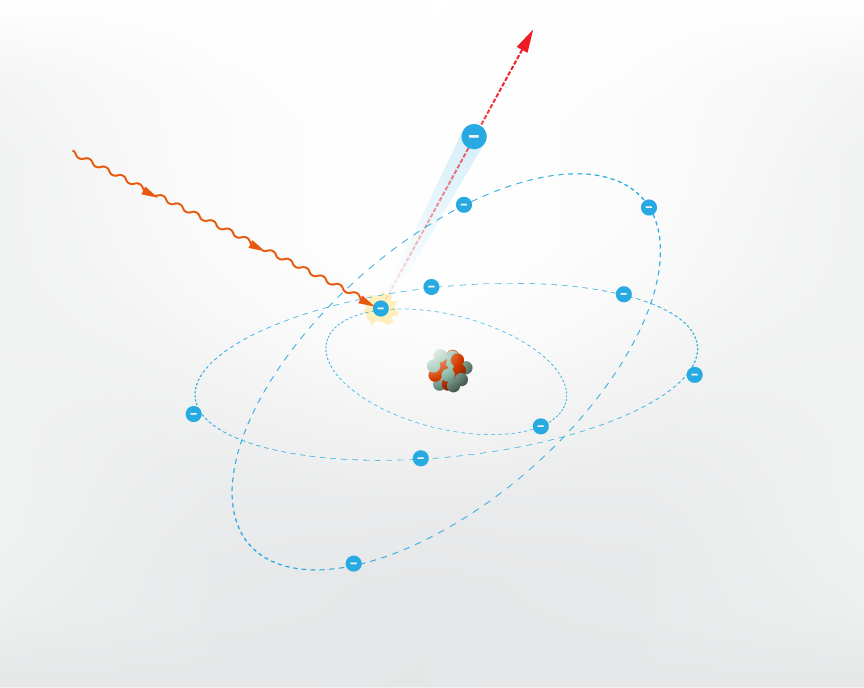
3.att. Iekšējā fotoefekta rezultātā palielinās materiāla elektrovadītspēja
2. solī tika apskatīta enerģijas mērvienība elektronvolts, kas tiek lietota ērtības nolūkos džoula vietā. Elektronvolta lielums nav izvēlēts nejauši. Ne velti salikums “elektronvolts” sastāv no diviem vārdiem “elektrons” un “volts”. Vienu elektronvoltu liela enerģija tiek piešķirta vienam elektronam, kurš elektriskajā laukā tiek pārvietots starp diviem punktiem, kuriem potenciālu starpība U vienāda ar 1 voltu (4. att.). Elektronam piešķirto enerģiju jeb padarīto darbu šādā gadījumā aprēķina pēc izteiksmes A = qU, kur
q – pārvietotā lādiņa lielums, C
U – potenciālu starpība, V
Šajā gadījumā lādiņa lielums vienāds ar elektrona lādiņu, tādēļ q = 1,6 · 10-19C, bet potenciālu starpība U = 1 V, līdz ar to A = 1,6 · 10-19J = 1 eV.
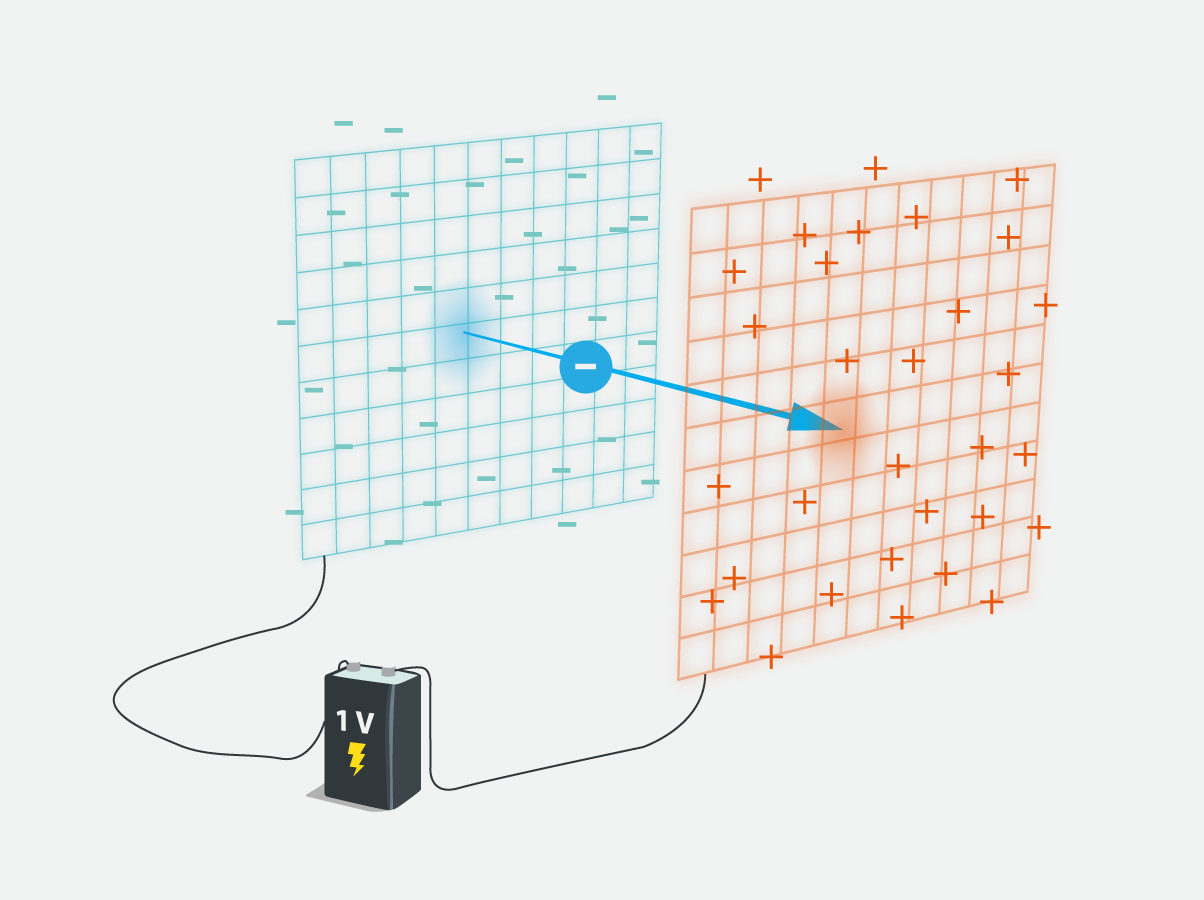
4.att. Darbs viena elektronvolta apmērā
Fiztēmā Molekulāri kinētiskā teorija 2. solī tika noskaidrots, ka gāzes daļiņas, triecoties pret trauka sieniņu, rada spiedienu (5. att. a). Tā kā gaisma arī ir daļiņu plūsma, kas var triekties pret kādu virsmu, tad jārēķinās ar tādu parādību kā gaismas spiediens. Gaismas spiediena izraisīšanā liela nozīme ir kvanta impulsam (līdzīgi kā gāzes spiedienā nozīmīgs ir gāzes daļiņas impulss). Gaismas kvanta impulsu (5. att. b) var aprēķināt, izmantojot formulup = hν : c vai p = h : λ, kur
h – Planka konstante, J·s
ν – gaismas frekvence, Hz
c – gaismas ātrums, m/s
λ – gaismas viļņa garums
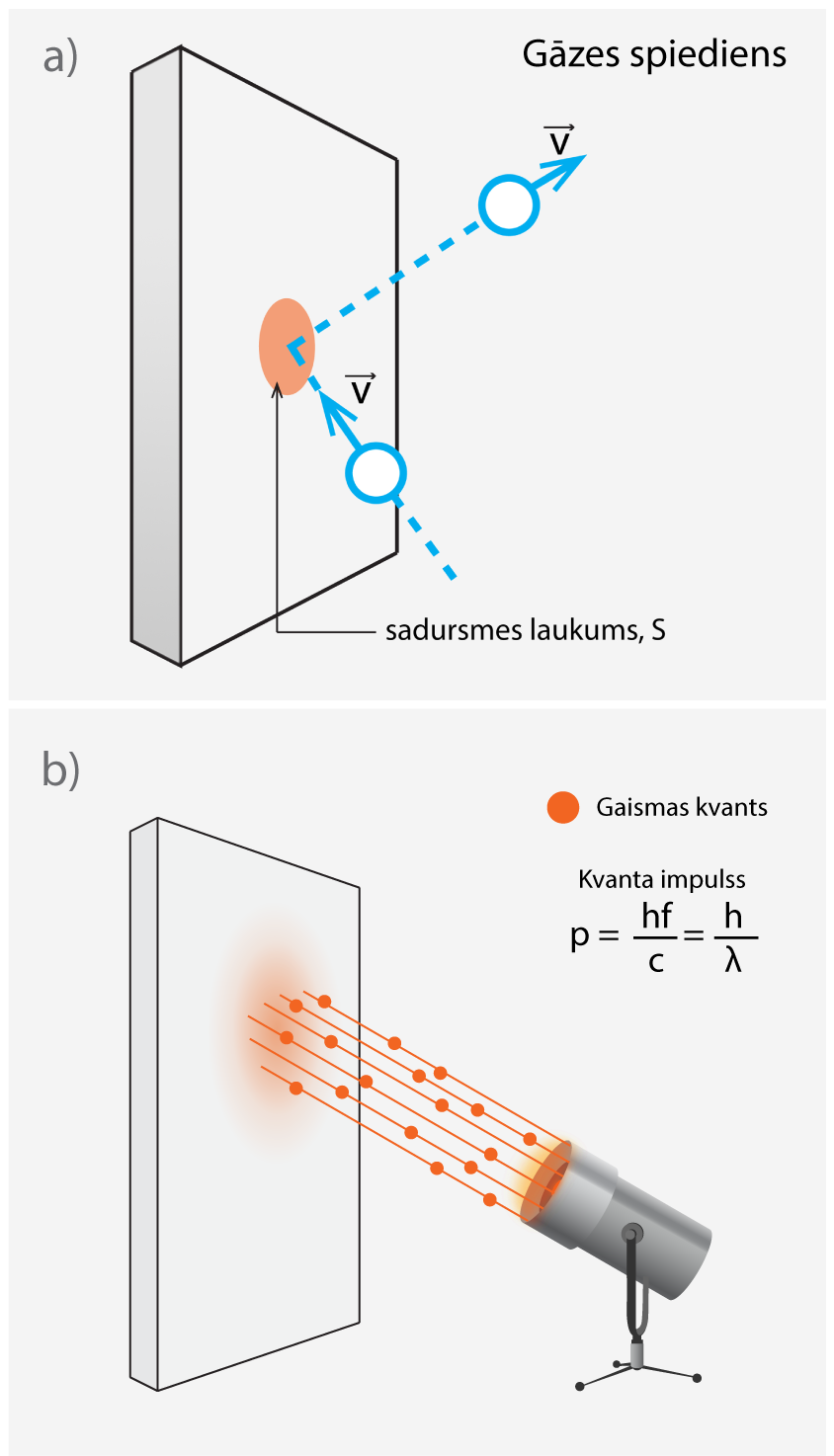
5.att. Spiedienu rada gāzes daļiņu sadursmes ar trauka sienu.
Uz Zemes gaismas spiediena efektu ir grūti novērot, jo traucē apkārtējo gāzu radītais atmosfēras spiediens. Taču nonākot atklātā kosmosā ne pārāk tālu no Saules, gaismas spiedienu var pat lietderīgi izmantot, piemēram, lietojot Saules buru (6.att.). Saules bura darbojas līdzīgi kā kuģa bura, tikai vēja vietā Saules bura "ķer" EM starojumu. Ar šādu Saules buru var veikt kosmisko aparātu manervus. Interesanti, ka pirmais cilvēks, kas pamatoja Saules buru izmantošanu kosmiskajos lidojumos, bija Rīgā dzimušais raķešu konstruktors Frīdrihs Canders.

6.att. Saules bura
Gaismas spiediens noteic arī to, ka komētām veidojas aste, kas vērsta prom no Saules (7. att.)

7.att. Komētas aste veidojas gaismas spiediena rezultātā