Šķidrums ir viens no vielas agregātstāvokļiem. Tas ir vienīgais agregātstāvoklis, kurā vielai ir konkrēts tilpums, bet nav noteiktas formas. Šķidrumam ir vairākas raksturīgas pazīmes, piemēram, plūstamība, laba sajaukšanās spēja, un fizikālās īpašības visos virzienos ir vienādas. Šķidrumus arī uzskata par praktiski nesaspiežamiem, tomēr, ja pieliek ļoti lielu spēku, tad šķidrumu tomēr nedaudz var saspiest. (1. att.)
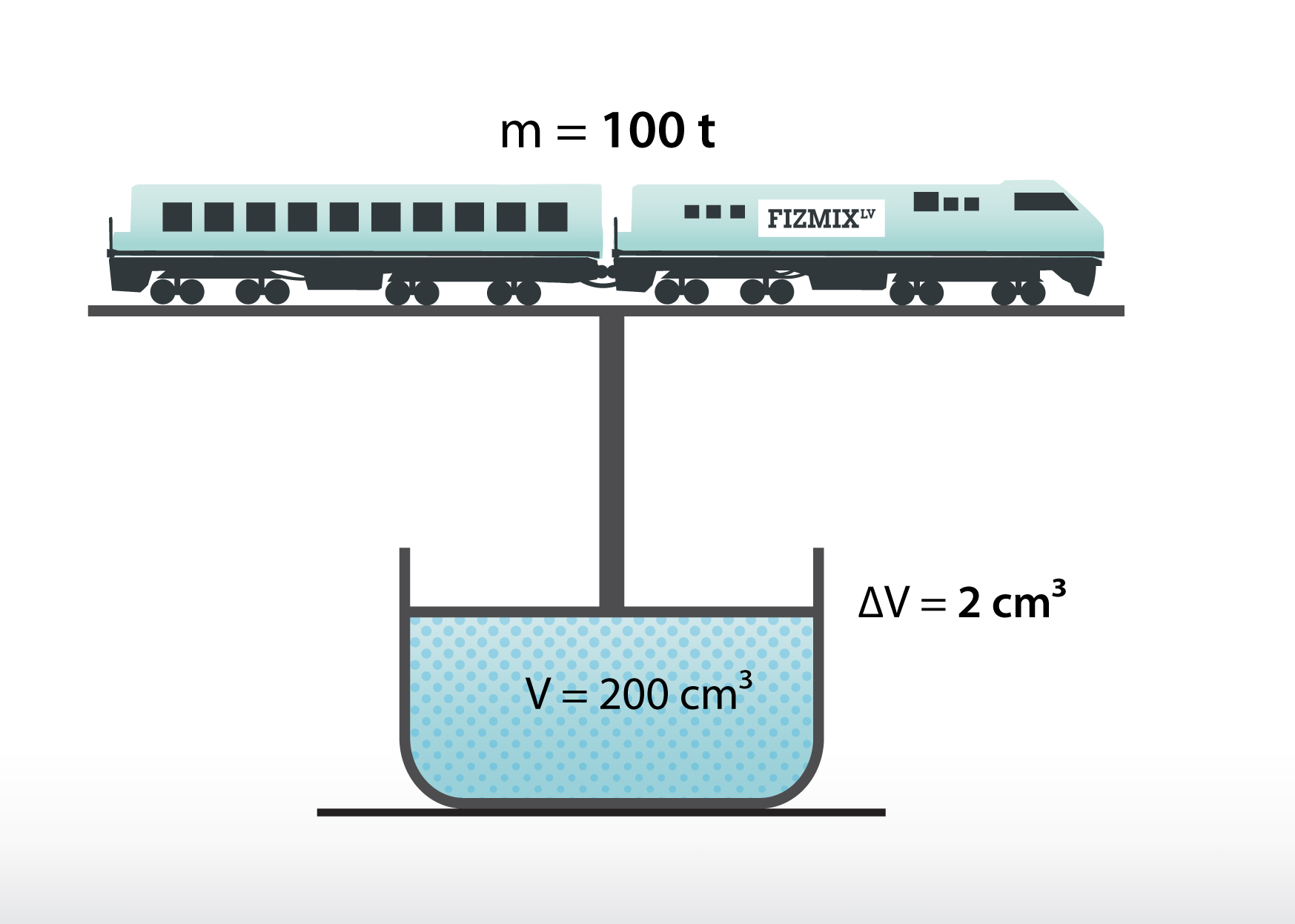
1.att. Šķidrumu ir ļoti grūti saspiest
Šķidrumu no apkārtējās vides atdala robežvirsma, ko sauc par šķidruma brīvo virsmu. Molekulas, kas atrodas šķidruma iekšpusē (2. att. a), no visām pusēm ir pakļautas apkārtējo molekulu iedarbībai, kas savstarpēji kompensējas (kopspēks Fa = 0). Bet uz virsmas esošās molekulas (2. att b) kaimiņi ieskauj tikai no vienas puses, no otras puses tās mijiedarbojas ar no šķidruma iztvaikojušajām vai gaisa sastāvā esošajām molekulām. Šī mijiedarbība ir daudzas reizes mazāka nekā mijiedarbība ar šķidrumā esošajā molekulām, tādēļ šķidruma virsmas molekulas tiek pakļautas spēkam Fb, kas tās velk iekšā šķidrumā. Šo spēku sauc par virsmas spraiguma spēku F, un tas nosaka, ka šķidruma virsma atrodas saspriegtā stāvoklī. Šī saspriegtā stāvokļa dēļ virsmai piemīt papildu potenciālā enerģija, ko sauc par virsmas enerģiju un apzīmē ar U.
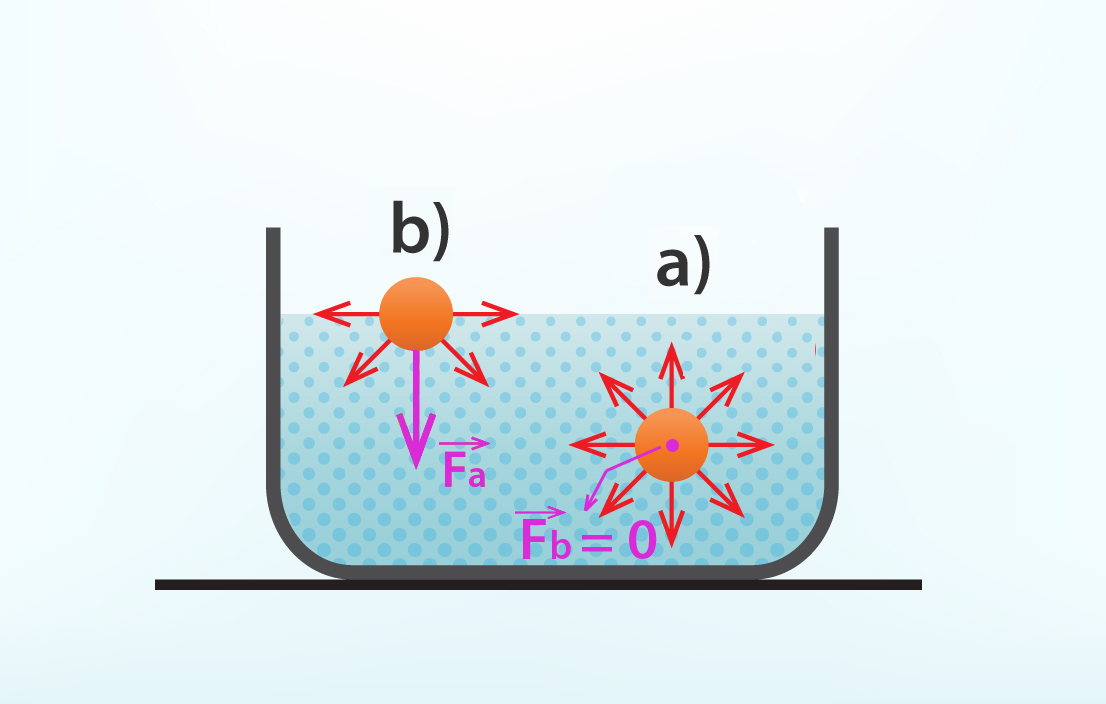
2.att. Uz šķidruma virsmas esošās molekulas pakļautas virsmas spraiguma spēkam
To, cik ļoti virsma ir saspriegta jeb cik ļoti tā tiecas sarauties, raksturo virsmas spraiguma koeficients σ. Ja šķidrumā iemērc kādu l garuma stieplīti un izmēra spēku F, kas jāpieliek, lai šo stieplīti atrautu no šķidruma (3. att.), tad σ = F: l. Virsmas spraiguma koeficients mainās temperatūras ietekmē. Ja temperatūru palielina, tad virsmas spraiguma koeficients samazinās. Virsas spraiguma koeficientu iespējams mainīt, izmantojot dažādus piejaukumus, piemēram, ziepes un citus mazgāšanas līdzekļus.
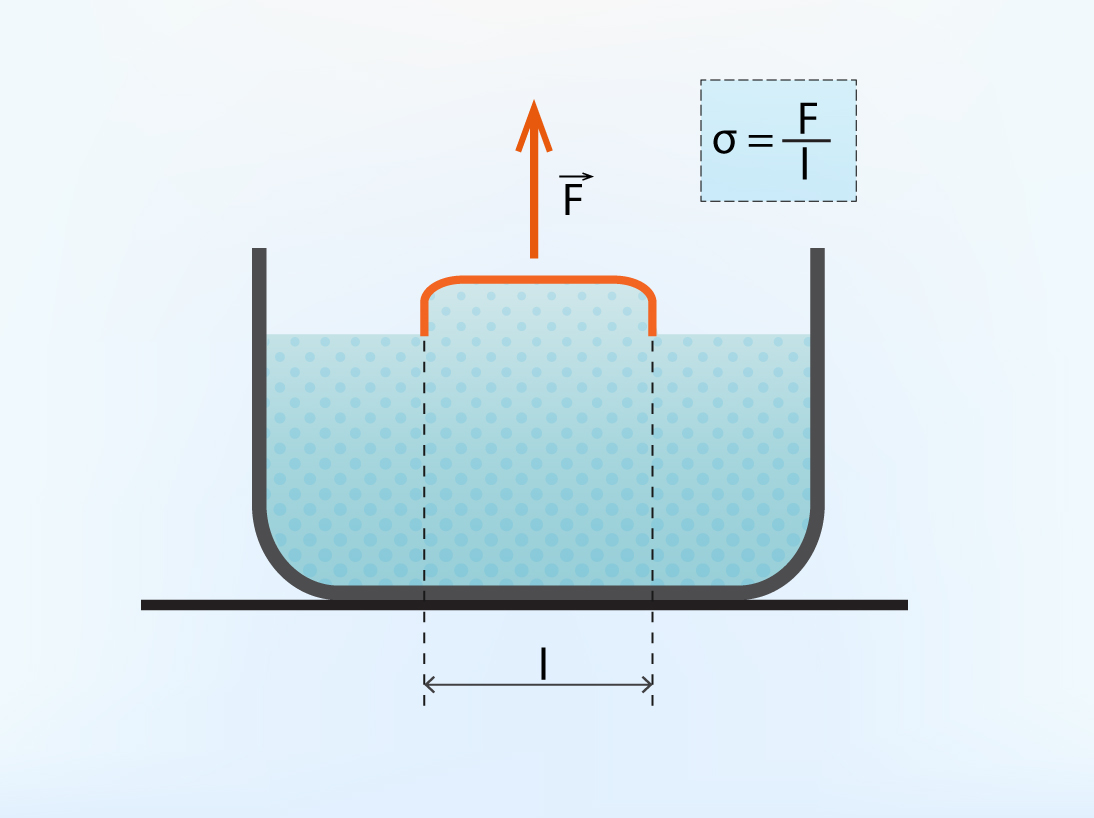
3.att. Virsmas spraiguma koeficients ir spēka attiecība pret garumu
Virsmas spraiguma spēks šķidruma virsmai piešķir elastīgas īpašības, tā uzvedas līdzīgi piepūsta košļenes burbuļa virsmai. Piemēram, uz šķidruma virsmas ir iespējams novietot vieglus priekšmetus, kuru materiāla blīvums pārsniedz šķidruma blīvumu (4. att. a), savukārt, ja traukā ielej nedaudz lielāku šķidruma tilpumu nekā trauks atļauj, tad līdz noteiktai robežai šķidrums nelīst pāri malām, bet veido tādu kā uzkalniņu (4. att. b).
Noskaties Jauno Fiziķu skolas nodarbības video par virsmas spraigumu!

4.att. Uz ūdens virsmas noturas metāla saspraude (a). Ūdens ieliets glāzē ar kaudzīti (b)
Virsmas spraiguma spēks vienmēr darbojas tā, lai pēc iespējas samazinātu šķidruma brīvās virsmas laukumu. Pie noteikta tilpuma vismazākais virsmas laukums ir sfērai, tādēļ, izlejot kādu šķidrumu, jārēķinās, ka tas sadalīsies pilienos. To, ka šķidruma piliens tiecas ieņemt sfērisku formu, var novērot pie piloša ūdens krāna (5. att.). Nelielu laika sprīdi pirms piles atdalīšanās no krāna var manīt, ka tā ir ieņēmusi sfērai līdzīgu formu, tomēr sasniegt ideāli sfērisku formu traucē citi spēki, piemēram, smaguma spēks.

5.att. Ūdens piliens spraiguma spēka ietekmē cenšas ieņemt lodveida formu
Noskaidrojām, ka piloša krāna gadījumā piles centienus ieņemt lodveida formu nodrošina šķidruma molekulu savstarpējā mijiedarbība, kas apkopojas virsmas spraiguma spēkā, un ka gravitācijas spēks šo lodveida formu deformē. Tomēr, ja šķidrums ir nonācis kontaktā ar cietu ķermeni (šajā gadījumā krānu), tad lielu lomu šķidruma uzvedībā var spēlēt šķidruma molekulu mijiedarbība ar cietā ķermeņa molekulām. Izrādās, ka šķidruma molekulas mijiedarbojas arī ar tā cietā ķermeņa molekulām, ar kuru tas ir nonācis kontaktā, un šo parādību sauc par slapināšanu. Ja šķidruma un cieta ķermeņa molekulu savstarpējās mijiedarbības spēki ir lielāki nekā šķidruma molekulu pievilkšanās spēki, tad saka, ka šķidrums virsmu slapina, bet pretējā gadījumā šķidrums virsmu neslapina. Ja traukā ielej šķidrumu, kas tā virsmu slapina, tad šķidruma virsma pie trauka sieniņas ir ieliekta (6. att. a), bet, ja šķidrums trauka materiāla virsmu neslapina, tad šķidruma virsma pie trauka sienas ir izliekta (6. att. b).
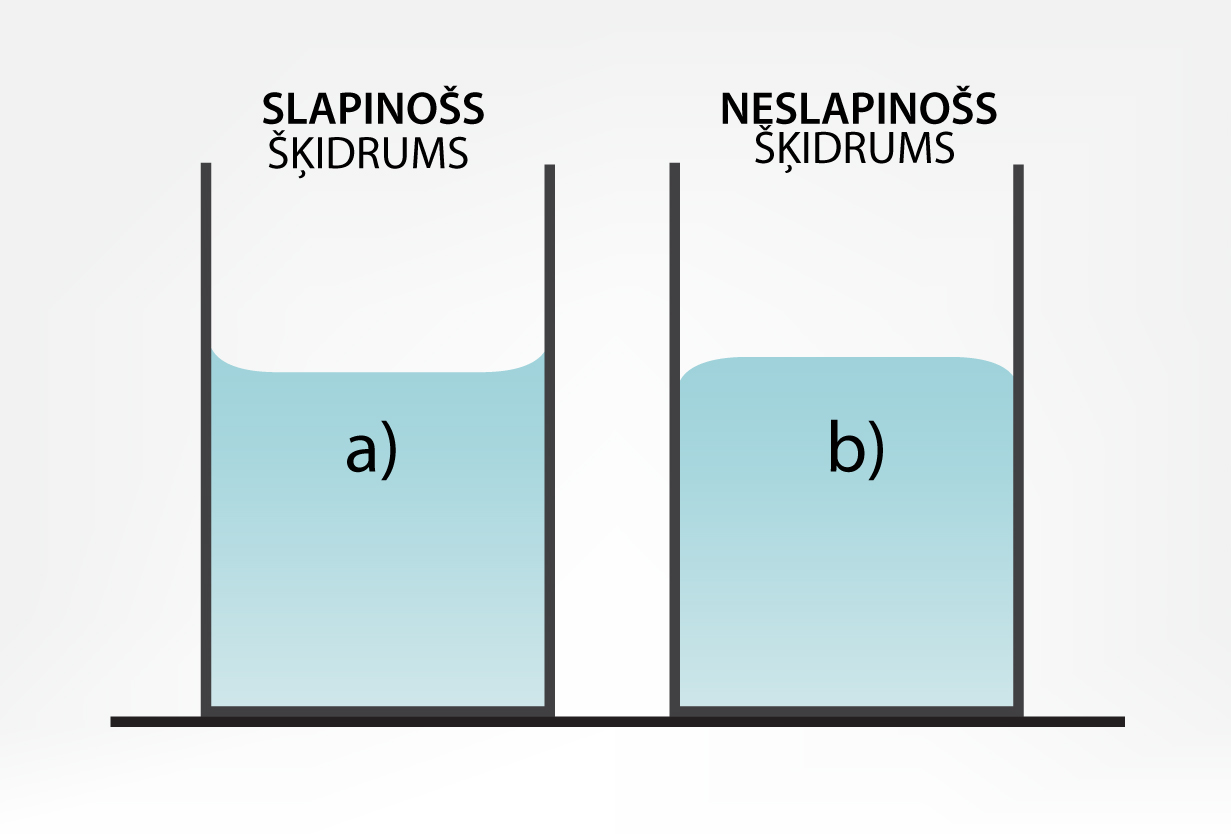
6.att. Trauka slapināšanas (a) un neslapināšanas (b) gadījums
Ja uz kādas virsmas nonāk šo virsmu slapinoša šķidruma pile, tad tā uz virsmas izplūst (7. att. a), piemēram, ja ūdens piles nonāk uz grīdas vai galda. Bet ja šķidrums ir neslapinošs, tad pile neizplūst (7. att. b un c). Tas novērojams speciāli apstrādātiem audumiem vai, piemēram, ja medus pilienus uzpilina uz svaiga kāposta lapas.

7.att. Virsmu slapinošs (a) un neslapinošs (b un c) šķidrums
Šķidruma virsmas spraigums un slapināšana īpaši izpaužas tievās caurulītēs, ko sauc par kapilāriem. Ja traukā ar šķidrumu iegremdē šādu kapilāru, tad slapināšanas gadījumā šķidruma līmenis kapilārā ir par h augstāks nekā traukā (8. att. a), bet ja slapināšana nenotiek, tad šķidruma līmenis ir pa h zemāks (8. att. b). Šo šķidruma līmeņu atšķirību kapilārā un traukā sauc par kapilārajām parādībām.
Augstumu h var aprēķināt pēc izteiksmes h = 2σ(ρgR), kur
σ - virsmas spraiguma koeficients
ρ- šķidruma blīvums
g - brīvās krišanas paātrinājums
R - kapilāra rādiuss
Šķidruma virsmai kapilārā ir pussfēras forma ar rādiusu R. Slapināšanas gadījumā šī virsma ir ieliekta (8. att. a), bet neslapināšanas gadījumā izliekta (8. att. b).
Ja kāds ķermenis satur kapilārus, tad slapināšanas gadījumā tie uzsūc ūdeni, piemēram, dažādi audumi, dvielis, augsne.
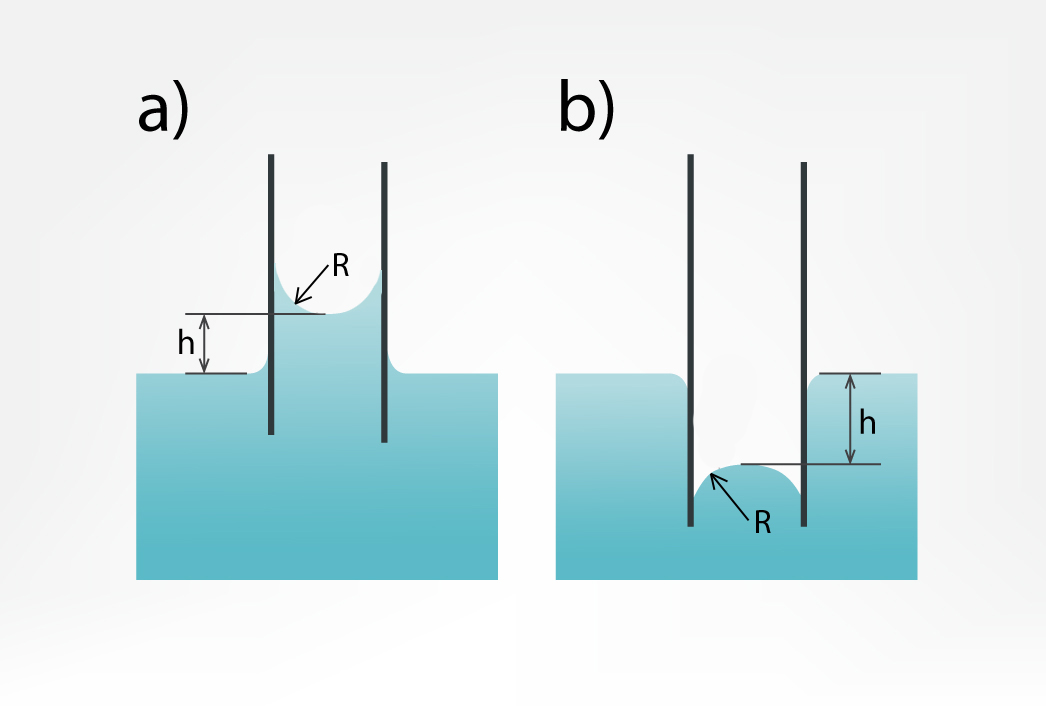
8.att. Kapilārās parādības slapināšanas (a) un neslapināšanas (b) gadījumā
Kapilārās parādības ir nozīmīgas dažādos bioloģiskos procesos, piemēram, kapilārajām parādībām ir pakļautas asinis smalkajos asinsvados – kapilāros. Acs ābola nepārtraukta mitrināšana ar asarām notiek caur divām tievām kapilāru “caurulītēm”. Arī augu barības vielu transportā liela nozīme ir kapilārajām parādībām, jo augu stumbrs sastāv no ļoti daudzu kapilāru sakopojuma.

9.att. Augu barības vielu transportā kapilārajām parādībā ir liela nozīme
Apskaties ar DZM materiālu par “Šķidruma virsmas īpašībām”.
Virsmas spraiguma spēku var novērtēt, izmantojot ziepjūdens plēvīti. Ja mēs no stieples izveidojam rāmīti, kuram ir viena kustīga mala garumā l (1. att. a), tad, iemērcot to ziepjūdenī, uz tā izveidojas ziepjūdens plēvīte (1. att. b), turklāt kustīgajai malai ir jābūt pieliktam spēkam F, kas kompensē ziepjūdens plēvītes virsmas spraiguma spēku Fs. Ja rāmīša kustīgo malu lēnām pārvieto par attālumu Δl (1. att. c) tā, ka nemainās plēvītes temperatūra, tad padarītais darbs A ir vienāds ar virsmas enerģijas pieaugumu ΔU = FΔl.
Virsmas enerģijas pieaugumu var izteikt kā ΔU = σΔS, kur
σ - virsmas spraiguma koeficients,
ΔS - virsmas laukuma pieaugums.
Līdz ar to virsmas spraiguma koeficientsσ = ΔU : ΔS.
Ņemot vērā, ka ΔU = σΔSun ΔU = Fs.Δl, kā arīΔS = lΔl, iegūstam iepriekš apskatīto formulu σ = FS : l .
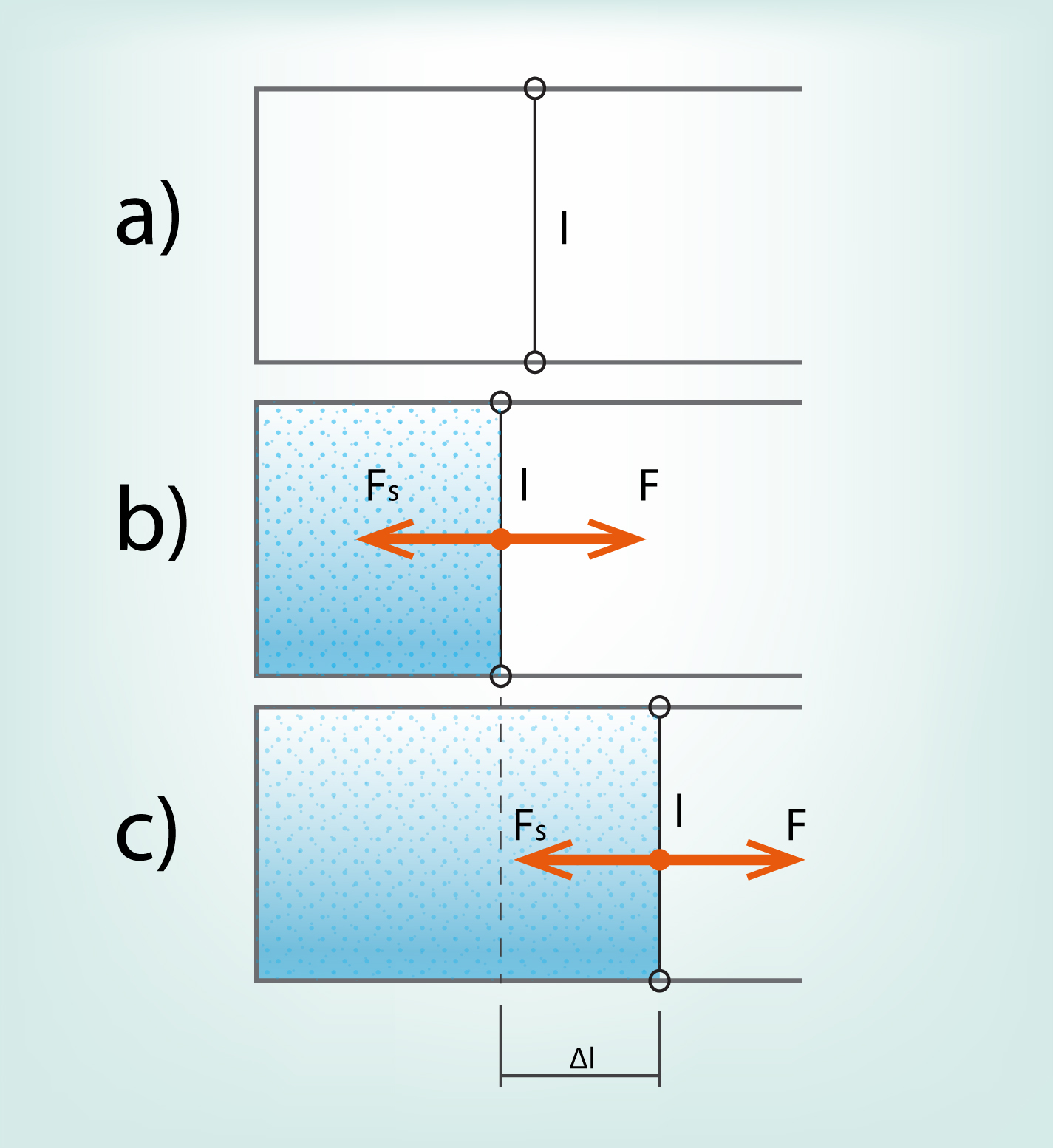
1.att. Ziepjūdens plēvīte uz rāmīša ar vienu kustīgu malu
Nosakot spēku, kas darbojas uz rāmīša kustīgo malu (1. att.), ir jāņem vērā, ka ziepjūdens plēvītei ir divas virsmas (2. att.), līdz ar to kopējais spēks veidosies no divu virsmu spraiguma spēku summas.
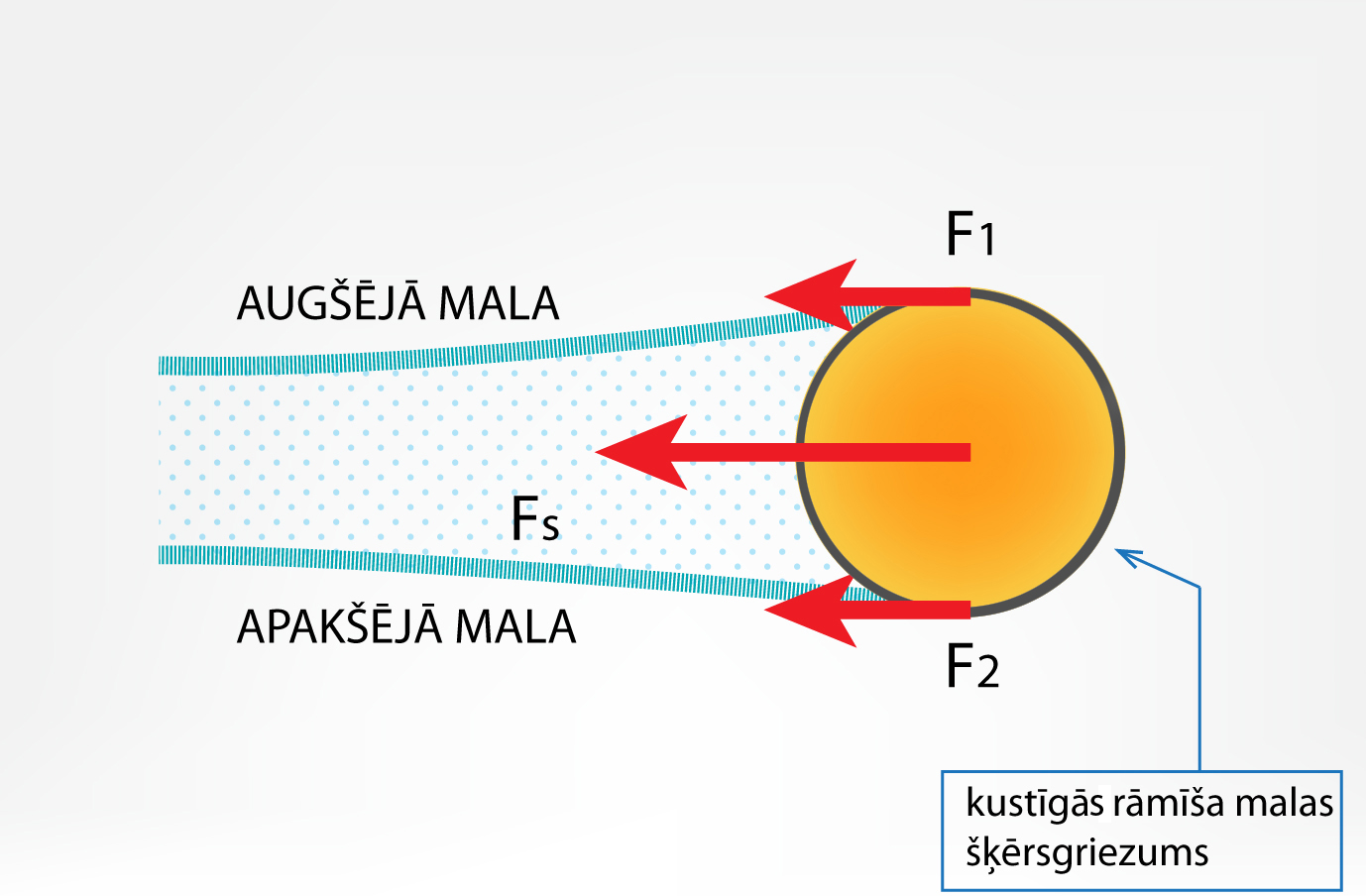
2.att. Ziepjūdens plēvītei ir divas virsmas
Dažādu vielu virsmas spraigumu koeficientu salīdzinājums redzams 3. att. Ļoti liels virsmas spraiguma koeficients ir dzīvsudrabam. Ja dzīvsudrabu šķidrā stāvoklī novieto uz kādas virsmas, tad tas savelkas sfēriskās bumbiņās. Ziepjūdens šķīdumam virsmas spraiguma koeficients ir teju 12 reizes mazāks, tomēr, ja mēs izveidojam no tā burbuli un palaižam gaisā, tad arī tas ieņem sfērisku formu (4. att.), jo gaisā esošo gāzu molekulu koncentrācija ir pārāk maza, lai mijiedarbība ar tām spēcīgi ietekmētu burbuļa sfērisko formu, un mazā svara dēļ smaguma spēka ietekme arī ir niecīga.
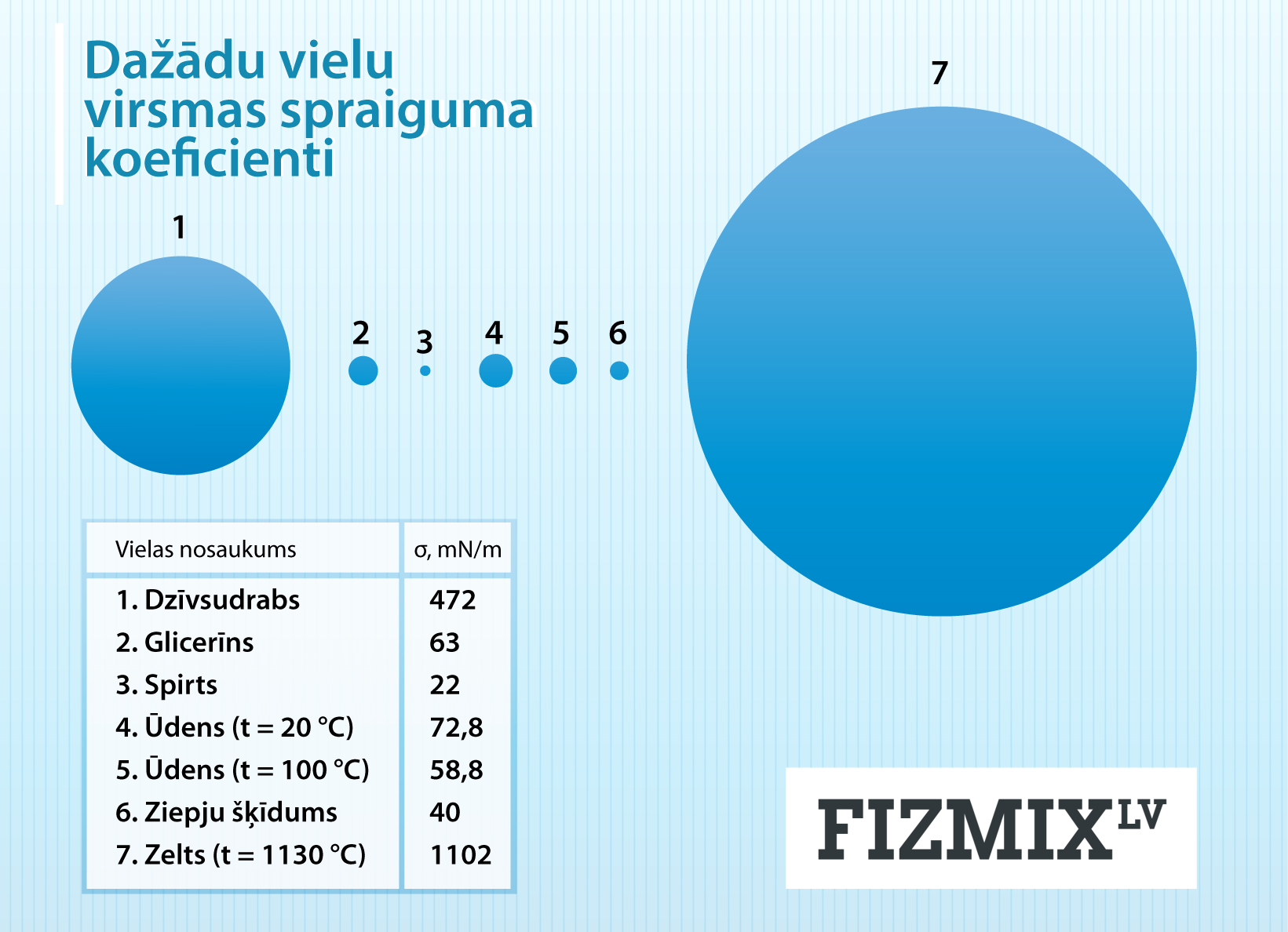
3.att. Dažādu vielu virsmas spraiguma koeficienti

4.att. Gaisā ziepjūdens burbuļi
Iepriekš apskatījām, ka tievos kapilāros šķidruma līmenis atšķiras no traukā esošā šķidruma līmeņa par augstumu h. Šo augstumu var noteikt, izmantojot 3. Ņūtona likumu. Kapilārā esošā šķidruma virsma ir izliekta, un izliekuma rādiuss ir vienāds ar kapilāra rādiusu R. Šķidruma sprieguma spēks FS, kas gar ieliektais virsmas kontūru ir vērsts vertikāli augšup, kompensē paceltā šķidruma smaguma spēku F = mg (5. att.). Virsmas spraiguma spēks šajā gadījumā ir FS = σ2πR, kur R ir kapilāra rādiuss, bet paceltā ūdens masa m = ρV = ρR2h, kur
V - paceltā ūdens tilpums,
ρ - šķidruma blīvums.
Ievērojot, ka F=FS jeb ρR2hg = σ2πR, iegūst izteiksmi h=2σ:(ρgR).
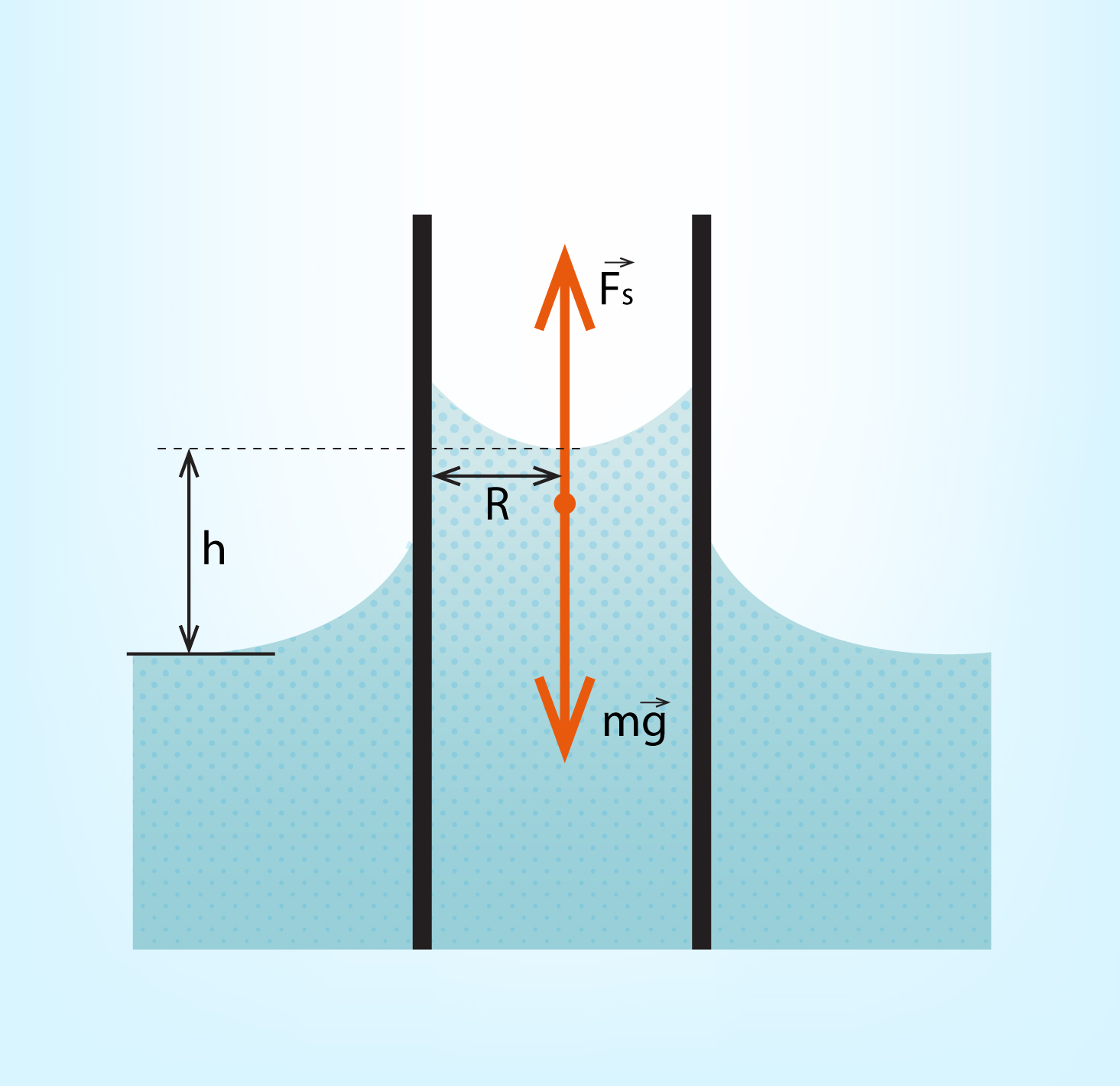
5.att. Uz kapilārā izliektās šķidruma virsmas darbojas 3. Ņūtona likums
Pamatojoties uz iegūto formulu, var izskaidrot, kādēļ, samazinot kapilāra rādiusu, šķidruma līmenis ir augstāks (6. att. a). Šeit gan jāatceras, ka ūdens līmenis kapilārā ir paaugstināts tad, ja šķidrums kapilāra virsmu slapina. Ja šķidrums virsmu neslapina, tad notiek līmeņa pazemināšanas (6. att. b), bet arī šajā gadījumā var lietot iegūto formulu, vienīgi šeit h būs augstums, par kādu pazeminās šķidruma līmenis.
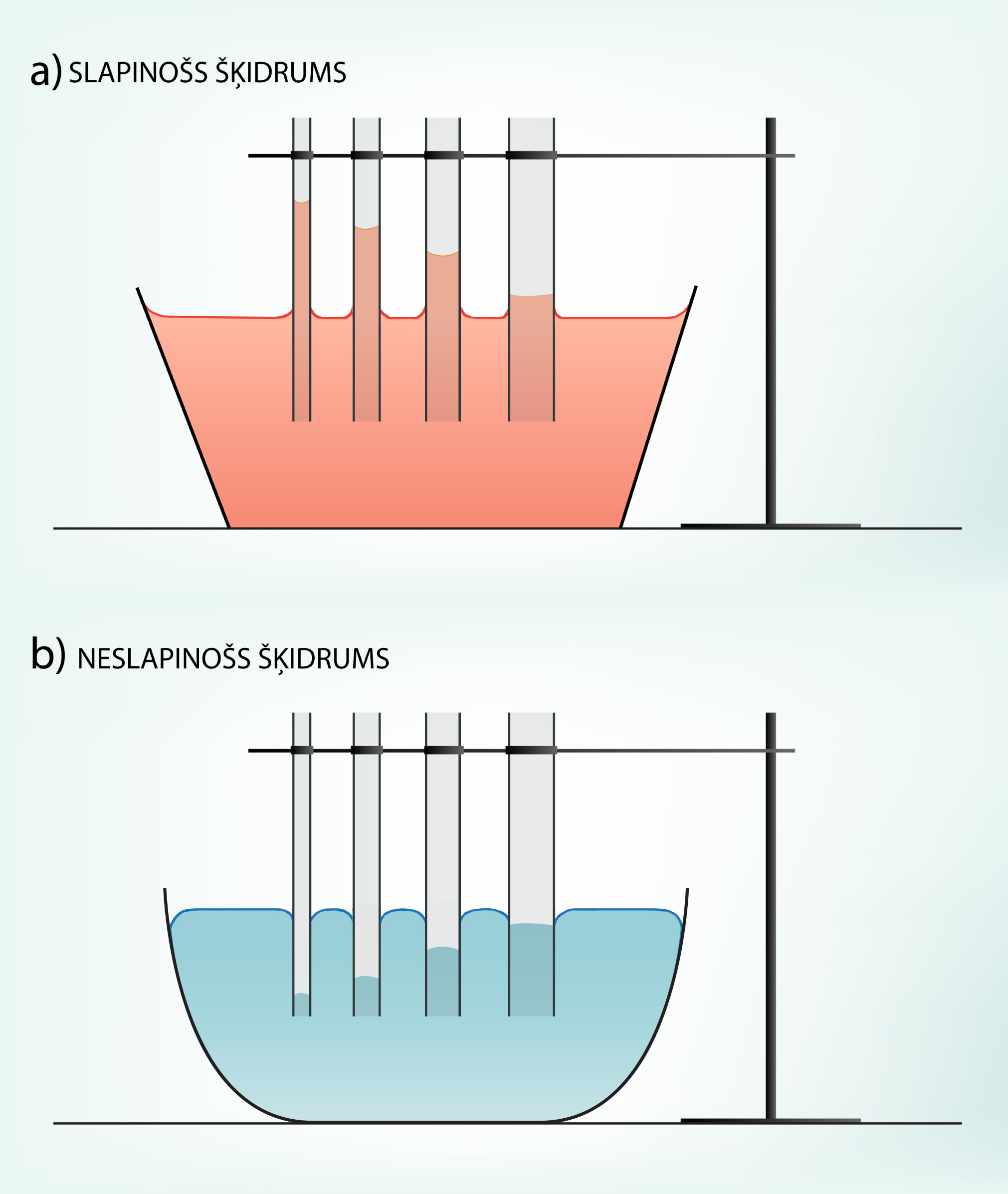
6.att. Ūdens līmeņa izmaiņas atkarībā no kapilāra diametra
Šķidruma virsmas spraiguma spēka dēļ šķidruma kārtiņa centīsies ieņemt tādu formu, lai tās virsmas laukums būtu pēc iespējas mazāks. Tas ir tādēļ, ka šķidruma kārtiņai piemīt brīvas virsmas enerģija E, kas ir proporcionāla virsmas laukumam S, un dabā ir iekārtots tā, ka sistēma cenšas ieņemt stāvokli ar vismazāko enerģiju. Brīvo virsmas enerģiju var aprēķināt pēc formulas E = σ.S, kur σ - virsmas spraiguma koeficients. Par šo faktu, ka šķidruma kārtiņa ieņems tādu formu, liecina tas, ka ziepjūdens burbuļi ieņem sfērisku formu, jo sfērai virsmas laukums pie noteikta tilpuma ir vislielākais. Ir, protams, arī citi apliecinājumi, piemēram, ja apskata ziepjūdens plēvītes formu dažādās rāmīšu konstrukcijās (1. att.), tad to izskats nav tāds, kā varbūt pirmajā brīdī šķiet, ka tam vajadzētu būt, jo ziepjūdens plēvīte ieņem stāvokli ar vismazāko virsmas laukumu.

1.att. Ziepjūdens plēvīte dažādās 3D konstrukcijās
Šķidruma slapināšanas parādības raksturošanai var lietot leņķi Θ, kādu šķidruma virsmas pieskare veido ar cieto virsmu (2. att.). Jo šis leņķis ir šaurāks (2. att. a), jo šķidrums virsmu vairāk slapina un tā pilieni uz cietās virsmas izplūst. Savukārt jo leņķis ir platāks (2. att. b), jo šķidruma piliens mazāk slapina virsmu un tā forma tiecas uz sfērisku pilienu.
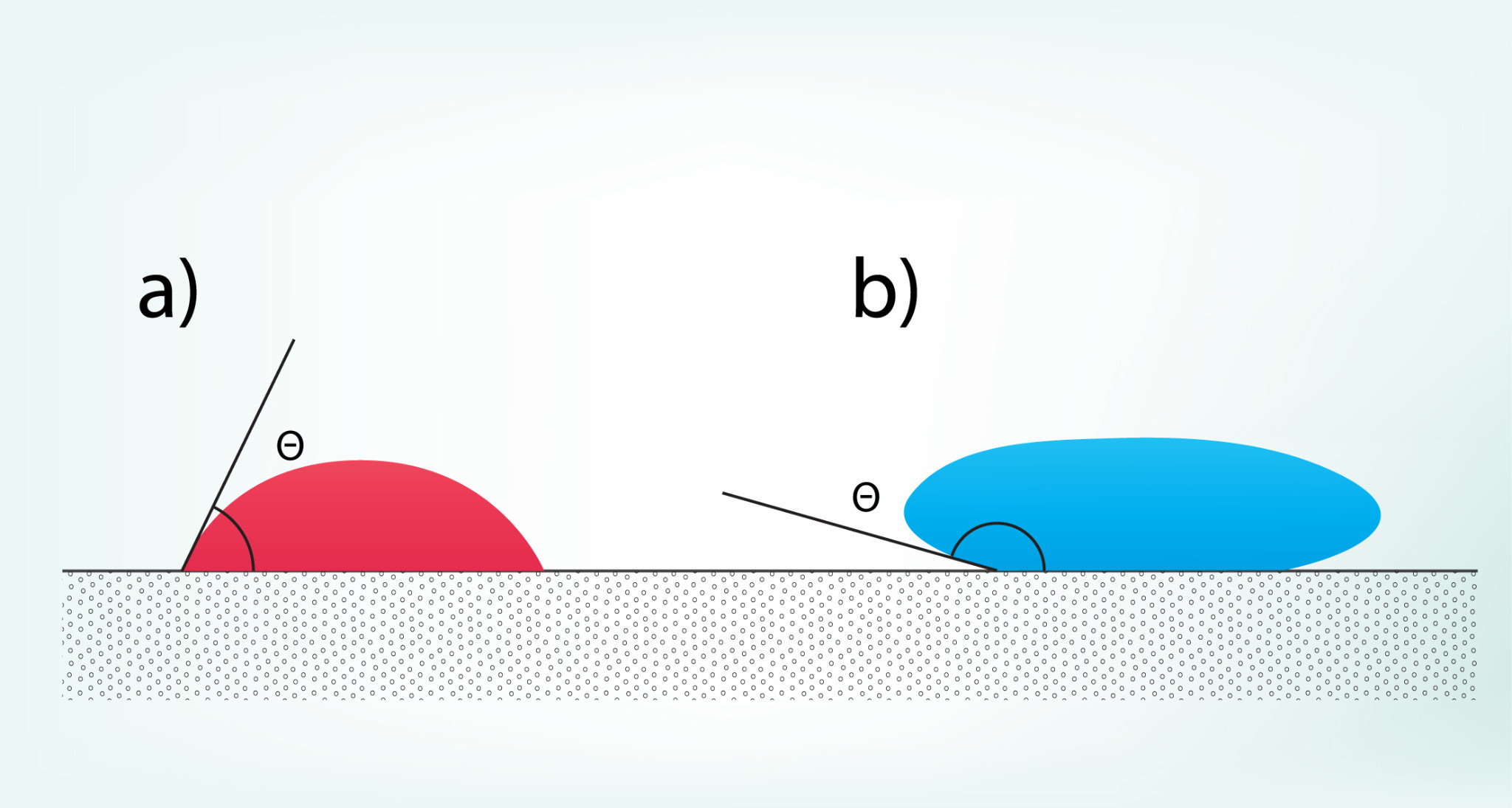
2.att. Šķidruma virsmas pieskares leņķis dažāds gadījumos
2. attēlā var redzēt, ka šķidrumiem, kas virsmu slapina mazāk, saskares laukums ar attiecīgo virsmu ir mazāks. Mazāks saskares laukums nozīmē, ka šo šķidrumu ir vieglāk atdalīt no virsmas. Šis princips darbojas, izmantojot mazgāšanas līdzekļus (3. att.). Ja uz virsmas ir eļļas (arī tauku) pilieni (3. att. a), tad tie virsmai ir pamatīgi pielipuši. Tad talkā nāk mazgāšanas līdzekļi, piemēram, ziepes, kas izveido kārtiņu ap eļļas pilienu (3. att. b). Šī kārtiņa nodrošina, ka eļļas piliens ar virsmu vairs tik intensīvi nemijiedarbojas, tādēļ tos ir vieglāk atdalīt (3. att. c).
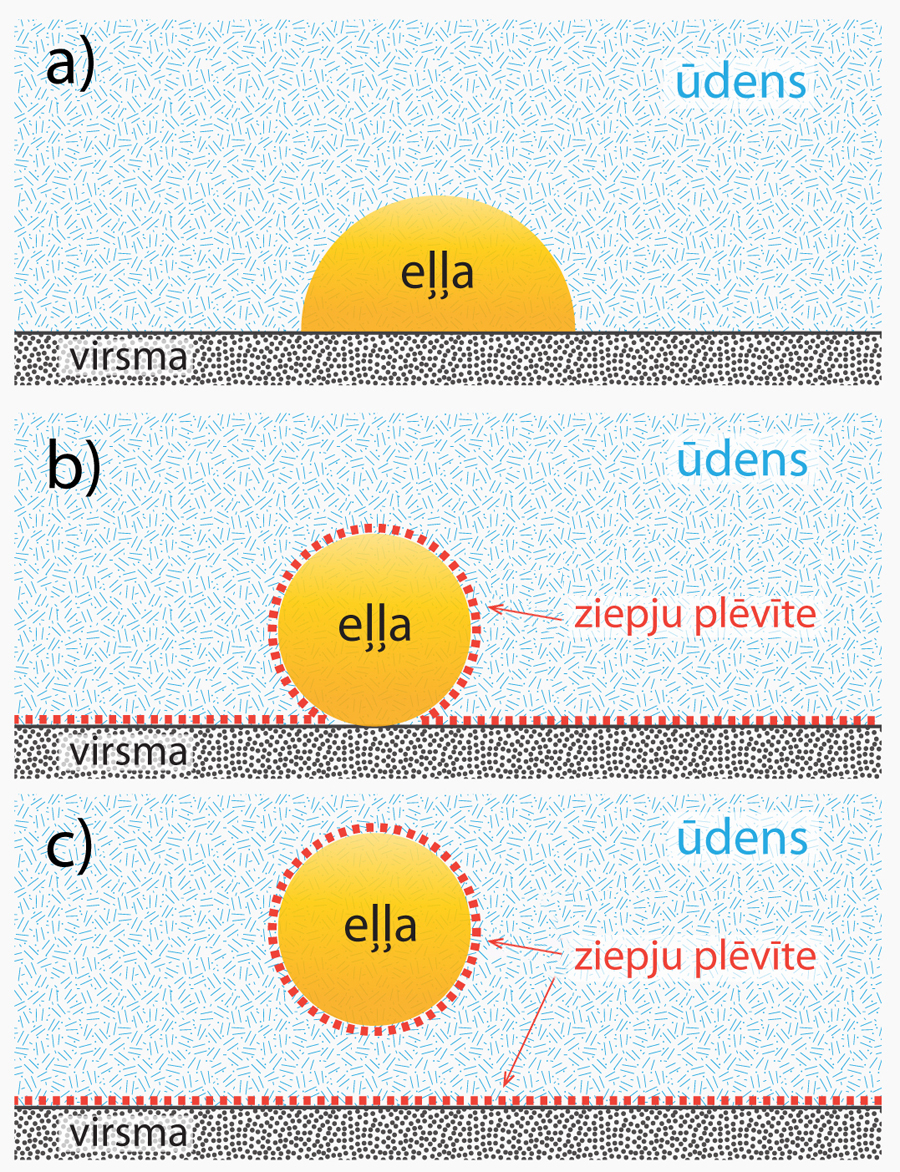
3.att. Mazgāšanas līdzeklis darbībā
2. solī, apskatot šķidruma augstuma izmaiņu kapilārā ar rādiusu R, tika pieminēts, ka spraiguma spēks kompensē paceltā šķidruma smaguma spēku, bet netika pieminēts, ka papildus šai kompensācijai spraiguma spēks veic korekcijas spiedienā, kas darbojas uz liekto virsmu (4. att.). Kopējo spiediena izmaiņu p var aprēķināt kā p = 2σ : R, kur
σ - virsmas spraiguma koeficients,
R - kapilāra rādiuss.
Ja virsma ir ieliekta (4. att. a), tad spiediens darbojas pretēji ārējam spiedienam un kopējo spiedienu uz virsmu samazina, bet, ja virsma ir izliekta (4. att. b), tad virsmas spraiguma spēka izraisītais spiediens rada papildu spiedienu uz virsmu.
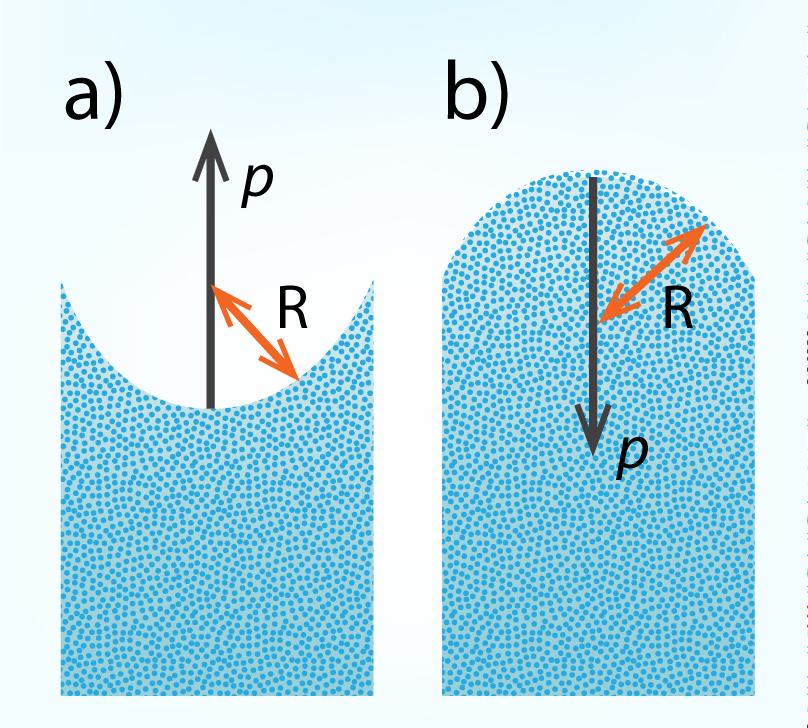
4.att. Uz liektām virsmām darbojas papildspiediens
Virsmas spraiguma dēļ no trauka caur sietu nelīst ārā šķidrums:
Skaties video par neparastajiem ziepju burbuļiem: