Spiediens šķidrumos un gāzēs
Nodaļā ''Cieta ķermeņa spiediens uz virsmu'' aplūkojām cieta ķermeņa spiedienu uz virsmu.
Spiediens (\(p\)) ir fizikāls lielums, kas raksturo, cik liels spēks darbojas uz virsmas laukuma vienību perpendikulāri virsmai: \(p=\frac{F_\mathrm{sp}}{S}\),
kur \(F_\mathrm{sp}\) – spiediena spēks, kas darbojas uz virsmu, bet \(S\) – tās laukums.
Spiediena mērvienība ir paskāls: \([p]=\frac{N}{m^2}=Pa\).
Spiediena rašānās mehānisms šķidrumos un gāzēs
Gāzes (un arī šķidruma) spiedienu uz trauka sienām rada gāzes molekulu triecieni.
Lūk, vienkāršots spiediena rašanās mehānisma apraksts. Iztēlosimies, ka gāze atrodas slēgtā nemainīga tilpuma traukā. Gāzes molekulas nepārtraukti un haotiski kustas, tādēļ tās triecas pret trauka sienām un atlec no tām. Katrai molekulai pirms sadursmes piemīt impulss \(mv\) kur \(m\) — molekulas masa, bet \(v\) — tās ātrums. Atlecot no trauka sienas, molekulas impulss mainās par \(\Delta (mv)\), un, atbilstoši impulsa nezūdamības likumam, šādu impulsu saņem trauka siena.
Līdz ar to, atbilstoši otrajam Ņūtona likumam, šī molekula uz trauka sienau iedarbojas ar spēku \(F_\mathrm{i} =\frac{\Delta (mv)}{\Delta t}\)
kur \(\Delta t\) — trieciena ilgums.
Tā kā molekulu ir ļoti daudz un tās kustas pilnīgi haotiski (visi kustības virzieni molekulām, kas kustas ar vienādu ātrumu, ir vienlīdz iespējami), molekulu triecienu spēkiem \(F_\mathrm{i}\) summējoties, to rezultējošais spēks \(F\), kas pielikts trauka sienai, ir vērsts perpendikulāri tai. Ja sienas laukums ir \(S\), tad uz to darbojas spiediens \(p = \frac{F}{S}\). (tuvāk gāzes spiediens aplūkots nodaļā ''Gāzes spiediens'').
Saskaņā ar Paskāla likumu, ko formulēsim šajā nodaļā, tāds pats gāzes spiediens darbojas arī visā gāzes tilpumā.
Protams, šādā sistēmā, kas sastāv no daudzām daļiņām, ir iespējamas spiediena fluktuācijas — neregulāras izmaiņas, kas ir jo jūtamākas, jo mazāks ir daļiņu skaits tilpuma vienībā. Ja gāze ir ļoti retināta, vai arī objekts, kas izjūt spiedienu ir mikroskopiski mazs, Paskāla likums lokāli var nebūt spēkā (skatīt nodaļu par Brauna kustību ''Vielas atomārā uzbūve'').
Šajā nodaļā aplūkosim, kā līdzsvarā esošs (būtībā nekustīgs) šķidrums vai gāze iedarbojas uz tajā iegremdētiem ķermeņiem, radot spiedienu uz tiem.
Gāzes no šķidrumiem būtiski atšķiras ar to dažādo saspiežamību. Gāzu saspiežamība ir liela, bet šķidrumus var uzskatīt par nesaspiežamiem - šķidruma blīvums (\(\rho=\frac{m}{V}\)) ārējas iedarbības rezultātā nemainās. Neraugoties uz šo atšķirību, līdzsvara stāvoklī gāzes un šķidrumi pakļaujas vieniem un tiem pašiem likumiem.
Ja uz šķidrumu vai gāzi, kas atrodas līdzsvarā (miera stāvoklī) cilindriskā traukā (1. attēls), spiež virzulis, tad, atbilstoši trešajam Ņūtona likumam, šķidrums darbojas uz virzuli ar skaitliski tik pat lielu, bet pretēji vērstu spēku.
Tieši uz virzuli darbojas tam tuvākais šķidruma slānis, bet uz to savukārt spiež dziļākie slāņi. Tāpēc virzuļa iedarbībā šķidrumā, līdzīgi kā cietā vielā, ārējā slodze rada spriegumu (skatīt nodaļu ''Mehāniskais spriegums''), kas pastāv visā šķidruma tilpumā. Statiskais spriegums šķidrumā būtiski atšķiras no tā sprieguma, ko ārējā iedarbība rada cietā vielā.
Šķidruma un gāzes slāņi, kā arī to molekulas, atšķirībā no cietu ķermeņu molekulām, var brīvi pārvietoties cita attiecībā pret citu visos virzienos.
Spiediena spēks šķidrumos un gāzēs
Varam iztēloties arī šķidrumā (vai gāzē) iegremdētu plānu plāksnīti vai vienkārši tilpuma elementu (1. attēls). Tā kā šķidrums atrodas līdzsvarā, šāds tilpuma elements nepārvietojas. Tātad - uz šādu ''plāksnīti'' šķidrumam no abām pusēm jādarbojas uz laukumu \(\Delta S\) ar spēkiem \(\Delta F\), kas, neatkarīgi no plāksnītes orientācijas, ir pretēji vērsti un skaitliski vienādi.
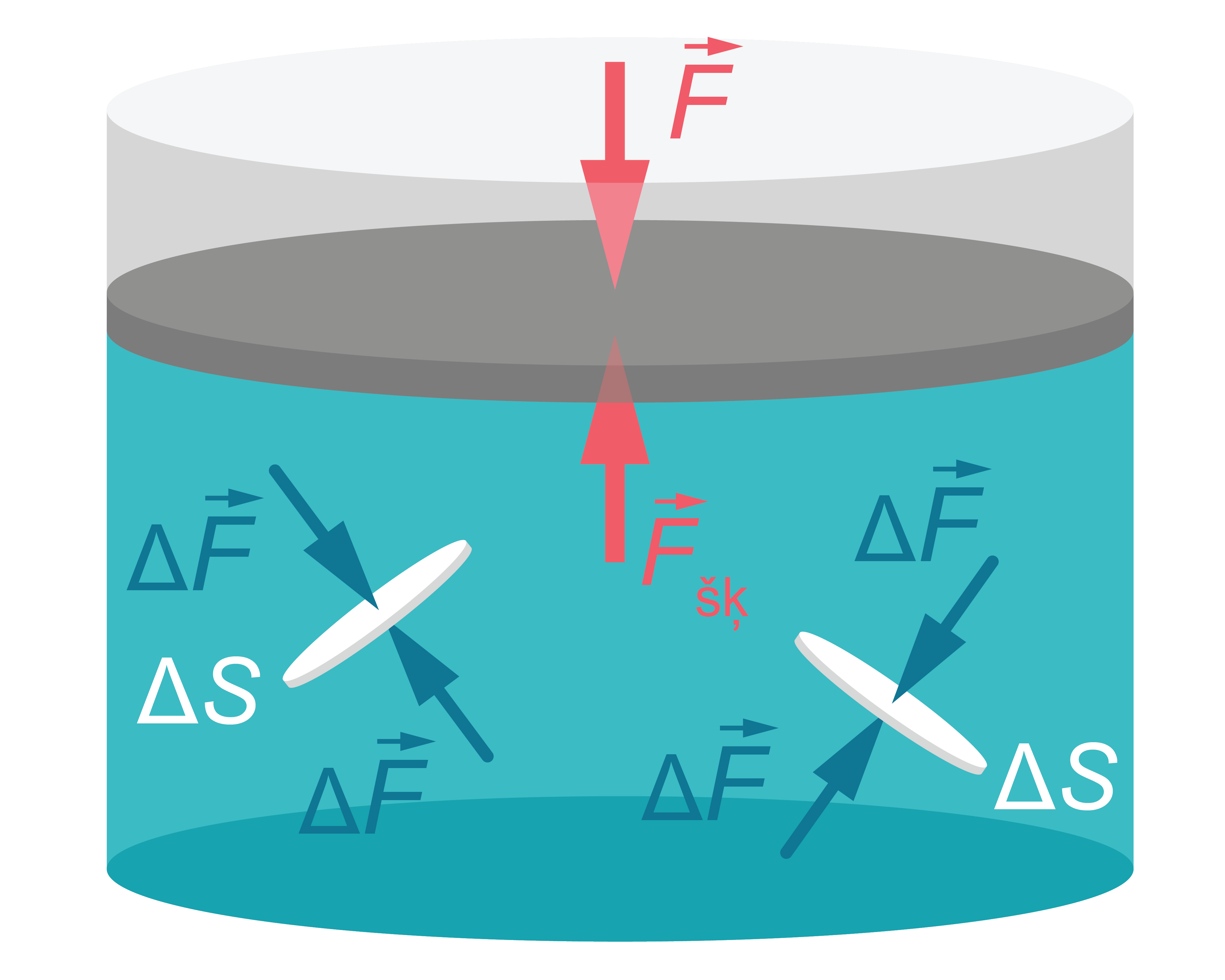
Secinājums – arī spriegums, kas darbojas uz ''plāksnītes'' virsmu, katrā punktā vienmēr ir vērsts tai perpendikulāri (pa normāli). Tas nozīmē, ka šķidrumā un gāzē nepastāv tangenciāli spriegumi.
Lai uzsvērtu atšķirību no mehāniskā sprieguma cietā vielā, spriegumu šķidrumā (vai gāzē) sauc par spiedienu \(p\).
Līdz ar to, spiediens ir spēks, kas šķidrumā vai gāzē darbojas uz jebkuru virsmas laukuma vienību un ir vērsts perpendikulāri šim laukumam.
Protams, tāpat, kā cieta ķermeņa spiedienam uz virsmu, spiediena SI mērvienība ir paskāls: \([p]=\frac{N}{m^2}=Pa\).
Saistībā ar spiedienu šķidrumos vai gāzēs nereti izmanto arī citas spiediena mērvienības:
- bārs (bar) - 100000 Pa
- tehniskā atmosfēra (at) - 1 kg/cm2 - 98066 Pa
- fizikālā atmosfēra (atm) - 101325 Pa (parasti ar ''atmosfēru'' saprot šo vērtību)
- tors (milimetr dzīvsudraba stabiņa) (mm Hg) - 133,322 Pa (izmanto atmosfēras spiediena raksturošanai meteoroloģijā).
Paskāla likums
Fakts, ka šķidrumā vai gāzē spiediens (tātad arī spiediena spēks) vienmēr darbojas uz jebkuru laukuma elementu perpendikulāri, ir noformulēts Paskāla likumā:
Mierā esoša šķidruma vai gāzes jebkurā punktā spiediens visos virzienos ir vienāds. Ja tā nebūtu, tad šķidrumā vienmēr varētu atrast tilpuma elementu, uz kuru darbojošies spēki nav līdzsvaroti un notiktu šķidruma kustība.
Šķidrumam vai gāzei pieliktais ārējais spiediens izplatās bez pārmaiņām visā šķidruma vai gāzes tilpumā un ir vienāds visos tā punktos.
Pēdējo apgalvojumu var pamatot, aplūkojot ar virzuli hermētiski noslēgtu trauku, kurā atrodas gāze (2. attēls).
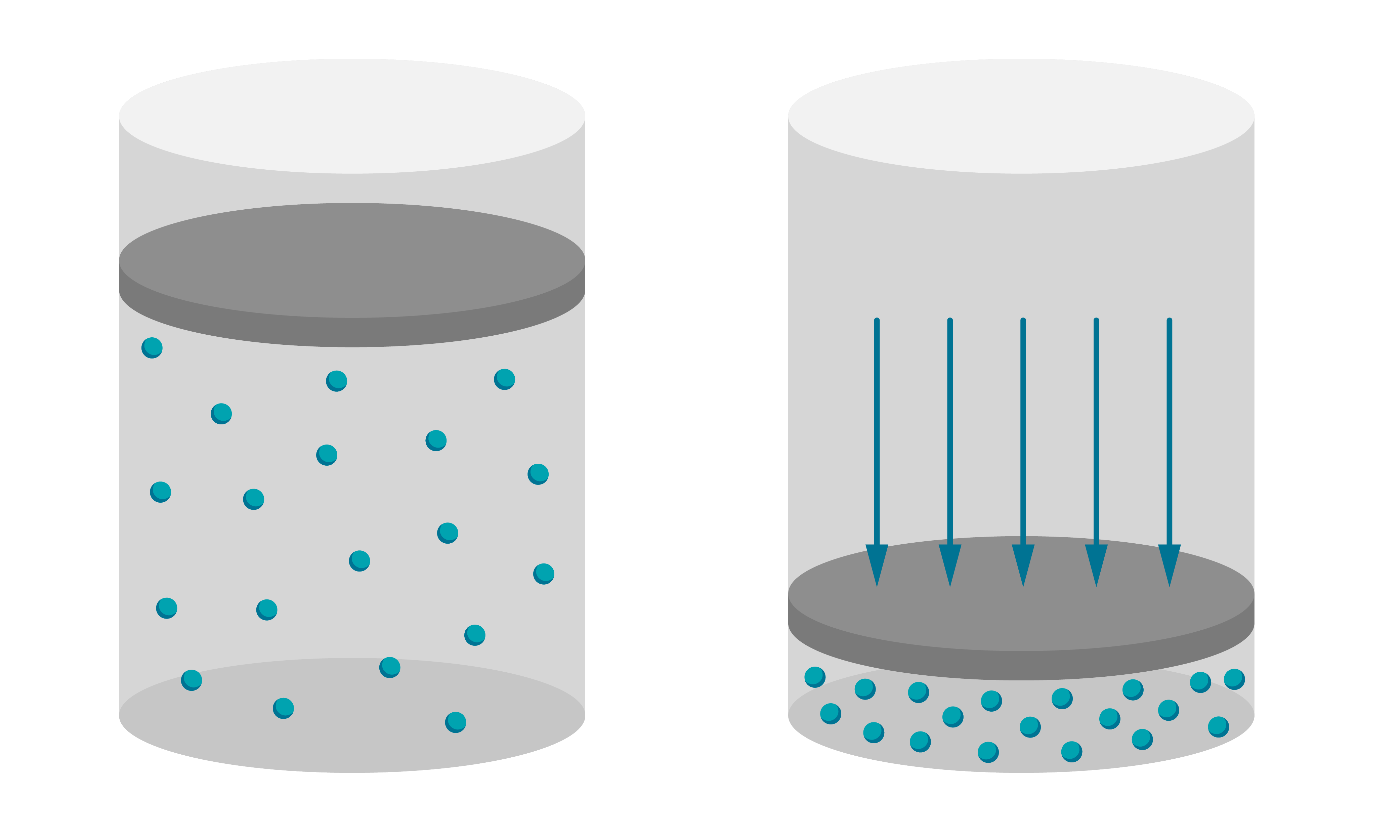
Gāzes molekulas ir vienmērīgi sadalītas visā trauka tilpumā. Gāzi saspiež - ārējā spēka iedarbībā tā ieņem jaunu, mazāku tilpumu, taču molekulu skaits paliek nemainīgs. Molekulas atkal izvietojas vienmērīgi visā trauka tilpumā.
Tā kā spiedienu gāzē rada molekulu triecieni, tad ārējā spēka darbības rezultātā spiediens ir vienādi palielinājies visos trauka punktos vienādi, jo vienādi ir palielinājusies molekulu koncentrācija - molekulu skaits tilpuma vienībā.
Pamatojoties uz Paskāla likumu, var izskaidrot dažādas parādības, izveidot hidrauliskas ierīces. Tās aplūkosim nodaļā ''Hidrostatiskais spiediens''.
Hidrostatiskais spiediens
Hidrostatiskais spiediens ir šķidruma spiediens uz trauka, kurā tas atrodas, sienām un dibenu.
Vērojot klasisku demonstrējumu (1. attēls) var pārliecināties, ka dziļākos šķidruma slāņos spiediens ir lielāks, nekā augšējos slāņos, kā rezultātā ūdens izplūst no traukā esošā cauruma ar lielāku ātrumu.
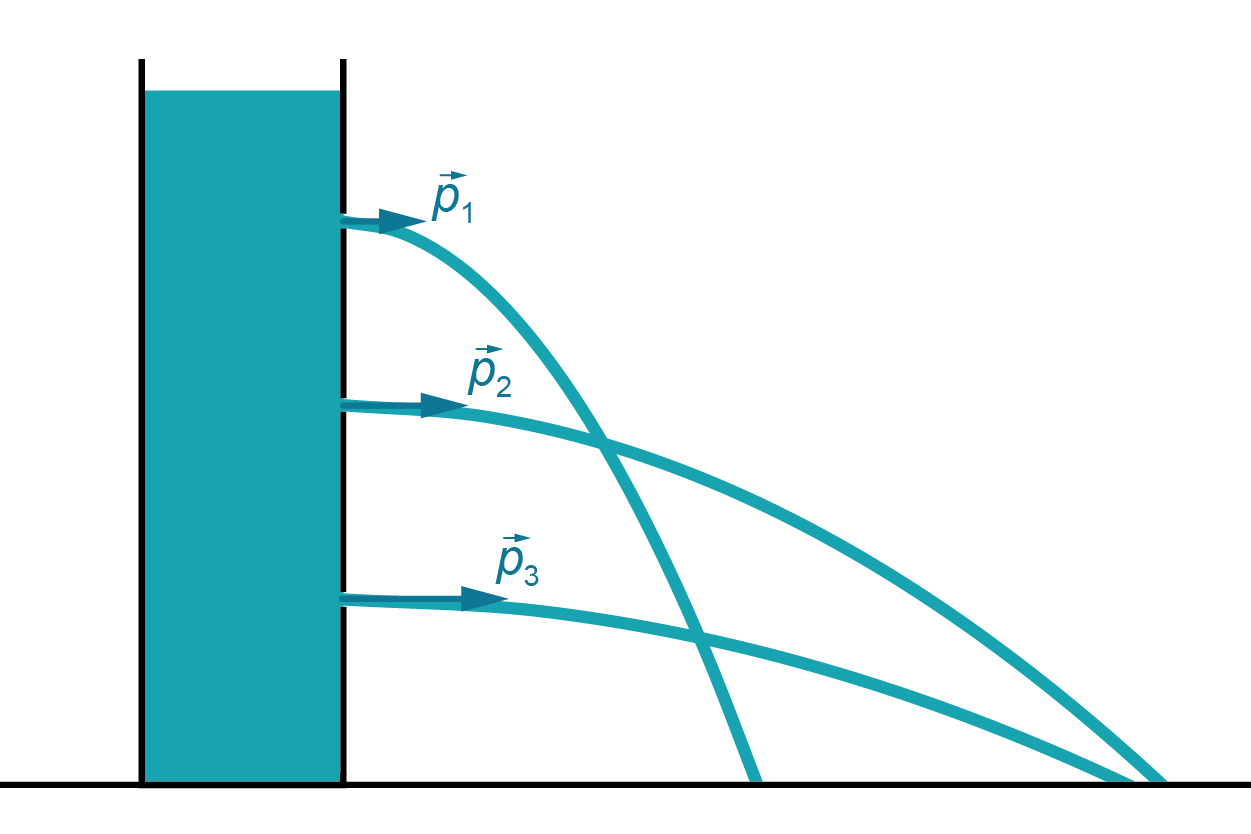
Tas ir tādēļ, ka uz šķidrumu vaļējā traukā darbojas atmosfēras spiediens, kā arī šķidruma augšējie slāņi smaguma spēka darbības rezultātā spiež uz dziļākajiem šķidruma slāņiem.
Neievērojot atmosfēras spiedienu, šķidruma ar blīvumu \(\rho\) stabs, kura augstums \(h\) un šķērsgriezuma laukumu \(S\), spiež uz laukumu ar savu svaru \(m g=\rho V g=\rho g h \cdot S\) (2. attēls a)
2.att. Hidrostatiskais spiediens
\(p_{\mathrm{šķ}}=\frac{\rho g h \cdot S}{S}=\rho g h \)
Ja ievēro arī atmosfēras spiedienu \(p_{a t m}\) un virzuļa radīto papildus spiedienu \(p_0=\frac{F_\mathrm{ā r}}{S}\), tad hidrostatiskais spiediens \(p=p_0+p_\mathrm{a t m}+\rho g h\)
Redzams, ka spiediens šķidrumā ir atkarīgs tikai no ārējā spiediena \(p_\mathrm{ ār}=p_0+p_\mathrm{a t m}\) un šķidruma staba augstuma \(h\). Līdz ar to, dažādas formas traukos, kuros vienādā līmenī ieliets viens un tas pats šķidrums, spiediens uz trauka dibenu un spiediens uz trauka sienām vienādā augstumā būs vienāds.
Ja ielejam šķidrumu traukos ar vienādiem pamata laukumiem, kuru pašu masu var neievērot, spēks ar kādu šķidrums spiež uz trauka dibenu, var būt gan lielāks, gan mazāks par trauka svaru – šo pretrunīgo faktu sauc par hidrostatisko paradoksu. Skaidrojums varētu būt šāds: saskaņā ar trešo Ņūtona likumu – ja šķidrums, atbilstoši Paskāla likumam, spiež uz trauka sienām perpendikulāri tām, tad trauka sienas spiež uz šķidrumu, ''palīdzot'' to noturēt vai arī iedarbojoties ar papildus spēku.
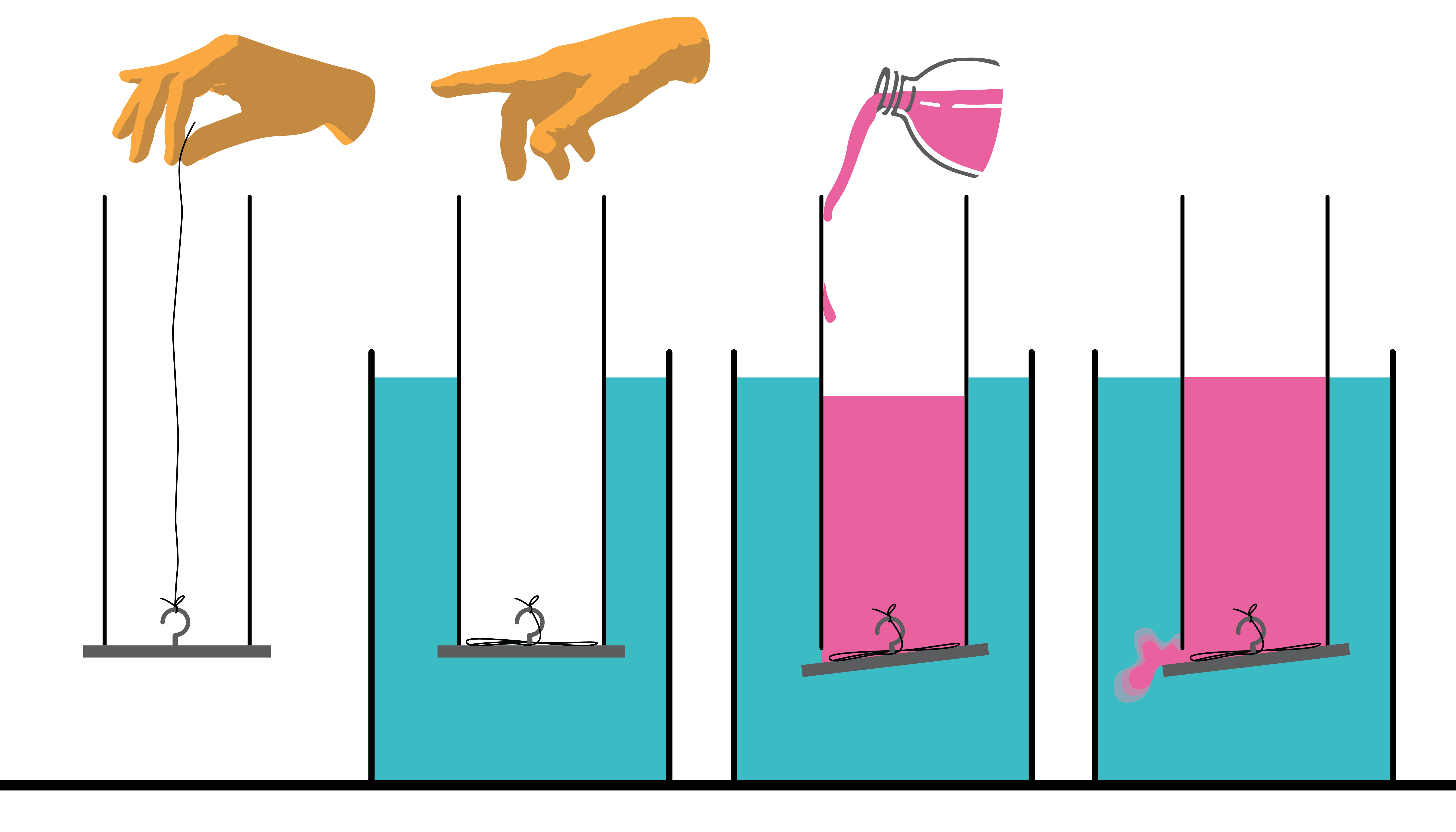
Hidrostatiskais spiediens ļauj izprast klasisko demonstrējumu, kurā izpaužas Paskāla likums: iegremdējot ūdenī stikla caurulīti, kurai viens gals aizverams ar plānu plāksnīti, to pieturot (3. attēls). Ūdenī plāksnīte turas pie cilindra, jo, atbilstoši Paskāla likumam, uz to no apakšas spiež ūdens. Tā nenokrīt arī tad, ja caurulīti ūdenī ievieto slīpi vai tajā ielej nedaudz iekrāsota ūdens. Plāksnīte atkrīt tikai tad, kad ūdens līmenis cilindrā ir vienāds ar ūdens līmeni traukā – ūdens spiediens no abām pusēm kļūst vienāds un plāksnīte nokrīt smaguma spēka darbības dēļ.
Izpratni par hidrostatisko spiedienu izmanto dažādos tehniskos risinājumos un ierīcēs.
Piemēram, būvējot aizsprostus, to apakšējo daļu veido biezāku, jo jāiztur lielāku ūdens spiedienu (4. attēls).
Jebkura līdzsvarā esoša (nekustīga) šķidruma virsma vienmēr būs horizontāla – smaguma spēka iedarbībā šķidruma daļiņas pārvietosies no augstākas vietas uz zemāku, līdz tās visas atradīsies vienlīdz zemu – cik tas būs iespējams. Šādu horizontālu virsmu sauc par šķidruma līmeni.
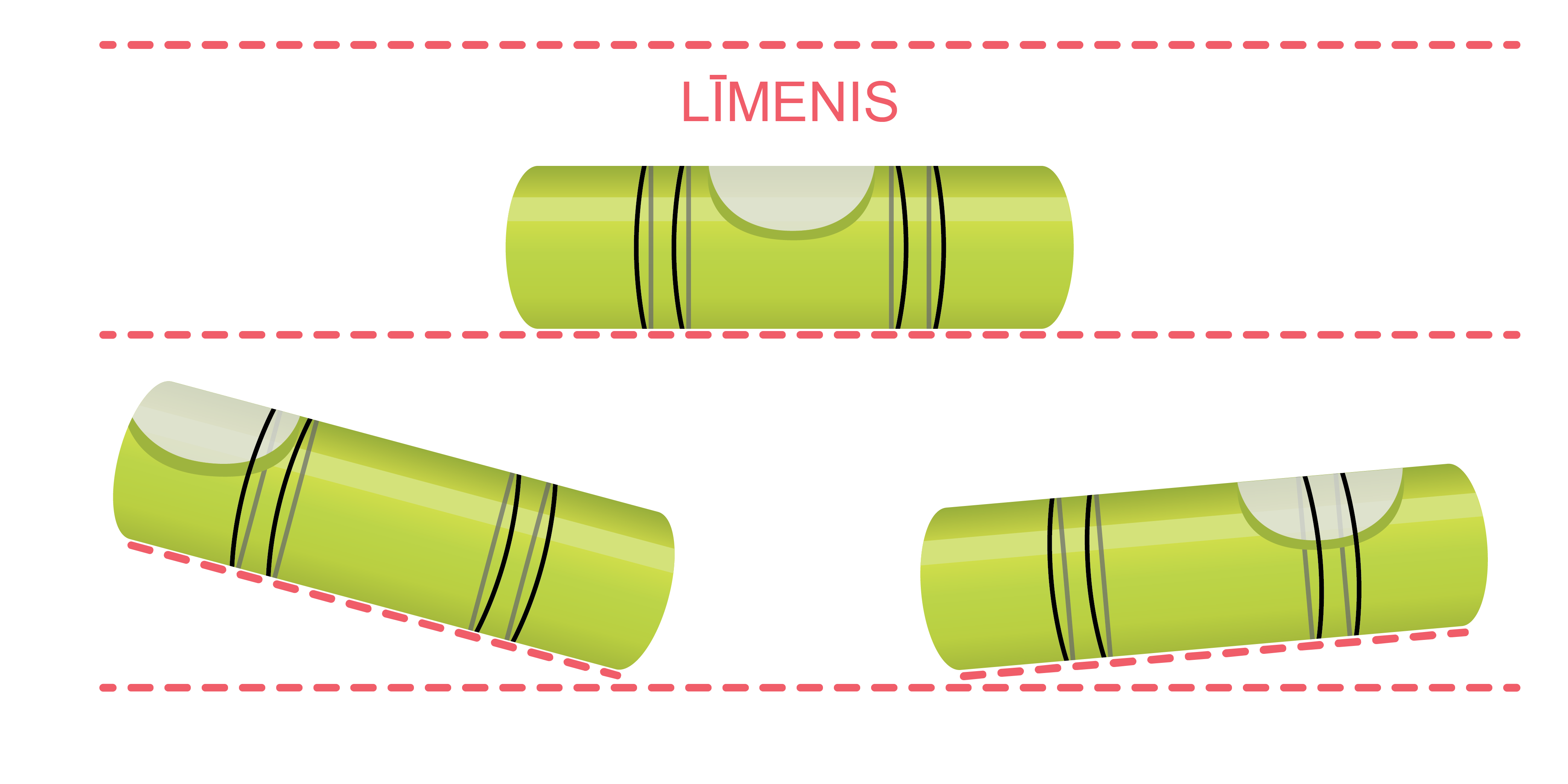
Fakts, ka šķidruma virsma vienmēr ir horizontāla, ir, piemēram, līmeņrāža darbības principa pamatā (5 .attēls) – gaisa burbulītis atradīsies caurulītes vidū tikai tad, ja tā būs novietota horizontāli:
Savienotie trauki
Paskāla likums un hidrostatiskais spiediens ļauj izskaidrot šķidruma līmeni savienotajos traukos.
Jebkurus divus vai vairākus savā starpā savienotus traukus, kuros šķidrums var brīvi pārplūst no viena trauka otrā, sauc par savienotajiem traukiem. Kādi ir šķidruma līdzsvara nosacījumi?
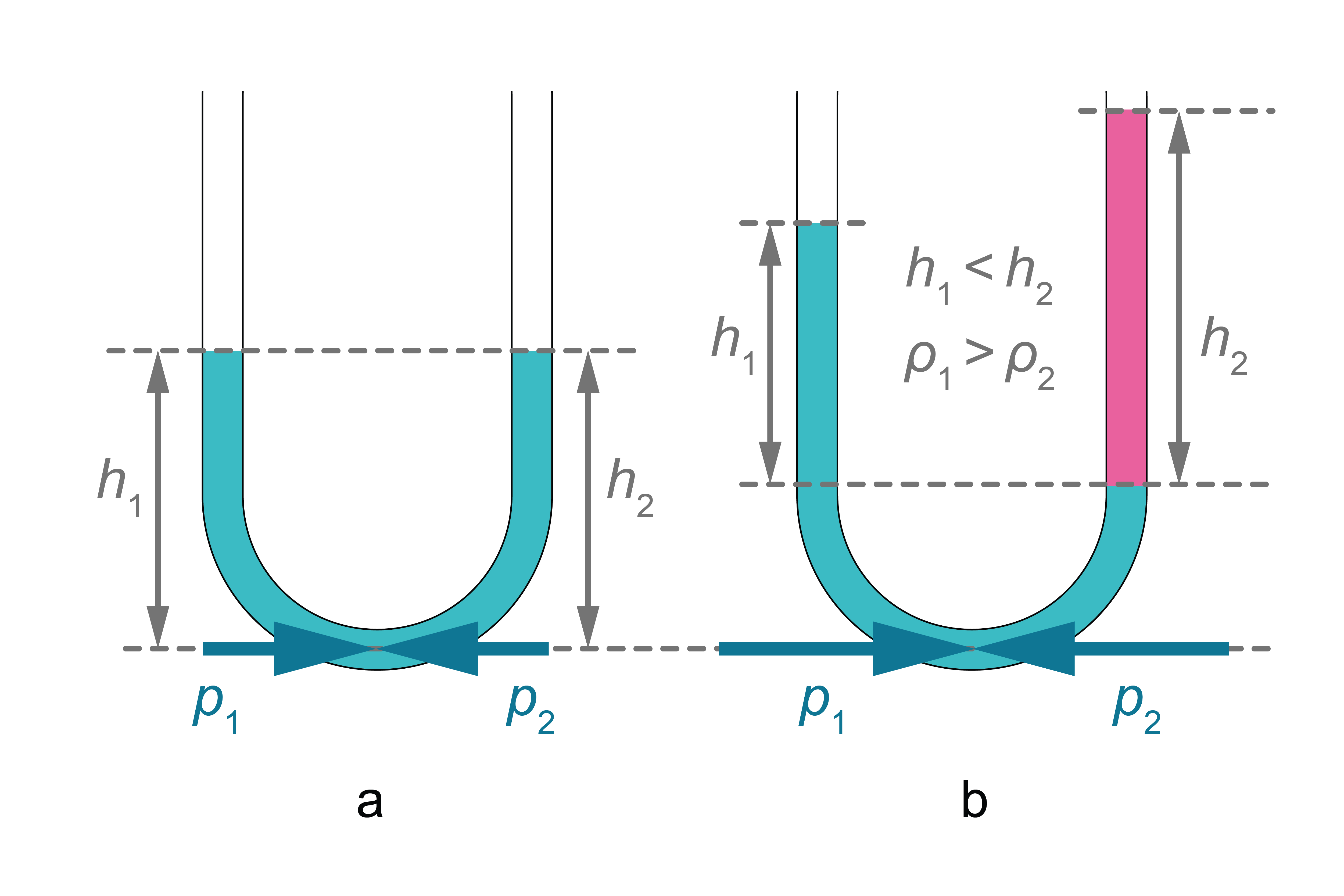
Aplūkosim šķidrumu U veida caurulītē. Šķidrums atrodas līdzsvarā, ja abu šķidruma stabu spiediens no abām pusēm uz jebkuru šķērsgriezuma laukumu ir vienāds. t. i., \(p_1=p_2\) (6. attēls).
Tas iespējams tikai tad, ja šķidruma līmeņi abos traukos ir vienādi: \(h_1=h_2\). Tad \(p_1=\rho g h_1\) un \(p_2=\rho g h_2\). (6. attēls a). Ja šķidruma stabu augstumi atšķirtos, šķidrums, spiediena spēku atšķirības dēļ, pārvietotos no trauka, kur līmenis ir augstāks, uz trauku, kur šķidruma līmenis ir zemāks, līdz spiedieni kļūtu vienādi.
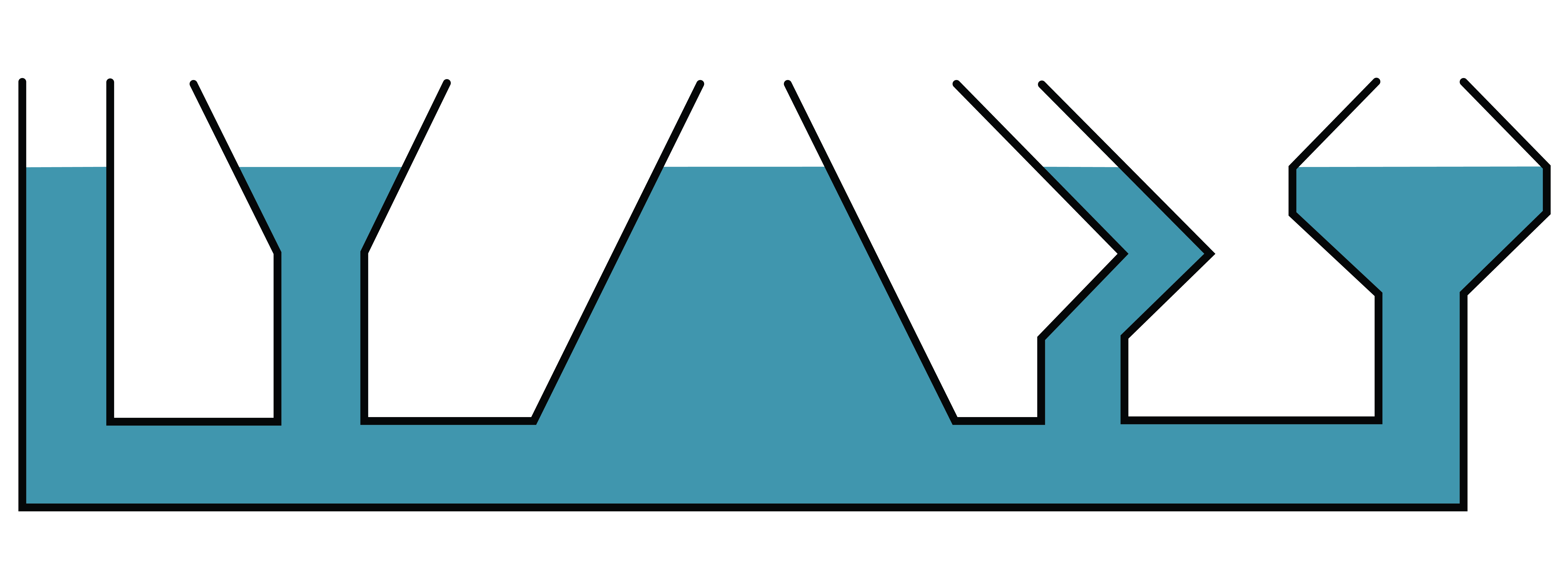
Tātad - jebkuras formas savienotajos traukos līdzsvarā esošā šķidruma līmeņi ir vienādā augstumā (7. attēls.).
Ja savienotajos traukos atrodas atšķirīgi šķidrumi, kuri nesajaucas, šķidruma stabu augstumi atšķiras (6. attēls b).
\(\rho_1 g h_1=\rho_2 g h_2\), tātad \(\rho_1 h_1=\rho_2 h_2\): tā šķidruma līmenis, kura blīvums ir mazāks, ir augstāks - šķidrumu līmeņu augstumi ir apgriezti proporcionāli šķidrumu blīvumiem.
Savienoto trauku principa pielietojumi
Savienoto trauku darbības princips ir pamatā daudzu sadzīvē lietojamo ierīču uzbūvei, arī ēku ūdensapgādei. Ūdeni uzsūknē ūdenstornī, kurš ir augstāks par visaugstāko namu (tvertne var atrasties ēkas bēniņos). No tvertnes pa caurulēm ūdens nokļūst namu ūdensvados, kur tas tiecas pacelties tikpat augstu kā tvertnē (8. attēls).
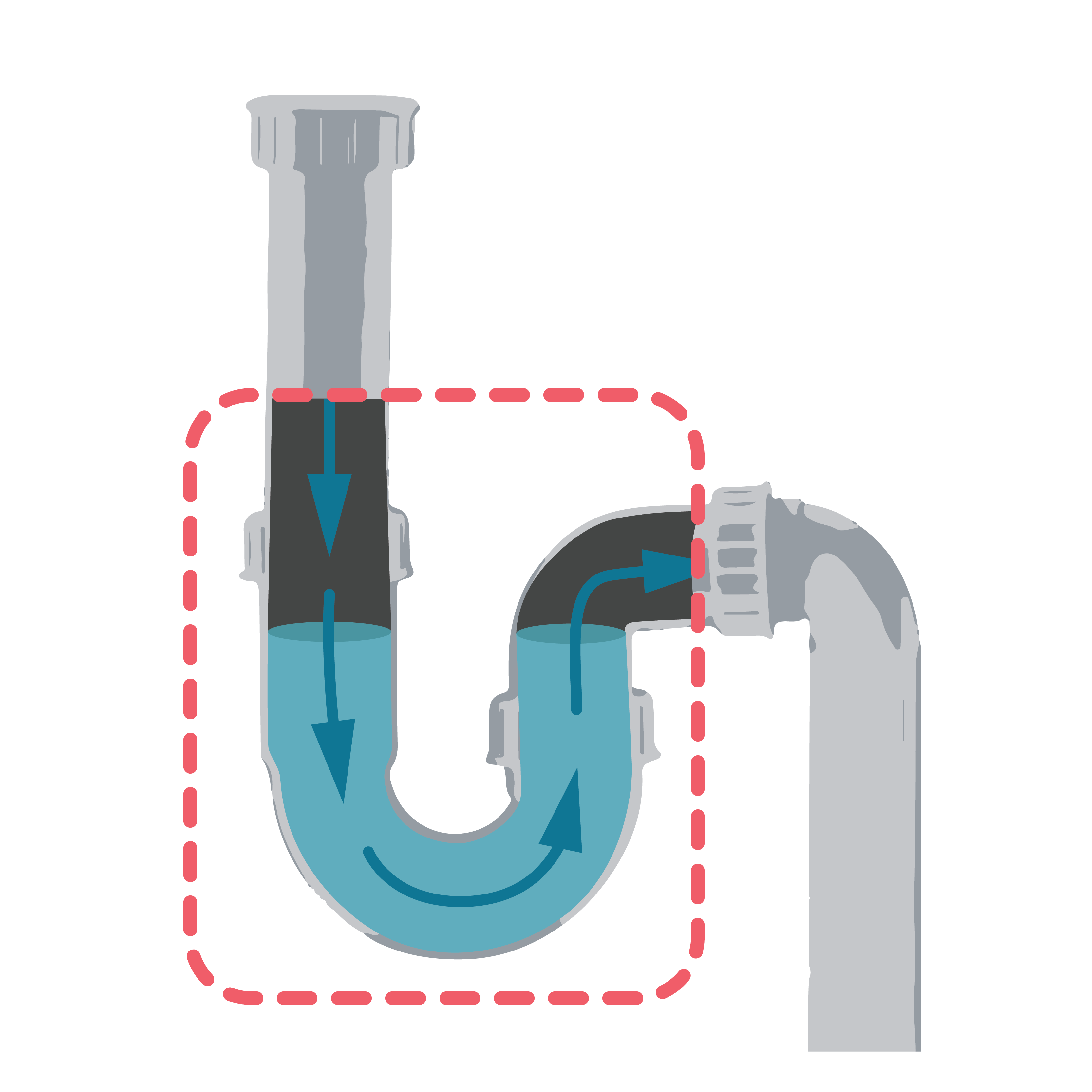
Šo principu izmanto arī, lai novērstu kanalizācijas smaku: zem izlietnes atrodas sifons - izliekta caurule. Sifonā palikušais tīrais ūdens neļauj smakai nokļūt telpā (9. attēls).
Arī upju un kanālu slūžu darbības pamatā ir savienoto trauku princips.
Paskāla likums un hidrostatiskā spiediena rašanās ir arī dažādu hidraulisku ierīču darbības pamatā.
Ja divi vertikāli cilindri noslēgti ar virzuļiem, ar ārēja spēka palīdzību šķidrumā var radīt spiedienu, kas daudzas reizes pārsniedz hidrostatisko spiedienu. Var uzskatīt, ka spiediens \(p\) visā sistēmā ir vienāds. Ja virzuļu laukumi ir \(S_1\) un \(S_2\), šķidrums uz virzuļiem darbojas ar spēkiem: \(F_1=p S_1\) un \(F_2=p S_2\) (10. attēls).
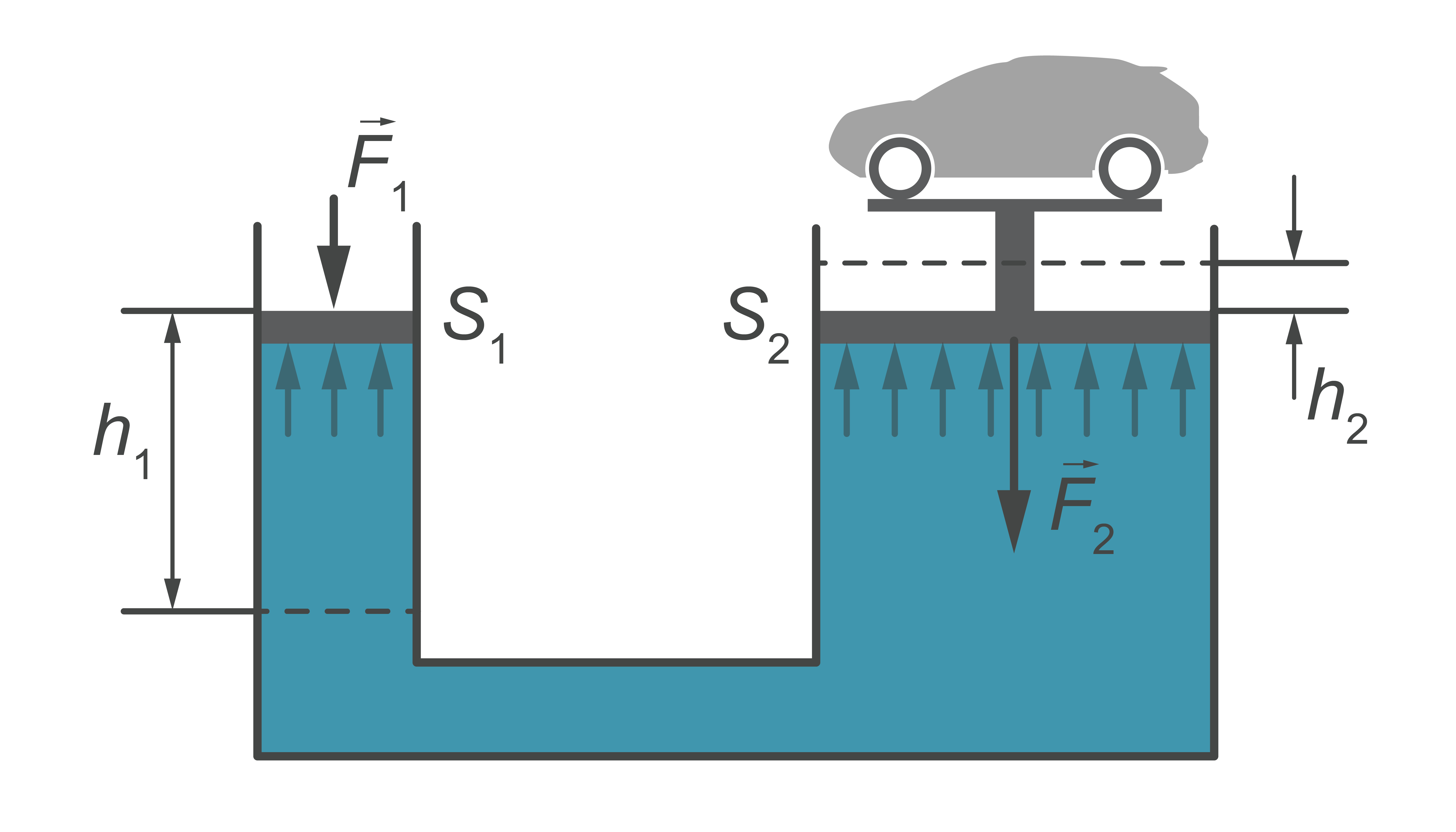
Tātad – hidrauliskā iekārta ļauj lielu spēku līdzsvarot ar mazu spēku.
Protams, darba ietaupījums nav iespējams – ja mazākais virzulis pārvietojas par attālumu \(h_1\), lielākais pārvietojas tikai par attālumu \(h_2\), jo šķidrums praktiski nav saspiežams un tā tilpums nemainās.
\(\begin{gathered} F_1 h_1=F_2 h_2 \\ h_2=h_1 \frac{S_1}{S_2} F_2=F_1 \frac{S_2}{S_1} \end{gathered}\)
Reālās situācijas, ievērojot to, ka šķidrums ir nedaudz saspiežams un darbojas berzes spēki, iegūtais spēka ietaupījums būs mazāks.
Uz šķidrumā vai gāzē iegremdētu ķermeni darbojas Arhimēda spēks, kas rodas hidrostatiskā spiediena atšķirības dēļ dažādā dziļumā zem šķidruma virsmas, to aplūkojam nodaļā ''Arhimēda spēks''.
Atmosfēras spiediens
Nodaļā ''Spiediens šķidrumos un gāzēs'' iepazināmies ar Paskāla likumu, nodaļā ''Hidrostatiskais spiediens'' aplūkojām, kā šķidruma vai gāzes ''stabs'' rada spiedienu uz ķermeņiem, kas šajā šķidrumā vai gāzē atrodas.
Atmosfēra ir gaisa slānis, kas aptver Zemi, un tā sniedzas aptuveni līdz 2000 km augstumam (atmosfēras biezums faktiski ir ''norunas lieta'', literatūrā atrodami arī citi dati).
Gaisa molekulas atrodas Zemes smaguma spēka laukā - uz katru molekulu darbojas smaguma spēks, kura ietekmē gaisa molekulas ''krīt'' tuvāk Zemes virsmai. Taču, molekulu haotiskās kustības dēļ, tās arī pārvietojas pretējā virzienā. Rezultātā gaisa blīvums atmosfērā ir atkarīgs no augstuma virs Zemes (2. attēls a). Mēs dzīvojam šā «gaisa okeāna» dibenā.
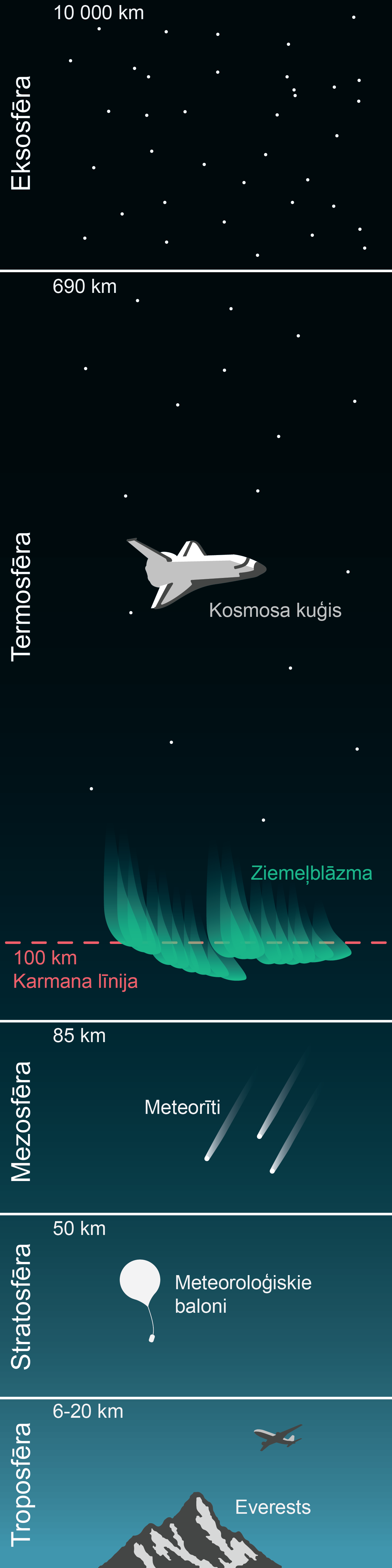
Atmosfēru atkarībā no augstuma virs Zemes mēdz iedalīt vairākos slāņos: troposfērā, stratosfērā, mezosfērā, termosfērā utt (1. attēls).
Ja paņemtu vienu kvadrāmetru lielu laukumu un saskaitītu kopā masu visām gaisā esošajām molekulām, kas virs tā atrodas, kopā iznāktu ap 10000 kg (2. att. b). Uz šādu masu darbojas aptuveni 100000 N liels gravitācijas spēks, kas, izdalot ar laukumu, uz vienu kvadrātmetru dod 100000 Pa lielu spiedienu - atmosfēras spiedienu.
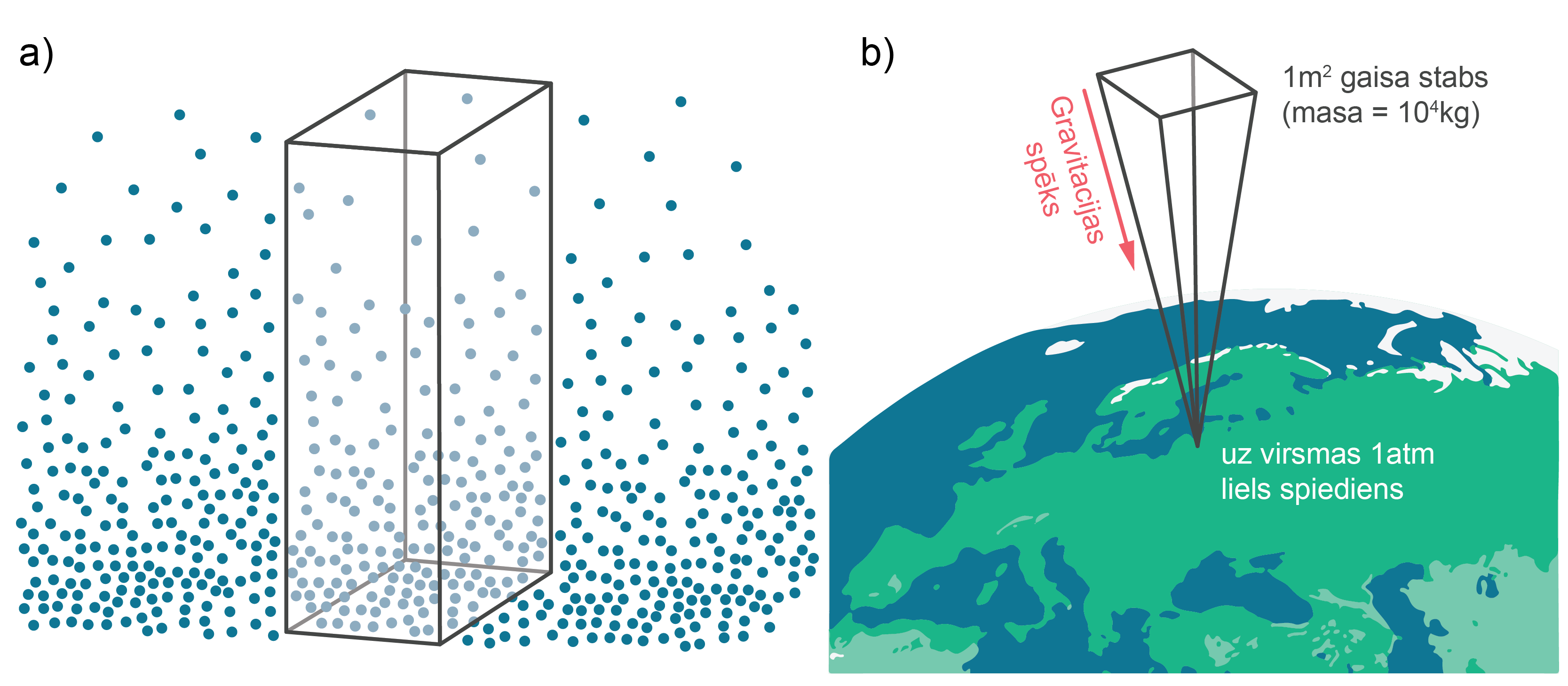
Savukārt, ja atmosfēra būtu homogēna un tās blīvums būtu 1,3 kg/m3, tā būtu tikai 8 km bieza.
78% kopējā atmosfēras tilpuma ir slāpeklis, 21% skābeklis, argons ir 0,9%, oglekļa(IV) oksīds 0,03% un neons, hēlijs, amonjaks, kriptons, slāpekļa oksīds, ūdeņradis, ozons kopā 0,07%.
Šo gāzu koncentrācijas un molmasas ir atšķirīgas, taču gaisa mehānisko īpašību un procesu analīzē gaisu var uzskatīt par viendabīgu gāzi, kuras molmasa ir 0,029 kg/mol.
Sausa gaisa blīvums 0 °C temperatūrā un vienas atmosfēras (101,308 kPa) spiedienā ir 1,293 kg/m3. Atmosfēras kopējā masa ir aptuveni 5,3∙1018 kg.
Augšējie gaisa slāņi spiež uz zemākajiem, atbilstoši Paskāla likumam radot spiedienu uz katru virsmu, kas atrodas gaisā. Gaisa smaguma spēka radīto hidrostatisko (aerostatisko) spiedienu sauc par atmosfēras spiedienu.
Tomēr atmosfēras spiedienu nevar rēķināt kā šķidruma hidrostatisko spiedienu uz trauka pamatu un sienām (\(p=\)\(p\)\(gh\)) – nepastāv konkrēta atmosfēras augstuma vērtība un gaisa blīvums mainās atkarībā no augstuma virs Zemes. Tādēļ atmosfēras spiedienu nosaka, to izmērot ar barometriem.
Toričelli eksperiments
Pirmoreiz atmosfēras spiedienu izmērīja E. Toričelli 1643. gadā (4. attēls). Metru garu stikla cauruli, kuras viens gals aizkausēts, piepildīja ar dzīvsudrabu, caurules vaļējo galu aizspieda, lai neizlītu, cauruli apvērsa ar aizkausēto galu uz augšu un vaļējo galu iegremdēja traukā ar dzīvsudrabu. Atbrīvojot caurules vaļējo galu, daļa dzīvsudraba izlija traukā, tomēr caurulē palika 760 mm augsts dzīvsudraba stabiņš virs dzīvsudraba līmeņa traukā. Caurules galā virs dzīvsudraba staba ir tikai dzīvsudraba tvaiki - Toričelli tukšums. E. Toričelli eksperimentu izskaidroja būtībā ar savienoto trauku principu – no vienas puses spiedienu rada atmosfēra, no otras puses – tikai dzīvsudraba stabiņš, un, atbilstoši Paskāla likumam, šiem spiedieniem jābūt vienādiem.
Tātad - uz dzīvsudraba virsmas atmosfēras spiediens ir vienāds ar dzīvsudraba staba spiedienu caurulē: \(p= \rho_\mathrm{Hg}gh\)
Atmosfēras spiediens mainās - tas nedaudz paaugstinās (anticiklons) vai pazeminās (ciklons) atkarībā no procesiem, kas notiek atmosfērā. 3. attēlā skatāms vidējais atmosfēras spiediens (hektopaskālos) jūras līmenī 15 gadu laikā vasarā un ziemā.
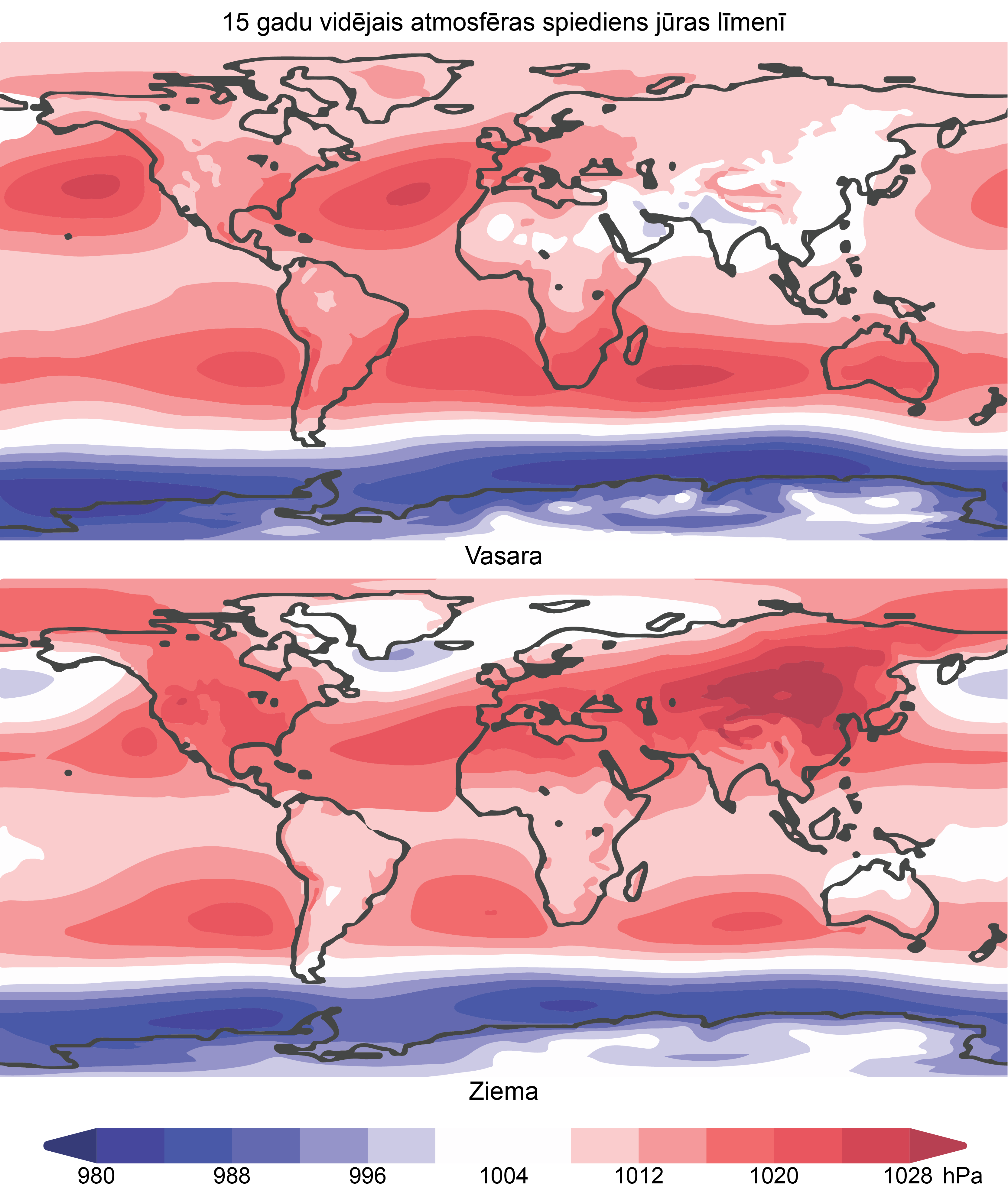
Par ''normālo'' atmosfēras spiedienu pieņem spiedienu, ko līdzsvaro 760 mm augsts dzīvsudraba stabiņš. Šis spiediens ir 101 325 Pa, jo dzīvsudraba blīvums ir 13 600 kg/m3.
Meteoroloģijā lieto arī spiediena vienību ''dzīvsudraba staba milimetrs'' (mm Hg) (1 mm augsta dzīvsudraba stabiņa radītais spiediens - 1 mm Hg=133 Pa) (4. attēls). Lieto arī mērvienības ''bārs'', ''atmosfēra'' un ''tehniskā atmosfēra''.

Barometri
Atmosfēras spiedienu mēra ar barometriem. Dzīvsudraba barometrs būtībā ir ''savienotie trauki'', vienam no kuriem gals ir aizkausēts (5. attēls a). Aizkausēto caurulīti piepilda ar dzīvsudrabu un novieto vertikāli un atmosfēras spiediens uz dzīvsudraba brīvo virsmu līdzsvaro dzīvsudraba staba spiedienu caurulītē. Uz skalas var nolasīt dzīvsudraba (Hg) staba augstumu milimetros. Šie barometri ir ļoti precīzi, bet neērti praktiskajai lietošanai, tādēļ tos izmanto tikai meteoroloģiskajos mērījumos.
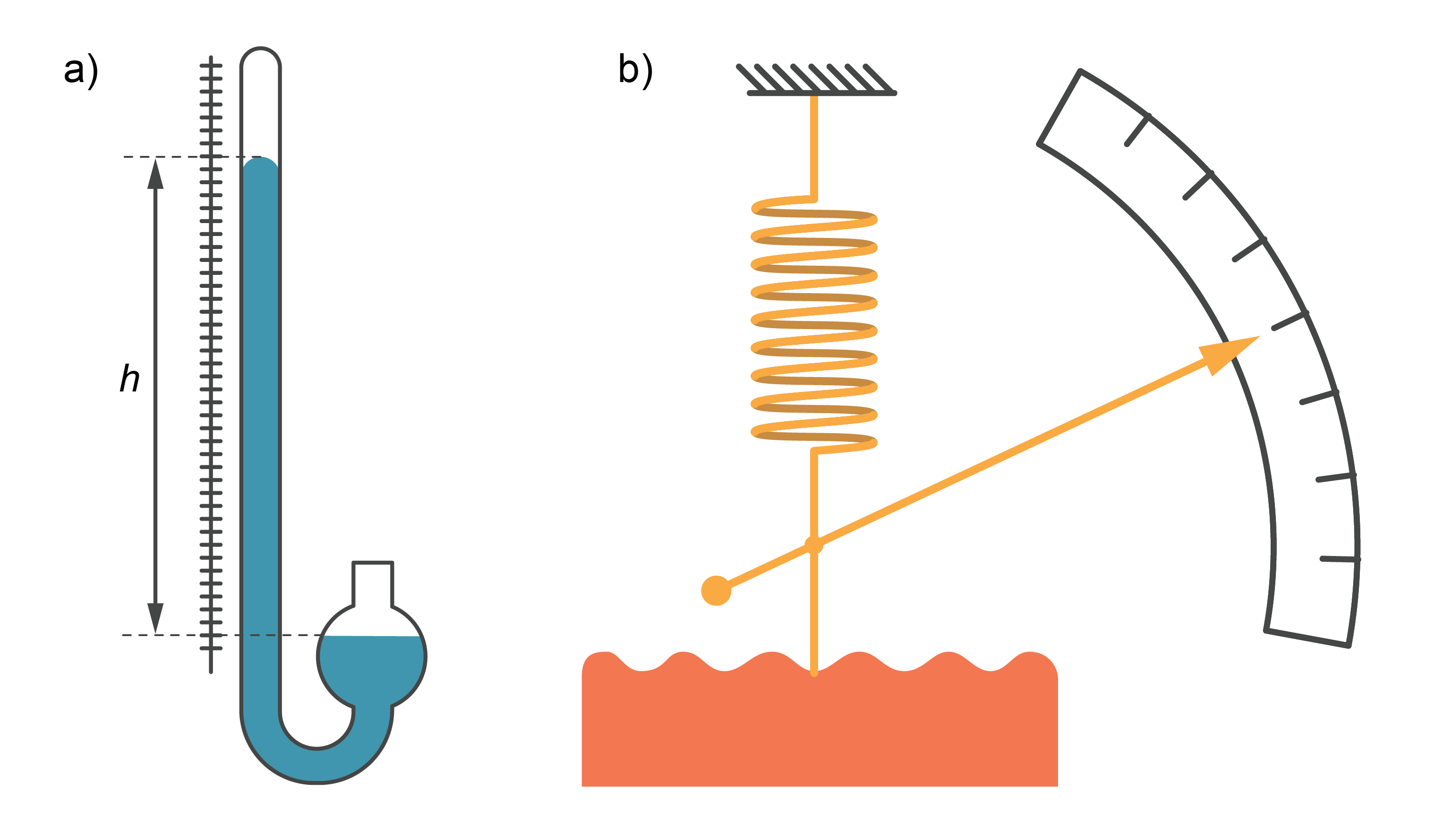
Metāla barometra - aneroīda galvenā sastāvdaļa ir slēgta metāla kārbiņa ar viļņotu virsmu (5. attēls b). No kārbiņas ir izsūknēts gaiss. Atspere neļauj kārbiņu saspiest. Mainoties atmosfēras spiedienam, mainās arī atsperes sastiepums. Ar atsperi savienotā rādītāja ''bultiņa'' pārvietojas gar skalu, kas graduēta spiediena vienībās. Tā kā atsperes elastība ir atkarīga no dažādiem faktoriem, aneroīds var būt neprecīzs.
Atmosfēras spiediena līdzsvarošana ar ūdens stabu
Atmosfēras spiediena mērīšanai varētu izmantot arī ūdeni, bet ūdens stabs, kas līdzsvaro atmosfēru, būtu pārāk augsts praktiskai lietošanai (10 metri).
Lūk piemērs (6. attēls):
Kad 2014. gadā FIZMIX aicināja piedalīties Ginesa rekorda uzstādīšanā, tapa video, kurā basketbola kluba VEF puiši centās pēc iespējas augstāk uzsūkt šķidrumu caur garu salmiņu. Video apgalvo, ka, balstoties uz fizikas likumiem, nebūs iespējams šķidrumu uzsūkt augstāk par aptuveni 10 m. Arī eksperiments apliecina, ka nevienam neizdodas uzsūkt šķidrumu augstāk par 8 m. Šī 10 m robeža ir tādēļ, ka šķidruma celšanos salmiņā nodrošina starpība starp ārējo spiedienu (atmosfēras spiedienu) un spiedienu salmiņā. Ideālā gadījumā salmiņā varētu rādīt vakuumu jeb spiediens būtu 0, tādā gadījumā spiedienu starpība būtu 1 atmosēra jeb aptuveni 100000 Pa. Ja aprēķina kādu hidrostatisko spiedienu rada 10 m augsts ūdens stabs, tad iznāk tie paši 100000 Pa. Līdz ar to atmosfēras spiediens darbojas pretī šķidruma hidrostatiskajam spiedienam.

Dažkārt tomēr arī dažādās iekārtās spiediens tiek mērīts šķidruma stabiņa milimetros. Piemēram, 7. attēlā redzams gāzes skaitītājs, kuram darba spiediens tiek mērīts ūdens stabiņa milimetros.

Atmosfēras spiediens dažādos augstumos virs jūras līmeņa
Jo tālāk no Zemes virsmas (jūras līmeņa), jo atmosfēras spiediens ir mazāks.
Tā kā gāzes ir stipri saspiežamas, atmosfēras spiediens pieaugot augstumam virs Zemes virsmas samazinās nevis lineāri (kā šķidrumos), bet gan eksponenciāli (8. attēls):
\(p \approx p_0 \cdot \exp \left(-\frac{g \cdot h \cdot M}{T_0 \cdot R_0}\right)\)
kur:
\(h\) – augstums virs jūras līmeņa
\(p_0\) – spiediens jūras līmenī 101325 Pa
\(M\) – gaisa vidējā molmasa 0.02896968 kg/mol
\(T_0\) – gaisa absolūtā temperatūra jūras līmenī (288.16 K)
\(g\) – brīvās krišanas paātrinājums jūras līmenī 9.80665 m/s2
\(R_0\) – universālā gāzu konstante 8.314462618 J/(mol·K)
Tomēr līdz apmēram 600 m augstumam spiediens samazinās vidēji par 1 mm Hg uz katriem 12 metriem.
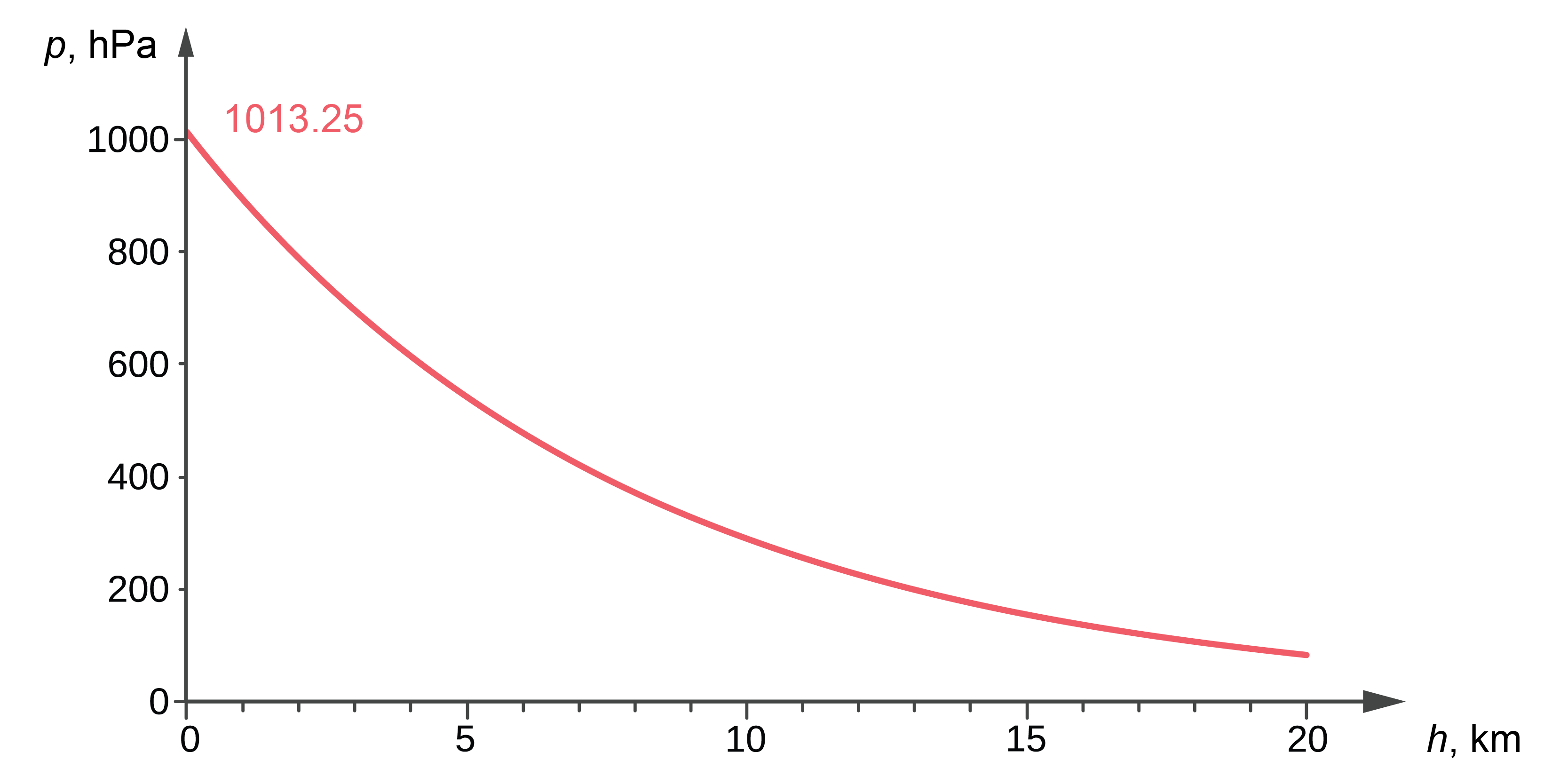
Sakarību starp spiedienu un augstumu virs Zemes var izmantot, lai noteiktu augstumu virs Zemes, izmantojot atmosfēras spiediena mērījumus. Aneroīdus, kuru skala ir graduēta augstuma vienībās (metros virs jūras līmeņa), sauc par altimetriem.
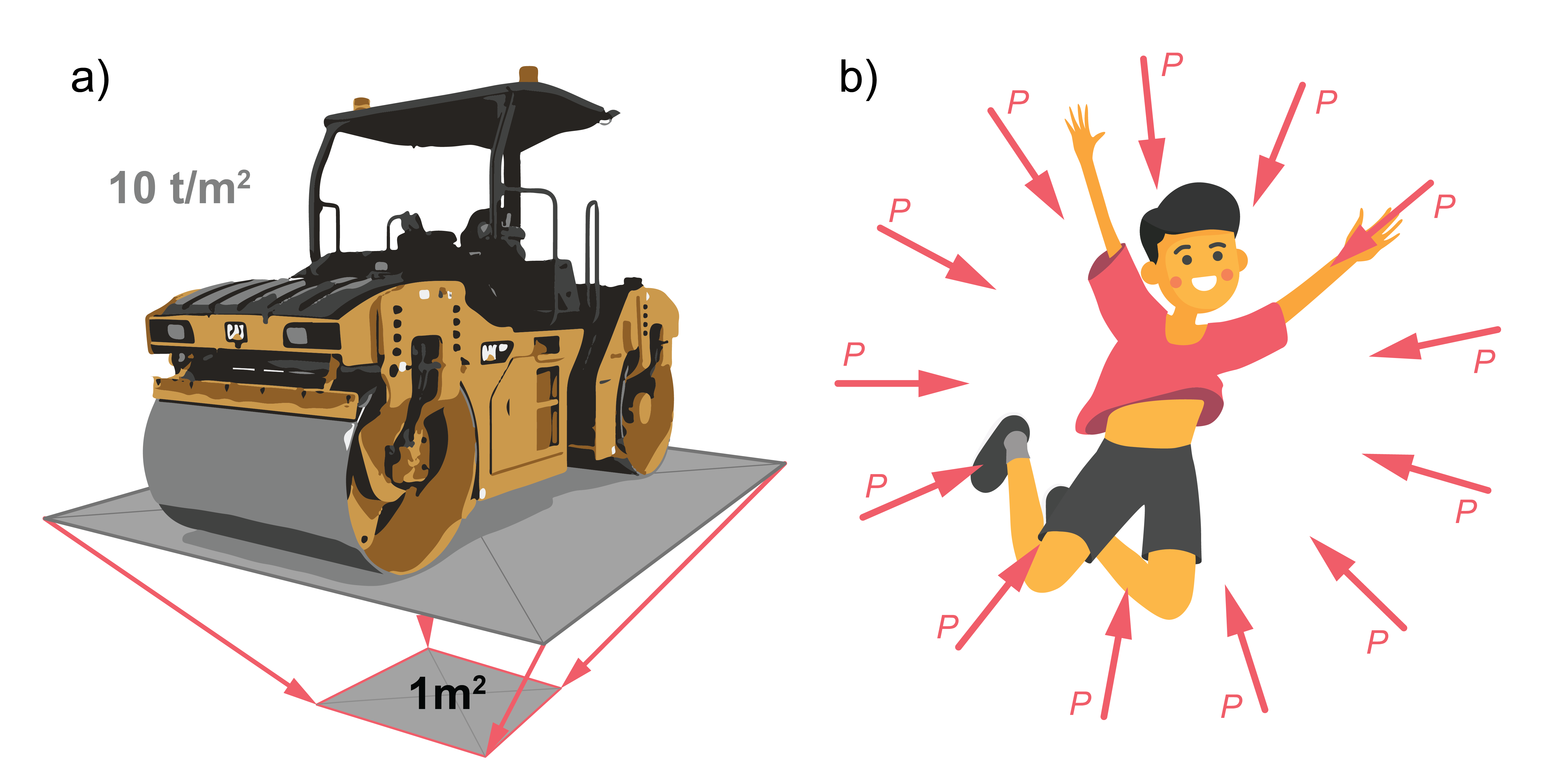
Jūras līmenī atmosfēras spiediens ir vienāds ar spiedienu, ko uz 1 m2 lielu laukumu radītu 10 t smags veltnis (9. attēls a). Mēs nejūtam apkārtējās atmosfēras spiedienu, jo spiediens mūsu ķermenī (audos, orgānos) ir aptuveni tāds pats kā atmosfēras spiediens ārpusē un spiediena spēki, kas darbojas uz mūsu ķermeni, ir līdzsvarā.
Arhimēda spēks
Uz šķidrumā vai gāzē iegremdētu ķermeni darbojas spēks, kas rodas hidrostatiskā spiediena atšķirības dēļ dažādā dziļumā zem šķidruma virsmas – Arhimēda spēks vai ''cēlējspēks'' (1. attēls)
Jo dziļāk šķidrumā, kas atrodas nenoslēgtā traukā, jo lielāks ir šķidruma hidrostatiskais spiediensun lielāks spiediens darbojas uz ķermeņa virsmu:
\(p=p_\mathrm{a t m}+\rho g h\)
Šķidrumā iegremdētam ķermenim – taisnstūra paralēlskaldnim ar augstumu \(h\) - uz tā virspusi un apakšpusi darbojas pretēji vērsti spēki \(F_1\) un \(F_2\), ko izraisa šķidruma slāņu radītais hidrostatiskais spiediens kopā ar atmosfēras spiedienu.
To, ka spēki ir pretēji vērsti, nosaka Paskāla likums – šķidrumā vai gāzē spiediena spēks vienmēr darbojas uz virsmu perpendikulāri tai, jo mierā esošā šķidruma vai gāzes jebkurā punktā spiediens visos virzienos ir vienāds. Tātad hidrostatiskā spiediena radītais spēks uz augšējo virsmu spiež no augšas, bet uz apakšējo – no apakšas. Arī uz sānu skaldnēm – perpendikulāru tām.
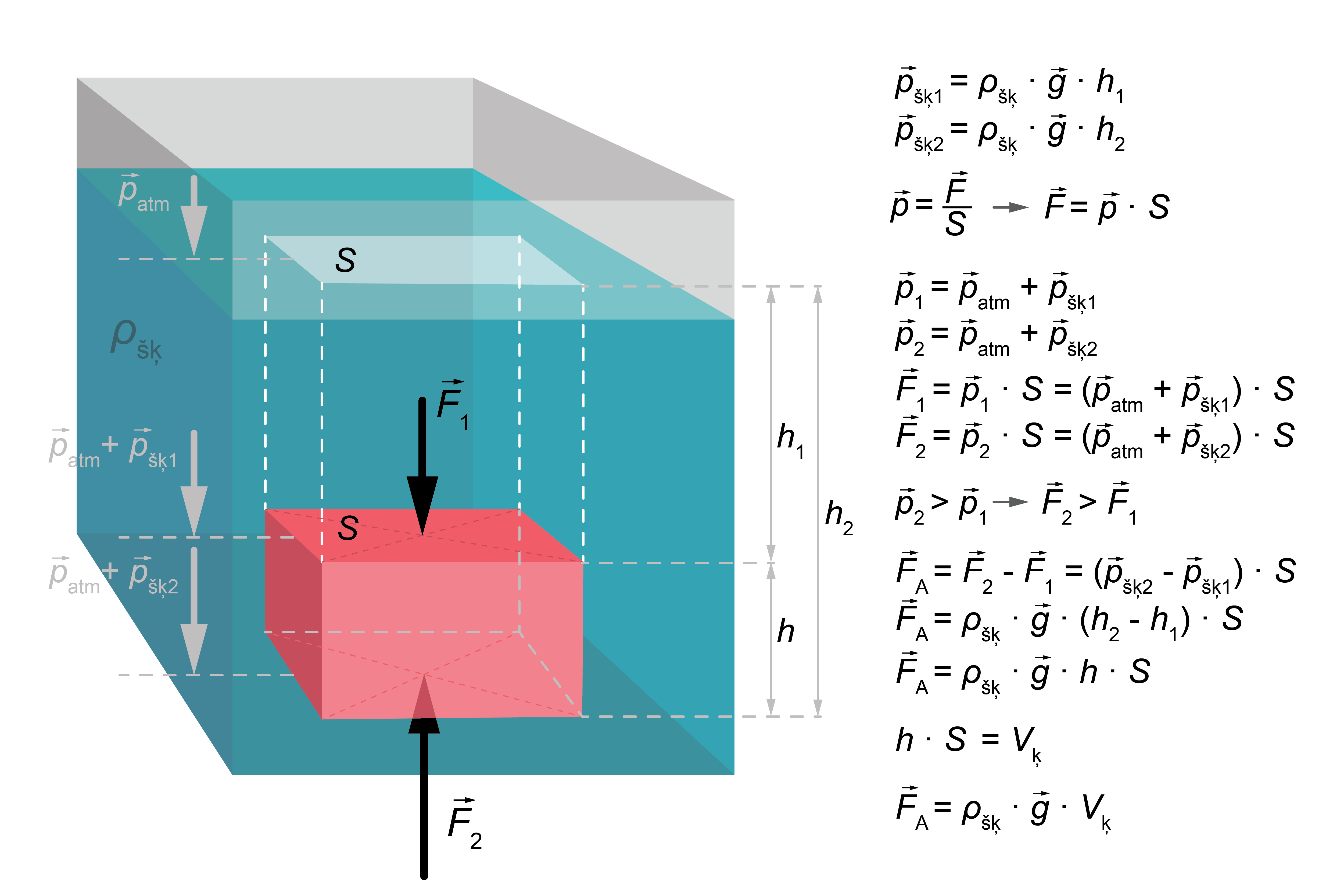
Šķidruma slānis, kas atrodas virs ķermeņa apakšējās daļas (augstums \(h_2\)), ir biezāks nekā tas, kas pārklāj ķermeņa virsmu (augstums \(h_1\)), tādēļ \(F_2\) ir lielāks nekā \(F_1\). Spēķi, kas darbojas uz sānu skaldnēm, savstarpēji kompensējas. Spēku saskaitīšanas rezultātā uz ķermeni darbojas augšup vērsts spēks, ko sauc par Arhimēda spēku (\(F_\mathrm{A}\)).
Tātad Arhimēda spēku aprēķina pēc formulas \(F_\mathrm{A}=\rho_{š ķ} \cdot g \cdot V\),
kur
\(\rho_{š ķ}\) - šķidruma blīvums, kurā iegremdēts ķermenis, kg/m3
\(g\) - brīvās krišanas paātrinājums, m/s2
\(V\) - ķermeņa tilpums, kas ir iegrimis šķidrumā, m3
Varētu iebilst, ka šī Arhimēda spēka aprēķina formulas der tikai taisnstūra paralēlskaldnim. Tomēr tā ir spēkā jebkuras formas ķermenim.
Pieņemsim, ka mierā esošā šķidrumā vai gāzē ar iedomātu virsmu nodalīts tilpums \(V_\mathrm{o}\) (2. attēls a). Tā kā šķidrums traukā atrodas līdzsvarā (nekustas), tad rezultējošam spēkam, kas pielikts tilpumā \(V_\mathrm{o}\) esošā šķidruma masas centram, jābūt vienādam ar nulli.
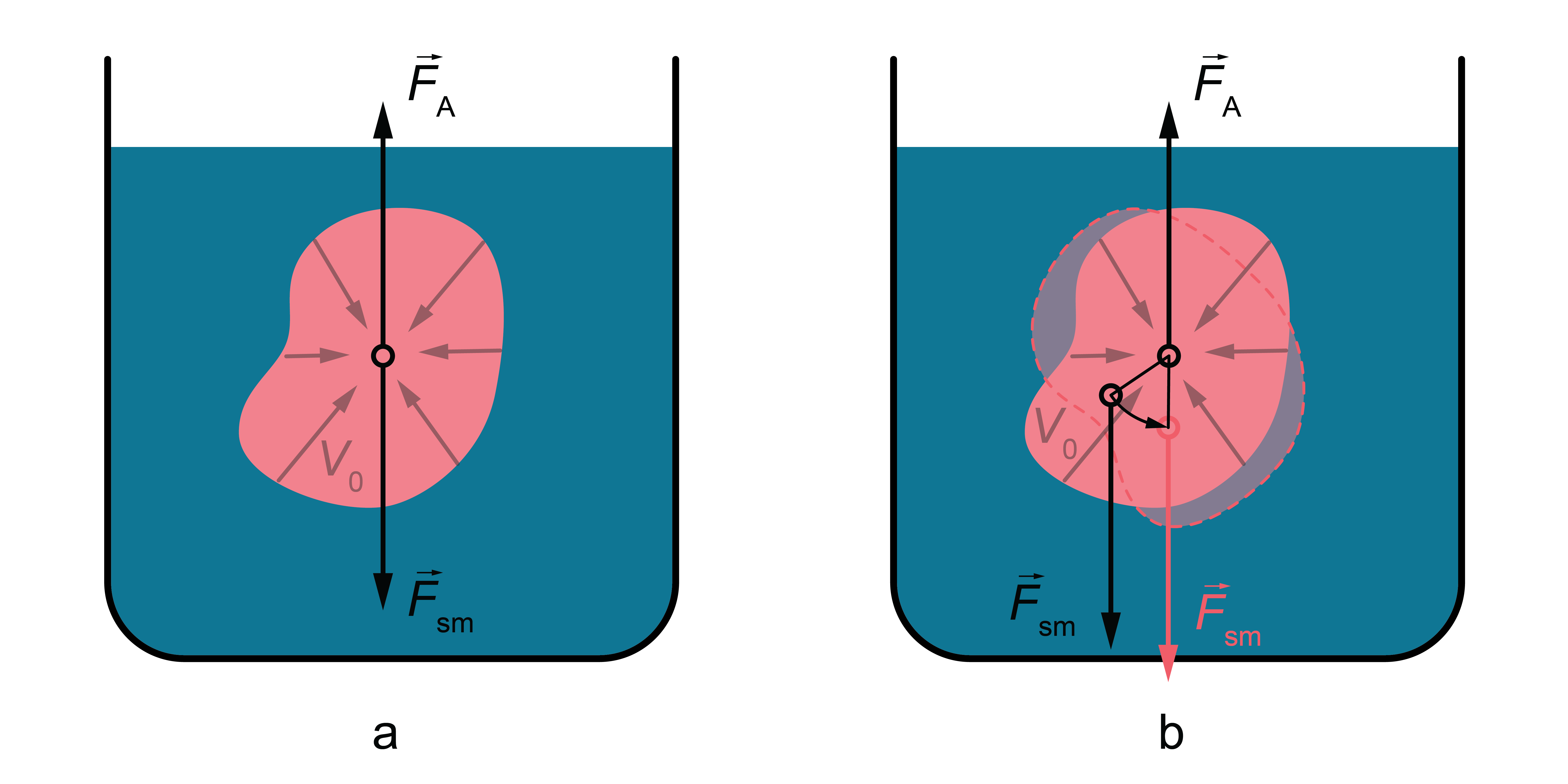
Uz šķidrumu tilpumā Vo darbojas divi spēki: smaguma spēks \(F_\mathrm{sm} = \rho_{šķ}V_\mathrm{o} g\) , kur \(\rho_{š ķ}\) — šķidruma blīvums, un apkārtējā šķidruma spiediena izraisītais spēks \(F_\mathrm{A}\). No līdzsvara nosacījuma var secināt, ka spēkiem jābūt skaitliski vienādiem: \(F_\mathrm{A}\) = \(F_\mathrm{sm}\) un pretēji vērstiem, tātad \(F_\mathrm{A}\) = \(\rho_{š ķ}V_\mathrm{o} g\) - tas vienāds ar izspiestā šķidruma (gāzes) svaru.
Arhimēda spēks un enerģijas nezūdamības likums
Arhimēda spēka rašanos var skaidrot arī no enerģijas nezūdamības likuma skatpunkta - sistēma vienmēr tiecas ieņemt stāvokli, kurā tās potenciālā enerģija būs cik iespējams mazāka.
Ja tilpumā \(V_\mathrm{o}\) šķidruma vietā iegremdē tādas pašas formas ķermeni, kurš ar apkārtējo šķidrumu atrodas līdzsvarā, tad nekādām izmaiņām šķidruma iedarbībā nevajadzētu notikt (2. attēls b). Tikai tagad spēks \(F_\mathrm{A}\) darbojas uz iegremdēto ķermeni. Šis spēks pēc moduļa vienāds ar izspiestā šķidruma (gāzes) svaru, pielikts izspiestā šķidruma masas centram un vērsts pretēji ķermeņa smaguma spēka darbības virzienam. Ja ķermeņa masas centrs nesakrīt ar izspiestā šķidruma masas centru, ķermenis šķidrumā pagriezīsies tā, lai abi spēki darbotos pa vienu taisni (3. attēls).
Saprotams, Arhimēda spēks darbojas uz ķermeni ne tikai šķidrumos, bet arī gāzēs, piemēram, gaisā.
Tomēr, kad ir runa par šķidrumā iegremdētu ķermeni, gaisa blīvums ir ļoti mazs, salīdzinot ar šķidruma blīvumu (\(\rho_\mathrm{gaiss}\) = 1,29 kg/m3), gaisa ietekmi var neievērot. Šajā gadījumā Arhimēda spēku (''cēlējspēku'') var izmērīt eksperimentāli – kā ķermeņa svara, tam atrodoties gaisā, un ķermeņa svara, kad tas iegremdēts šķidrumā, starpību (4. attēls)
\(F_\mathrm{A} = P_\mathrm{GAISĀ} - P_\mathrm{ŠĶIDRUMĀ}\)
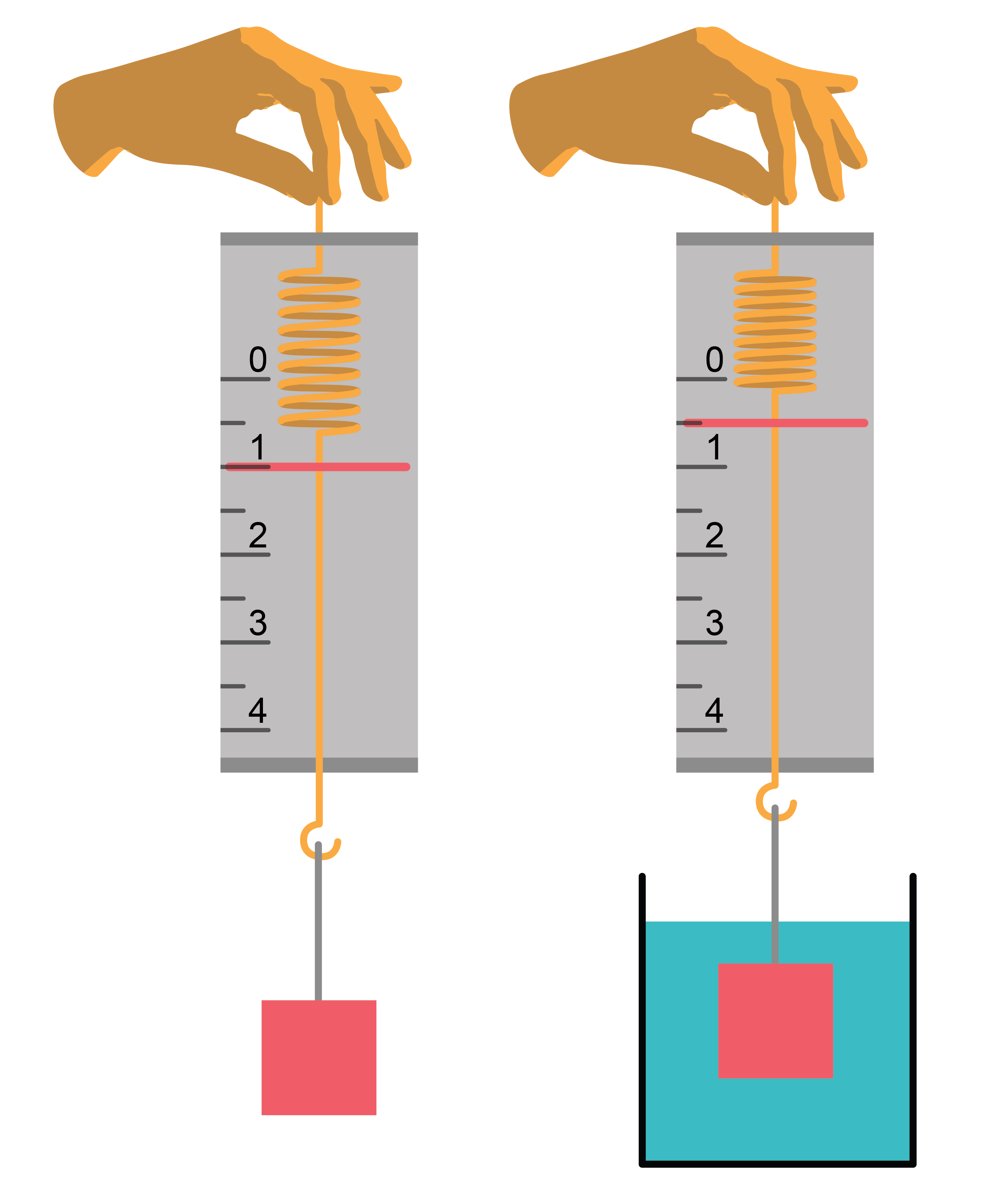
Skaidrs, ka viss iepriekš secinātais attiecināms arī uz šķidrumā tikai daļēji iegremdētu ķermeni - tad šķidruma spiediens no augšas vienāds ar nulli.
Arhimēda spainītis
Nereti izmanto arī šādu Arhimēda likuma formulējumu: uz šķidrumā vai gāzē pilnīgi vai daļēji iegremdētu ķermeni darbojas cēlējspēks, kas vērsts vertikāli augšup un ir vienāds ar ķermeņa iegrimušās daļas izspiestā šķidruma (gāzes) svaru.
Eksperimentā ar ''Arhimēda spainīti'' (5. attēls) var pārliecināties arī par šā formulējuma patiesumu:
Lai gan gaisa blīvums ir neliels, tomēr Arhimēda spēku, kas darbojas uz ķermeni gaisā ir jāņem vērā – ikviens ķermenis gaisā sver mazāk, kā vakuumā. To noteikti jāņem vērā, ja ķermeņa masu jānosaka ļoti precīzi.
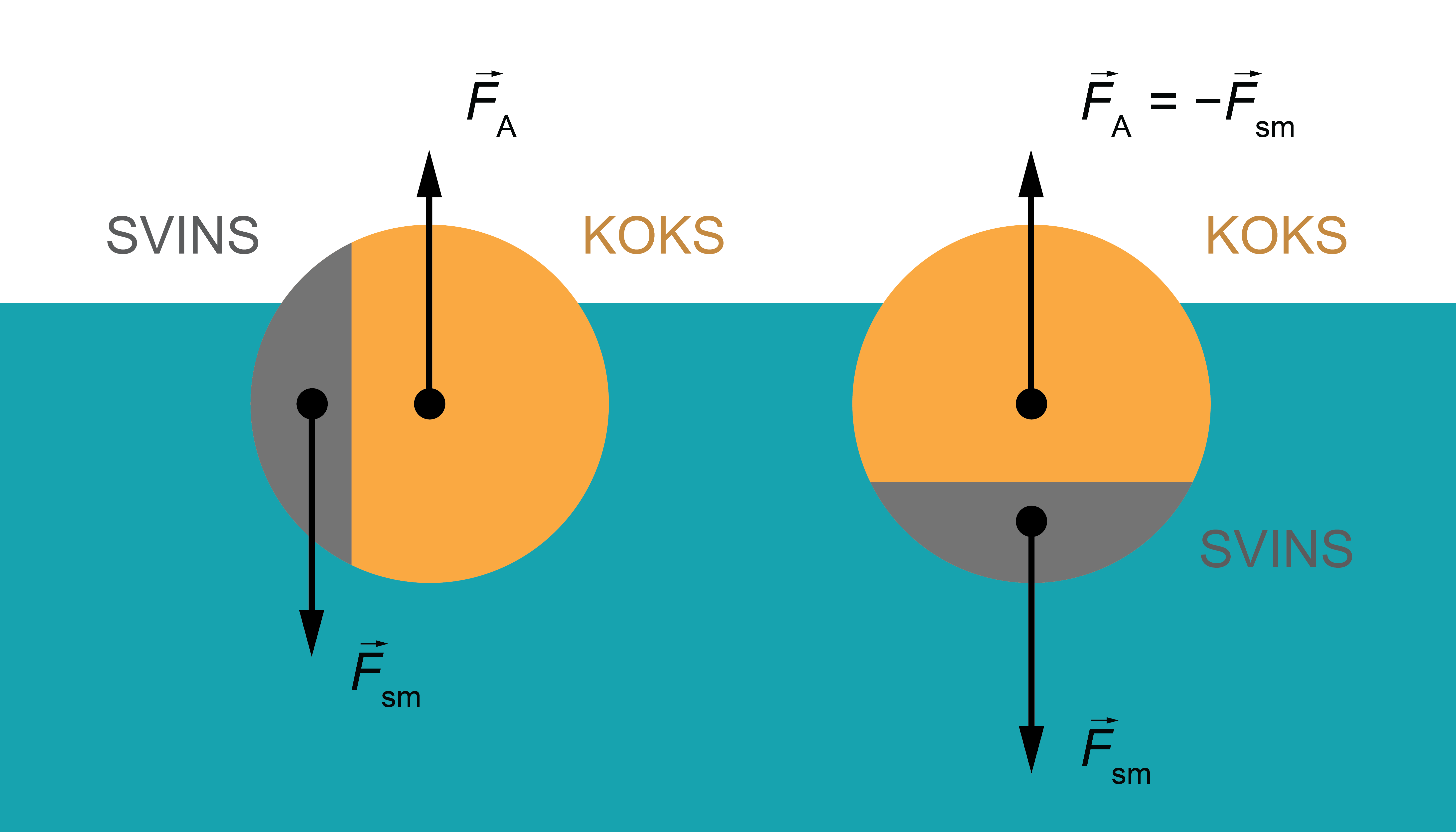
Arī klasiskajai bērnu dienu mīklai: ''Kas sver vairāk – kilograms vates vai kilograms dzelzs?'' pareizā atbilde pārsteidzošā kārtā ir: ''Protams, kilograms dzelzs'' (6. attēls).
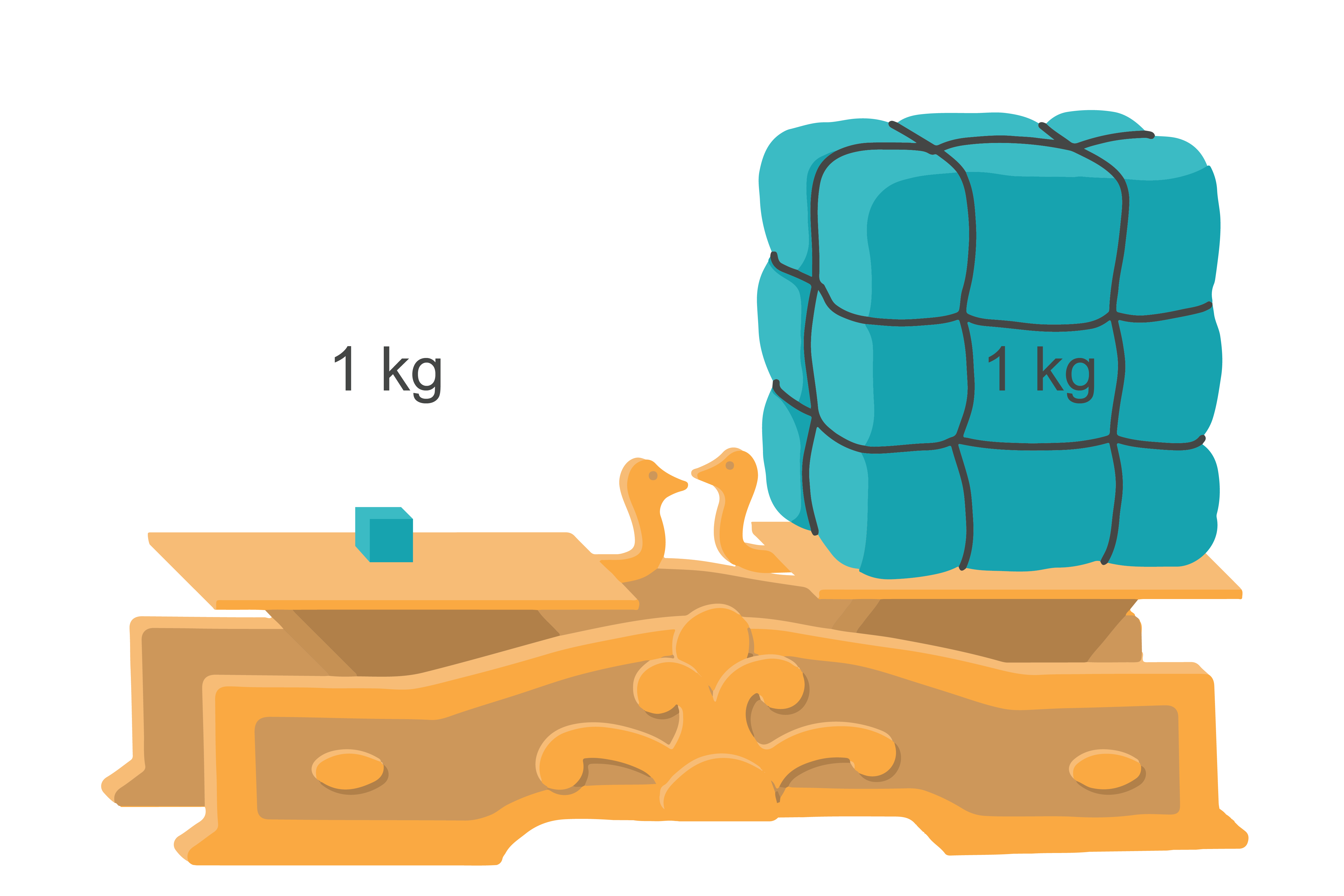
Kilograms dzelzs aizņem daudz mazāku tilpumu, kā kilograms vates, tādēļ uz vati darbojas lielāks augšup vērstais Arhimēda spēks, kamēr smaguma spēki ir vienādi.
Virsmas spraigums
Šķidrumu no apkārtējās vides atdala robežvirsma, ko sauc par šķidruma brīvo virsmu. Molekulas, kas atrodas šķidruma iekšpusē), (1. attēls) no visām pusēm ir pakļautas apkārtējo molekulu iedarbībai, kas savstarpēji kompensējas (kopspēks vienāds ar nulli). Bet uz virsmas vai tuvu virsmai esošās molekulas to ''kaimiņi'' ieskauj tikai no vienas puses. No otras puses tās mijiedarbojas tikai ar no šķidruma iztvaikojušajām vai gaisa sastāvā esošajām molekulām. Šī mijiedarbība ir daudzas reizes vājāka nekā mijiedarbība ar šķidruma molekulām, tādēļ šķidruma virsmas molekulas tiek pakļautas spēkam \(F\), kas tās ''velk'' iekšā šķidrumā - molekulu savstarpējās mijiedarbības kopspēks, kas darbojas uz molekulām šķidruma virsmas slānī, vērsts uz šķidruma iekšieni perpendikulāri tā virsmai (līdz, molekulām satuvinoties, savstarpējās atgrūšanās spēki to līdzsvaro).
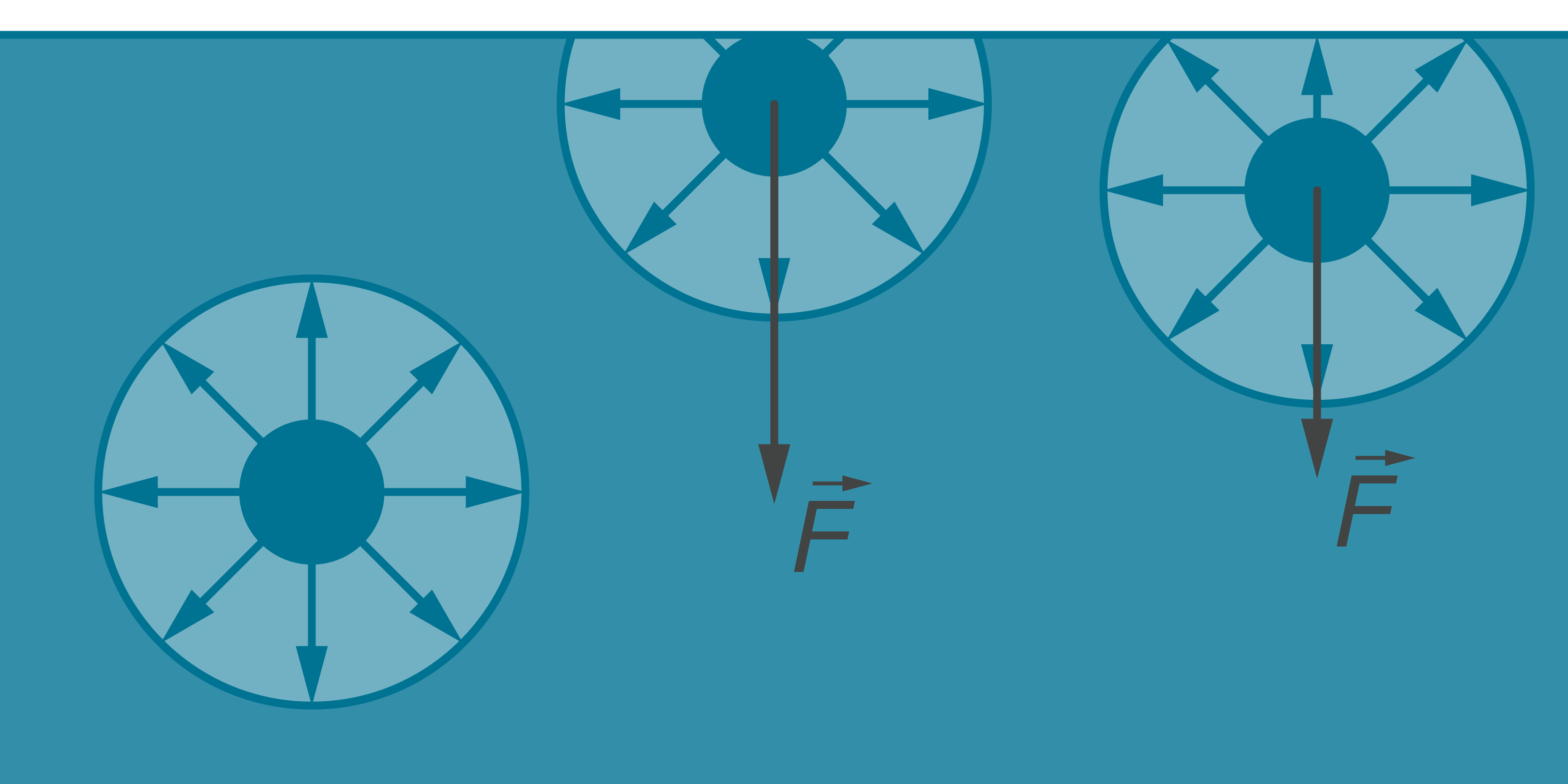
Lai molekulu pārvietotu no šķidruma iekšienes uz virskārtu, ir jāveic darbs šā molekulu pievilkšanās spēku kopspēka pārvarēšanai. Tas nozīmē, ka virsmas slāņa molekulām piemīt lielāka potenciālā enerģija kā šķidruma iekšienē esošajām molekulām. Līdz ar to virsmas slānim piemīt papildus iekšējā enerģija, salīdzinot ar līdzīga biezuma slāni šķidruma iekšienē – virsmas brīvā enerģija (\(U\)), kas proporcionāla virsmas laukumam.
Zināms, ka jebkura sistēma tiecas ieņemt stāvokli, kurā tās enerģija ir pēc iespējas mazāka, tādēļ, iespēju robežās, notiek virsmas saraušanās. Tātad – rodas spēki, kas nodrošina šo virsmas laukuma samazināšanos.
Molekulu mijiedarbības spēku ietekmē šķidruma virsma samazinās līdz vismazākajam iespējamajam izmēram, tātad šķidruma virskārta ir līdzīga nostieptai plēvītei. Tomēr pastāv būtiska atšķirība: izstiepjot, piemēram, gumijas plēvīti, virskārtas molekulu skaits paliek nemainīgs, bet palielinās attālumi starp tām. Izstiepjot šķidruma virsmas ''plēvīti'', molekulu skaits tajā pieaug, bet attālumi starp tām nemainās. Tādēļ spēks, kas nepieciešams, lai izstieptu šķidruma virsmas plēvīti, paliek nemainīgs - tas nepakļaujas Huka likumam.
Virsmas spraiguma spēks
Šādu šķidruma virskārtas stāvokli sauc par virsmas spraigumu un spēkus, kas darbojas pa šķidruma virsmas pieskarēm un nodrošina šo virsmas laukuma samazināšanos – par virsmas spraiguma spēkiem (\(F_\mathrm{S}\)). Tos rada šķidruma molekulu savstarpējās pievilkšanās spēki.
Lai novērtētu virsmas spraiguma spēku, aplūkosim sekojošu situāciju (2. attēls a):
Rāmīti ABCD, kura viena mala AB var bez berzes slīdēt pa malām AD un CB iegremdē ziepjūdenī vai citā šķīdumā (2. attēls a). Rāmīša kontūrā ABCD veidojas plēvīte, kurai ir divas virsmas (2. attēls b). Kontūra malai AB pieliek spēku \(F\), kurš, izstiepjot plēvīti un pretdarbojoties virsmas spraiguma spēkiem \(F_\mathrm{S}\), pārvieto malu AB stāvoklī A’B’ - par attālumu \(\Delta x\). Lai palielinātu virsmu par \(\Delta S\), spēks ir padarījis darbu \(A = F \Delta x\). Ja rāmīša kustīgo malu pārvieto lēni - tā, ka nemainās plēvītes temperatūra - tad padarītais darbs \(A\) ir vienāds ar virsmas enerģijas pieaugumu \(\Delta U\). Tā kā virsmas ir divas,
\(\Delta x =\frac {\Delta S}{2l}\) un \(A = F_S(\frac{\Delta S}{l})\)
Šo sakarību var izteikt:
\(A = \Delta U = \sigma \Delta S\), kur \(\sigma = \frac{F_\mathrm{S}}{l}\).
Lielums \(\sigma\) interpretējams divējādi.
No vienas puses, \(\sigma\) ir īpatnējā virsmas enerģija – lielums parāda, par cik pieaug virsmas brīvā enerģija \(U\), virsmas laukumam pieaugot par \(\Delta S\). Šajā gadījumā SI mērvienība ir J/m2.
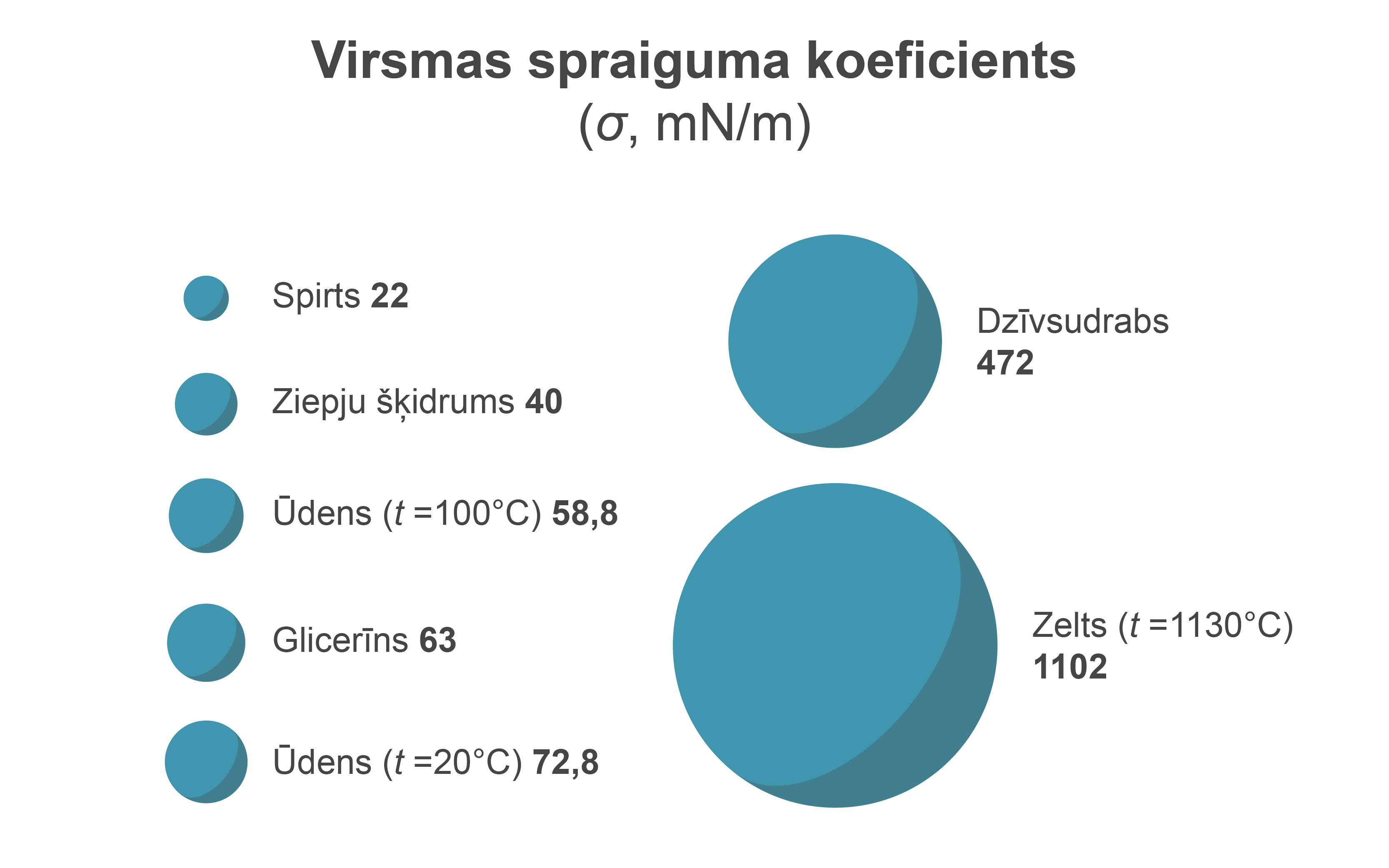
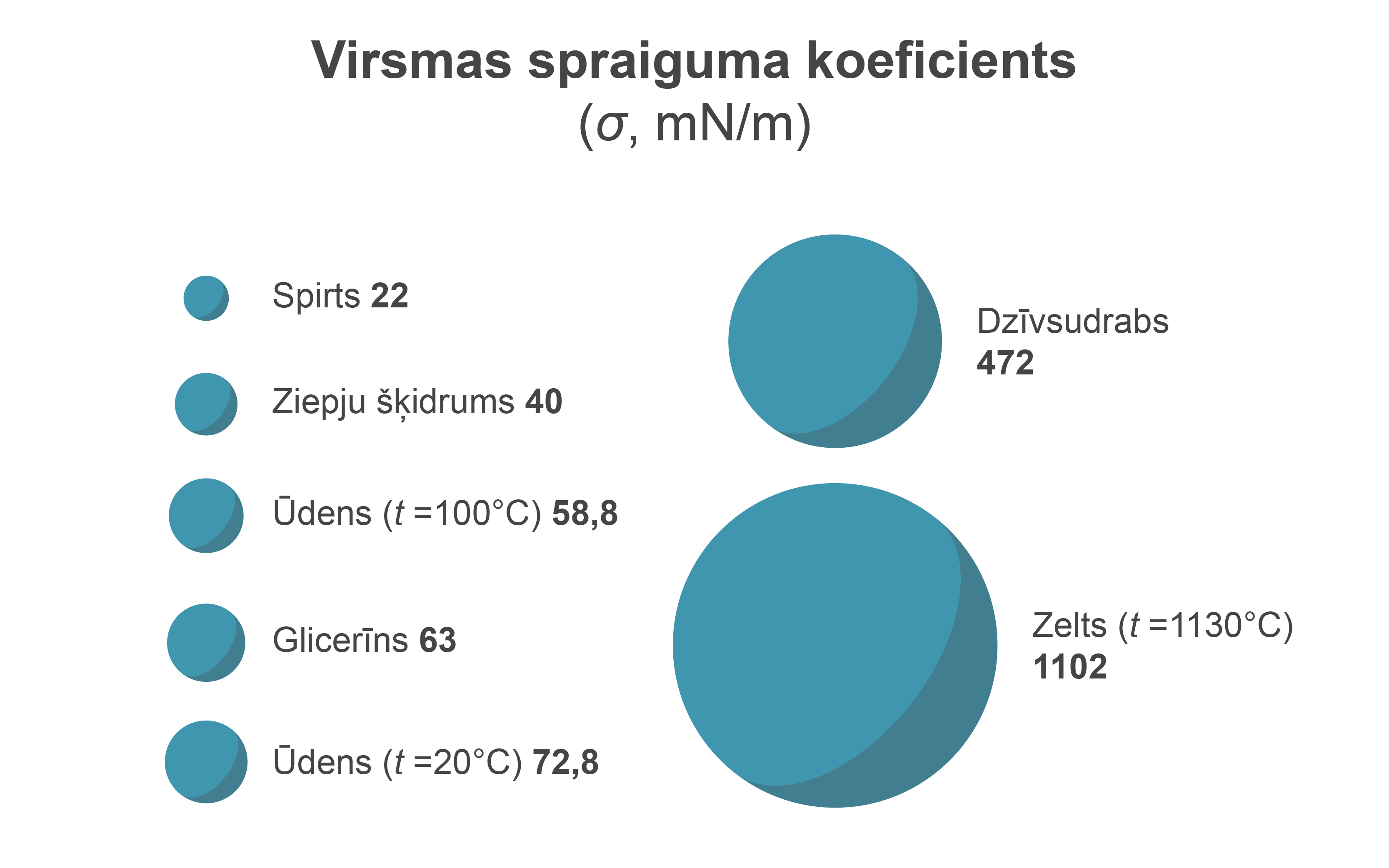
No otras puses – šis lielums \(\sigma\) ir skaitliski vienāds ar virsmas spraiguma spēku \(F_\mathrm{S}\), kas darbojas uz vienu kontūra malas garuma vienību, un šo lielumu sauc arī par virsmas spraiguma koeficientu. Šajā gadījumā SI mērvienība ir N/m.
Dažādu vielu virsmas spraigumu koeficienti doti 3. attēlā.
Tomēr jāņem vērā, ka virsmas spraigums ir atkarīgs ne tikai no paša šķidruma īpašībām, bet arī no tā, ar kādu vielu šķidruma virsma ir kontaktā. Istabas temperatūrā ūdens virsmas spraigums ir 72,8 mN/m, bet, ja ūdens virsma robežojas ar, piemēram, ēteri, virsmas spraigums ir tikai 12,2 mN/m.
Virsmas spraiguma izpausmes
Virsmas spraiguma spēks šķidruma virsmu padara elastīgu - tā uzvedas līdzīgi piepūsta balona virsmai. Tādēļ, piemēram, uz šķidruma virsmas ir iespējams novietot vieglus priekšmetus, kuru materiāla blīvums pārsniedz šķidruma blīvumu (4. attēls b), savukārt, ja traukā ielej nedaudz lielāku šķidruma tilpumu nekā trauks atļauj, tad līdz noteiktai robežai šķidrums nelīst pāri malām, bet veido tādu kā uzkalniņu (4. attēls a).
Noskaties Jauno Fiziķu skolas nodarbības video par virsmas spraigumu!
Tā kā virsmas spraiguma spēks vienmēr darbojas, lai pēc iespējas samazinātu šķidruma brīvās virsmas laukumu, un no matemātikas zināms, ka sfērai ir vismazākais virsmas laukums salīdzinot ar citiem tāda paša tilpuma ķermeņiem, ''brīvs'' šķidrums vienmēr tiecas ieņemt lodveida formu. Tādēļ, lejot kādu šķidrumu, jārēķinās, ka tas sadalīsies pilienos. To, ka šķidruma piliens tiecas ieņemt sfērisku formu, var novērot pie piloša ūdens krāna (5. attēls a). Neilgu laika sprīdi pirms piles atdalīšanās no krāna var manīt, ka tā ir ieņēmusi sfērai līdzīgu formu, tomēr sasniegt ideāli sfērisku formu traucē citi spēki, piemēram, smaguma spēks. Arī kosmosa stacijā bezsvara stāvoklī ''izlijis'' šķidrums ieņem lodveida formu (5. attēls b).
Avots: https://commons.wikimedia.org/wiki/File:S130E012778_-_STS-130_-_Patrick_with_Water_Droplet_on_MDDK_-_DPLA_-_548e89e6b7aa47e90d52b8ecc56e1fe0.jpg
Ja mēs izpūšam ziepjūdens burbuli un palaižam gaisā, tad arī tas ieņem sfērisku formu (6. attēls), jo gaisā esošo gāzu molekulu koncentrācija ir pārāk maza, lai mijiedarbība ar tām spēcīgi ietekmētu burbuļa sfērisko formu, un mazā svara dēļ smaguma spēka ietekme arī ir niecīga.

Brīva šķidruma lodveida formu var skaidrot arī, neizmantojot enerģijas jēdzienu, ''ģeometriski'': tā kā uz šķidruma virskārtas molekulām darbojas spēks, kas ir perpendikulārs šķidruma virsmai, tad šķidruma daļa, kas nav pakļauta ārējo spēku iedarbībai, pieņem lodes formu, jo tikai tādā gadījumā molekulu mijiedarbības spēki līdzsvarojas.
Ir arī citi apliecinājumi tam, ka šķidrums vienmēr ieņems stāvokli ar mazāko brīvās virsmas laukumu. Piemēram, ja apskata ziepjūdens plēvītes formu dažādās rāmīšu konstrukcijās (7. attēls), tad to izskats nav tāds, kā pirmajā brīdī šķiet, kādam tam vajadzētu būt, jo ziepjūdens plēvīte ieņem stāvokli ar vismazāko virsmas laukumu.

Labi zināms, ka, piemēram, slapjas smiltis vai slapji mati salīp. Tas tādēļ, ka šķidruma plēvītes, kas aptver matus vai smiltis, cenšas samazināt savu virsmas laukumu un, saskaroties, izveido vienu, kopīgu ūdens slānīti (8. attēls a, b).
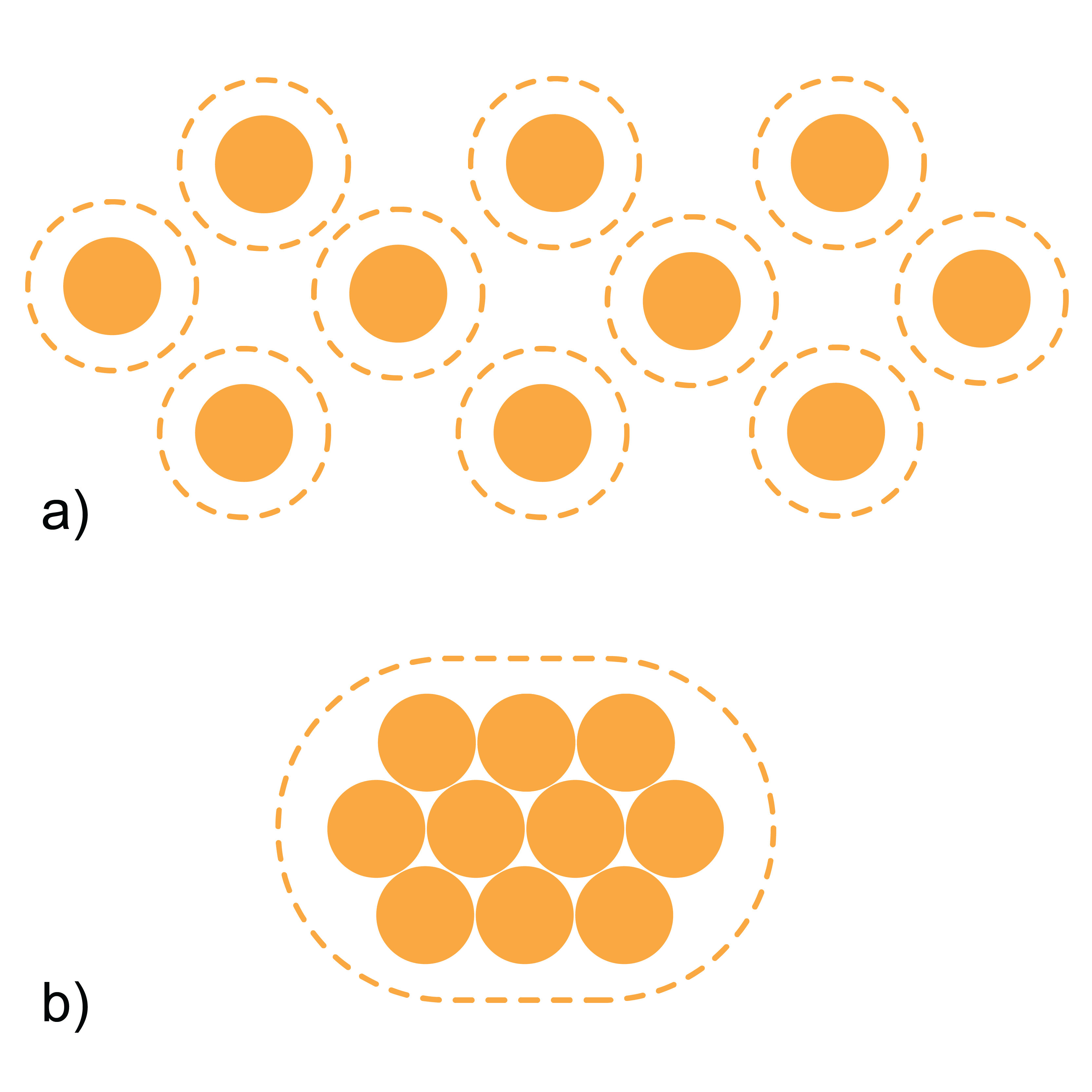
Šķidruma virsmas enerģiju var samazināt ne tikai samazinot šķidruma brīvās virsmas laukumu.
Virsmas aktīvās vielas
Ja šķidruma sastāvā ir vairākas atšķirīgas vielas, virsmas slānī koncentrējas tās vielas molekulas, kurai virsmas enerģija ir mazāka. Tā rezultātā šķidruma virsmas slāņa un visa pārējā šķidruma sastāvi atšķiras.
Vielas, kuras, samazinot virsmas enerģiju, uzkrājas robežslānī starp divām vidēm, sauc par virsmas aktīvām vielām. Šāda vielas ir, piemēram, ziepes, ēteris u.c.
Ziepju spēja putot un tādējādi veicināt mazgāšanu ir saistīta tieši ar šo īpašību.
Par virsmas spraiguma spēku darbību un virsmas aktīvo vielu ietekmi var pārliecināties šādā demonstrējumā (9. attēls).

Šķīvī ielej ūdeni, kura brīvajai virsmai uzkaisa piparus, talku vai citas sīkas daļiņas, kas peld uz ūdens virsmas. Var pārliecināties, ka, pieliekot tīru pirkstu piparu kārtiņa saglabājas. Ja piparu slānītim pieskaras ar mazgāšanas līdzeklī samērcētu pirkstu vai, piemēram, iepilina ētera pilienu, var novērot, ka sīkās daļiņas ļoti ātri attālinās uz trauka malām. Tas parāda, ka mazgāšanas līdzekļa šķīduma vai ētera virsmas spraiguma koeficients ir daudz mazāks nekā tīram ūdenim.
Ir arī vielas, kas virsmas spraigumu palielina (piemēram, vārāmā sāls, cukurs u. c.).
Slapināšana
Virsmas spraiguma spēki vienmēr darbojas tā, lai šķidruma brīvās virsmas laukums būtu pēc iespējas mazāks (skatīt nodaļu ''Virsmas spraigums''). Pie nemainīga tilpuma vismazākais virsmas laukums ir sfērai.
Tomēr šķidruma molekulas mijiedarbojas arī ar cietā ķermeņa molekulām, ar kuru tas ir nonācis kontaktā. Šķidruma piliens uz cietas virsmas var izplūst, bet var arī ieņemt gandrīz sfērisku formu. Šo parādību sauc par slapināšanu.
Leņķi \(\Theta\), ko veido cietā ķermeņa virsma ar šķidruma virsmas pieskari, sauc par malas leņķi.
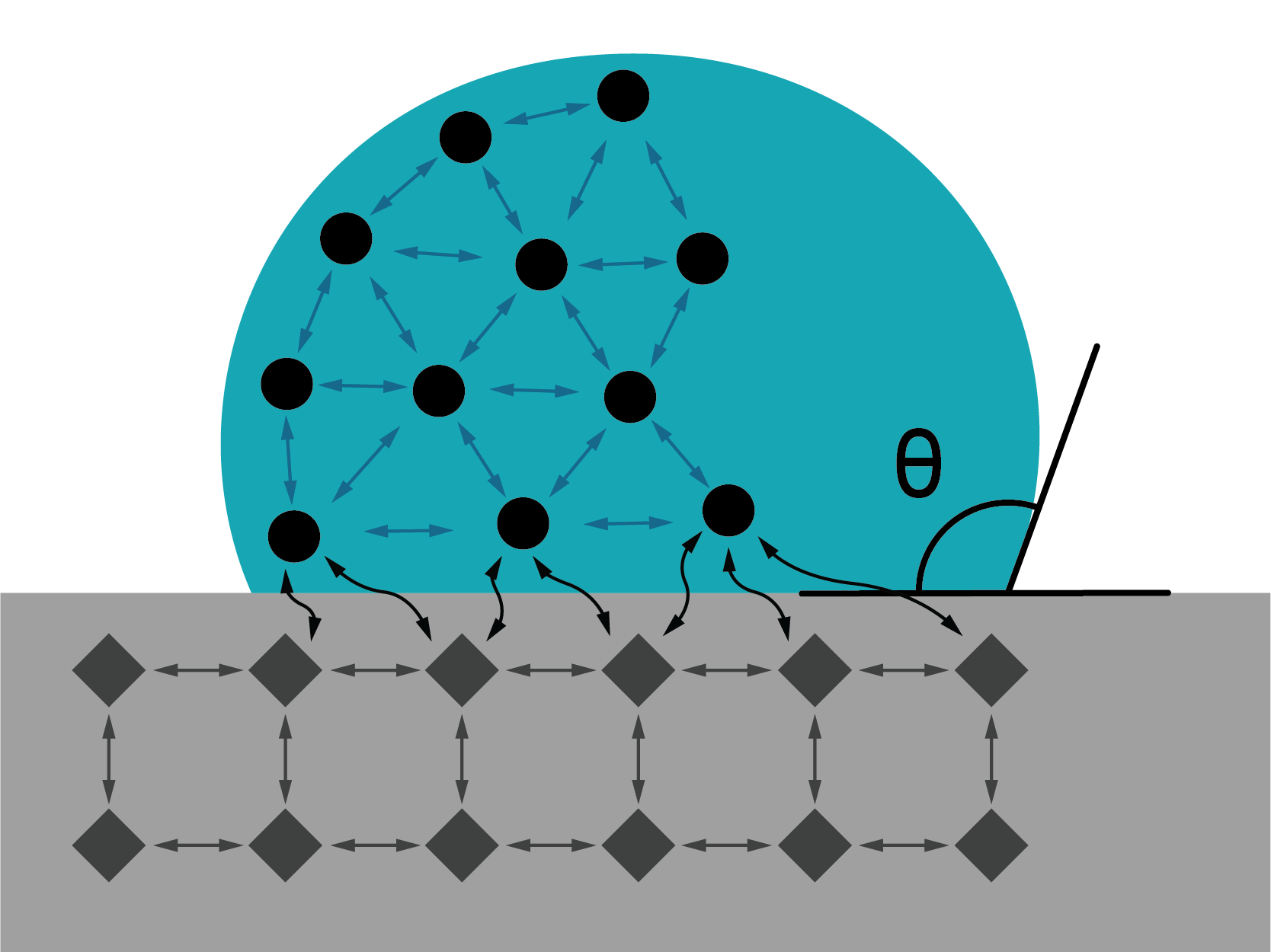
Ja šķidruma un cieta ķermeņa molekulu savstarpējās mijiedarbības spēki ir lielāki nekā šķidruma molekulu savstarpējās pievilkšanās spēki, tad šķidrums cenšas palielināt saskares virsmas laukumu ar cieto ķermeni. Šajā gadījumā šķidrumu sauc par slapinošu šķidrumu, malas leņķis ir mazāks nekā 90° (2. attēls a,b).
Jo slapinošāks ir šķidrums, jo vairāk tas izplūst pa virsmu, jo mazāks ir leņķis \(\Theta\). Ja šķidrums pilnīgi slapina cieto ķermeni (\(\Theta\) = 0°), tad šķidrums izplūst pa cietā ķermeņa virsmu ļoti plānā kārtiņā.
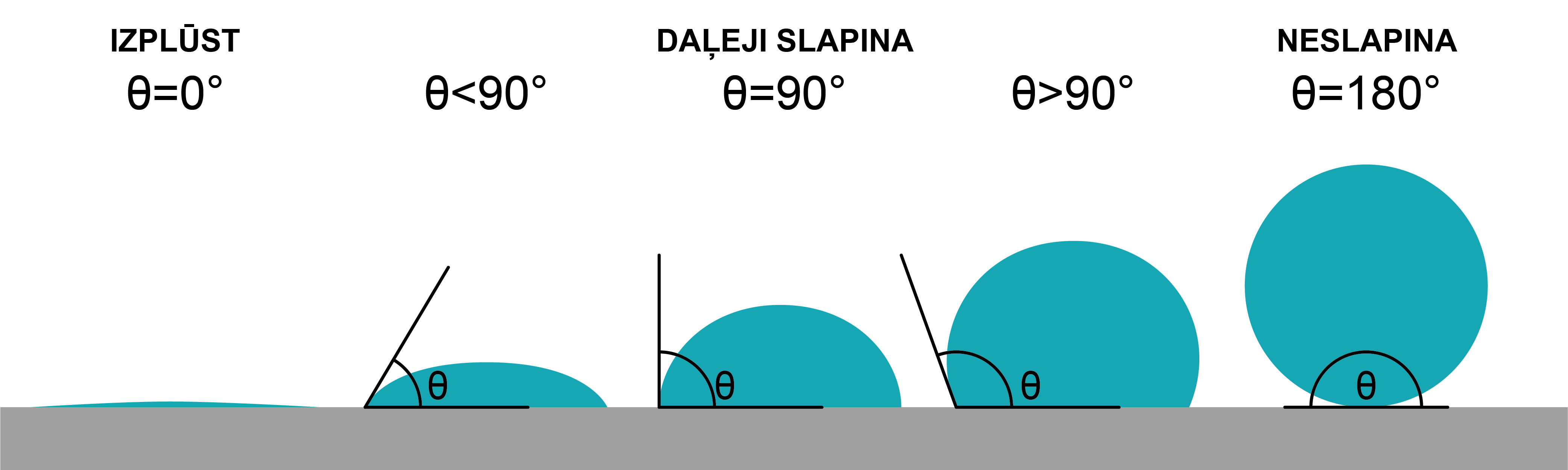
2.att. Virsmu slapinoši un neslapinoši šķidrumi
Savukārt, ja šķidruma molekulu pievilkšanās spēki ir lielāki par šķidruma un cietās vielas molekulu savstarpējās pievilkšanās spēkiem, tad šķidrums cenšas samazināt saskares virsmas laukumu ar cieto ķermeni, pēc iespējas attālinoties no tā – šajā gadījumā gadījumā šķidrums virsmu neslapina. Virsmas, ko neslapina ūdens, sauc par hidrofobām.
Šķidruma piliens uz horizontālas cieta ķermeņa virsmas smaguma spēka darbības rezultātā pieņem saplacinātas lodes formu (2. attēls d,e).
Neslapinošam šķidrumam \(\Theta\) > 90°. Pilnīgas neslapināšanas gadījumā \(\Theta\) = 180°.
Slapināšana un neslapinašana ir relatīvi jēdzieni — šķidrums, kas slapina vienu virsmu, kādu citu virsmu var neslapināt. Tā, piemēram, ūdens slapina stiklu, bet neslapina vasku, dzīvsudrabs slapina varu, bet neslapina stiklu.
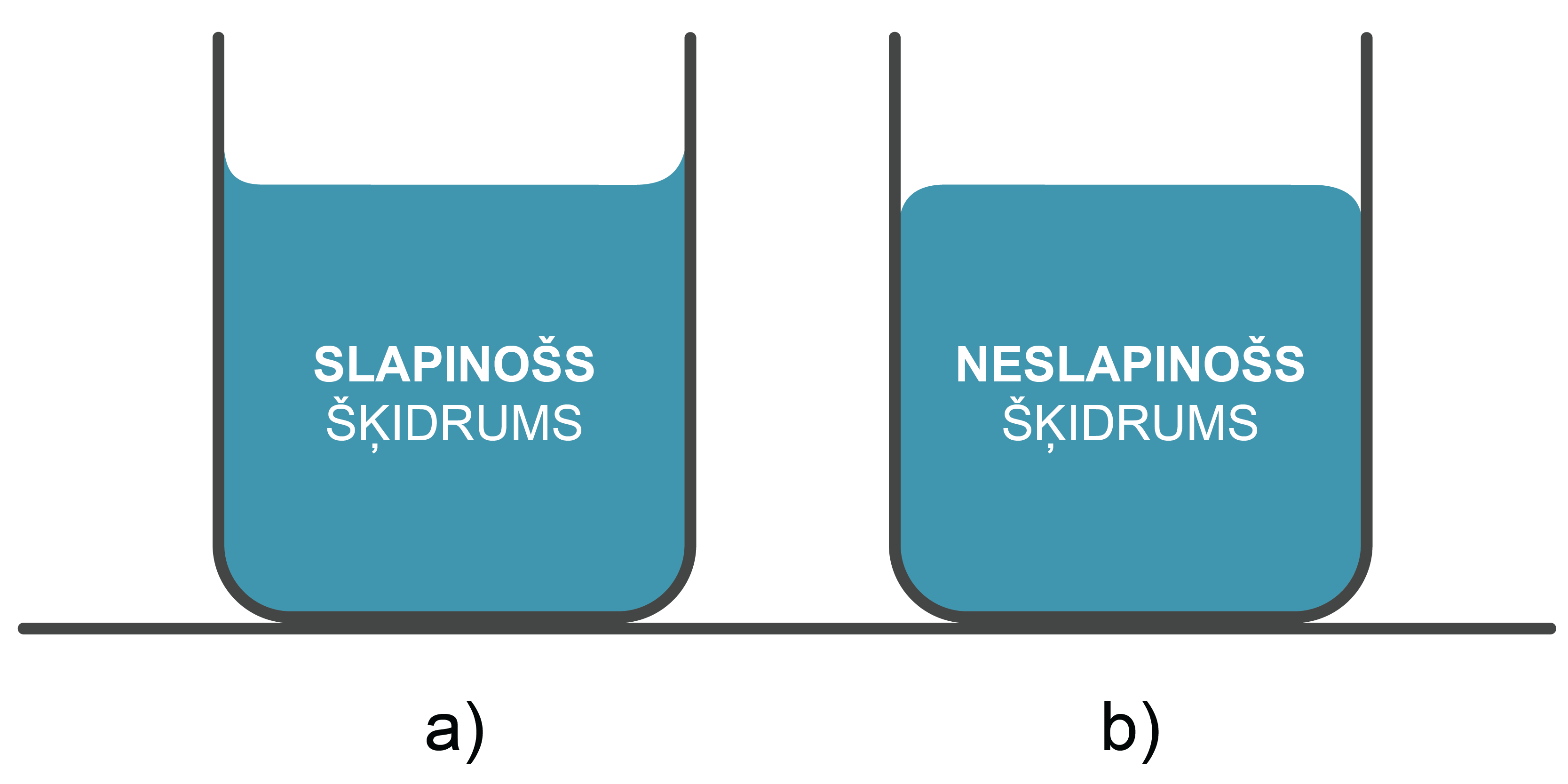
Ja šķidrums atrodas traukā, tad pie trauka sienas novēro šķidruma pacelšanos uz augšu (slapināšanas gadījumā) (3. attēls. a), vai līmeņa pazemināšanos (neslapināšanas gadījumā) (3. attēls b).
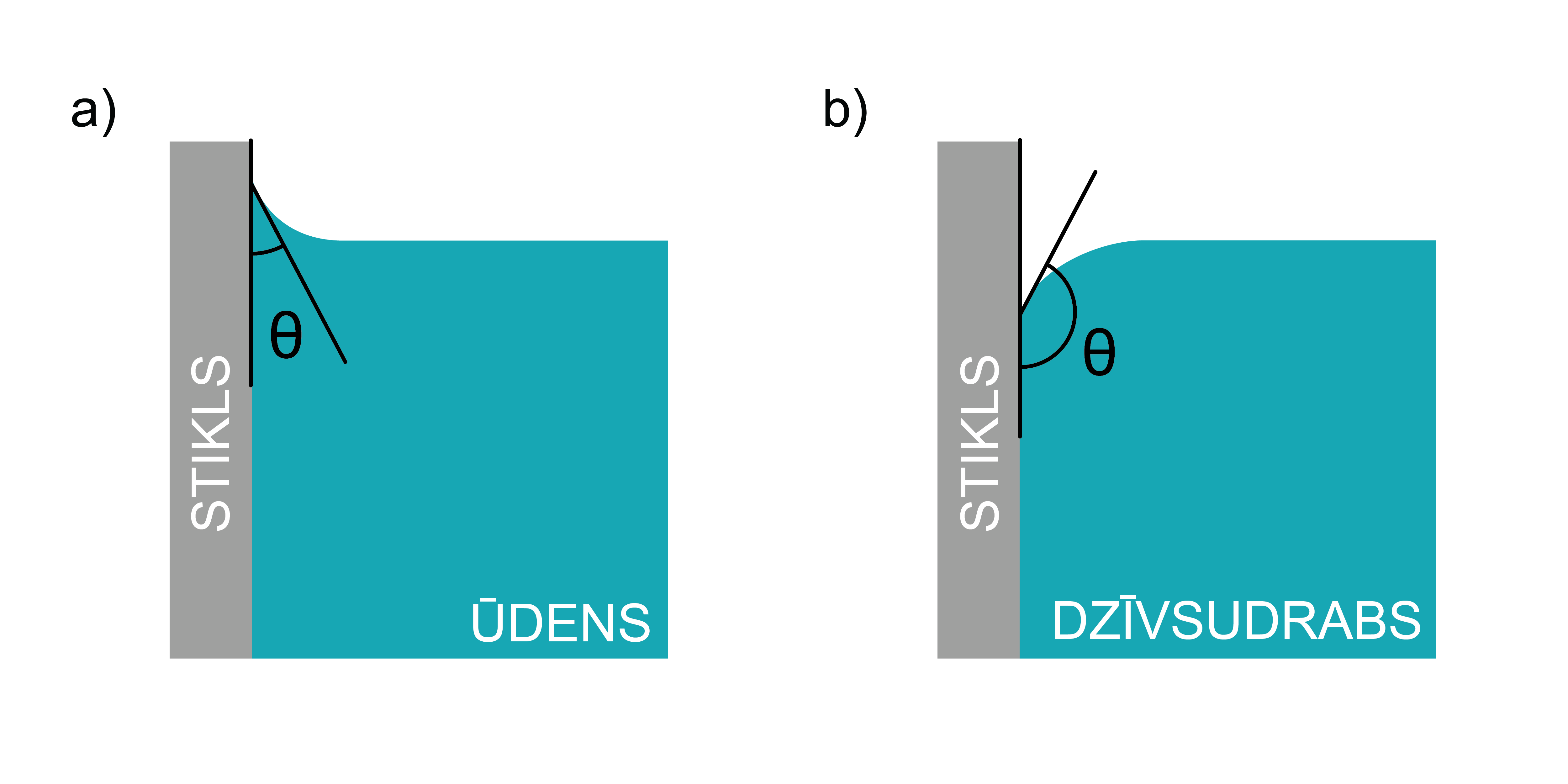
Malas leņķis pie vertikālas trauka sienas ir praktiski tikpat liels kā tādai pašai šķidruma/cietas vielas kombinācijai uz horizontālas virsmas, jo to nosaka molekulu mijiedarbība. Slapināšnas (neslapināšanas) dēļ šķidrums ļoti tievās caurulītēs var pacelties vai nolaisties – šo parādību aplūkosim nodaļā ''Kapilārās parādības''.
Slapināšana dabā un sadzīvē
Dažādās tehnoloģijās ir būtiski, lai izmantotās vielas un materiāli slapinātu viens otru, piemēram, līmēšanā, lodēšanā, krāsošanā un lakošanā.
Arī mazgāšanas līdzekļiem ir jāslapina mazgājamie priekšmeti. Mazāks saskares laukums nozīmē, ka šo šķidrumu ir vieglāk atdalīt no virsmas. Šis princips darbojas, izmantojot mazgāšanas līdzekļus (3. attēls). Vienkāršots skaidrojums ir šāds: ja uz virsmas ir eļļas (vai tauku) pilieni (3. att. a), tad tie virsmai ir pamatīgi pielipuši. Tad talkā nāk mazgāšanas līdzekļi, piemēram, ziepes, kas izveido kārtiņu ap eļļas pilienu (3. att. b). Šī kārtiņa nodrošina, ka eļļas piliens ar virsmu vairs tik intensīvi nemijiedarbojas, tādēļ tos ir vieglāk atdalīt (3. att. c).
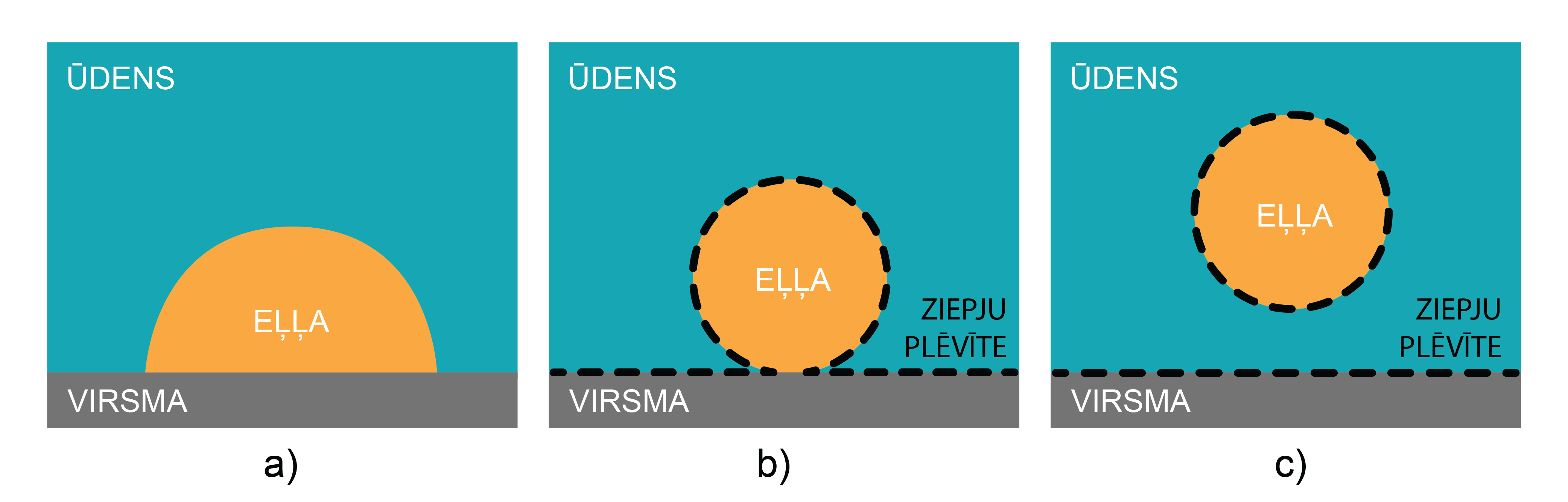
Tas, vai šķidrums virsmu slapina, ir atkarīgs ne tikai no šīdruma un virsmas materiāla (vielas), bet arī no virsmas faktūras.
Tā zinātnieki atklāja ''lotosa esfektu'' – pamanīja, ka ūdens praktiski neslapina lotosa lapas, ūdens pilieni praktiski uzreiz noripo no lapas, līdzi aiznesot putekļu daļiņas. Šādi virsma praktiski vienmēr saglabājas tīra. Līdzīgs efekts novērojams arī raspodiņu un lupīnu lapām (5. attēls).

Avots: https://commons.wikimedia.org/wiki/File:Lupins_with_superhydrophobic_water_droplet_capture.jpg
Vienkāršoti skaidrojot, tam par iemeslu ir ļoti sīkie ''izcilnīši'' augu lapu virsmā, kuru dēļ ūdens nevar mijiedarboties ar lapas virsmu.
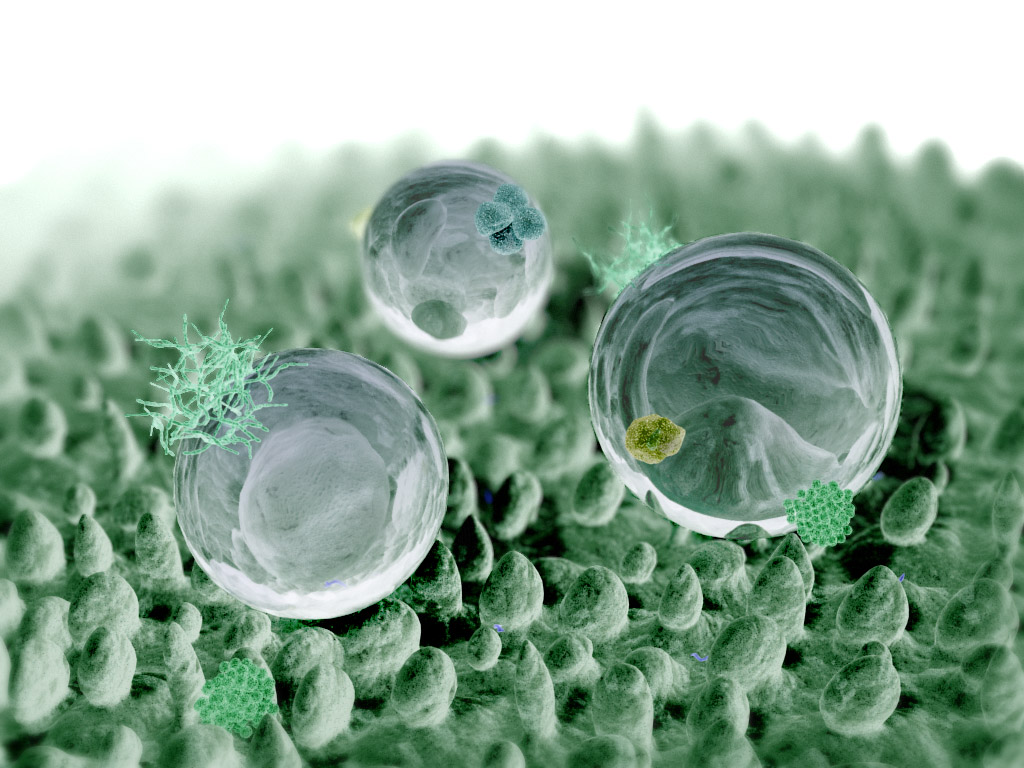

5.att.
Šo principu zinātnieki izmantoja, radot jaunus nanomateriālus – hidrofobus audumus un debesskrāpju logu stiklus, kurus būtu ļoti grūti vai neērti mazgāt.
Kapilāras parādības
Nodaļā ''Slapināšana'' aplūkojām parādību, ka, ja traukā ielej šķidrumu, kas tā virsmu slapina, tad šķidruma virsma pie trauka sieniņas ir ieliekta (1. attēls. a), bet, ja šķidrums trauka materiāla virsmu neslapina, tad šķidruma virsma pie trauka sienas ir izliekta (1. attēls. b).
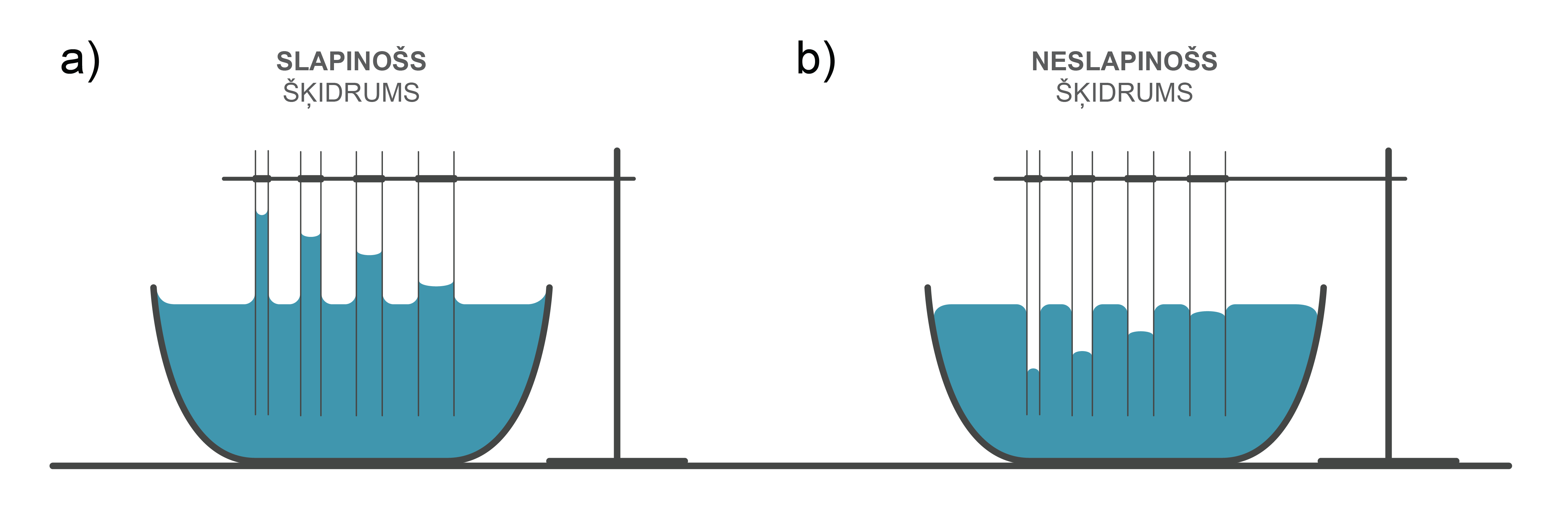
Šķidruma virsmas spraigums un slapināšana īpaši izpaužas tievās caurulītēs, ko sauc par kapilāriem. Ja traukā ar šķidrumu iegremdē šādu kapilāru, tad slapināšanas gadījumā šķidruma līmenis kapilārā ir par \(h\) augstāks nekā traukā (2. attēls. a), bet neslapinoša šķidruma līmenis ir pa \(h\) zemāks (2. attēls. b). Šādas šķidruma līmeņu atšķirības kapilāros sauc par kapilārajām parādībām.
Šķidruma virsmai kapilārā ir pussfēras forma ar rādiusu \(R\). Slapināšanas gadījumā šī virsma ir ieliekta (8. att. a), bet neslapināšanas gadījumā izliekta (2. attēls b).
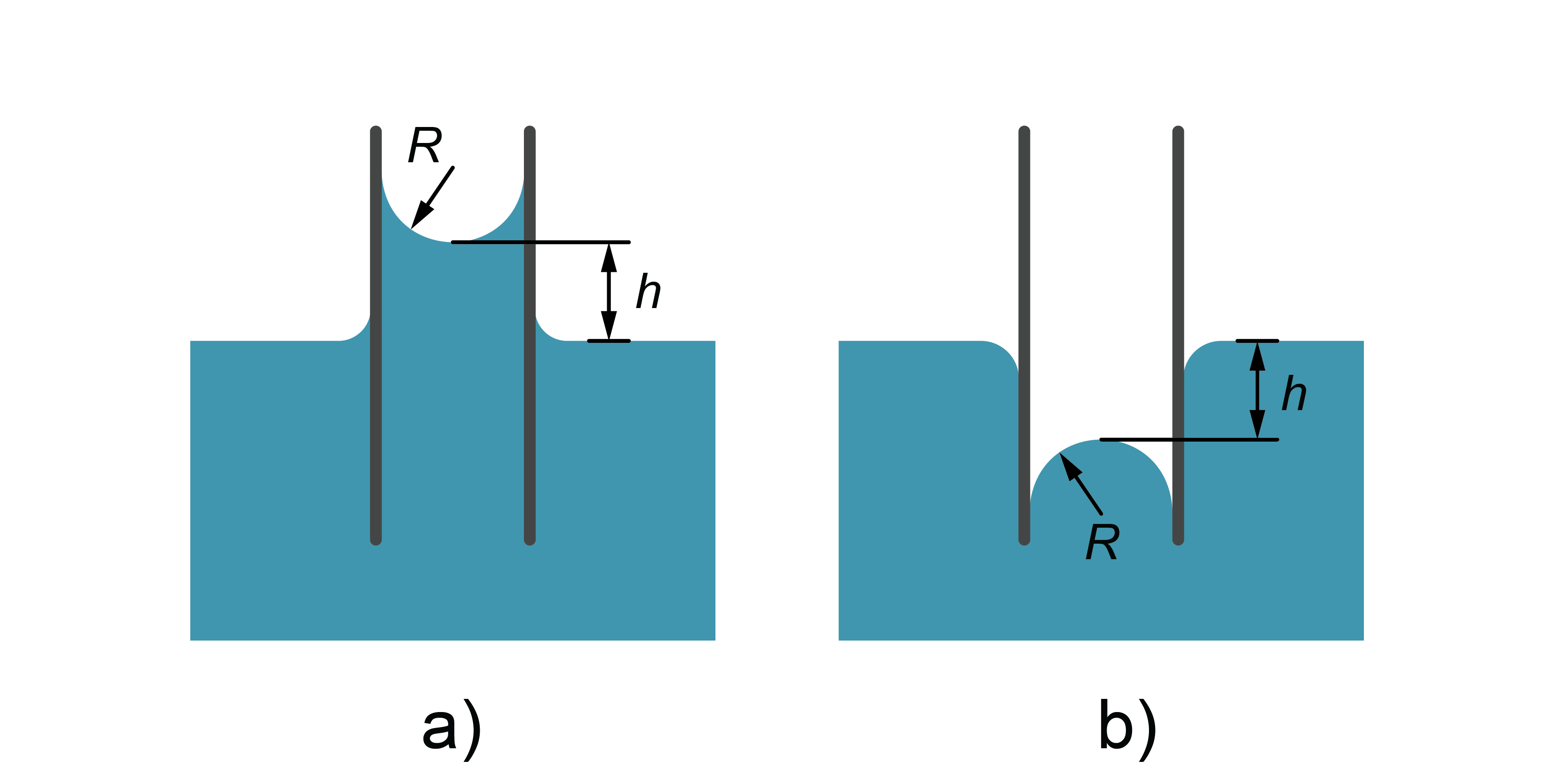
Kapilārā esošā šķidruma virsmas liekuma rādiuss ir vienāds ar kapilāra rādiusu R – veidojas menisks.
Zem liektas šķidruma virsmas rodas papildspiediens (\(\Delta p\)). Slapinošā šķidrumā un neslapinošā šķidrumā šis papildspiediens \(\Delta p\) ir vērsts pretējos virzienos (3. attēls). Ja virsma ir ieliekta (3. att. b), tad spiediens darbojas pretēji ārējam spiedienam un kopējo spiedienu uz virsmu samazina, bet, ja virsma ir izliekta (3. att. a), tad virsmas spraiguma spēka izraisītais spiediens palielina kopējo spiedienu uz virsmu.
Sfēriskas virsmas gadījumā šā spēka lielumu aprēķina pēc formulas \(\Delta p =\frac {2\sigma}{R}\).
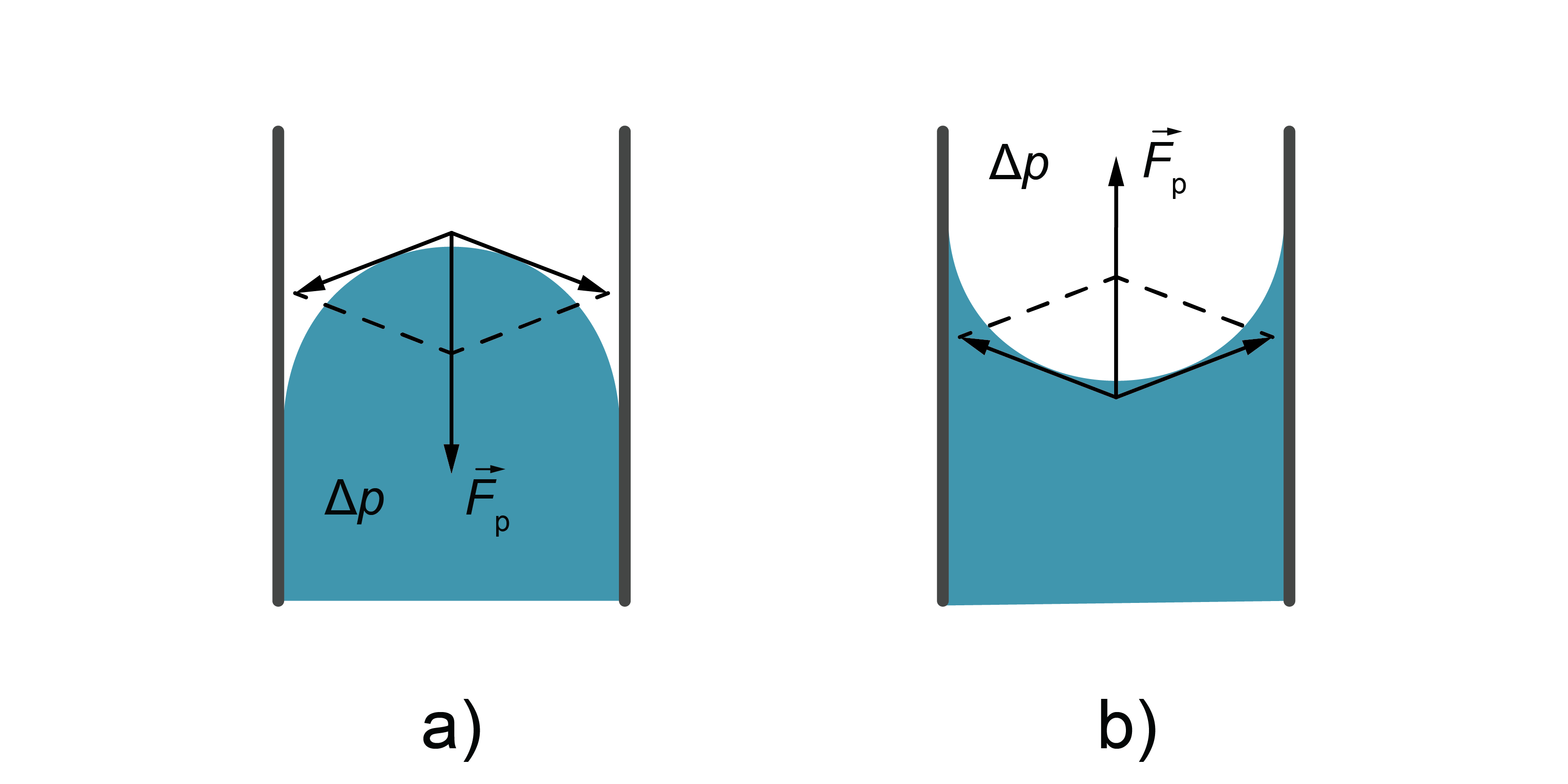
kur \(\Delta p\) — spiedienu starpība (šķidrumā un ārpus šķidruma), \(R\) — kapilārās caurulītes un, tātad, arī meniska rādiuss.
Papildspiediens zem liektas virsmas spilgti izpaužas demonstrējumā (4. attēls)
Caurulītes galus A un B ieliek traukā ar ziepjūdeni uz izņem no tā, pārklājot tos ar šķiduma plēvīti. Atverot krāniņus 1 un 2, piepūš ziepju burbuli A. Tad krānu 2 aizver, atver krāniņu 3 un piepūš mazāka rādiusa burbulīti B. Aizverot krāniņu 1 un atkal atverot 2 var ieraudzit šķietami negaidītu rezultātu - mazākais burbulītis kļūst mazāks, bet lielākais uzpūšas lielāks. Atmosfēras spiediens uz abiem burbuļiem ir vienāds, tātad gaisa plūsmu varēja radīt tikai papildspiediens zem burbuļu liektās virsmas.
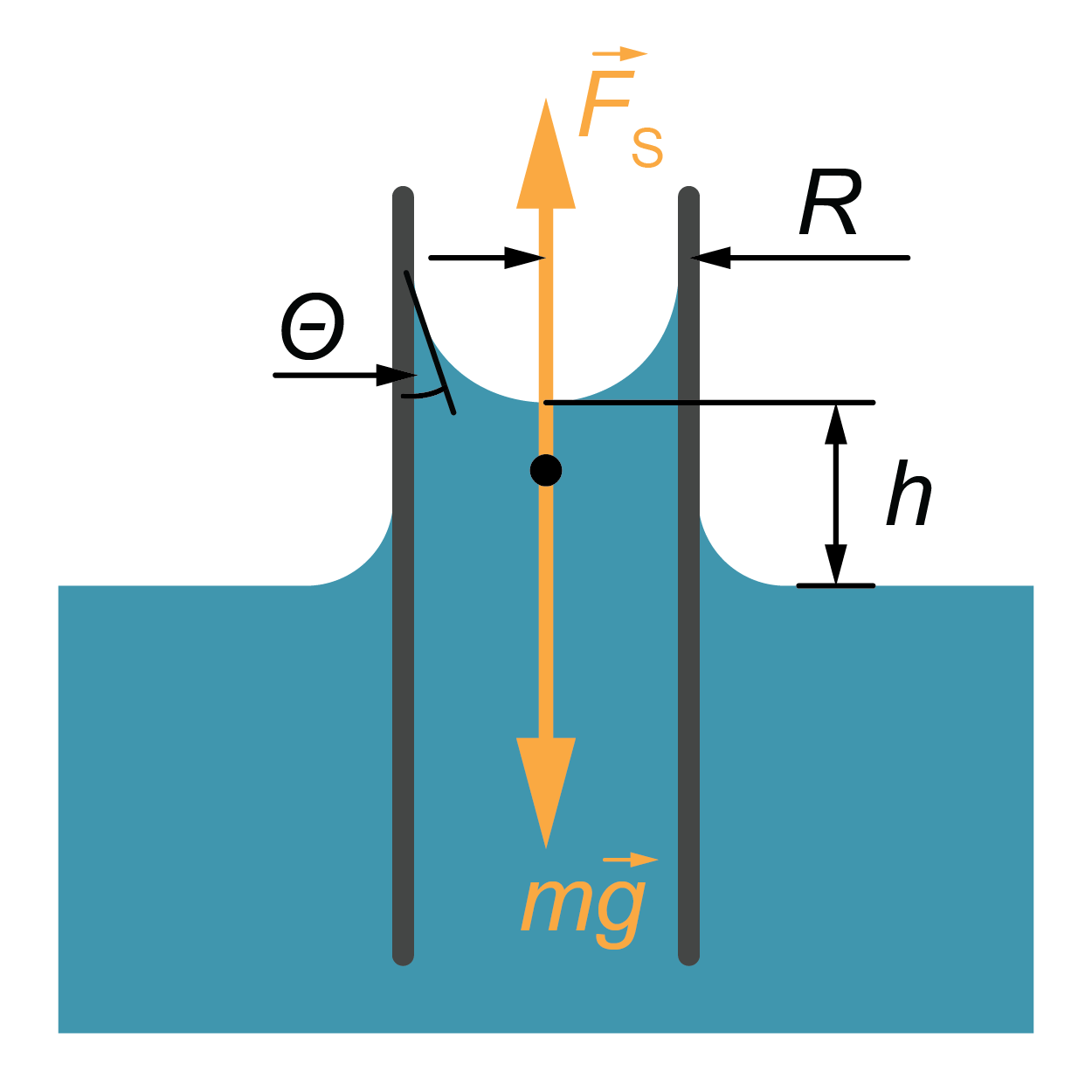
Šķidruma stabiņš kapilārā atrodas līdzsvarā, ja šķidruma virsmas spraiguma spēks \(F_\mathrm{S}\), kas gar ieliektās šķidruma virsmas kontūru ir vērsts vertikāli augšup, kompensē paceltā šķidruma smaguma spēku \(F_\mathrm{g} = mg\) (5. attēls). Virsmas spraiguma spēks šajā gadījumā \(F_\mathrm{S} = \sigma 2 \pi R\), kur \(\sigma\) - virsmas spraiguma koeficients, \(R\) - kapilāra rādiuss, bet paceltā ūdens masa (pieņemot, ka šķidruma stabiņš kapilārā ir cilindriskas formas) \(m = \rho V = \rho R^2h\), kur \(V\) - paceltā ūdens tilpums, bet \(\rho\) - šķidruma blīvums un \(g\) - brīvās krišanas paātrinājums.
Tātad, ja \(F_\mathrm{g} = F_\mathrm{S}\) jeb \(\rho R^2hg = \sigma 2 \pi R\), iegūst izteiksmi
\(h = \frac{2 \sigma} {(\rho g R)}\)
Ja ņem vērā arī meniska izliekumu un to, ka šķidruma stabiņš tomēr nav cilindrisks, tad, zinot malas leņķi, šķidruma stabiņa augstums kapilārā izsakāms šādi:
\(h = \frac {2 \sigma\cos\Theta} {(\rho g R)}\)
Pamatojoties uz šīm sakarībām, var izskaidrot, kādēļ, samazinot kapilāra rādiusu, šķidruma līmenis ir augstāks (6. att. a). Šeit gan jāatceras, ka ūdens līmenis kapilārā ir paaugstināts tad, ja šķidrums kapilāra virsmu slapina. Ja šķidrums virsmu neslapina, tad notiek līmeņa pazemināšanas (6. att. b), bet arī šajā gadījumā var lietot iegūtās formulas, vienīgi šeit h būs augstums, par kādu pazeminās šķidruma līmenis.
Ja kāda ķermenī ir kapilāri, tad slapināšanas gadījumā tas uzsūc ūdeni, piemēram, dažādi audumi, porolons, augsne.
Kapilārās parādības dabā
Kapilārās parādības ir nozīmīgas dažādos bioloģiskos procesos, piemēram, kapilārajām parādībām ir pakļautas asinis smalkajos asinsvados – kapilāros. Acs ābola nepārtraukta mitrināšana ar asarām notiek caur divām tievām kapilāru ''caurulītēm''. Arī augu barības vielu transportā liela nozīme ir kapilārajām parādībām, jo augu stumbrs faktiski ir veidots kā ļoti daudzu kapilāru sakopojums (7. attēls).

Arī augsnes virskārtā nepieciešamais mitrums var saglabāties, ja vienlaikus ar ūdens iztvaikošanu notiek tā pacelšanās kapilāros. Līdzīgi izskaidrojama arī dzēšpapīra vai sveces dakts darbība un citas līdzīgas parādības.