Spēki un mijiedarbība

Ja uz ķermeni, kas var brīvi griezties ap kādu asi, visu spēku momentu summa ir 0, tad ķermenis atrodas līdzsvarā (1. att. a), bet ja spēka momentu līdzsvars nav nodrošināts, tad sistēma griežas jeb rotē tajā virzienā, kurā spēka momentu summa ir lielāka (pozitīvajā vai negatīvajā virzienā). Lai rotējoši ķermeņi kustētos pēc iespējas līdzenāk, it sevišķi pie lieliem rotācijas ātrumiem, to masas centram jāsakrīt ar rotācijas centru. Novirzes gadījumā paša ķermeņa svars veido spēka momentu, kas padara saraustītu rotācijas kustību un var izraisīt gan diskomfortu (kratās un dreb kā traks), gan sabojāt rotējošo iekārtu. Tādēļ, piemēram, nepieciešams pārbaudīt automašīnas riepu balansu un nepieciešamības gadījumā pievienot papildus atsvariņus, kas izmaina riepas masas centra novietojumu (1. att. b).

1. att. Spēka momenti rotācijā un riteņu balansēšana

Tomēr ne vienmēr mums ir vajadzīga līdzena rotācijas kustība. Ja rotējošs disks nav nobalansēts, tad tas rotējot izraisa vibrācijas, kuras var izmantot, piemēram, mobilajos telefonos skaņas signāla vietā. Šis vibrācijas rada speciāls motoriņš, kura sastāvā ir nenobalansēts rotācijas disks (2. att.) 

2. att. Vibrozvanu izraisoša motoriņa uzbūve

Izmantojot spēka momenta līdzsvara nosacījumu, var izskaidrot to, kādēļ ar trīšiem var ietaupīt spēku. Ja trīsis ir nekustīgs (3. att.), tad spēka pleci l₁ un l₂, kas atbilst ķermeņa smaguma spēkam F₁ un pieliktajam spēkam F₂, ir vienādi, līdz ar to ietaupījums uz spēka lielumu netiek iegūts, tomēr pielikt uz leju vērstu spēku, lai paceltu kravu, nereti ir ērtāk.

3. att. Nekustīgs trīsis

Ja virves vienu galu nostiprina un tajā iekār trīsi, tad iegūst kustīga trīša sistēmu (4. att.). Atšķirībā no nekustīgas trīšu sistēmas (3. att.), šajā gadījumā spēka plecs l₂  spēkam, kas nodrošina kravas pacelšanu, ir divas reizes lielāks par spēku plecu l₁, kas atbilst kravas smaguma spēkam. No spēku momentu līdzsvara nosacījuma F₁l₁=F₂l₂ seko, ka F₂=F₁/2. Tas nozīmē, ka kravas pacelšanai ir jāpielie divreiz mazāks spēks nekā tai atbilstošais smaguma spēks.

4. att. Kustīgs trīsis

Praksē tiek lietotas trīšu sistēmas, kas sastāv gan no kustīgiem, gan nekustīgiem trīšiem. Kombinējot abus trīšu veidus, var panāk gan ērtāku kravu ceļošā spēka pielikšanas virzienu, gan arī ietaupījumu uz ceļošā spēka lielumu. 2012. gada maijā Latvijas Universitātes Dabaszinātņu un matemātikas izglītības centrs rīkoja pasākumu skolēniem, kurā viņiem bija jāveic dažādi ar dabaszinātnē saistīti uzdevumu. Fizikas posmā skolēniem vajadzēja uzbūvēt trīšu sistēmu, lai ar pēc iespējas mazāka spēka pielikšanu paceltu kādu no saviem komandas biedriem (5. att.).

5. att. Skolēnu komanda veido trīšu sistēmu, lai paceltu savu komandas biedru

Ja ķermenis ir novietots uz stabila pamata, tad tas negāzīsis, ja no smaguma centra novilkta vertikāle atradīsies atbalsta laukuma robežās (6. att. a). Tiklīdz tas neizpildās, ķermeni apgāž paša svara izraisīts spēka moments (6. att. b). Tādēļ ķermeņu stabilitātē ir svarīgs masas centra novietojums. Ja masas centra atrodas virs atbalsta laukuma, tad par ārēji nestabila sistēma negāzīsies (6. att. c). Ja mēģina līdzsvara stāvoklī novietot zīmuli uz tā asā gala, tas ir praktiski neiespējams uzdevums, kaut gan var atrast stāvokli, kad masas centrs atrodas virs atbalsta laukuma. Tomēr šis atbalsta laukums ir tik niecīgs, ka apkārtējo apstākļu paša zīmuļa mikroskopisku efektu ietekme izbīda zīmuli no līdzsvara stāvokļa, apskati video.

6. att. Ķermeņu līdzsvars

Cilvēks, pieceļoties no sēdus stāvokļa, vienmēr intuitīvi paliecas uz priekšu, lai savu masas centru novirzītu ārpus atbalsta laukumam, atvieglojot piecelšanos. Tāpēc, lai apturētu kāda cilvēka piecelšanos, pietiek pielikt tam pie pieres vienu pirkstu, tādējādi neļaujot paliekties uz priekšu, un sēdošajam cilvēkam, pat pieliekot lielas pūles, vairs neizdodas piecelties (7. att.).

7. att. Tā var apturēt picelšanos tikai ar vienu pirkstu

Jo tālāk no atbalsta laukuma tiek pielikts spēks, jo sistēma ir nestabilāka. To jāievēro, vedot uz velosipēda stūres kādu kravu, piemēram, iepirkuma maisiņu. Jo tālāk maisiņš atrodas no stūre centra, jo liekāks spēka moments darbojas uz velosipēdu un tas kļūst nestabilāks (8. att.)

8. att. Dažās iepirkuma maisiņa novietojums uz velosipēda stūres

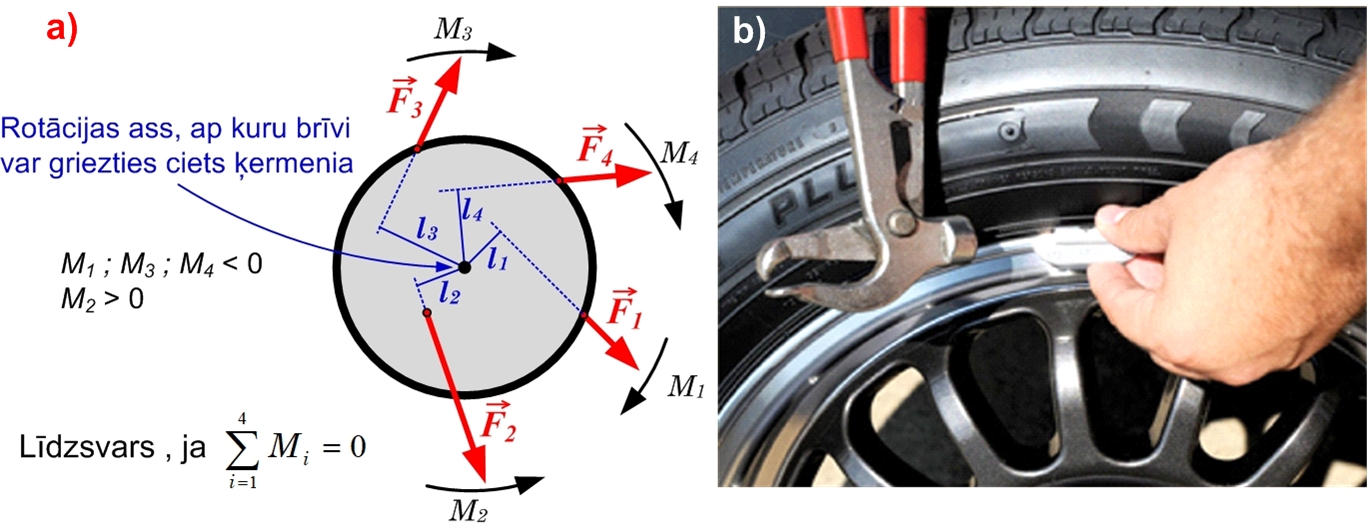
Sadaļā par inerci tika noskaidrots, ka masa ir ķermeņa inerces mērs. Ja ķermenim ir lielāka masa,  to ir grūtāk iekustināt un paātrināt, vai arī tieši otrādi - nobremzēt un apstādināt. Ja ķermenis atrodas rotācijas kustībā, tad tāda gadījumā inerce vairs nav atkarīga tikai no kermeņa masas, bet arī no attāluma līdz rotācijas asij. Lai aprakstītu rotējoša ķermeņa inerci, izmanto inerces momentu. Ja masas punkts kustas pa riņķa līniju, tad inerces momentu aprēķina I=mR², kur 
m - masa, kg
R - riņķa līnijas rādiuss, m
Par masas punktu, kas rotē ap noteiktu centru, var uzskatīt nelielu ķermeni, kas tiek griezt tievā saitē (1. att.). 

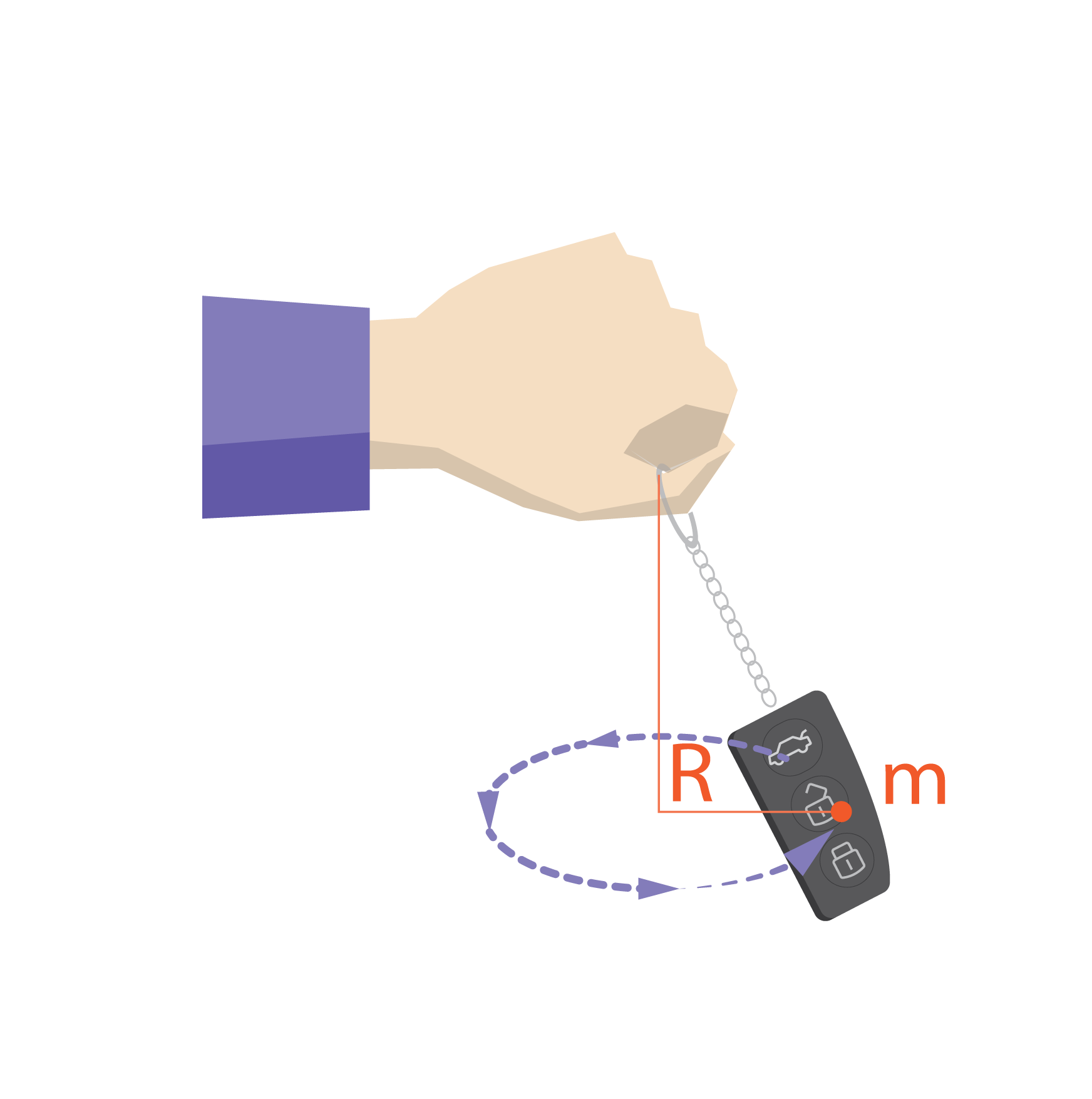
1. att. Inerces momenta aprēķināšana

Ja ķermeni nevar uzskatīt par masas punktu, tad dažādi ķermeņa punkti atrodas dažādos attālumos no rotācija ass. Lai iegūtu šāda ķermeņa inerces momentu, ir jāsaskaita visu ķermeņa punktu inerces momenti, piemēram, Zemei (2. att.) visi ķermeņa punkti neatrodas vienāda attāluma no rotācijas ass. Tādēļ lai iegūtu kopējo inerces momentu, ir jāsaskaita kopā visu ķermeņa punktu inerces momenti.

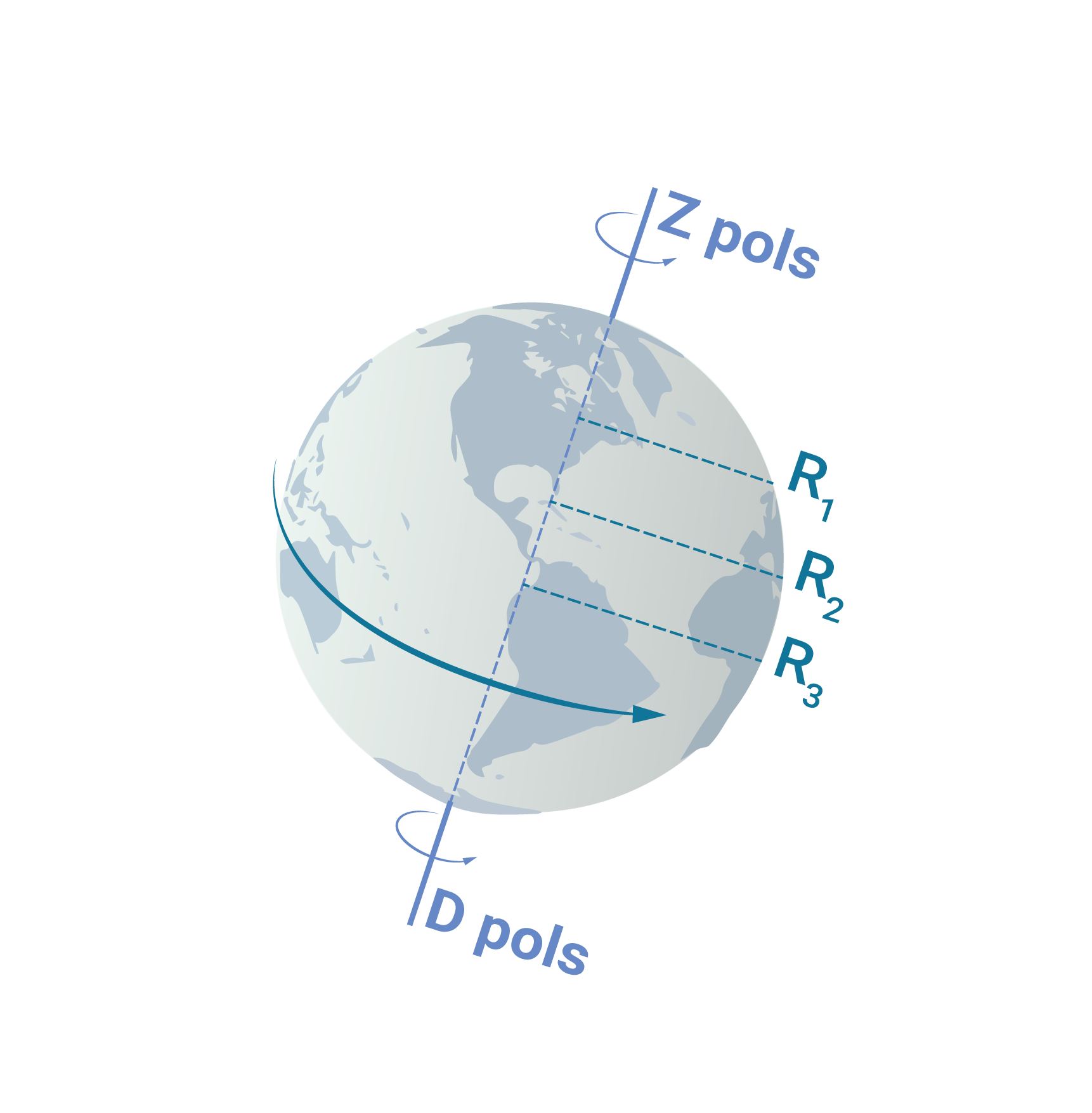
2. att. Zemes rotācija

Inerces momentu var aprēķināt arī patvaļīgas formas ķermenim, tomēr ja ķermenim ir regulāra forma, tad inerces momentu var izteikt ar vienkāršām formulām, kurā ietilps ierasti ķermeņa parametri (3. att.).

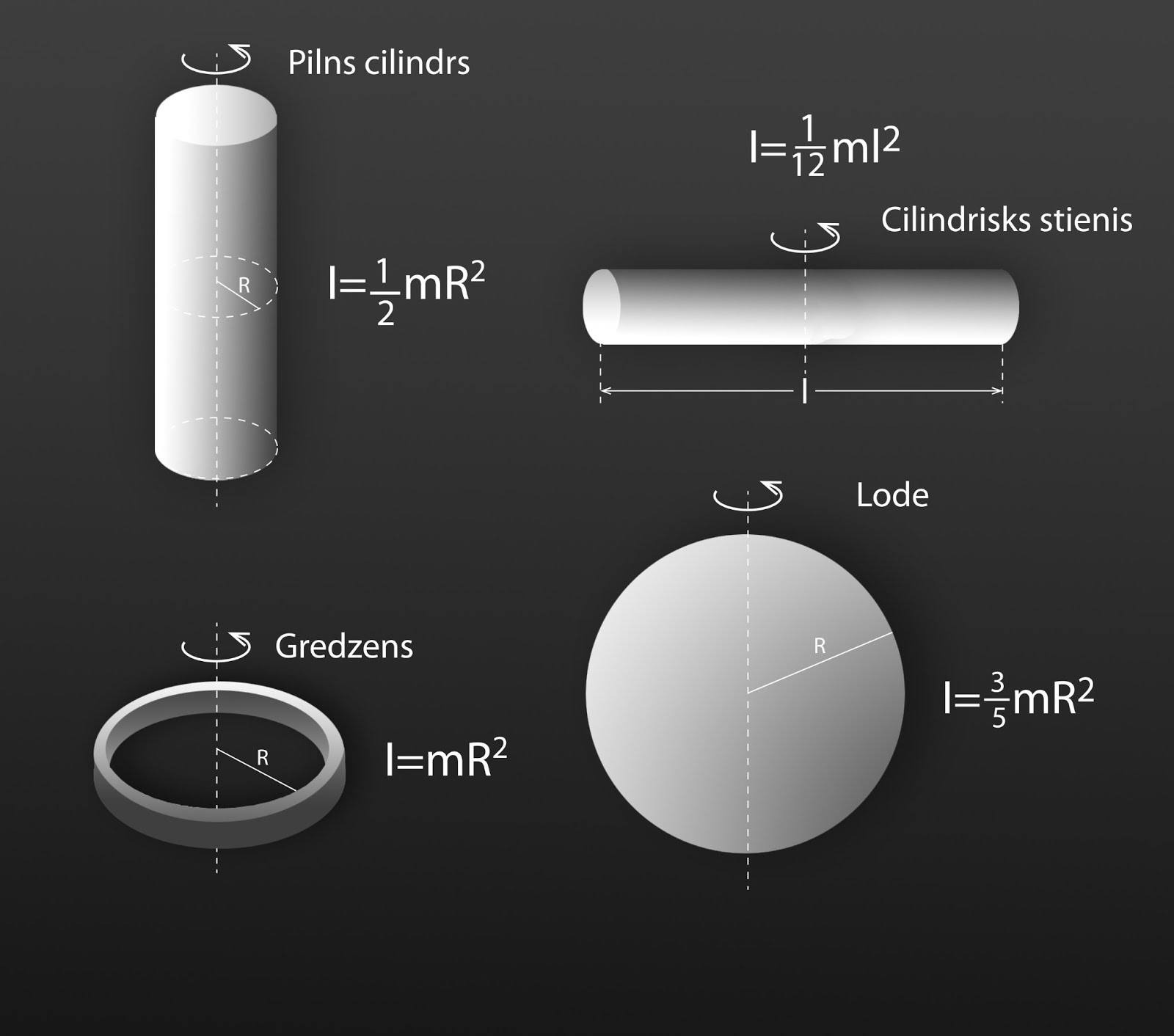
3. att. Dažādu regulāru ķermeņu inerces momenti

3. attēlā arī redzams, ka viena un tā paša ķermeņa inerces moments var būt atkarīgs no rotācijas ass izvēles. To var sajust, izmantojot slotas kātu. Ja mēs slotu kātu grozam pa gareno asi, tad visa masa atrodas tuvu rotācijas asij un šādu darbību veikt ir samērā viegli (4. att. a). Savukārt, ja mēs paņemam kātu aiz viena gala un griežam ap to, tad griezt ir daudz grūtāk (4. att. b), jo masa šādā gadījumā atrodas tālāk no rotācijas ass un ķermeni raksturo lielāks inerces moments.

4. att. Slotas kāta griešana ap dažādām asīm

Inerces momenta īpašības izmanto dažādu transporta līdzekļu dzinējos, lai padarītu to darbību vienmērīgāku, proti, dzinēja vienā galā ir piemontēts liels, apaļs un smags spara rats, kuram ir liels inerces moments (5. att.). Sadegot degvielai, motorā enerģija roda tikai noteiktos laika brīžos, nevis nepārtraukti, tādēļ spara rata lielais inereces moments nodrošina enerģijas uzkrāšanu un vienmērīgu atdošanu tajos brīžos, kad motorā enerģija nerodas.

5. att. Dzinēja spararats

Ar inerces momentu ir jārēķinās arī dejojot. Kad deju pāris griežas, tad pāra inerces moments ir atkarīgs no attāluma starp deju partneriem. Jo mazāks ir šis attālums, jo inerces moments ir mazāks, līdz ar to ir vieglāk iegriezties. Ja dejas laikā deju partneris cenšās piekļauties pēc iespējas tuvāk savai deju partnerei, tas var liecināt par vēlmi kārtīgi izgriezties dejas laikā (6. att.). Protams, mērķi var būt arī citi.
 

6. att. Deju partnere griezienā

Vēl viens moments fizikā ir impulsa moments L. Atšķirība no iepriekšējiem momentiem, šajā gadījumā momenta lielumu aprēķina L=mvR=pR, kur
m - masa, kg
v - kustības ātrums, m/s
R - attālums no rotācijas ass, m
p - impulss, kg·m/s
Ja ir zināms ķermeņa inerces moments I un rotācijas leņķiskais ātrums ω, tad otrs veids kā aprēķināt impulsa momentu ir L=Iω. Šīs pēdējās izteiksmes dēļ impulsa momentu dēvē arī par leņķisko momentu.  Ja impulss ir vērsts pret pulksteņa rādītāja virzienu, tad impulsa moments ir vērsts augšup, pretējā gadījuma impulsa momenta vērsums ir uz leju (7. att.).

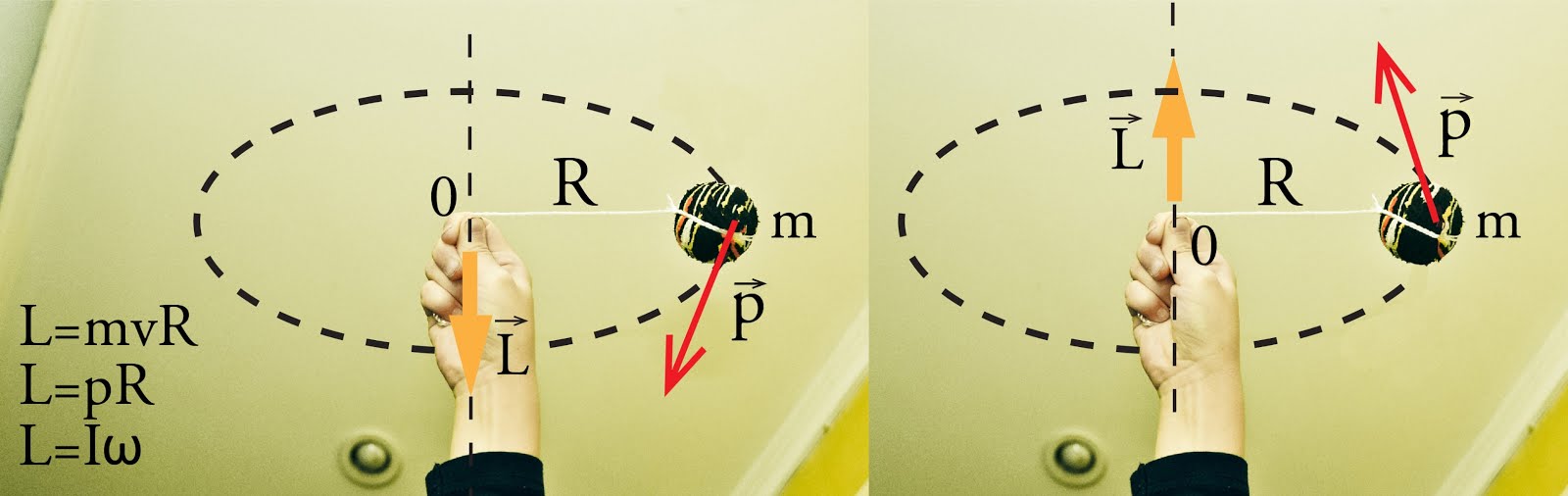
7. att. Impulsa momenta aprēķināšana un virziena noteikšana

Rotējoši ķermeņi ir pakļauti impulsa momenta nezūdamības likumam: ja ķermenis rotē un uz to nedarbojas spēka moments, tad impulsa moments nemainās jeb L=Iω=const. Par impulsa nezūdamību var pārliecināties, izmantojot rotējošu platformu (8. att.). Ja cilvēks ar izstieptām rokā iegriežas uz rotējošas platformas (8. att. a), tad tam piemīt noteikts inerces moments I un rotācijas leņķiskais ātrums ω. Piekļaujot rokas klāt (8. att. b), samazinās I, līdz ar to pēc impulsa momenta L nezūdamības likuma ir jāpalielinās rotācijas leņķiskajam ātrumam ω, ko arī šajā gadījumā var novērot. Daiļslidošanas trikos arī tiek izmantots impulsa momenta saglabāšanās likums. Kad, piemēram, daiļslidotāja veic kādu rotācijas kustību, tad vispirms iegriešanās tiek veikta ar izstieptām rokām, pēc tam rokas tiek piekļautas, lai iegūtu lielāku rotācijas ātrumu. Noskaties video!

8. att. Kārlis uz rotējošas platformas

Zemes griešanās ap savu asi un no tās izrietošā dienas un nakts maiņa ir ierasta lieta mūsu dzīvēs. Un izrādās, ka Zemes griešanās arī ir saistīta ar impulsa momenta nezūdamības likumu. Kad Saules sistēma, kurā atrodas mūsu Zeme, bija vēl tikai veidošanās stadīja, tā sastāvēja no rotējoša gāzu un putekļu mākoņa (9. att.), kuru raksturoja noteikts impulsa moments. Kad vēlāk no šiem putekļiem sāka veidoties lieli sablīvējumi - planētas, tad, lai saglabātos impulsa moments, arī planētai bija jārotē. 
 

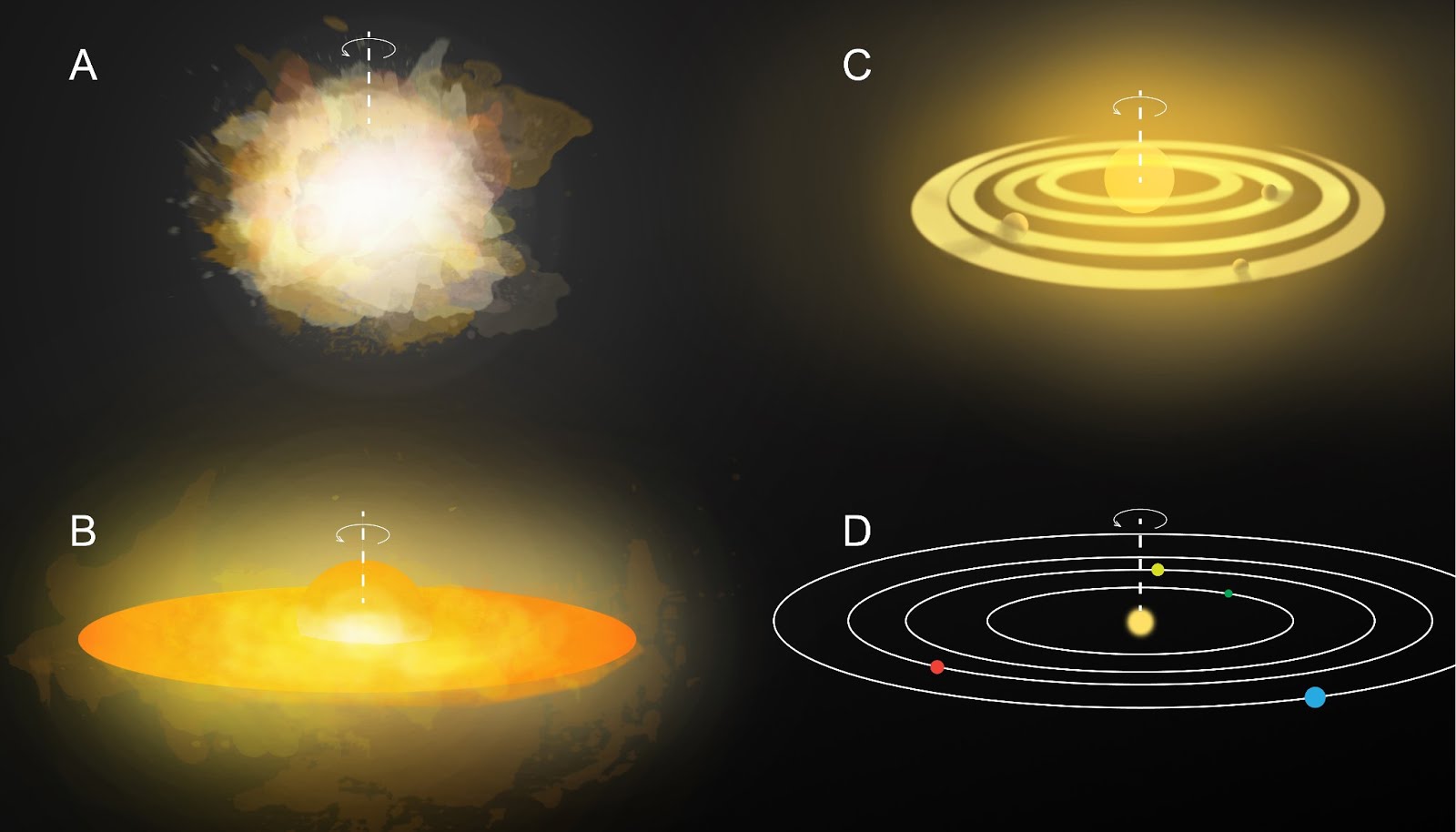
9. att. Saules sistēmas veidošanās