Ja divi spēki darbojas uz vienas taisnes, tad izšķir divus gadījumus. Tie var darboties vienā virzienā (1. att. a) vai pretēji viens otram (1. att. b). Pirmajā gadījumā kopsēka vērtību iegūst, saskaitot abus spēkus (1. att. a), bet otrajā gadījumā spēki darbojas pretējos virzienos un daļēji viens otru kompensē, tādēļ kopsēks būs vērsts lielākā spēka virzienā un tā vērtībā iegūstama no lielākā spēka atņemot mazāko (1. att. b).
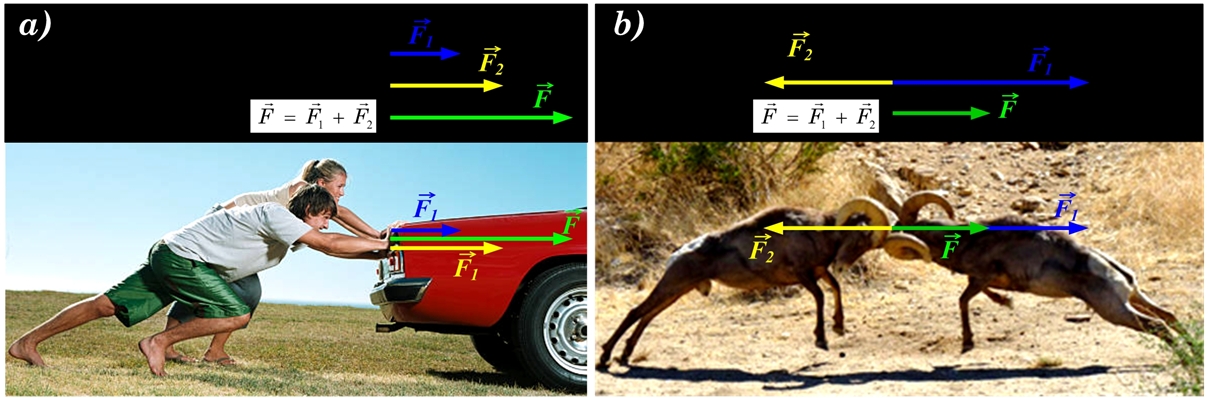
1. att. Spēku saskaitīšana uz vienas taisnes
Ja divi spēki ir vērsti perpendikulāri, tad kopsēks vērsts pa diagonāli četrstūrim, kura divas malas veido spēku vektori, bet pārējas divas iegūst no katram vektoram paralēlām līnijām. Šādā gadījumā kopspēka aprēķināšanai jāizmanto Pitagora teorēma (2. att.). Perpenidkulāru spēku gadījumā kopsēks nav vērsts neviena no atsevišķā spēka virzieniem (2. att.).
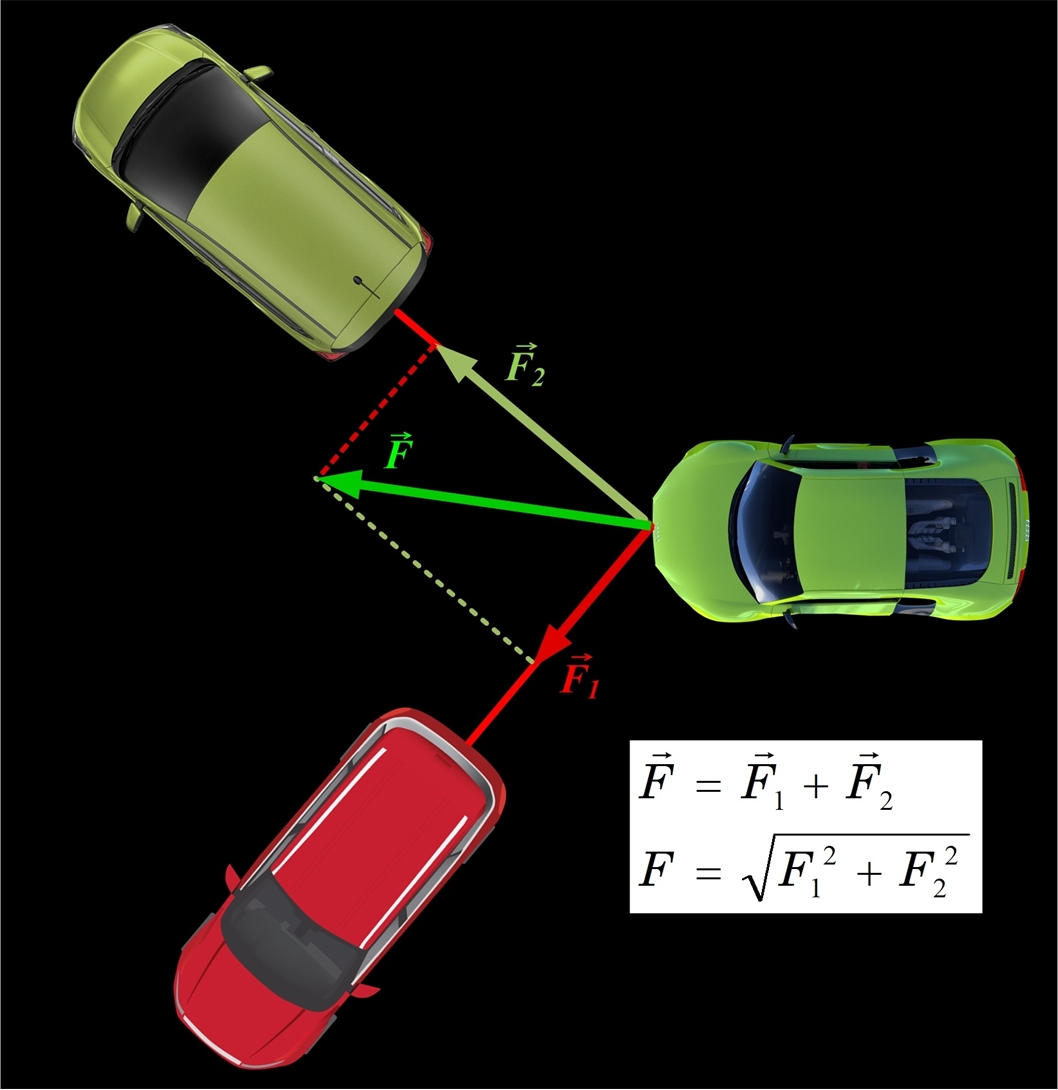
2. att. Perpendikulāru spēku saskaitīšana
Ja divi spēki ir vērsti perpendikulāri, tad kopsēks vērsts pa diagonāli četrstūrim, kura divas malas veido spēku vektori, bet pārējas divas iegūst no katram vektoram paralēlām līnijām. Šādā gadījumā kopspēka aprēķināšanai jāizmanto Pitagora teorēma (2. att.). Perpenidkulāru spēku gadījumā kopsēks nav vērsts neviena no atsevišķā spēka virzieniem (2. att.).
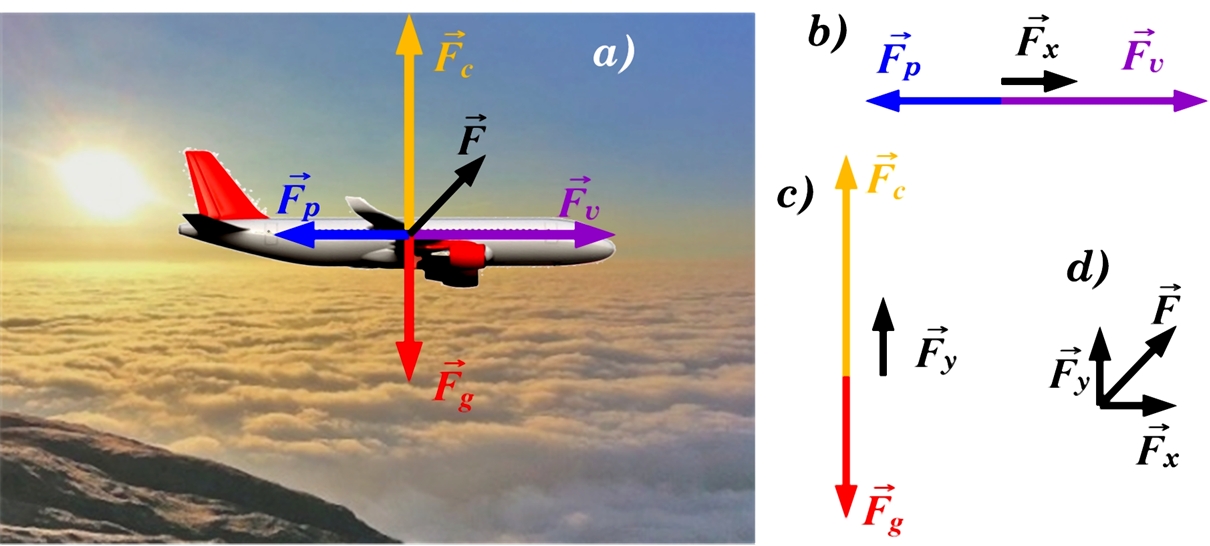
3. att. Vairāk nekā divu perpendikulāri vērstu spēku saskaitīšana
Ja perpendikulāri ir vērsti vairāk nekā divi spēki, tad vispirms ir jāveic to spēku saskaitīšanas, kas atrodas uz vienas taisnes un pēc tam jāsaskaita perpendikulārie kopspēki pa katru taisni. Piemēram, apskatīsim gaisa balonu uz kuru darbojas četri spēki: Arhimēda cēlējspēks FA, vēja radītais vilcējspēks FV, smaguma spēks FG un pretestības spēks FP (3. att. a). Lai iegūtu kopspēku, virspirms tiek saskaitīti spēki pa x-asi, iegūstos kopsēku x-ass virzienā FX (3. att. b). Tas pats tiek izdarīts pa y-asi (3. att. c). Visbeidzot tiek saskaitīti spēki FX un FY, iegūstot četru spēku kopspēku F (3. att. d).
Ja divi vektori ir vērsti patvaļīgos virzienos, tad vektoru saskaitīšanai var izmantot paralelogramma likumu. Ja abus vektorus atliek no viena punkta, tad summas vektors vienāds ar paralelogramma diognāli, kas iziet no kopīgā sākuma punkta (1. att.)
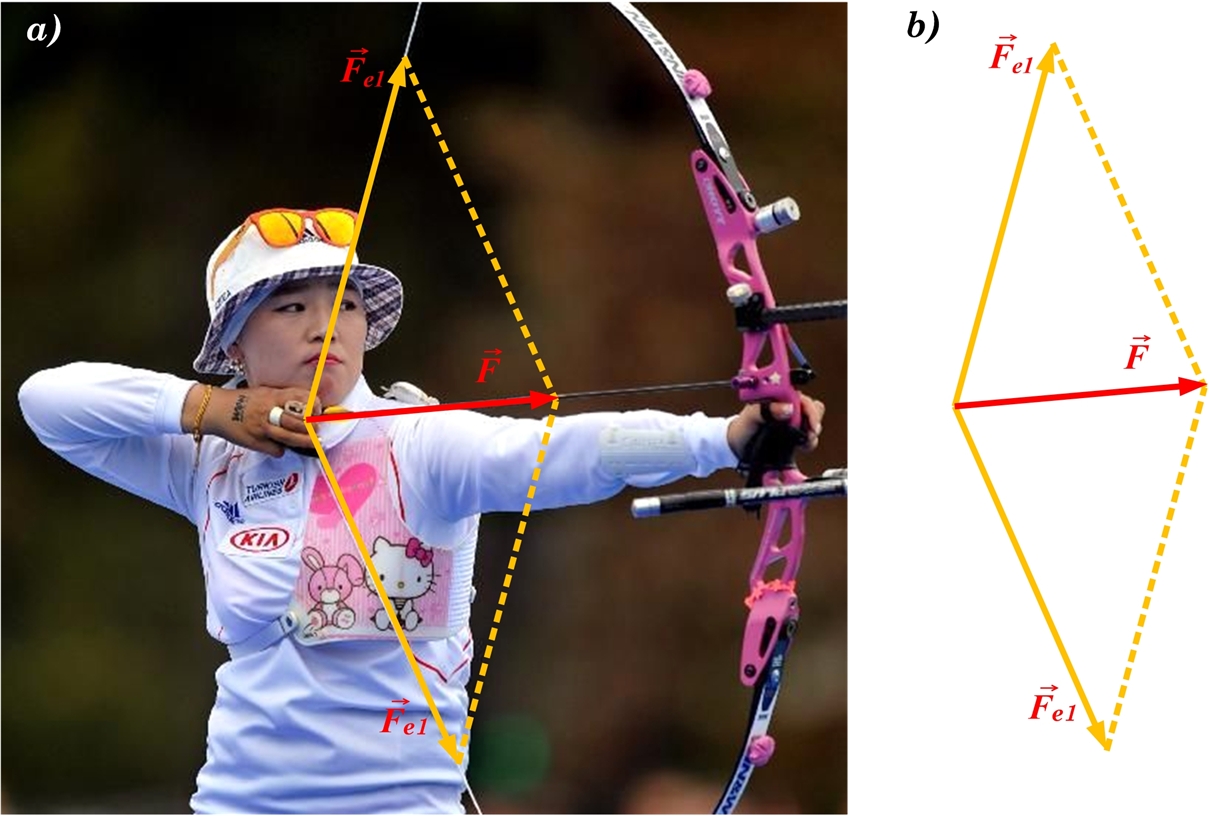
1. att. Divu patvaļīgi vērstu spēku saskaitīšana
Ja saskaitāmo vektoru skaits ir lielāks nekā divi un tie vērsti patvaļīgos virzienos, tad saskaitīšanai ērti izmantot daudzstūra likumu. Šajā gadījumā ir jānofiksē viens vektors un jāpievieno pārējie vektori tā, lai katra nākamā vektora sākuma punkts sakrīt ar iepriekšējā vektora beigu punktu. Summas vektors ir vērsts no pirma vektora sākuma punkta līdz pat pēdējā vektora beigu punktam. Secība, kādā atliek vektorus un kuru izvēlās par pirmo, nav svarīga! Piemēram, 2. att. norādīti četri spēki, kas darbojas uz lidmašīnu. Izmantojot daudzstūra likumu, nav svarīgi kādā secībā tiek sakārtoti vektor, taču kopspēks būs vienāds ar vektoru, kas savieno pirmā vektora sākumpunktu ar pēdējā vektora galapunktu!
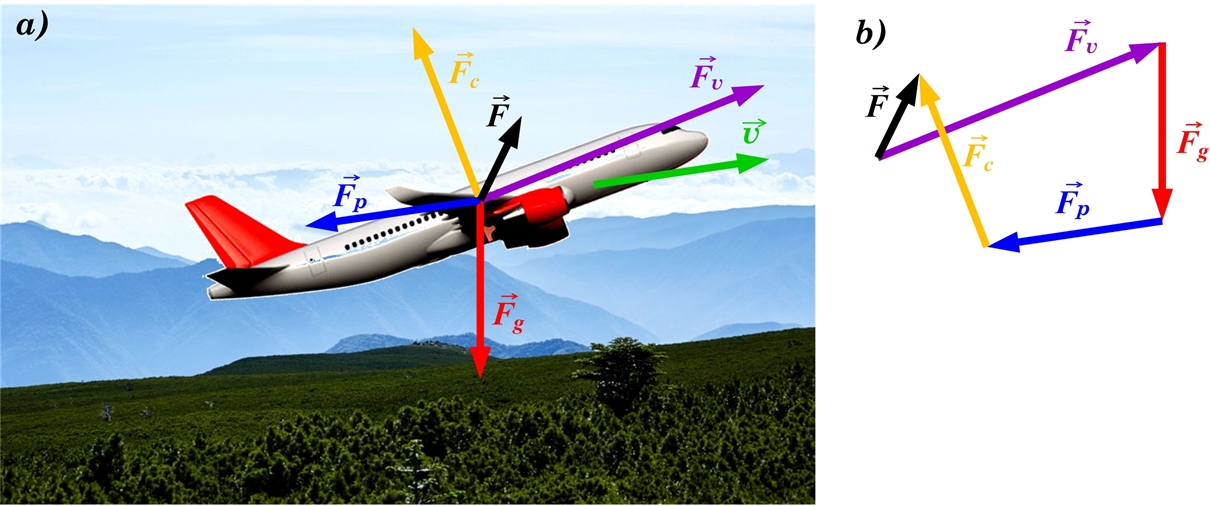
2. att. Uz lidmašīnu darbojošais kopspēks
Ja tiek apskatīta kustība pa taisni, tad jāņem vērā kāds ir spēku darbība pa šo taisni. Piemēram, ja uz putekļu sūcēju iedarbojas ar spēku F (3. att. a) un mums interesē kā putekļu sūcējs kustas horizontālajā virzienā, tad jānoskaidro cik liels spēks darbojas tieši šajā virzienā. Ērtības labad jāievieš koordinātu sistēma, kurā x-ass izvēleta pa kustības asi. Spēka lielums ass virzienā ir vienāds ar tā projekciju. Ja spēks F ar X-asi veido leņķi α, tad projekcija FX vienāda ar Fcosα (3. att. b). Ja nepieciešams noskaidrot spēka darbību citā virzienā, piemēram, perpendikulārajā virzienā kurā ir vērsta koordinātu sistēmas Y-ass, tad jātrod spēka projekcija uz šo asi. To var aprēķināt FY=Fsinα (3. att. b).
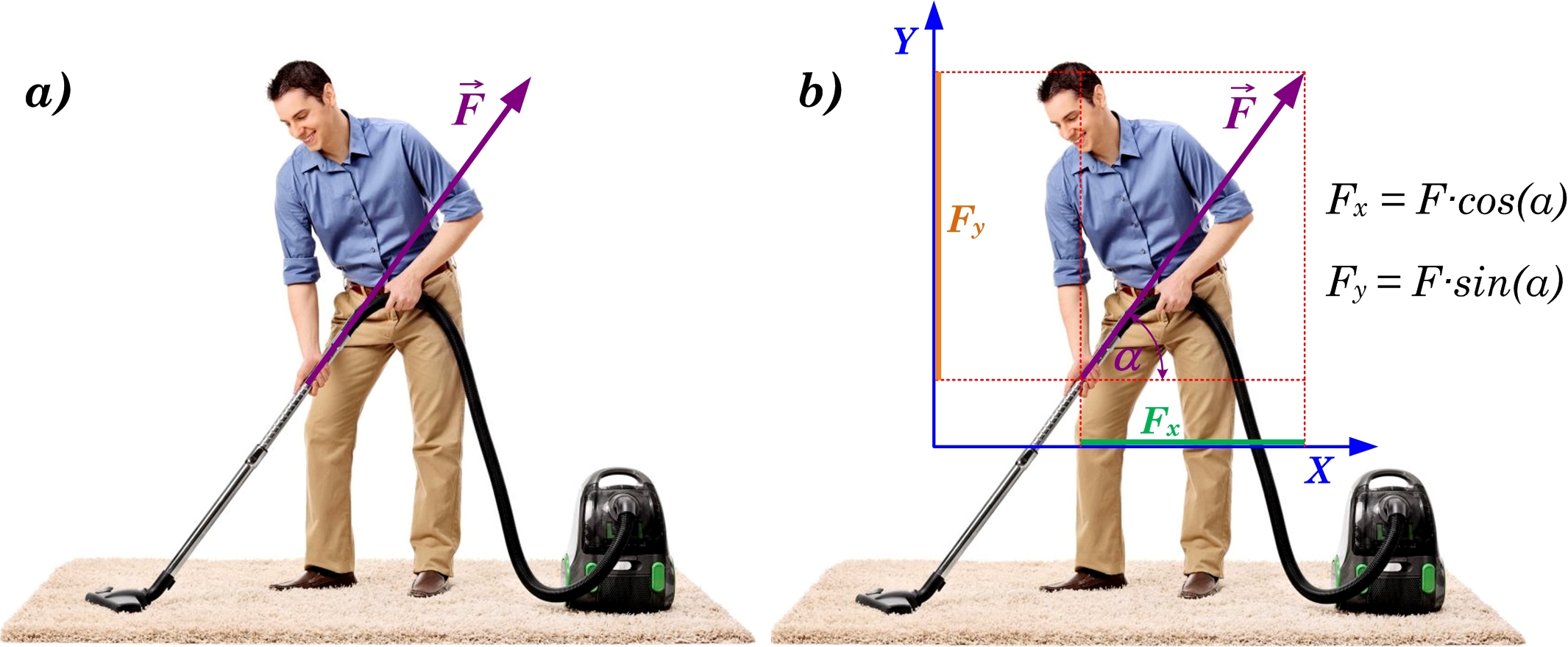
3. att. Spēka projekcija dažādos virzienos
Ja kustība notiek pa slīpu virsmu, tad koordinātu sistēmu ērti izvēlēties, saistot to ar kustības virzienu. Piemēram, ja ar ragaviņām brauc no kalna un jāatrod smaguma spēka FG ieguldījums kustībā, tad koordinātu sistēma jāizvēlas tā, lai X-ass būtu vērsta paralēli kalna virsmai, līdz ar to Y-ass vērsums būs perpendikulārs kalna virsmai (4. att.). Aprēķinot spēka projekcijas iznāk, ka projekcija FGX parāda kāds spēks darbojas kustības virzienā, bet projekcija FGY spēku ar kādu ragaviņas spiež uz kalnu smaguma spēka ietekmē (4. att.).
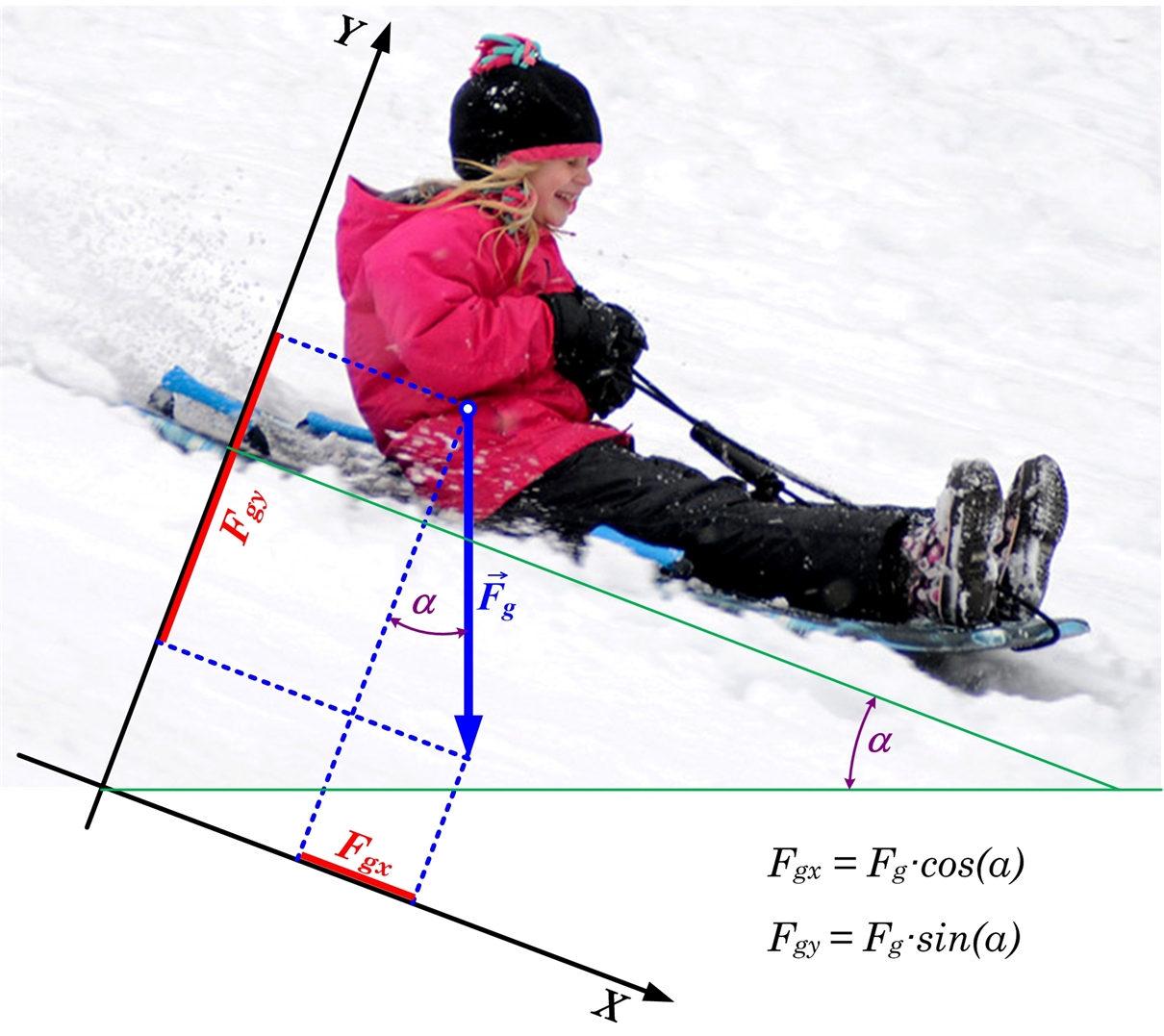
4. att. Koordinātu ass izvēle slīpa plaknes gadījumā
Analizējot objekta kustību pa slīpu plakni, jāapskata visi spēki, kas darbojas. 2. solī tika noskaidrots, ka smaguma spēks FG darbojas gan paralēli (projekcija FGX), gan perpendikulāri (projekcija FGY) slīpas plaknes virsmai (1. att.). Ja objekts atrodas mieras stāvoklī vai vienmērīgā taisnlīnijas kustībā uz leju pa slīpo plakni, tad no 1. Ņutona likuma seko, ka kopspēkam uz objektu jābūt 0, līdz ar to bez smaguma spēku ir citi spēki, kas to kompensē. Smaguma spēka komponenti FGX kompensē berzes spēks FB, bet komponenti FGY - balsta reakcijas spēks FR (1. att.).
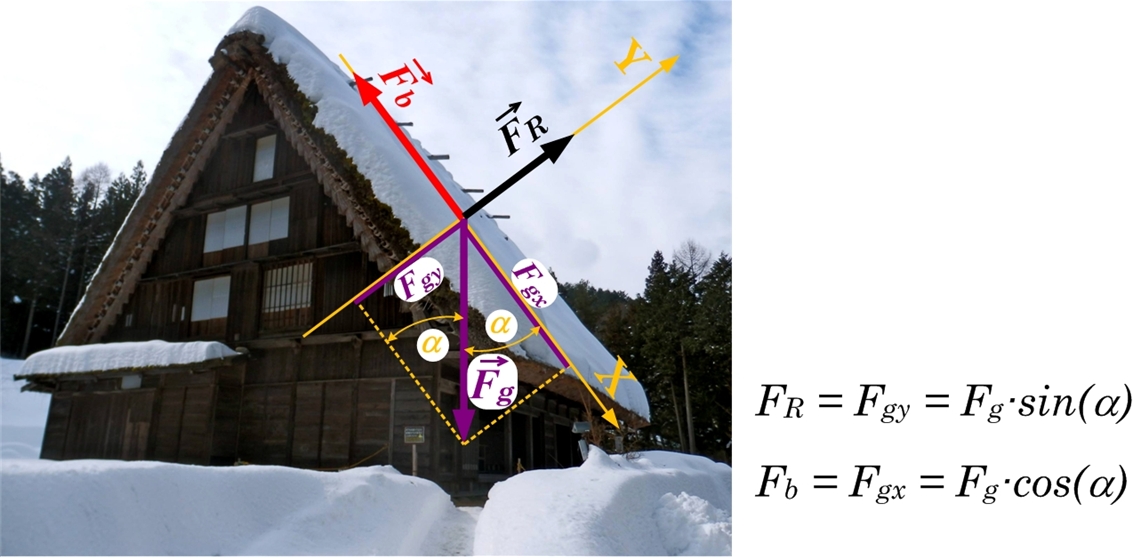
1. att. Objekts uz slīpās plaknes (sniegs uz jumta), kas atrodas miera stāvoklī
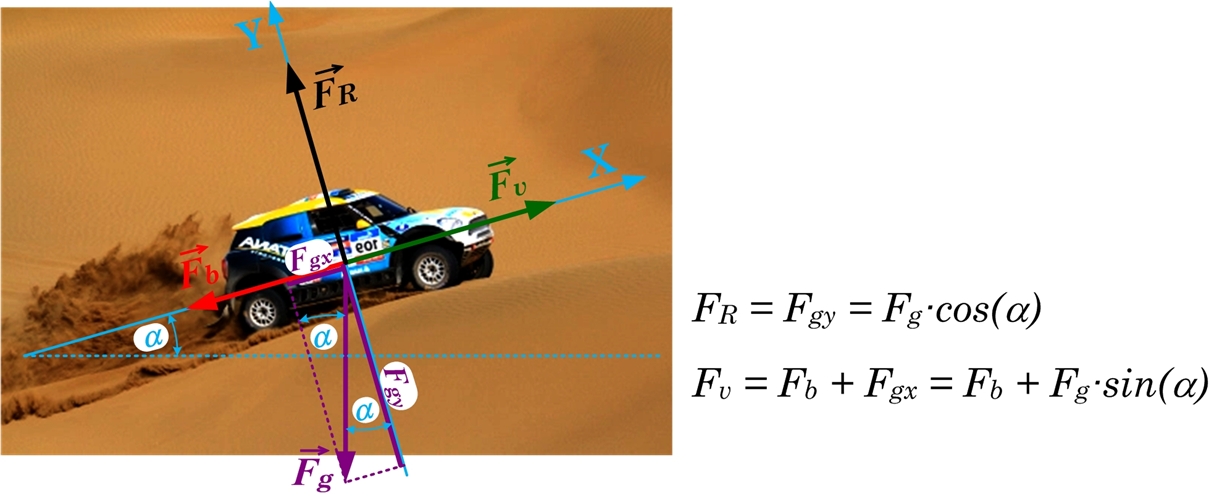
Ja objekts vienmērīgi kustas pa slīpo plakni uz augšu, tad ar smaguma spēku kā kustību izraisošo spēku vien nepietiek, ir jābūt kādam vilcējspēkam Fv (2. att.). Reakcijas spēku šajā gadījumā aprēķina identiski kā iepriekšējā piemērā (1. att.), bet izmaiņas ir spēku sadalījumā pa X-asi. Atšķirībā no 1. att. gadījuma, šeit berzes spēks darbojas otrā virzienā, jo kustība notiek uz augšu. Līdz ar to vilcējspēks vienāds ar berzes spēka un smaguma spēka X-ass projekcijas summu (2. att.)
2. att. Objekts uz slīpās plaknes, kas atrodas vienmērīgā taisnlīnijas kustībā uz augšu
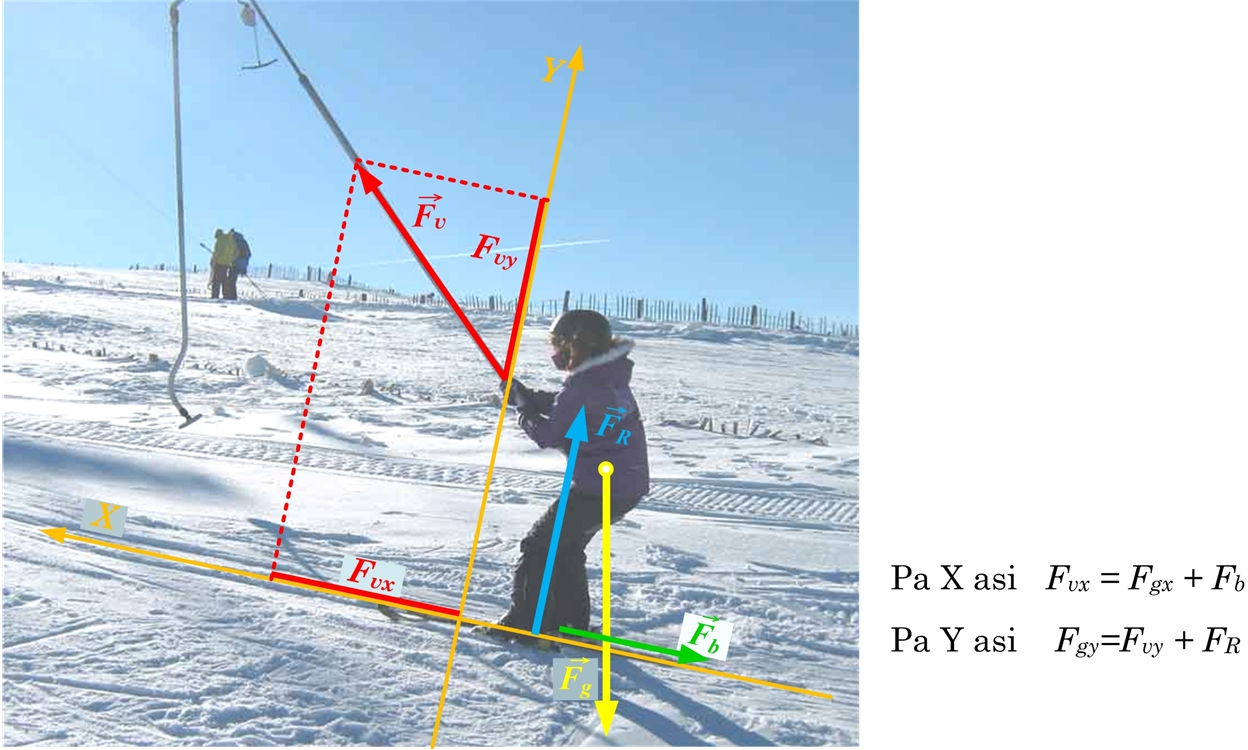
Ja vilcējspēks tiek pielikts lenķī pret slīpās plaknes virsmu, tad, analizējot objekta kustību, arī vilcējspēkam jāatrod projekcijas uz X un Y asīm, kuras pēc tam tiek izmantotas spēka vienādojumu sastādīšanā (3. att.)
3. att. Slīpi pielikts vilcējspēks uz slīpās plaknes kustošu objektu