Svars ir viens no cilvēku raksturojošajiem parametriem, kuru esam pieraduši noteik, izmantojot svarus. Tomēr svari patiesībā neparāda mūsu svaru, bet gan masu. Ja svari parādītu svaru, tad uzrādītais skaitlis būtu aptuveni 10 reizes lielāks jeb, pecīzāk, g reizes lielāks, kur g ir brīvās krišanas paātrinājums. Svaru fizikā definē kā spēku ar kādu ķermenis iedarbojas uz balstu perpendikulāri tā virsmai vai arī nostiepj vertikālu saiti. Cilvēks, pateicoties smaguma spēkam, var spiest uz kādu virsmu ar svaru P (1. att. a) vai arī ar to pašu svaru nostiept vertikālu saiti, piemēram, virvi (1. att. b). Abos gadījumos svaru aprēķina P=mg, kur
m - ķermeņa masa, kg
g - brīvās krišanas paātrinājums, m/s2
Ja cilvēks palecas, tad uz īsu brīdi tas atrodas bezsvara stāvoklī jeb tā svars P=0, jo atrodoties gaisā tas ne nostiepj saiti, ne spiež uz kādu virsmu (1. att. c).

1. att. Ķermeņa svars dažādās situācijās
Lai mainītos ķermeņa svars, ir jāmainās vai nu ķermeņa masai vai paātrinājumam. Ķermeņa masa var mainīties tad, ja notiek izmaiņas pašā ķermenī, tādēļ vieglāk svaru ir mainīt, izmainot paātrinājumu. Svara aprēķina formulā P=mg ir iekļauts brīvās krišanas paātrinājums g, kas noteiktā zemeslodes vietā ir praktiski nemainīgs lielums. Tomēr brīvās krišanas pātrinājums nav vienīgais paātrinājums, kas var darboties uz ķermeni. Ja uz ķermeni darbojas kāds papildus paātrinājums a, tad arī tas var ietekmēt ķermeņa svaru. Atrodoties liftā, kura paātrinājums a=0 (lifts miera stāvoklī vai vienmērīgā kustībā), svars ar kādu tajā esošie cilvēki iedarbojas uz lifta grīdu ir jau iepriekš apskatītais lielums P=mg (2. att. a). Ja lifts kustas uz augšu ar paātrinājumu a, tad cilvēka svars pieaug (2. att. b) un kļūst vienāds ar P=m(g+a). Savukārt, ja lifts kustas uz leju ar paātrinājumu a (2. att. c), tad cilvēka svars samazinās un ir aprēķināms šādi: P=m(g-a). Svara izmaiņas liftā ir pietiekoši lielas, lai tās varētu sajust, līdz ar to mēs pēc sajūtam varam noteikt, kad lifts atrodas paātrinātā kustībā!
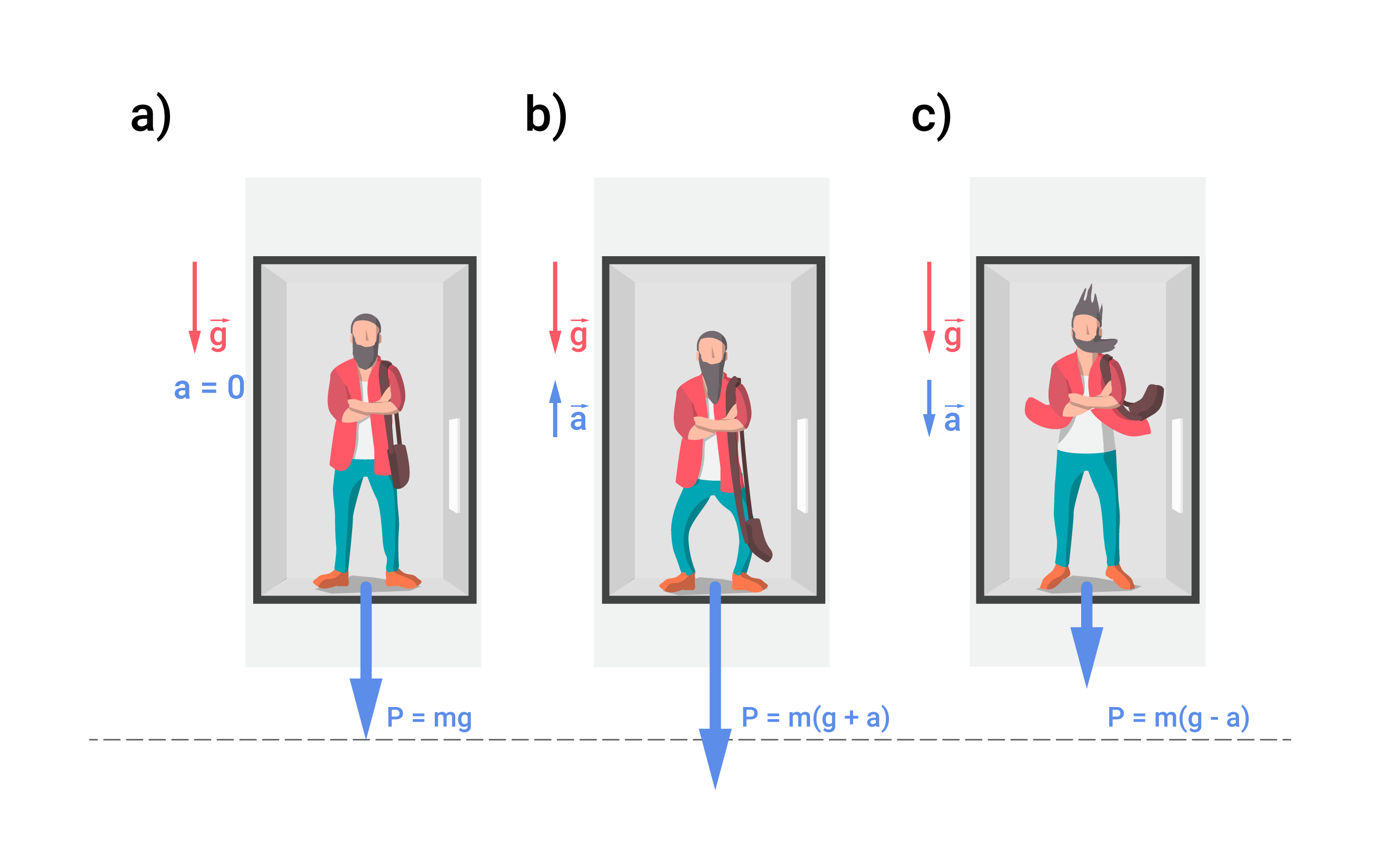
2. att. Svara izmaiņas liftā
Lai gan dažādās Zemeslodes vietās ir atšķirīgs brīvās krišanas paātrinājums, atšķirības ir tik niecīgas, ka praktiski nav sajūtamas. Lai izjustu brīvās krišanas paātrinājuma izmaiņas ietekmi uz svaru, būtu jādodas uz citām Saules sistēmas planētām un citiem objektiem. 3. att. redzams brīvās krišanas paātrinājums uz dažādām Saules sistēmas planētām. Jo lielāks brīvās krišanas paātrinājums, jo lielāks ķermeņa svars uz planētas. Piemēram, ja uz Zemes ķermeņa svars ir 1 N, tad uz Jupitera tas ir 2,5 N, bet uz Marsa zem 0,5 N. Tātad, ja nepieciešams izdevīgi pārdod sveramu preci, tad svēršanas darbība jāveic uz Jupitera, bet ja esi pircēja lomā, tad darījums izdevīgāks būs uz Marsa vai Merkura (3. att.).
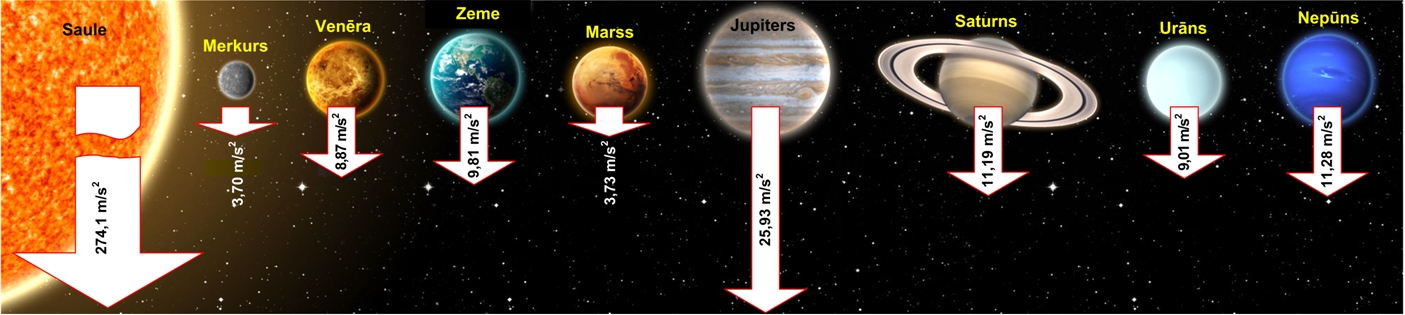
3. att. Brīvās krišanas paātrinājums uz dažādām planētām
Smaguma spēks FG ķermenim ir pielikts masas centrā, bet svars P - balstam, turklāt perpendikulāri tā virsmai (1. att.)! Mierā vai vienmērīgā kustībā esoša ķermeņa gadījumā svaru nodrošina smaguma spēks. Horizontālas virsmas gadījumā ķermeņa svars ir vienāds ar smaguma spēku, jo abi šie spēki ir vērsti vienā virzienā (1. att. a). Ja ķermeni novieto uz slīpas virsmas, tad smaguma spēka virziens vairs nesakrīt ar virsmai perpendikulāro virzienu, kurā ir vērsts ķermeņa svars. Ja šāda gadījumā koordinātu sistēmu izvēlas tā, ka X-ass ir paralēla virsmai uz kuras atrodas ķermenis, tad svars ir vienāds ar smaguma spēks FG projekciju uz Y-ass. Ja virsma ar horizontu veido leņķi α, tad P=FGY=mgcosα (1. att. b).
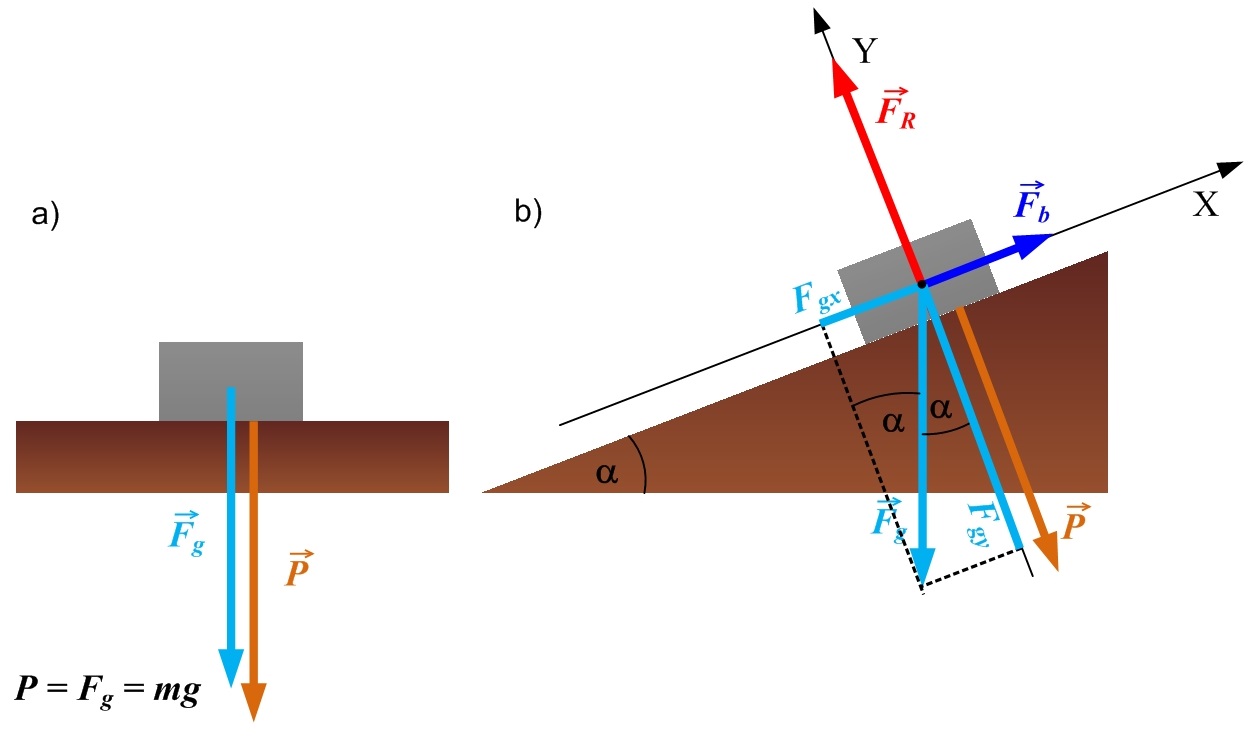
1. att. Ķermeņa svars uz horizontālas un slīpas virsmas
Ja ķermenis atrodas miera stāvoklī nevis uz slīpas, bet uz liektas virsmas tās virsotnē vai ieplakā, tad svars ir vienāds ar smaguma spēku. Piemēram, BMX braucējiem trase sastāv no ļoti daudz liektām virsmām, bet ja braucējs apstājas kāda paugura virsotnē vai ieplakā tad tā svars vienāds ar smaguma spēku. Šeit gan jāatceras, ka BMX braucējs spiež uz virsmu vismaz divas vietās (abas BMX riepas), tādēļ svars veidojas ņemot vērā smaguma spēka darbību visās saskares vietās (2. att.).
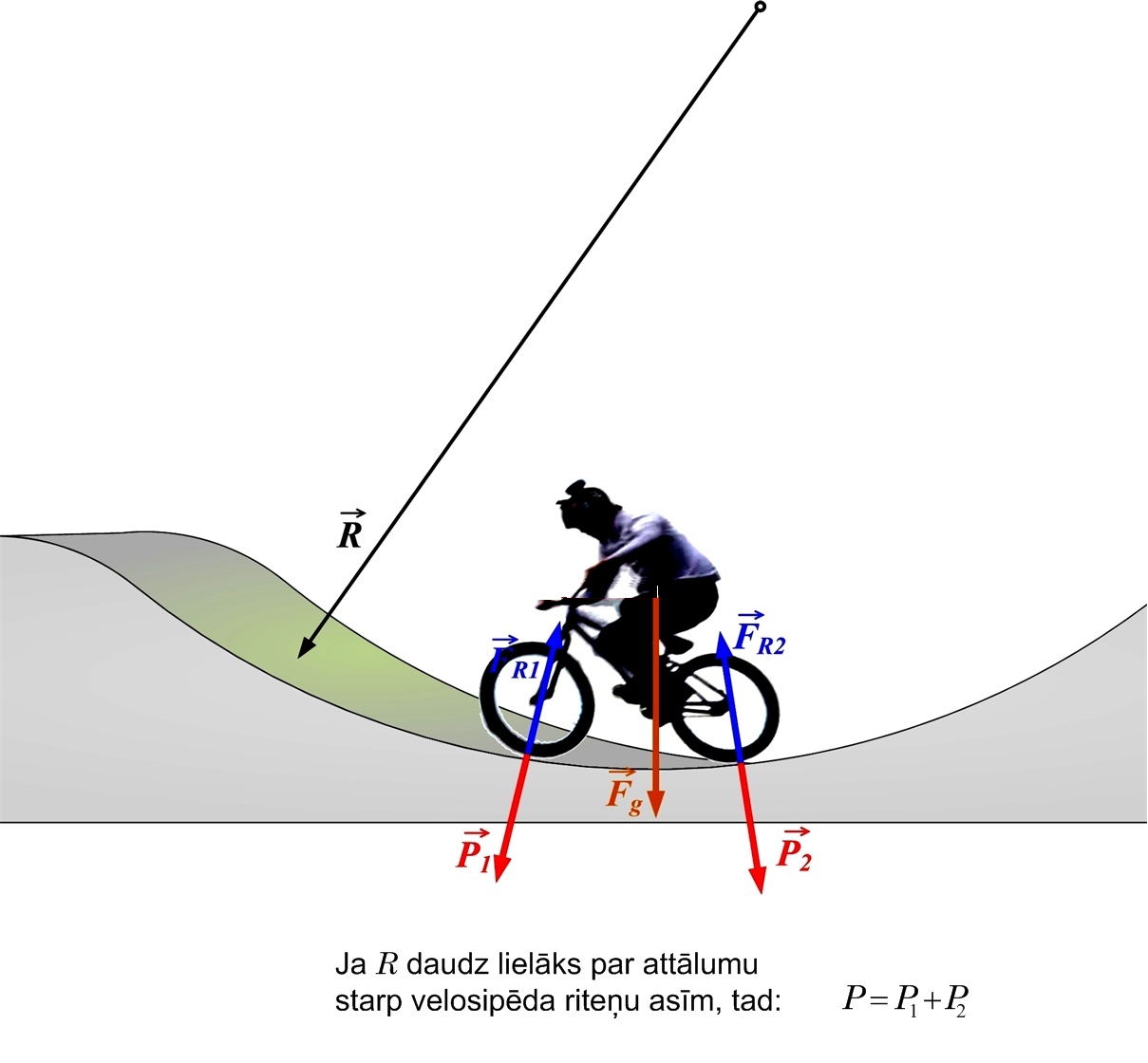
2. att. Uz liektas virsmas stāvošs ķermenis
Ja ķermenis pa pauguru brauc ar ātrumu v, tad tā svars atšķiras no smaguma spēka. Braucot ar ātrumu v pa pauguru, kura liekuma rādiuss ir R, ķermenis atrodas kustībā pa riņķa līniju un līdz ar to uz to darbojas centrtieces paātrinājums ac=v2/R. Centrtieces paātrinājumu nodrošina smaguma spēks un tieši par tik lielu vērtību arī samazinās ķermeņa svars (3. att.), kuru šajā gadījumā aprēķina P=m(g-v2/R), kur
m - ķermeņa masa, kg
v - ķermeņa ātrums, m/s
R - liekuma rādiuss, m
Braucot pa BMX trasi, sportisti pauguru virsotnēs tiešā nozīmē var justies atviegloti, un jo ātrāk tie brauc, jo vieglāk paliek (3. att.). Protams, ja ātrums ir pārāk liels, tad sportisitiem iestājas bezsvara stāvoklis un tie atraujas no trases virsmas!
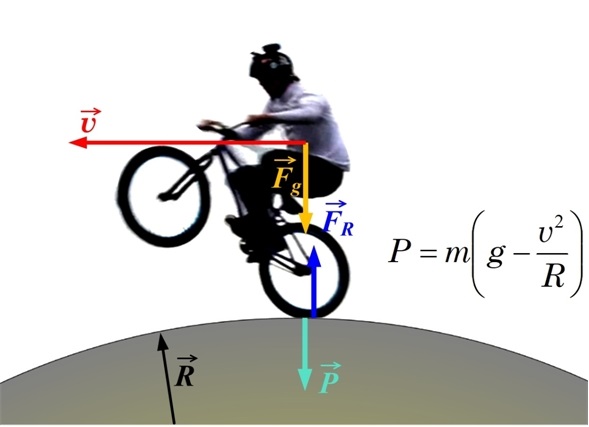
3. att. Ķustīga ķermeņa svars uz paugura
Ja ķermenis, kustoties ar ātrumu v, nonāk ieplakā, tad tā svars palielinās un to aprēķina P=m(g+v2/R), kur
m - ķermeņa masa, kg
v - ķermeņa ātrums, m/s
R - liekuma rādiuss, m
Tā jau saka, ka dzīvē pēc kāpumiem nāk kritumi, arī BMX trasē pēc trases virsotnēm, kurās BMX braucēji var justies vieglāki, nāk ieplakas, kurās sportisti svars palielinās (4. att.) un tie kļūst smagāki. Bet nekas, drīz jau atkal seko pauguri un to virsotnes.
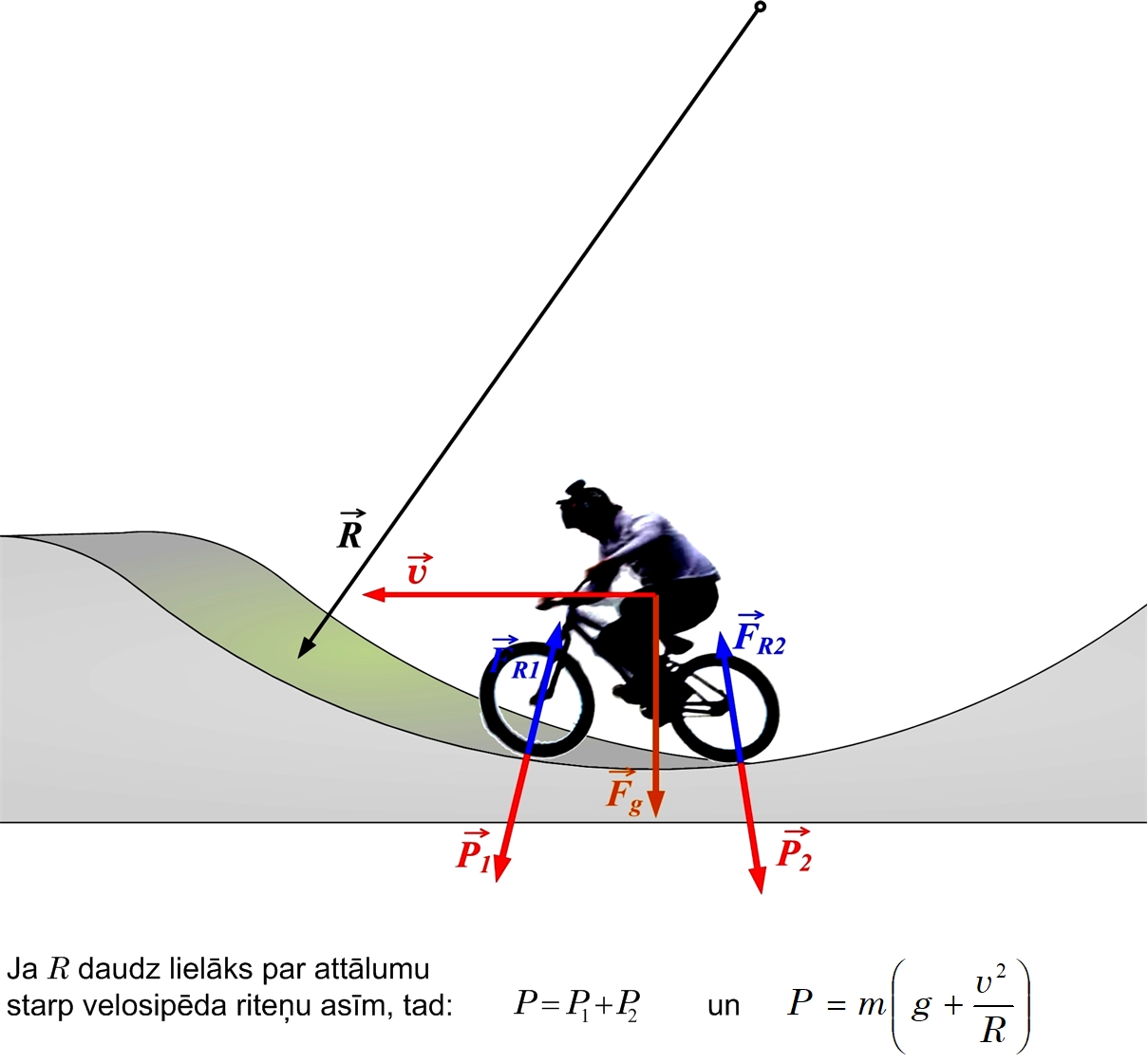
4. att. Ķustīga ķermeņa svars ieplakā
Svara izmaiņas centrtieces paātrinājuma dēļ notiek arī tad, kad ķermenis atrodas uz kāda rotējoša objekta. Piemēram, mēs visi atrodamies uz Zemes, kas rotē. Rotācijas dēļ uz mums darbojas centrtieces spēks FC, kas notur mūs kustībā pa riņķveida trajektoriju (5. att.). Arī šajā gadījumā centrtieces spēku nodrošina smaguma spēks un tieši tik daudz tiek atņemts mūsu svaram uz Zemes. Jāsaka gan, ka tā ir ļoti niecīga vērtība. Salīdzinot ar svaru Zemes polos, kur nav centrtieces paātrinājums, un uz ekvatora, kur ir vieslielākais centrtieces paātrinājums Zemes rotācijas dēļ, cilvēka svars atšķiras par 0,3 %! Vēl 0,2 % dod tas, ka uz ekvatora cilvēks atrodas tālāk no Zemes centra nekā polos. Kopā iznāk, ka uz ekvatora esam par 0,5 % vieglāki nekā polos.
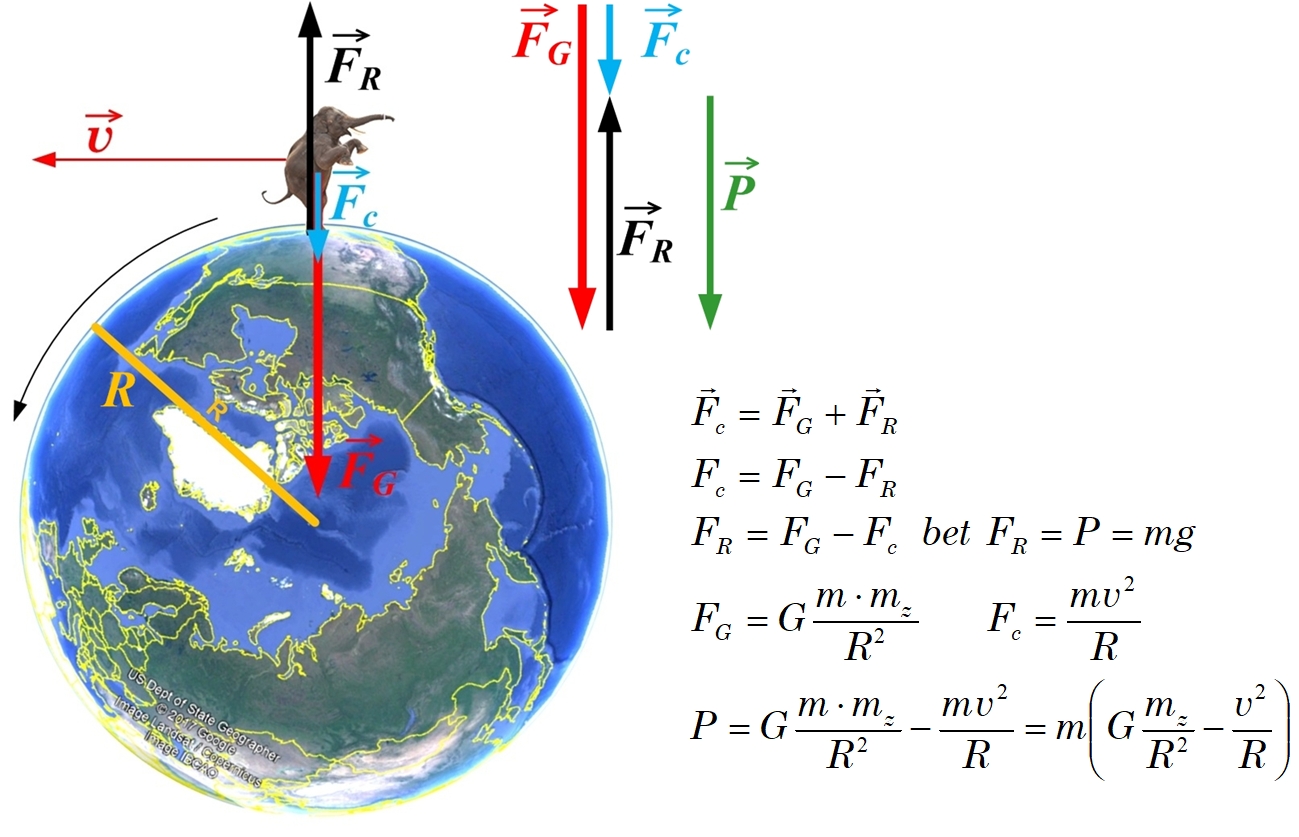
5. att. Ķermenis uz rotējošas Zemes
Svara izmaiņas var nodrošināt ne tikai centrtieces paātrinājums. Sežot vienmērīgi braucošas mašīns krēslā, mēs ar savu smaguma spēku iedarbojamies gan uz sēdvirsmu ar svaru P1, gan uz atzveltni ar svaru P2 (6. att. a). Bet ja automašīna sāk kustēties vienmērigi paātrināti, tad cilvēks svars uz atzveltni palielinās par ma, kur
m - cilvēka masa, kg
a - paātrinājums, m/s
Gala rezultātā paātrinātā kustībā cilvēks spiež uz krēsla atzveltni ar svaru P3=P2+ma (6. att. b). Šo svara palielinājumu atzveltnes virzienā mēs sajūtam kā “iespiešanu krēslā” brīdī, kad automašīna “uzņem ātrumu”. Un jo lielāks ir automašīnas uzrāviens, jo vairāk mēs to izjūtām. Salīdzinot ar automašīnu, liels paātrinājums ir lidmašīnai, uzsākot kustību pa skrejceļu. Tas ir brīdis, kad pasažieri tiek pamatīgi “iespiesti krēslos”!
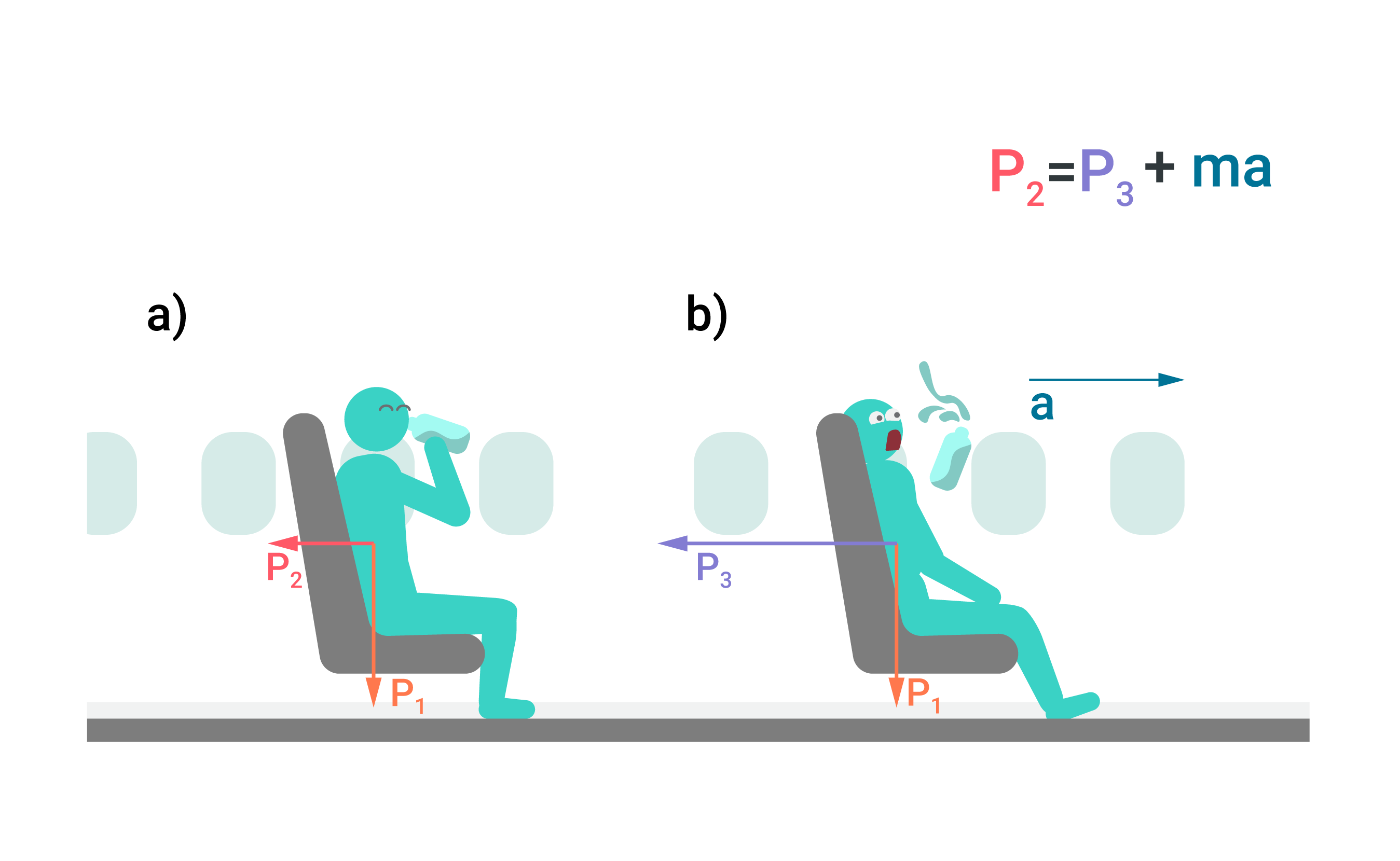
6. att. Autovadītāja radītais svars uz mašīnas krēslu
Iepriekš minēto “iespiešanas krēslā” efektu var izmantot mākslīgās gravitācijas radīšanai. Ja cilvēks ilgi atrodas bezsvara stāvoklī, tad tā organisms sāk piedzīvot nevēlamas izmaiņas. Tādēļ kosmonautiem, kam plānota ilga uzturēšanās bezsvara stāvoklī, jādomā risinājumi mākslīgai gravitācijas radīšanai. Viena no iespējām ir iegriezt kosmosa kuģi (7. att. a). Tad centrtieces paātrinājuma dēļ kosmonauts iedarbosies uz virsmu ar svaru P=mac=mω2R, kur
m - kosmonauta masa, kg
a - centrtieces paātrinājums, m/s2
ω - leņķiskais ātrums, rad/s
R - attālums līdz rotācijas asij, m
Šādā mākslīgās gravitācijas ideja tika izmantota filmā Elizeja, kur bagātnieki apdzīvoja rotējošu kosmosa staciju (7. att. b).
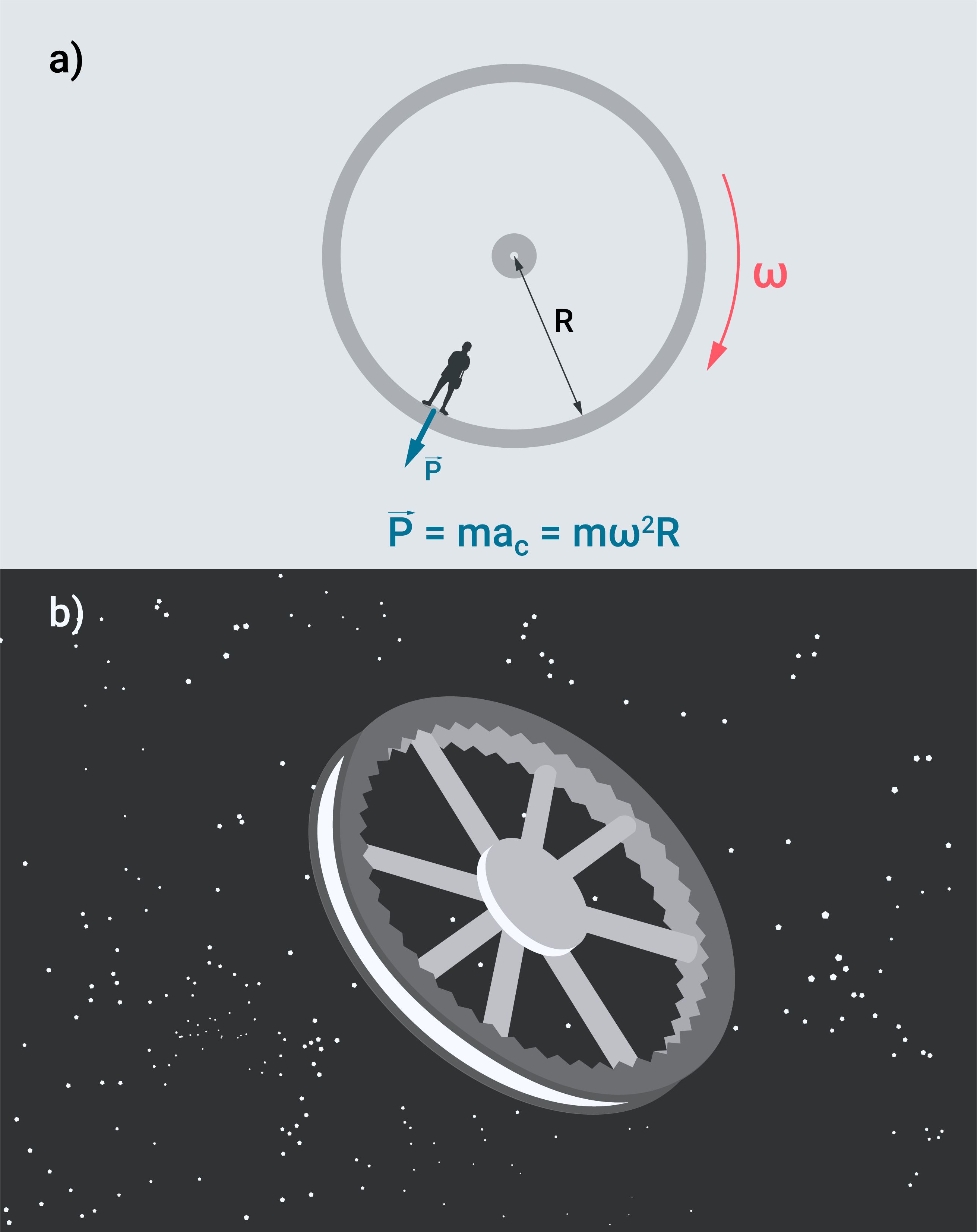
7. att. Mākslīgās gravitācijas radīšana
Ja paātrinājums dēļ cilvēkam pieaug svars, tad ķermenim rodas pārslodze. Tās lielumu raksturo tas cik reizes ķermeņa svars paātrinātā kustībā ir lielāks nekā miera stāvoklī. Cilvēka pārslodzes vērtības dažādās situācijās attēlotas 8. att.
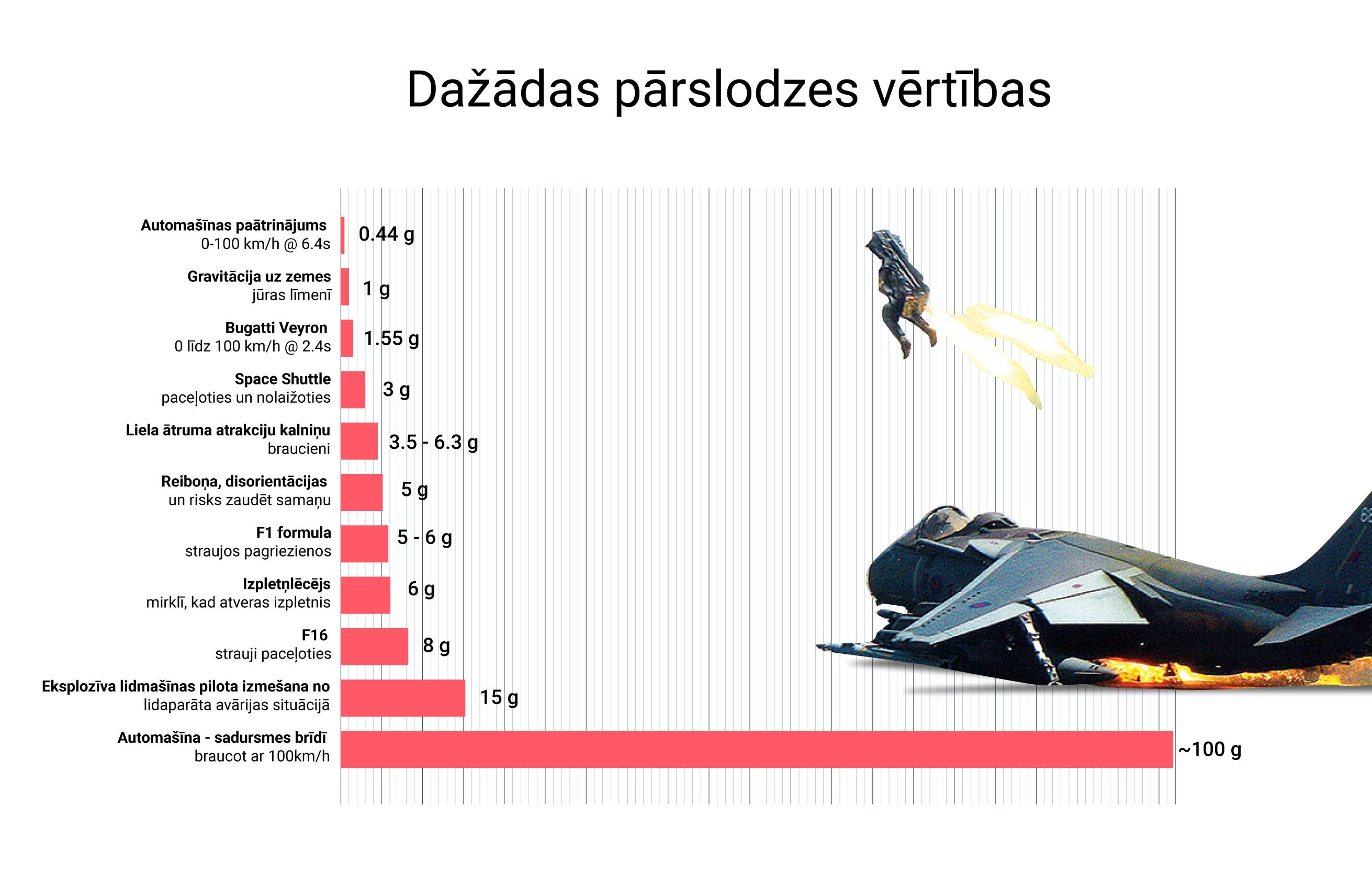
8. att. Dažādas pārslodzes vērtības
Lai aprēķinātu svaru automašīnai, kas atrodas izliekta tilta virsotnē un kustas ar āturmu v (1. att.) jāatceras, ka smaguma spēks FG nodrošina gan centrieces spēku FC, gan automašīnas svaru P. Smaguma spēku aprēķina FG=mg, kur
m - automašīnas masa, kg
g - brīvās krišanas paātrinājums, m/s2
Bet centrtieces spēks FC=maC=mv2/R, kur
aC - centrtieces paātrinājums, m/s2
v - kustības ātrums, m/s
R - tilta liekuma rādiuss, m
Līdz ar to smaguma spēks FG=P+FC, no kurienes seko, ka automašīnas svars P=FG-FC=mg-mv2/R=m(g-v2/R).
Izmantojot šo vienādojumu, var aprēķināt kādam ir jābūt ātrumam, lai automašīna šajā punktā atrastos bezsvara stāvoklī. Ja P=0, tad g-v2/R=0, no kurienes seko, ka v=(gR)0,5.
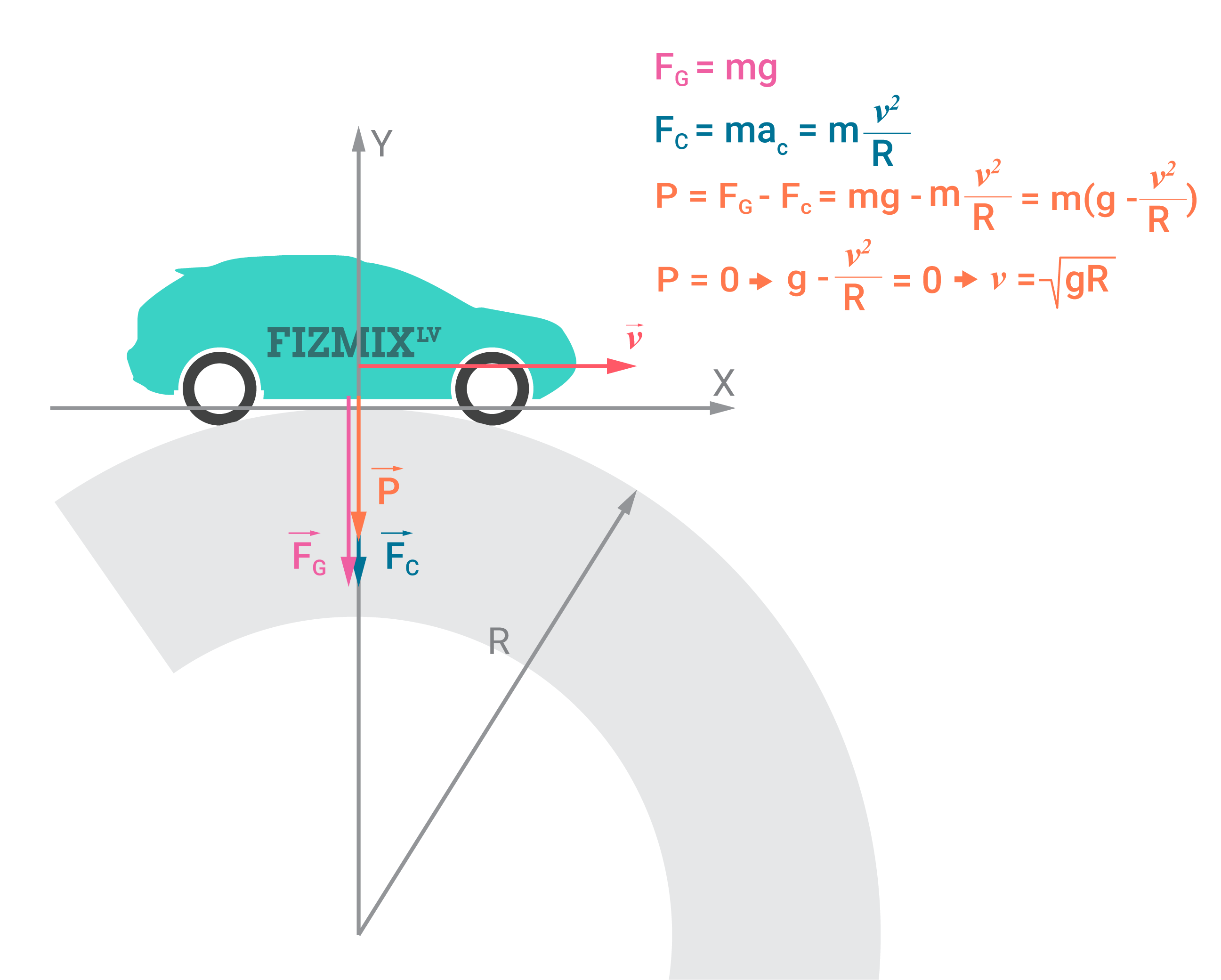
1. att. Automašīnas svars izliekta tilta virsotnē
Ja automašīna brauc pāri izliektam tiltam ar nemainīgu ātrumu v, tad tās svars visu laiku mainās. Lai aprēķinātu automašīnas svaru noteiktā tilta punktā, ērti ieviest koordinātu sistēmu, kurā X-ass ir vērsta pa pieskari tiltam, bet Y-ass - perpendikulārajā virzienā (2. att.). Smaguma spēks FG ir vērst uz leju un veido leņķi α ar Y-asi. Ja automašīna stāvētu uz vietas, tad svars būtu vienāds ar smaguma spēka projekciju uz Y-ass FGY=mgcosα, bet tā kā automašīna kustas pa riņķa līnijas loku, tad uz to darbojas centrtieces spēks FC=maC=mv2/R. Līdz ar to smaguma spēka projekcija FGY nodrošina gan ķermeņa svaru, gan centrtieces spēku un varam rakstīt, ka FGY=P+FC, no kurienes seko, ka automašīnas svars P=FGY-FC=mgcosα-mv2/R (2. att.).
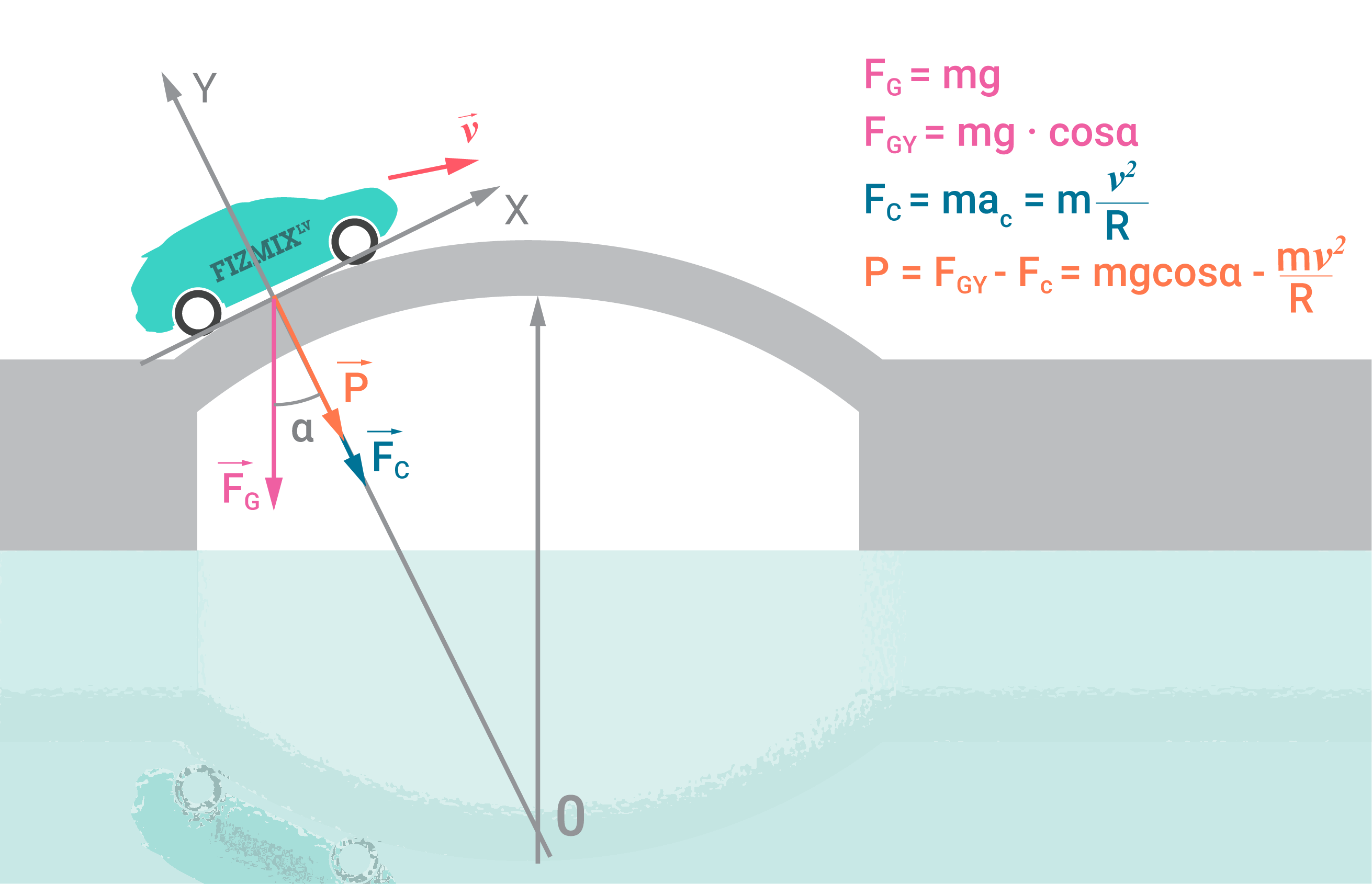
2. att. Automašīnas svars, braucot pār izliektu tiltu
Svars mainās arī gumijlēkšanas aktivitātes laikā (3. att. a). Grafikā redzams (3. att. b), ka lecienā sākumā cilvēka svars ir 0, jo tas vēl nav sācis iedarboties uz elastīgo saiti (gumiju). Grafika punktā A (3. att. b) svars sāk pieaugt, jo cilvēks sāk izstiept elastīgo saiti. Punktā B cilvēks atrodas zemākajā pozīcijā un svars ir maksimālais, jo saite ir maksimāli iztiepta (papildus paātrinājumu rada saites elastības spēks). Tālāk atkal sākas kustība augšup. Punktā C cilvēkas atkal ir bezsvara stāvoklī, jo elastīgajā saitē uzkrātā enerģija ir uzmetusi cilvēku gaisā. Svārstīšanas pamazām norimst līdz cilvēka svars vai nemainās un ir vienāds ar P=mg, kas grafikā atbilst punktam D!

3. att. Svara izmaiņas, lecot ar gumiju