Lai gan ar mērierīcēm tiek izmērītas noteiktas fizikālā lieluma vērtības, tomēr tās nav iespējams izmērīt pilnīgi precīzi, jo katram mērinstrumentam ir noteikta kļūda, ko tas rada mērījuma rezultātos, kā arī pastāv dažādi ārējie apstākļi, kas ietekmē mērījuma rezultātu. Kļūdas var iedalīt dažādos veidos. Pēc būtības kļūdas iedala absolūtajā un relatīvajā kļūdā. Absolūtā kļūda ir cieši saistīta ar mērinstrumenta mērīšanas iespējām. Ja lieto mērinstrumentu ar sīkām iedaļām, tad absolūtā kļūda, kuru apzīmē ar ∆, ir vienāda ar mērinstrumenta vienas iedaļas vērtību. Piemēram, ja mēra termokrūzes augstumu h ar lineālu (1. att. a), kura sīkākās iedaļas vērtība ir 1 mm, tad ∆=1 mm. Tā kā izmēritais fizikālai lielums h=17,7 cm (1. att. b), tad iegūto 0x1F6C0 rezultātu var pierakstīt h±∆h=(17,7±0,1) cm.
Apskatīsim piemēru vienam pētījumam un kā tajā atklājas mērīšanas precizitāti. Pārvietojoties lauku teritorijās, nākas saskarties ar dažādiem teritorijas segumiem un šķēršļiem mūsu ceļā, piemēram, pļavām, vagām, meža ceļiem, grāvjiem, lāci, kokiem. Atkarībā no mūsu pārvietošanās veida katrs no šiem elementiem kustību ietekmē citādāk, jo sastapšanās ar lāci, ejot kājām vai braucot mašīnā, ir nedaudz citādāka. Noskaidrosim, kurš pārvietošanās līdzeklis mūsu izvēlētā maršrutā būtu visātrākais. Pieņemsim, ka mūsu rīcībā ir velosipēds, automašīna – visurgājējs, kā arī varam iet kājām. Pētījumā tiks izmantoti visi šie pārvietošanās līdzekļi, lai noskaidrotu, kurš izvēlētajā maršrutā (1. att.) ir visātrākais. Šim nolūkam tika veikta viena un tā pati distance l un izmērīts kustības laiks t. Lai pārliecinātos par rezultātu ticamību, katrā reizē tika arī izmērīta veiktā distance l, kaut arī vienmēr maršruts bija viens un tas pats.
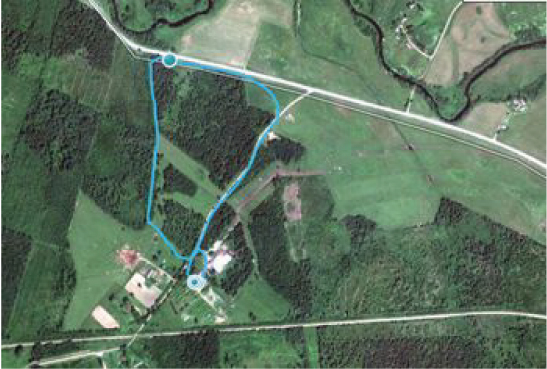
1.att. Izvēlētais maršruts
Apskatīsim veiktos mērījumus automāšīnas kustībai. Viedtālrunis (2. att.) uzskatāms par digitālo mērinstrumentu, tādēļ nolasīto rezultātu absolūtā kļūda ir vienāda ar mērskaitļa pēdējā cipara kārtu, līdz ar to automašīnas veiktajai distancei l=1,90 km, kas tika nolasīta no mērinstrumenta, absolūtā kļūda ∆l=0,01 km. Savukārt nolasītajam kustības laikam t=333 s absolūtā kļūda ∆t=1 s (2. att.). Aprēķinot relatīvās kļūdas rl=∆l:l·100 %=0,01:1,90·100 %=0,53 %, un rt=∆t:t·100 %=1:333·100 %=0,30 % (2. att.).

2.att. Pētījumā izmantotais viedtālrunis ar GPS un iegūtie rezultāti automašīnai
3. attēlā redzmi iegūti rezultāti visiem trīs pārvietošanās veidiem. Veiktais attālums visos gadījumos ir vienāds, tādēļ tā absolūtā un relatīvā kļūda visos trīs gadījumos ir vienāda, bet kustības laikam lai arī absolūtā kļūda katru reizi ir 1 s, tomēr kustības laiks katru reizi ir atšķirīgs, līdz ar to atšķirīgas ir arī relatīvās kļūdas. Jo mazāka ir fizikāla lieluma vērtība pie tās pašas absolūtās kļūdas, jo lielāka ir relatīvā kļūda (3. att.).

4.att. Mērījumu un aprēķinu rezultāti
Gan attālums l gan laiks t tika mērīti tieši, tas nozīmē, ka apskatīta relatīvas kļūdas rēķināšanas metode der tiešajai mērīšanai. Netiešajā mērīšanā iegūto mērskaitli veido divi vai vairāk tieši izmērīti lielumi, kuram katram var būt sava absolūtā un relatīvā kļūda. Tomēr arī šādā gadījumā ir iespējams aprēķināt relatīvo kļūdu, izmantojot, piemēram, relatīvo kļūdu saskaitīšanas metodi. No iepriekšējā piemērā tieši iegūtajiem mērījumiem ir iespējams aprēķināt automašīnas vidējo ātrumu vvid=l:t. Vidējā ātruma relatīvo kļūdu iegūst saskaitot attāluma un laika relatīvās kļūdas rvvid=rl+rt=0,53+0,30=0,83 %.
Pēc izcelsmes kļūdas iedala trīs veidos:
1) sistemātiskās kļūdas;
2) gadījuma kļūdas;
3) rupjās kļūdas.
Sistemātiskās kļūdas rodas mērierīču dēļ, un tās ir iespējams samazināt vai novērst. Iepriekšējā solī aplūkotajā pētījumā sistemātisko kļūdu nosaka, tas ar kādu precizitāti fizikālos lielumus nosaka telefons, kuram pieejama GPS funkcija.
Gadījuma kļūdas rodas dažādu ārējo apstākļu dēļ, kas ir mainīgi un kuru ietekmi nevar paredzēt. Šīs kļūdas nav iespējams novērst. Veiktajā eksperimentā gadījuma kļūdas varētu radīt vēja virziena maiņa, kas apgrūtina katru pārvietošanās līdzekli citādāk, smilšu graudu ieķeršanās velosipēda rites sistēmā, nepareiza motora apgriezienu izvēle pārnesuma pārslēgšanai, paklupšana uz līdzenas vietas u.c. Gadījuma kļūda var rasties arī tad, ja neatbilstošā leņķī paskatās uz mērinstrumenta skalu (1. att.).

1.att. Gadījuma kļūdas avots
Par rupjām kļūdām sauc kļūdas, kuras ievērojami pārsniedz konkrētajos apstākļos sagaidāmo kļūdu. Šādas kļūdas var izraisīt gan bojāti mēraparāti, gan eksperimenta veicēja neuzmanība, gan arī negaidīti liela ārējo apstākļu ietekme (2. att.).
Nosakot fizikālās vērtības kļūdu, tiek ņemta vērā gan sistemātiskā, gan gadījuma kļūda, un to sauc par pilno kļūdu, bet rupjās kļūdas ir jāizslēdz no mērījumu rezultātiem (DZM materiāls par kļūdu cēloņiem).

2.att. Dzīvnieki uz ceļa - pēkšņi kāds gadījums ietekmē rezultātu
Lai noskaidrotu, ar kādu precizitāti attālumus var noteikt, izmantojot GPS, proti, sistemātisko kļūdu, ir jānoskaidro, pēc kāda principa GPS strādā. GPS pamatā ir vairāk nekā divdesmit satelītu, kas lido pa noteiktām orbītām apkārt zemeslodei aptuveni 20 000 km augstumā. Katrā satelītā ir uzstādīts ļoti precīzs atompulkstenis, kas ļauj izrēķināt satelīta pozīciju attiecībā pret Zemi jebkurā laika momentā. Šie satelīti katru brīdi izstaro radio signālu, ko uztver GPS uztvērējs uz Zemes (mūsu piemērā tas ir telefons). Uztverot signālu, ir zināms, kurš satelīts kurā brīdi to ir sūtījis un kāda pozīcijā tas ir atradies, līdz ar to, zinot radiosignāla izplatīšanās ātrumu, var aprēķināt, cik tālu uztvērējs ir no satelīta. Ja šāda informācija ir iegūta no vairākiem satelītiem (3. att.), tad ar ģeometriska aprēķina palīdzību ir iespējas noteikt atrašanās vietu uz Zemes.
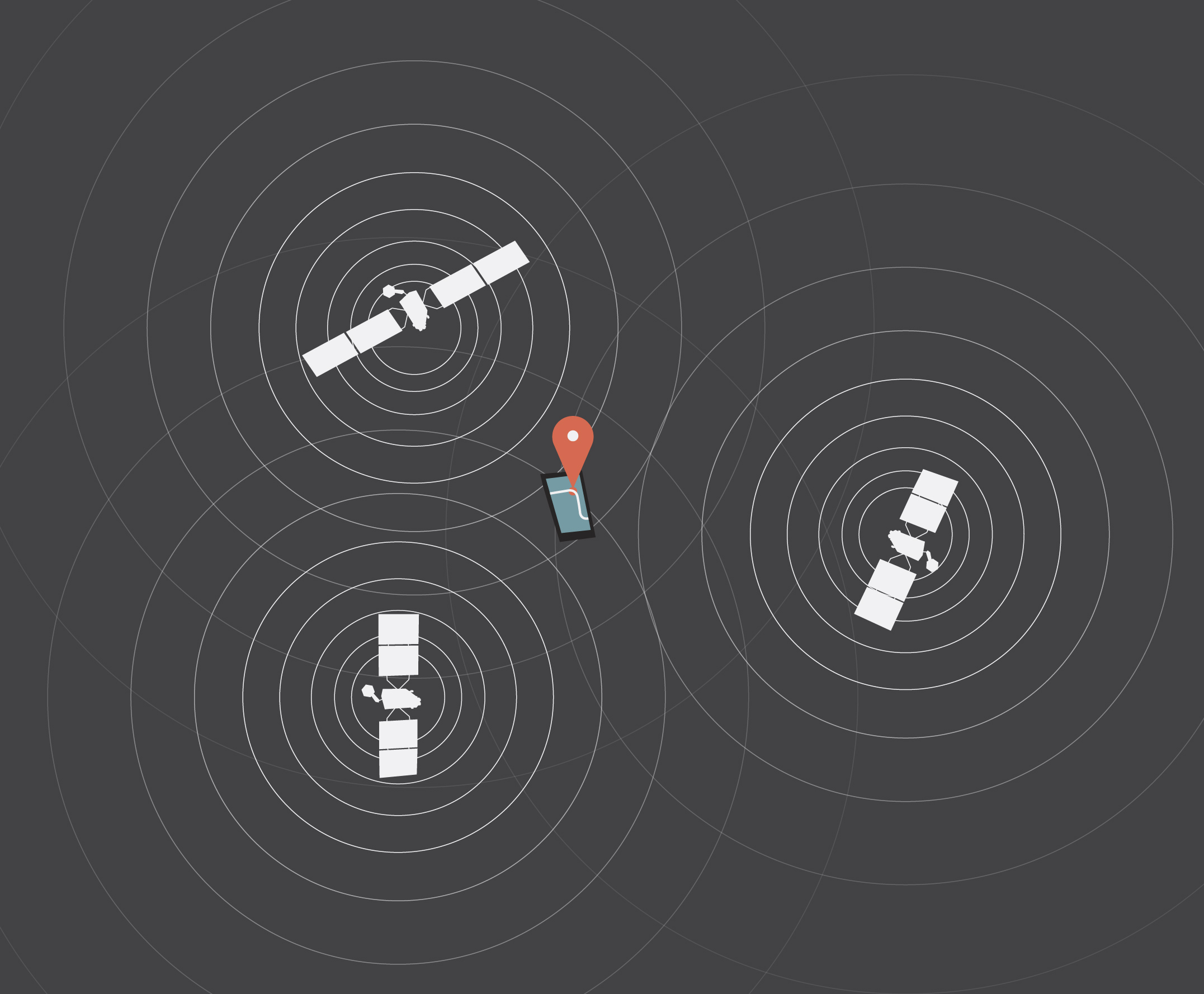
3.att. Satelītu saziņa ar GPS aparātu
Ir nepieciešams signāls vismaz no četriem satelītiem, lai noteiktu konkrētu atrašanās vietu. Atrašanās vietas noteikšanas precizitāti ietekmē vairāki faktori, daļa no tiem ir apkopoti 4. attēlā, klāt arī norādot to radītas kļūdas apmēru. Saskaitot visas kļūdas kopā, iznāk, ka atrašanās vietu GPS var noteikt ar ± 12 m precizitāti. Telefonā, kas tika lietots attāluma mērīšanai, neuzrādīja mērījuma kļūdu, tādēļ par mērījuma kļūdu jāpieņem viena mazākā iedaļa no iegūtās fizikālā lieluma vērtības.
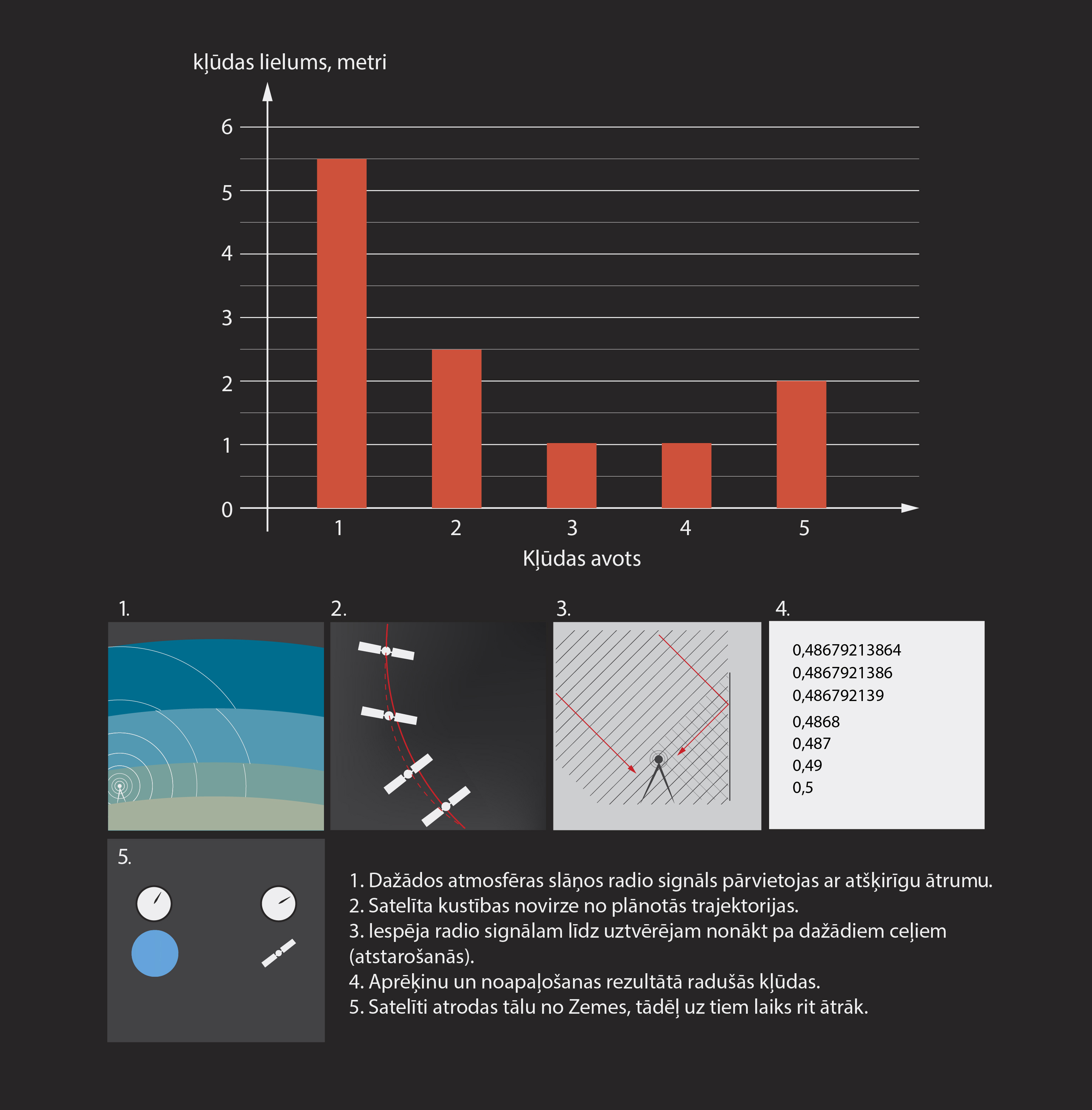
4.att. GPS kļūdu avoti un to radītais kļūdas apmērs