Jebkura vide sastāv no daļiņām. Ja kāda vide nav deformēta, tad rezultējošais spēks, kas darbojas uz vidi veidojošajām daļiņām, ir vienāds ar nulli. Piemēram, 1. att. a) redzams atsperē iekārts lemurs (multfilma Madagaskara), kas rokā satvēris vecas telefona līnijas vadu. Šis vads ir taisni nostiepts un rezultējošais spēks, kas uz to darbojas, ir nulle. Tad lemurs sāk kustību uz augšu (1. att. b). Redzams, ka vada gals, kas ir lemuram rokās, pārvietojas līdzi, bet tālākā vada kustība atpaliek no lemura rokas.
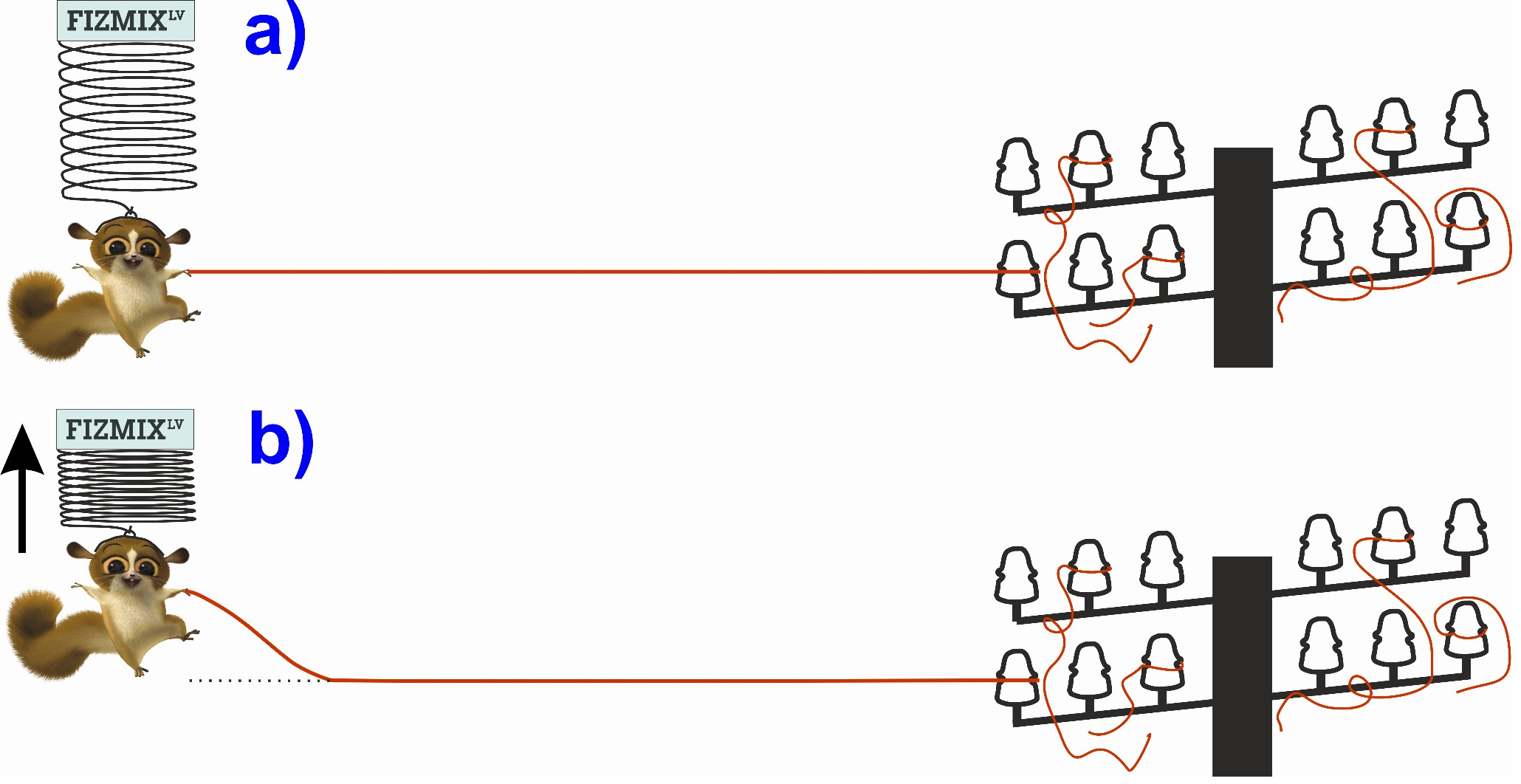
1. att. Lemurs kā viļņu avots
Ja lemurs turpina savu kustību augšup un lejup (2.att. c, d, e), tad redzams, ka tā izraisīta vada gala svārstību kustība turpina izplesties tālāk pa vadu. Tas notiek tādēļ, ka kustībā esošās vides daļiņas iedarbojas uz blakus esošajām daļiņām un “parauj” tās līdzi. Tādā veidā vadā ir sācis izplatīties mehāniskais vilnis, kas ir kādas vides daļiņu mehānisko svārstību izplatīšanos attiecīgajā vidē. DZM materiāls.
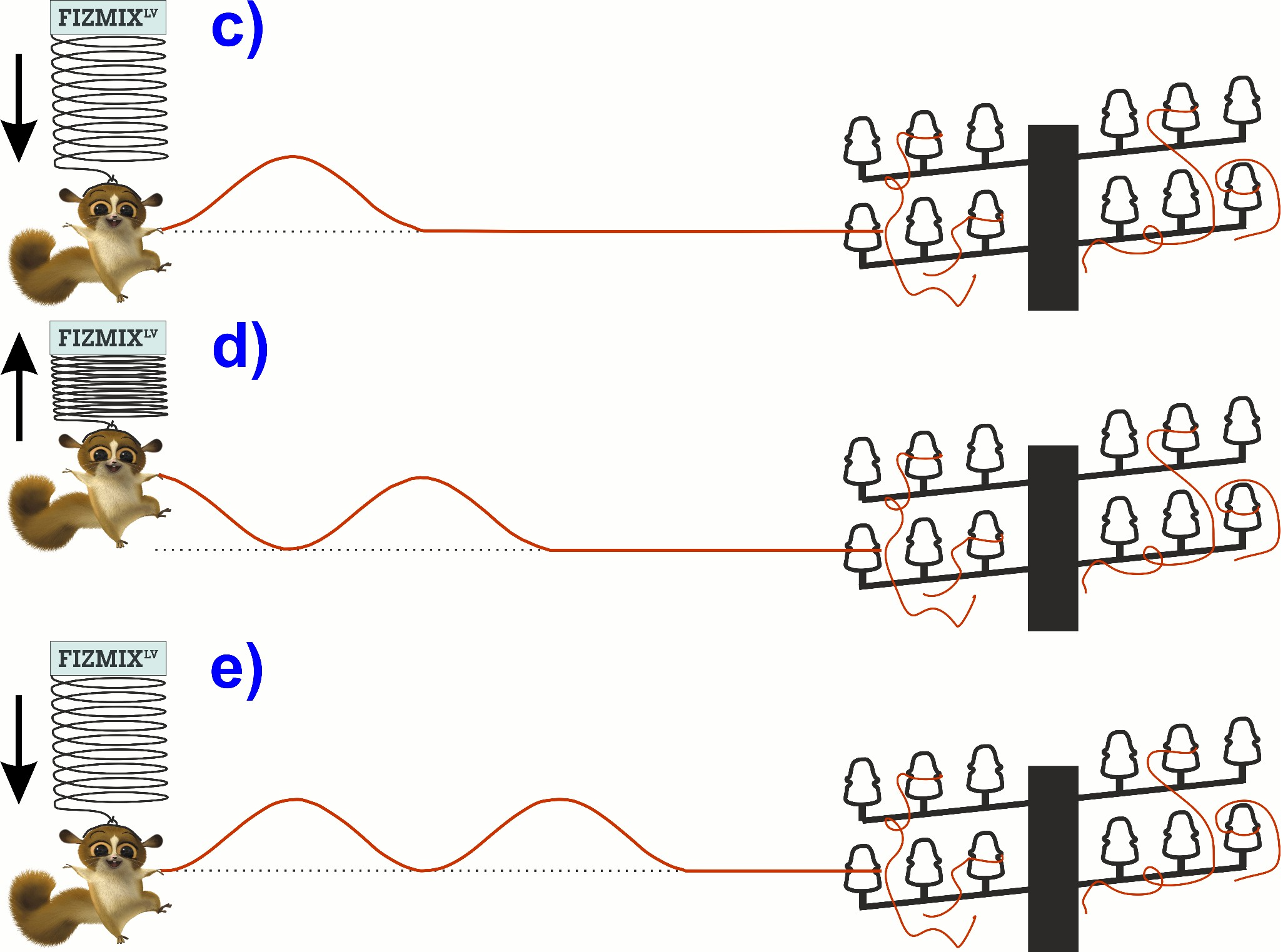
2. att. Viļņa izplatīšanās vadā
Vilņa raksturošanai var izmantot dažādus parametrus. 3. att. redzams, ka lemurs turpina darboties ap vadu. Lemura radītā viļņa izplatīšanās nodrošina, ka dažādas vada daļas jeb šo vidi veidojošās daļiņas svārstās atšķirīgi, jo kādā noteiktā laika momentā atšķiras to novietojumos attiecībā pret sākuma līdzsvara stāvokli. Tomēr ir arī daļiņas, kuras svārstās vienādi. Attālumu starp tuvākajām daļiņam, kas svārstās vienādi, sauc par viļņa garumu, savukārt maksimālo daļiņas novirzi no līdzsvara stāvokļa sauc par amplitūdu.
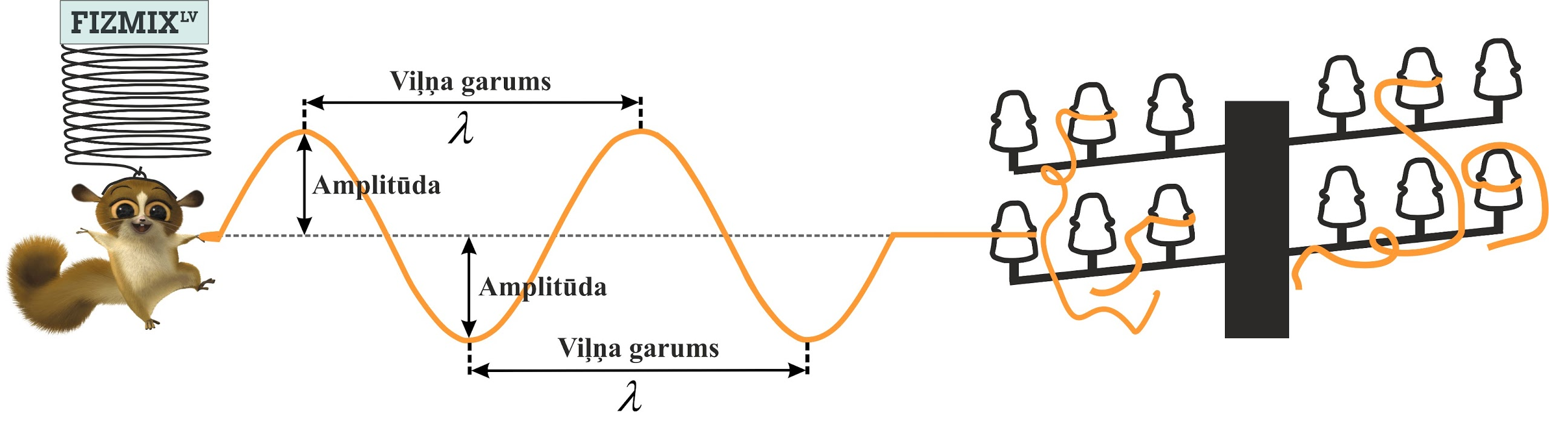
3. att. Vilņa raksturojošie lielumi
Viļņi var atšķirities pēc tajos svārtošo vides daļiņu kustības virziena atiecību pret viļņa izplatīšanās virzienu (4. att.). Šādā veidā viļņus var iedalīt:
1) Šķērsviļņos (4. att. a);
2) Garenviļņos (4. att. b).
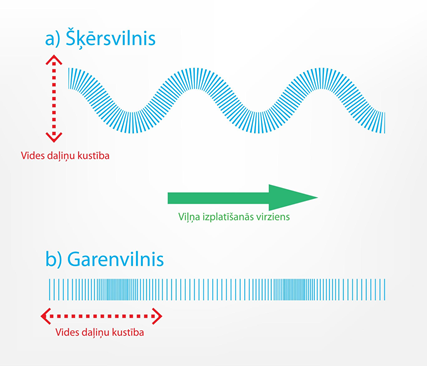
4. att. Šķērsvilņi un garenvilņi
Viļņu pārklāšanos vidē sauc par interferenci. Pārklājoties diviem vai vārakiem viļņiem, summējas to svārstību amplitūdas (5. att.), tādēļ kopējā svārstību amplitūda var būt gan mazāka (5. att. a), gan lielāka (5. att. b) par atsevisķo viļņu svārstību amplitūdām.
Video no macibuvideo.lv par difrakciju
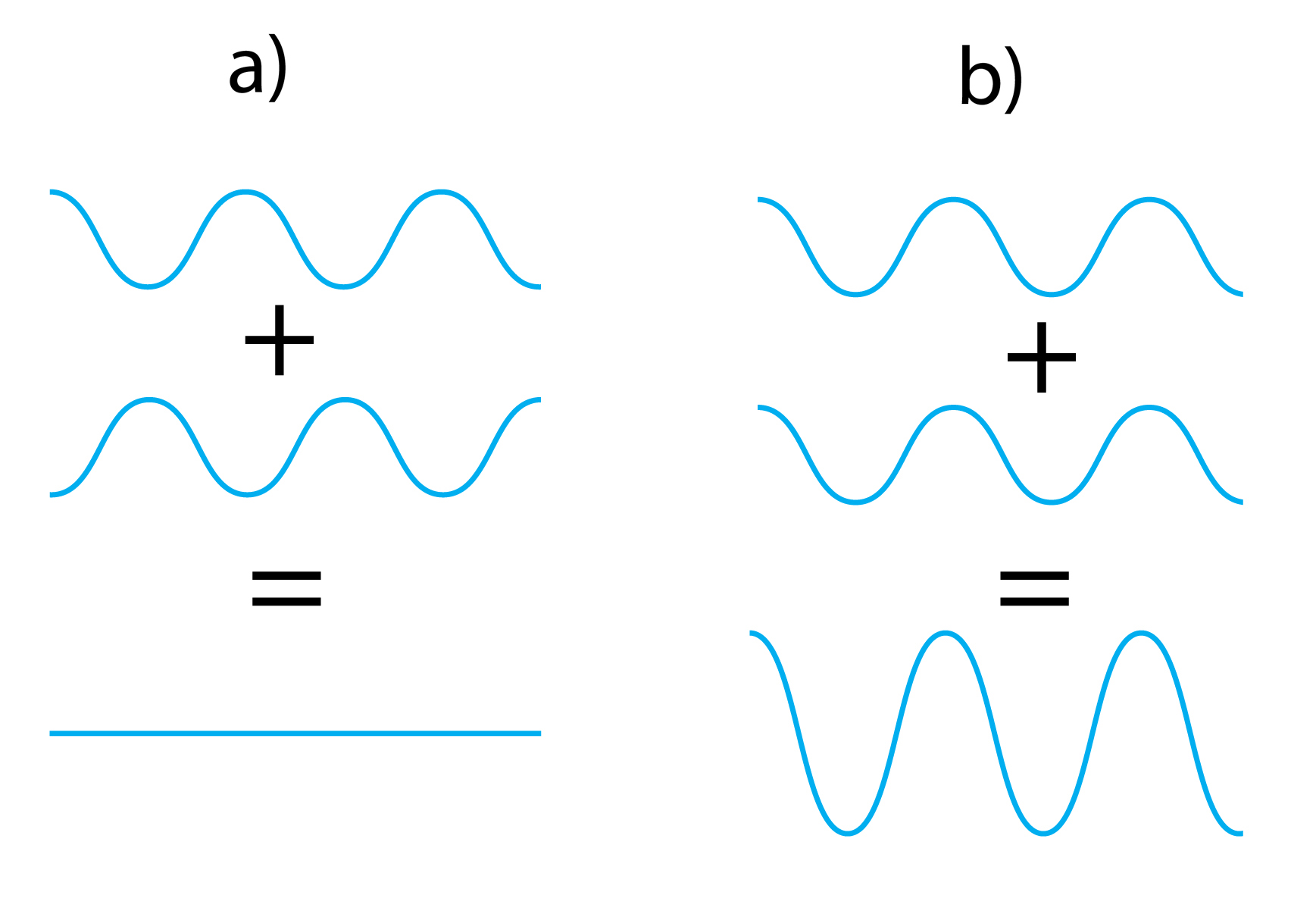
5. att. Viļņu interference
Ja vilnis savā ceļā sastop šķērsli, tad atkarībā no škēršļa izmēra un viļņa garuma, tas vairāk vai mazāk apliecas ap šķersli. To sauc par viļņu difrakciju. Ja šķēršļa izmēri ir daudz lielāki par viļņa garumu , tad apliekšanās ir neliela (6. att. a), bet ja viļņu garums ir aptuveni tāds pats kā šķēršļa izmērs, tad apliekšanās ir ievērojami liela (6.att. b).
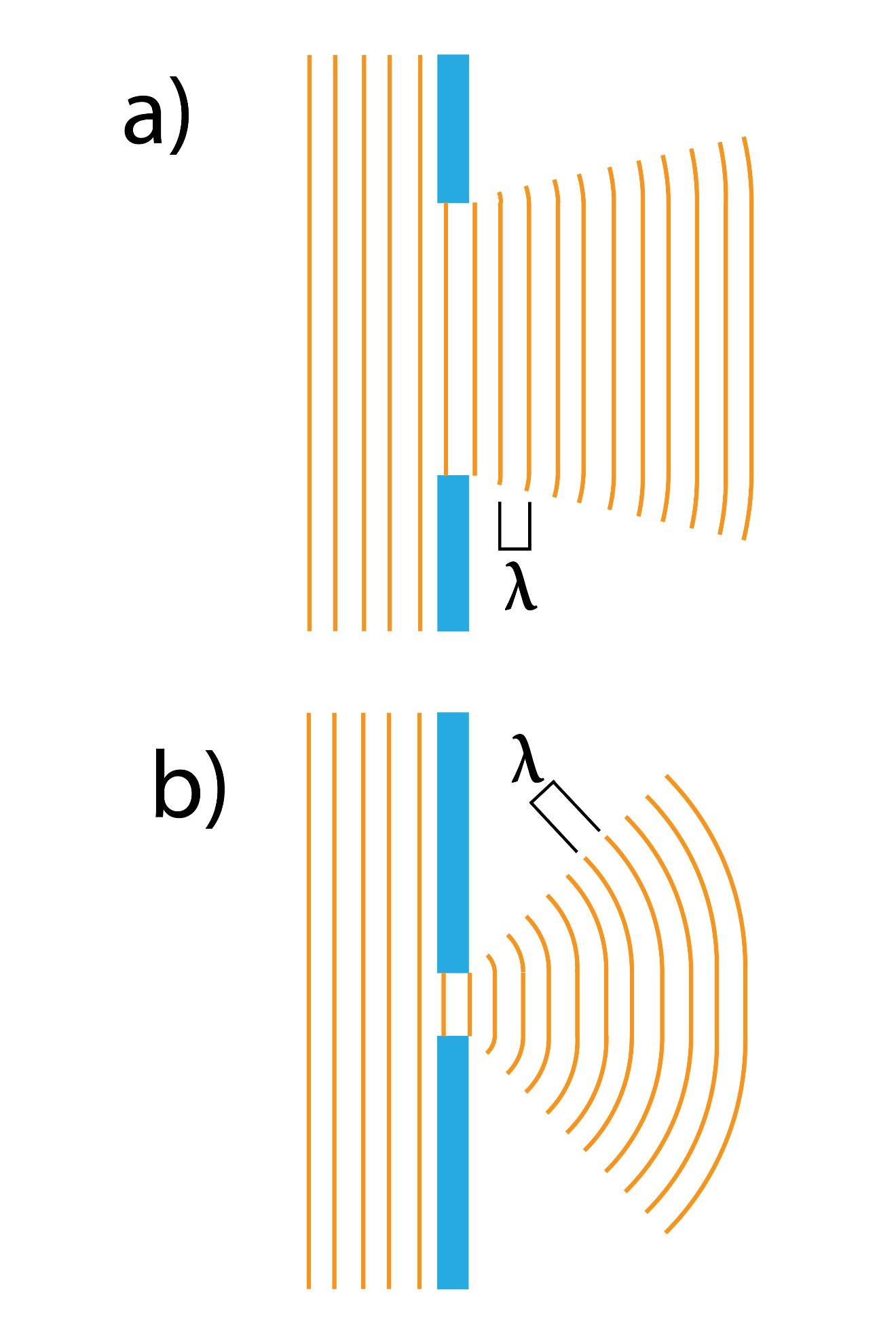
6. att. Viļņu difrakcijas lieluma atkarība no viļņu izmēra
Viļņus varam novērot, piemēram, ūdens bļodā, palēnām tajā pilinot ūdens pilienus (1. att.).

1. att. Viļņi bļodā ar ūdeni
Ja mēs kāda laika momentā “noķertu” vilni, kas izplatās brokastu pārslu šķīvī (2. att.), tad varētu novērtēt dažādu brokastu pārslu novirzi no sākotnēja līdzsvara stāvokļa. Lai gan attēlā vilnis ir “notverts”, reāli tas pārvietojas ar noteiktu ātrumu v (2. att.). Laika momentu, kurā vilnis pārvietojas par vienu viļņa garumu, sauc par periodu T, līdz ar to ir spēkā sakarība λ=vT.

2. att. Viļņa periods un pārvietošanās ātrums
Viļņu izplatīšanas ātrums ir atkarīgs no vides, kurā tas izplatās. Piemēram, ja mēs paņemsim veļas auklu, un ar rokas kustību radītu tājā skrejošu vilni (3. att. a), tad šī viļņa ātrums nebūs tāds pats, ja mēs paņemtu pārlocītu segu un ierosinātu tajā skrejošu vilni (3. att. b), jo atšķirīgas ir vidi veidojošo materiālu elastības īpašības.

3. att. Viļņu ātrums dažādās vidēs ir atšķirīgs
Šķērsviļņos vides daļiņa izplatās perpendikulāri viļņa kustības virzienam. Piemēram, ja kādai žurkai ir izdevies tikt klāt interneta optiskajam vadam (4. att. a), tad tā ir tik priecīga par savu guvumu, ka aiz priekiem sāk lēkāt (4. att. b,c,d,e). Tad lai gan žurkas lēkāšanas notiek augšup-lejup, vilnis izplatās modema virzienā.

4. att. Šķērsviļņa izplatīšanās optiskajā vadā
Šķersviļņi veidojas visu stīgu instrumentu stīgās, kad instrumenta spēlētājs ir pielicis stīgai spēku un to iesvārstījis (5. att.).

5. att. Šķērsviļņi ģitāras stīgā
Ja vides daļiņas izplatās paralēli viļņa kustības virzienam, tad tādu vilni sauc par garenvilni. Šāda tipa vilni var novērot atsperē, ja tiek satverts viens atsperes gals (6. att. a) un ar strauju rokas kustību radīts sablīvējums atsperes galā (6. att. b), tad atsperes sablīvējums jeb garenvilnis pārvietojas pa atsperi (6. att. c,d,e), tieši tajā pašā virzienā, kurā notiek daļiņu svārstības.
6. att. Garenvilņa izplatīšanās
Mēs spējam sadzirdēt dažādas skaņas tādēļ, ka pa gaisu pārvietojas garenviļņi. Ja netālu no cilvēka auss ir kāds svārstību radošs objekts (7. att.), tad šī objekta svārstības iesvārsta gaisā esošās molekulas. Ja svārstības ir pieteikoša spēcīgas, lai skaņas vilnis nonāktu līdz cilvēka ausij un iekustinātu bungādiņu, tad mēs sadzirdam skaņu.
7. att. Skaņas viļņi gaisā
Skaņas viļņi ir pakļaut interferences parādībai. Šo faktu izmanto, piemēram, automāšīnu izpūtējos (8. att. a), kur speciāli izveidotā nodalījumā (8. att. b) punktā A izplūdes gāzes tiek sadalītas divās daļās. Plūsmas tiek sadalītas tā, lai, satiekoties punktā B, izpildītos interferences minimuma nosacījums un skaņa tiktu slāpēta.
8. att. Skaņas interference automašīnu izpūtējos
Viļņu difrakciju, savukārt, var novērot ūdens viļņiem, kad tie virzās cauri kādai spraugai, kuras platums salīdzināms ar ūdens viļņu garumu (9. att.).
9. att. Ūdens viļņu difrakcija
Svārstību un viļņu raksturošanai izmanto arī fāzes jēdzienu. Viena svārstību perioda laikā vides daļiņa veic vienu pilnu svārstību ciklu, izejot cauri visiem svārstību stāvokļiem un atgriežās sākotnēja stāvoklī. Fāze norāda kurā stāvoklī atrodas svārstības konkrētajā laikā momentā. Parasti apskata fāžu starpību vides daļiņu svārstībām viena viļņa ietvaros (1. att.), kā arī fāžu starpību atsevišķiem viļņiem (2. att. a un b). Fāzi un fāzu starpību nosaka grādos. Viens svārstību cikls atbilst 2π radiāniem jeb 360 grādiem.
1. att. Fāzu starpība vilnī svārstošām daliņām
Ja vilnī attālums starp daliņām ir vienāds ar viļņa garumu λ, tad fāzu starpība vienāda ar 360 grādiem un saka, ka daļiņas svārstas vienā fāzē, savukārt ja attālums ir λ/2, tad fāzu starpība ir 180 grādi un daļiņas svārstās pretējās fāzēs (1.att.). Ja apskata divu viļņu fāzu starpības (2.att.), tad ja fāzu starpība ir 0, tad saka, ka viļņi ir vienādā jeb vienā fāzē (2. att. a), bet ja starpība starp viļņiem ir λ/2, tad viļņi ir pretfāzē (2. att. b).
2. att. Viļņu fāze un pretfāze
Par koherentiem viļņiem sauc tādus viļņus, kuri pārklājoties veido laikā nemainīgu interferences ainu. Koherentiem viļņiem:
a) jābūt ar vienādu viļņu garumu;
b) jāsaglabājas fāžu starpībai.
Ja viļņu avoti rada koherentus viļņus, tad tos sauc par koherentiem viļņu avotiem. 3. att. redzama interferences aina, kas veidojas pārklājoties divu koherentu avotu radītajiem viļņiem. Ar gaisāku un tumšāku krāsu ir atzīmēti svārstību amplitūdas maksimumi un minimumi.
3. att. Divu koherentu avotu interferences aina
4. att. a) redzams, ka punktā M pārklājās divu koherentu viļņu avotu veidotie viļņi. Attālums no pirmā viļņu avota līdz punktam M ir d1, bet attālums no otrā avota ir d2. Fāzu starpību punktā M noteiks starpība |d2-d1|, ko sauc par gājuma starpību d. Svārstību amplitūda pārklāšanās punktā būs vislielākā, ja gājuma starpība vienāda ar pāra skaitu pusviļņu garumiem (2·λ/2, 4·λ/2, 6·λ/2 ...) , jo tad abi viļņi ir fāzē. Savukārt, ja d vienāds ar nepāra skaitu pusviļņu garumiem (1·λ/2, 3·λ/2, 5·λ/2 ...) , tad amplitūda ir minimālā (4.att. b). Citos punktos, kuros neizpildās kāds no abiem iepriekš minētājiem nosacījumiem, amplitūda ir robežās starp maksiālo un minimālo.
4. att. Gājuma starpība
Ja kādreiz iznāk stāvēt ceļa malā brīdī, kad garām pabrauc operatīvais transporta līdzeklis ar ieslēgtu sirēnu, tad var dzirdēt, ka, pabraucot garām, mainās sirēnas skaņas augstums. Šī parādība ir izskaidrojama ar Doplera efektu. Par Doplera efektu sauc avota izstarotā viļņa garuma un novērotāja uztvertā viļņu garuma atšķirības, kas rodas avota un novērtotāja savstarpējās kustības dēļ. 5. att. redzams, ka ja avots kustas virzienā uz novērotāju, tad uztvertā viļņa garums ir mazāks nekā tad, ja avots kustas prom no novērotāja. Šis izpildās arī tad, ja kustas novērotājs.
5. att. Doplera efekts
Doplera efektu var izmantot medicinā, lai noteiktu asins plūsmas ātrumu. Šādam nolūkam tiek izmantota ultra skaņa, ko laiž virsū asinsvadiem. Ultraskaņa atstarojas no asinīs esošajamiem sarkanajiem asinsķermenīšiem, bet tā kā sarkanie asinsķermenīši kustas līdzi asinīm, tad Doplera efekta dēļ atstarotā skaņa ir ar lielāku viļņa garumu. Nosakot cik liela ir starpība starp sākotnējās un atstarotās ultraskaņas viļņu garumiem, var aprēķināt asinsķermenīšu un līdz ar to arī asins plūsmas ātrumu (6. att.).
6. att. Doplera efektu izmantošana asins ātruma noteikšanai asinsvados