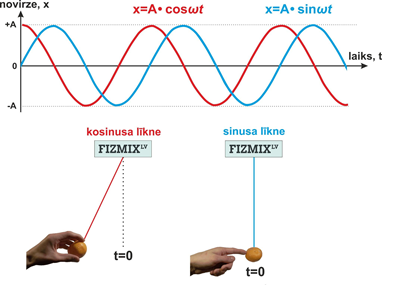
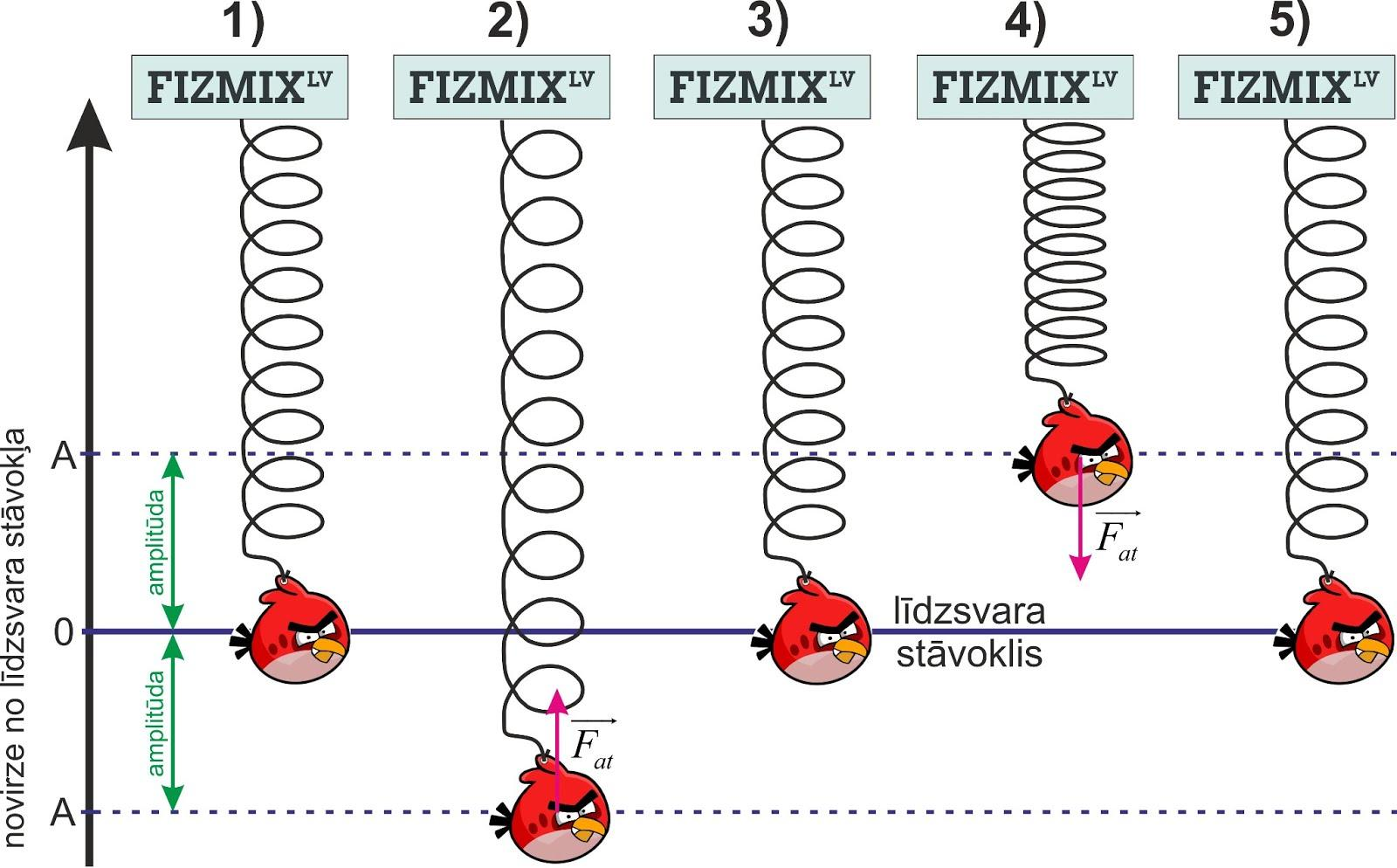
Ja ķermeni izvirza no stabila līdzsvara stāvokļa un tas perodiski tajā atgriežās, tad attiecīgo kustību sauc par mehāniskajām svārstībām. Piemēram, ja mēs paņemam dusmīgo putnu un iekaram to atsperē, tad šī sistēma ieņem līdzsvara stāvokli (1. att.). Ja kādā brīdi dusmīgais putns tiek izvirzīts no līdzsvara stāvokļa, tad rodas atgriezējspēks Fat (1. attēls, 2. stāvoklis), kas cenšas dusmīgo putnu nogādāt atpakaļ līdzsvara stāvoklī. Tas arī notiek, bet inerces dēļ dusmīgais putns aiztraucas līdzsvara stāvoklim garām un atkal rodas atgriezējspēks, tikai šoreiz pretējā virzienā (1. attēls, 4. stāvoklis), un tā dusmīgais putns ir sācis svārstīties.
2. att. Svārstību kustība
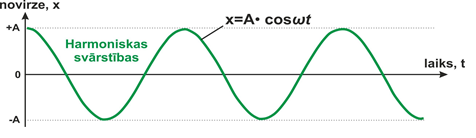
Svārstības raksturo dažādi raksturlielumi.
Par svārstību periodu T sauc laiku, kādā notiek viena pilna svārstība.
Svārstību frekvence f vienāda ar svārstību skaitu laika vienībā. Ja laika vienība ir sekunde, tad frekvences mērvienība ir Hz. Svārstību periods un frekvence ir apgriezti lielumi: f=1/T un T=1/f. Piemēram, ja frekvence ir 50 Hz, tad, katra svārstība notiek 1:50 sekundēs.
Par svārstību amplitūdu A sauc ķermeņa maksimālo novirzi no līdzsvara stāvokļa.
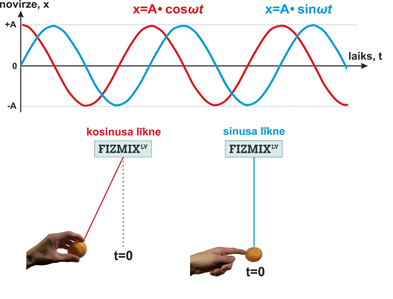
Ķermenis var svārstīties dažādos veidos, piemēram, to pašu dusmīgo putnu varam iekārt nevis atsperē, bet diegā (2. att.). Arī šādā gadījumā, novirzot dusmīgo putnu no līdzsvar stāvokļa un palaižot vaļā, un to darbojas atgriezējspēks, un dusmīgais putns sāk svārstīties. Šīs svārstības var raksturot ar iepriekš apskatītajiem raksturlielumiem.
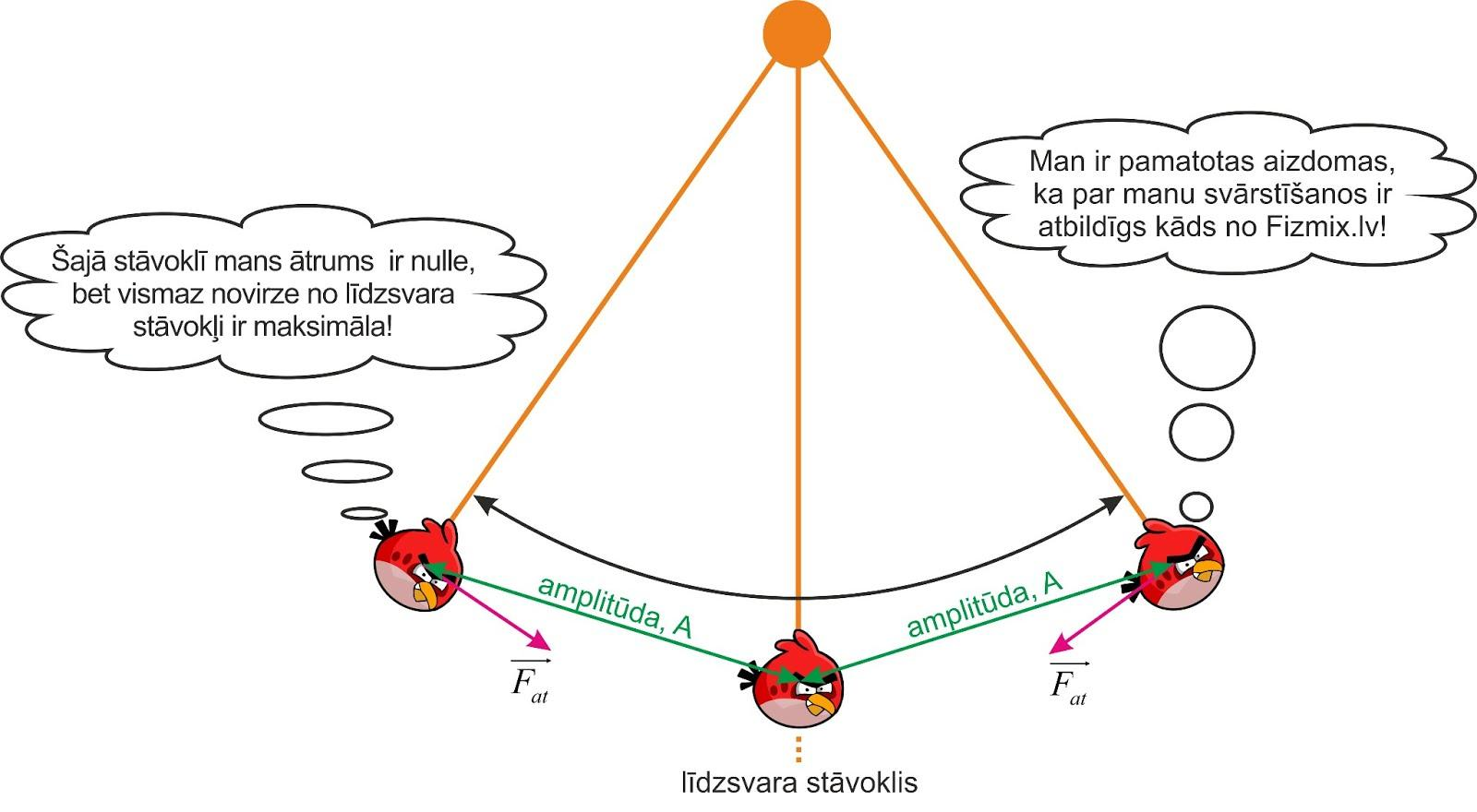
2. att. Svārstību raksturlielumi
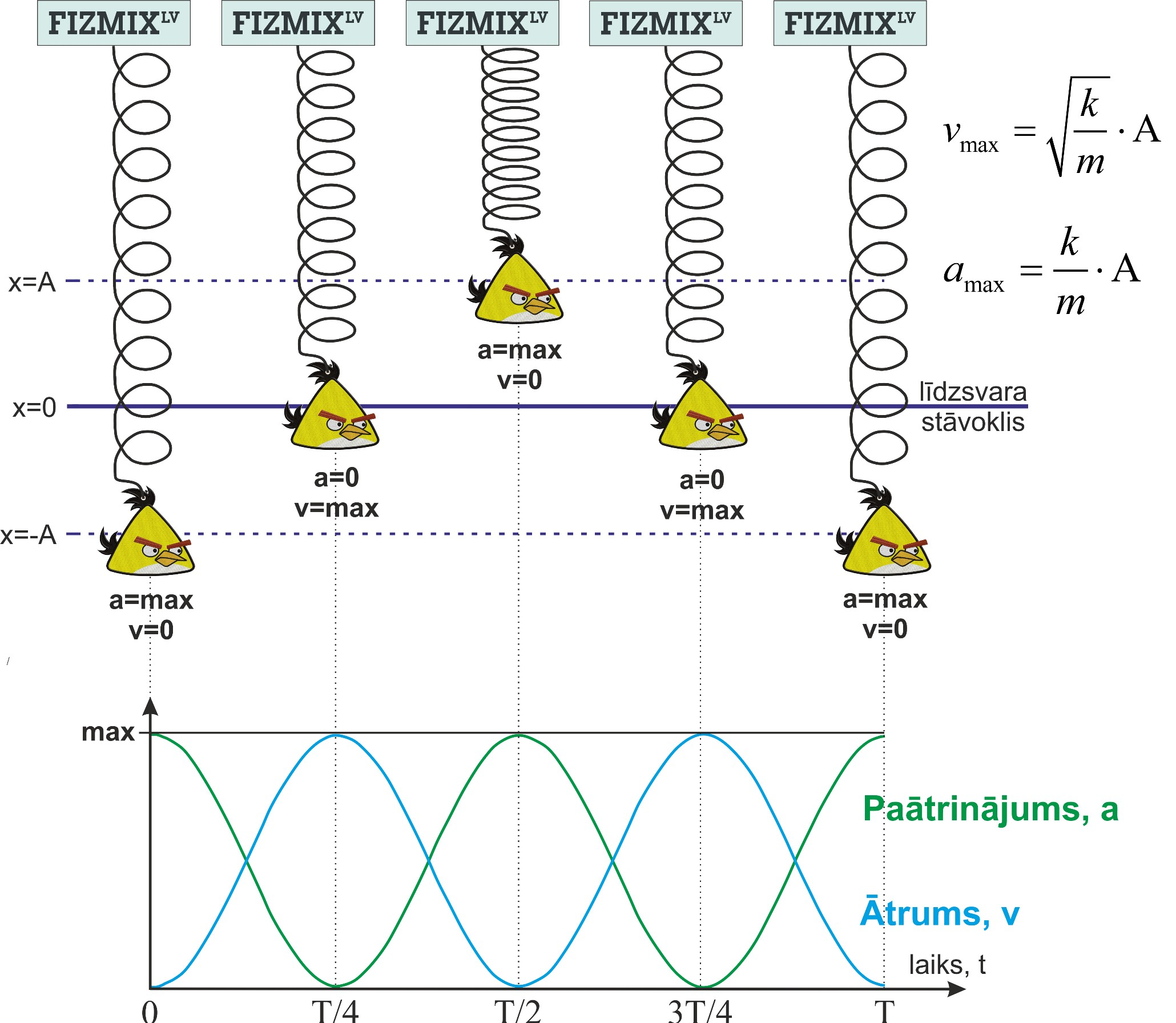
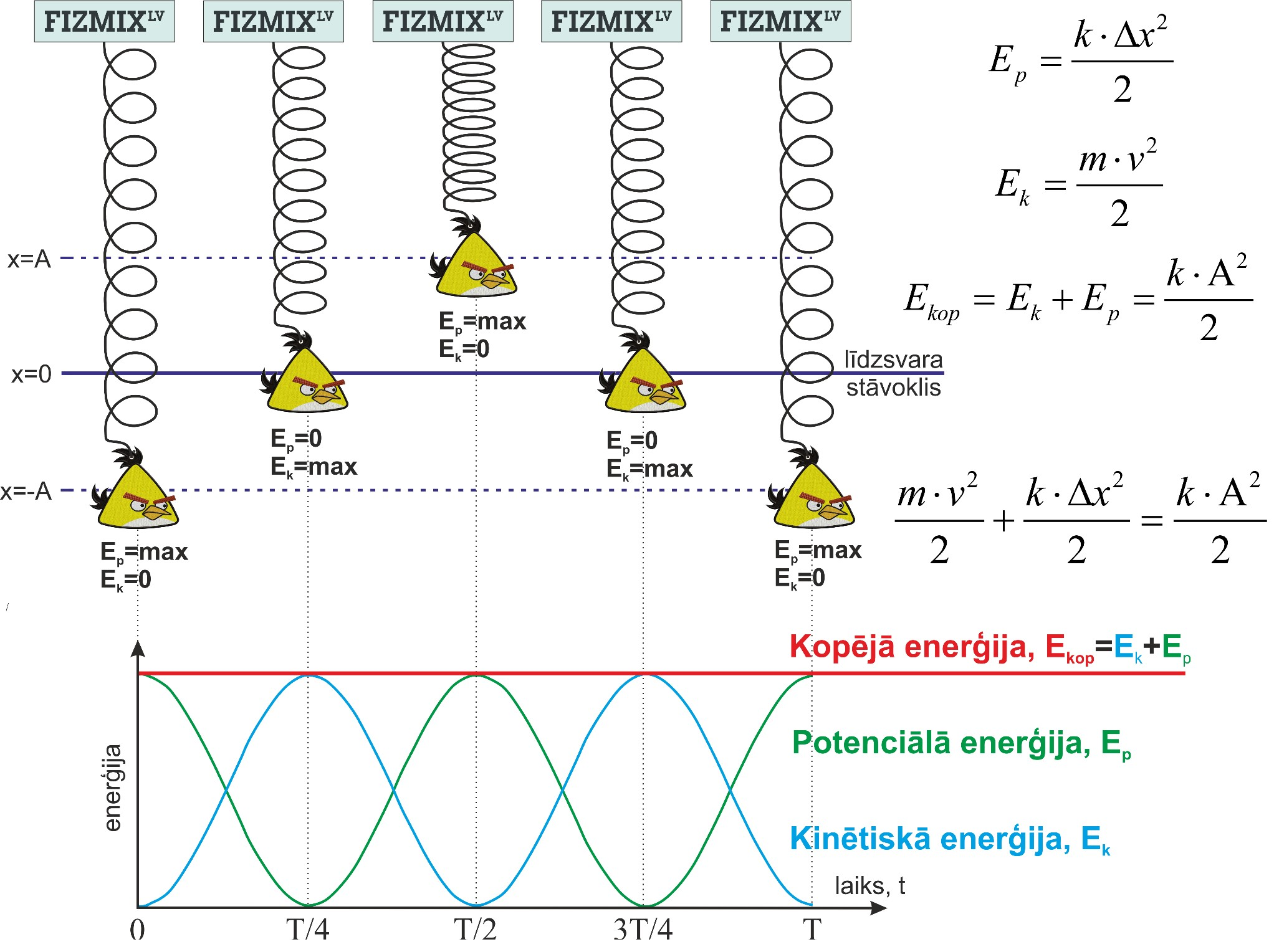
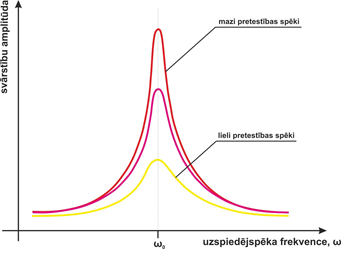
Atsperes svārsts sastāv no atsperē vai elastīgā auklā iekārta ķermeņa. Ja ķermeni izvirza no līdzsvara stāvokļa par lielumu ∆x, tad rodas elastības spēks Fe=k∆x, kur k ir atsperes vai auklas stinguma koeficients. Palaižot ķermeni vaļā, elastības spēks darbojas kā atgriezeniskais spēks, kas cenšas ķermeni nogādāt atpakaļ līdzsvara stāvoklī, līdz ar to nodrošinot atsperes svārsta kustību (1. att.). Svārstības notiek ar periodu, kas atkarīgs no iekārtā ķermeņa masas un stinguma koeficienta (3. att.).
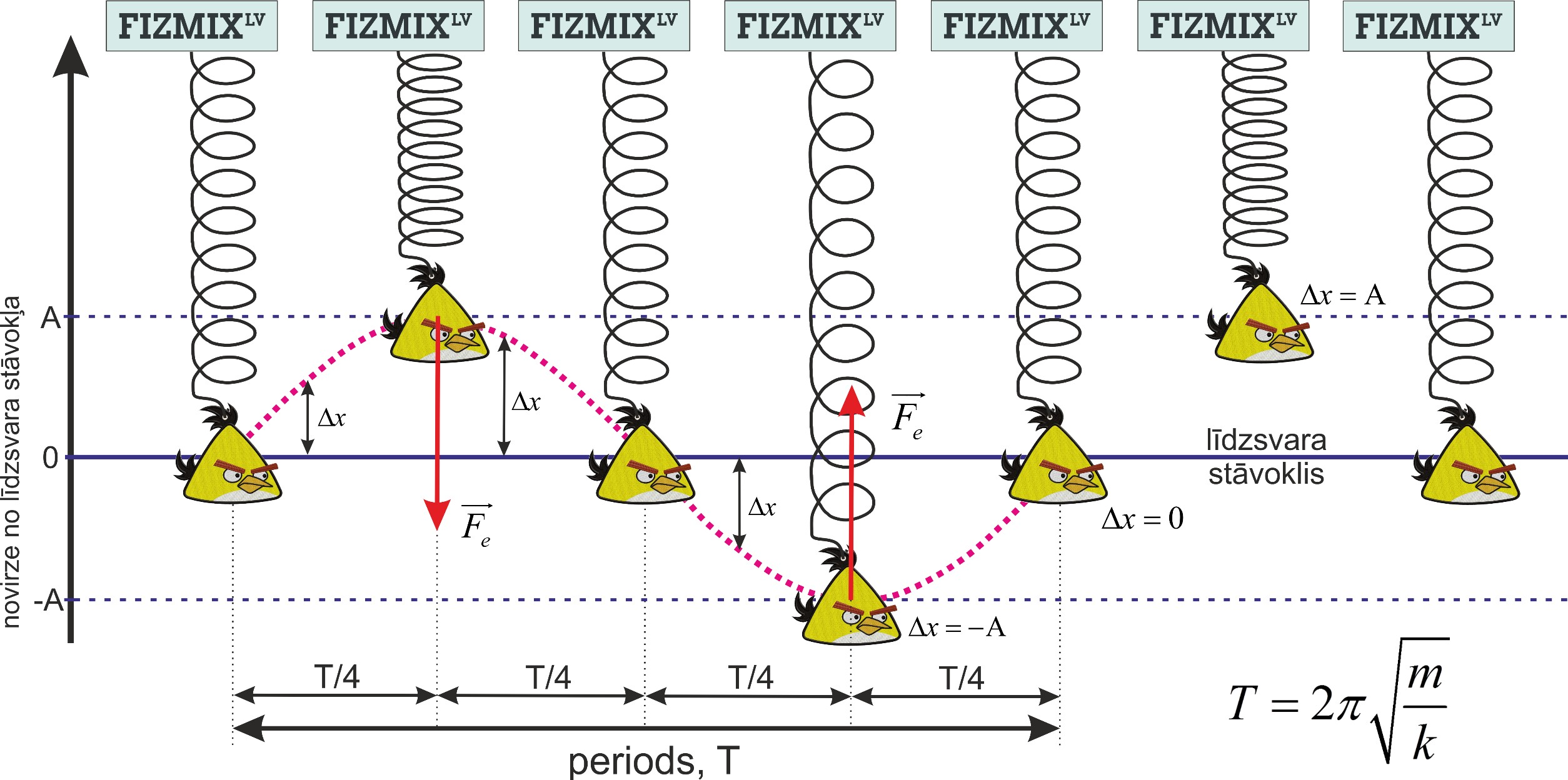
3. att. Atsperes svārsta kustība
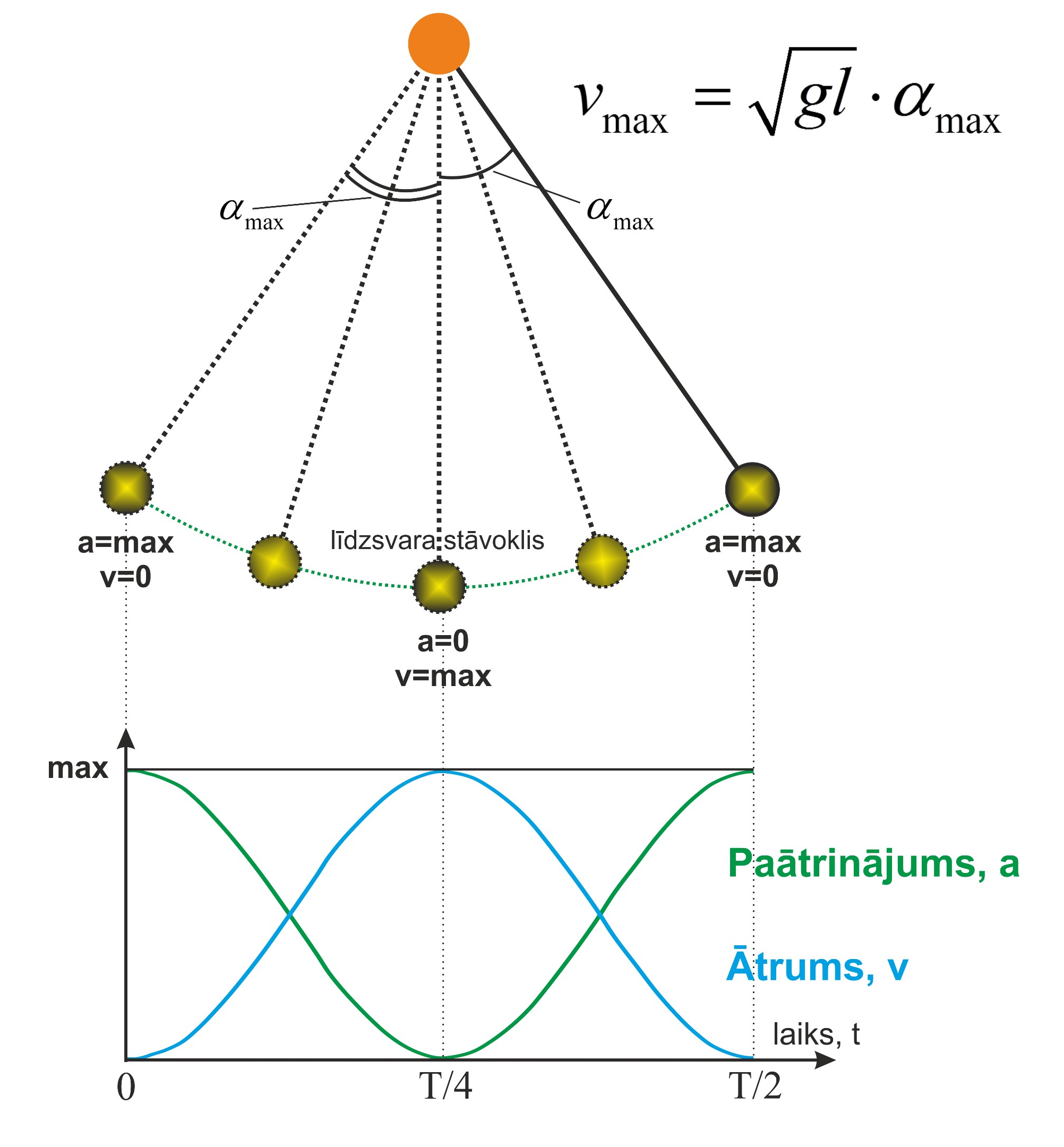
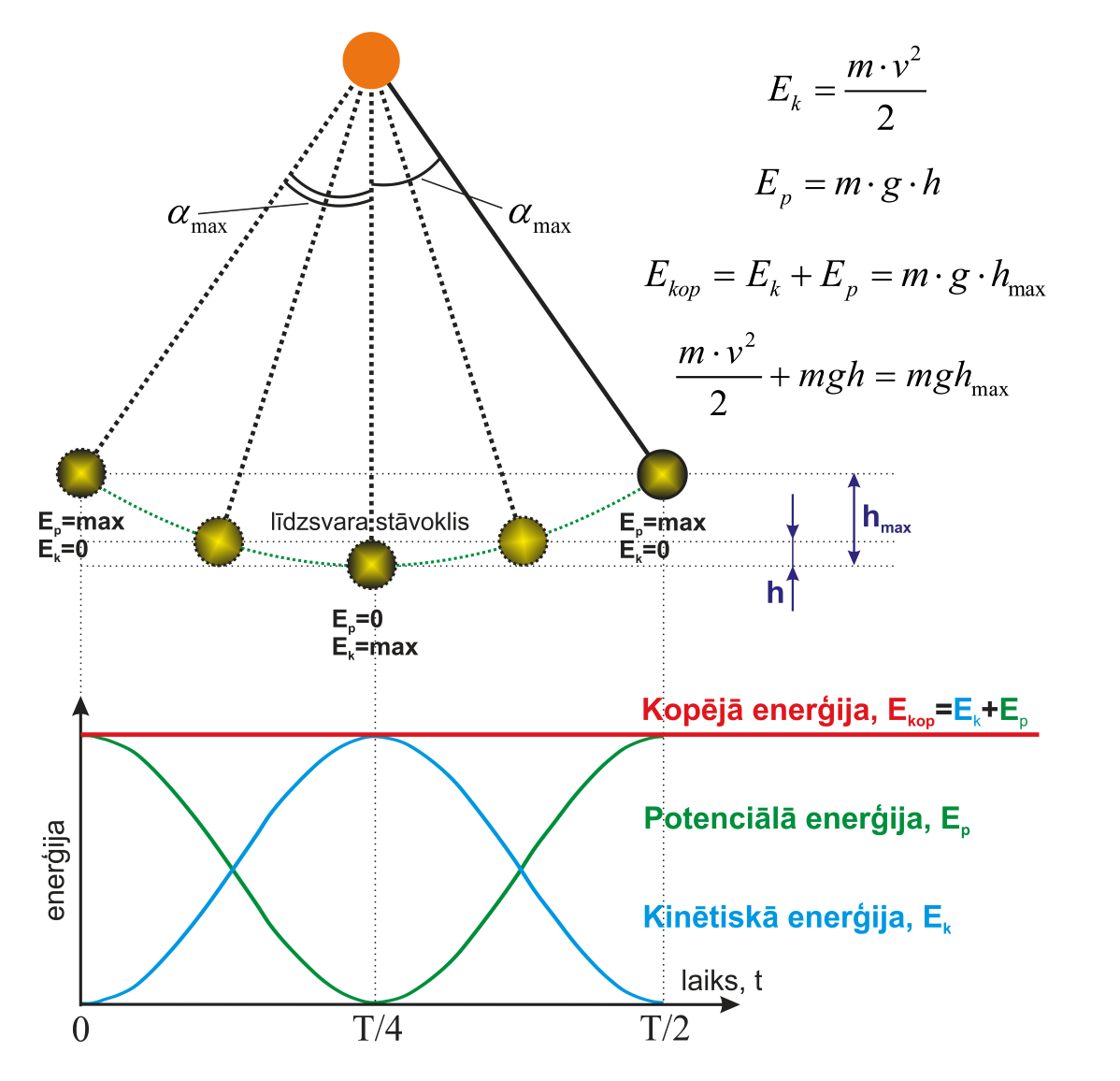
Ja tievā diegā vai auklā iekar ķermeni, turklāt, diega vai auklas masa ir niecīga un ķermeni var uzskatīt par masas punktu, tad šādu objektu sauc par matemātisko svārstu. Ja diegā iekārto ķermeni izvirza no līdzsvara stāvokļa par leņķi α, tad rodas nekompensēts smaguma spēks Fat=mgsinα, kur
m - ķermeņa masa, kg
g - ir brīvās krišanas paātrinājums, m/s2
Smaguma spēks, palaižot ķermeni vaļā, darbojas kā atgriezeniskais spēks, kas noteic svārsta kustību (4. att.). Svārstības notiek ar periodu, kas atkarīgs no svārsta garuma l un brīvās krišanas paātrinājuma (4. att.).
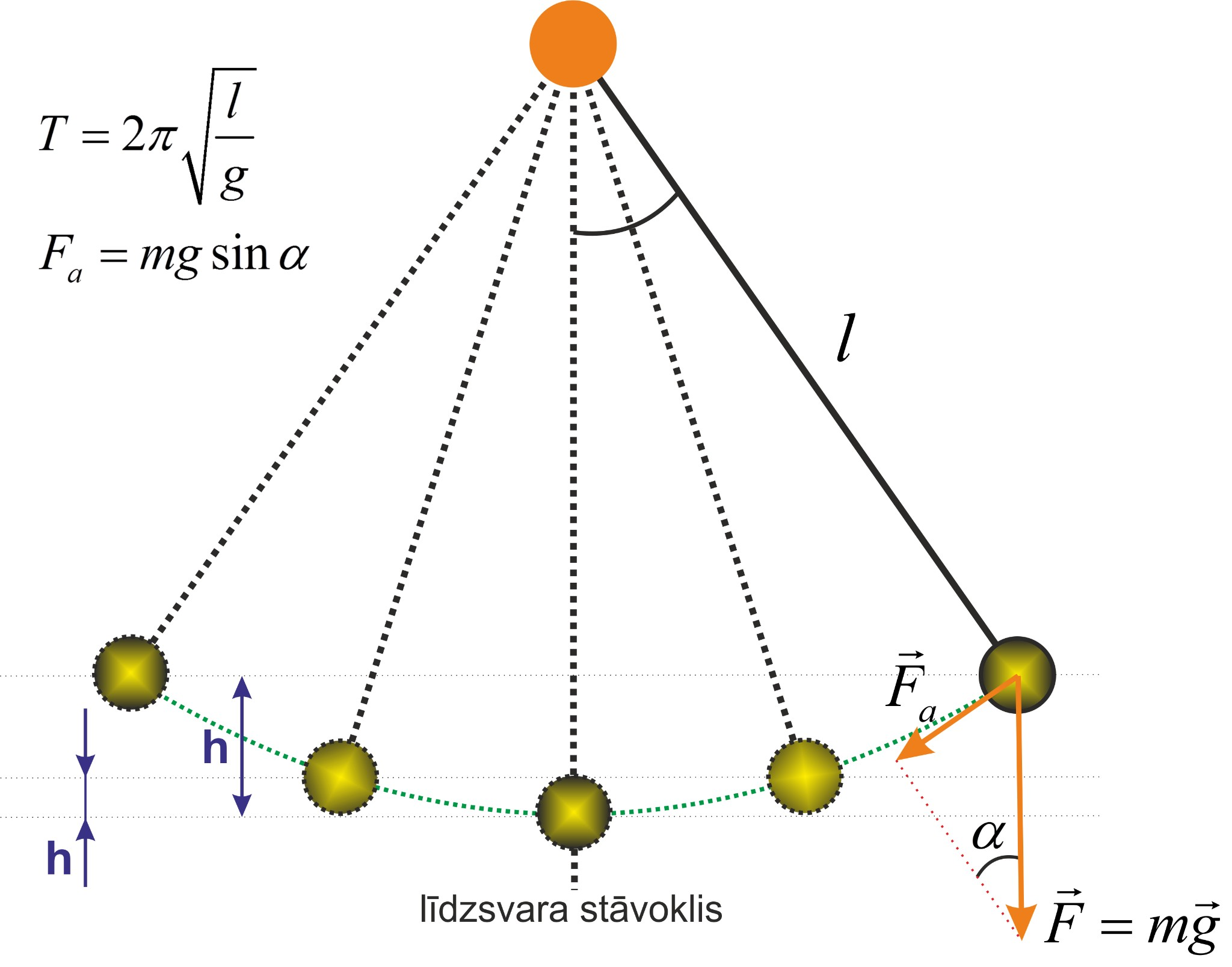
4. att. Matemātiskā svārsta kustība