Kustībai var būt dažāds raksturs. Piemēram, vienu un to pašu attālumu maratona distancē sportisti veic dažādos laikos. Lai varētu raksturot dažādu sportistu tempu distancē, lieto vidējo ātrumu. Par vidējo ātrumu vvid sauc veiktā ceļa l attiecību pret kustības laiku t jeb vvid = l : t. Mūsdienās skrējēji lieto GPS iekārtas un velosipēdi (1. att.) un mašīnas ir aprīkotas ar spidometriem, kas parāda vidējo ātrumu izvēlētajā distancē.

1.att. Vidējā ātruma attēlošana sporta pulkstenī
Tomēr ne visiem spidometriem ir funkcija parādīt vidējo ātrumu, jo to pamatfunkcija ir attēlot momentāno ātrumu (2. att. a). Ja ātrumu nosaka kādā noteiktā laika momentā vai trajektorijas punktā, tad to sauc par momentāno ātrumu (2. att. b). Momentānais ātrums ir vektoriāls lielums, to raksturo gan virziens, gan arī skaitliskā vērtība, bet vidējam ātrumam ir tikai vērtība.
2.att. Momentālais ātrums
Ja kustības laikā nemainās ātruma vektora modulis un virziens, tad to sauc par vienmērīgu taisnlīnijas kustību. Bet, tiklīdz mainās vektora modulis (3. att. a) vai vektora virziens (3. att. b), tā uzreiz jārunā par paātrinātu kustību.

3.att. Paātrināta kustība
Ja vienmērīgi mainās ātruma modulis, nemainoties virzienam, tad tā ir vienmērīgi mainīga (paātrināta vai palēnināta) taisnlīnijas kustība, kurā ātruma izmaiņas straujumu raksturo paātrinājums a. Ja ir zināms kustības sākuma ātrums v0 un beigu ātrums v, kā arī laiks t, kurā notikusi ātruma izmaiņa, tad paātrinājumu aprēķina a = (v - v0) : t. Paātrinājums ir vektors, kuram ir gan vērtība, gan virziens, un ja šis vektors ir vērsts ātruma virzienā, tad tā ir vienmērīgi paātrināta kustība (4. att. a), bet ja paātrinājuma vektors ir vērsts pretēji ātrumam, tad tā ir vienmērīgi palēnināta kustība (4. att. b).
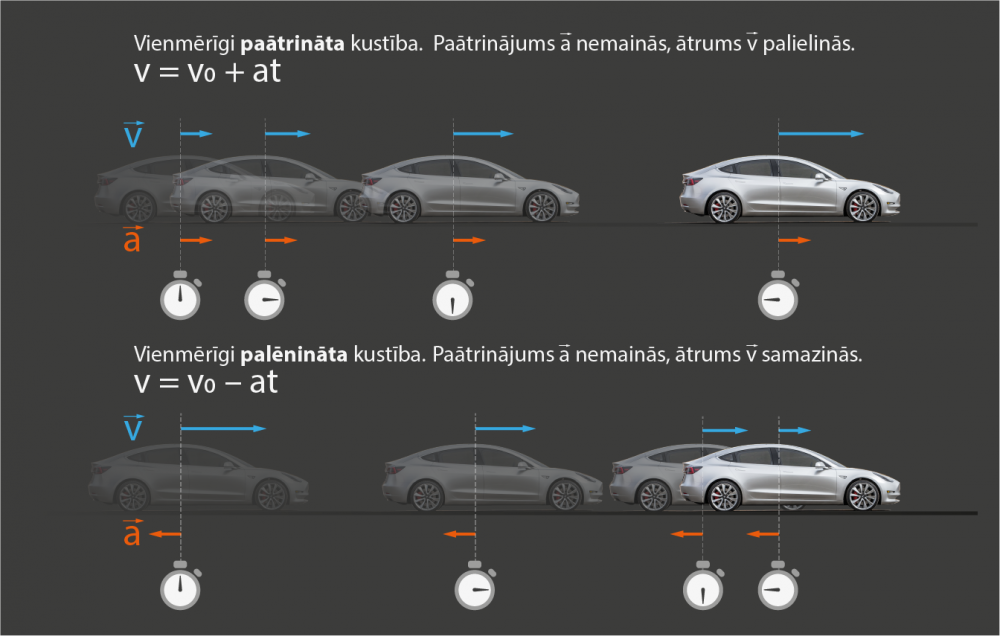
4.att. Paātrinājums
Dažādu ātrumu piemēri redzami 5. un 6. attēlā.
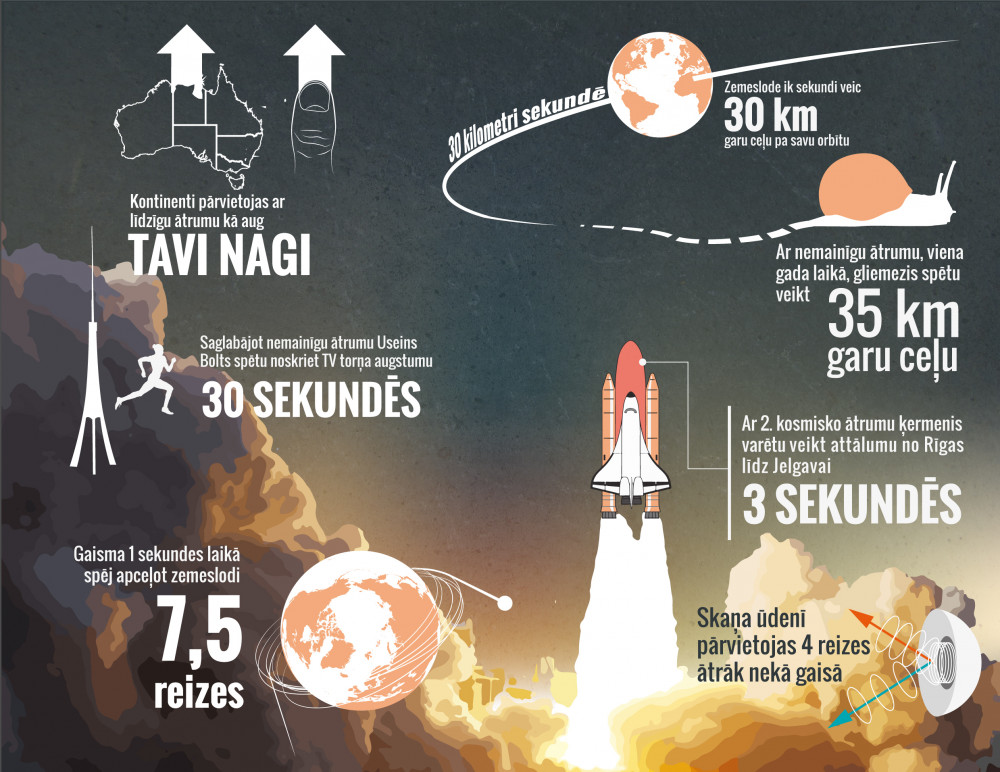
5.att. Dažādu ātrumu piemēri
6.att. Ātrumi var būt ļoti atšķirīgi
Lai aprakstītu skeitera taisnvirziena kustību, ir jāievieš koordinātu sistēmu, kas šajā taisnvirziena kustības gadījumā sastāv no vienas koordinātu ass (1. att.). Pret šo koordinātu sistēmu skeiteris var kustēties dažādos virzienos. Viens virziens sakrīt ar X asi (1. att. a) , bet otrs virziens ir pretējs (1. att. b). Ātrums vienmēr ir pozitīvs lielums, bet, tā ka ātrums ir vektors un tas var būt dažādi novietots pret koordinātu asi, tad tā projekcija var būt gan pozitīva, gan negatīva. Piemēram, apskatot kustību pa X-asi, ja ātrums ir vērsts ass virzienā, tad projekcija vx ir pozitīva un vienāda ar vektora moduli vx = v (1. att. a). Ja tomēr ātrums ir vērsts pretēji X-asij (1. att. b), tad projekcija ir negatīva jeb tās vērtība ir vienāda ar negatīvu vektora moduļa vērtību vx = -v.
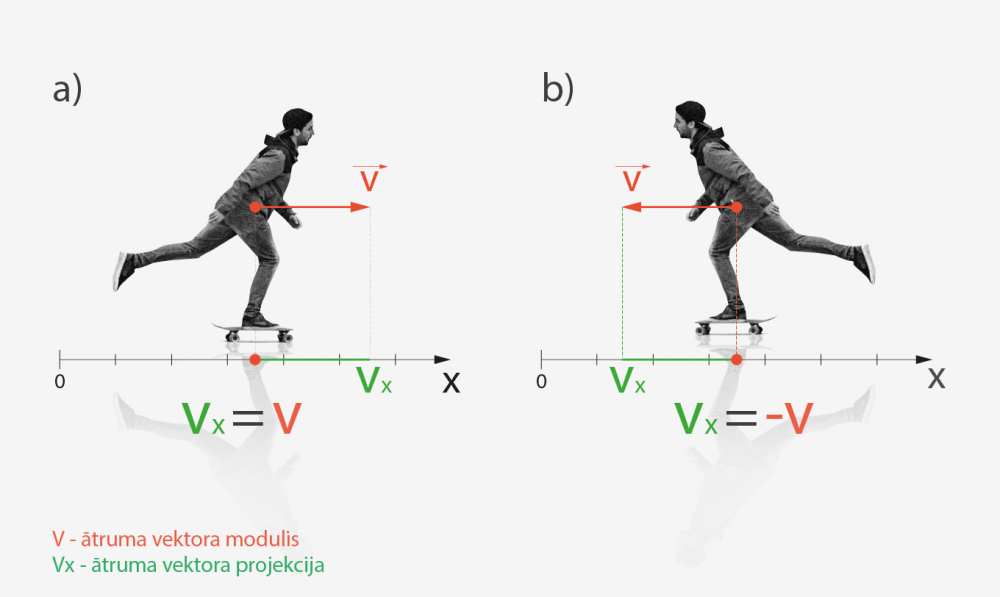
1.att. Pozitīva un negatīva ātruma projekcija
Vienmērīgā kustībā ātruma vērtība nemainās, tādēļ gadījumā, ja attēlotu ātruma atkarību no laika, tad pie dažādiem ātrumiem iegūtu grafika līnijas, kas paralēlas laika asij (2. att.)
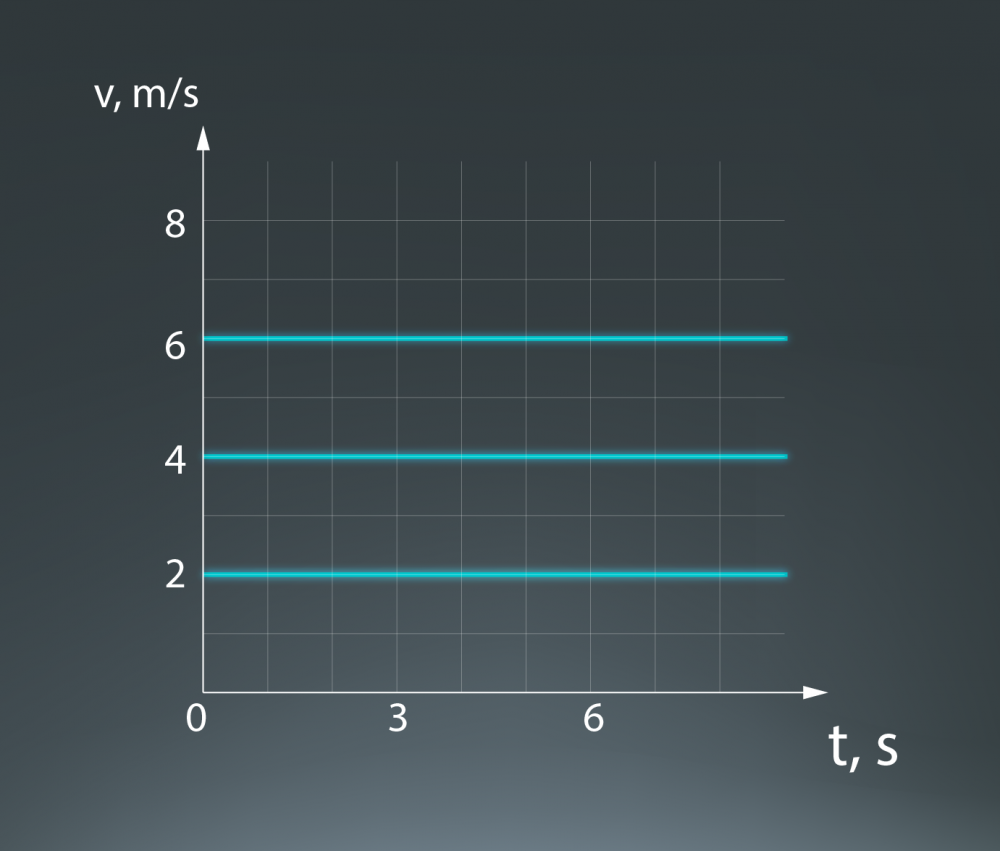
2.att. Ātruma grafiki vienmērīgā taisnlīnijas kustībā
Koordinātes maiņu vienmērīgā taisnlīnijas kustībā apraksta vienādojums x = x0 + vxt, kur
x0 – sākuma koordināte, m
vx – ātruma projekcija, m/s
t – laiks, s
Zīmējot koordinātes grafiku, jāpievērš uzmanība, vai kustība notiek ass virzienā vai pretēji, jo tas izmaina grafika virzienu (3. att. a). Pie dažādiem kustības ātrumiem koordinātu grafikam ir dažāds slīpums. Jo lielāks ir ātrums, jo lielāks ir grafika slīpuma leņķis (3. att. b). 3. attēla c gadījumā redzams piemērs trīs koordinātru grafikiem ar dažādiem ātrumiem, kad kustība ir sākusies no koordinātu sākuma punkta.
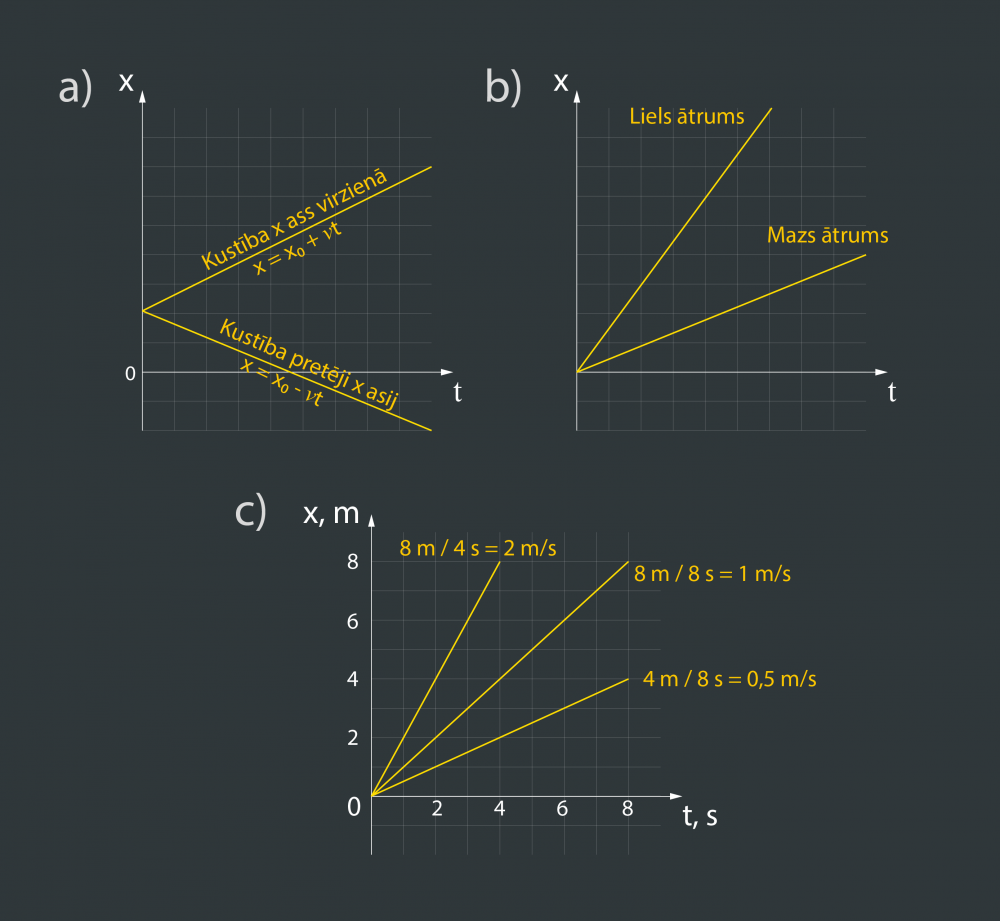
3.att. Vienmērīgas taisnlīnijas kustības koordinātu grafiki
Vienmērīgi paātrinātā taisnlīnijas kustībā ātruma vērtība mainās, un tās izmaiņu apraksta vienādojums vx = v0x + axt, kur
vx – beigu ātrums, m/s
v0x – sākuma ātruma projekcija, m/s
ax – paātrinājuma projekcija, m/s2
t – laiks, s
Uzzīmējot grafiku ātruma atkarībai no laika, var redzēt: jo lielāks ir kustības paātrinājums, jo stāvāks ātruma grafiks (4. att.).
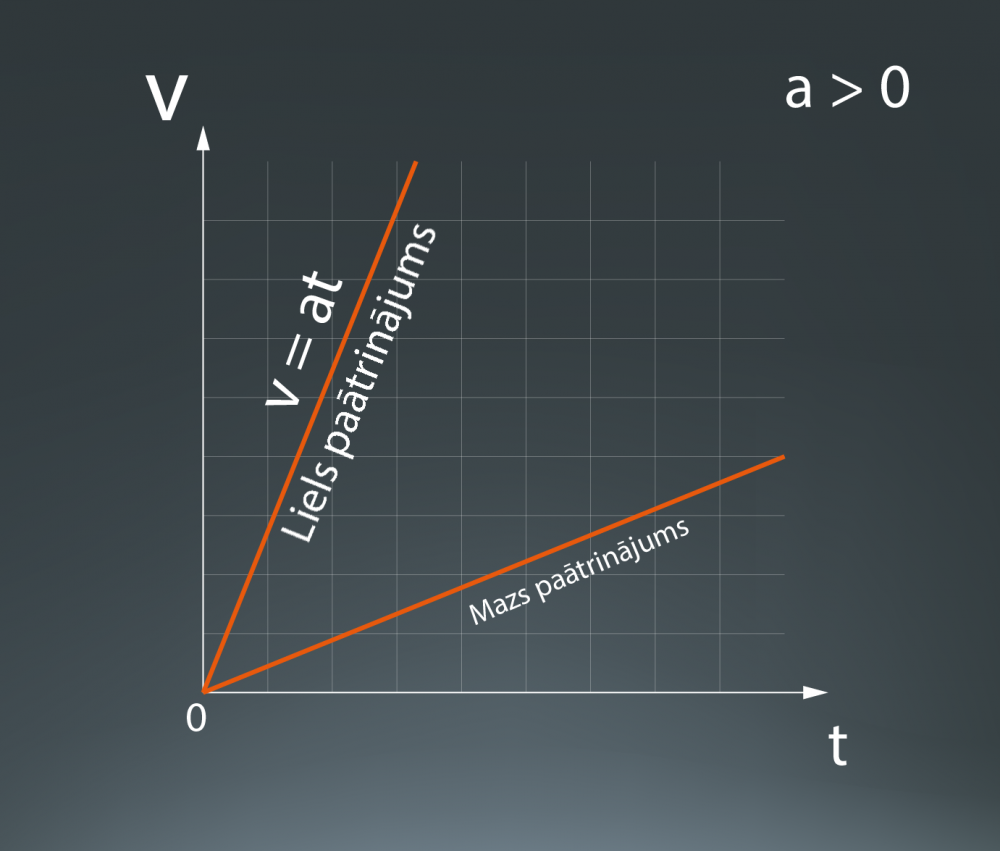
4.att. Ātruma grafiks vienmērīgi paātrinātā kustībā
Koordinātas grafiks vienmērīgi paātrinātai taisnlīnijas kustībai ir x = x0 + v0xt + axt2 : 2, kur
x0 – sākuma koordināte, m
v0x – sākuma ātruma projekcija, m/s
t – laiks, s
ax – paātrinājuma projekcija, m/s2
Šādam gadījumam koordinātu grafiks vairs nav taisne, bet gan parabola (5. att.).
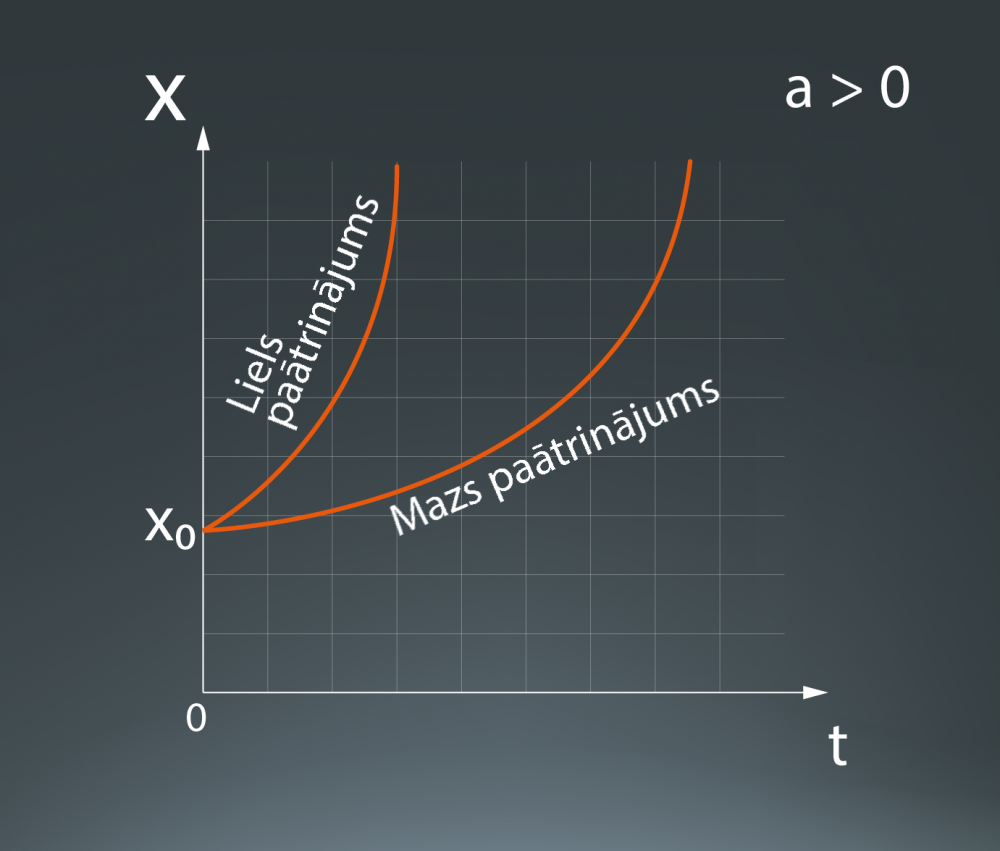
5.att. Koordinātas grafiks vienmērīgi paātrinātā kustībā
Lai aprēķinātu kustības laikā veikto ceļu, var izmantot grafisko metodi, proti, veiktais ceļš ir vienāds ar laukumu, ko ierobežo ātruma taisnes nogrieznis un laika ass. Šī metode darbojas gan vienmērīgā taisnlīnijas kustībā (6. att. a), gan arī vienmērīgi paātrinātā taisnlīnijas kustībā (6. att. b).
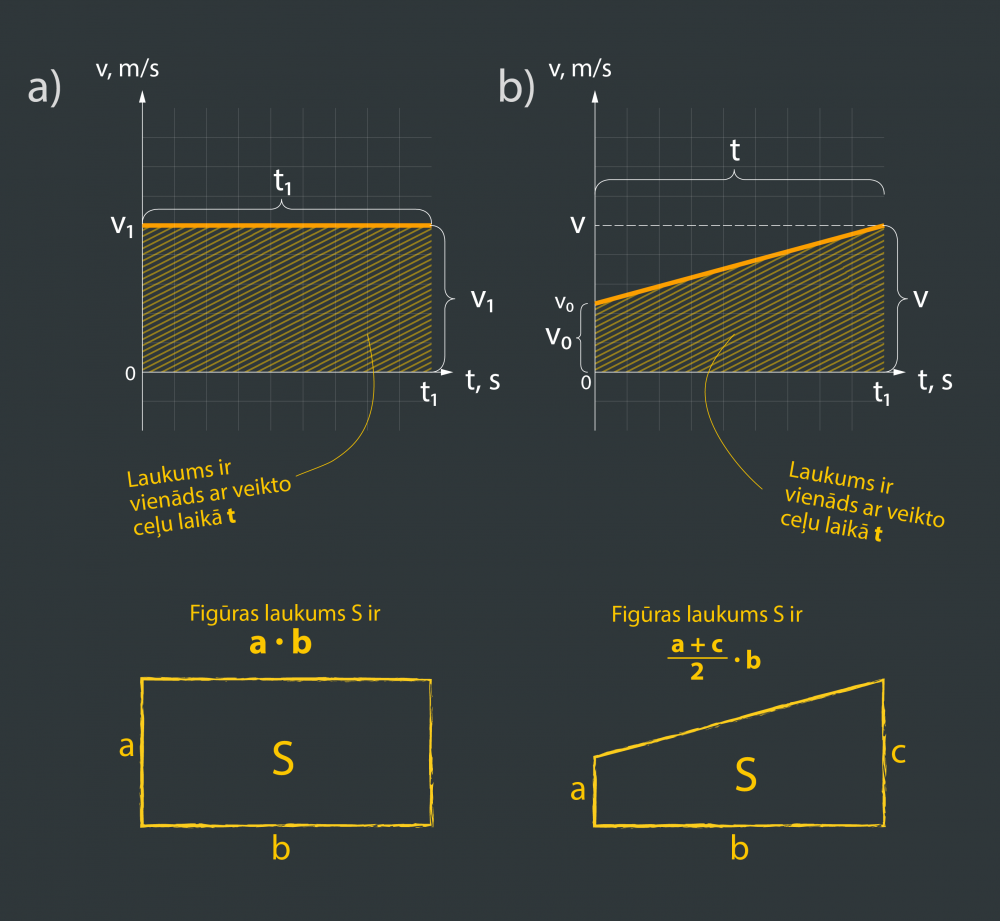
6.att. Grafiskā metode veiktā ceļa aprēķinam
7. attēlā redzams kustības vienādojumu un grafiku apkopojums.
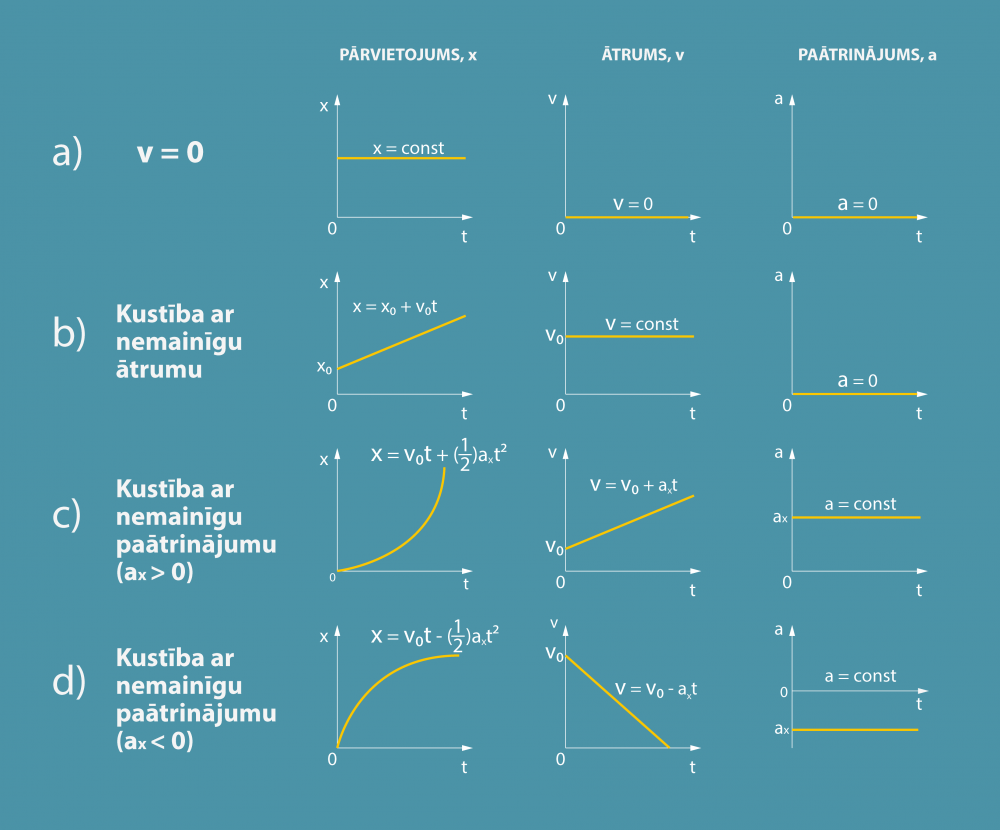
7.att. Kustības vienādojumu un grafiku apkopojums
Tā kā ātrums ir vektoriāls lielums, tad ātrumu saskaitīšana jāveic ģeometriski. Ja putns lido ar ātrumu v1, bet tam no sāniem pūš vējš ar ātrumu v2, tad rezultējošais ātrums v = (v12 + v22)½ (1. att.)
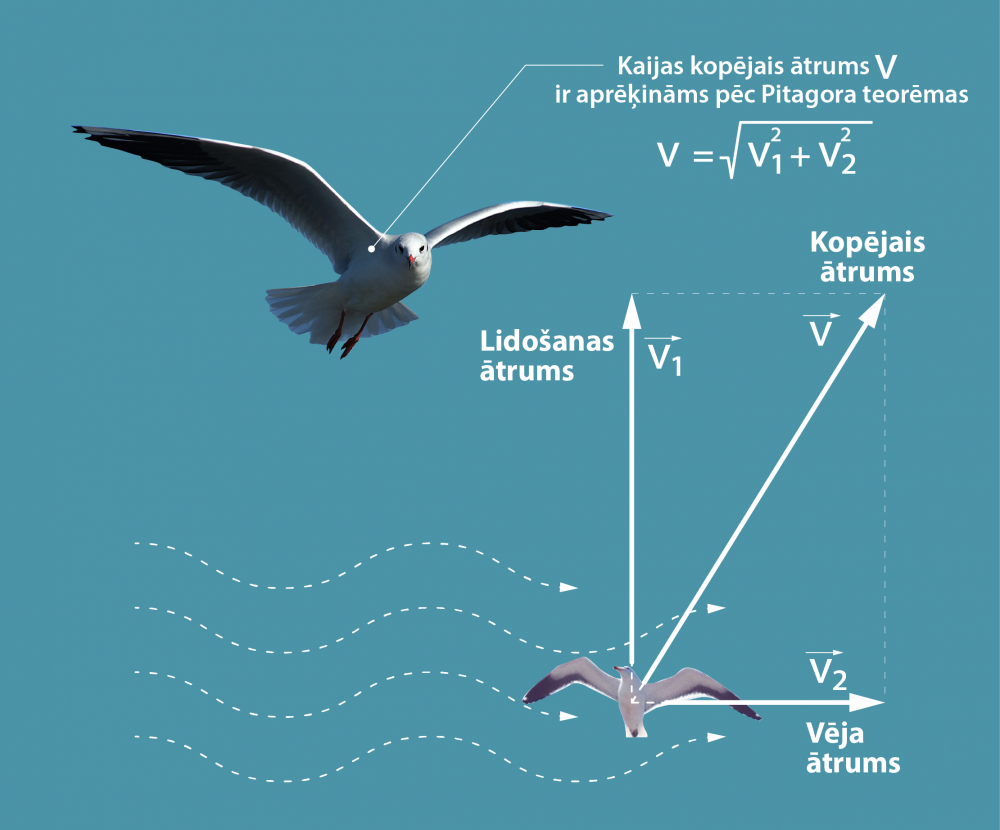
1.att. Putna kopējais ātrums
Kustību var pētīt, izmantojot stroboskopiskos attēlus (2. att.). Stroboskopiskā attēlā ir redzams ķermeņa novietojums pēc vienādiem laika momentiem. Tie ir kā vairāki momentuzņēmumi, kas salikti kopā. Ja ir dots mērogs, pēc stroboskopiskā attēla var noteikt cik lielu ceļu veic ķermenis starp katru uzņēmumu. Tālāk, ja ir zināms zibšņa periods T (2. att.), tad var noteikt pārējos kustības parametrus. Ja ķermenis kustas vienmērīgi, tad tas starp zibšņiem veic vienu un to pašu ceļa gabalu (2. att. a). Ja ķermenis kustas vienmērīgi paātrināti, tad katra nākamā zibšņa laikā ķermeņa noietais ceļš pieaug par vienu un to pašu vērtību (2. att. b), savukārt ja paātrinājums ir negatīvs, tad starp zibšņiem noietais ceļš samazinās par vienu un to pašu vērtību (2. att. c).

2.att. Stroboskopiskie attēli vienmērīgā un vienmērīgi paātrinātā kustībā
3. attēlā redzami koordinātas, ātruma un paātrinājuma grafiki kustībai, kas sastāv gan no vienmērīgas, gan vienmērīgi paātrinātas kustības.
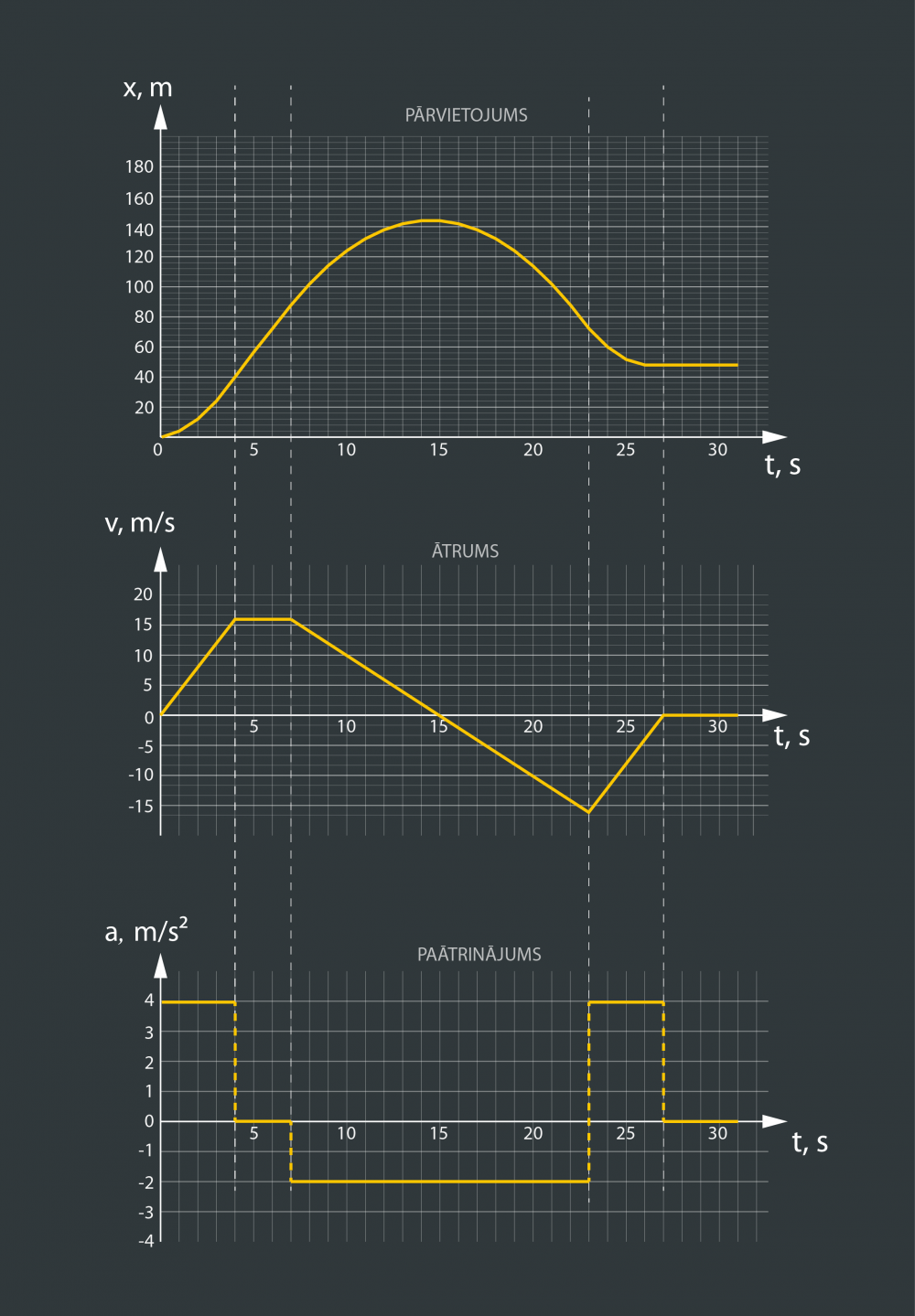
3.att. Kompleksas kustības koordinātas, ātruma un paātrinājuma grafiks