Ja elektroenerģijas avotam jāpieslēdz vairāki patērētāji, pastāv vairāki veidi, kā tos savā starpā savienot. Slēgumu, ja patērētāji savienoti cits aiz cita, sauc par virknes slēgumu (1. att. a). Ja virknē saslēgti n patērētāji, tad to kopēja pretestība R = R1 + R2 + ... + Rn, kur R1, R2, … Rnir katra atsevišķā patērētāja pretestība. Arī kopējais spriegums U veidojas, saskaitot sprieguma kritumus (ikdienā lietojam vienkārši „spriegums”) katrā patērētājā: U = U1 + U2 +...+ Un. Virknes slēgumā caur katru patērētāju plūst viena un tā pati strāva I, tādēļ strāvas stiprums caur visiem patērētājiem ir vienāds I = I1 = I2 = ... = In. Tas ir līdzīgi kā upē: lai arī cik kritumu tajā būtu, aizplūdušā ūdens daudzums upē visu laiku ir vienāds (1. att. b).
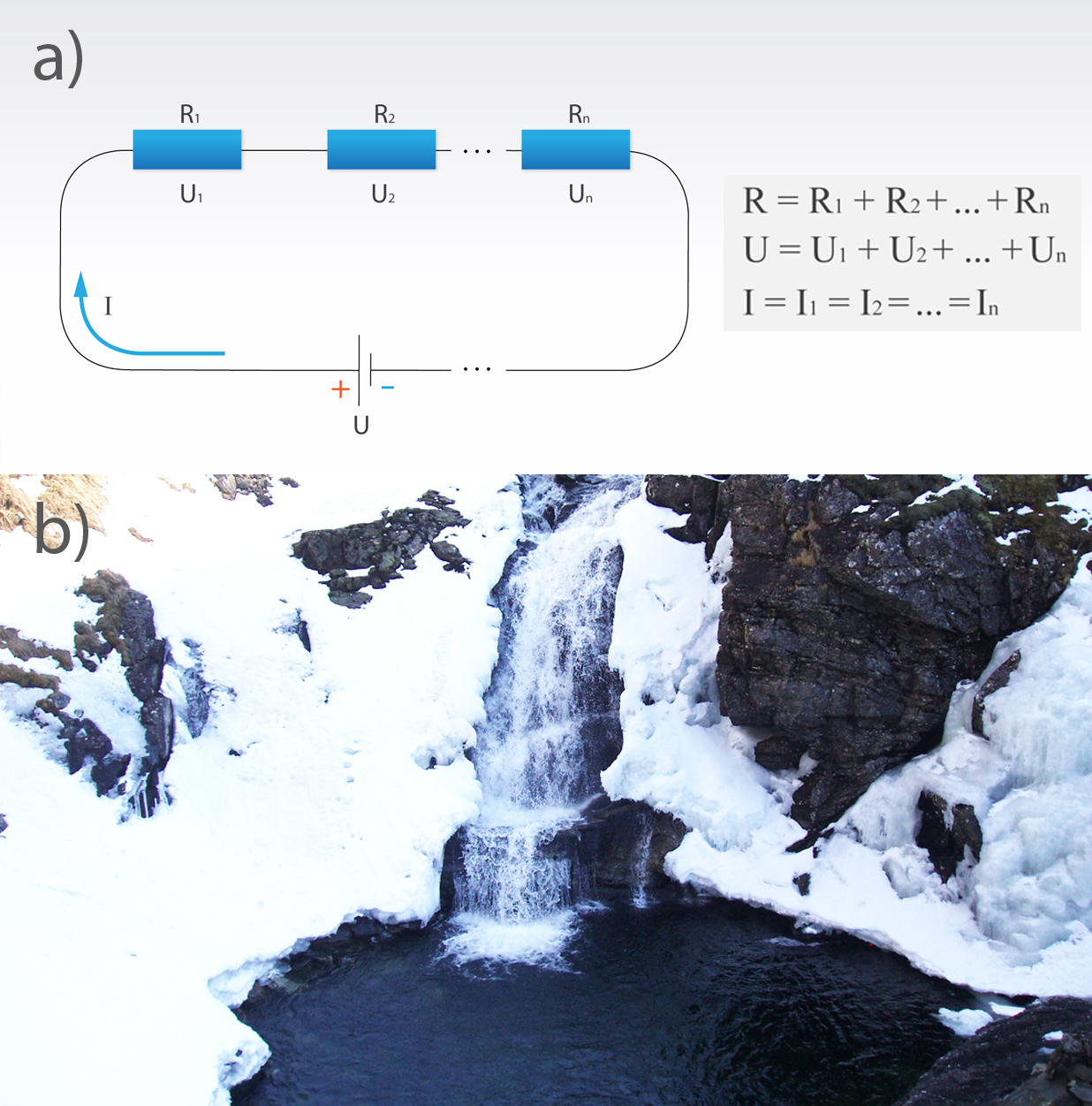
1.att. Virknes slēgums ar n patērētājiem
Ja spriegumam U ir pieslēgti divi virknē saslēgti patērētāji (2. att.) ar pretestībām R1 un R2, tad kopējā pretestība R = R1 + R2. Kā jau iepriekš minēts, visā ķēdē plūst viena un tā pati strāva, tādēļ strāvas stiprums I visā ķēdē ir vienāds: I = I1 = I2. Izmantojot Oma likumu U = IR, var iegūt sprieguma kritumus U1 un U2 katram patērētājam; to summa ir vienāda ar kopējo ķēdes spriegumu U = U1 + U2. Sprieguma kritums uz paterētāja ir proporcionāls tā pretestībai, tādēļ, jo lielāka ir virknē ieslēgta patērētāja pretestība, jo lielāku daļu no kopējā sprieguma krituma tas “savāc” sev (2. att.).
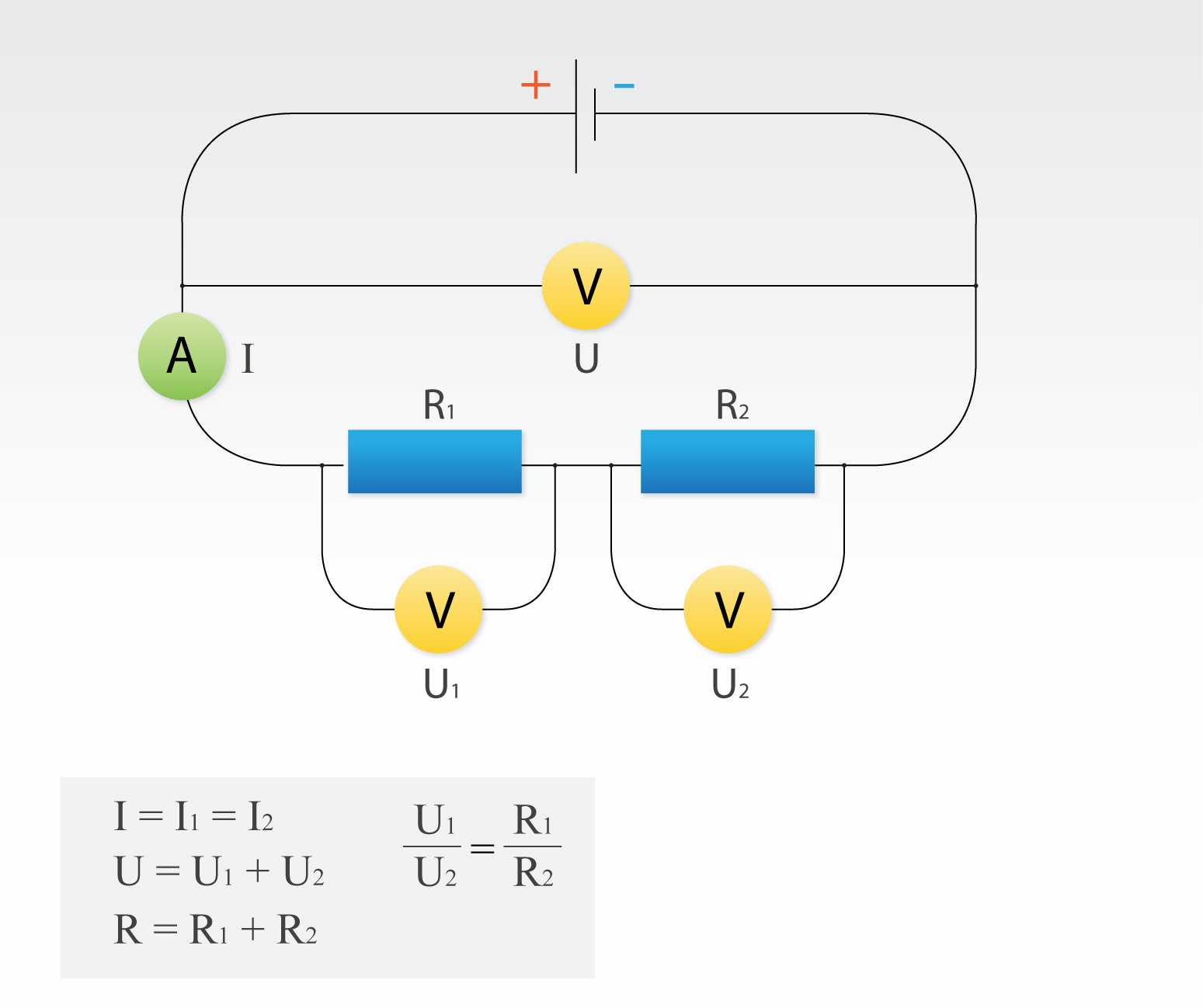
2.att. Virknes slēgums ar 2 patērētājiem
Ja n patērētājiem savieno attiecīgos izvadus un pēc tam tos pieslēdz elektroenerģijas avota poliem, veidojas sazarota ķēde (3. att. a). Šādu slēgumu sauc par paralēlo slēgumu. Paralēlajam slēgumam raksturīgi, ka kopējais sprieguma kritums U ir vienāds ar sprieguma kritumu uz katra atsevišķā patērētāja, proti, U = U1 = U2 = ... = Un, savukārt kopējais strāvas stiprums I veidojas no katram patērētājam cauri plūstošās strāvas stipruma: I = I1 + I2 + ... + In. Te atkal vietā līdzība ar upi – lai arī tā sadalās vairākos plūšanas kanālos, kopējais izplūdušā ūdens daudzums visos kanālos būs vienāds ar to, kas plūst cauri nesazarotai upei (3. att. b). Nedaudz neierasta situācija ir ar pretestībām, kurām darbojas apgriezto lielumu saskaitīšanas likums:, saskaitot katra patērētāja pretestības apgrieztos lielumus, iegūst ķēdes kopējās pretestības R apgriezto lielumu: 1 : R = 1 : R1 + 1 : R2 + ... + I : Rn.
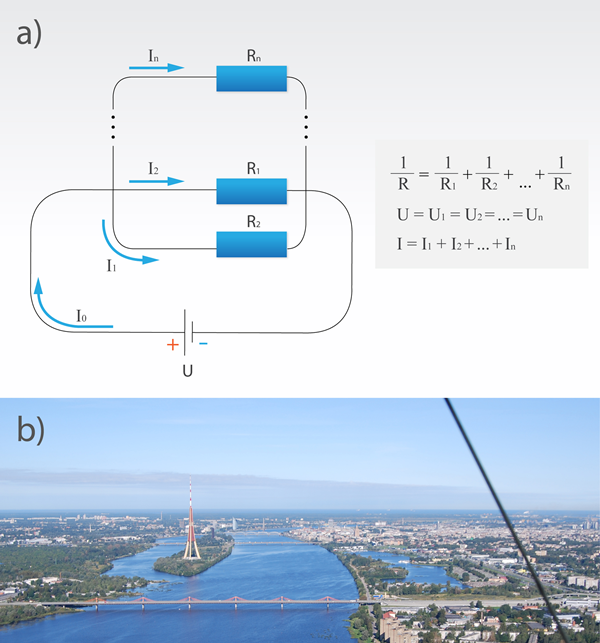
3.att. Paralēlais slēgums ar n patērētājiem
Saslēdzot paralēli divus patērētājus (4. att.) ar pretestībām R1un R2, tie abi ir pakļauti vienam un tam pašam sprieguma kritumam U = U1 = U2. Sazarotajā ķēdē kopējais strāvas stiprums I sadalās divās daļās: I = I1 + I2; tāpat ūdens plūsma sadalās ap upē esošu salu. Lai iegūtu slēguma kopējo pretestību, jālieto aprēķinu formula paralēlajam slēgumam: 1 : R = 1: R1 + I: R2. No šis formulas var iegūt izteiksmi R = R1R2 : (R1 + R2) (4. att.).
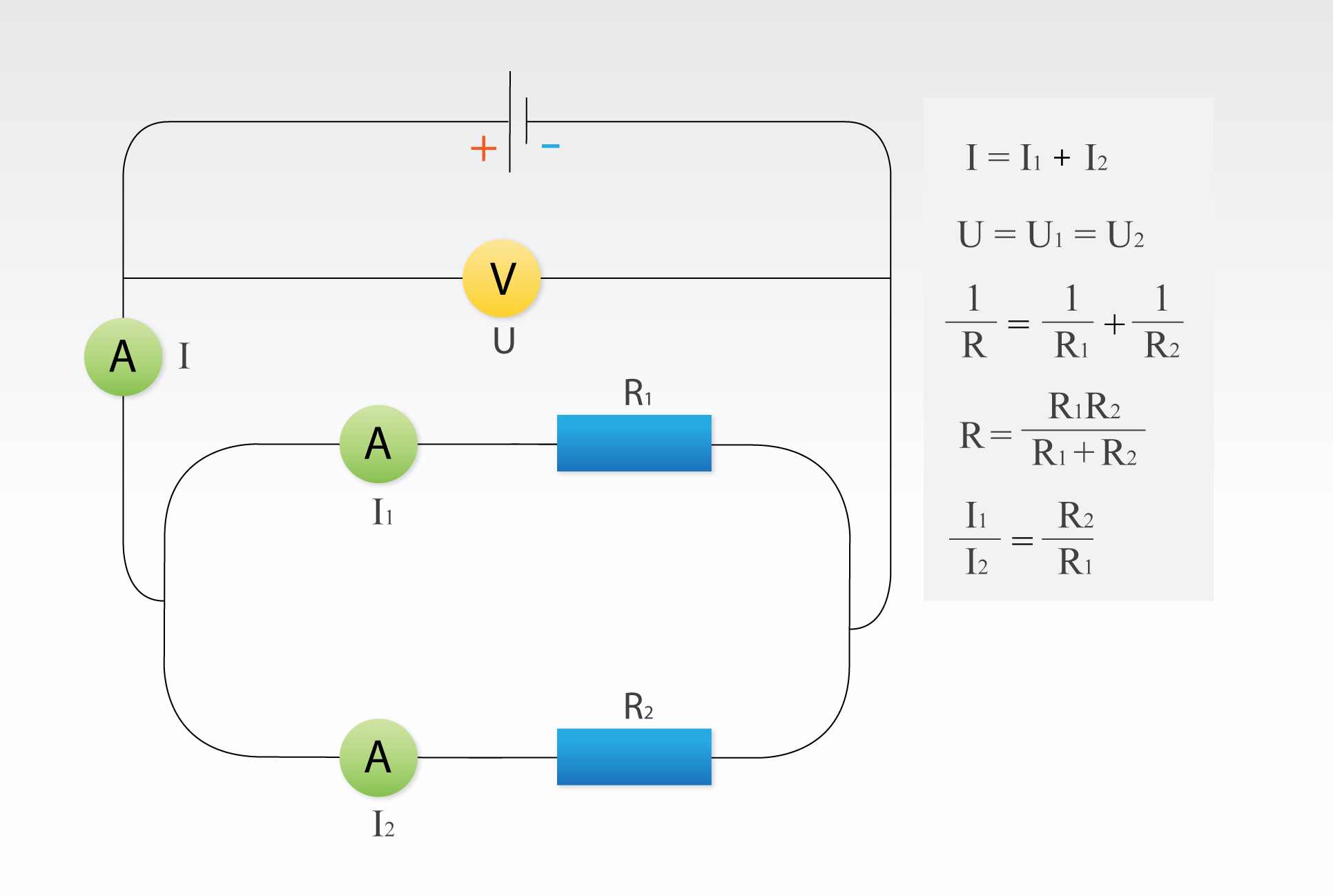
4.att. Paralēlais slēgums ar 2 patērētājiem
Ja patērētājus saslēdz tādā slēgumā, kurā ir elementi gan no virknes, gan paralēlā slēguma, tad to sauc parjaukto slēgumu. 5. attēlā redzams trīs patērētāju jauktā slēguma piemērs . Patērētāji R2 un R3 ir slēgti paralēli, tomēr šis paralēlais slēgums ir ieslēgts virknē kopā ar patērētāju, kura pretestība R1. Lai šādam slēgumam aprēķinātu, piemēram, kopējo pretestību R, vispirms būtu jāizrēķina pretestība R2,3, kas ir kopējā pretestība R2un R3paralēlajam slēgumam, un tad klāt jāpieskaita R1, jo R2,3 un R1slēgti virknē. Gala rezultātā R = R2R3 : (R2 + R3) + R1.
Apskaties DZM materiālu par elektriskajiem slēgumiem.
Izmanto simulāciju, lai saprastu, kā darbojas slēgumi!

5.att. Trīs patērētāju jauktais slēgums
Pievienojot trīs patērētāju virknes slēgumu spriegumam U (1. att.), ķēdē sāk plūst strāva ar stiprumu I. Strāvas stiprumu nosaka lādiņa lielums q, kas laika vienībā izplūst caur patērētājiem. Virknes slēgumam nav atzaru, tādēļ, pēc lādiņu nezūdamības likuma, caur visiem patērētājiem izplūst viens un tas pats lādiņš un līdz ar to strāvas stiprums visos patērētājos ir vienāds ar kopējo ķēdes strāvas stiprumu: I = I1 = I2 = I3. Katram patērētājam ir sava pretestība R1, R2un R3. Pēc Oma likuma var izrēķināt sprieguma kritumu katrā patērētājā: U1 = I · R1, U2 = I · R2un U3 = I · R3. Sprieguma kritumu patērētājos rada sprieguma avots, tādēļ kopējais sprieguma kritums vienāds ar visu atsevišķo patērētāju sprieguma kritumu summu: U = U1 + U2 + U3. Kopējā ķēdes pretestība no Oma likuma izsakāma kā R = U : I. Ievietojot U vietā iepriekš apskatīto summu, iegūst R = (U1 + U2 + U3) : I = U1 : I + U2 : I + U3 : I = R1 + R2 + R3. Rezultātā kopējā slēguma pretestība vienāda ar atsevišķo patērētāju pretestību summu.
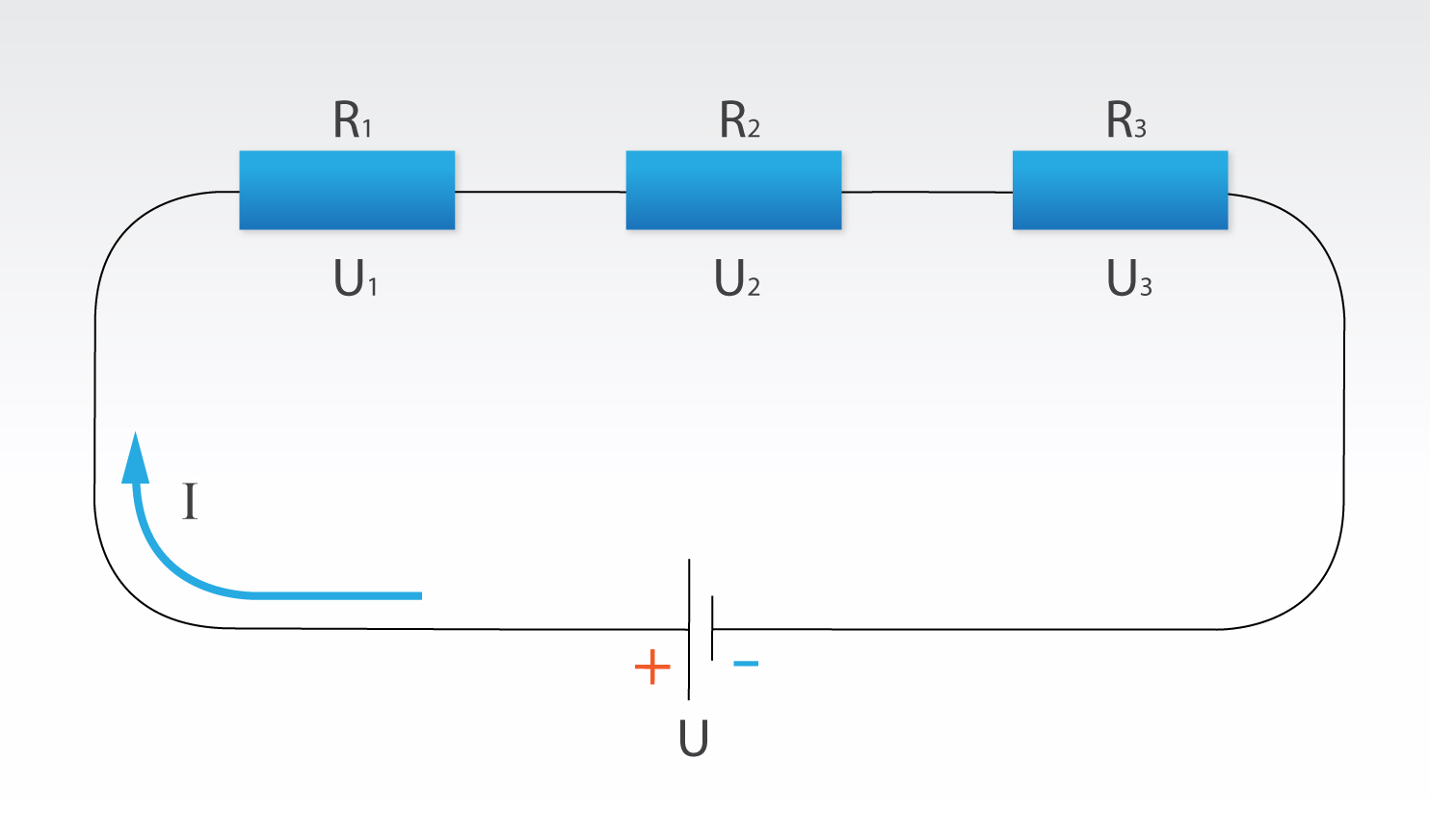
1.att. Virknes slēgums
Virknes slēgumam laba analoģija ir ūdens plūsma noslēgtā sistēmā. Ja noslēgtā cauruļu sistēmā plūst šķidrums, tad šaurāks caurules posms pielīdzināms lielākai elektriskajai pretestībai, bet platāks caurules posms – mazākai elektriskajai pretestībai (2. att.), jo ūdenim ir vieglāk plūst caur plašāku vietu. Taču, lai arī kāda būtu šo vadu posmu diametru attiecība, vienā laika vienībā caur tiem izplūst viens un tas pats ūdens daudzums, kas elektriskajā ķēdē pielīdzināms vienai un tai pašai lādiņu plūsmai laika vienībā jeb strāvas stiprumam I.

2.att. Virknes slēguma analoģija ar ūdens plūsmu caurulēs
Ar virknes slēgumu ļoti bieži nākas saskarties Ziemassvētku laikā (3. att. a), jo lielāka daļa Ziemassvētku lampiņu virtenes ir slēgtas pēc virknes slēguma shēmas. Tas tā tiek darīts, lai ietaupītu elektrības vadus, jo, ja lampiņas būtu slēgtas paralēli, tad uz katru mazo lampiņu vajadzētu vilkt divus elektrības vadus, bet virknes slēguma gadījumā, cauri visām lampiņām iet viens vads. Šādam tehnoloģiskajam risinājumam ir arī savas ēnas puses, jo tiklīdz kāda lampiņa izdeg, tā tiek pārtraukta strāva visa ķēdē, līdz ar to vienas lampiņas iziešana no ierindas var izraisīt tumšus Ziemassvētkus. Virknes slēgums sastopams arī mikroshēmas, kur noteiktu elektrisko īpašību iegūšanai, ķēdes elementi slēgti virknē (3. att. b). I.
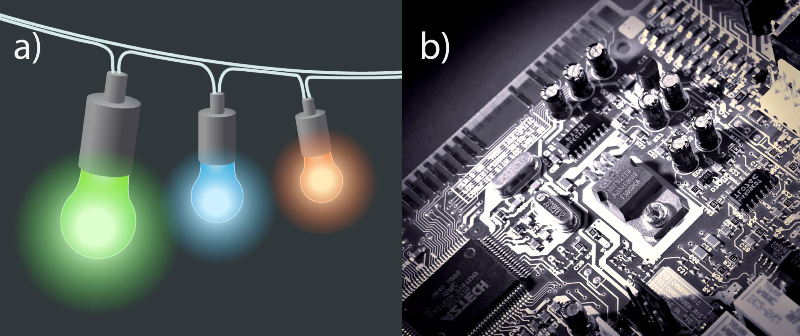
3.att. Virknes slēguma pielietojumi
Virknes slēgumam nav sazarojumu, tādēļ strāvas stiprums visā ķēdē ir viens un tas pats. Ja ķēde sazarojas, tad sadalās arī strāvas stiprums. Ja ķēdes posms, kurā plūst strāva I, sadalās divās daļas, tad arī strāvas stiprums I sadalās divās daļās I1un I2tā, ka I1 + I2 = I(4. att. a). Līdzīgi notiek arī dabā ar upes tecējumu. Upei sadaloties divās daļās, tajā plūstošais ūdens daudzums arī sadalās divās daļās (4. att. b).
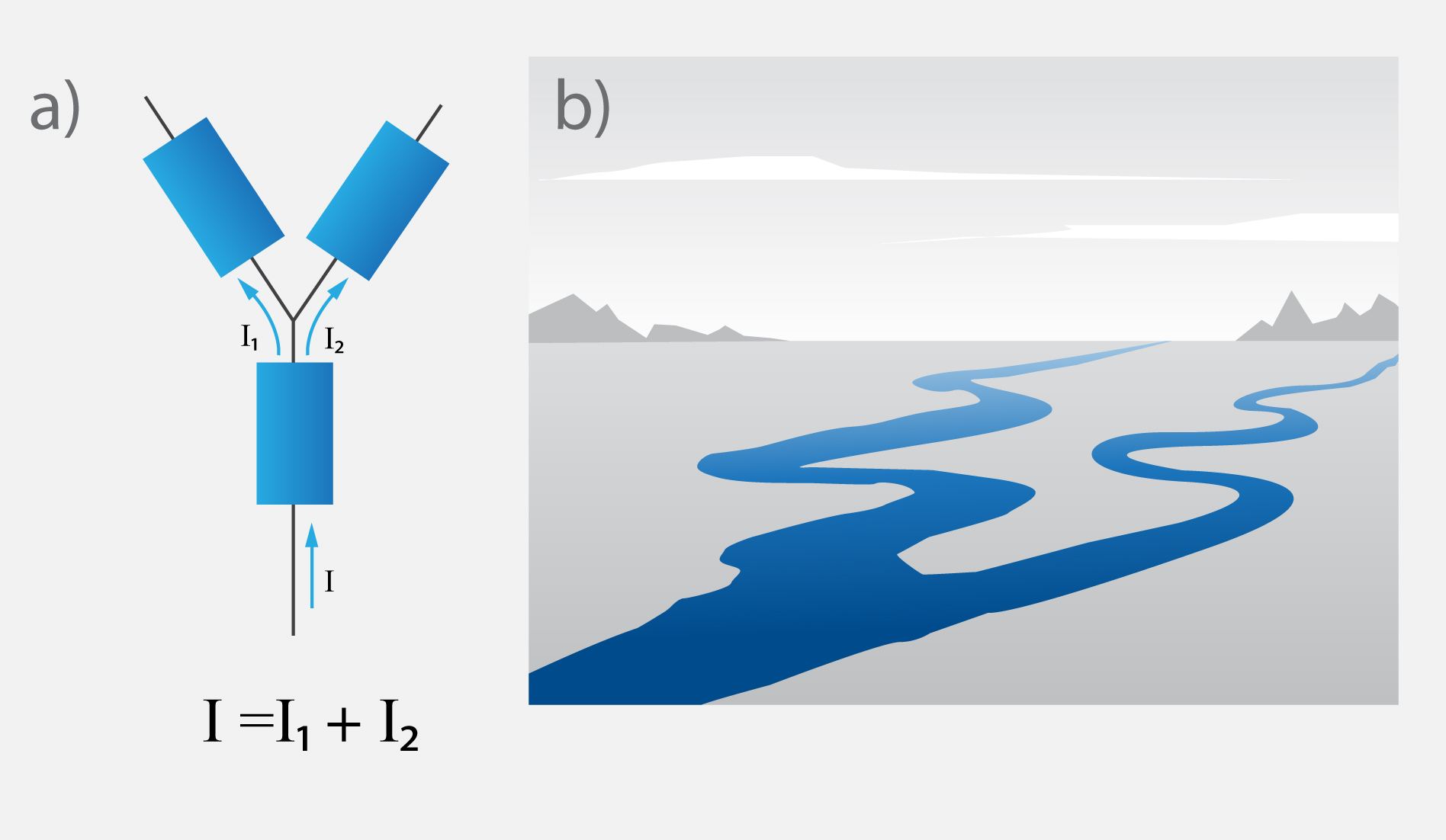
4.att. Strāvas stipruma sazarošanās un tās analoģija ar upes tecējumu
Atšķirībā no virknes slēguma paralēlajam slēgumam ir raksturīgi sazarojumi. Ja paralēli slēgti trīs patērētāji ar pretestībām R1, R2un R3, tad kopējais strāvas stiprums I sazarojuma vietā sadalās trīs strāvas plūsmās I1, I2un I3, turklāt I = I1 + I2 + I3. Zinot pretestību un kopējo ķēdes spriegumu U, var aprēķināt strāvas stiprumu katrā patērētājā: I1 = U : R1, I2 = U : R2, I3 = U : R3. No šīm sakarībām izriet, ka paralēlajā slēgumā caur patērētāju ar lielāku pretestību plūst mazāka stipruma strāva. Izmantojot Oma likumu pilnai ķēdei R = U : I un izsakot no tā apgriezto lielumu pretestībai, iegūst 1 : R = I : U. Ņemot vērā, ka I = I1 + I2 + I3un ievietojot katra strāvas stipruma izteiksmes, iegūstam 1 : R = (I1 + I2 + I3) : U = I1 : U + I2 : U + I3 : U = 1 : R1 + 1 : R2 + 1 : R3; tā ir ķēdes kopējās pretestības izteiksme paralēlajam slēgumam. Ja paralēlajā slēgumā ir saslēgti n vienādas pretestības patērētāji, tad kopējā pretestība R = Ri : n, kur Riir viena patērētāja pretestība.
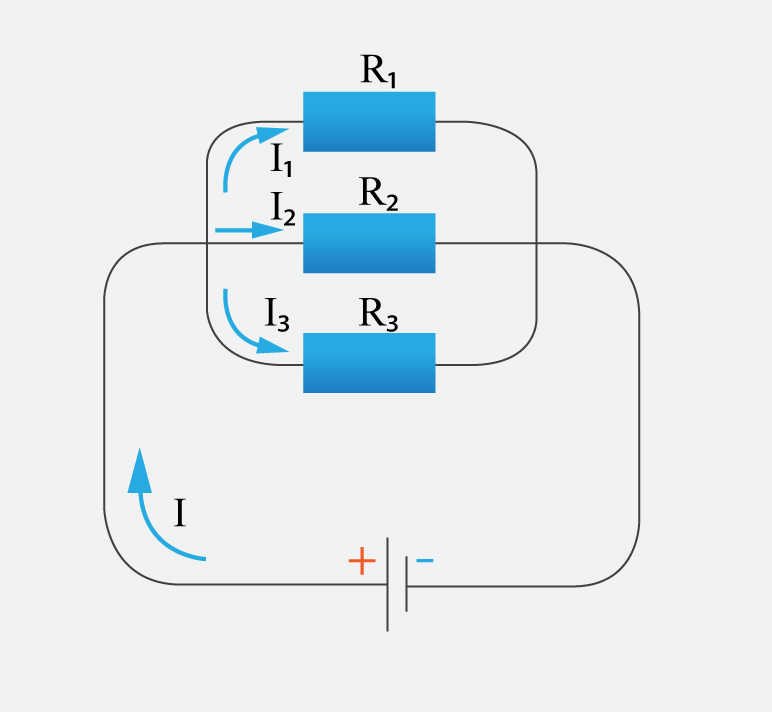
5.att. Paralēlais slēgums
Arī paralēlajam slēgumam ir analoģija ar ūdens plūsmu caur noslēgtu cauruļu sistēmu. Šajā gadījumā cauruļu sistēma sadalās divos zaros ar atšķirīgiem caurules diametriem (6. att.). Šaurākā caurule atbilst lielākajai elektriskajai pretestībai R1, bet platākā caurule – mazākajai elektriskajai pretestībai R2. Ūdens plūsma labprātāk plūst pa resnāko cauruli, jo tā mazāk pretojas plūdumam. Tādēļ arī paralēlajā slēgumā lielāks strāvas stiprums plūst caur patērētāju ar zemāko pretestību.
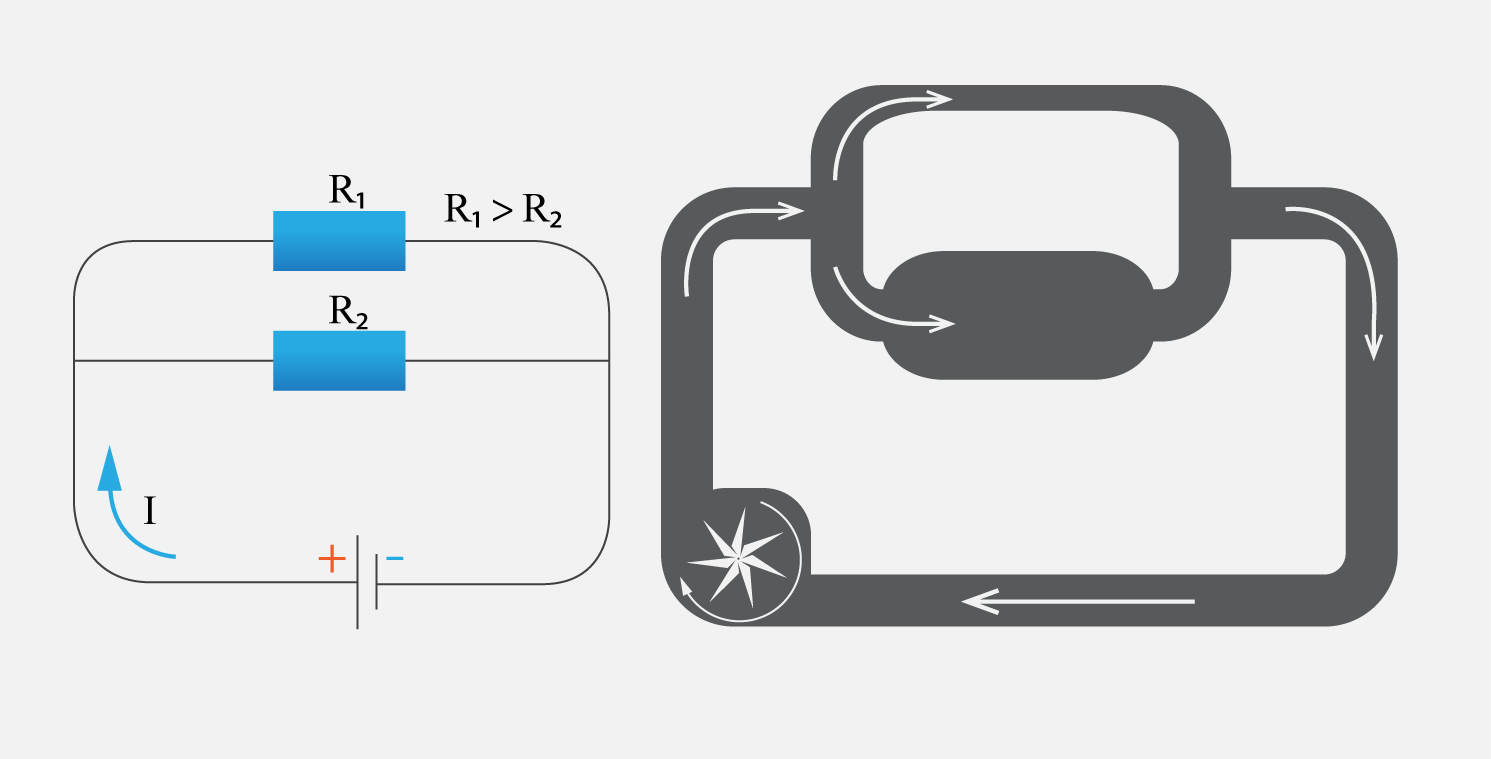
6.att. Paralēlā slēguma analoģija ar ūdens plūsmu caurulēs
Ar paralēlo slēgumu mēs atklāti sastopamies daudz biežāk nekā ar virknes slēgumu. Piemēram, automašīnu elektriskās sistēmas ir ļoti sarežģītas (7. att. a), it sevišķi mūsdienās, kad elektrība darbina faktiski visu. Taču, ja šo sistēmu uzmanīgi izpētītu, tad atklātos, ka lielākā daļa elektronisko komponenšu automašīnā ir slēgtas paralēli. Līdz ar to, ja brauc ar automašīnu lietainā un tumšā laikā, tad zini, ka ieslēgtās tuvās gaismas, gabarītlukturi, miglas lukturi, logu tīrītāji un paneļa apgaismojums (7. att. b) automašīnas elektriskajā sistēmā ir saslēgti paralēli.

7.att. Paralēlā slēguma lietojums automašīnās
Lielākajā daļā mājsaimniecību elektriskais tīkls sastāv no vienas fāzes, kas būtībā nozīmē to, ka mājai elektrību pievada caur diviem vadiem (8. att. a). Tādēļ, ieejot savā istabā un ieslēdzot dažādus elektroenerģijas patērētājus, piemēram, galda lampu, datoru, telefona lādētāju un istabas apgaismoju (8. att. b), tie visi visticamāk atrodas paralēlajā slēgumā.

8.att. Paralēlā slēguma lietojums mājas apstākļos
Ja slēgums sastāv gan no paralēli, gan virknē slēgtām komponentēm, tad kopējās pretestības aprēķināšanas nolūkā ķēde ir pakāpeniski jāvienkāršo, aizstājot vairāku pretestību slēgumus ar vienu ekvivalentu pretestību. 1. attēlā ir jauktā slēguma, kas sastāv no septiņām pretestībām, piemērs. Šī slēguma kopējo pretestību R aprēķina četros soļos:
1) R2, R3 un R5 kopējo pretestību aprēķina pēc 1. soļa beigu daļā iegūtās formulas un aizstāj ar atbilstošu pretestību R2,3,5, bet R6 un R7 kopējo pretestību rēķina, izmantojot virknes slēguma sakarības, un pēc tam aizstāj šīs divas pretestības ar ekvivalentu pretestību R6,7.
2) Tālāk pēc paralēlā slēguma sakarībām tiek aprēķināta R4un R2,3,5 kopēja pretestība un slēguma aizstāta ar R2,3,4,5 pretestību.
3) Šajā solī tiek aprēķināta R1, R2,3,4,5 un R6,7 kopējā pretestība, izmantojot virknes slēguma sakarības, un beigās šīs trīs pretestības tiek aizstātas ar kopējo pretestību R.
4) Tagad atliek vien priecāties, ka septiņu pretestību vietā esam ieguvuši vienu pretestību, kas atbilst kopējai slēguma pretestībai R.
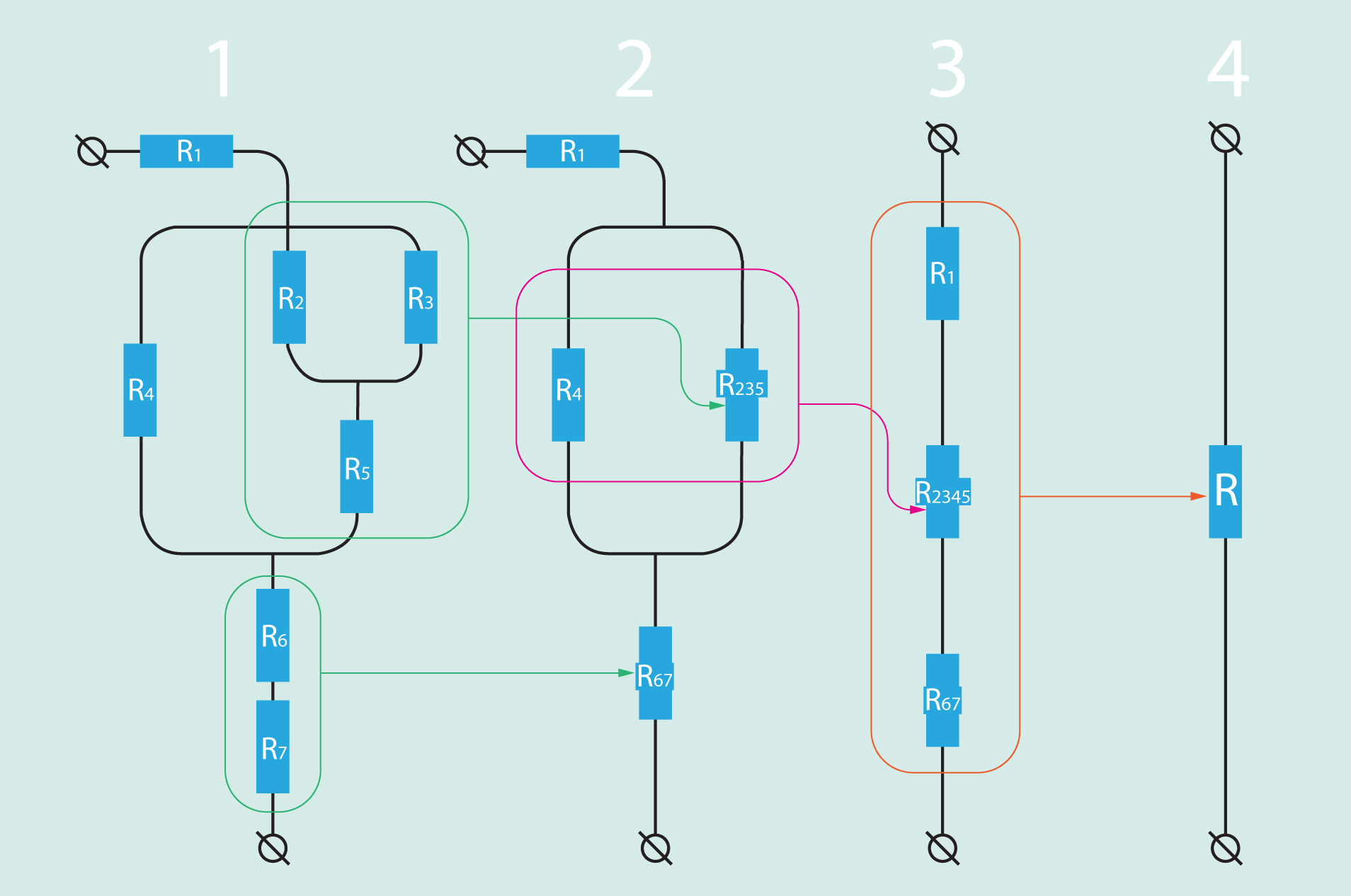
1.att. Jauktā slēguma pretestības aprēķināšana
Jauktajam slēgumam ir līdzība ar ūdens plūsmu sazarotā kaskādē. Elektriskajā ķēdē, kurā jauktajā slēgumā saslēgtas četras pretestības (2. att. a), strāvas plūsma sadalās līdzīgi kā ūdens plūsma kaskādē, kas attēlota blakus (2. att. b). Dažādie augstumi ūdens kaskādē h1, h2, h3 un h4 atbilst dažādām patērētāju potenciālu starpībām U1, U2, U3 un U4, savukārt tievākas vai resnākas caurules atbilst lielākai vai mazākai patērētāja pretestībai.
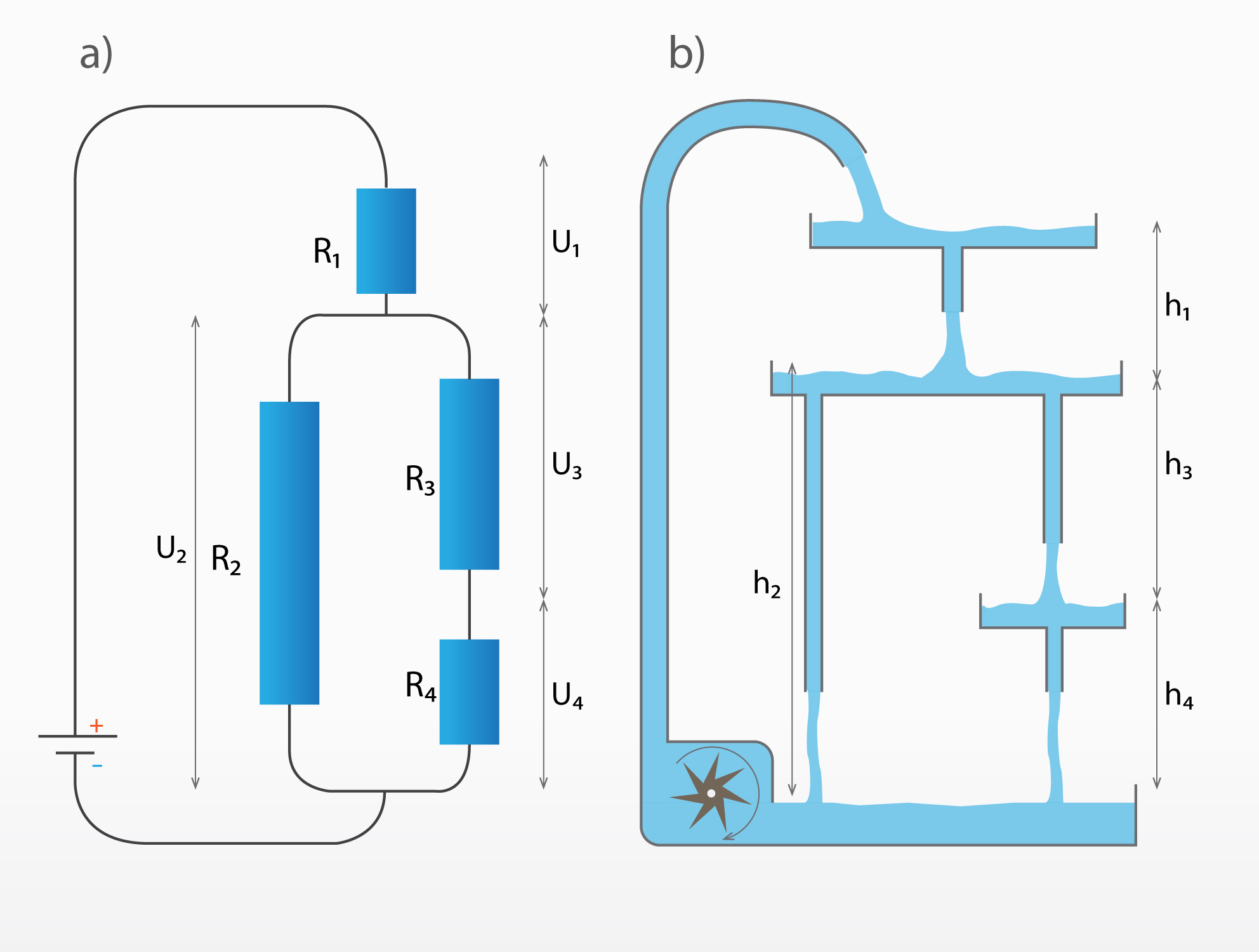
2.att. Jauktā slēguma ūdens plūsmas ekvivalents
Līdz šim tika apskatīti patērētāji, kuriem ir nemainīga elektriskā pretestība. Izmantojot šādus elementus, elektriskajās ķēdē ir ierobežotas iespējas veikt jebkādas parametru izmaiņas. Tādēļ tiek lietoti patērētāji ar maināmu pretestību, ko sauc par reostatiem (3. att. a). Reostata galvenās sastāvdaļas ir materiāls ar tam piemītošu elektrisko pretestību un slīdkontakts, kas nosaka to, cik lielai pretestību radošā materiāla daļai ķēdes strāva plūdīs cauri (3. att. b).
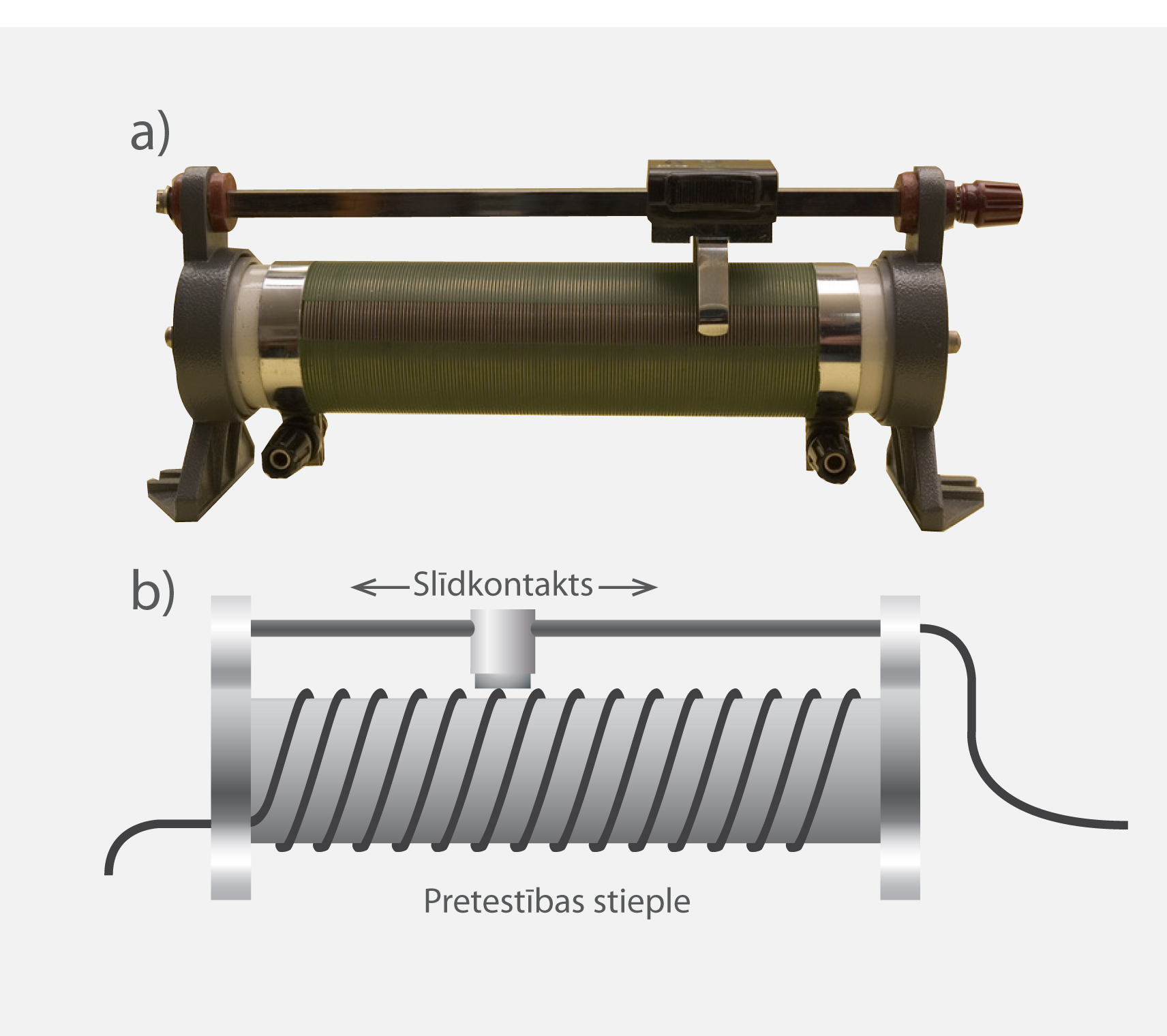
3.att. Reostats
Ja reostatu ieslēdz ķēdē (4. att. a), tad, pārvietojot tā slīdkontaktu, ir iespējams mainīt strāvas stiprumu, kas plūst ķēdē. No Oma likuma I = U : R varam secināt: jo lielāku pretestību uzstāda reostatam, jo vājāka strāva plūst cauri ķēdei. Ja rezistoru ieslēdz ķēdē tā, kā parādīts 4. att. b, tad šādā gadījumā, pārbīdot slīdkontaktu, tiek mainīts spriegums UR (4. att. b). Šādu ierīci sauc par potenciometru, un tā ir domāta sprieguma regulēšanai elektriskajās shēmās (4. att. c).
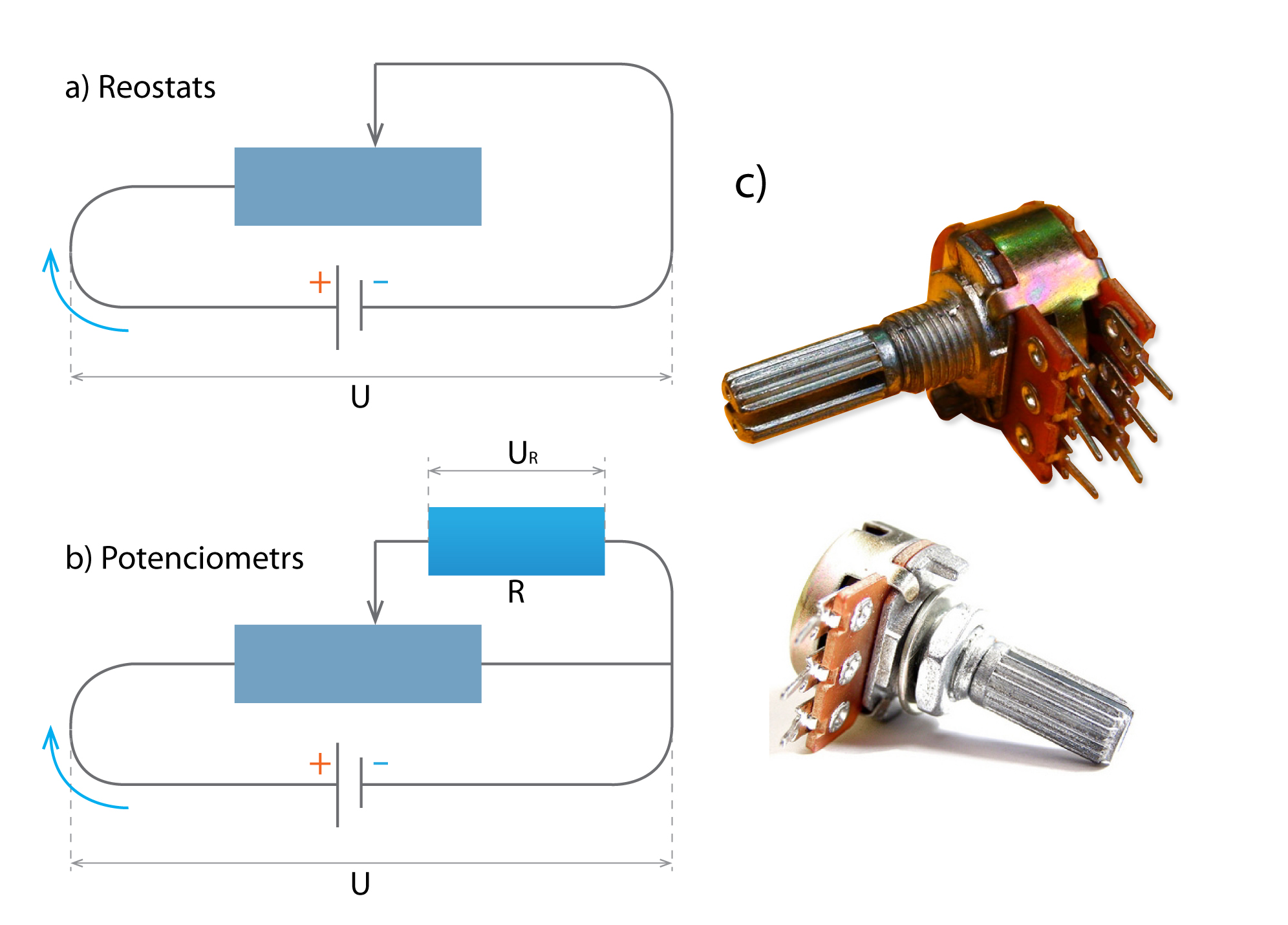
4.att. Reostats un potenciometrs
Potenciometram elektronikā ir daudzveidīgs lietojums. Pirmkārt, dažādām audio aparatūrām ar potenciometru palīdzību regulē skaļumu (5. att. a) un ne tikai, arī citi skaņas parametri pakļaujas potenciometra regulējumam, tādēļ audio pultīs to lieto plaši (5. att. b). Potenciometrus izmanto arī automašīnu elektrosistēmā, lai regulētu paneļa apgaismojuma spilgtumu. Ar potenciometru regulē spilgtumu un kontrastu arī televizoros (5. att. c).

5.att. Potenciometra lietošanas veidi
Pastāv slēgumi, kurus nevar sadalīt vienkāršākos virknes un paralēlos slēgumos. Tāds, piemēram, ir tilta slēgums, kurā noteiktā secībā savirknētas piecas pretestības (6. att.) Ņemot talkā Oma likumu, U2 = I2R2 un U3 = I3R3, tilta slēguma funkcionalitāte atklājas faktā, ka ir iespējams atrast tādas pretestību R1, R2, R3 un R4 kombinācijas, ka strāva caur R5 neplūst. Tādā brīdī tiltu sauc par līdzsvarotu. Līdzsvara gadījumā potenciālu starpība starp a un b punktiem ir nulle, līdz ar to spriegumi U1 un U4, kā arī U2 un U3 ir vienādi (6. att.). Izsakot spriegumus U1 un U4, iegūst U1 = I2R1, U4 = I3R4. Ja spriegumu attiecībā U2 : U1 = U3 : U4 ievieto izteiktos spriegumus, iegūst pretestību attiecību R2 : R1 = R3 : R4 no kuras var izteikt, piemēram, pretestību R4 = R1R3 : R2.
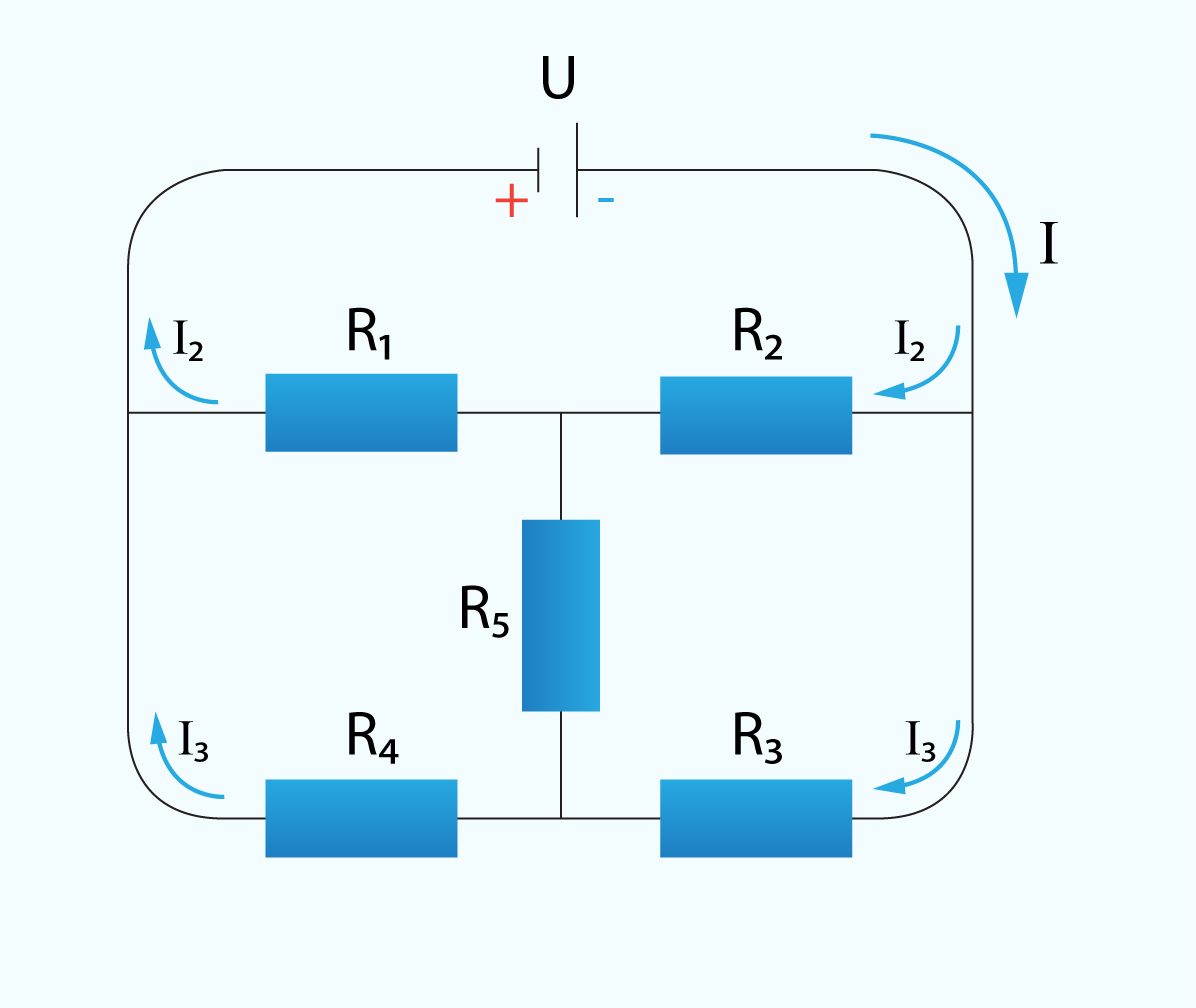
6.att. Tilta slēgums
Ja tilta slēgums (6. att.) tiek modificēts tā, ka R5 pretestības vietā ievieto voltmetru, R3 vietā ievieto rezistoru, bet R4 vietā ieliek nezināmu pretestību X (7. att.), tad, mainot R3 pretestību un atrodot stāvokli, kad voltmetrs rāda nulles spriegumu (līdzsvarots tilts), nezināmo pretestību var aprēķināt: X = R1R3 : R2.
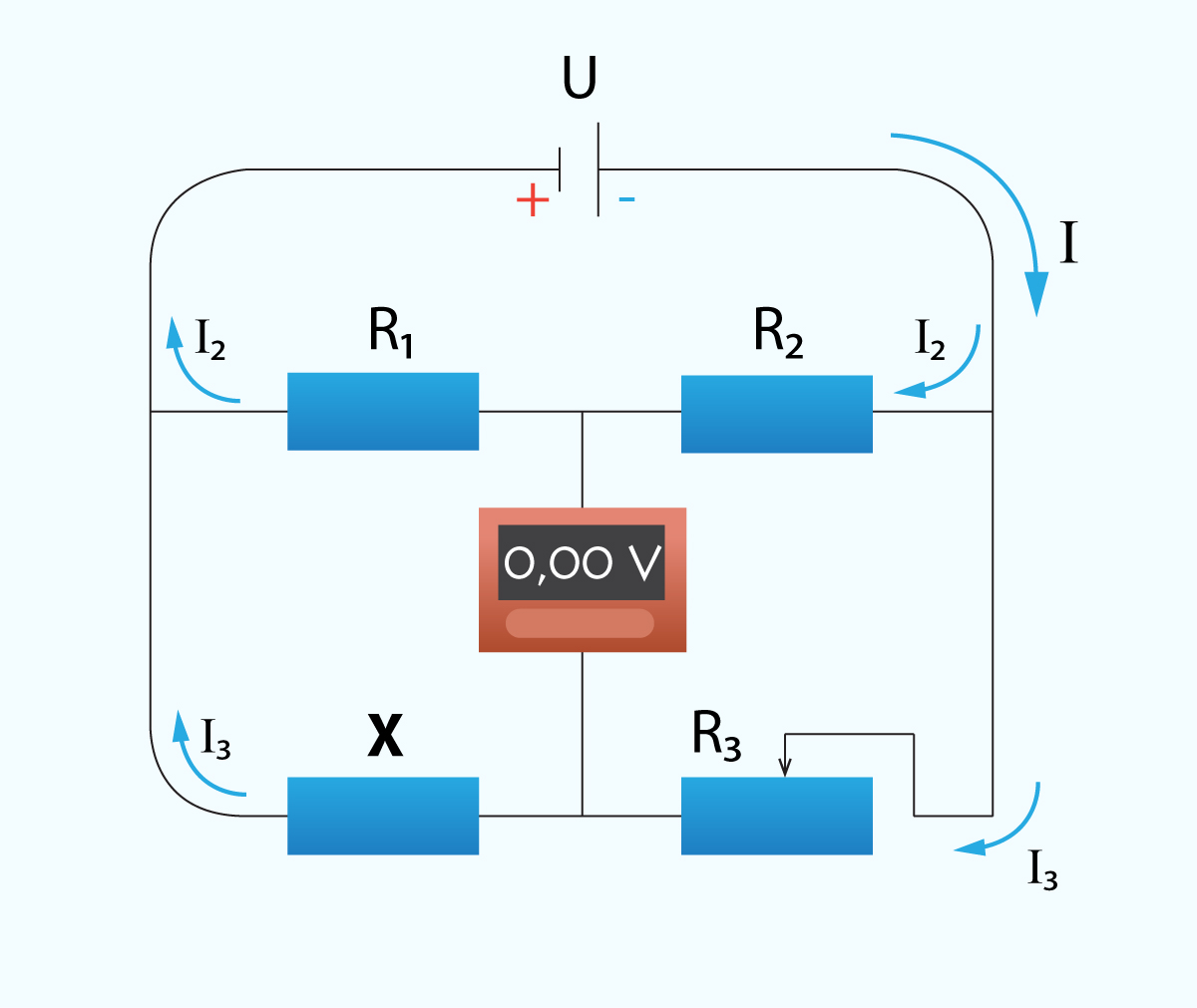
7.att. Mērīšanai pielāgots tilta slēgums