Fizmix Mehānisko svārstību un viļņu sadaļā par viļņu īpašībām tika apskatītas tādas mehānisku viļņu īpašības kā interference, difrakcija un Doplera efekts. Mehāniskais vilnis ir vides daļiņu mehānisko svārstību izplatīšanās elastības spēka ietekmē (1. att. a). Lai gan gaisma ir elektromagnētiskais vilnis, kurā vides daļiņu vietā svārstās elektriskais un magnētiskais lauks (1. att. b), arī šiem viļņiem piemīt daudzas mehānisko viļņu īpašības, piemēram, interference.
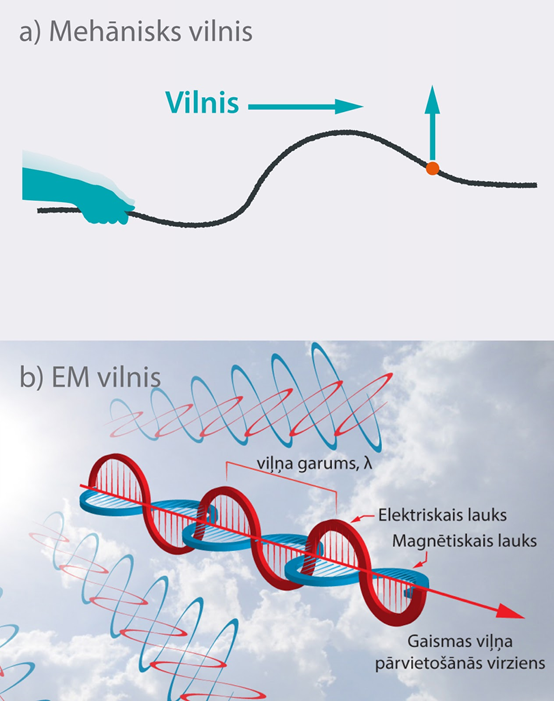
1.att. Mehānisks un EM vilnis
Par interferenci sauc viļņu pārklāšanos vidē. Pārklājoties diviem vai vairākiem viļņiem, summējas to svārstību amplitūdas. Kopējā svārstību amplitūda var būt gan mazāka (2. att. a), gan arī lielāka (2. att. b) par atsevišķo viļņu svārstību amplitūdu. Mazākas amplitūdas gadījuma interferenci sauc par destruktīvu (2. att. a), bet lielākas amplitūdas gadījumā – par konstruktīvu (2. att. b).
Noskaties video no macibuvideo.lv par difrakciju (iekļauj interferenci).
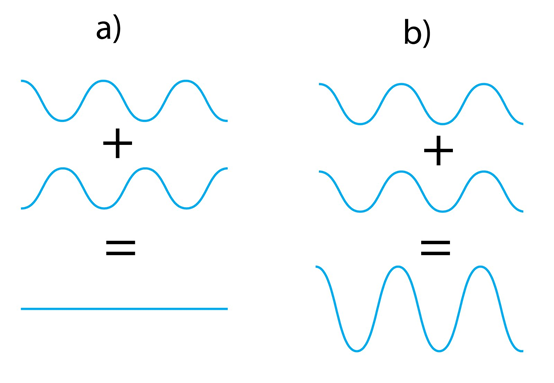
2.att. Destruktīvā un konstruktīvā interference
Lai, pārklājoties gaismas viļņiem, veidotos interferences aina, šiem viļņiem ir jābūt savstarpēji koherentiem (tādiem, kuriem viļņu procesu norises saskaņotas laikā) (3. att. a). Viļņi ir koherenti tad, ja ir spēkā īpaši nosacījumi. Pirmkārt, viļņu svārstību frekvencēm ir jāsakrīt, tātad viļņiem ir jābūt monohromatiskiem. Otrkārt, viļņu svārstību fāzei ir jābūt nemainīgai. Var gadīties, ka viļņiem frekvence ir vienāda, bet fāžu starpība mainās, tādā gadījumā viļņi nav koherenti (3. att. b). Treškārt, abiem viļņiem ir jāsakrīt elektriskā lauka svārstību virzienam telpā. Gaismas vilnis ir šķērsvilnis, kurā elektriskais lauks svārstās perpendikulāri izplatīšanās virzienam, līdz ar to ir iespējami daudz un dažādi svārstību virzieni. Lai divi viļņi būtu koherenti, šiem svārstību virzieniem jāsakrīt.
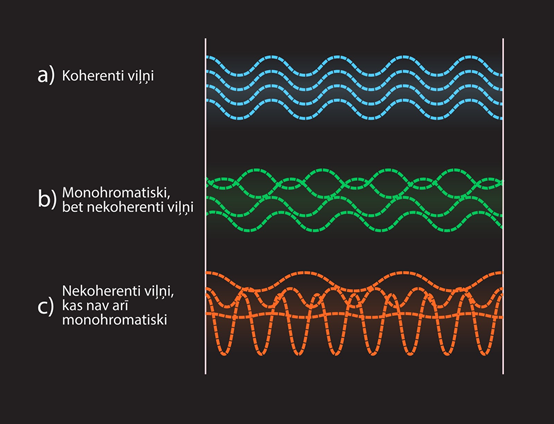
3.att. Koherentu un nekoherentu viļņu piemēri
Ja kādā punktā pārklājas divi koherenti gaismas viļņi, tad atkarībā no viļņu fāžu nobīdes ir iespējami dažādi punkta apgaismojumi. Fāžu nobīdi var noteikt, ja apskata viļņu ģeometrisko ceļu starpību. Piemēram, ja divi koherenti viļņi ceļo no dažādām vietām uz punktu M (4. att. a), tad viens vilnis līdz punktam noiet attālumu x1, bet otrs vilnis – attālumu x2 (4. att. a). Noietā ceļa starpība vienāda ar Δx = |x2 - x1|. Modulis tiek lietots tādēļ, ka nav svarīgi, kura viļņa noietais ceļš ir garāks. Ja Δx ir vienāds ar gaismas viļņa garuma daudzkārtni kλ, kur k = 0, 1, 2, 3, … , tad izpildās interferences maksimuma nosacījums (4. att. a) un viļņu sastapšanās punkts ir maksimāli gaišs. Ja Δx ir vienāds ar nepāra skaitu pusviļņu garumu jeb Δx = (2k + 1)λ : 2, kur k = 0, 1, 2, 3, tad izpildās interferences minimuma nosacījums (4. att. b) un punkts ir maksimāli tumšs. Ja neizpildās ne minimuma, ne maksimuma nosacījums, tad punkta apgaismojums ir kaut kas starp maksimālo un minimālo vērtību.
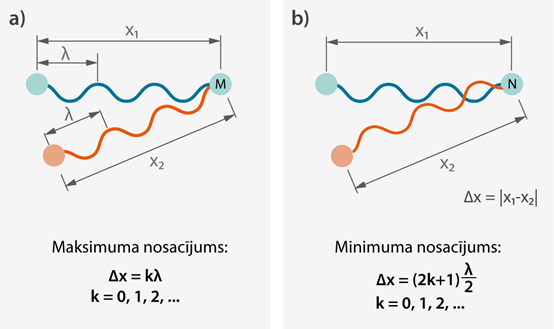
4.att. Interferences maksimuma un minimuma nosacījums
Divu punktveida gaismas avotu maksimumu un minimumu nosacījumi veido tādu struktūru, kāda redzama 5. attēlā. Tumšajās vietās izpildās minimuma nosacījumi, bet gaišās vietiņas ir atvēlētas reģioniem, kuros izpildās interferences maksimuma nosacījums.
Aplūko materiālu mar gaismas interferenci!
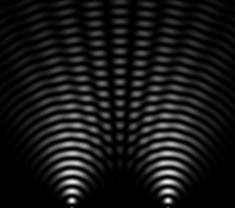
5.att. Divu punktveida gaismas avotu interference
Lai iegūtu interferences ainu, ir jāiegūst koherentas gaismas stari. No parastas lampiņas nākoši gaismas stari nav koherenti, jo lampiņa gaismas viļņus izstaro haotiski visos virzienos (1. att. a). Tomēr no šīs lampiņas izstarotajiem viļņiem ir iespējams iegūt koherentus gaismas starus. Sadaļā par Gaismas izplatīšanos 3. solī tika apskatīts Heigensa princips – “katru jau esošas viļņu frontes punktu var uzskatīt par jaunu punktveida viļņu avotu”. Tomēr šajā sadaļā netika pieminēta nozīmīga jauno punktveida avotu īpašība, proti, ka tie ir koherentu viļņu avoti. Līdz ar to, ja mēs lampiņas ceļā noliekam vienu spraugu, iegūstot punktveida gaismas avotu, bet pēc tam šī punktveida avota ceļā noliekam divas tuvu esošas spraugas, tad šīs spraugas kļūst par koherentu viļņu avotiem (1. att. b) un šo avotu radītie viļņi pārklājoties veido interferences minimuma un maksimuma nosacījumus (1. att. c). Fizikā tās sauc par Janga dubultspraugām.
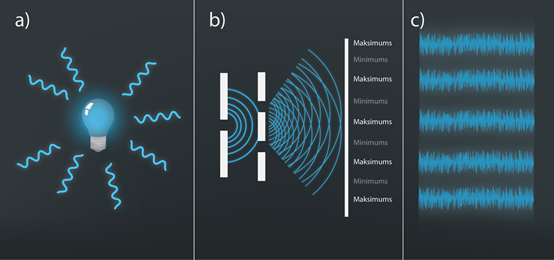
1.att. Nekoherenti un koherenti gaismas avoti
Ja uz Janga dubultspraugām krīt baltā gaisma, tad interferences ainā šī baltā krāsa sadalās spektrā (2. att. a). Tas ir tādēļ, ka katras krāsas gaismai ir savs viļņu garums un līdz ar to savi minimuma un maksimuma nosacījumi. Ja uz dubultspraugu krīt tikai vienas krāsas gaisma, piemēram, zaļa, tad arī interferences ainu veido tikai šī krāsa (2. att. b).
Aplūko sīklietotni par Junga dubultspraugas eksperimentu!

2.att. Baltās un zaļās gaismas interferences ainas
Interferences ainu var iegūt arī tad, ja gaisma spīd uz kādu plānu kārtiņu, piemēram, ziepjūdens plēvīti (3. att.). Attēlā redzams, ka gaismas stars krīt uz ziepjūdens plēvīti un viena daļa no gaismas atstarojas, bet otra lūst un nonāk ziepjūdens plēvītē. Pēc vēl vienas atstarošanās pret ziepjūdens plēvītes otru virsmu un vēl vienas lūšanas ziepjūdens plēvītes virspusē satiekas divi koherenti gaismas stari 1 un 2 (3. att.). Tā kā gaismas stars 2 ir nogājis garāku ceļu, tad starp staru 1 un 2 ir izveidojusies gājienu starpība un ir iespējams novērot interferences ainu. Pēc vairākkārtējas atstarošanās arī otrā ziepjūdens plēvītes pusē izveidojas interferences ainas novērošanai labvēlīgi apstākļi, jo tur nonāk koherenti gaismas stari 3 un 4 (3. att.).
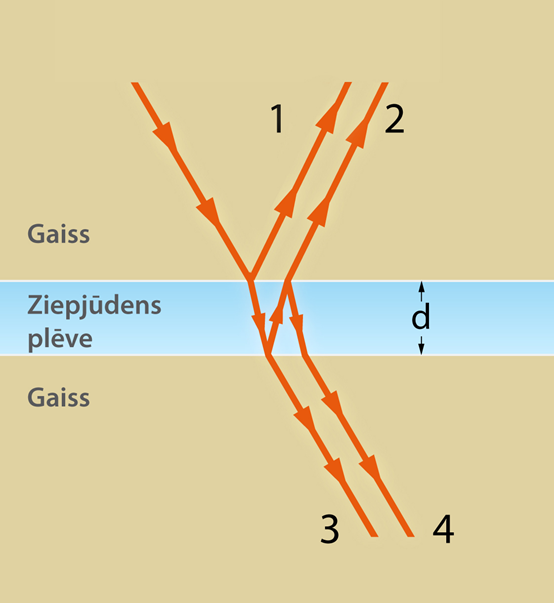
3.att. Interference plānā kārtiņā
Interferences ainu ziepjūdens plēvītē iespējams apskatīt, spēlējoties ar ziepjūdens burbuļiem. Pret ziepjūdens plēvīti atstarojas un tajā lūst apkārtējās gaismas stari un acij paveras krāšņa interferences aina (4. att. a). Par plāno kārtiņu, kurā var notikt gaismas interference, labi kalpo arī eļļas slānītis. Ja kādu eļļas lāsi iepilina ūdens rezervuārā vai arī gadās izliet eļļu uz mitras virsmas, tad šis eļļas pleķis, Saules apspīdēts, zaigo visās varavīksnes krāsās (4. att. b), un to izraisa tieši interference plānā kārtiņā.

4.att. Ziepjūdens burbuļa un eļļas kārtiņas interferences ainas
Interesanta interferences aina veidojas tad, ja uz plakanas virsmas novieto lēcu ar lielu liekuma rādiusu (5. att. a). Ja lēca ir kvalitatīva, tad interferences aina sastāv no koncentriskiem riņķiem (5. att. b). Ņūtona gredzeni veidojas, interferējot gaismas stariem, no kuriem viens atstarojas pret lēcu, bet otrs pret plakano virsmu, tādējādi veidojot gājienu starpību (5. att. a).
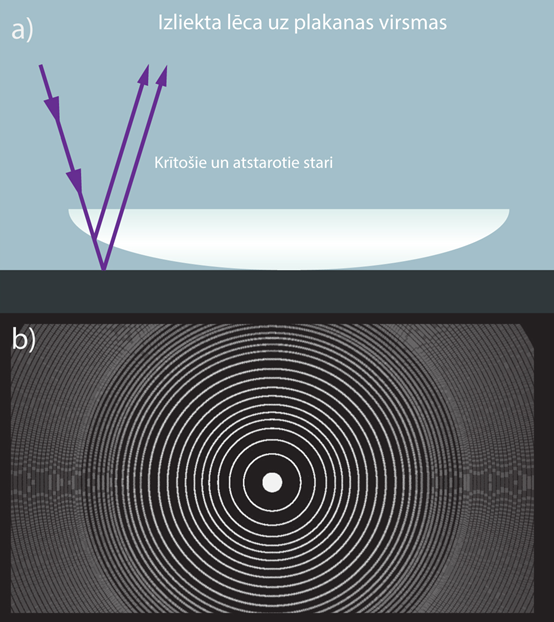
5.att. Ņūtona gredzeni no kvalitatīvas lēcas
Ņūtona gredzenus var izmantot, lai noteiktu lēcas kvalitāti. Ja Ņūtona gredzeni veidojas apaļi un koncentriski (5. att. b), tad lēca ir perfekti sfēriska, bet, ja Ņūtona gredzeni ir kropļoti (6. att.), tad lēcai ir novirzes no sfēriskas formas.
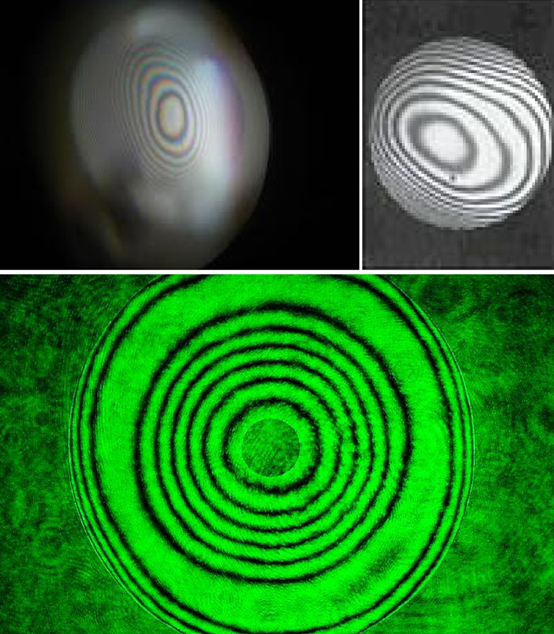
6.att. Ņūtona gredzeni no nekvalitatīvām lēcām
Ziepju burbulis un eļļas kārtiņa (4. att.) atmirdz visās varavīksnes krāsās tādēļ, ka uz tās virsmas notiek dažādu krāsu gaismas viļņu konstruktīvā interference. Atstarotajā gaismā dominē tā krāsa, kurai izpildās interferences maksimuma nosacījums, un, tā kā ziepju burbulim un eļļas kārtiņai dažādās vietās ir atšķirīgs biezums, tad dažādās vietās mainās atstarotās gaismas viļņu garums. Dažādās optiskajās ierīcēs, piemēram, fotoaparātos atstarotā gaisma ir nevēlama parādība, jo fotogrāfijas uzņemšanai ir nepieciešas savākt pēc iespējas vairāk gaismas. Šādās optiskajās ierīcēs izmanto tā saukto optisko materiālu dzidrināšanu, kuras pamatā ir pretējs process konstruktīvajai interferencei, kas notiek ziepjūdens burbulī. Dzidrināšanas procesā lēca (7. att. a) tiek pārklāta ar pārklājumu, kura laušanas koeficients ir mazāks nekā lēcai (7. att. a). Pārklājumu uzklāj tādā biezumā, lai atstarotajai gaismai būtu spēkā interferences minimuma nosacījums jeb iestātos destruktīvā interference un gaisma neatstarotos. Tādā veidā tiek palielināts caurizgājušās gaismas apjoms, tomēr visus zudumus, kas rodas atstarošanās dēļ, novērst nevar, jo interferences minimuma nosacījums izpildās tikai vienam viļņu garumam. Dzidrinātas lēcas var atpazīt pēc tā, ka dzidrinošā kārtiņa rada dzeltenu vai violetu nokrāsu (7. att. b). Ikdienas fotoaparāta objektīvus izgatavo, lai dzidrinātu zaļos gaismas starus, jo cilvēka acs pret tiem ir visjūtīgākā! Tāpēc, skatoties objektīvā pretējā virzienā, redzam to violetu, jo šos gaismas starus tas atstaro.
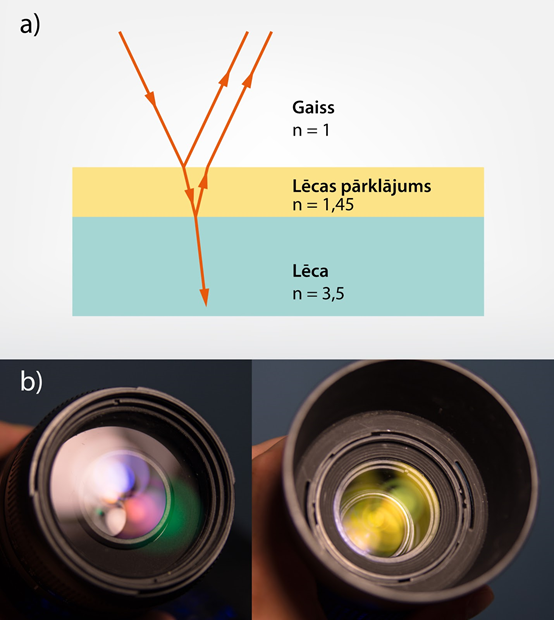
7.att. Optisko materiālu dzidrināšana
Interferences parādība tiek izmantota, izstrādājot hologrammas, ar kurām var iegūt telpisku priekšmeta attēlu. Hologrammas iegūšanai nepieciešams spēcīgs monohromatiskas gaismas avots, piemēram, lāzers (8. att.). Koherentā gaisma tiek sadalīta divas daļās. Viena daļa krīt uz objektu un nonāk uz hologrāfiskās plates, bet otra daļa atstarojas pret spoguli un arī nonāk uz hologrāfiskās plates. Starp šie abiem gaismas kūļiem veidojas gājiena diference, tādēļ uz hologrāfiskās plates notiek šo staru kūļu interference, kuras rezultātā tiek iegūta hologramma. Šādi iegūtas hologrammas sauc par plānajām hologrammām. Pastāv arī citi hologrammu iegūšanas veidi.
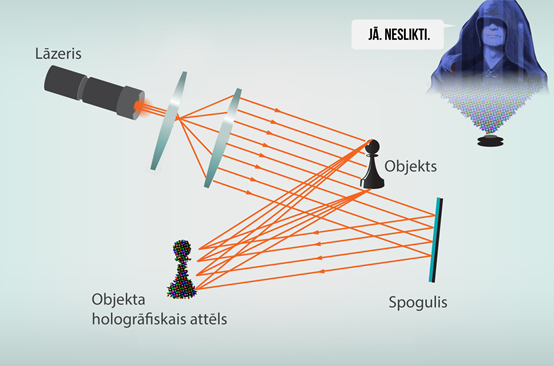
8.att. Hologrammas iegūšana
Hologrammas var lietot gan preču zīmju un vērtīgu dokumentu aizsardzībai, gan arī reklāmas nolūkos, jo ar hologrammām var iegūt spilgtus un mainīgus attēlus, kas piesaista pircēju uzmanību. Ikdienā ar hologrammām var saskarties, izmantojot papīra naudu, jo banknotēm ir hologrāfiskā iestrāde (9.att. a), tāda ir arī uz bankas kartēm (9. att. b).

9.att. Hologrammu iegūšana
Ja uz Junga dubultspraugu krīt baltā gaisma, tad uz ekrāna pretī spraugām veidojas balts maksimums, bet uz malām izvietojas dažādu krāsu maksimumi dažādos attālumos (1. att.). Tas ir tādēļ, ka katras gaismas interferences maksimuma nosacījums ir atkarīgs no leņķa, kādā gaisma noliecas pēc iziešanas caur dubultspraugu. Apskatīsim divus starus, kas iziet cauri Junga dubultspraugai leņķī α un nonāk uz ekrāna vienā punktā (1. att.). Gājuma diference starp abiem stariem ir Δx = x2 - x1. Tā kā parasti attālums d starp spraugām ir daudzas reizes mazāks nekā attālums R no spraugām līdz ekrānam, tad abi stari ir faktiski paralēli un Δx ≈ dsinα. Interferences maksimuma nosacījums izpildās tad, ja Δx = kλ, kur k = 0,1,2, … . Gala rezultātā kλ ≈ dsinα. No iegūtās sakarības var secināt, ka gaismas viļņi ar lielāku garumu noliecas vairāk no centra nekā mazāka viļņu garuma gaisma, kā tas arī redzams 1. attēlā. Centrālais maksimums ir baltā krāsā, jo tur bez lūšanas nonāk visu krāsu gaismas stari.
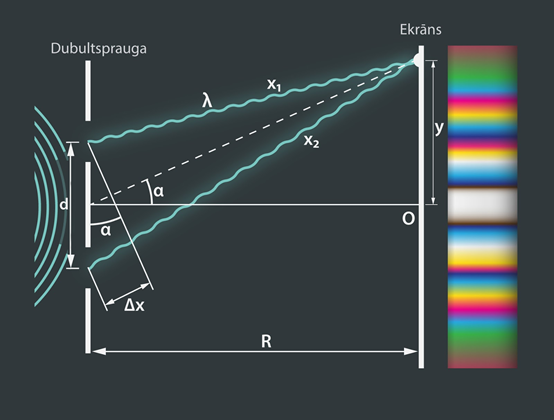
1.att. Baltās gaismas interference Junga dubultspraugā
Ja gaismas stars atstarojas, tad papildus tam, ka notiek izplatīšanās virziena maiņa, ir iespējamas arī izmaiņas gaismas viļņa svārstību fāzē. Izmaiņas notiek tad, kad stars no vides ar zemāku laušanas koeficientu atstarojas pret vidi, kurai tas ir augstāks. Piemēram, ja stars pārvietojas vidē, kurai laušanas koeficientsn = 1, un atstarojas pret plāno kārtiņu, kurai laušanas koeficients n>1, tad atstarošanās brīdī viļņu svārstību fāze izmainās par 180⁰ grādiem jeb π radiāniem (2. att.). Ja atstarošanās notiek pret vidi, kurai laušanas koeficients ir mazāks, lēciens svārstību fāzē nenotiek. Šāda situācija realizējas plānajā kārtiņā, kad gaismas stars atstarojas pret otru kārtiņas virsmu (2. att.)
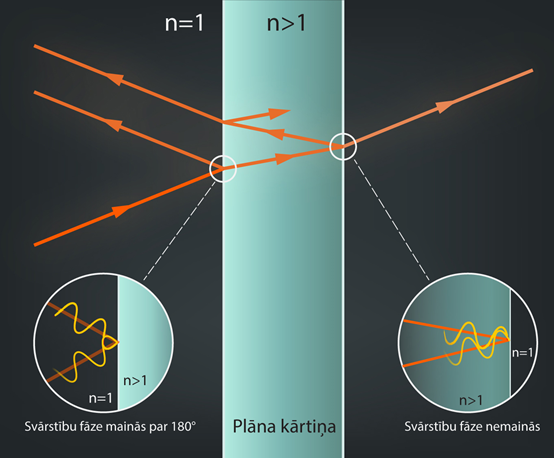
2.att. Svārstību fāzes maiņa atstarošanās procesā
Svārstību fāzes lēciens ir jāņem vēra tad, ja vēlas aprēķināt plānās kārtiņas biezumu, lai kādas noteiktas krāsas gaismai izpildītos interferences minimuma vai maksimuma nosacījums. Ja uz plāno kārtiņu krīt stars 1, tad interference notiek starp staru 2, kas ir atstarotais stars, un staru 5, kas veidojas no lauztā stara 3 un atstarotā stara 4 (3. att.). Gājuma starpība stariem 2 un 5 vienāda ar Δx = n(BC + CD) – AB + λ : 2. Attālums BC + CD ir papildu ceļš, kas jānoiet staram plānajā kārtiņā. Šis attālums ir pareizināts ar vides absolūto laušanas koeficientu n, jo plānajā kārtiņā gaismas laušanas koeficients ir lielāks nekā gaisā, tādēļ gaisma pārvietojas lēnāk, līdz ar to tās optiskais ceļš palielinās. Pusviļņa garums λ : 2 tiek pieskaitīts tādēļ, ka, atstarojoties no plānās kārtiņas, notiek fāzes lēciens par 180 grādiem, kas atbilst pusviļņa garumam. Attālums AB ir jāatņem nost, jo tas ir ceļš, ko paspējis noiet stars 2. Ja Δx = kλ, kur k = 0, 1, 2,... , tad izpildās interferences maksimuma nosacījums, bet ja Δx = (2k + 1)λ : 2, kur k = 0, 1, 2,... , tad izpildās interferences minimuma nosacījums.
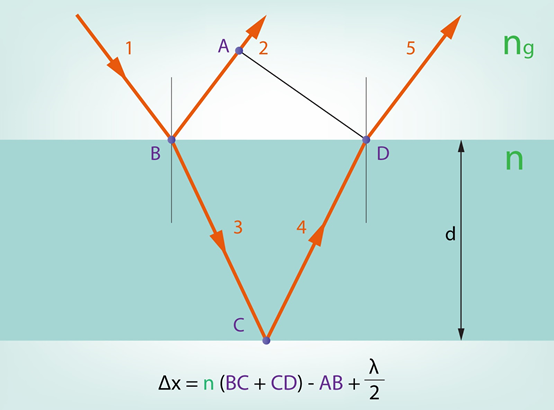
3.att. Gājuma starpības veidošanās plānajā kārtiņā
Lai aprēķinātu, kāds būs rādiuss rk k-tajam Ņūtona gredzenam, ir jāapskata tuvāk gredzenu veidošanās mehānisms (4. att.). Staru diference veidojas ķīļveida spraugā starp lēcu un virsmu. Šo ķīļveida spraugu tuvināti var uzskatīt par trijstūrveida, tās mala Δx ir vienāda ar pusi no gājuma starpības (staram šis attālums jānoiet divas reizes, turp un atpakaļ). Trijstūrim AOB (4. att. b) ir spēkā Pitagora teorēma: R2 = rk2 + (R - Δx)2 = rk2 + R2 - 2RΔx + Δx2. No šīs izteiksmes iegūst rk2 - 2RΔx + Δx2 = 0. Attālums Δx ir mazs, līdz ar to Δx2 ir vēl daudzas reizes mazāks lielums, tādēļ tuvinātos aprēķinos to var neņemt vērā. Tādējādi rk2 - 2RΔx ≈ 0 un Δx ≈ rk2 : 2R. Lai izpildītos interferences maksimuma nosacījums, 2Δx = 2kλ : 2 – λ : 2 un 2Δx = (2k - 1)λ : 2. Pusviļņa garums λ : 2 tiek atņemts nost, jo ir jākompensē fāzes lēciens par 180 grādiem, kas rodas, atstarojoties no lēcas virsmas. Ievietojot Δx vietā no Pitagora teorēmas iegūto vērtību, 2rk2 : 2R ≈ (2k - 1)λ : 2. Tātad rk2 ≈ R(2k - 1)λ : 2.
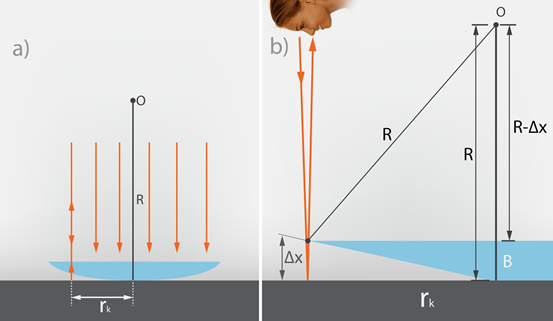
4.att. Ņūtona gredzenu veidošanās
Izsekojot līdzīgā veidā, kā veidojas staru gājuma starpība dzidrinātās optikas gadījumā, var iegūt izteiksmi, kas saista pārklājuma biezumu d un viļņu garumu λ gaismai, kuras atstarošanos ir vēlme nomākt: d = λ : 4np; npir dzidrinātā pārklājuma gaismas laušanas koeficients (5. att.).
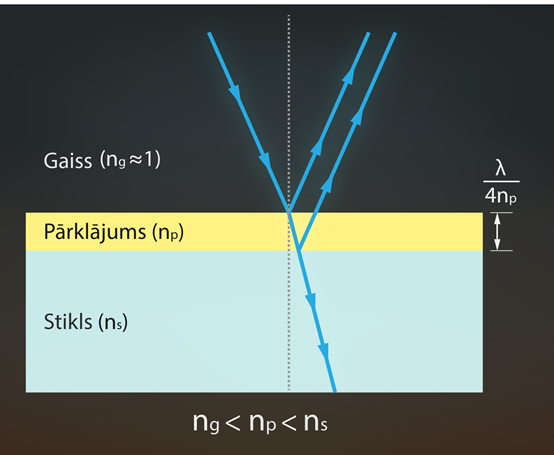
5.att. Ņūtona gredzenu veidošanās
Interferences svarīgs lietošanas veids ir precīziem mērījumiem, ko var veikt ar mērinstrumentu – interferometru (6. att.). Šajos mērinstrumentos izmanto gaismas interferences parādību, lai ar augstu precizitāti varētu mērīt attālumu, mazas deformācijas, gaismas laušanas koeficientu vai noteikt gaismas viļņa garumu. Piemēram, ar Releja interferometru (6. att.) var izmērīt gaismas laušanas koeficientu. Šajā interferometrā divi koherenti gaismas kūļi tiek laisti cauri divām kivetēm K1 un K2. Kivete ir neliels stikla trauks, ko izmanto optiskajā aparatūrā, ar kuru pētī šķidruma īpašības. Vienā kivetē esošajai vielai gaismas laušanas koeficients n1 ir zināms, bet otrā kivetē esošās vielas gaismas laušanas koeficients n2 nav zināms. Ja vielām atšķiras laušanas koeficienti, tad atšķiras arī ātrums, ar kādu gaisma šajā vidē pārvietojas. Tā rezultātā starp abiem stariem veidojas gājienu starpība un uz ekrāna var novērot interferences ainu. Analizējot šo interferences ainu, var noteikt gaismas laušanas koeficientu starpību abas kivetēs.
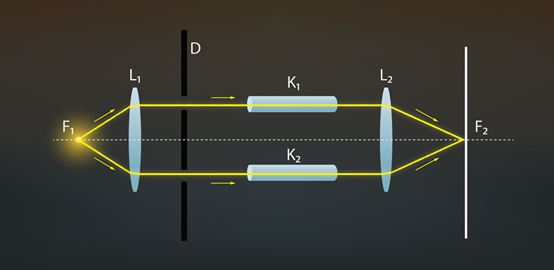
6.att. Interferometra darbība