Ja magnētiskajā laukā B ievieto vadu, pa kuru plūst strāva I, tad magnētiskais lauks uz vadu iedarbojas ar spēku FA (1. att.), ko sauc par Ampēra spēku. Šo spēku var aprēķināt, izmantojot izteiksmi FA=BIlsinα, kur
B – magnētiskā lauka stiprums jeb indukcija, T
I – vadā plūstošās strāvas stiprums, A
l – vada daļas garums, kas pakļauts magnētiskajam laukam, m
α – leņķis starp magnētiskā lauka indukcijas un vadā plūstošās strāvas virzieniem,
Ampēra spēka virziena noteikšanai izmanto kreisās rokas likumu: ja atvērta kreisās rokas plauksta ir novietota tā, ka magnētiskā lauka līnijas “duras” plaukstā un izstieptie pirksti vērsti strāvas plūšanas virzienā, tad atvāztais īkšķis norāda Ampēra spēka virzienu (1. att).
Apskaties DZM materiālu par šo tēmu!
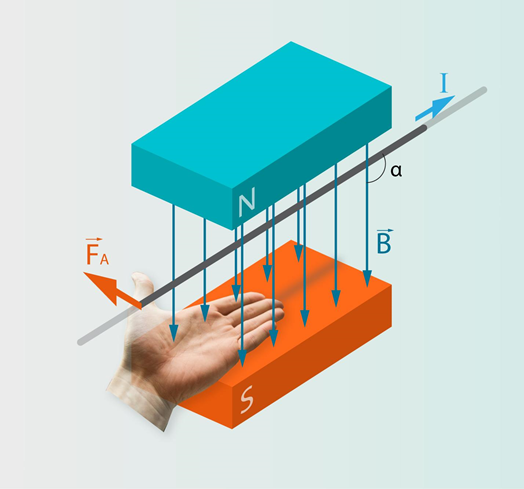
1.att. Kreisās rokas likums Ampēra spēka virziena noteikšanai
Ampēra spēku var izmantot, lai noteiktu magnētiskā lauka indukcijas B lielumu. Ja perpendikulāri magnētiskā lauka līnijām novieto strāvas kontūru ar vienu kustīgu malu (2. att. a), tad, palaižot kontūrā strāvu, uz kustīgo malu darbojas Ampēra spēks. Magnētiskā lauka indukcijas līnijas ir perpendikulāras kontūra kustīgajai malai, tādēļ Ampēra spēks FA=BIl. Ja izmēra Ampēra spēku, tad magnētiskā lauka indukcija B=FA:(Il). Ja kustīgo vadu apskata no gala (2. att. b), tad redzams, kāds izskatās magnētiskais lauks ap šo vadu. Vada radītais magnētiskais lauks mijiedarbojas ar magnētisko lauku, kurā vads atrodas, kā rezultāta kopējais magnētiskais lauks veido izliekumu ap vadu (2. att. b). Magnētiskā lauka līnijas darbojas līdzīgi elastīgām saitēm, tādēļ vads sajūt spēku.
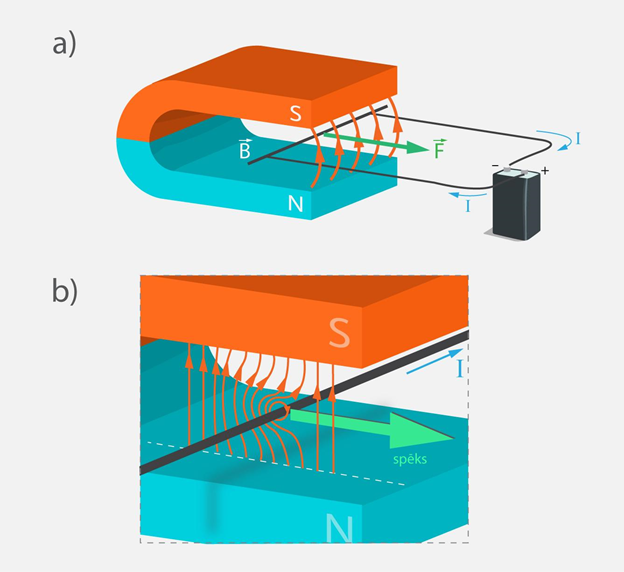
2.att. Ampēra spēka iedarbība uz kustīgo rāmīša malu
Ja magnētiskajā laukā perpendikulāri tā indukcijas līnijām ielido lādēta daļiņa, tad uz to darbojas Lorenca spēks FL(3. att.), kuru aprēķina pēc formulas FL=Bqv, kur
B–magnētiskā lauka indukcija, T
q–lādiņa lielums, C
v–lādētās daļiņas ātrums, m/s
Lorenca spēka virziena noteikšanai arī lieto kreisās rokas likumu. Izstiepta plauksta ir jānovieto tā, lai magnētiskā lauka līnijas ieietu plaukstā (3. att.). Ja daļiņa ir pozitīvi lādēta, tad izstieptie plaukstas pirksti jāvērš lādētās daļiņas kustības virzienā, bet ja daļiņa ir lādēta negatīvi, tad pretēji. Ja atvērta plauksta novietota kā teikts iepriekš, tad atliekts īkšķis norāda Lorenca spēka darbības virzienu (3. att.).
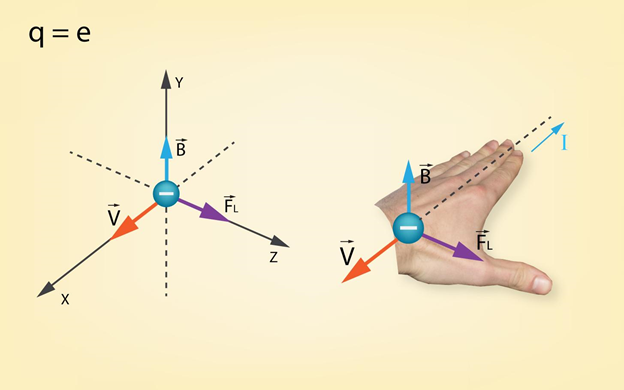
3.att. Lorenca spēka virziens
Ja lādētā daļiņa neielido perpendikulāri magnētiskā lauka līnijām, bet ātruma virziens veido leņķi α ar magnētiskā lauka līnijām (4. att.), tad Lorenca spēka lielums ir atkarīgs no tās ātruma vektora komponentes, kas vērsta perpendikulāri magnētiskā lauka indukcijās līnijām (4. att.). Šādā gadījumā Lorenca spēku izsaka izteiksme FL=Bqvsinα. Ja lādētā daļiņa lido paralēli magnētiskā lauka līnijām, tad uz to nedarbojas Lorenca spēks.
Izpēti Lorenca spēku pats!
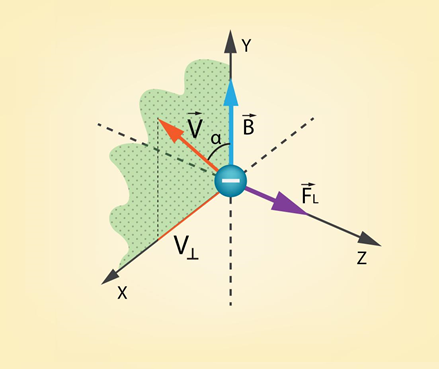
4.att. Lorenca spēku nosaka magnētiskajam laukam perpendikulārā ātruma vektora komponente
Ja blakus novieto divus vadus, pa kuriem plūst strāva I, tad vadi Ampēra spēka ietekmē var gan pievilkties, gan atgrūsties (1. att.). Kurš no minētajiem scenārijiem realizēsies, atkarīgs no strāvu virziena vados. Ja abos vados strāva plūst vienā virzienā (1. att. a), tad abu vadu radītie magnētiskie lauki cenšas apvienoties un rezultātā vadi savstarpēji pievelkas (1. att. a). Ja strāva vados plūst pretējos virzienos, tad abu vadu magnētiskie lauki nodalās viens no otra un vadi savstarpēji atgrūžas (1. att. b).
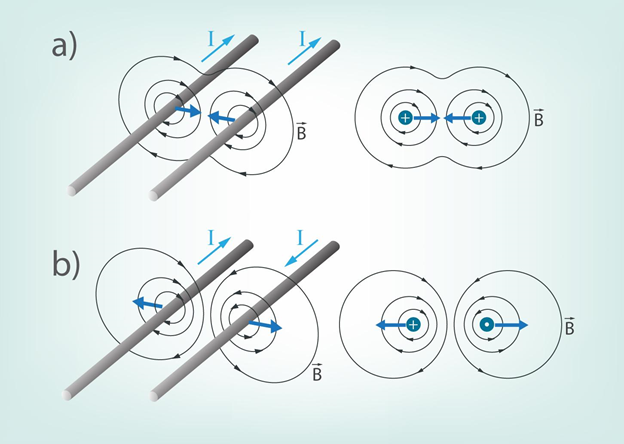
1.att. Vadu pievilkšanās un atgrūšanās Ampēra spēka ietekmē
Sadaļā par elektriskās strāvas stiprumu tika minēts, ka ampērs tiek definēts, izmantojot mijiedarbības spēku starp diviem taisniem, paralēliem un ļoti gariem vadiem (2. att.). Spēks, kura rezultātā vadi mijiedarbojas, ir Ampēra spēks. Izmantojot izteiksmi magnētiskā lauka indukcijas vērtības aprēķināšanai attālumā R no strāvas vada iegūst B1=μ0I1:(2πR), kur
B1–magnētiskā lauka indukcija ap pirmo strāvas vadu, T
μ0–magnētiskā konstante
I1–strāvas stiprums, kas plūst vadā, A
R–attālums no vada, kurā apskata magnētisko lauku, m
Ja attālumā R no pirmā vada atrodas otrs vads (2. att.), tad uz to darbojas Ampēra spēks FA=B1I2l, kur l ir vada posma garums, uz kuru tiek apskatīta Ampēra spēka ietekme. Ja šajā izteiksmē ievieto pirmā vada magnētiskā lauka indukcijas B1izteiksmi, tad iegūst FA=μ0I1I2l:(2πR).
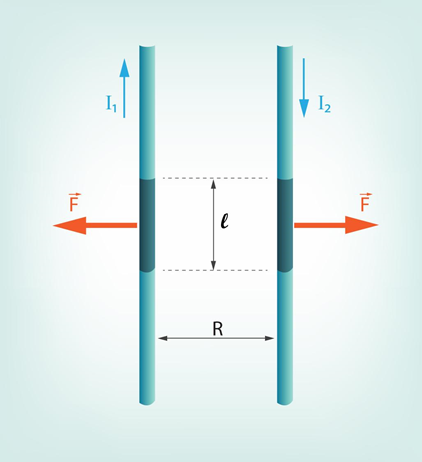
2.att. Divu tievu, garu un paralēlu vadu atgrūšanās
Šobrīd zinātnieki visā pasaulē strādā pie tā, lai visu SI mērvienību definīcijas varētu piesaistīt fundamentālajiem fizikas likumiem un mikropasaules konstantēm. 1 Ampēru liela strāva atbilst noteiktam elektrona lādiņu skaitam sekundē, tādēļ jauno strāvas etalonu ir plānots izbūvēt kā ļoti precīzo elektronu skaitītāju. Lai varētu ātri un precīzi skaitīt atsevišķus elektronus. Arī Latvijas fiziķi aktīvi piedalās šajā procesā: Dr. Vjačeslavs Kaščejeva vadībā izstrādātais "sabrukuma kaskāžu modelis" (3. att.), kas modelē kvantu punktos notiekošos procesus, ir kļuvis par pamatu pasaulē precīzākiem elektronu skaitītājiem. Latvijas Universitātes teorētiķi kopā ar Vācijas un Lielbritānijas metroloģijas laboratoriju eksperimentatoriem turpina darbu pie strāvas kvantu etalona izveides, lai nākamajā SI sistēmas pārskatīšana reizē varētu mainīt Ampēra definīciju.

3.att. Modeļa attēlojums
Ja no vada, pa kuru plūst strāva, izveido rāmīti un ievieto to magnētiskajā laukā tā, kā parādīts 3. attēlā, tad uz rāmīša ass AB paralēlajām malām, kas atrodas perpendikulāri magnētiskā lauka līnijām, darbojas Ampēra spēks, turklāt uz katru no malām Ampēra spēks darbojas pretēja virzienā (4. att.). Ampēra spēka virzienu var noteikt, izmantojot kreisās rokas likumu. Ja rāmīša plakne nav perpendikulāra magnētiskā lauka līnijām, tad rāmīts ir pakļauts griezes momentam, kas cenšas to pagriezt ap asi AB (4. att. a). Tiklīdz rāmīša plakne nonāk perpendikulāri magnētiskā lauka līnijām, tā Ampēra spēks rāmīti vairs negriež, bet tikai deformē, velkot katru malu uz savu pusi (3. att. b). Šādu strāvas rāmīšu griešanos izmanto, piemēram, elektromotoros, kuros ir daudz strāvas rāmīšu (tinumu), kas griežas magnētiskajā laukā.
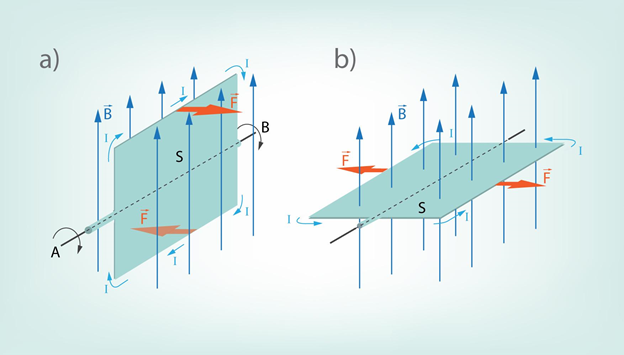
4.att. Strāvas rāmīša griešanas magnētiskajā laukā
Ja lādēta daļiņa, piemēram, elektrons, ielido homogēnā magnētiskajā laukā perpendikulāri tā indukcijas līnijām, tad uz to sāk darboties Lorenca spēks, kura virzienu var noteikt, izmantojot kreisās rokas likumu (5. att.). Lorenca spēks ir vērsts perpendikulāri elektrona kustības virzienam, līdz ar to tas darbojas kā centrtieces spēks, kura rezultātā elektrons sāk pārvietoties pa riņķveida trajektoriju, kuras rādiuss ir R (5. att.). Uz elektronu darbojas Lorenca spēks, kas vienāds ar FA=evB, kur
e–elektrona lādiņš, C
v–elektrona ātrums, m/s
B–magnētiskā lauka indukcija, T
Centrtieces spēku FC, kas darbojas uz rotējošu elektronu, iespējams izteikt kā FC=mv2:R, kur
m–elektrona masa, kg
R–riņķveida trajektorijas rādiuss, m
Tā kā Lorenca spēks šajā gadījumā ir centrtieces spēks, tad FA=FC, līdz ar to mv2:R=evB, no kā var izteikt riņķveida trajektorijas rādiusu R=mv:(eB).
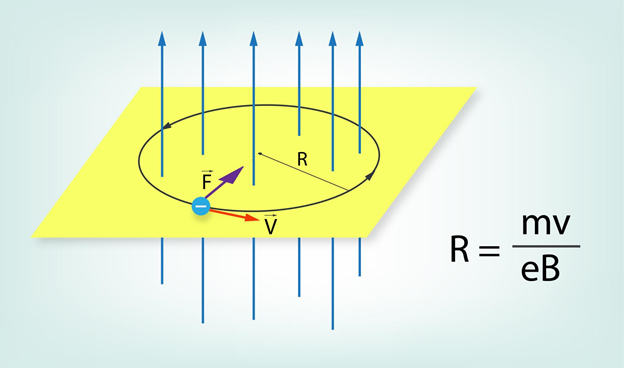
5.att. Elektrona trajektorija, ielidojot homogēnā magnētiskajā laukā
Ja elektrons vai kāda cita lādēta daļiņa homogēnā magnētiskajā laukā ielido nevis perpendikulāri pret lauka līnijām, bet leņķī α , tad kustības trajektorija ir spirāle (6. att.). Spirāles liekuma rādiusu R var aprēķināt, lietojot iepriekš iegūto formulu, vienīgi šajā gadījumā daļiņas ātruma v vietā jaizmanto magnētiskā lauka līnijām perpendikulārā ātruma komponente vp=vsinα, līdz ar to R=mvsinα:(eB).
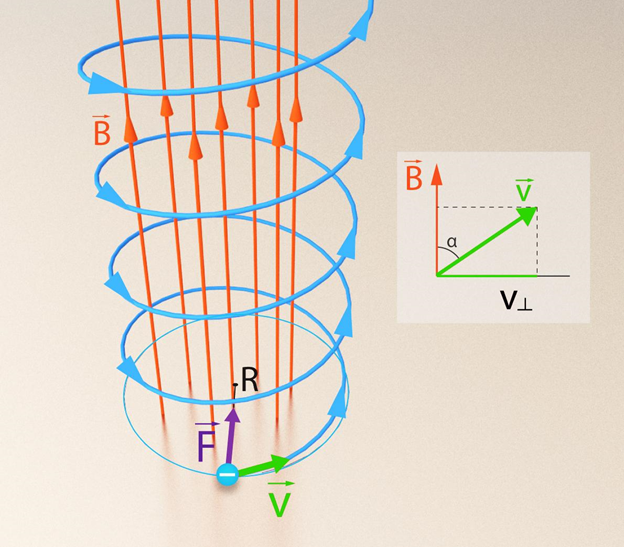
6.att. Lādētas daļiņas trajektorija, ielidojot leņķī pret magnētiskā lauka līnijām
Esam noskaidrojuši, ka kustībā esoša lādēta daļiņa sāk kustēties pa spirāli ar rādiusu R, nonākot leņķī α pret homogēnā magnētiskā lauka līnijām (7. att. a). Tomēr magnētiskais lauks mēdz būt nehomogēns, kā rezultātā magnētiskā lauka indukcija pieaug vai samazinās spirāles vīšanas virzienā (7. att. b,c). Ja magnētiskā lauka indukcija B pieaug spirāles vīšanās virzienā, tad spirāles rādiuss arvien samazinās (7. att. b), bet ja B samazinās, tad rādiuss kļūst aizvien lielāks (7. att. c). Tas nozīmē, ka lādētā daļiņa it kā “tinas” ap magnētiskā lauka indukcijas līnijām.
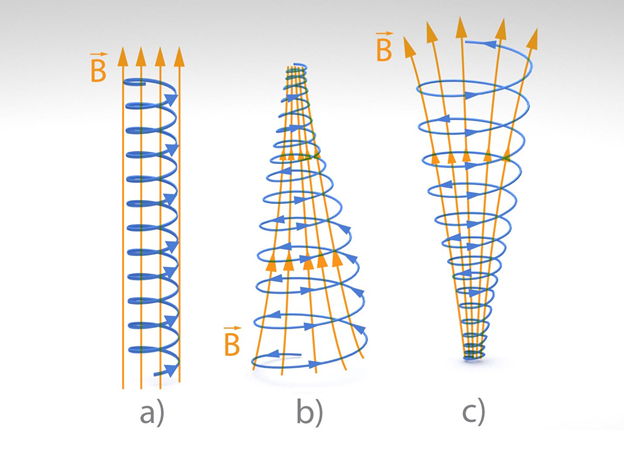
7.att. Lādētas daļiņas trajektorija homogēnā un nehomogēnā magnētiskajā laukā
Arī elektriski lādētās daļiņas, kas nonāk Zemes magnētiskajā laukā, vijas ap Zemes magnētiskā lauka līnijām (8. att.), līdz saduras ar atmosfērā esošajām molekulām vai nonāk līdz Zemes virsmai. Pateicoties Zemes magnētiskā lauka formai, lādētās daļiņas tiek novirzītas uz zemes magnētiskajiem poliem. Atšķirība starp negatīvi lādētām daļiņām, piemēram, elektroniem, un poziīvi lādētām daļiņām, piemēram, protoniem, ir tā, ka tie ap magnētiskā lauka līnijām vijas pretējos virzienos. To lādiņi ir pretējas zīmes, līdz ar to uz katru no daļiņām Lorenca spēks darbojas pretējos virzienos.
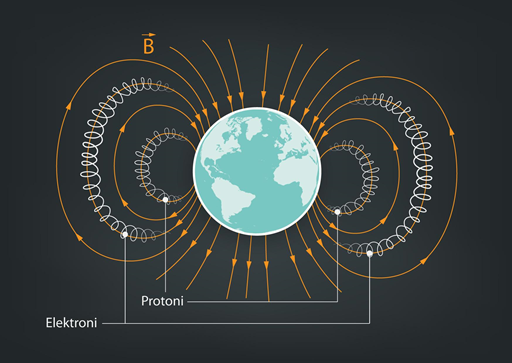
8.att. Lādētas daļiņas vijas ap Zemes magnētiskā lauka līnijām
Ja strāvas rāmīti ievieto magnētiskajā laukā, ir iespējama tā rotācijas kustība ap asi AB (1. att a). Rotācijas kustību nodrošina spēka moments M. Sadaļā par dažādiem momentiem fizikā noskaidrojām, ka spēka momentu nosaka spēka un spēka pleca reizinājums. Šajā gadījumā spēks ir Ampēra spēks FA, kas darbojas uz rāmīša rotācijas asij paralēlajām malām, bet spēka plecs, ko šajā gadījumā apzīmēsim ar s, ir atkarīgs no tā, kādā stāvoklī atrodas rāmītis. Ja rāmīti apskata no gala (1. att. b), tad rāmīša plakne ar magnētiskā lauka līnijām veido leņķi β. Spēka plecs ir vienāds ar rāmīša rotācijas rādiusa d projekciju uz magnētiskā lauka līnijām, kas ir atkarīga no leņķa βjeb s=dcosβ. Maksimālais spēka moments, kas var darboties uz vienu rāmīša malu, vienāds ar FAd, bet tā kā Ampēra spēks darbojas uz divām rāmīša malām, tad maksimālais spēka moments, kas var darboties uz rāmīti, vienāds ar M=2FAd. Ja rāmīša rotācijas ass ir perpendikulāra magnētiskā lauka līnijām, tad arī Ampēra spēks FAir maksimāls: FA=BIl. Ievietojot šo maksimālā spēka momenta izteiksmē, iegūst M=2BIld=BIS, kur S ir rāmīša laukums.
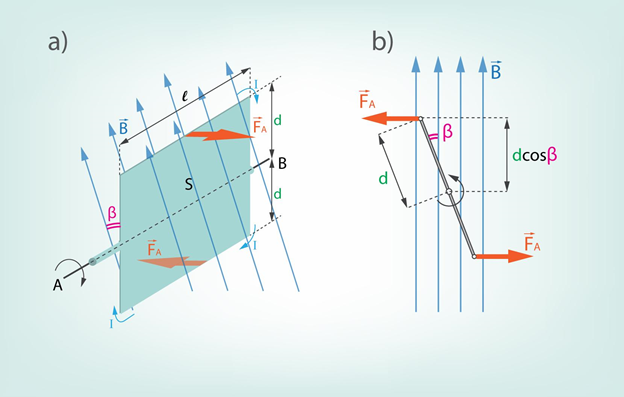
1.att. Uz strāvas rāmīti magnētiskajā laukā var darboties spēka moments
Iepriekšējā solī tika pieminēts, ka strāvas rāmīša pagriešanos magnetiskajā laukā izmanto līdzstrāvas elektromotoros. Vienkāršs līdzstrāvas motors sastāv no pastāvīgā magnēta, rotējoša rāmīša (rotora) un strāvas pievada (statora) (2. att. a). Stators nodrošina to, ka pēc katra pus apgrieziena mainās strāvas virziens rotorā, lai uz rāmīti vienmēr darbotos spēka moments, kas to griestu. Līdzstrāvas motorus izmanto elektriskajos instrumentos, kas darbojas uz baterijām, piemēram, elektriskajos skrūvgriežos. Automašīnas starteris ir līdzstrāvas motors (2. att. b), kam, izmantojot akulumatora enerģiju, jāiegriež automašīnas dzinējs. Līdzstrāvas motors sastopams arī mobilajos telefonos. Telefona vibrēšana tiek panākta ar līdzstrāvas motoriņu, kuram ir nevienmērīgi sadalīta masa uz rotora, tādā veidā izraisot tā vibrēšanu.
Apskaties, kā darbojas līdzstrāvas motors!
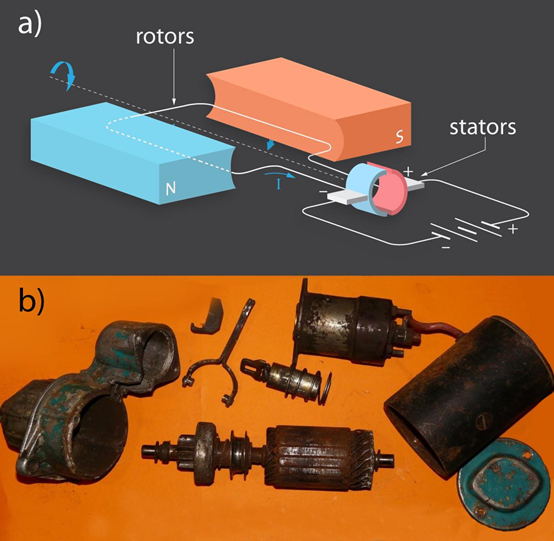
2.att. Līdzstrāvas motors
Strāvas rāmīša pagriešanos magnētiskājā laukā var izmantot arī dažādos mērinstrumentos, piemēram, ampērmetrā. Ampērmetrs sastāv no kustīga vadu tinuma jeb spoles, kas ievietota pastāvīgā magnētiskajā laukā (3. att.). Kad spoli pievieno strāvai, tad spole pagriežas Ampēra spēka ietekmē. Spoles pagriešanos kavē atspere, tomēr, jo spēcīgāka strāva plūst spolē, jo lielāks spēka moments darbojas uz spoli un jo vairāk tā pagriežas. Tad tikai atliek spolei pievienot rādītāju un skalu, nokalibrēt to, un ampērmetrs gatavs (3. att.).
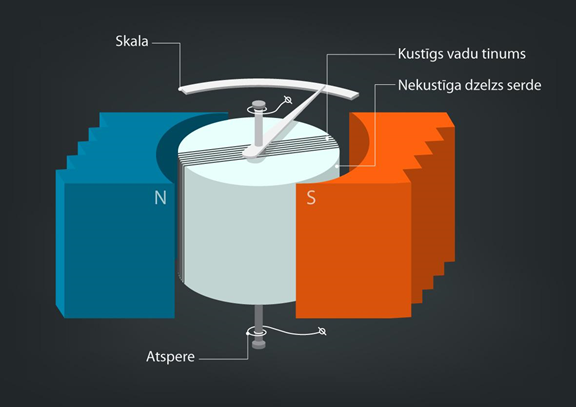
3.att. Ampērmetra uzbūve
Ja elektroni ielido magnētiskajā laukā, tad, pateicoties Lorenca spēkam, tie sāk pārvietoties pa riņķveida orbītām. Šo parādību var vizuāli novērot, ja izmanto caurspīdīgu trauku, kas pildīts ar inertu gāzi zemā spiedienā (4. att.). Traukā vēl jāievieto elektronu lielgabals un spole magnētiskā lauka radīšanai. Pēc 2. solī iegūtas formulas R=mv:(eB) redzams, ka trajektorijas rādiusu var ietekmēt, izmanojot elektronu ātrumu v un magnētiskā lauka indukcijas B vērtību. Palielinot elektronu ātrumu, rādiuss pieaugs, savukārt, palielinot magnētiskā lauka indukcijas vērtību, rādiuss samazināsies.

4.att. Elektronu orbītas vizualizācija
Lorenca spēka radīto izliekumu lādētu daļiņu kustības trajektorijā var izmantot, lai atdalītu dažādu masu lādētas daļiņas, izmantojot masspektrogrāfu (5. att.) Viena no masspektrogrāfa galvenajām sastāvdaļām ir ātruma filtrs, kurā darbojas elektriskais Kulona un magnētiskais Lorenca spēks. Šie spēki ir vērsti tā, lai Kulona spēks FK=qEun Lorenca spēks FL=qvBdarbotos viens otram pretī, līdz ar to no ātruma filtra izlidotu daļiņas, kurām v=E:B. Šīs daļiņas tālāk ieliedo magnētiskajā laukā ar indukciju B0(5. att.). Izmantojot formulu R=mv:(eB), var paredzēt –jo lielāka ir daļiņas masa, jo lielāks ir riņķa līnijas rādiuss, pa kuru tā kustēsies un tādēļ nonāks tālāk uz foto plates (5. att.).

5.att. Masspektrogrāfa darbība
Izmantojot Lorenca spēku, iespējams virzīt lādētas daļiņas pa vēlamo trajektoriju. Šo Lorenca spēka priekšrocību izmanto Lielajā hadronu paātrinātājā, kura vairāk nekā 26 km garajā galvenajā tunelī lādētas daļiņas tiek noturētas vajadzīgajā trajektorijā, izmantojot spēcīgus magnētus (6. att.).

6.att. Lielais hadronu paātrinātājs jeb LHC