Ja ķermenis, kura masa m, ir pacelts virs Zemes augstumā h, tad ķermenim piemīt potenciālā enerģija Ep (Fiztēma par enerģiju), ko nosaka smaguma spēks F, kas darbojas uz ķermeni (1. att. a). Līdzīga situācija ir ar elektriskajiem spēkiem. Ja virs kāda negatīvi lādēta ķermeņa attālumā d atrodas pozitīvs lādiņš +q (1. att. b), tad tas tiecas virzīties negatīvā ķermeņa virzienā. Tātad arī pozitīvajam lādiņam piemīt potenciālā enerģija, ko apzīmē ar W. Lādiņa potenciālo enerģiju izraisa spēks, ko noteic negatīvi lādētā ķermeņa elektriskais lauka intensitāte E. Tas nozīmē, ka elektriskā lauka intensitāte raksturo spēku, kas darbojas uz lādiņu, bet arī lādiņa potenciālās enerģijas raksturošanai ir nepieciešams kāds fizikāls lielums. Un tam ir izvēlēts tāds jēdziens kā elektriskā lauka potenciāls.
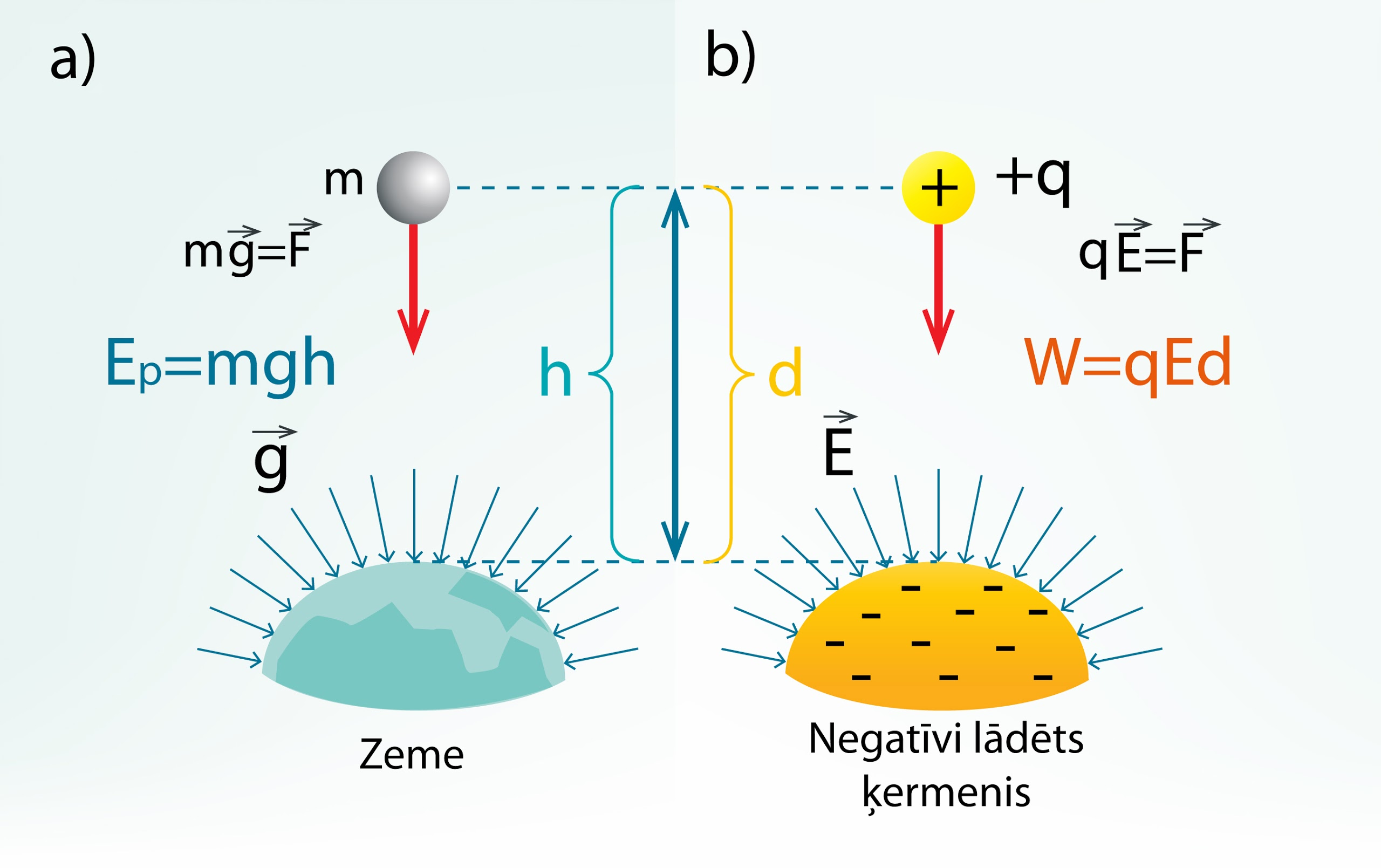
1.att. Potenciālā enerģija gravitācijas un elektriskajā laukā
Ja starp divām pretēji uzlādētām plātnēm atrodas pozitīvs lādiņš q (2. att.), tad tas gribot negribot tiecas negatīvās plates virzienā, jo šim lādiņam dotajā elektriskajā laukā ir potenciālā enerģija attiecībā pret šo plati. Potenciālo enerģiju, kas mīt elektriskajā laukā ievietotos lādiņos, apraksta elektriskā lauka potenciālsφ = W : q, kur
W - lādiņa potenciālā enerģija, džouli (J)
q - lādiņa lielums, kulonos (C)
Potenciāla φ mērvienība ir volts (V).
Ja lādiņš q atrodas attālumā d1no negatīvas plates un tā potenciālā enerģija ir W1 (2. att.), tad elektriskā lauka potenciāls šajā stāvoklī ir φ1 = W1 : q. Ja lādiņš nonāk uz negatīvas plates, tam vairs nav, kur tālāk virzīties, līdz ar to šajā punktā lādiņa potenciālā enerģija W2 = 0 un līdz ar to šoreiz elektriskā lauka potenciāls φ2 = W2 : q = 0 (2. att.).
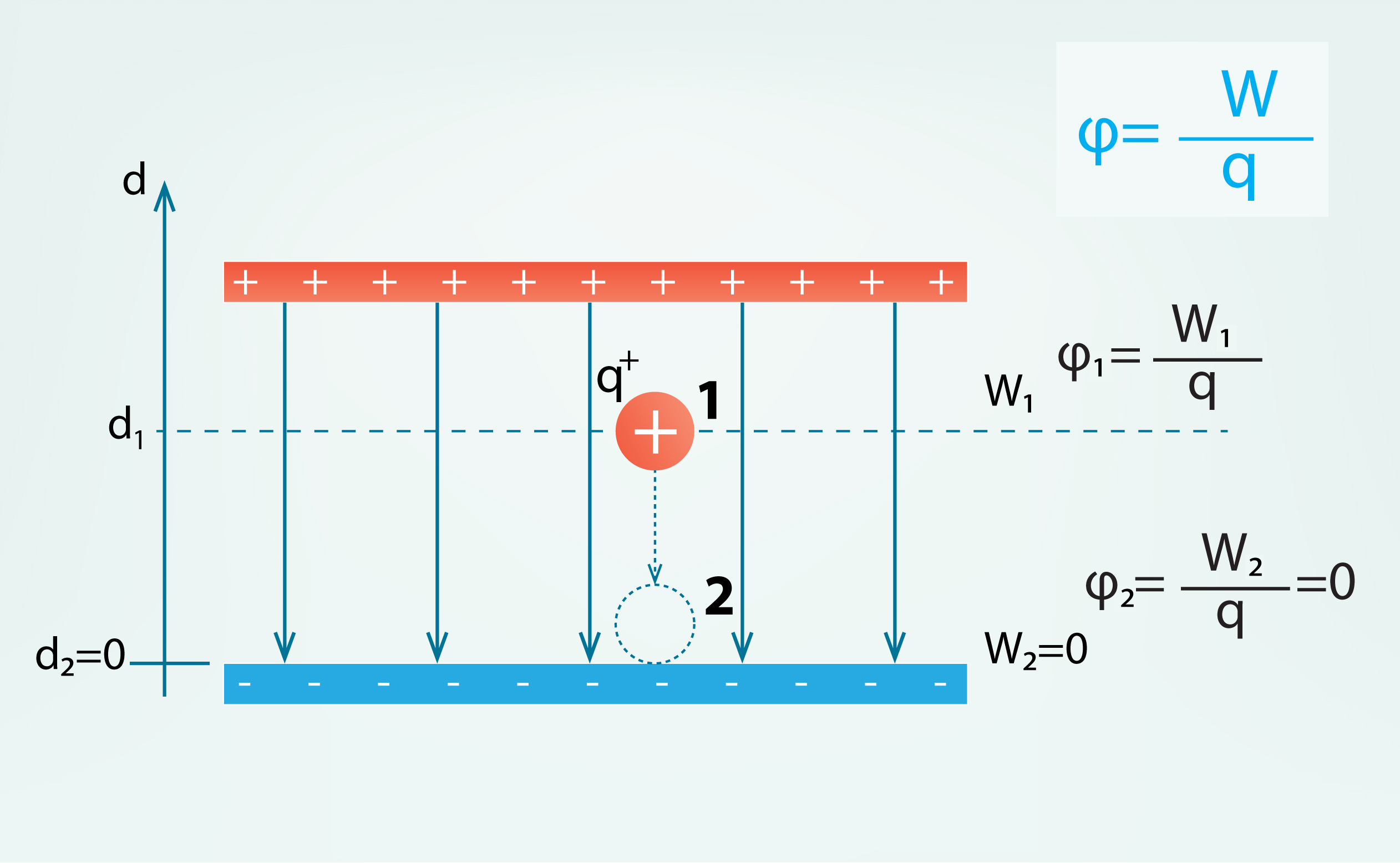
2.att. Elektriskā lauka potenciāls φ
Ja elektriskajā laukā pārvietojas lādiņš un izmainās tā potenciālā enerģija, tad tiek paveikts darbs, turklāt paveiktais darbs A ir vienāds ar potenciālās enerģijas izmaiņu. Ja lādiņš q atrodas telpas punktā ar potenciālu φ1 (3. att.), tad šajā punktā tā potenciālā enerģija ir W1 = qφ1. Ja lādiņš tiek pārvietots uz telpas punktu, kurā elektriskā lauka potenciāls ir φ2(3. att.), tad šajā vietā W2 = qφ2. Paveiktais darbs A ir vienāds ar potenciālās enerģijas izmaiņu, tādēļ A = W2 - W1 = qφ1 - qφ2 = q(φ1 - φ2). No šīs sakarības izriet, ka nav svarīgi, pa kādu trajektoriju lādiņš tiek pārvietots (3. att.), jo paveiktais darbs ir atkarīgs no potenciālu starpības abos galapunktos.
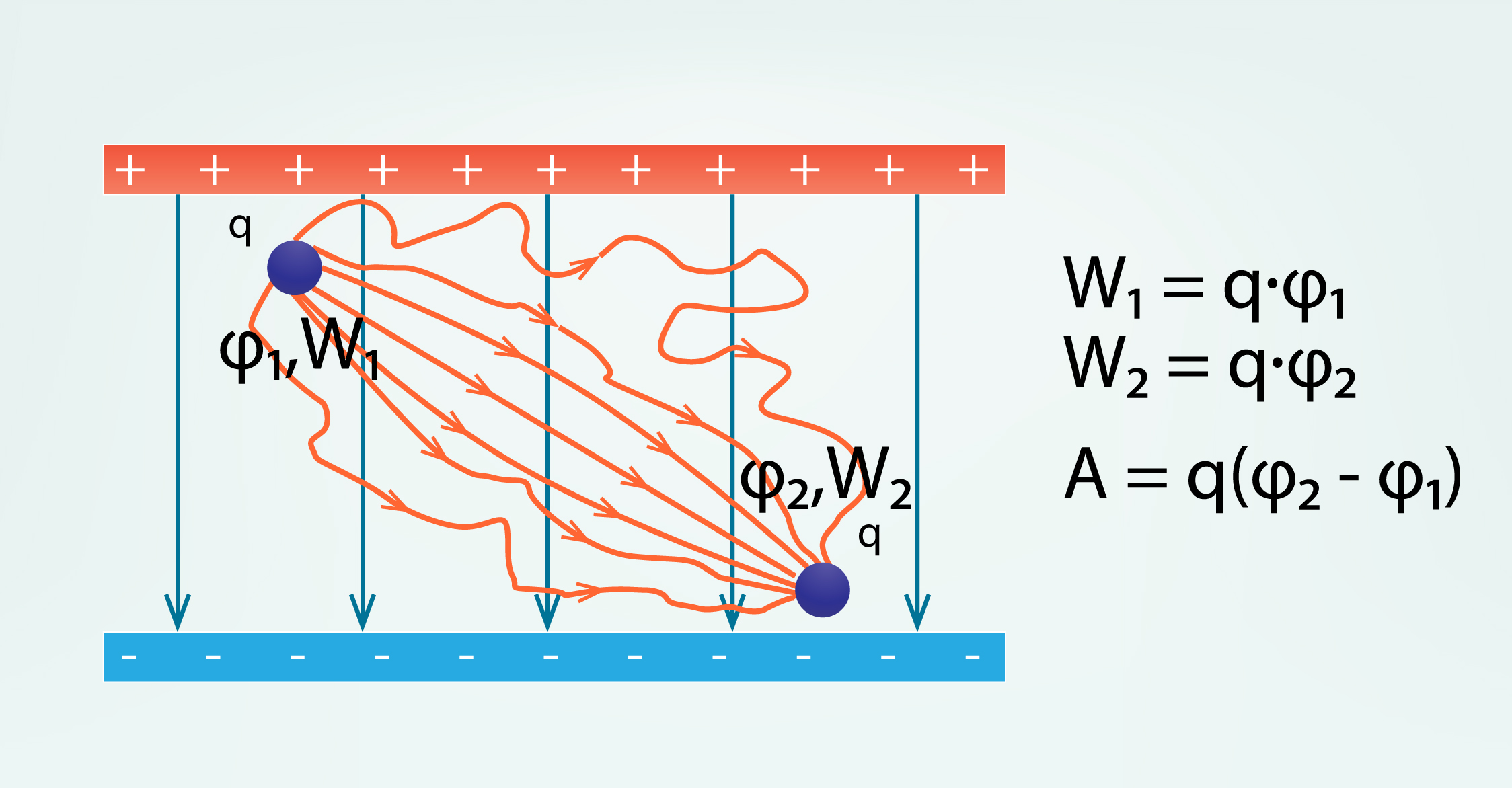
3.att. Elektriskā lauka darbs
Tātad, lai aprēķinātu elektriskā lauka veikto darbu lādiņa pārvietošanas procesā, jāzina šī lauka potenciāls. Piemēram, punktveida lādiņam (4. att.) to izsaka formula φ = kq : R, kur
k - Kulona spēka konstante, (Nm2 : C2)
q - punktveida lādiņa lielums kulonos (C)
R - attālums līdz punktveida lādiņam metros (m)
Izmēģini Kolorādo Universitātes simulāciju vai apskati DZM materiālus!
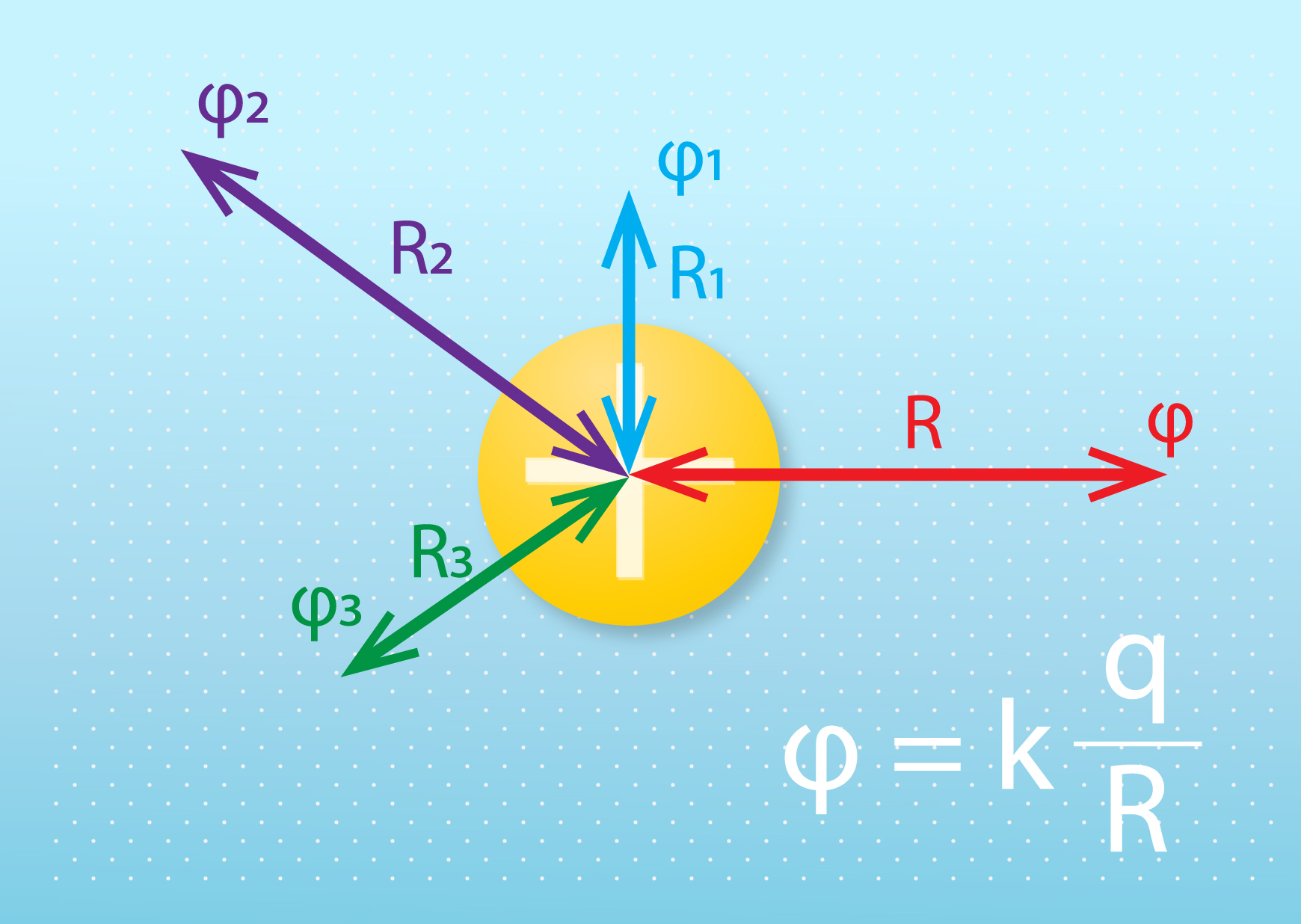
4.att. Punktveida lādiņa potenciāls
Tā kā paveiktais darbs ir atkarīgs no potenciālu starpības abos galapunktos, nevis potenciālu vērtībām, tad ir vērts ieviest fizikālu lielumu, kas raksturo šo potenciālu starpību. Šāds fizikālais lielums ir spriegums. Potenciālu starpība jeb spriegums norāda, cik liels darbs A ir jāveic elektriskajam laukam, lai pārvietotu vienu vienību lielu lādiņu no viena lauka punkta uz citu. Līdz ar to U = A : q.
Ja, piemēram, pretēji uzlādētām plātnēm vienas plātnes potenciāls ir φ1, bet otras plātnes potenciāls φ2, tad spriegums starp plātnēm U12 = φ2 - φ1 (1. att. a). Sprieguma mērvienība ir tāda pati kā potenciālam - volts (V). Automašīnu akumulatoriem ierasta sprieguma vērtība ir 12 V, tas nozīmē, ka līdz ar patērētāja pieslēgšanu elektriskajam laukam jārēķinās ar 12 V spriegumu, lai lādiņu pārvietotu no vienas akumulatora spailes un otru (1. att. b).
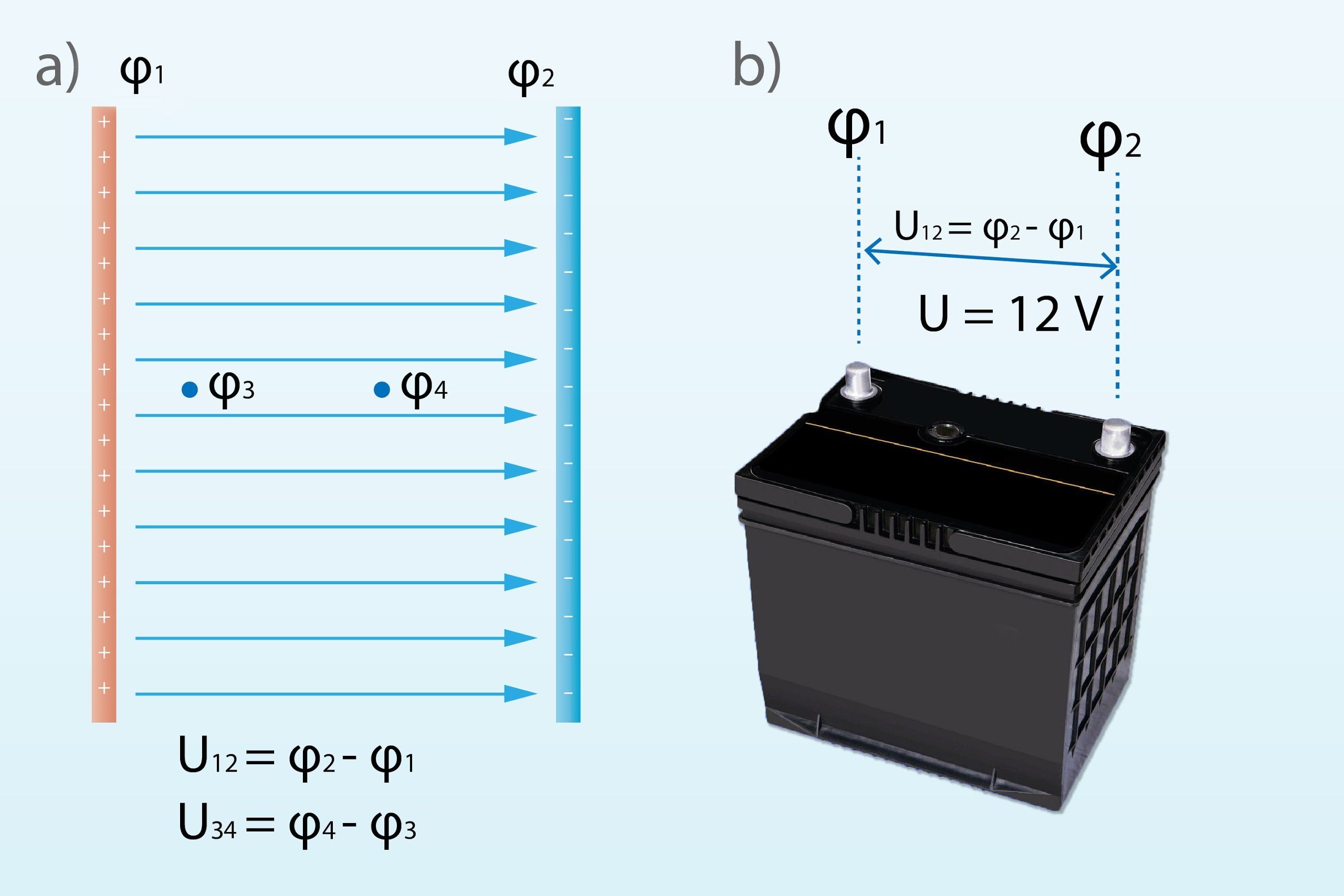
1.att. Potenciālu starpību sauc par spriegumu
Iepriekš tika noskaidrots, ka elektriskā lauka veiktais darbs, pārvietojot lādiņu, ir atkarīgs no potenciālu starpības starp pārvietojuma sākumu un beigu punktu. Līdz ar to, ja sākuma un beigu punktu potenciāli sakrīt, tad elektriskais lauks darbu nav veicis. Elektriskajā laukā kāda noteikta potenciāla vērtība nav tikai vienā punktā, bet tās veido nemainīga potenciāla līnijas, ko sauc par ekvipotenciālajām līnijām. Divu plakņu elektriskajam laukam ekvipotenciālās līnijas ir taisnas līnijas, kas paralēlas cita citai (2. att). Ja kāds lādiņš tiek pārvietots pa kādu ekvipotenciālo līniju, tad elektriskā lauka veiktais darbs vienāds ar nulli.
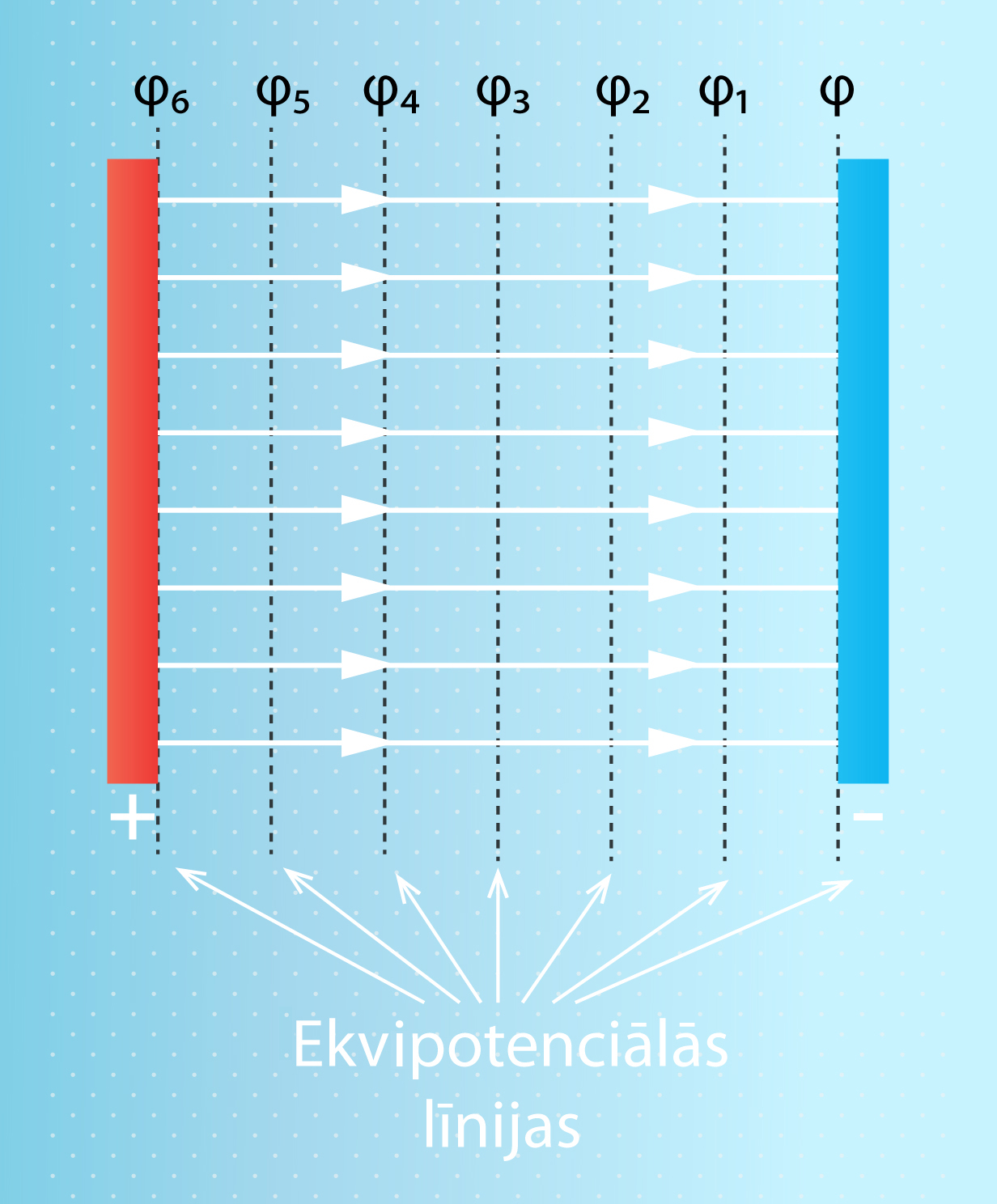
2.att. Plakņu elektriskā lauka ekvipotenciālās līnijas
Līdzību ar elektriskā lauka ekvipotenciālajām līnijām var atrast gravitācijas laukā, piemēram, atrodoties uz jumta (3. att.). Ja uz jumta mēs pārvietojamies paralēli jumta korei, tad mēs pārvietojamies pa kādu ekvipotenciālo līniju. Tādā gadījumā gravitācijas spēks mums netraucē un arī nepalīdz pārvietoties. Bet, ja mēs sākam pa jumtu pārvietoties augšup vai lejup, tad gravitācijas spēka ietekme ir jūtama, jo gravitācijas spēks sāk veikt darbu, kas mums attiecīgi atvieglo vai sarežģī kāpšanas procesu. Ja gribi dzīvē pārbaudīt šeit rakstīto rindu patiesību, tad atceries, ka izpētes procesā ir svarīgi, lai kādam neaizbrauc jumts!

3.att. Plakņu elektriskā lauka ekvipotenciālo līniju ekvivalents gravitācijas laukā
Punktveida lādiņam elektriskā lauka līnijas vairs nav paralēlas, bet veido koncentriskus riņķus ap doto punktveida lādiņu (4. att. a). Arī, piemēram, pozitīva punktveida lādiņa ekvipotenciālajām līnijām var atrast līdzību dabā. Šajā gadījumā tas būtu simetrisks un diezgan spics paugurs (4. att. b), kura smaile atbilst punktveida lādiņa centram. Ja mēs uzkāptu līdz šāda paugura vidum un tad sāktu staigāt apkārt pa kādu ekvipotenciālo līniju, tad gravitācijas lauks mums lieki netraucētu to darīt, bet, tiklīdz mēs sāktu kāpt augstāk vai zemāk, gravitācijas spēks sāktu darīt savu darbu. Negatīvam punktveida lādiņam būtu jāmeklē līdzības ar kādu bedri.
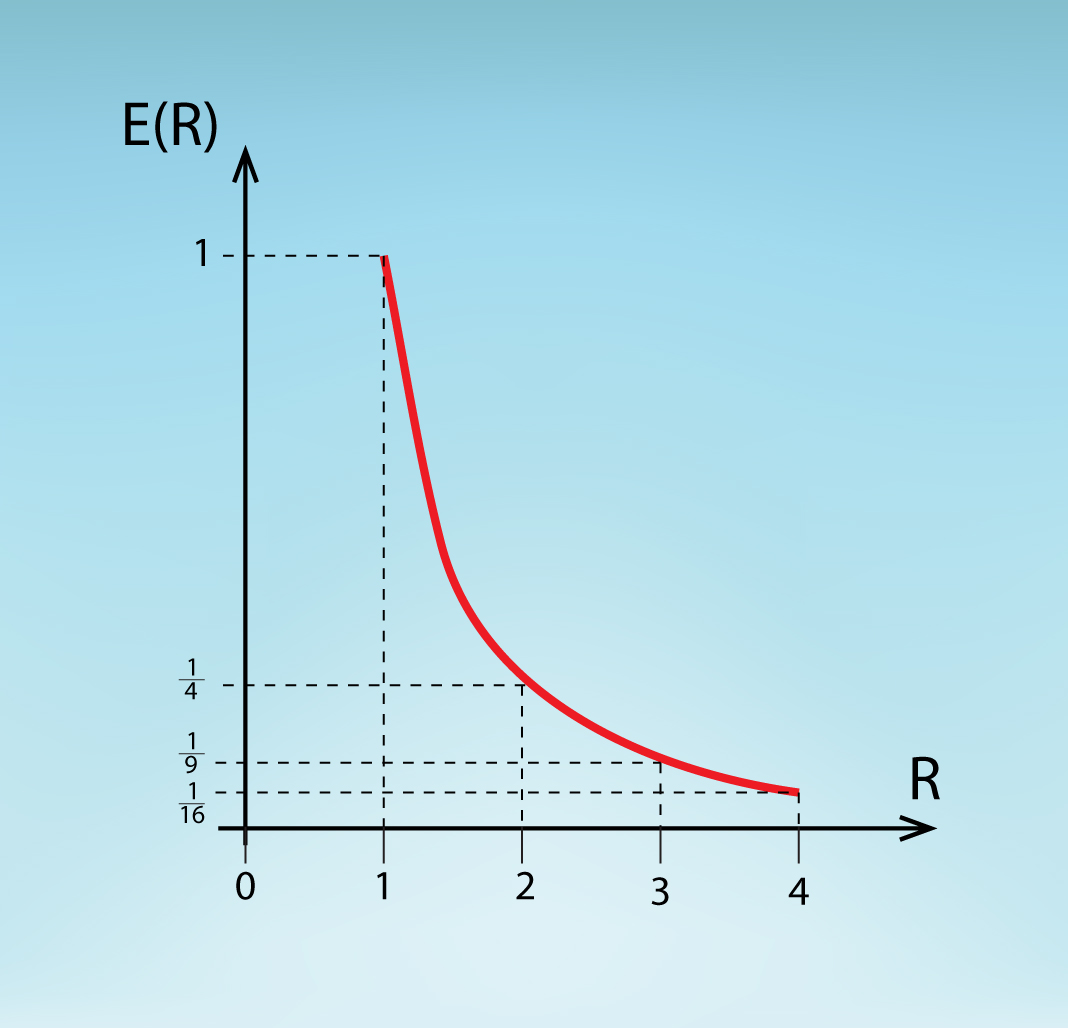
4.att. Punktveida lādiņa elektriskā lauka ekvipotenciālās līnijas
Punktveida lādiņa radīto potenciālu φ var aprēķināt pēc formulas φ = kq : R. Izmantojot šo izteiksmi, var iegūt divu punktveida lādiņu sistēmas potenciālās enerģijas W izteiksmi. Punktveida lādiņa q1potenciāls punktā A (5. att.) ir φ1 = kq1 : R. Ja šajā punktā novietotu otru punktveida lādiņu q2, tad tā potenciālā enerģija ir W = q2φ, ievietojot φ vietā φ1izteiksmi, iegūst divu punktveida lādiņu potenciālās enerģijas izteiksmi, tiem atrodoties attālumā R vienam no otra: W = q1q2k : R.
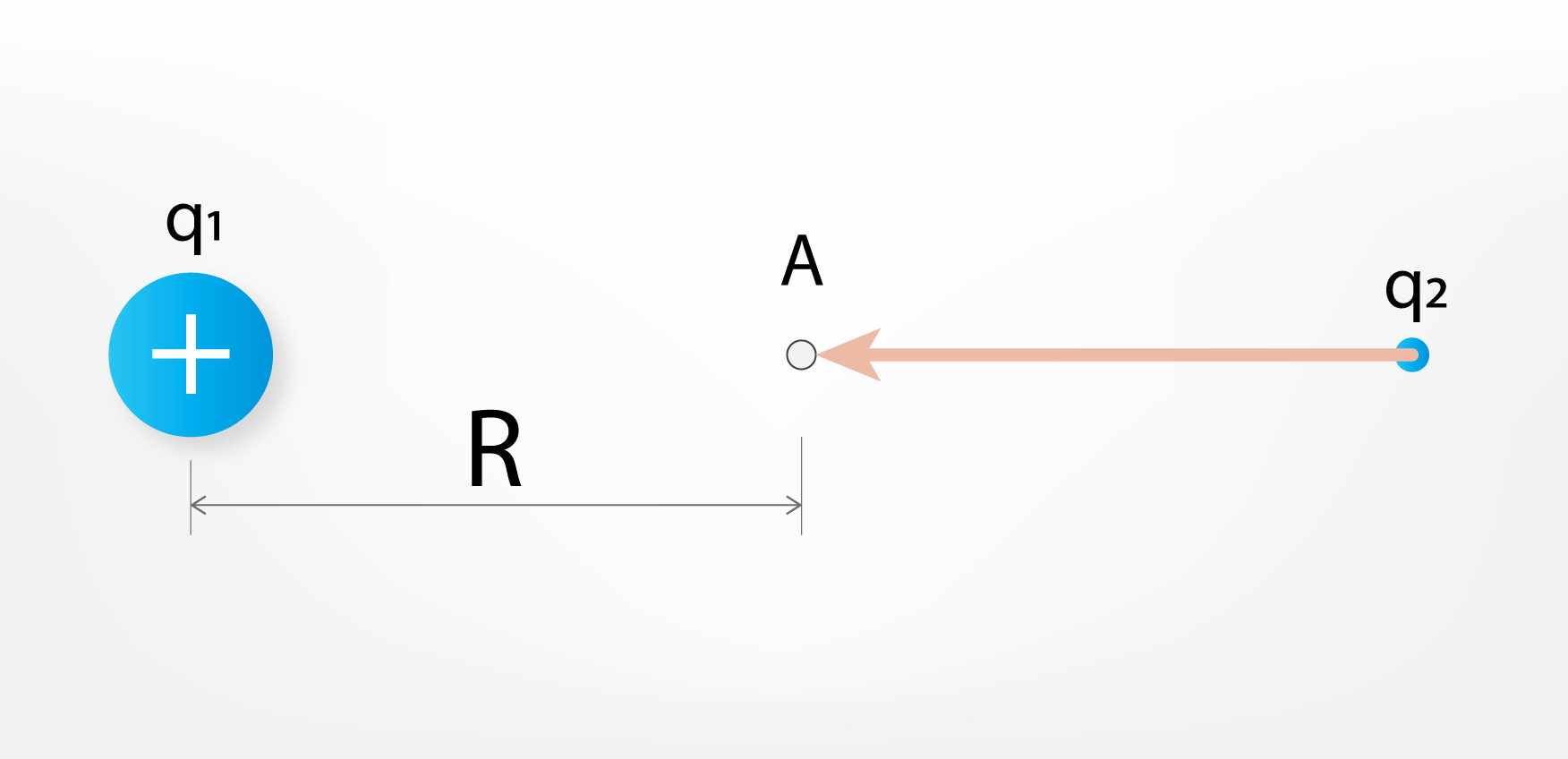
5.att. Divu punktveida lādiņu sistēma
1. solī tika apskatīts elektriskā lauka potenciāls φ = W : q, no kura var iegūtlādētas daļiņas potenciālās enerģijas atkarību no elektriskā lauka potenciāla φ un lādiņa q lieluma, proti, W = qφ. Potenciālo enerģiju homogēnam laukam var izteikt arī caur elektriskā lauka intensitāti E. Jāatceras, ka potenciālās enerģijas izmaiņa ΔW ir vienāda ar spēka F paveikto darbu A, pārvietojot lādiņu attālumā Δd, proti, ΔW = A = FΔd. Elektriskā lauka intensitāti definē kā E = F : q, no tā izsakot spēku, iegūst F = Eq. Šo spēka izteiksmi ieliek ΔW izteiksmē un iegūst ΔW = EqΔd (6. att.).
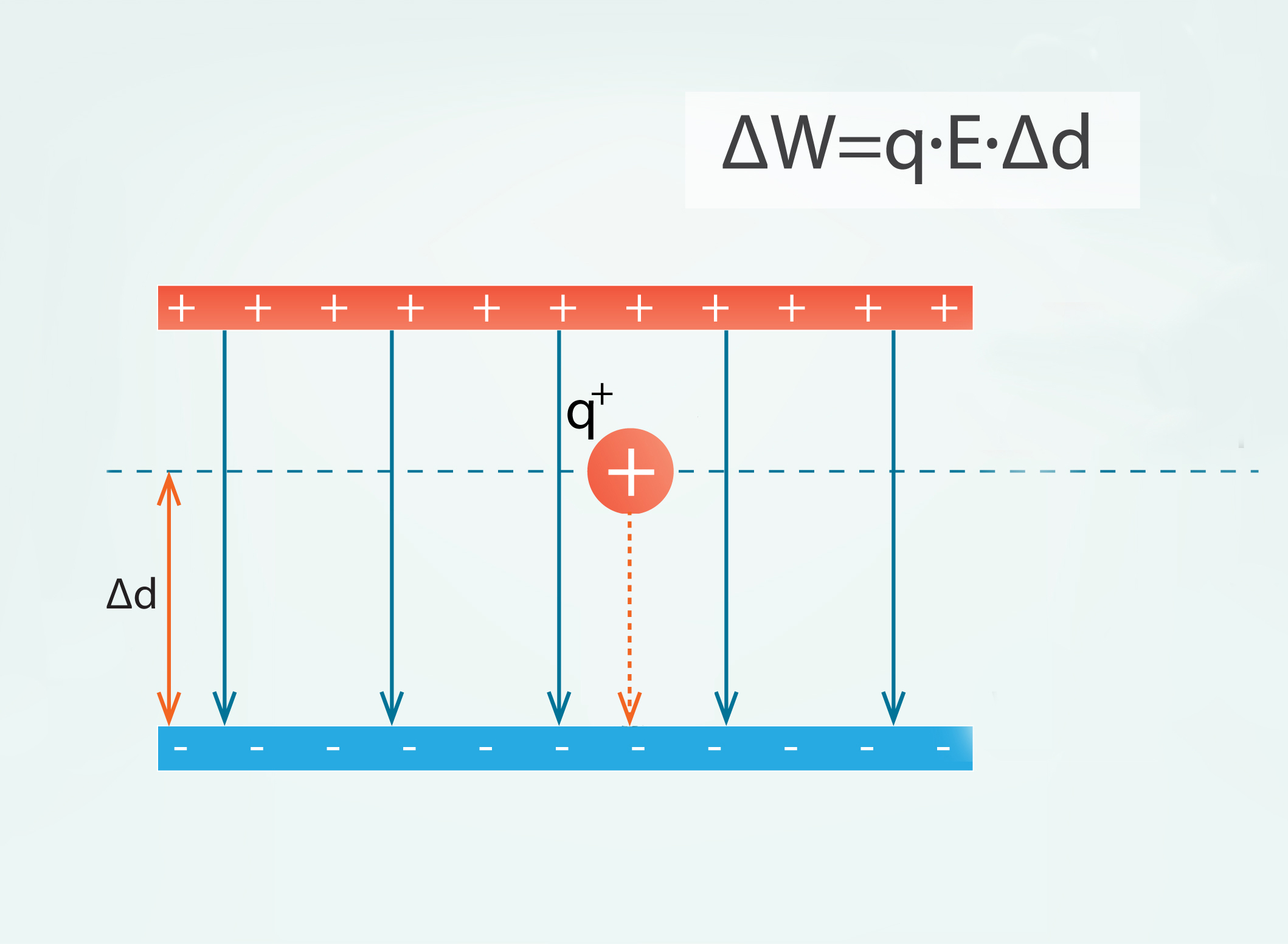
6.att. Lādētas daļiņas potenciālā enerģija elektriskajā laukā
Ja ΔW izsaka kā ΔW = q(φ2 - φ1) = qUun šo izteiksmi ievieto sakarībā ΔW = EqΔd, tad iegūst qU = EqΔd, no kā izriet, ka E = U : Δd. Šī sakarība apstiprina, ka elektriskā lauka intensitāti var mērīt ar mērvienību V : m.
Var uzskatīt, ka starp divām pretēji lādētām plaknēm pastāv homogēns elektriskais lauks (1. att.). Ja šajā laukā tiek pārvietots lādiņš q no punkta 1 uz punktu 2, tad pēc iepriekšējā soļa beigās apskatītās izteiksmes elektriskā lauka darbu varam aprēķināt, izmantojot formulu A = qU, kur U ir spriegums starp punktiem 1 un 2. Homogēnam elektriskajam laukam ir īpašība, ka uz tajā esošu lādiņu darbojas viens un tas pats Kulona spēks F, lai arī kurā punktā lādiņš atrastos. Tādēļ padarīto darbu ir iespējams izteikt caur spēku. Kulona spēks ir vērsts perpendikulāri plaknēm, tādēļ, ja kustība notiek leņķi α pret šī spēka virzienu, tad noietajam ceļam s ir jāatrod pieliktā spēka virzienā vērstā komponente Δd (1. att.). Līdz ar to A = FΔd = Fscosα.
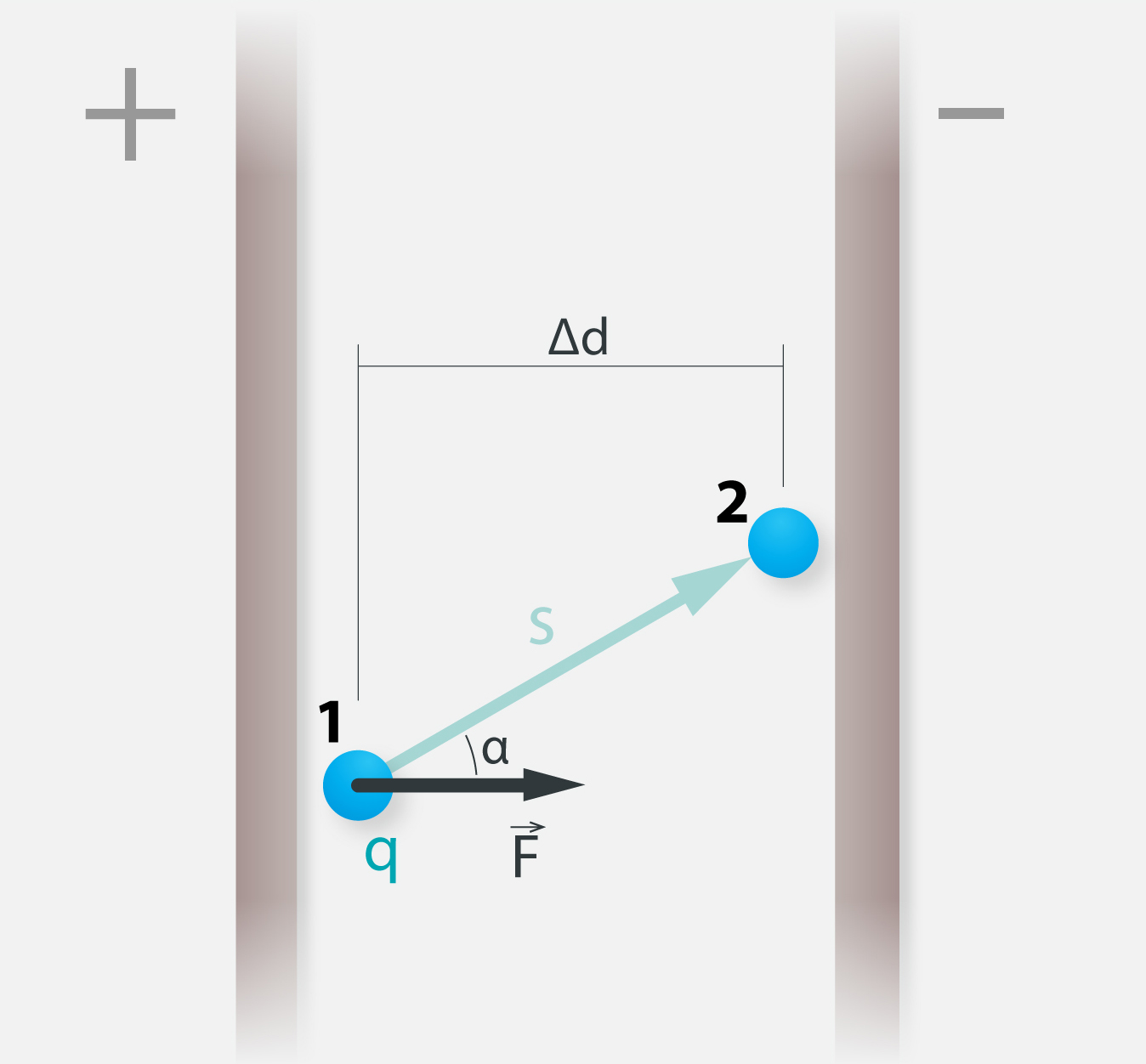
1.att. Lādiņa pārvietošana homogēnā elektriskajā laukā
Apskatot elektriskā lauka intensitātes un ekvipotenciālās līnijas, kas atrodas starp divām uzlādētām plaknēm, redzams, ka šīs līnijas ir perpendikulāras (2. att. a). Izrādās, ka šāds līniju savstarpējais novietojums saglabājas jebkāda avota elektriskajam laukam, vienīgi, ja elektriskā lauka intensitātes līnijas nav paralēlas, tad šī perpendikularitāte nav tik atklāti redzama. Piemēram, punktveida lādiņam ekvipotenciālās līnijas ir riņķa līnijas (2. att. b), tomēr, ja šīs ekvipotenciālās līnijas apskata ļoti mazā apkārtnē ap intensitātes līniju, tad perpendikularitāte atklājas pilnā spožumā.
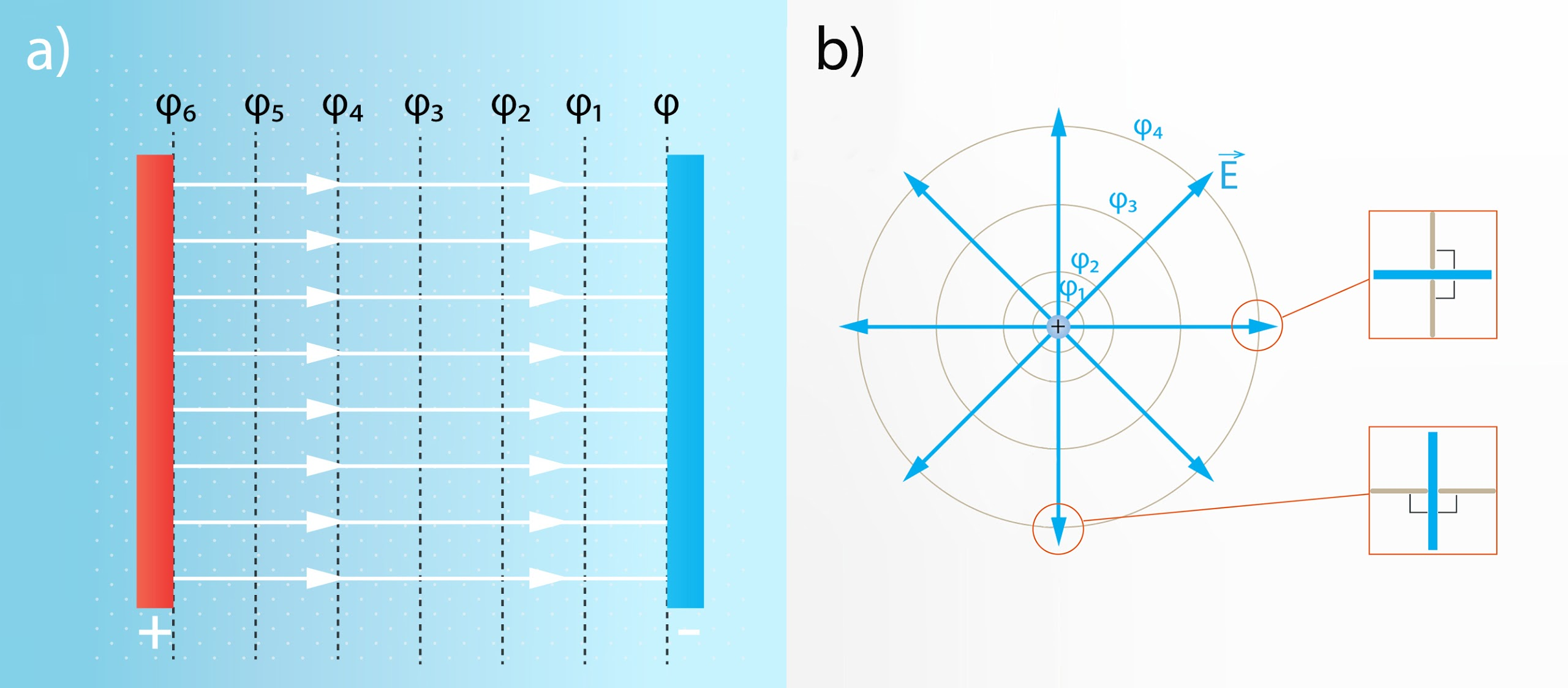
2.att. Elektriskā lauka intensitātes ekvipotenciālās līnijas
Izmantojot apskatīto faktu, ka ekvipotenciālās līnijas ir perpendikulāras elektriskā lauka intensitātes līnijām, mēs varam izmantot iepriekš apskatītu lādiņu sistēmu elektrisko lauku intensitātes attēlojumu un tam pievienot klāt ekvipotenciākās līnijas, piemēram, kā tas izdarīts 3. attēlā.
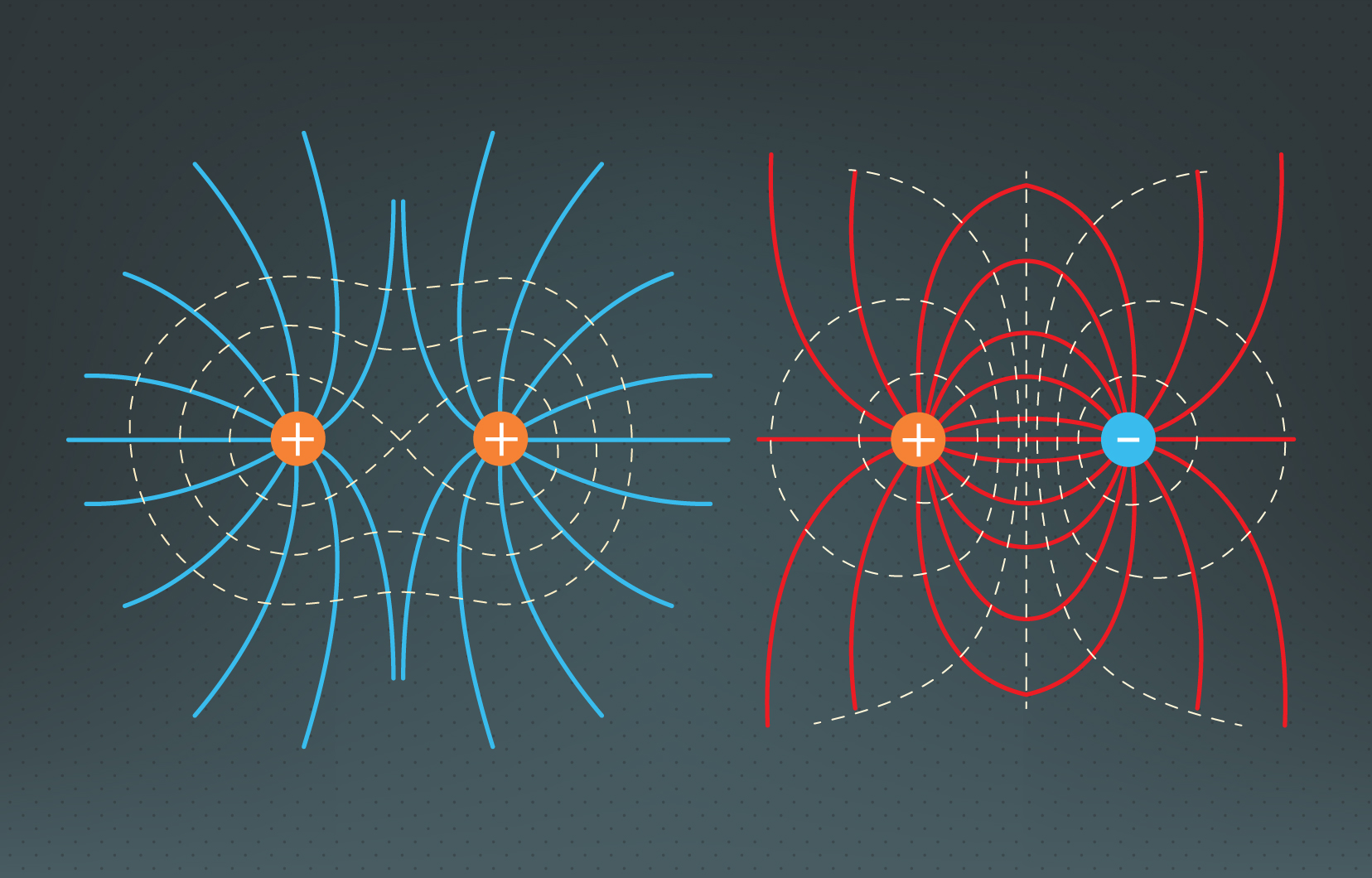
3.att. Elektriskā lauka intensitātes ekvipotenciālās līnijas divu lādiņu sistēmai
Uz Zemes arī dabiski pastāv elektriskais lauks. Par elektriskā lauka nulles līmeni pieņemta zeme. Cilvēks parasti atrodas kontaktā ar zemi, līdz ar to cilvēka ķermenis strādā kā nulles līmeņa paaugstinātājs. Šī iemesla dēļ Zemes elektriskā lauka intensitātes un ekvipotenciālās līnijas izliecas ap cilvēku (4. att.)
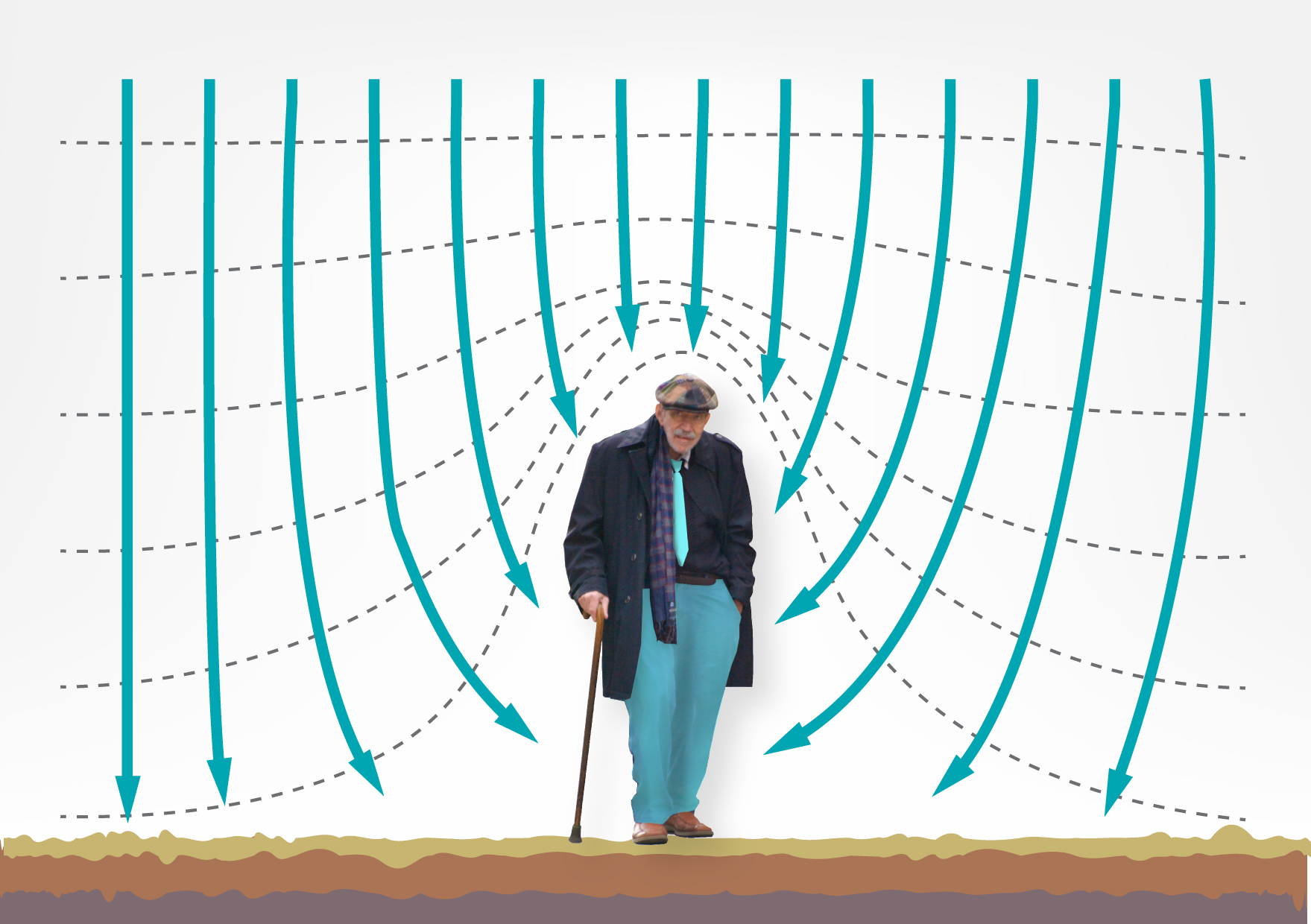
4.att. Cilvēku aptverošais elektriskais lauks