Lai varētu salīdzināt, cik daudz lādiņu ir spējīgs uzņemt kāds vadītājs, tiek lietots kapacitātes jēdziens. Kad vadītājs ir uzlādēts ar lādiņu q, ap to veidojas elektriskais lauks un tā virsma iegūst potenciālu φ. Par vadītāja elektrisko kapacitāti C sauc šo fizikālo lielumu attiecību: C = q : φ (1. att. a). Kapacitātes mērvienība ir farads (F). Kapacitāti ietekmē, piemēram, ķermeņa izmērs. Starp viena materiāla, bet dažāda rādiusa lodītēm jo lielāka ir lodīte, jo lielāka ir tās kapacitāte (1. att. b).
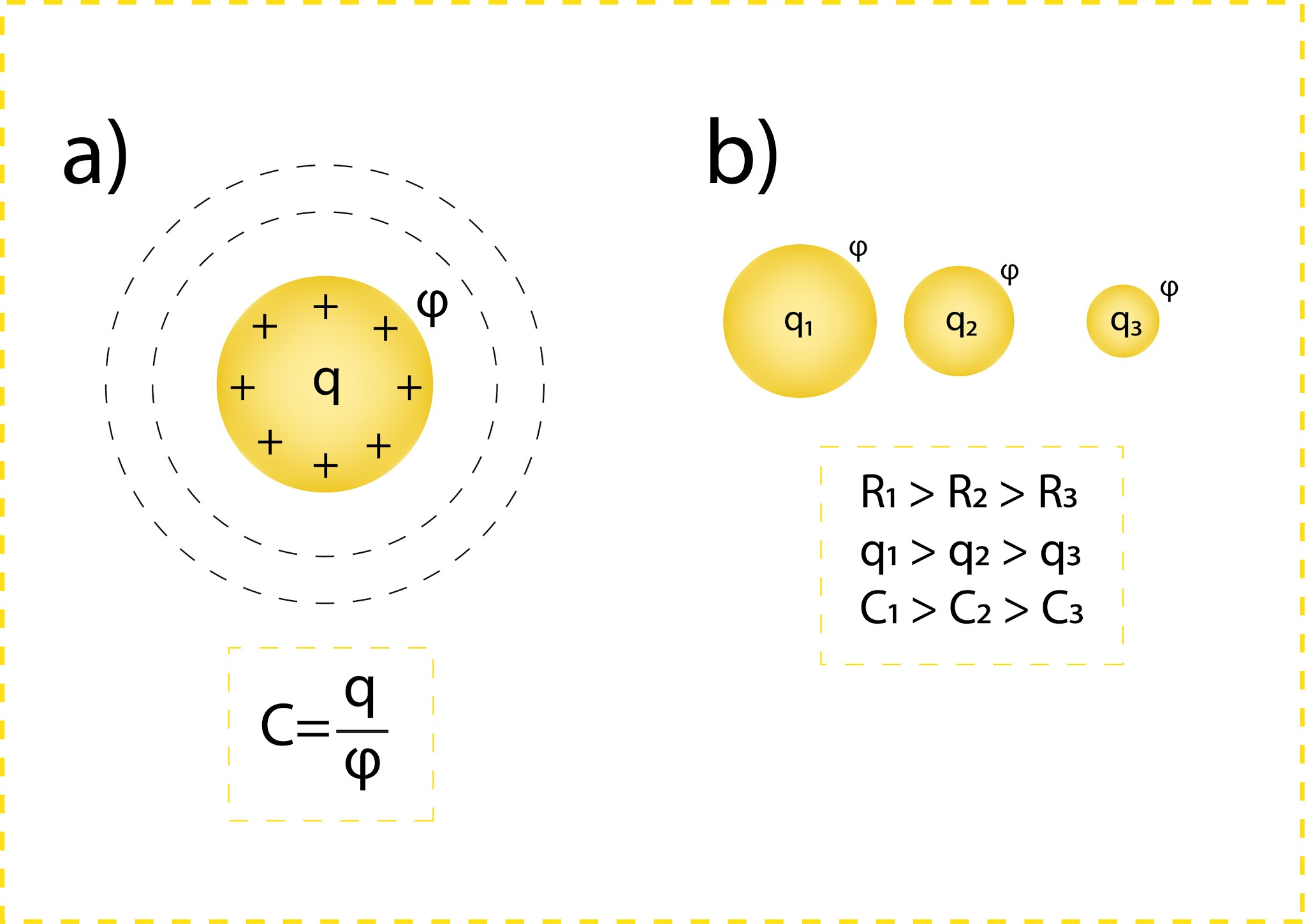
1.att. Vadītāja kapacitāte
Dažādās tehnoloģijās lādiņa uzkrāšanai tiek lietoti kondensatori. Kondensatoru var izveidot no divām vadītāja plāksnēm, kas uzlādētas ar vienāda lieluma q, bet pretēju zīmju lādiņiem. Šo sauc par plakņu kondensatoru. Šāda kondensatora elektriskā kapacitāte C = q : U, kur U ir potenciālu starpība jeb spriegums starp plāksnēm (2. att.). Izmantojot kondensatora ģeometriskos izmērus, kapacitāti var izteikt ar formulu C = ε0εS : d, kur
ε0- elektriskā konstante, ε0 ≈ 8,85*10-12 F / m
ε -relatīvā dielektriskā caurlaidība
S- plākšņu laukums, m2
d - attālums starp plāksnēm, m
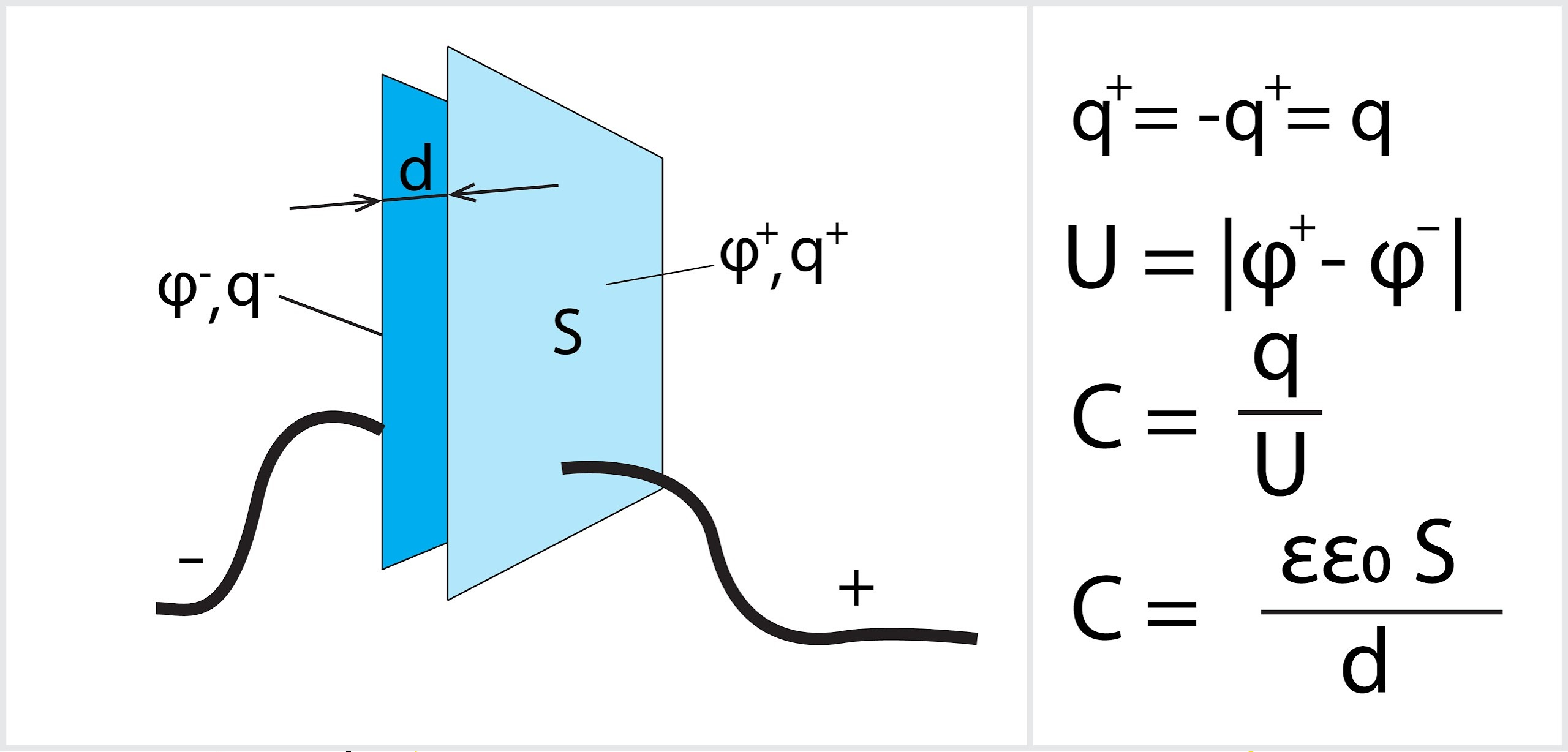
2.att. Plakņu kondensators
Lai iegūtu dažādas kapacitātes vērtības, kondensatorus ir iespējams slēgt dažādu veidu slēgumos. Kondensatoru slēgumu sauc par kondensatoru bateriju. Viens no slēguma veidiem ir virknes slēgums, kurā kondensatori saslēgti cits aiz cita (3. att.). Šādā slēguma kopējo kapacitāti C, kopējo spriegumu U un kopējo lādiņu q ar katra atsevišķā kondensatora raksturlielumiem saista šādas sakarības (3. att.):
1:C = 1:C1 + 1 : C2 + ... + 1 : Cn
U = U1 + U2 +...+ Un
q = q1 = q2 =...= qn
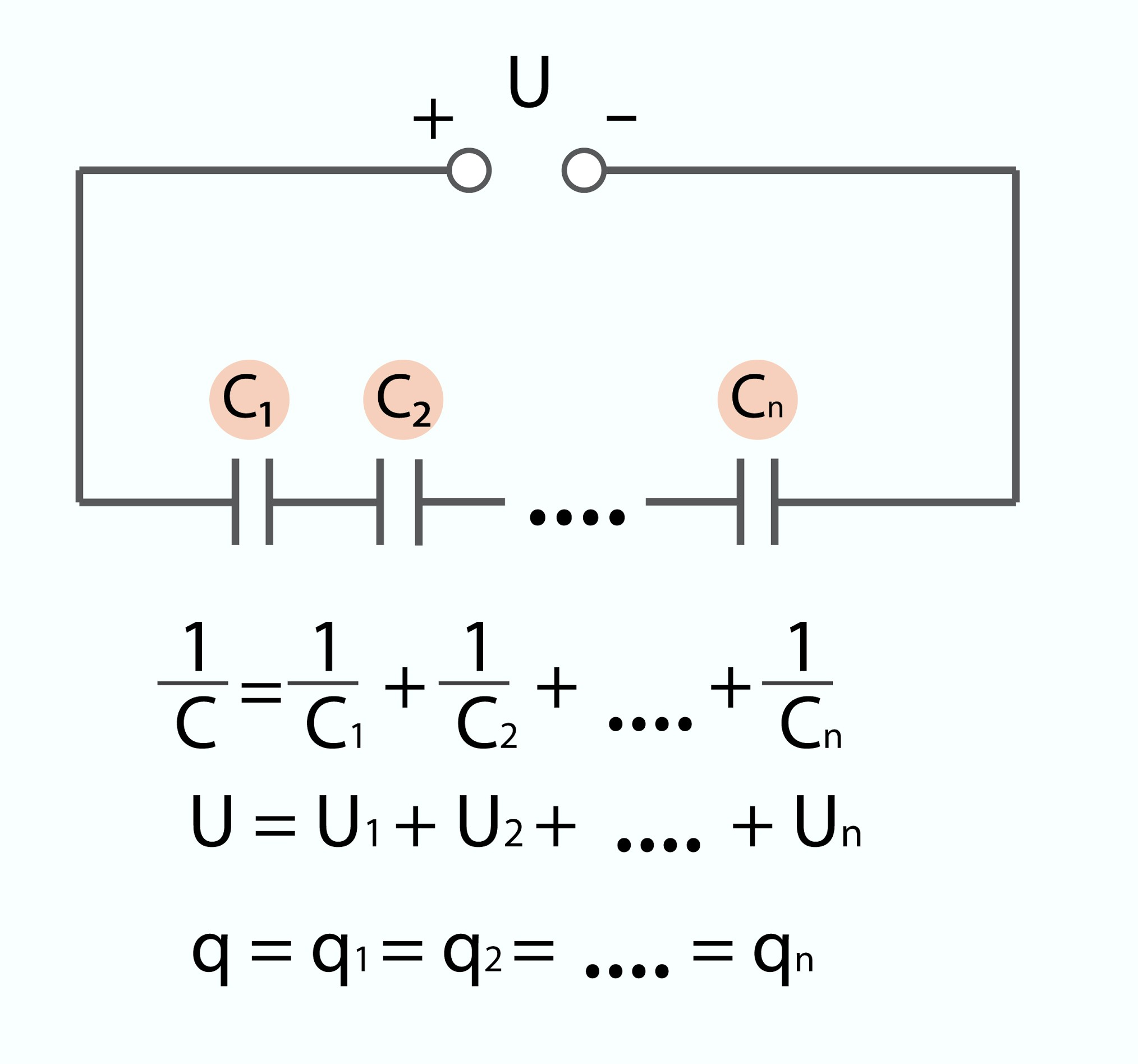
3.att. Kondensatoru virknes slēgums
Kondensatoru paralēlajā slēgumā savienotas visu kondensatoru pozitīvās plaknes, kā arī visas negatīvās (4. att.). Šādā gadījumā kondensatora baterijas raksturlielumi pakļaujas šādām sakarībām:
C = C1 + C2 + ... + Cn
U = U1 = U2 = ... = Un
q = q1 + q2 + ... + qn
Spied uz iekrāsotā vārda un izmēģini saslēgt kondensatoru slēgumus!
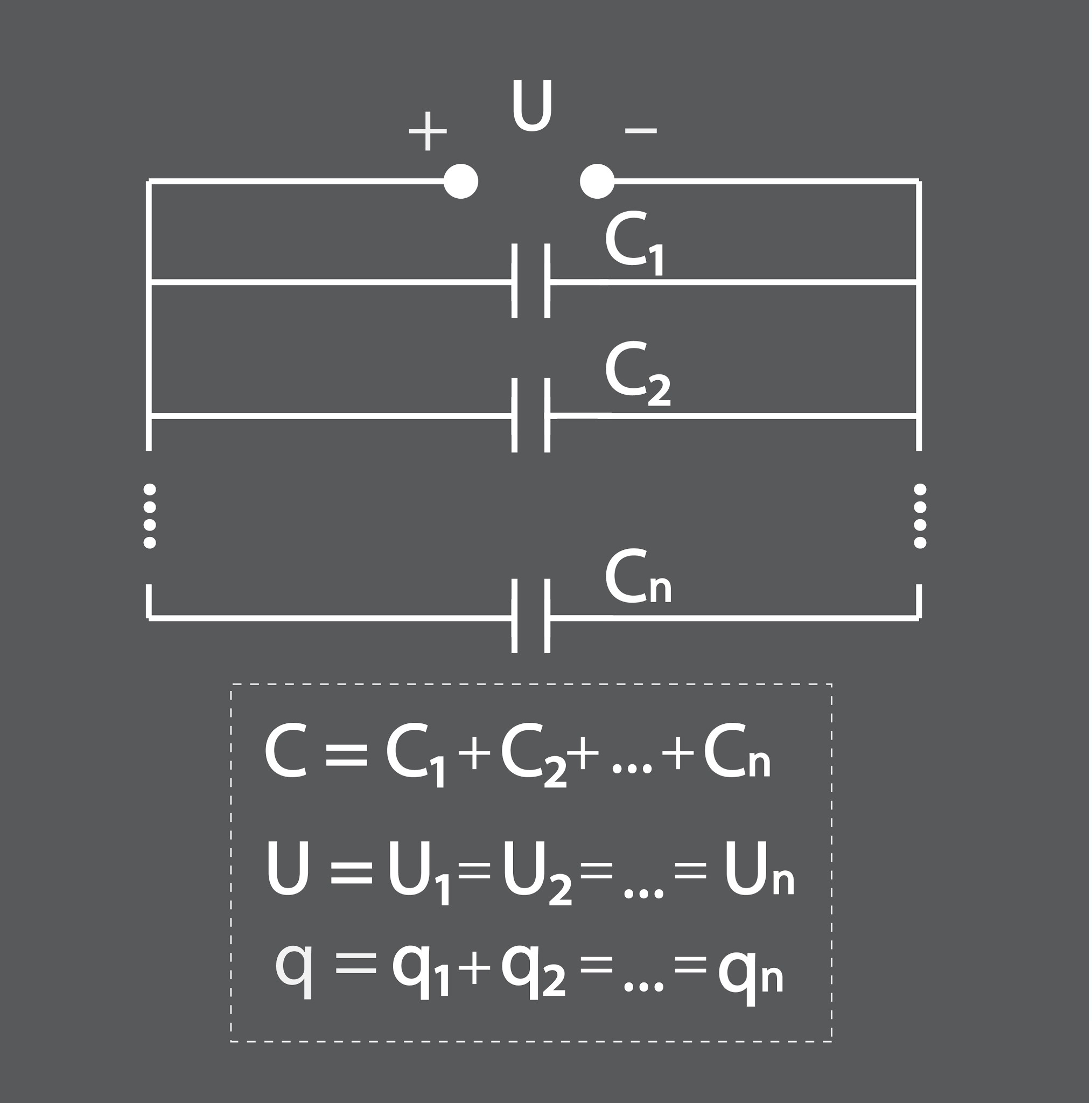
4.att. Kondensatoru paralēlais slēgums
Uzlādētā kondensatorā vai kondensatoru baterijā ir noglabāts zināms daudzums elektriskā lauka enerģijas W, kuru var aprēķināt, zinot kondensatora sistēmas raksturlielumus. Ja ir zināma kondensatora kapacitāte C un spriegums U, tad W = CU2 : 2. Savukārt ja sprieguma vietā ir zināms lādiņš q, kas noglabāts kondensatorā, tad W = q2 : 2C.
Izmēģini kondensatoru laboratoriju!
Ja mēs kādam ķermenim, kas uzlādēts ar lādiņu q+, vēlamies pievienot papildu lādiņu q, tad pievienošanas procesā mums ir jāpārvar spēks F= qE, ko rada uzlādētā ķermeņa elektriskais lauks (1. att.). Ja pievieno papildu lādiņu, tad ķermeņa kopējais lādiņš palielinās. Līdz ar to palielinās elektriskā lauka intensitāte, ko rada šis uzlādētais ķermenis, tādēļ nākamo lādiņu pievienot būs grūtāk.
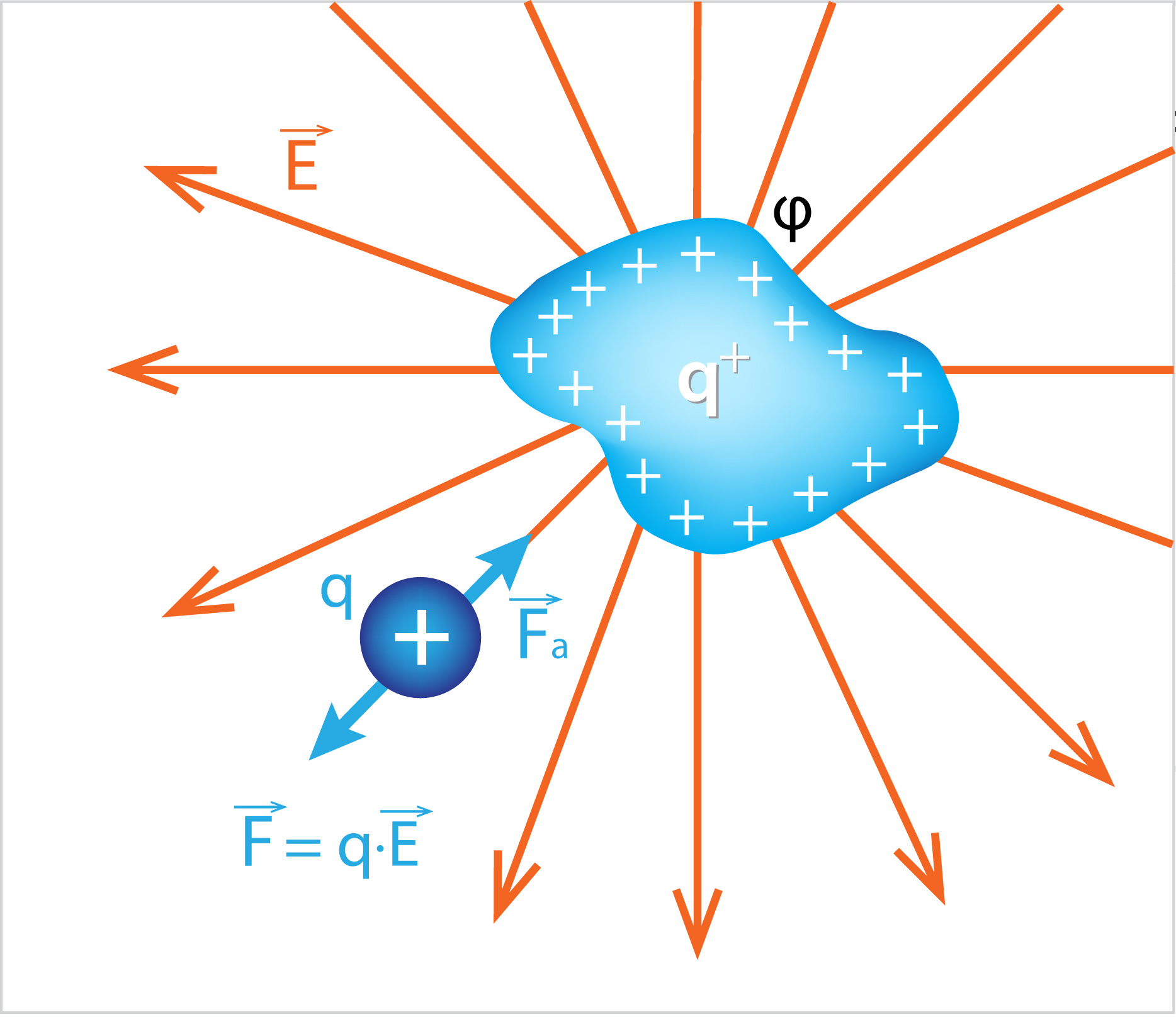
1.att. Lādiņa pievienošana uzlādētam ķermenim
Lādiņu sistēmai, kas sastāv no diviem pretēji uzlādētiem ķermeņiem ar lādiņiem q+un q-, papildu lādiņu pievienot ir vieglāk, jo attiecīgās vietās abu ķermeņu radītie elektriskie lauki viens otru kompensē, līdz ar to papildu lādiņam ir jāpārvar mazāks spēks F = qE (2. att.). Šādai sistēmai kapacitāte C ir lielāka nekā vienam pašām uzlādētam ķermenim (1. att.). Tātad kapacitāte norāda to, cik viegli sistēmai ir pievienot papildu lādiņu. Jo vieglāk to ir izdarīt, jo lielāka ir sistēmas kapacitāte.
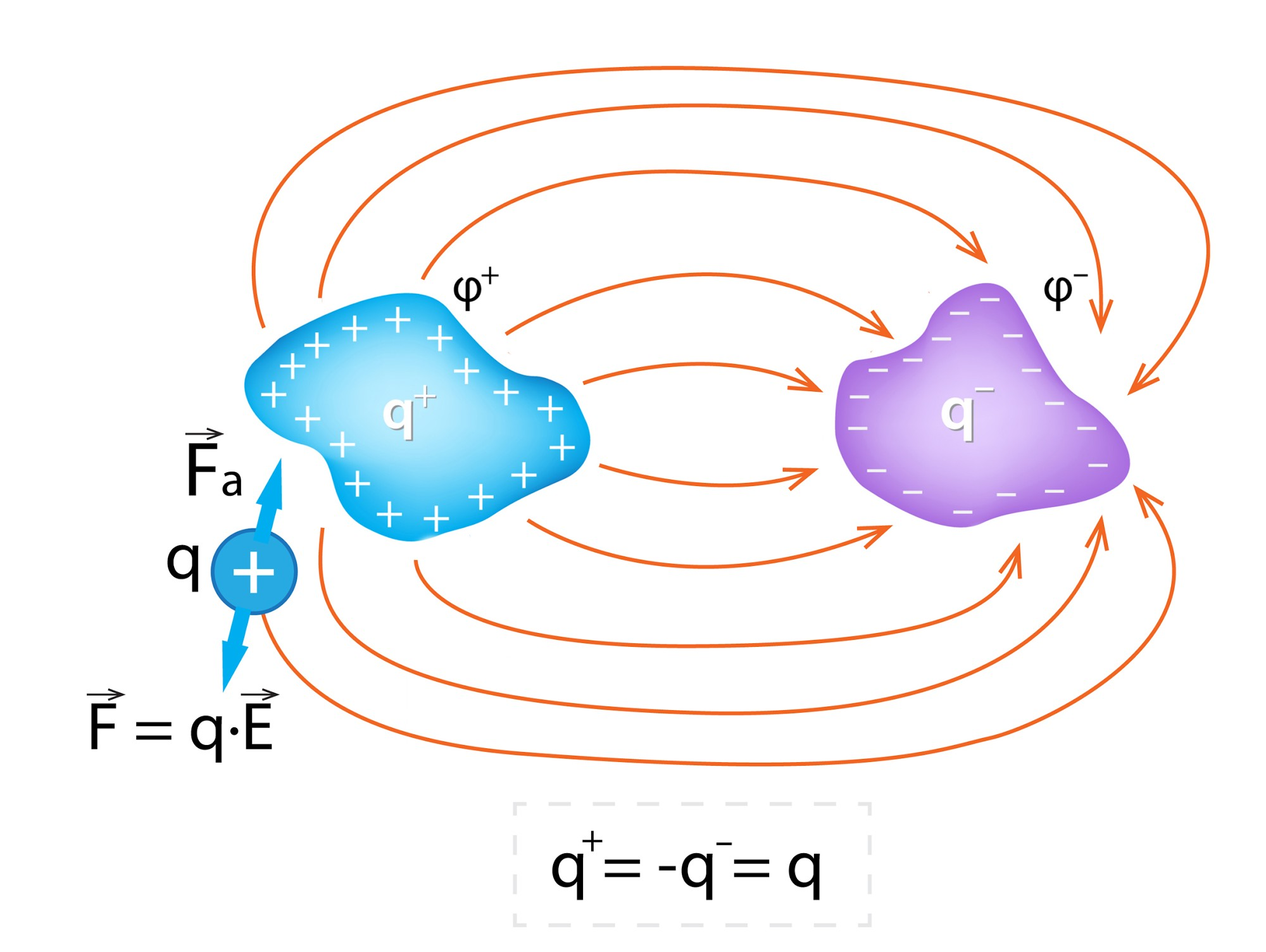
2.att. Lādiņu sistēma ar diviem pretēji lādētiem ķermeņiem
To var salīdzināt ar sabiedrisko autobusu. Ja autobuss ir tukšs, pasažieriem tajā iekāpt ir viegli. Kad autobuss jau ir piepildījies (3. att.), tad katram nākošajam pasažierim ir jāsastopas ar zināmu piepūli, lai iekļūtu autobusā. Līdz ar to, jo lielāks ir autobuss (lielāka kapacitāte), jo vairāk cilvēku tajā var iekāpt, un vēlāk iestājas tas brīdis, kad katram nākošajam pasažierim ir jāpiespiežas, lai tiktu iekšā.

3.att. Pārpildīts autobuss Dienvidāzijā
Plakņu kondensators ir sistēma, kas sastāv no diviem pretēji uzlādētiem ķermeņiem – plaknēm. Starp plaknēm abu plakņu radītie elektriskie lauki ir vērsti vienā virzienā, tādā veidā viens otru pastiprinot, taču ārpus plaknēm elektriskie lauki ir vērsti pretēji viens otram (4. att. a), tādēļ tie viens otru dzēš. Gala rezultātā ārpus plaknēm elektriskā lauka faktiski nav, tas ir koncentrēts starp plaknēm (4. att. b), tādēļ šādam kondensatoram ir viegli pievienot lādiņus no ārpuses, jo nav elektriskā lauka, kas aizturētu lādiņu pievienošanai. Tas ļauj sasniegt augstu kondensatora kapacitāti.
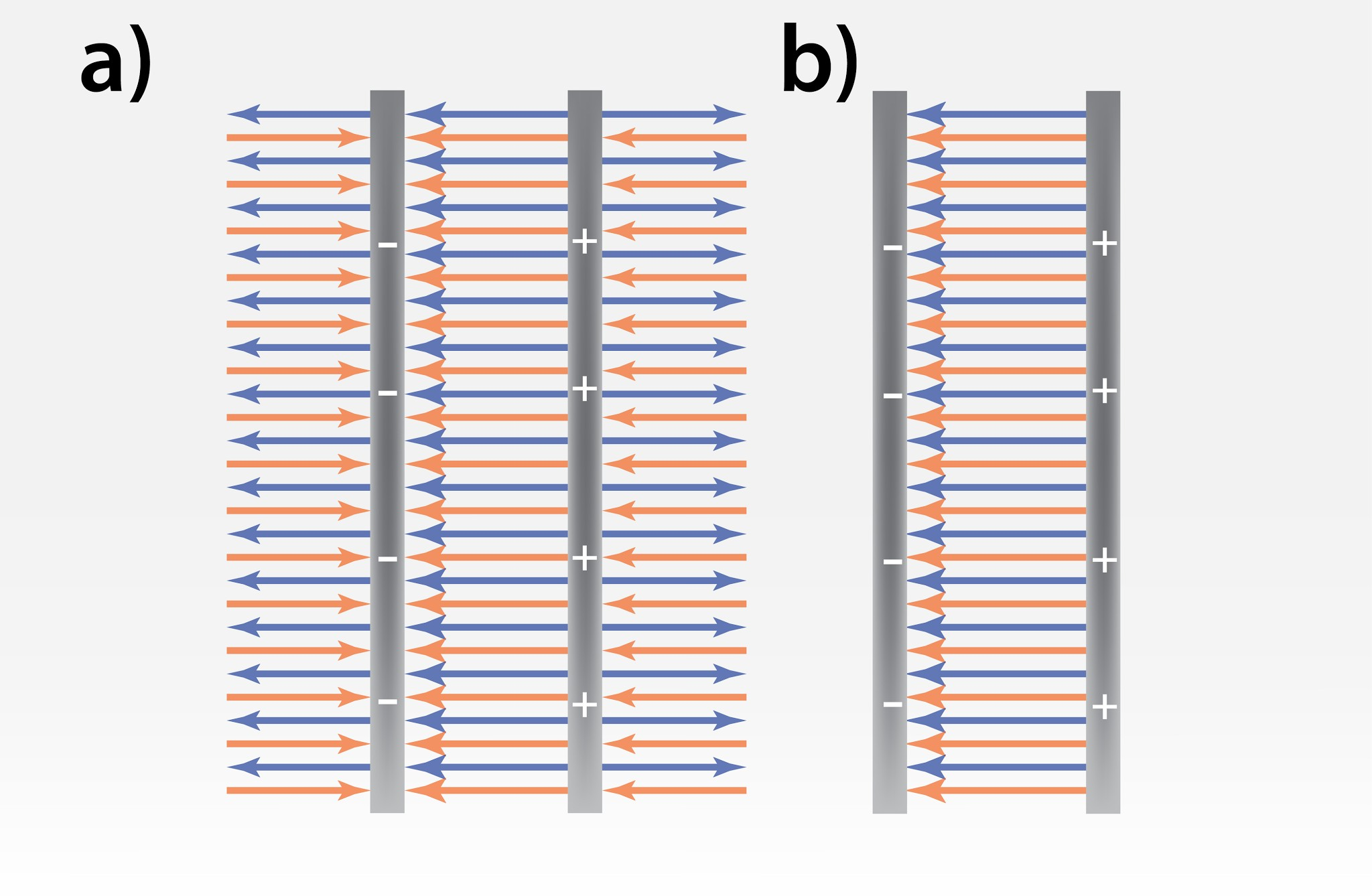
4.att. Plakņu kondensatora elektriskais lauks
Pēc kapacitātes definīcijas C = q : U. Plakņu kondensatoram lādiņš q = σS, kur σ ir lādiņu blīvums (C : m2), bet S ir plaknes laukums (m2). Spriegumu U (V) starp plaknēm var izteikt kā U = Ed, kur d ir attālums starp plaknēm metros, bet E ir plakņu radītā elektriskā lauka intensitāte E = σ : (ε0ε). Apvienojot visas minētās formulas, iegūst plakņu kondensatora elektriskās kapacitātes formulu C = ε0εS : d.
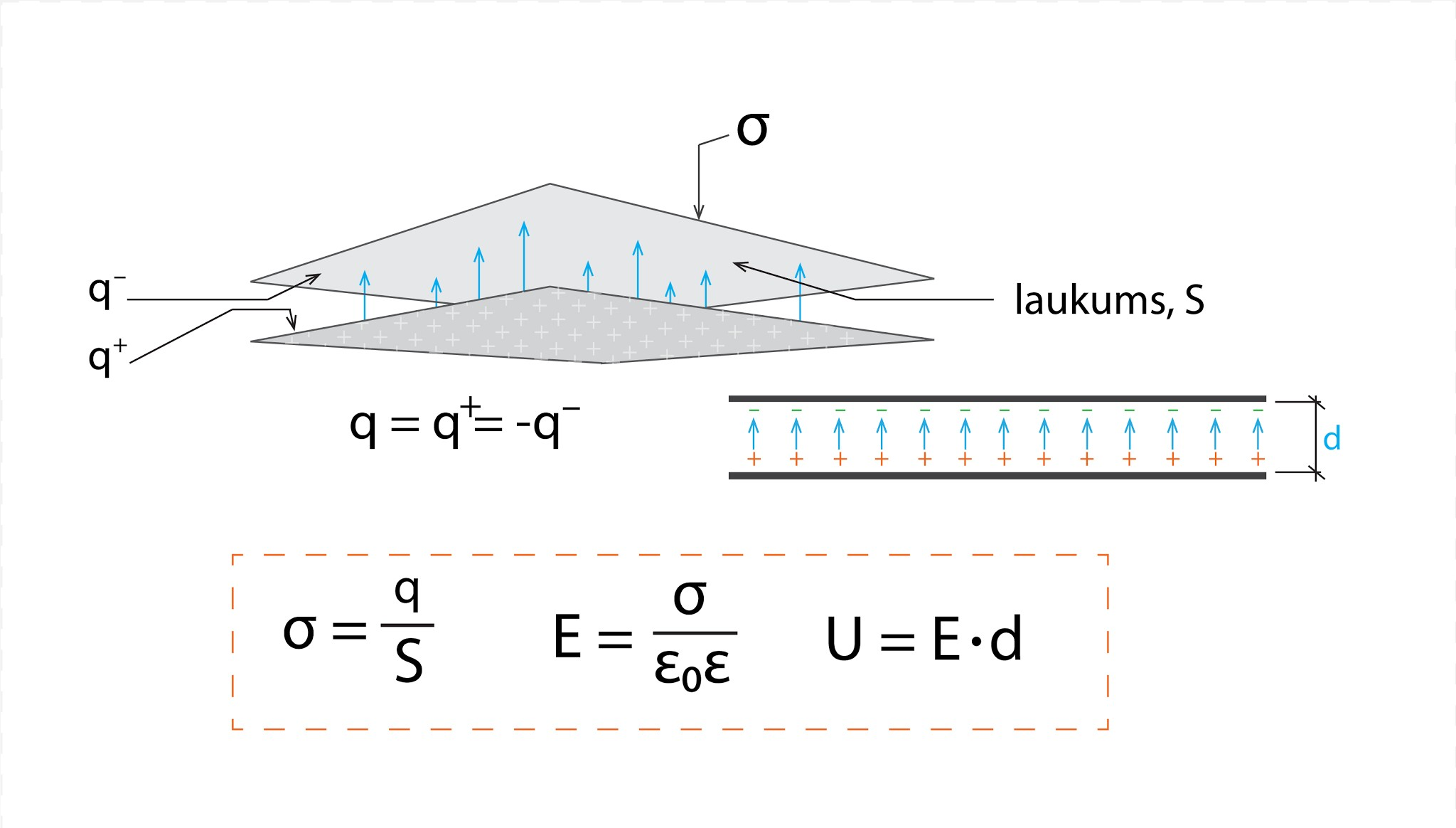
5.att. Plakņu kondensatora raksturlielumi
Kondensatoru virknes slēgumā kondensatoru plaknes savienotas cita aiz citas. Viena kondensatora plakne ir pievienota strāvas avota pozitīvajam polam, tādēļ tā iegūst pozitīvu lādiņu q+, otra kondensatora plakne elektrostatiskās indukcijas dēļ uzlādējas ar negatīvu lādiņu q-. Tā tas notiek viscaur virknei, tādēļ visiem kondensatoriem šajā slēgumā ir viens un tas pats lādiņš q = q+ = -q-. Līdz ar to spriegums katram kondensatoram (6. att.): U1 = q : C1 un U2 = q : C2. No šī izriet, ka virknes slēguma mazākais spriegums ir kondensatoram ar lielāko kapacitāti.
Kondensatoru virknes slēguma kopējais spriegums ir vienāds ar katra atsevišķā kondensatora spriegumu summu, līdz ar to divu kondensatoru sistēmai U = U1 + U2 = q : C1 + q : C2 = q(1 : C1 + 1 : C2) (6. att.).
Kondensatoru baterijas kopējo kapacitāti izsaka izteiksme 1 : C = 1 : C1 + 1 : C2 +...+ 1 : Cn. Divu kondensatoru virknes slēguma gadījumā 1 : C = 1 : C1 + 1 : C2, ko var pārveidot uz C = C1C2 : (C1+C2) (6. att.).
Ja virknē ir saslēgti n vienādi kondensatori un katra kondensatora kapacitāte ir C0, tad kopējo virknes kapacitāti C var izteikt ar formulu C = C0 : n.
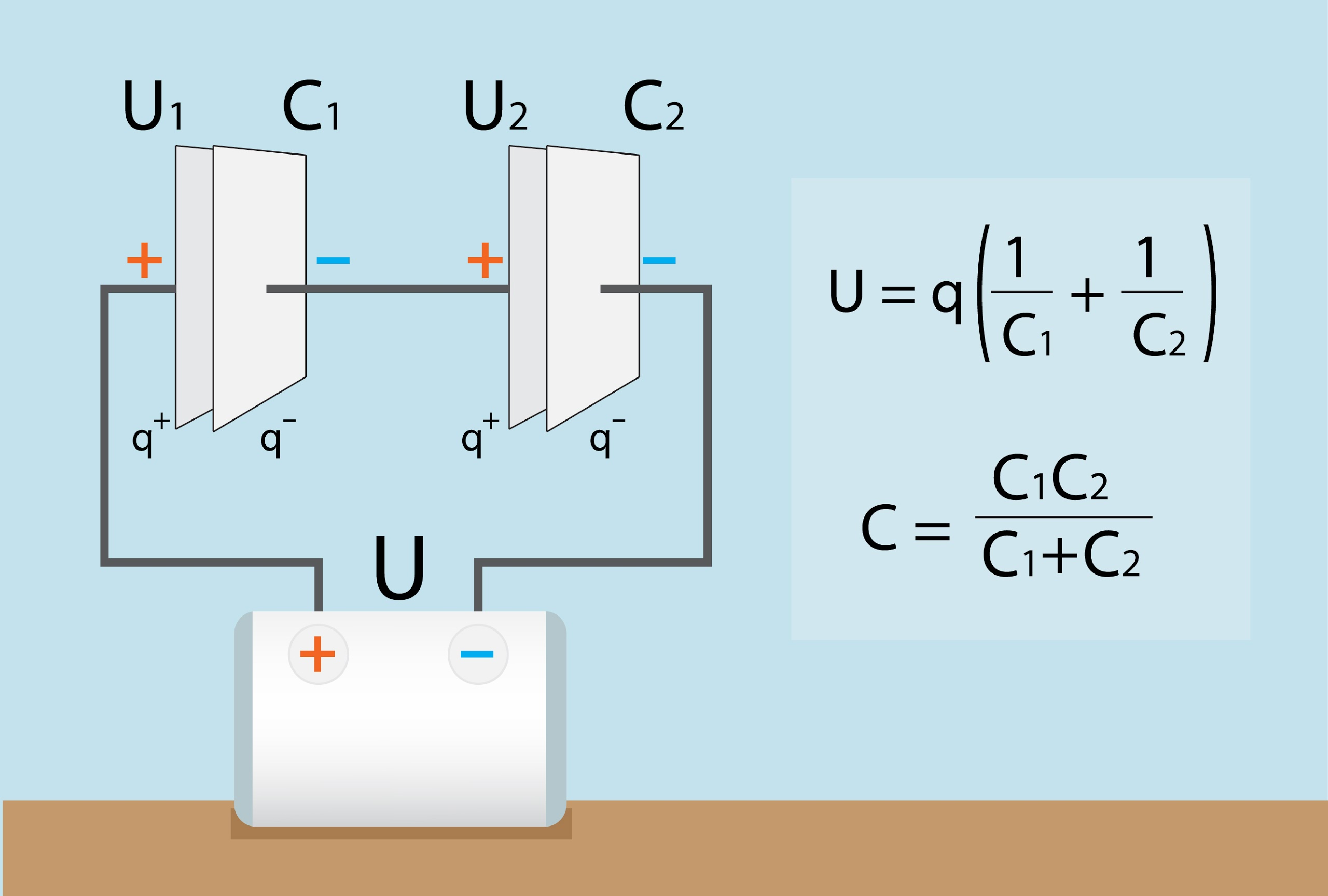
6.att. Divu kondensatoru virknes slēgums
Ja divus kondensatorus ar kapacitātēm C1un C2saslēdz paralēli (7. att.), tad spriegums visiem kondensatoriem ir vienāds: U = U1 = U2. Tas ir tādēļ, ka katra kondensatora pozitīvā plakne saskaras ar strāvas avota pozitīvo polu un attiecīgi katra kondensatora negatīvā plate saskaras ar strāvas avota negatīvo polu, līdz ar to tiek iegūts tas pats spriegums, kāds ir starp strāvas avota spailēm, proti, U.
Paralēlajā slēgumā lādiņa lielumu q, kas uzkrājas katrā kondensatorā, nosaka attiecīgā kondensatora kapacitāte. Jo lielāka kapacitāte, jo lielāks lādiņš uzkrājas (7. att.). Kā jau paralēlajam slēgumam, kopējā kondensatoru baterijas kapacitāte ir vienāda ar atsevišķo kapacitāšu summu: C = C1 + C2.
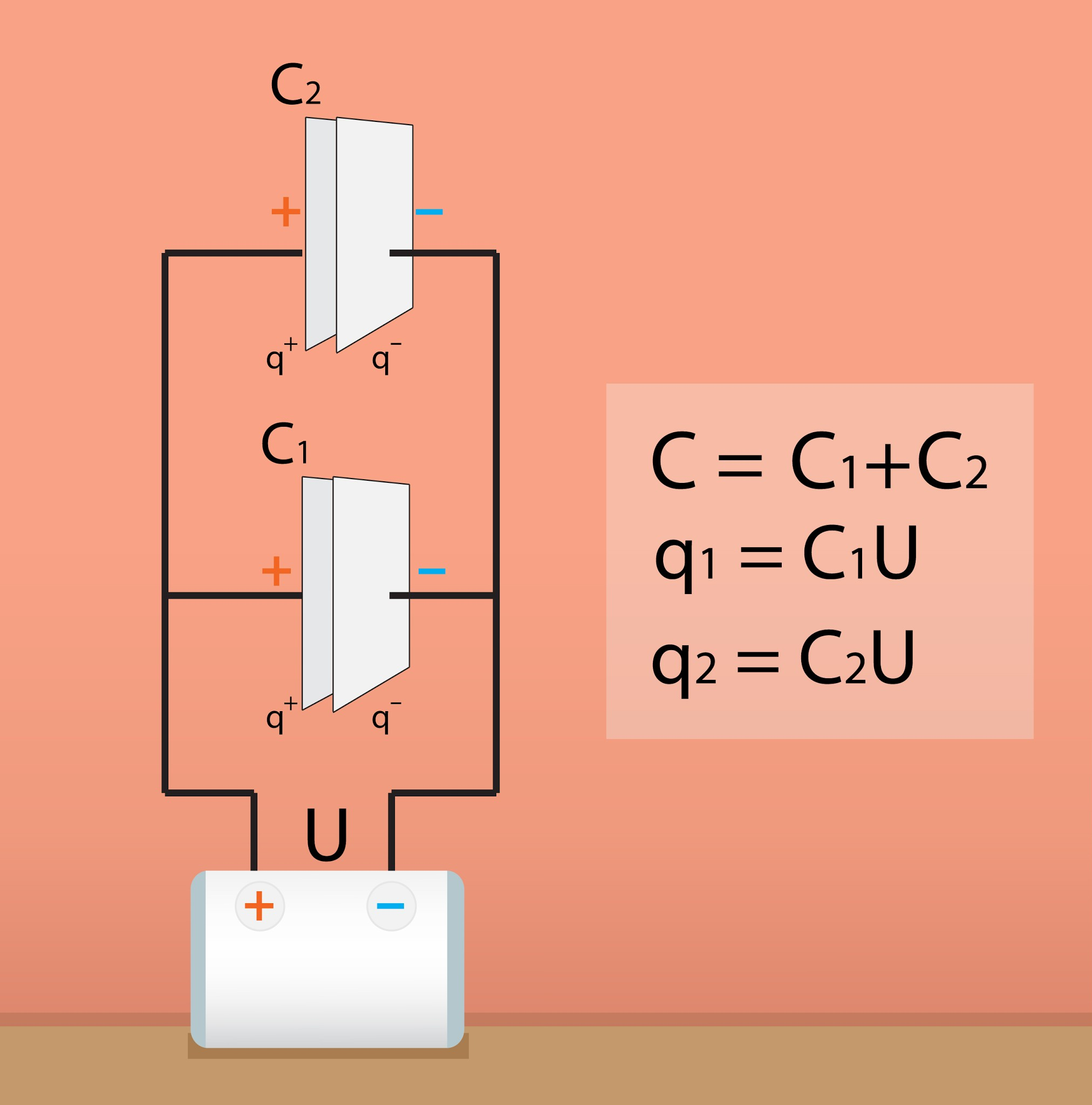
7.att. Divu kondensatoru paralēlais slēgums
Uzlādētā kondensatorā ir uzkrājusies elektriskā lauka enerģija, jo uzlādes procesā elektriskais lauks ir pārvietojis daļu lādiņu no vienas kondensatora plates uz otru (8. att.). Sadaļā par elektriskā lauka potenciālu tika aplūkota lādiņa potenciālās enerģijas izteiksme elektriskajā lauka: W = Eqd, kur
E - elektriskā lauka intensitāte (V : m),
q - lādiņa lielums (C),
Δd - attālums līdz potenciāla nulles līmenim (m).
Šo izteiksmi var izmantot, lai iegūtu uzlādēta kondensatora elektriskā lauka enerģiju, apskatot kondensatora pozitīvi uzlādēto plakni kā lādiņu q, kas atrodas attālumā d no elektriskā lauka avota – negatīvi uzlādētās plaknes (8. att.).
Iegūta kondensatora elektriskā lauka enerģijas formula W = CU2 : 2, kur
C - kapacitāte, F
U - spriegums, V
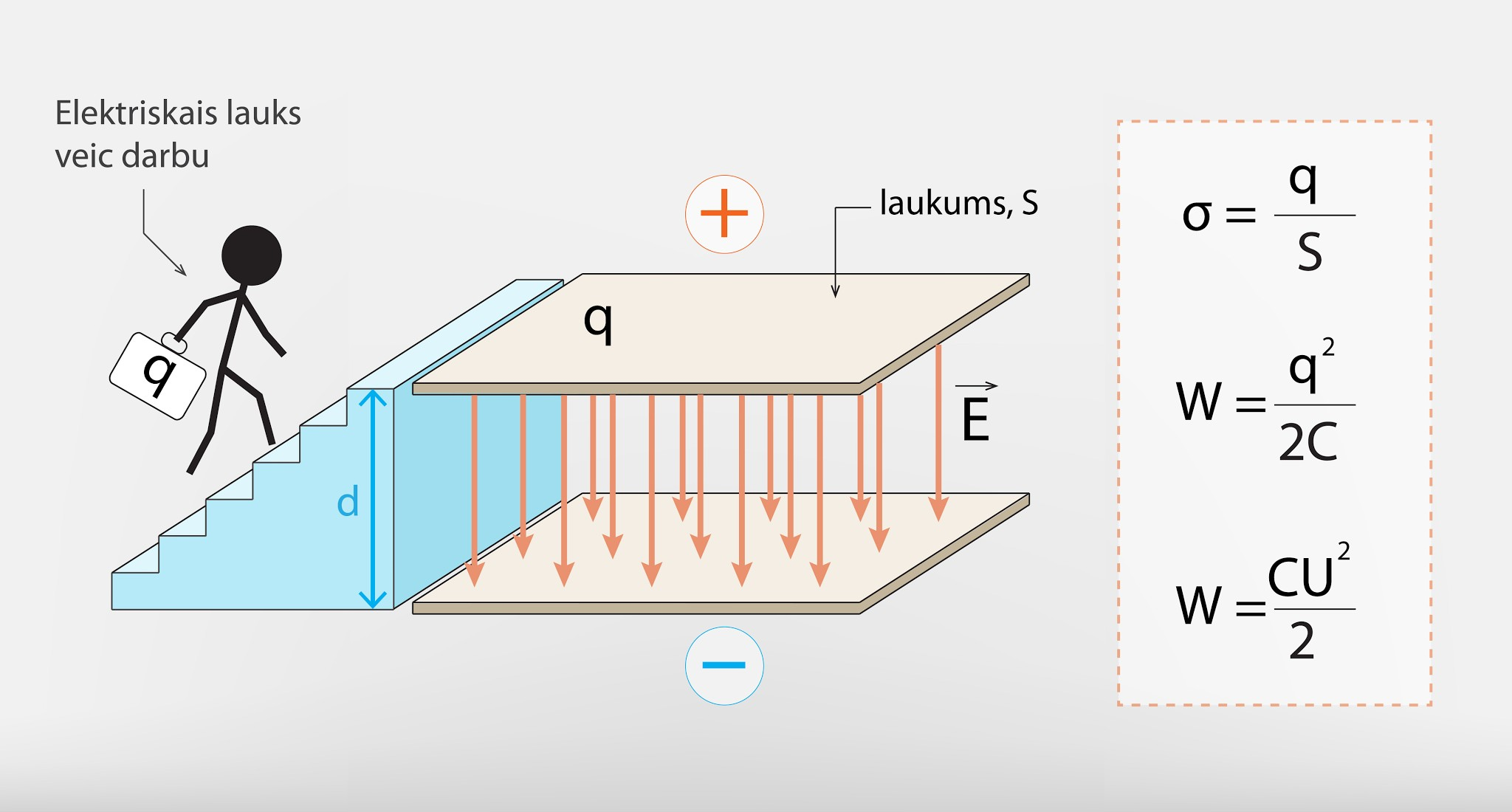
8.att. Uzlādēta kondensatora enerģija
Ja kondensators ir tukšs, tad spriegums starp tā klājumiem U = 0. Lai kondensatoru uzlādētu, tas ir jāpieslēdz kādam strāvas avotam (1. att. a). Kamēr spriegumu atšķirība starp strāvas avotu un kondensatoru ir liela, ķēdē plūst stipra strāva un lādiņi pamazām tiek pārvietoti no vienas kondensatora plates uz otru (1. att. b), tādā veidā pieaudzējot spriegumu uz kondensatora plaknēm. Kad kondensatora spriegums sāk tuvoties strāvas avota spriegumam, strāva ķēdē sāk samazināties (1. att. c), līdz beidzot vispār pārstāj plūst, kad kondensatora spriegums kļūst vienāds ar strāvas avota spriegumu (1. att. d).
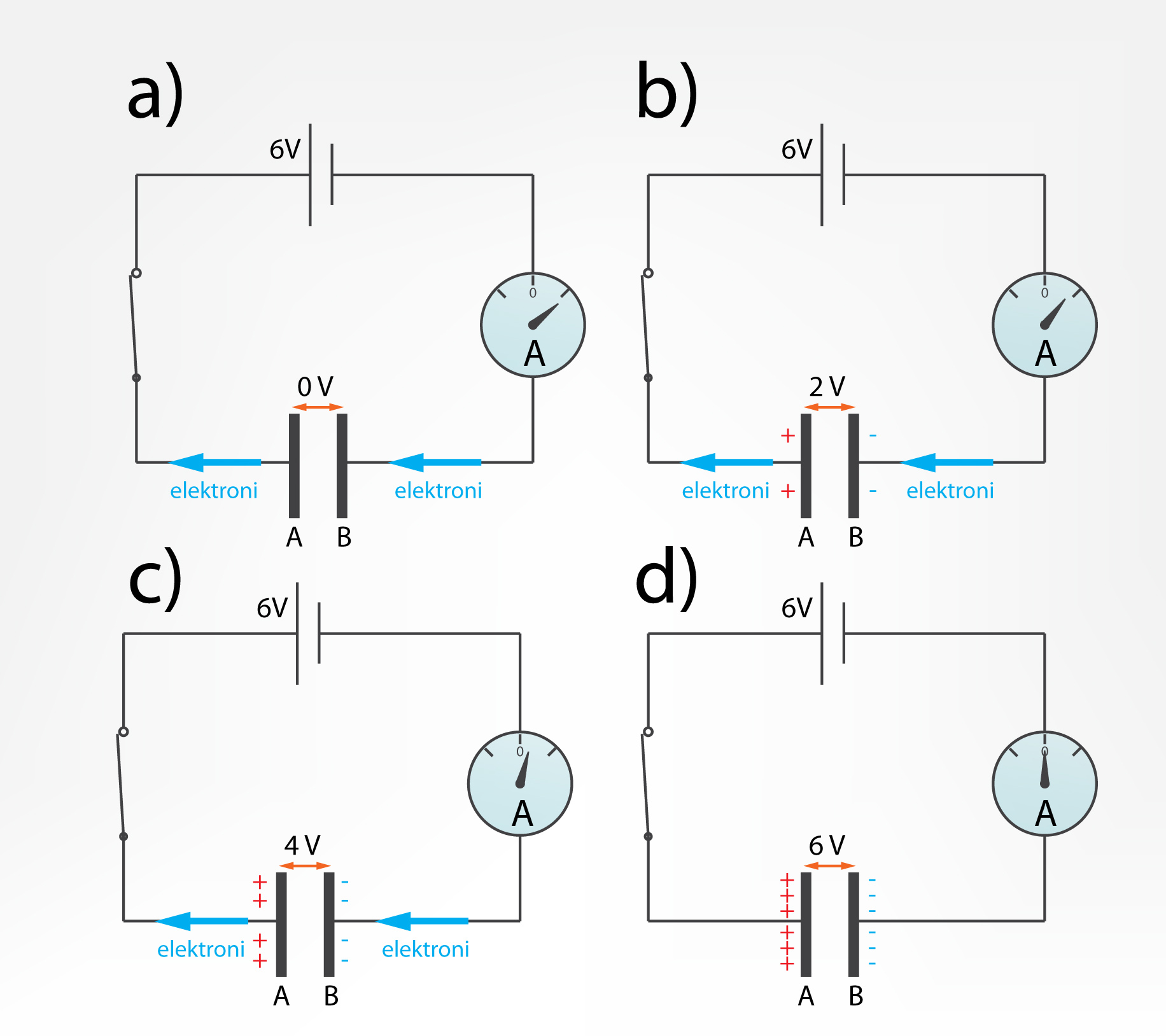
1.att. Kondensatora uzlādēšana
Kondensatora uzlādes procesā tam piešķirto enerģiju var aprēķināt ar grafisko metodi. Ja grafikā atliek kondensatora sprieguma atkarību no kondensatoram piešķirtā lādiņa (2. att.), tad kondensatora enerģija vienāda ar plaknes laukumu, ko ierobežo grafika līnija un lādiņa ass. Līdz ar to W = qU : 2. Šī sakarība iet roku rokā ar iepriekš apskatītajām elektriskā lauka enerģijas aprēķināšanas izteiksmēm. Izsakot no kapacitātes definīcijas U = q : C un ievietojot to W = qU : 2, iegūst W = q2 : 2C, kas ir viena no iepriekš apskatītajām formulām (2. solis, 8. att.).
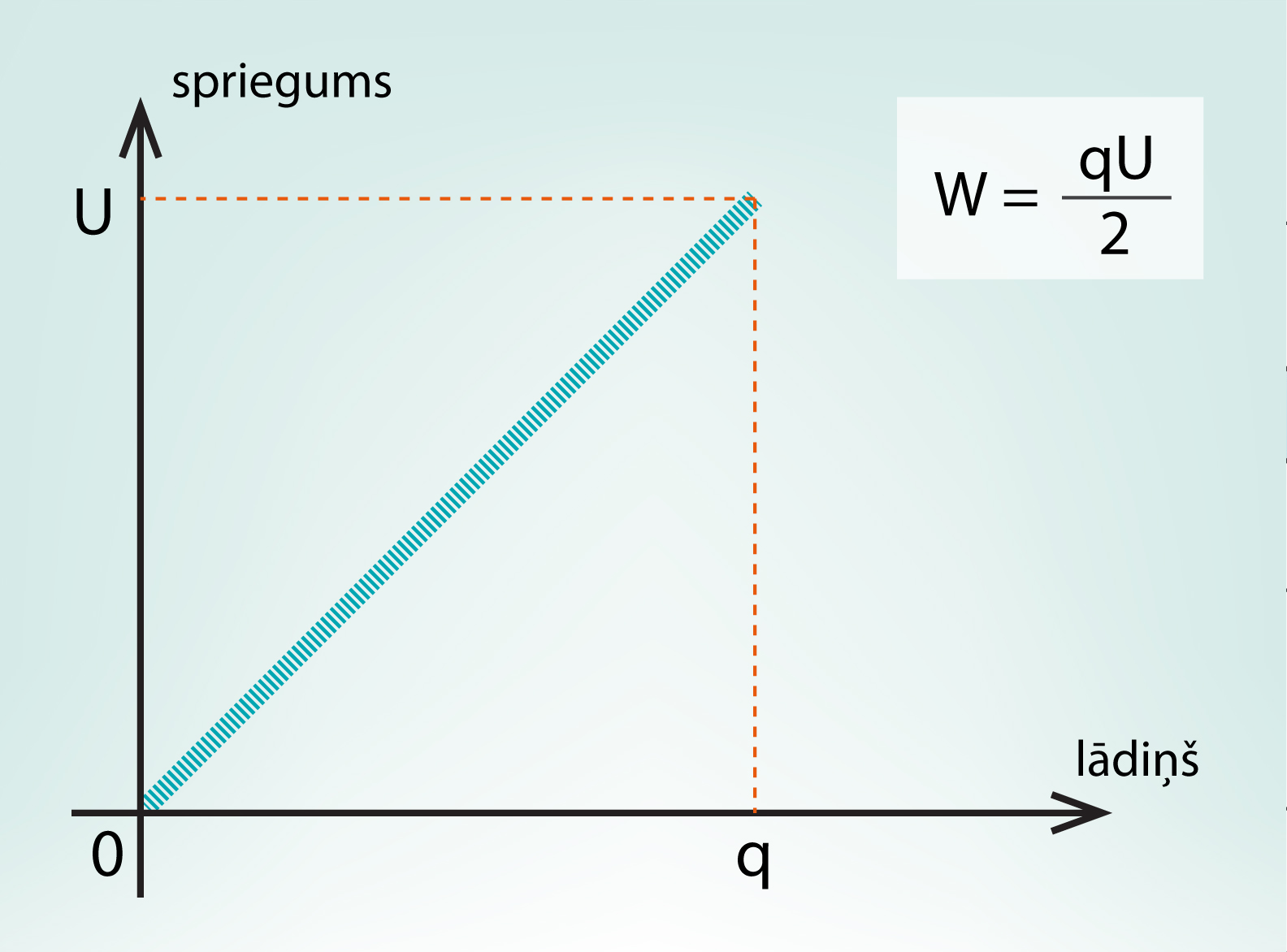
2.att. Kondensatora uzlādes grafiks
Dažādās tehnoloģijās svarīgāk ir tas, cik ātri kondensators spēj atdot uzkrāto lādiņu jeb izlādēties. Lai to pārbaudītu, var izmantot shēmu, kurā kondensatoru ar slēdža palīdzību var pārslēgt no strāvas avota (uzlādēšana) uz kādu patērētāju ar elektrisko pretestību R (izlādēšana), piefiksējot sprieguma izmaiņas atkarību laikā (3. att. a). Izlādes grafikos (3. att. b) redzams, ka izlādes ātrums ir atkarīgs gan no kondensatora kapacitātes C, gan arī no patērētāja, kas pieslēgts kondensatoram, elektriskās pretestības R. Kondensatorus izmanto fotoaparātu zibspuldzēs, jo tur nepieciešama ļoti strauja izlāde, lai nodrošinātu īslaicīgi spēcīgu gaismu.
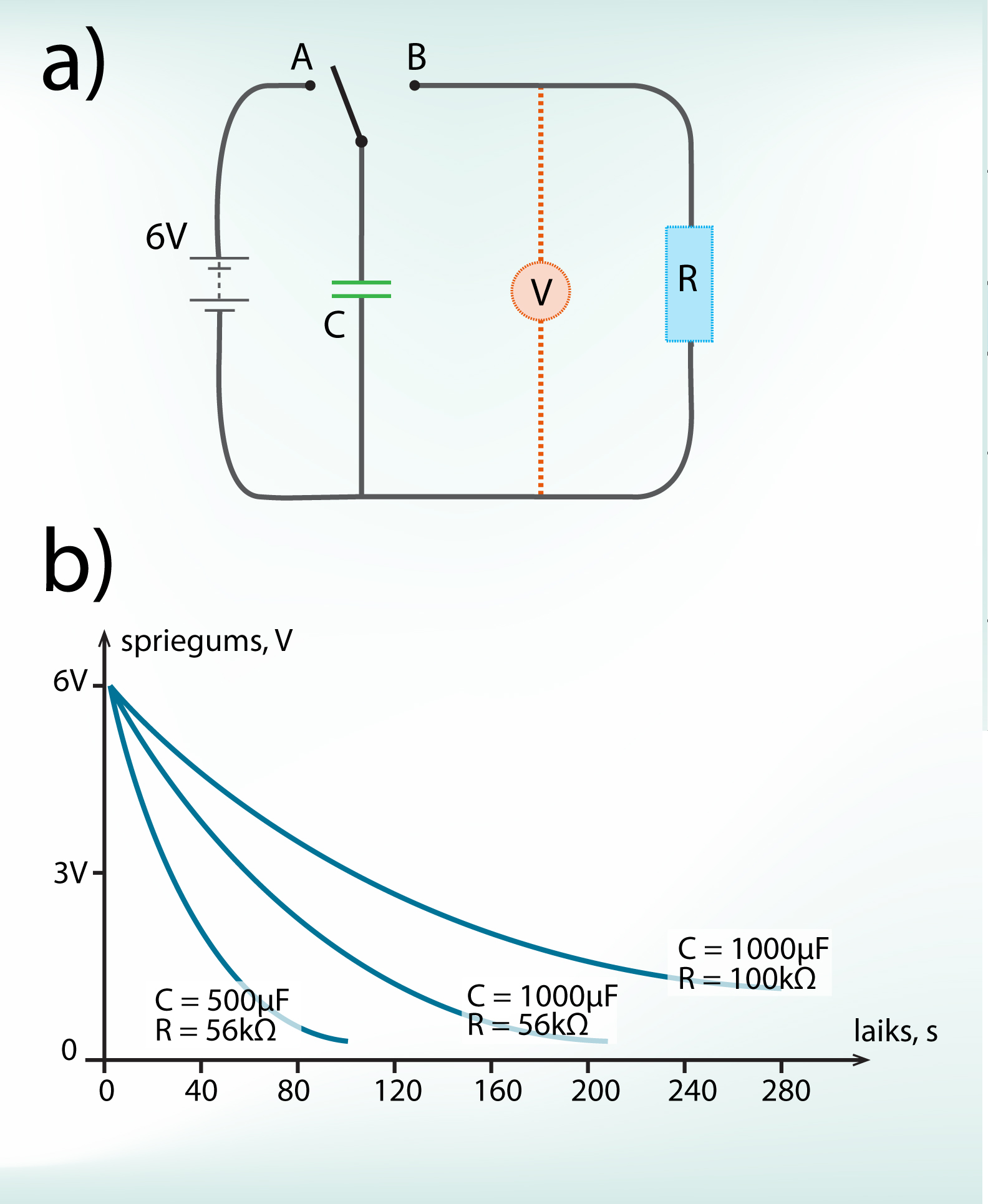
3.att. Kondensatoru izlāde
Plakņu kondensators ir tikai viens no kondensatoru uzbūves veidiem (4. att. a). Pastāv iespēja plakņu kondensatoru sarullēt, tādā veido iegūstot cilindriska veida kondensatoru, kas pēc būtības ir plakņu kondensators (4. att. b). Var cilindrisku kondensatoru veidot uzreiz, kad ap centrālo elektrodu apvij cilindriskas formas klājumu (4. att. c). Nedaudz eksotiskāks ir sfēriskas formas kondensators (4. att. d). Kondensatoru var uzbūvēt tā, ka tam ir iespēja mainīt kapacitāti, piemēram, vairāk vai mazāk pārklājot plakņu klājumus (4. att. e).
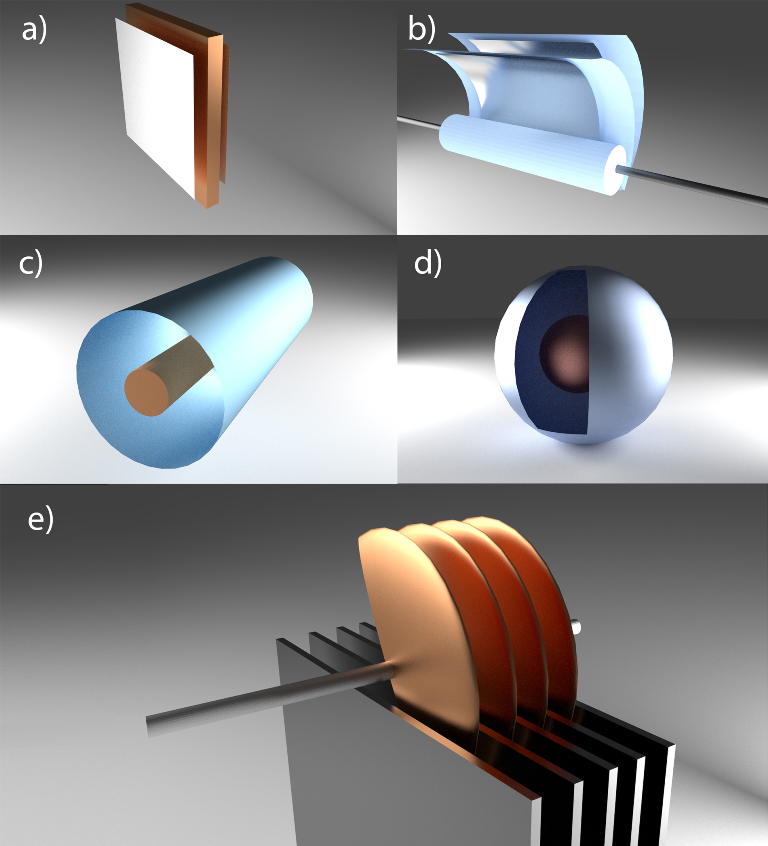
4.att. Dažādi kondensatoru ģeometriskie risinājumi
Cik dažādi ir kondensatoru ģeometriskie risinājumi, tik dažādi ir arī kondensatoru rūpnieciskie izpildījumi (5. att.). Kondensatori ir gan lieli, gan mazi, gan apaļi, gan kantaini, bet laikam viena no nozīmīgākajām to īpašībām ir kapacitāte C. Kapacitātes mērvienība ir farads (F), vienīgi šī mērvienība ir ļoti liela, tādēļ kapacitāti mēdz izteikt mazākās vienībās:
mikrofarados (1 μF = 10-6F)
nanofarados (1 nF = 10-9F)
pikofarados (1 pF = 10-12F)

5.att. Dažādi kondensatori