Pavadoņu rotācijas periods
Zemes mākslīgo pavadoņa rotācijas periods
Shematiskajā attēlā (1. attēls) parādīts ZMP, kas atrodas augstumā \(h\) virs Zemes virsmas. Tādēļ tā rotācijas rādiuss \(r\) ap Zemes centru ir vienāds ar \(r=R+h\), kur \(R\) – Zemes rādiuss.
.png)
1.att.
Gravitācijas spēks \(F_\mathrm{gr}\) piešķir pavadonim centrtieces paātrinājumu \(a_\mathrm{ct}\).
Lai noteiktu ZMP rotācijas periodu \(T\) augstumā \(h\), izmantosim gravitācijas spēka formulu \(F_\mathrm{gr}=G\frac{Mm}{r^2}\) (centrtieces spēks), otrā Ņūtona likuma formulu \(F_\mathrm{gr}=ma_\mathrm{ct}\) un centrtieces paātrinājuma formulu \(a_\mathrm{ct}=\frac{4\pi^2r}{r^2}\) kur \(M\) – Zemes masa, \(m\) – pavadoņa masa.
Iegūstam \(G\frac{Mm}{r^2}=m\frac{4\pi^2r}{T^2}\) vai \(G\frac{Mm}{(R+h)^2}=m\frac{4\pi^2(R+h)}{T^2}\). Nosakām rotācijas periodu: \(T=2\pi\sqrt{\frac{(R+h)^3}{GM}}\).
Satelītu kustība ap Zemi
Aplūkosim satelīta rotācijas periodu ap Zemi. Pavadoņa (satelīta) rotācijas periods \(T\) ap Zemi vienāds 24 h – liekas, ka pavadonis visu laiku atrodas virs konkrēta Zemes punkta. Noteiksim pavadoņa augstumu virs Zemes.
No formulas \(T=2\pi\sqrt{\frac{(R+h)^3}{GM}}\) izteiksim augstumu \(h\) un ieliksim skaitliskās vērtības: \(h=\sqrt[3]{\frac{T^2GM}{4\pi^2}}-R=\sqrt[3]{\frac{(24\cdot{3600})^2\cdot{6,67\cdot{10^{-11}}\cdot{6}\cdot10^{24}}}{4\pi^2}}-6,4\cdot{10}^6\approx{3,6}\cdot{10}^7\) \(m\) \(=36000\) \(km\).
GPS sistēmas pavadoņi veic divus pilnas apriņķojumus diennakts laikā un atrodas virs Zemes virsmas augstumā ap 20 000 km.
Eratostēna eksperiments
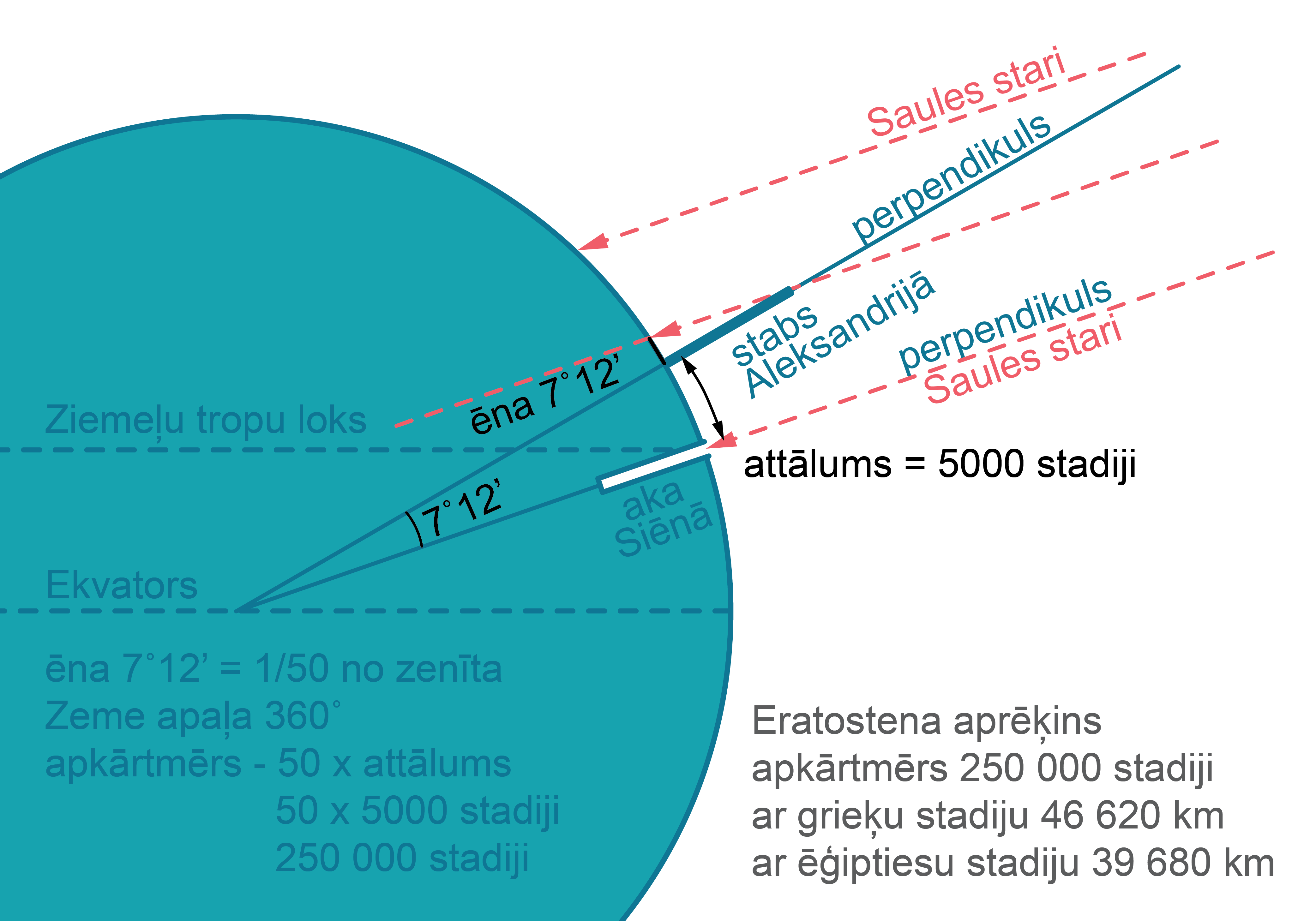
Eratostens noteica Zemes apkārtmēru nepametot Ēģipti (1. attēls). Viņš zināja, ka vasaras saulgriežos, pusdienlaikā Siēnā (senpilsēta netālu no pilsētas Asuana), Saule bija zenītā, tieši virs galvas. Viņš izmērīja Saules leņķi savā dzimtajā pilsētā, Aleksandrijā, arī saulgriežos, pusdienlaikā, un atklāja, ka tās leņķis ir par 1/50 daļu uz dienvidiem no zenīta.
1.att.
Pieņemot, ka Zeme ir apaļa (360°) un ka Aleksandrija ir tieši uz ziemeļiem no Siēnas, viņš secināja, ka attālumam no Aleksandrijas līdz Siēnai jābūt 1/50 daļai no Zemes apkārtmēra. Viņš zināja, ka gadu laikā, paaudzēm ceļojot starp abām pilsētām, bija noskaidrojies, ka attālums starp tām ir 5000 stadiju jeb 927,7 kilometri. Šo pieņēmumu apstiprināja, izpētot laiku, kādā kamielis var nokļūt no Siēnas līdz Aleksandrijai.
Eratostens noapaļoja rezultātu līdz 700 stadijām uz 1 grādu, kas norāda, ka Zemes apkārtmērs ir 252 000 stadiju. Tiek diskutēts par viņa izmantoto stadiju lielumu. Grieķu stadija bija apmēram 185 metrus gara, kas nozīmētu 46 620 kilometrus lielu Zemes apkārtmēru, kurš no patiesā atšķiras par 16,3%. Taču, ja pieņem, ka viņš izmantoja ēģiptiešu stadiju, kas ir apmēram 157,5 metrus gara, tad viņa mērījumi dotu 39 680 kilometrus lielu Zemes apkārtmēru, kurš no patiesā atšķiras tikai par 1,6%.
Fuko svārsts
Fuko svārsts ir ierīce, ko izmanto, lai pierādītu Zemes griešanos ap savu asi. Ierīce nosaukta par godu Leonam Fuko, svārsta eksperimenta pirmās demonstrācijas veicējam.
Fuko svārstam piemīt īpašība nemainīt savu svārstību plaknes novietojumu telpā atkarībā no Zemes rotācijas ap savu asi. Fuko svārsta pirmā demonstrācija 1851. gadā bija viens no pirmajiem vienkārši uztveramajiem pierādījumiem Zemes rotācijai.
Mūsdienās Fuko svārsti ir uzstādīti vairākās universitātēs un zinātnes muzejos. Eksperimenta gaitā smaga lode tiek iekārta vadā (visbiežāk 12–30 m garā), kas piestiprināts lielā augstumā. Zem lodes atrodas virsma, uz kuras ir atzīmēti leņķi. Nereti eksperimenta veikšanai ik pēc noteikta attāluma apkārt virsmai tiek novietoti priekšmeti, kuri, svārstam sasniedzot konkrēto leņķi, tiek apgāzti (1. attēls).

1.att.
Brīvās krišanas paātrinājuma atkarība no augstuma virs Zemes virsmas
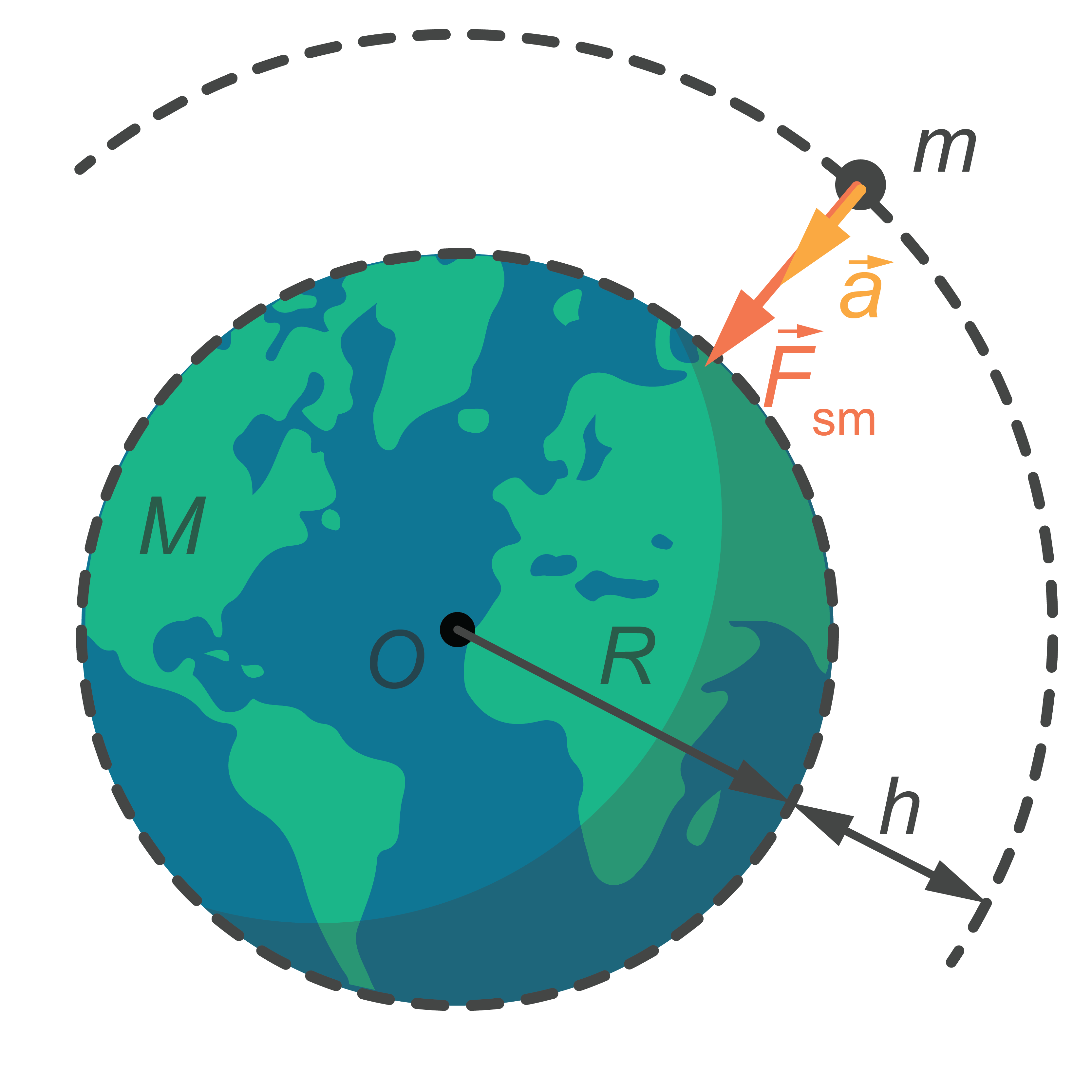
Attēlā ķermenis ar masu \(m\) atrodas \(h\) augstumā virs Zemes virsmas (1. attēls).
1.att.
Izmantosim gravitācijas likuma formulu \(F_\mathrm{gr}=G\frac{m_1m_2}{r^2}\) ar konkrētiem lielumiem: \(m_1\) vietā ieliksim Zemes masu \(M\), \(m_2\) vietā – ķermeņa masu \(m\), \(r\) vietā – Zemes rādiusa \(R\) un pacelšanas \(h\) augstuma summu \(R+h\). Iegūstam formulu \(F_\mathrm{gr}=F_\mathrm{sm}=G\frac{Mm}{(R+h)^2}\). Smaguma spēks ir vērsts virzienā uz Zemes centru.
Ja uz ķermeni darbojas tikai smaguma spēks (gaisa pretestības spēku neņem vērā), tad ķermenis brīvi krīt. Noteiksim ķermeņa krišanas paātrinājumu vai brīvās krišanas paātrinājumu \(g_\mathrm{h}\) augstumā \(h\) virs Zemes virsmas.
Saskaņā ar otro Ņūtona likumu, smaguma spēks \(F_\mathrm{sm}\) piešķir ķermenim paātrinājumu \(a\): \(F_\mathrm{sm}=ma\) vai \(G\frac{Mm}{(R+h)^2}=ma\). Iegūstam \(a=G\frac{M}{(R+h)^2}\). Izteiksmi \(G\frac{M}{(R+h)^2}\) apzīmēsim ar \(g_\mathrm{h}\) un nosauksim to par brīvās krišanas paātrinājumu augstumā \(h\) virs Zemes virsmas.
Par brīvās krišanas paātrinājuma augstumā \(h\) noteikšanu (piemēri):
1. Noteikt brīvas krišanas paātrinājumu augstumā \(h=nR\) virs Zemes virsmas (\(R\) - Zemes rādiuss).
\(g_\mathrm{h}=G\frac{M_\mathrm{Z}}{(R+h)^2}=G\frac{M_\mathrm{Z}}{(R+nR)^2}=G\frac{M_\mathrm{Z}}{R^2(n+1)^2}=\frac{g}{(n+1)^2}\). Piezīme: \(g=G\frac{M_\mathrm{Z}}{R^2}\approx10\) \(\frac{m}{s^2}\)
2. Kādā augstumā \(h\) brīvās krišanas paātrinājums būs \(n\) reizes mazāks, nekā uz Zemes virsmas?
\(g_\mathrm{h}=\frac{1}{n}g\) ⇒ \(G\frac{M_\mathrm{Z}}{(R+h)^2}=\frac{1}{n}G\frac{M_\mathrm{Z}}{R^2}\) ⇒ \(\frac{1}{(R+h)^2}=\frac{1}{n}\cdot{\frac{1}{R^2}}\) ⇒ \(R+h=\sqrt{nR}\) ⇒ \(h=(\sqrt{n}-1)R\).
Faktori, kas ietekmē brīvās krišanas paātrinājuma vērtību
Brīvās krišanas paātrinājums nav vienāds visur uz Zemes. Parasti izmantotā vērtība aptuveni atbilst ķermeņa krišanas paātrinājumam 45° platumā un jūras līmeņa augstumā.
Faktori, kas ietekmē novirzi no standarta vērtības, ir sekojoši:
- Zemes griešanās. Zemes griešanās dēļ, rodoties ''centrbēdzes'' spēkam, ķermeņa brīvās krišanas paātrinājums uz poliem ir augstāks nekā uz ekvatora.
- Zemes forma. Zeme nav ideāla sfēra, bet tai ir polos saplacināta forma.
- Augstums virs jūras līmeņa.
- Zemes neviendabība.
Brīvās krišanas paātrinājuma emperiskā formula
Brīvās krišanas paātrinājuma skaitlisko vērtību nelielos augstumos \(h\) (metros) virs jūras līmeņa ģeogrāfiskajā platumā \(\varphi\) (grādos) var iegūt aptuveni no šādas formulas (formula iegūta empīriski):
\(g=9,780327(1+0,0053024sin^2\varphi-0,0000058sin^22\varphi)-3,086\cdot10^{-6}\)\(h\)
Brīvas krišanas paātrinājums dažādos augstumos virs jūras līmeņa
Mākslīgā gravitācija
Viena no metodēm, kā iegūt mākslīgo gravitāciju, ir rotējošu centrifūgu izmantošana.
1.att.
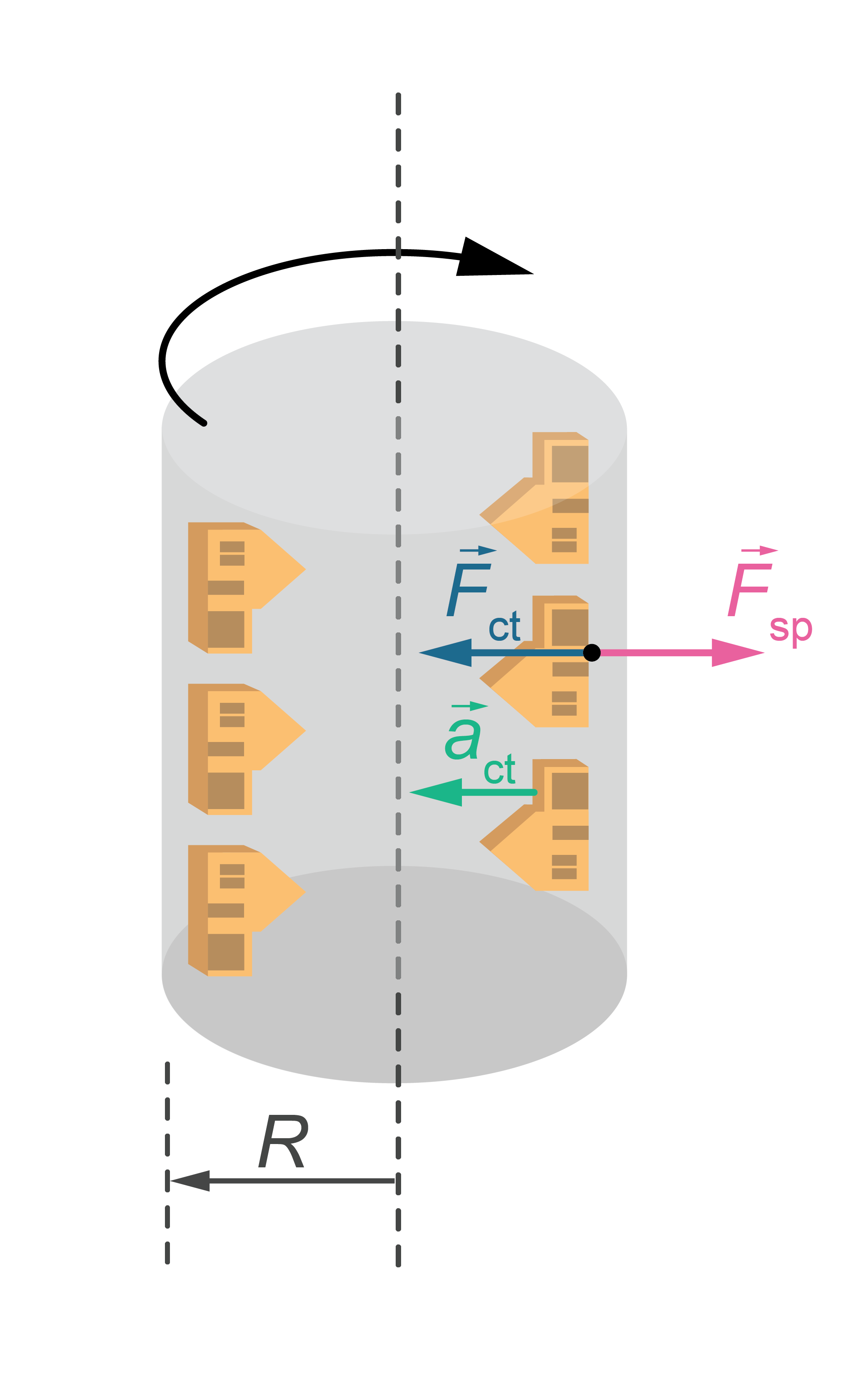
Attēlā ir parādīts cilindrs (centrifūga), kas griežas ap savu asi. Aplūkosim ķermeni, kas atrodas uz cilindra iekšējās sānu virsmas. Rotācijas laikā uz jebkuru ķermeni darbojas centrtieces spēks \(F_\mathrm{ct}\), kas piešķir ķermenim centrtieces paātrinājumu \(a_\mathrm{ct}\) (1. attēls). Kosmosa kuģī centrtieces spēku, kas darbojas uz cilvēku, izraisa cilindra sānu virsma. Saskaņā ar trešo Ņūtona likumu, ķermenis darbojas ar tik pat lielu pēc moduļa spiediena spēku \(F_\mathrm{sp}\) uz cilindra sānu virsmu.
Centrtieces spēku var aplūkot kā virsmas reakcijas spēku. Tad spiediena spēks ir ķermeņa mākslīgais smaguma spēks vai svars.
Smaguma spēka formula \(F_\mathrm{sm}=mg\), kur \(m\) – ķermeņa masa. Centrtieces spēka \(F_\mathrm{ct}\) formula \(F_\mathrm{ct}=ma_\mathrm{ct}\). Pielīdzināsim \(mg=ma_\mathrm{ct}\), saīsināsim masu \(m\), un iegūsim \(g=a_\mathrm{ct}\).
Centrtieces paātrinājuma formula \(a_\mathrm{ct}=\omega^2R\), kur \(\omega\) - cilindra rotācijas leņķiskais ātrums, \(R\) – rotācijas rādiuss.
No izteiksmes \(g=\omega^2R\) noteiksim kosmosa kuģa (cilindra) rotācijas leņķisko ātrumu \(\omega=\sqrt{\frac{g}{R}}\).
Uzdevuma risināšanas piemērs
Centrifūgas rādiuss \(R=5\) \(m\). Cik liels rotācijas leņķiskais ātrums nodrošina Zemes gravitāciju?
Ieliksim formulā \(\omega=\frac{g}{R}\) skaitliskās vērtības: \(\omega=\sqrt\frac{10}{5}\approx{1,4}\) \(s^{-1}\).
Tādā gadījumā rotācijas frekvence \(f=\frac{\omega}{2\pi}=\frac{1,4}{6,28}\approx0,22\) \(Hz\). Rotācijas periods \(T=\frac{1}{f}=\frac{1}{0,22}\approx{4,5}\) \(s\).
Zemes kustība Visumā
Zeme kosmiskajā telpā atrodas dažādās kustības (vairāk, nekā desmit). Galvenās no tām:
1. Rotācija ap savu asi. Rotācijas periods 23 h 56 min 4 s.
2. Rotācija ar Sauli. Rotācijas periods 365 diennaktis 6 h. Ātrums ap 30 \(\frac{km}{s}\).
3. Rotācija kopā ar Saules sistēmu ap Galaktikas centru. Rotācijas periods ap 250 miljonu gadi. Ātrums ap 230 \(\frac{km}{s}\).
4. Rotācija kopā ar Mēnesi ap kopējo masas centru. Rotācijas periods 27,3 diennaktis.
5. Zemes ass precesija. Pašlaik Zemes ass virzīta aptuveni Polārzvaigznes virzienā. Precesijas periods ir aptuveni 25 770 gadi.
1.att.
1. attēlā shematiski parādīta Zemes vieta Visumā, atkarībā no mēroga.