Gravitācijas likums
Ņūtons 1667. gadā izteica hipotēzi, ka starp visiem ķermeņiem darbojas savstarpējās mijiedarbības spēki. Šos spēkus nosauca par vispasaules gravitācijas spēkiem. Gravitācijas mijiedarbībai ir pakļauti bez izņēmuma visi ķermeņi (planētas, Zemes mākslīgie pavadoņi, Saule un citas zvaigznes, molekulas utt.).
Ap visiem ķermeņiem, kuriem piemīt masa, pastāv gravitācijas lauks. Ķermeņi mijiedarbojas viens ar otru ar gravitācijas lauka starpniecību.
Vispasaules gravitācijas likums:
Divi ķermeņi savstarpēji pievelkas ar spēku, kura modulis ir tieši proporcionāls abu ķermeņu masu reizinājumam un apgriezti proporcionāls attāluma kvadrātam starp ķermeņu masas centriem. Šie savstarpējās pievilkšanās gravitācijas spēki vērsti pa taisni, kas savieno ķermeņu masas centrus, to moduļi ir vienādi un virzieni – pretēji (1. attēls).
1.att.
Vispasaules gravitācijas likuma formula:
\(F_\mathrm{gr}=G\frac{m_1m_2}{r^2}\) , kur \(F_\mathrm{gr}\) – gravitācijas spēka modulis, \(m_1\) un \(m_2\) – ķermeņu masas, r – attālums starp ķermeņiem (starp ķermeņu masas centriem), \(G\) – gravitācijas konstante.
Mijiedarbības attālums starp ķermeņiem ir neierobežots. Tās nozīmē, ka mijiedarbojas ķermeņi, kas atrodas jebkuros attālumos viens no otra.
Gravitācijas mijiedarbības izpausme dabā.
Zvaigznēm un lielām planētām piemīt lodveida forma. Visas daļiņas, no kurām sastāv ķermenis, cenšas nokļūt ķermeņa centrā, gala rezultātā izveidojot lodveida formu (2. attēls).

2.att.
Gravitācijas likuma pielietojuma robežas:
1) ķermeņus, kas pievelkas, var uzskatīt par masas punktiem;
2) ķermeņi ir lodes un \(r\) – attālums starp ložu centriem;
3) viens ķermenis ir lode, bet otrs – neliela izmēra jebkuras formas ķermenis, piemēram, zemeslode un jebkurš ķermenis uz Zemes.
Gravitācijas spēkam ir vairākas raksturīgas īpašības:
1. Gravitācijas spēks vienmēr ir ķermeņu savstarpējās pievilkšanās spēks, bet nekad nav atgrūšanās spēks.
2. Gravitācijas spēka darbību nav iespējams norobežot, jo nav tādas vielas vai lauka, kas to varētu ekranēt.
3. Ja starp ķermeņiem darbojas tikai gravitācijas spēki, tad tie var atrasties tikai paātrinātā kustībā.
Gravitācijas konstante \(G\) nav atkarīga no ķermeņu masas, to formas vai sastāva. \(G\) ir koeficients vispasaules gravitācijas likumā. Gravitācijas konstante nemainās arī laikā. Gravitācijas konstante ir viena no universālajām fizikas konstantēm. Tā skaitliski vienāda ar spēku, ar kādu savstarpēji pievelkas divas lodes, ja to masas ir l kg un ja tās atrodas l m attālumā viena no otras, proti, \(G=6,67\cdot{10^{-11}}\frac{N\cdot{m^2}}{kg^2}\) (3. attēls). Kā redzams, šis spēks \(6,67\cdot{10^{-11}}N\) – ir ļoti mazs. Tieši tādēļ ikdienā nenovērojam divu ķermeņu tuvošanos (pievilkšanos), jo to kompensē berzes vai elastības spēki. Gravitācijas spēki ir noteicošie Visumā, kur debess ķermeņu masas ir milzīgas.
3.att.
Piemēri gravitācijas spēka aprēķināšanai:
1. Novērtēt gravitācijas spēku starp diviem 10. klases skolēniem. Pieņemam, kā skolēnu masas ir pa \(60\) \(kg\), attālums starp tiem \(1\) \(m\).
\(F_\mathrm{gr}=G\frac{m_1m_2}{r^2}=6,67\cdot{10^{-11}}\cdot\frac{60\cdot{60}}{1^2}\approx2,4\cdot{10^{-7}}N\)
Ar ko salīdzināt rezultātu? Fizikas kabinetos laboratorijas darbos izmanto dinamometrus ar iedaļas vērtību \(0,05\) \(N\) vai \(5\cdot10^{-2}\) \(N\). Starpība starp iegūto gravitācijas spēka moduli un dinamometra iedaļas vērtību ir piecas kārtas vai 100 000 reizes. Skaidrs, kā sadzīvē gravitācijas mijiedarbība starp cilvēkiem nav novērojama!
2. Noteikt gravitācijas mijiedarbības spēku starp Zemi un Mēnesi. No tabulas paņemam planētu masas un attālumu starp tām: Zemes masa \(M_\mathrm{z}=6,0\cdot10^{24}\) \(kg\), Mēness masa \(M_\mathrm{M}=7,4\cdot10^{22}\) \(kg\), attālums starp Zemi un Mēnesi \(r=3,8\cdot{10^8}\) \(m\).
\(F_\mathrm{gr}=G\frac{m_1m_2}{r^2}=G\frac{M_\mathrm{Z}M_\mathrm{M}}{r^2}=6,67\cdot{10^{-11}}\cdot\frac{6,0\cdot{10^{24}}\cdot7,4\cdot{10^{22}}}{(3,8\cdot{10^8})^2}\)\(N\)
Spēka modulis milzīgs, salīdzinājumā ar ''sadzīves'' spēkiem. Piemēram, jauna cilvēka izdarīta sitiena spēks ir ap \(2\cdot{10^3}\) \(N\). Atšķirība ir acīm redzama.
Par gravitācijas konstanti
Gravitācijas konstantes skaitlisko vērtību 1798. gadā aprēķināja H. Kavendišs.
Kavendiša eksperimentā tiek mērīts gravitācijas spēks ar kādu pievelkas svina lodes (4. attēls a). Kvarca diegā iekārts stienītis, kura galos atrodas nelielas svina lodītes ar masām \(m\). Tā kā lielo ložu masa ir daudz lielāka par mazo lodīšu masu, tad gravitācijas spēka iedarbībā mazās lodītes pievirzās tuvāk lielajām lodēm. Rezultātā stienītis pagriežas ap vertikālo asi un savērpj diegu, radot tajā elastības spēku. Diega elastības spēks bremzē gravitācijas spēku izraisīto stieņa griešanos. Stienis griežas līdz brīdim, kad elastības spēka moments līdzsvaro gravitācijas spēku pāra momentu. Elastības spēka moments ir tieši proporcionāls diega vērpes leņķim. (Pirms šā eksperimenta nosaka diega elastības spēka atkarību no vērpes leņķa.) Izmērot diega savērpuma leņķi \(\alpha\), var aprēķināt gravitācijas konstantes skaitlisko vērtību.
Arī Fizikas un matemātikas fakultātē atrodas šāda eksperimentālā iekārta (4. attēls b), bet jāteic, ka eksperiments ir ļoti jutīgs – mērījuma rezultāti tiek negatīvi ietekmēti pat tad, ja \(200\) \(m\) attālumā garām pabrauc tramvajs.
4.att.
Brīvās krišanas paātrinājums
Teorija par brīvas krišanas paātrinājumu
Gravitācijas spēks ir vispārīgais jēdziens – spēks kas darbojas starp ķermeņiem jebkuros attālumos. Īpašajā gadījumā, ja ķermenis atrodas uz planētas virsmas (vai tuvu planētas virsmai), gravitācijas spēka vietā var izmantot jēdzienu "smaguma spēks''. Smaguma spēks \(F_\mathrm{sm}\) ir spēks, ar kādu Zeme (vai cita planēta) pievelk ķermeni, kas atrodas tās virsmas tuvumā.
Ķermenis ar masu \(m\) atrodas uz Zemes virsmas (1. attēls). Izmantosim gravitācijas likuma formulu \(F_\mathrm{gr}=G\frac{m_1m_2}{r^2}\) ar konkrētiem lielumiem: \(m_1\) vietā ieliekot Zemes masu \(M\), \(m_2\) vietā – ķermeņa masu \(m\), \(r\) vietā – Zemes rādiusu \(R\). Iegūstam formulu \(F_\mathrm{gr}=F_\mathrm{sm}=G\frac{Mm}{R^2}\) . Smaguma spēks ir vērsts virzienā uz Zemes centru. Ja ķermenis attēlots uz kādas virsmas vai iekārts auklā, tad smaguma spēku attēlo vērstu uz leju.
1.att.
Aplūkosim ķermeņa krišanu no neliela augstuma, kas ir ļoti mazs, salīdzinājumā ar Zemes rādiusu. Ja uz ķermeni darbojas tikai smaguma spēks (gaisa pretestības spēku neņem vērā), tad ķermenis brīvi krīt.
Noteiksim ķermeņa krišanas paātrinājumu (brīvās krišanas paātrinājumu).
Saskaņā ar otro Ņūtona likumu, smaguma spēks \(F_\mathrm{sm}\) piešķir ķermenim paātrinājumu \(a\): \(F_\mathrm{sm}=ma\) vai \(G\frac{Mm}{R^2}=ma\) . Iegūstam, ka \(a=G\frac{M}{R^2}\) . Izteiksme \(G\frac{M}{R^2}\) ir atkarīga tikai no Zemes (vai citas planētas) parametriem. Paātrinājumu \(a\) apzīmē ar \(g\) un nosauc par brīvās krišanas paātrinājumu. Tātad, smaguma spēks \(F_\mathrm{sm}\), kas darbojas uz ķermeni, ir vienāds ar ķermeņa masas m un brīvās krišanas paātrinājuma \(g\) reizinājumu: \(F_\mathrm{sm}=mg\) .
Var teikt arī šādi: smaguma spēks \(F_\mathrm{sm}\) piešķir ķermenim paātrinājumu, ko sauc par brīvās krišanas paātrinājumu \(g\). Tiešā Zemes tuvumā brīvās krišanas paātrinājuma \(g\) skaitliskā vērtība ir vienāda ar \(9,81\) \(m/s^2\). Brīvās krišanas paātrinājuma skaitliskā vērtība dažādās vietās uz Zemes var mazliet atšķirties. Iemesli var būt sekojoši: Zeme nav homogēnā lode; vietas augstums virs jūras līmeņa ir atšķirīgs, …
Praktiski brīvās krišanas paātrinājumu izmērīja Galilejs 1589. gadā Pizā.
Brīvās krišanas paātrinājuma īpašības
1) Paātrinājums nav atkarīgs no ķermeņa masas un visi ķermeņi vienā un tajā pašā vietā uz Zemes krīt ar vienādu paātrinājumu. Protams, tikai tad, ja eksperiments notiek bezgaisa traukā (2. attēls).
2.att.
2) Visumā katra ķermeņa virsmas tuvumā ir savs brīvās krišanas paātrinājums, jo katram ķermenim ir sava noteikta masa un rādiuss. Tā, piemēram, brīvās krišanas paātrinājums uz Mēness ir \(1,62\) \(m/s^2\) (3. attēls).

3.att.
3) Brīvās krišanas paātrinājums samazinās, ja palielinās attālums no planētas virsmas. Apzīmējums \(g_\mathrm{h}\) – brīvas krišanas paātrinājums \(h\) augstumā virs Zemes virsmas (4. attēls).
4) Pārvietojoties planētas centra virzienā, brīvās krišanas paātrinājums lineāri samazinās. Planētas centrā brīvās krišanas paātrinājums vienāds ar nulli (4. attēls).
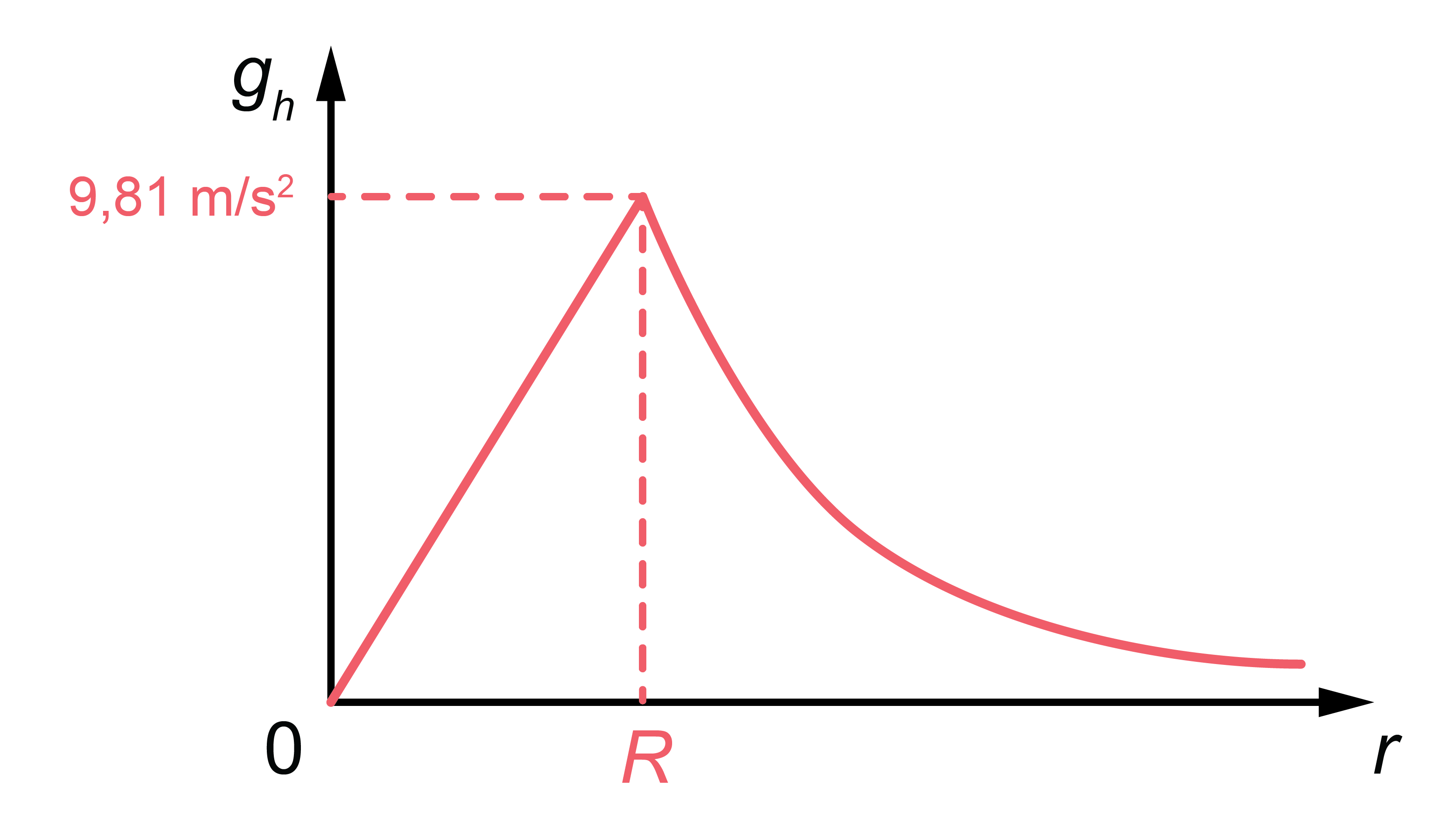
4.att.
Brīvās krišanas paātrinājums Zemes iekšienē
Ķermenis ar masu \(m_0\) atrodas A punktā (5. attēls). No sākuma pierādīsim, ka uz ķermeni darbojas tikai tas Zemes slānis, kas atrodas dziļāk, nekā pats ķermenis (attēlā – P apgabals).
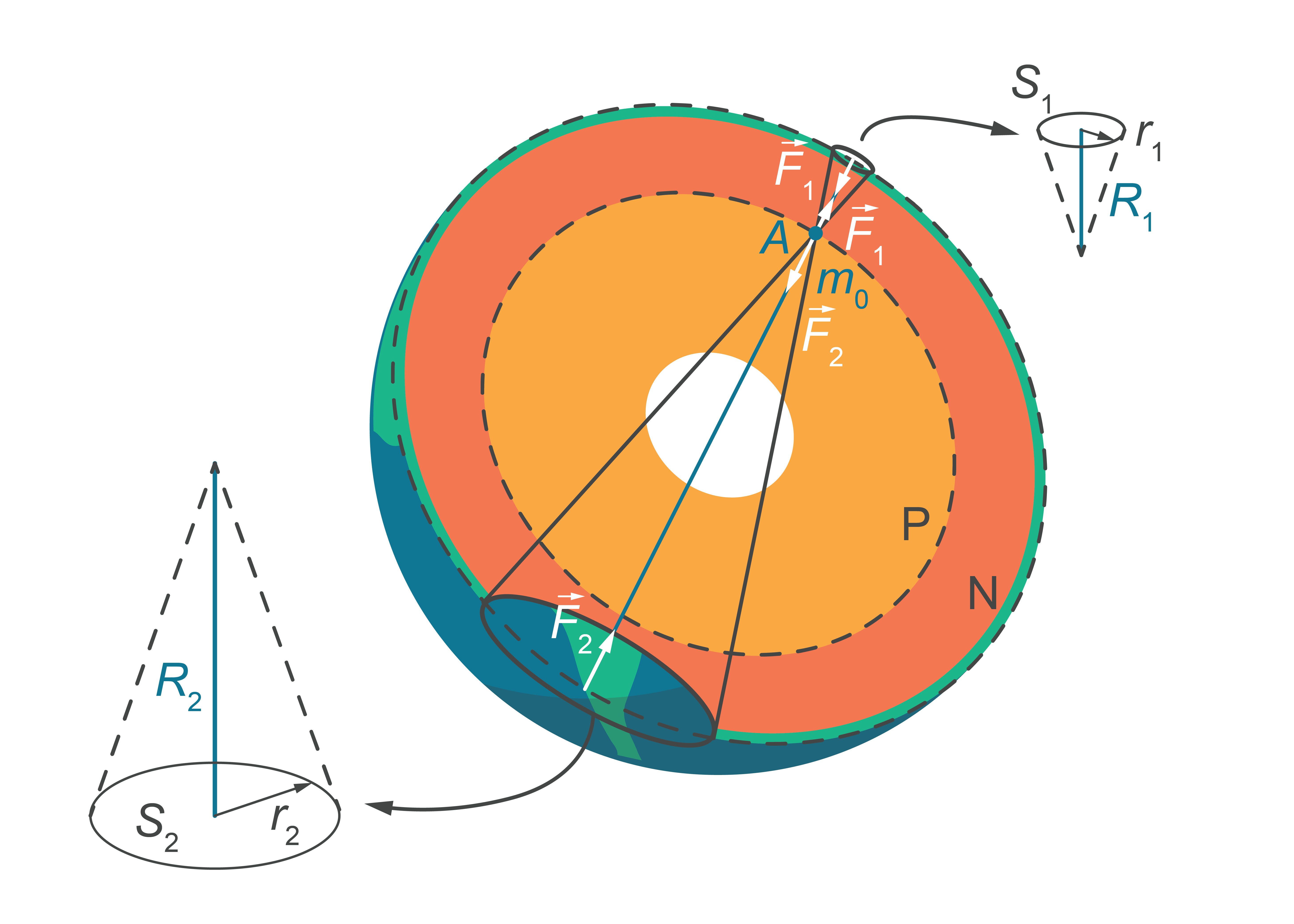
5.att.
Sadalīsim Zemi plānās čaulās ar biezumu \(d\).
Izdalīsim Zemes iekšienē divus konusus ar virsotnēm punktā A. Konusu pamati ir čaulas fragmenti ar rādiusiem \(r_1\) un \(r_2\). Konusu augstumi \(R_1\) un \(R_2\) (\(r_1\)≪ \(R_1\) un \(r_2\)≪ \(R_2\)). Tātad, konusu pamatus var aplūkot, ka plānus diskus.
Čaulas fragmentu masas izteiksim šādi: \(M_1=\rho{S_1}d\) un \(M_2=\rho{S_2}d\), kur \(\rho\) – Zemes blīvums.
Fragmentu laukumus \(S_1\) un \(S_2\) izteiksim šādi: \(S_1=\pi{r}^2_1\) un \(S_2=\pi{r}^2_2\) .
Salīdzināsim spēkus \(\overrightarrow{F}_1\) un \(\overrightarrow{F}_2\) . Spēks \(\overrightarrow{F}_1\) – pievilkšanās spēks starp ķermeni \(m_0\) un čaulas fragmentu ar laukumu \(S_1\), spēks \(\overrightarrow{F}_2\) – pievilkšanas spēks starp ķermeni \(m_0\) un čaulas fragmentu ar laukumu \(S_2\). Čaulas fragmenti ir uzskatāmi par ļoti maziem ķermeņiem.
Saskaņā ar gravitācijas likuma formulu, spēku \(\overrightarrow{F}_1\) un \(\overrightarrow{F}_2\) moduļi izskatās šādi:
\(F_1=G\frac{M_1m_0}{R^2_1}\) un \(F_2=G\frac{M_2m_0}{R^2_2}\) .
Ņemot vērā fragmentu masu formulas, iegūsim:
\(F_1=G\frac{\rho{S_1dm_0}}{R^2_1}=G\frac{\rho{\pi{r}_1^2}dm_0}{R^2_1}\) un \(F_2=G\frac{\rho{S_2dm_0}}{R^2_2}=G\frac{\rho{\pi{r}_2^2}dm_0}{R^2_2}\) .
Izteiksim spēku formulas citādi: \(F_1=G\rho\pi{dm}_0(\frac{r_1}{R_1})^2\) un \(F_2=G\rho\pi{dm}_0(\frac{r_2}{R_2})^2\) .
Attēlā redzamie konusi ir līdzīgas figūras. Tad \(\frac{r_1}{r_2}=\frac{R_1}{R_2}\) vai \(\frac{r_1}{r_1}=\frac{R_2}{R_2}\) . Tātad spēki \(F_1\) un \(F_2\) vienādi, un Zemes slāņi (attēlā – N apgabals), kas atrodas tuvāk Zemes virsmai, nekā ķermenis, neiedarbojas uz ķermeni.
Secinājums – uz ķermeni \(m_0\) darbojas tikai tie Zemes slāņi, kas atrodas dziļāk, nekā ķermenis (attēlā – P apgabals).
Iegūsim formulu, kā mainās brīvas krišanas paātrinājums Zemes iekšienē. Apzīmējumi: \(M\) – Zemes masa, \(M\)* – masa sfērai ar rādiusu \(r\) (6. attēls).
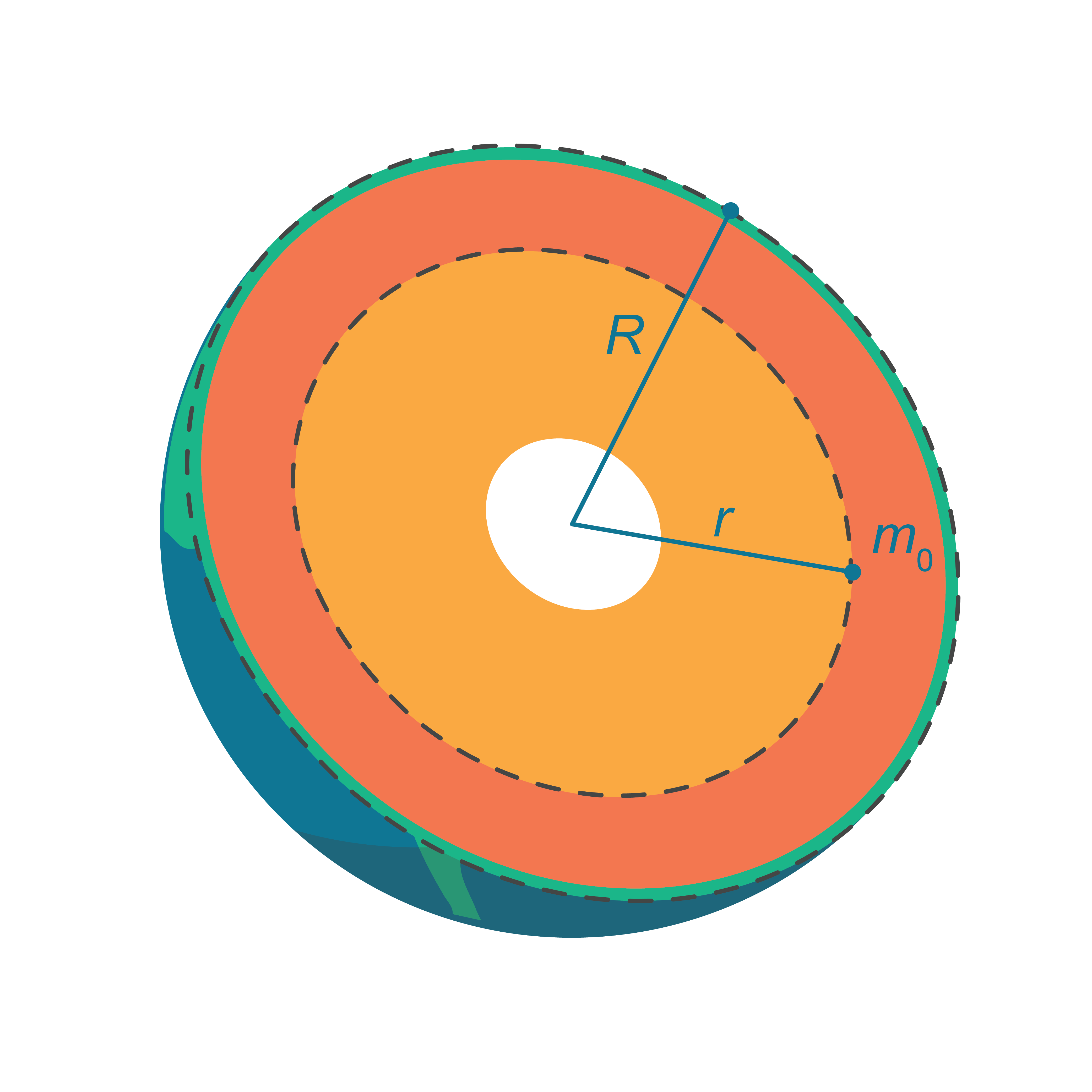
6.att.
Izteiksim masas \(M\) un \(M\)* citādi: \(M=\rho\frac{4}{3}\pi{R}^3\) un \(M\)*\(=\rho\frac{4}{3}\pi{r}^3\) , kur \(\rho\) – Zemes blīvums.
Sastādīsim proporciju: \(\frac{M^*}{M}=\frac{r^3}{R^3}\) .
Spēks \(F\), kas darbojas uz ķermeni \(m_0\): \(F=G\frac{Mm_0}{r^2}\) .
No proporcijas izteiksim \(M^*=M\frac{r^3}{R^3}\) un ieliksim spēka formulā: \(F=G\frac{M\frac{r^3}{R^3}m_0}{r^2}=G\frac{Mm_0}{R^3}r\) .
Izteiksim formulu citādi: \(F=G\frac{Mm_0}{R^2}\frac{r}{R}\).
Izteiksme \(G\frac{M}{R^2}=g\) – brīvas krišanas paātrinājums uz Zemes virsmas.
Tātad, \(F=m_0{g}\frac{r}{R}\) .
Secinājums – Zemes iekšienē brīvās krišanas paātrinājums lineāri samazinās no \(9,81 \) \(m/s^2\) (uz Zemes virsmas) līdz nullei (Zemes centrā).