Skolēns uzņēma kvēlspuldzes un rezistora voltampēru raksturlīkni (attēlā).
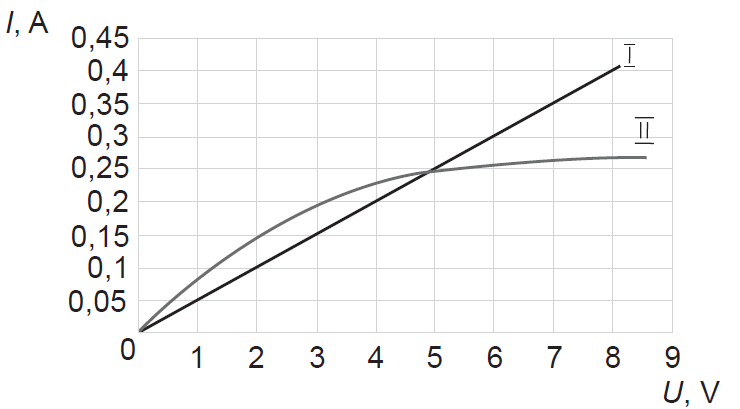1. Izskaidro, kura līkne atbilst kvēlspuldzei!
2. Pie kāda sprieguma kvēlspuldzes un rezistora pretestības ir vienādas? Paskaidro!
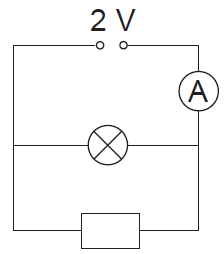
3. Skolēns kvēlspuldzi un rezistoru saslēdza paralēli un pieslēdza sprieguma avotam, kura spriegums ir 2 V. Attēlā dota šī slēguma shēma. Izmantojot grafiku, nosaki, cik lielu strāvas stiprumu rādīs ampērmetrs!
4. Skolēns gribēja saglabāt kvēlspuldzes spožumu, vienlaikus samazinot kopējo slēguma jaudu. Skolēns pieslēdza rezistoram virknē vēl vienu tādu pašu rezistoru. Nosaki, cik lielu strāvas stiprumu tagad rādīs ampērmetrs! Skaidro, vai skolēnam ir izdevies samazināt kopējo slēguma jaudu, saglabājot kvēlspuldzes spožumu!
1. punkts
Kvēlspuldzei, atšķirībā no rezistora, pretestība mainās. Pieaugot spriegumam \(U\) un, līdz ar to, arī strāvas stiprumam \(I\), kvēlspuldzes metāla kvēldiegs uzkarst un tā pretestība pieaug. Datu bukletā atrodama atbilstoša sakarība \(R=R_0(1+\alpha\Delta T)\).
Tā rezultātā, pieaugot spriegumam, strāvas stiprums vairs nepieaug lineāri.
Savukārt rezistora elektrisko pretestību var uzskatīt par nemainīgu, tādēļ, saskaņā ar datu bukletā atrodamo sakarību – Oma likumu \(I=\frac{U}{R}\), strāvas stiprums mainās tieši proporcionāli spriegumam un sakarības grafiks ir lineārs – taisne, kas iet caur koordinātu sākumpunktu. Tātad, kvēlspuldzei atbilst II līkne.
Par elektriskās strāvas siltumdarbību (https://www.fizmix.lv/fiztemas/lidzstrava-9/stravas-darbs-un-jauda) un metālu pretestības maiņu uzkarstot (https://www.fizmix.lv/fiztemas/lidzstrava-9/elektriska-strava-metalos-un-skidrumos) var lasīt Fizmix portālā.
Atbilde: kvēlspuldzei atbilst II līkne attēlā.
2. punkts
Tā kā, saskaņā ar Oma likumu, \(R=\frac{U}{I}\), kvēlspuldzes un rezistora pretestības būs vienādas, ja pie vienādām sprieguma \(U\) vērtībām arī strāvas stipruma \(I\) vērtības ir vienādas.
Grafikā redzams, ka šāda situācija ir pie sprieguma \(U\approx5\space\mathrm{V}\), kad strāvas stiprums \(I\approx0{,}25\space\mathrm{A}\).
\(R=\frac{U}{I}=\frac{5}{0{,}25}=20\space\mathrm{\Omega}\) (šīs aprēķins NAV obligāts).
Atbilde: kvēlspuldzes un rezistora pretestības būs vienādas pie sprieguma \(U=4{,}9\space\mathrm{V}\) (tiek pieņemtas atbildes robežās no \(4{,}8\space\mathrm{V}\) līdz \(5{,}0\space\mathrm{V}\)). Pretestības būs vienādas, ja pie vienādām sprieguma vērtībām arī strāvas stipruma vērtības ir vienādas.
3. punkts
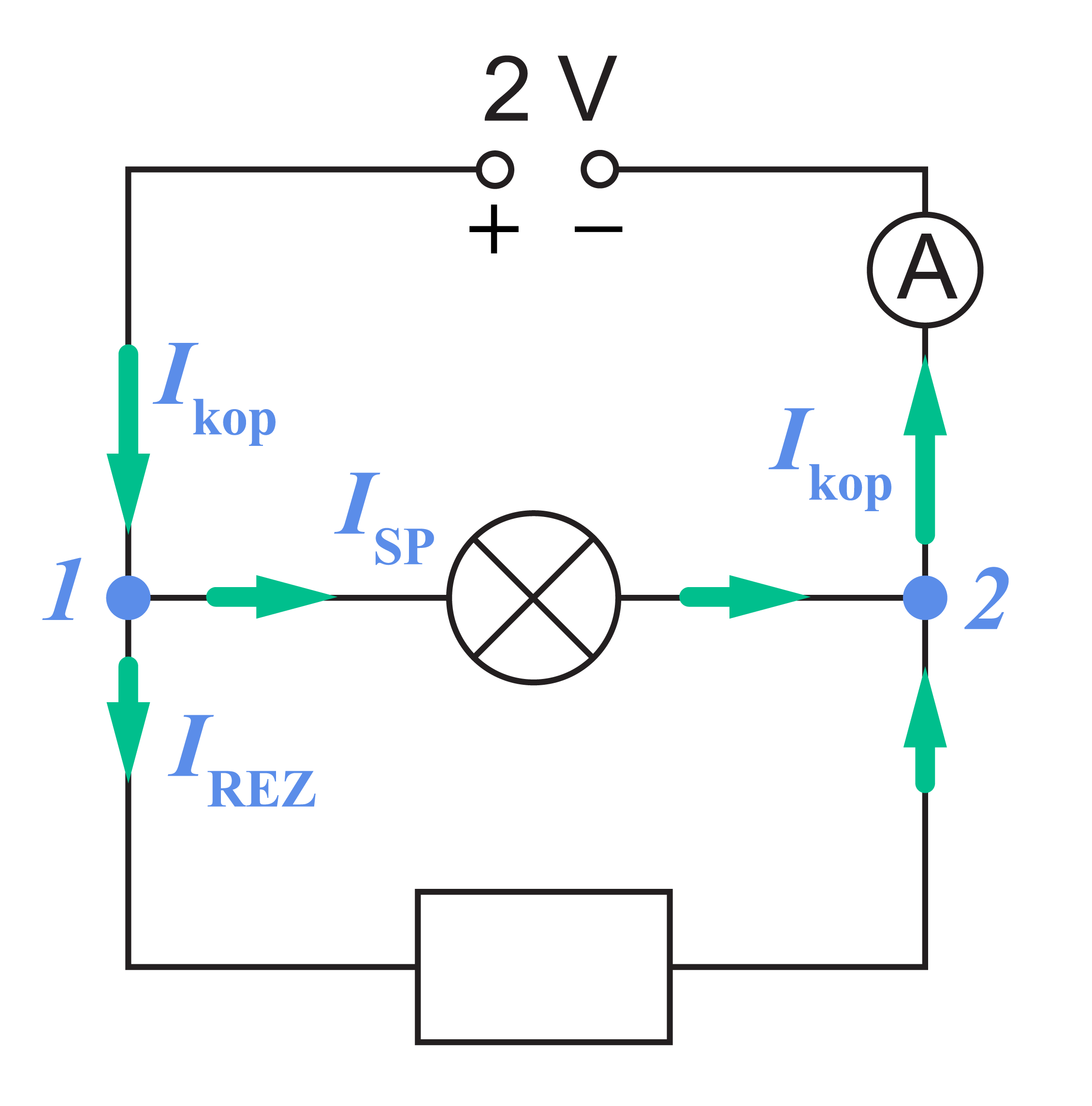Attēlā redzams, ka ampērmetrs ieslēgts divu paralēli slēgtu rezistoru kopējā vadā. Paralēlajā slēgumā strāvas stiprums kopējā vadā vienāds ar atsevišķo paralēli slēgto rezistoru strāvas stiprumu summu.
Tā kā abi ķēdes elementi sprieguma avotam pieslēgti paralēli viens otram (tie abi pieslēgti ķēdes punktiem 1. un 2.), tad spriegums uz katra no tiem ir \(2\space\mathrm{V}\).
No grafika nolasa, ka strāvas stiprums vienā elementā ir \(I_\mathrm{sp}=0{,}15\space\mathrm{A}\), bet otrā \(I_\mathrm{rez}=0{,}1\space\mathrm{A}\).
Ampērmetrs rāda kopējo strāvas stiprumu \(I_{\mathrm{kop}}=I_{\mathrm{sp}}+I_{\mathrm{rez}}=0{,}15+0{,}1=0{,}25\space\mathrm{A}\).
Var spriest arī savādāk: izmantojot datus no grafika, aprēķina rezistora un spuldzes pretestības.
\(R_\mathrm{sp}=\frac{U}{I_\mathrm{sp}}=\frac{2}{0{,}15}\approx13{,}3\space\mathrm{\Omega}\)
\(R_\mathrm{rez}=\frac{U}{I_\mathrm{rez}}=\frac{2}{0{,}1}=20\space\mathrm{\Omega}\)
Paralēli saslēgtiem patērētājiem to pretestību apgriezto vērtību summa vienāda ar kopējās pretestības apgriezto vērtību.
Tātad, diviem paralēli slēgtiem patērētājiem \(R_\mathrm{kop}=\frac{R_\mathrm{sp}R_\mathrm{rez}}{R_\mathrm{sp}+R_\mathrm{rez}}=\frac{13{,}3\cdot20}{13{,}3+20}\approx8\space\mathrm{\Omega}\).
Tad \(I_{\mathrm{kop}}=\frac{U}{R_\mathrm{kop}}=\frac{2}{8}=0{,}25\space\mathrm{A}\).
Atbilde: ampērmetrs rādīs \(0{,}25\space\mathrm{A}\) lielu strāvas stiprumu.
4. punkts
Pieslēdzot virknē ar rezistoru vēl vienu tādu pašu rezistoru, veidojas jauktais slēgums.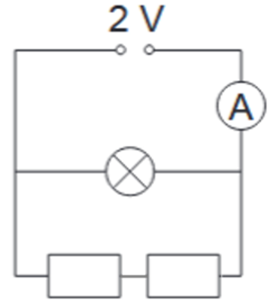 
Tā kā abi ķēdes posmi – spuldze un divu rezistoru virknes slēgums ir slēgti paralēli, tad spriegums uz katra paralēli slēgtā posma ir \(2\space\mathrm{V}\).
No grafika nolasa, ka strāvas stiprums spuldzē ir \(I_\mathrm{sp}=0{,}15\space\mathrm{A}\) (nav mainījies).
Strāvas stiprums otrā paralēli slēgtajā posmā samazinājies divas reizes, jo virknē ieslēgta otra tāda pati pretestība un virknes slēgumā pretestības summējas: \(I_\mathrm{2}=\frac{0{,}1}{2}=0{,}05\space\mathrm{A}\).
Ampērmetrs rāda kopējo strāvas stiprumu \(I_\mathrm{kop}=I_\mathrm{sp}+I_2=0{,}15+0{,}05=0{,}20\space\mathrm{A}\).
Spuldzes spožums saglabājas, jo strāvas stiprums caur to (spriegums uz tās) nav mainījies.
Slēguma kopējā jauda samazinās, jo samazinājies kopējais strāvas stiprums (\(P=I\cdot U\)).
Iespējami arī citi risināšanas veidi.
Četru punktu iegūšanai pietiek ar spriedumu, ka spuldzei spriegums un strāvas stiprums, tātad arī jauda (spožums) nemainās, bet slēguma kopējā jauda samazinās – pieaugot viena paralēlā posma pretestībai, pieaug arī visa slēguma kopējā pretestība , tātad jauda \(P=\frac{U^2}{R}\) samazinās (vai – samazinās kopējais strāvas stiprums, tātad arī jauda \(P=I\cdot U\)).
Iespējams spriedums, ka spožums nedaudz pieaugs, jo strāvas stiprums pievados samazināsies un, ja to pretestību arī ņemtu vērā, sprieguma kritums uz pievadiem būs mazāks.
Atbilde: spuldzes spožums saglabājas, jo strāvas stiprums caur to un spriegums uz tās nav mainījies.
Slēguma kopējā jauda samazinās, jo pieaug slēguma kopējā pretestība un samazinās kopējais strāvas stiprums.
1. punkts
Uzdevuma izpilde eksāmenā – 52,7%.
Vērtēšanas kritēriji
Pareizi nosaka līkni, kas atbilst kvēlspuldzei – 1 punkts.
Paskaidro, ka kvēlspuldzes pretestība mainās (vai paskaidro, ka rezistora pretestība, visdrīzāk, nemainās) – 1 punkts.
Skaidro, ka kvēldiegs uzkarst un tā pretestība pieaug, tādējādi strāva vairs nepieaug tik strauji – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 3 punktiem.
2. piemērs: risinājums novērtēts ar 3 punktiem.
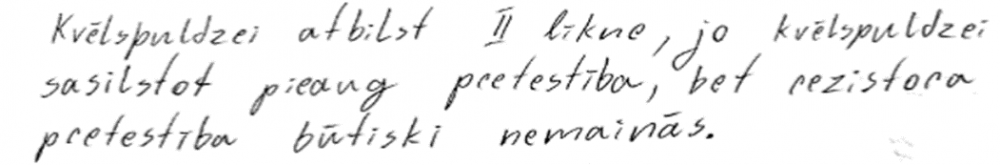
3. piemērs: risinājums novērtēts ar 2 punktiem. Nav pamatojuma pretestības maiņai un/vai tās ietekmei uz līknes formu.
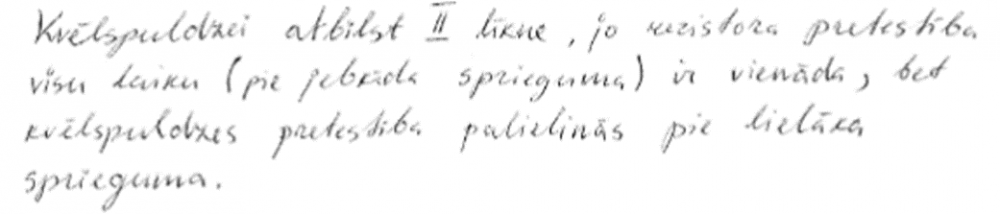
4. piemērs: risinājums novērtēts ar 1 punktu. Ir atbilde, bet nav pamatojuma.
2. punkts
Uzdevuma izpilde eksāmenā – 85,3%.
Vērtēšanas kritēriji
Nosaukta pareiza sprieguma vērtība (robežās no \(4{,}8\space\mathrm{V}\) līdz \(5{,}0\space\mathrm{V}\)) un ir pamatojums ar Oma likuma formulu vai tekstu – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 1 punktu.
2. piemērs: risinājums novērtēts ar 1 punktu.
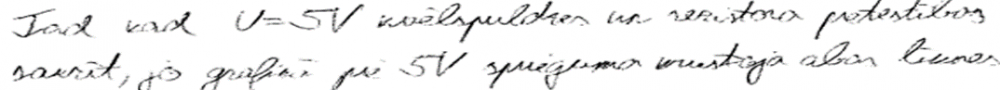
3. piemērs: risinājums novērtēts ar 1 punktu.
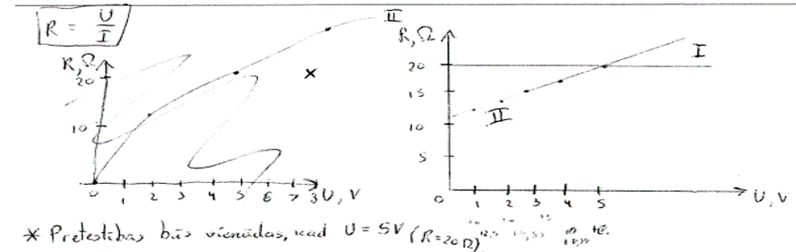
4. piemērs: risinājums novērtēts ar 0 punktu. Nepareizi noteikta sprieguma vērtība.
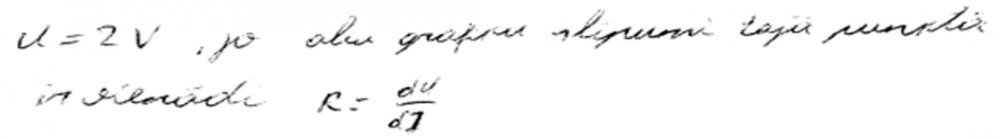
5. piemērs: risinājums novērtēts ar 0 punktu. Trūkst pamatojuma.
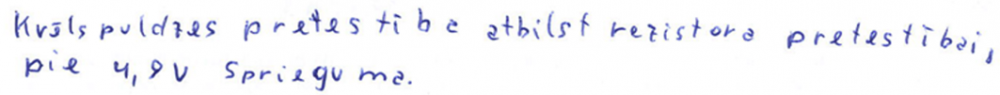
3. punkts
Uzdevuma izpilde eksāmenā – 52,3%.
Vērtēšanas kritēriji
Atpazīst paralēlo slēgumu. Tas var nebūt nosaukts vārdā, bet saprotams no teksta, ka spriegums uz ķēdes elementiem vienāds un strāvu stiprums nesazarotajā ķēdes posmā ir vienāds ar visos patērētajos plūstošu strāvas stiprumu – 1 punkts.
Iegūst ampērmetra rādījumu (nolasot no grafika vai aprēķinot) – 1 punkts.
Zīmīgo ciparu skaitu atrisinājumā nevērtē.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 2 punktiem.
2. piemērs: risinājums novērtēts ar 2 punktiem.
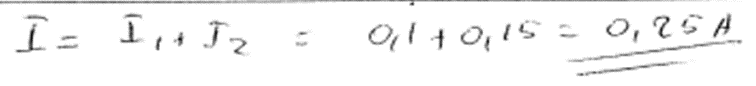
3. piemērs: risinājums novērtēts ar 2 punktiem.
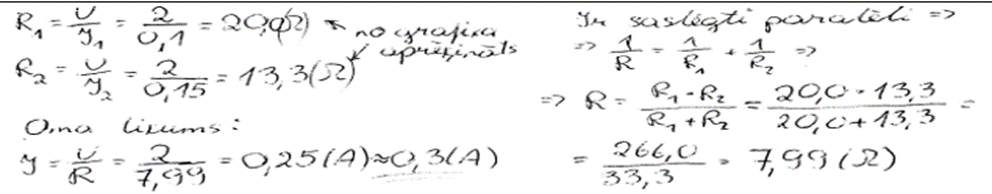
4. piemērs: risinājums novērtēts ar 1 punktu. Paralēlais slēgums ir atpazīts, par ko 1 punkts.
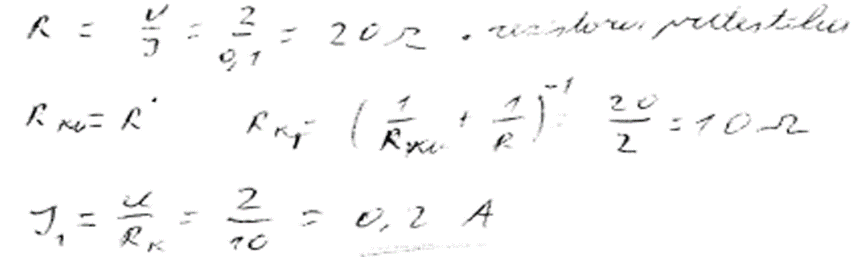
5. piemērs: risinājums novērtēts ar 0 punktu. Nav pamatojuma.
6. piemērs: risinājums novērtēts ar 0 punktu. Nav atpazīts slēgums, spriedums neatbilst attēlotajai situācijai.
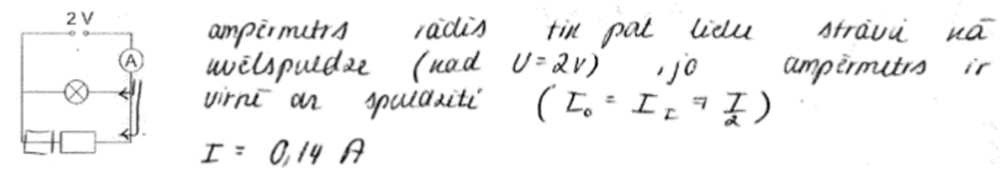
4. punkts
Uzdevuma izpilde eksāmenā – 34,2%.
Vērtēšanas kritēriji
Shēmā redzams vai aprakstā nolasāms pareizs jauktais slēgums – 1 punkts.
Novērtēts, ka strāvas stiprums spuldzē nemainās, bet divu rezistoru virknes slēgumā tas samazinās, salīdzinot ar viena rezistora gadījumu, sarēķināta kopējā strāva (skaidrojums var nebūt, var izmantot iepriekš iegūtu rezistora pretestību) – 1 punkts.
Secināts un pamatots, ka spuldzes spožums saglabājas (ir spriedums par spožuma saistību ar jaudu) – 1 punkts.
Secina un pamato, ka kopējā jauda samazinās – 1 punkts.
Shēma var nebūt, bet, ja ir, noteikti jāskatās, kas sazīmēts/sarakstīts shēmā!
Faktiski var vērtēt līmeņos – ir seši momenti, kam jābūt:
- uzzīmēts/risinājumā ieraugāms pareizs slēgums;
- novērtēts, ka strāvas stiprums spuldzē nemainās, tātad nemainās jauda;
- spožums saistīts ar jaudu;
- novērtēts, ka strāvas stiprums otrā paralēlajā posmā samazinās, jo pretestība pieaug 2x, tātad jauda samazinās;
- aprēķināts strāvas stiprums;
- secināts par kopējās jaudas samazināšanos.
Lai iegūtu visus 4 punktus, kaut kas no pirmajiem četriem var nebūt uzrakstīts.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 4 punktiem.
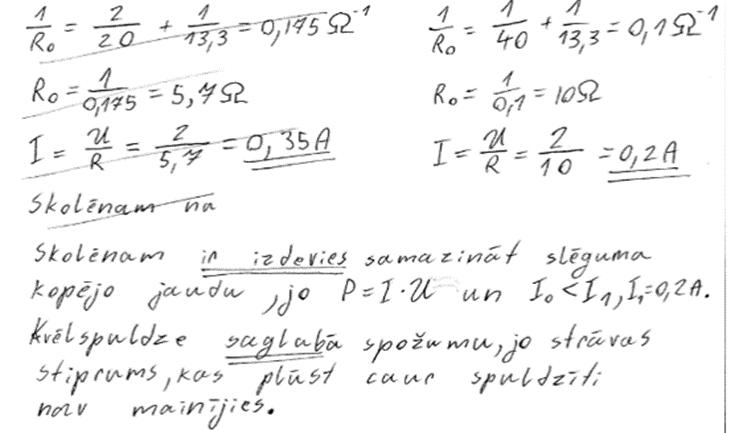
2. piemērs: risinājums novērtēts ar 4 punktiem.
3. piemērs: risinājums novērtēts ar 4 punktiem.
4. piemērs: risinājums novērtēts ar 3 punktiem. Nepareizs secinājums par spuldzes spožumu.
5. piemērs: risinājums novērtēts ar 3 punktiem. Spriedumi pareizi, kļūda pretestības aprēķinā.
6. piemērs: risinājums novērtēts ar 2 punktiem. Ir slēgums, ir jaudas formula, pretrunīgi novērtēts strāvas stiprums caur virknē saslēgtajiem rezistoriem.
7. piemērs: risinājums novērtēts ar 1 punktu. Ir spriedums par spožuma saistību ar jaudu un jaudas formula.
8. piemērs: risinājums novērtēts ar 0 punktu. Kļūdains secinājums bez pamatojuma.
