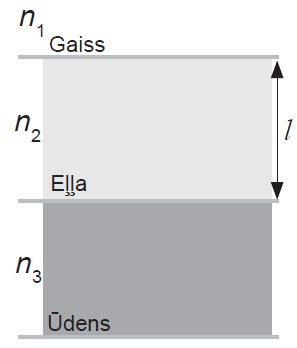
Gaismas interferences dēļ, piemēram, ziepju burbulis vai plānas eļļas kārtiņa uz ūdens, dažu tauriņu spārni, izskatās krāsaini. Interferences ainu plānās kārtiņās ietekmē krītošās gaismas viļņa garums, plānās kārtiņas biezums l un gaismas laušanas koeficienti.
1. Uzzīmē shematiski staru gaitu plānā kārtiņā, kuras rezultātā veidojas interference atstarotajai gaismai! Salīdzini kādām n vērtībām parādība ir iespējama!
Fotokamerās objektīvā nereti tiek izmantotas vairākas lēcas cita aiz citas. Gaisma, atstarojoties no šo atšķirīgo lēcu virsmām, ietekmē attēla kvalitāti. Lai novērstu šos efektus, lēcas pārklāj ar plānu magnija fluorīda kārtiņu. Magnija fluorīds MgF2 ir balts kristālisks sāls ar gaismas laušanas koeficientu nkārt = 1,38. Tas ir optiski caurspīdīgs plašā elektromagnētisko viļņu garumu diapazonā – no 0,110 μm līdz 7,5 μm. MgF2 komerciāli izmanto, izgatavojot logus, lēcas un prizmas, tostarp arī tās, kuras izmanto kosmiskajos teleskopos.
2. Vai magnija fluorīds ir caurspīdīgs gamma starojumam? Atbildi pamato!
3. Uz lēcu, kas pārklāta ar magnija fluorīda kārtiņu, krīt gaismas viļņi, kuru garums ir 550 nm. Gaismas laušanas koeficients stiklā nst = 1,52. Gaismas laušanas koeficients MgF2 plānajā kārtiņā nkārt = 1,38. Aprēķini, cik lielam jābūt minimālajam magnija fluorīda kārtiņas biezumam, lai novērstu atstarošanos no lēcas virsmas!
4. Kāda lēca – ar lielāku vai ar mazāku – plānās kārtiņas biezumu būtu jāizmanto, lai novērstu gaismas atstarošanos no lēcas virsmas, ja būtu jāfotografē sarkanā gaismā? Atbildi pamato!
1. punkts
Pirms risināt konkrēto uzdevumu, aplūkosim gaismas interferenci plānās kārtiņās.
"Vienādiem" (ar vienādu viļņu garumu un vismaz daļēji vienādu elektriskā un magnētiskā lauka svārstību virzienu) gaismas viļņiem pārklājoties, to rezultējošais vilnis veidojas kā atsevišķu viļņu summa. Šo parādību sauc par viļņu interferenci. Rezultējošā viļņa amplitūda ir atkarīga no atsevišķo viļņu amplitūdām un fāžu starpībām.
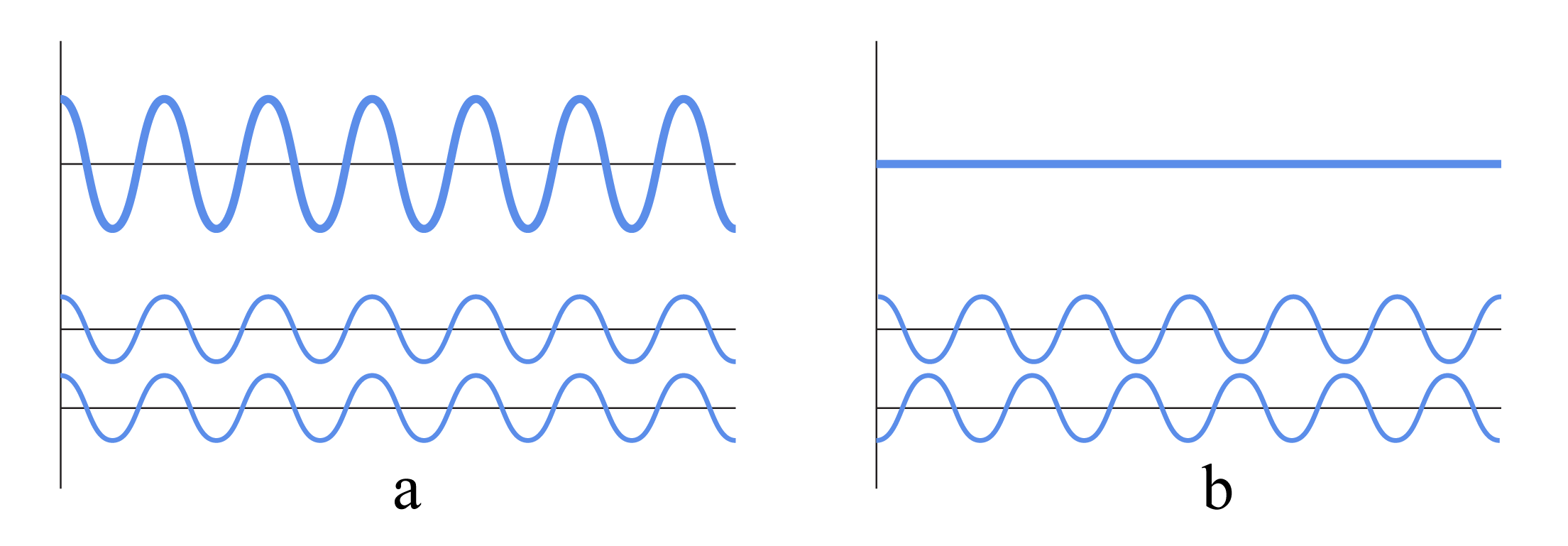
Ja divi vienādi gaismas viļņi kādā telpas punktā sastopas vienādās fāzēs, tad novērojama rezultējošās amplitūdas palielināšanās – notiek konstruktīva interference (1. attēls a). Interference ir konstruktīva, ja interferējošo viļņu fāzu nobīde ir \(2\pi k\), kur \(k\) ir vesels skaitlis, tad viļņu fāzes pārklāšanās vietā sakrīt. Pieņemot, ka interferē divi viļņi, kuru avoti svārstās vienā fāzē, gājumu starpībai abiem interferējošajiem viļņiem jābūt veselam viļņu garumu skaitam: \(\Delta x=k\lambda\).
Ja viļņi sastopas pretējās fāzēs, tad rezultējošā viļņa amplitūda ir vienāda ar nulli un tas "dzēšas" – notiek destruktīva interference (1. attēls b). Interference ir destruktīva, ja interferējošo viļņu fāzu nobīde ir \((2k+1)\frac{\pi}{2}\), kur \(k\) ir vesels skaitlis, tad viļņu fāzes pārklāšanās vietā ir pretējas. Pieņemot, ka interferē divi viļņi, kuru avoti svārstās vienā fāzē, gājumu starpībai abiem interferējošajiem viļņiem jābūt pusveselam viļņu garumu skaitam: \(\Delta x=(2k+1)\frac{\lambda}{2}\).
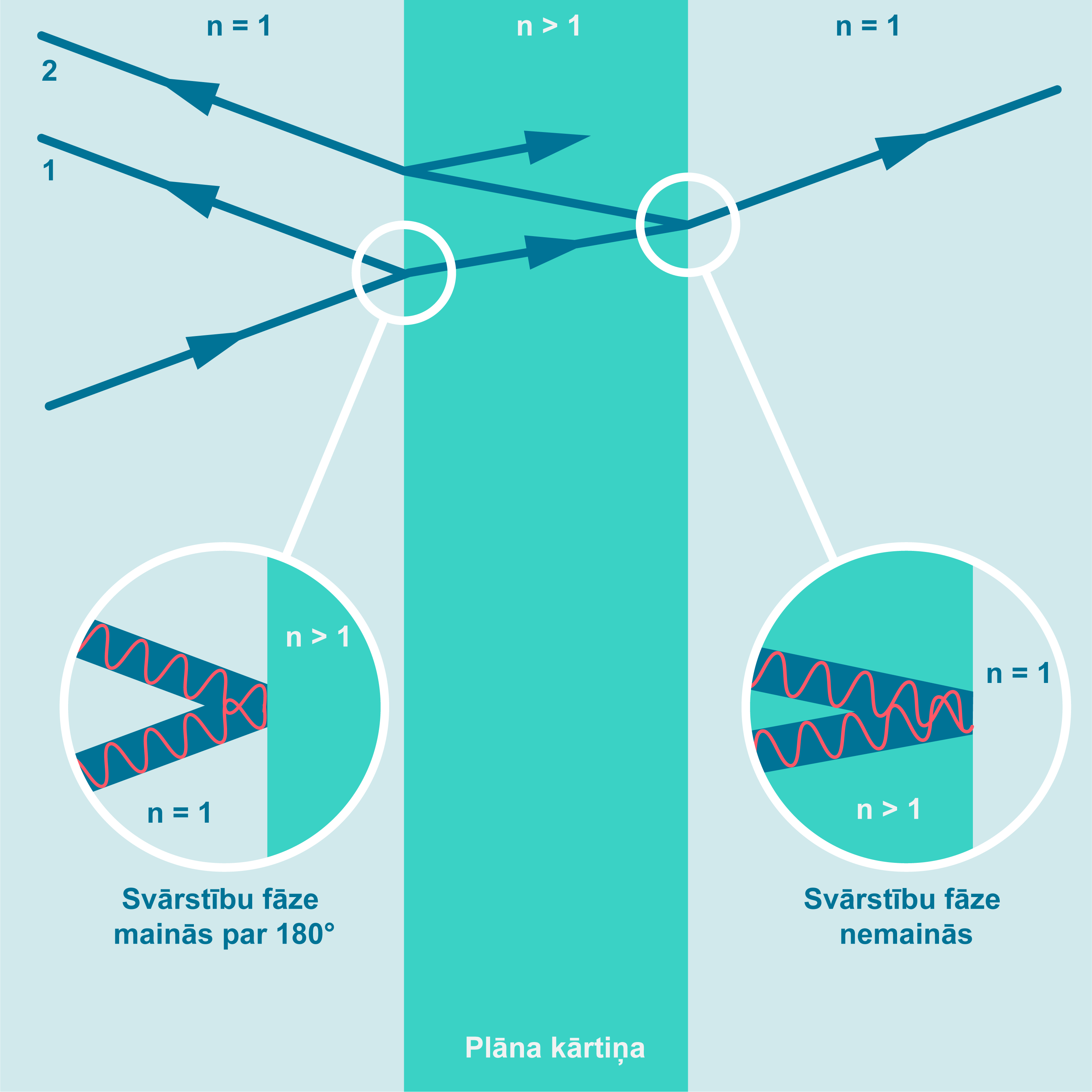
Interferences ainu var iegūt, piemēram, tad, ja monohromatiska gaisma krīt uz kādu plānu kārtiņu, piemēram, ziepjūdens plēvīti (2. attēls). Attēlā redzams, ka gaismas stars krīt uz plēvīti un daļa gaismas atstarojas, bet otra – lūst un nonāk plānajā kārtiņā. Šis lauztais stars vēlreiz atstarojas pret kārtiņas otru virsmu un vēlreiz lūst uz pirmās virsmas. Ja kārtiņa ir plāna, abus gaismas viļņus var uzskatīt par koherentiem – "vienādiem". Tā kā gaismas stars 2 ir nogājis garāku ceļu, tad starp staru 1 un 2 ir izveidojusies gājienu starpība un veidojas interferences aina.
Pēc vairākkārtējas atstarošanās arī otrā ziepjūdens plēvītes pusē var veidoties interferences aina.
Gaisma atstarojas no robežvirsmas starp divām vidēm tad, ja šīs vides ir "optiski atšķirīgas" – ja atšķiras to gaismas laušanas koeficienti. Ja tie ir vienādi, gaismas stars uz robežvirsmas netiek lauzts un netiek arī atstarots.
Ja gaisma atstarojas, tad, papildus tam, ka notiek izplatīšanās virziena maiņa, var mainīties arī gaismas viļņa svārstību fāze. Ja gaisma atstarojas pret vidi, kurai gaismas laušanas koeficients ir augstāks, tad, atstarojoties, viļņa svārstību fāze izmainās par 180⁰ grādiem jeb \(\pi\) radiāniem. Ja atstarošanās notiek uz robežvirsmas ar vidi, kurai laušanas koeficients ir mazāks, šāds lēciens svārstību fāzē nenotiek. Šāda situācija parādīta 2. attēlā (piemēram – ziepju burbulītī).
Svārstību fāzes lēcienu ir jāņem vēra, ja jāaprēķina plānās kārtiņas biezumu, lai kādas noteiktas krāsas gaismai izpildītos interferences minimuma vai maksimuma nosacījums.
Ja gaisma krīt uz plāno kārtiņu, tad interference notiek starp staru 1, kas ir atstarotais stars, un staru 2, kas veidojas no lauztā stara un atstarotā stara.
Šo divu staru gājumu starpības \(\Delta x\) aprēķins no ģeometrijas skatpunkta tuvāk aplūkots Fizmix portāla Fiztēmās.
Tomēr samērā viegli var iztēloties, ka, gaismai uz kārtiņu krītot praktiski perpendikulāri, 2. stars no 1. stara atpaliek par attālumu, ko tas veic "turp un atpakaļ", izplatoties kārtiņā, tātad šī gājumu starpība telpā vienāda ar divkāršotu kārtiņas biezumu. Iegūto "ģeometrisko" gājumu starpību ir jāreizina ar kārtiņas vides absolūto laušanas koeficientu \(n_2\), jo plānajā kārtiņā gaisma pārvietojas lēnāk, līdz ar to tās optiskais ceļš palielinās. Turklāt, gadījumā, ja fāzes lēciens notiek tikai uz vienas virsmas (piemēram, ziepju slānītim abās pusēs ir gaiss), jāpieskaita \(\frac{\lambda}{2}\), jo fāzes lēciens par 180 grādiem atbilst pusviļņa garumam.
1. punkta atrisinājums un atbilde
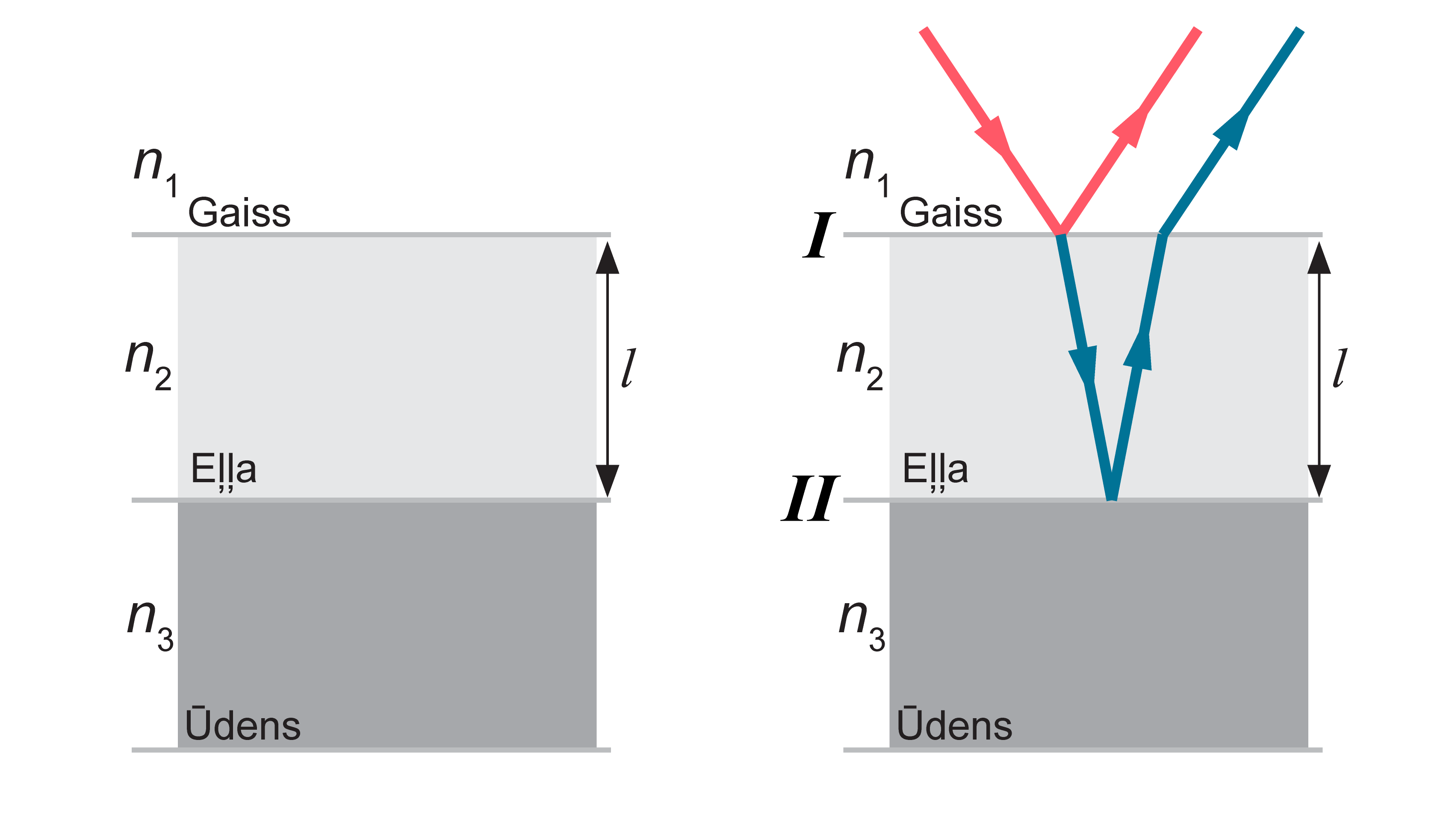
- gaismas stars, kas krīt pret virsmu (I), daļēji atstarojas no tās (zaļais stars 1) un daļēji lūzt uz robežvirsmas starp gaisu un plānās kārtiņas virsmu;
- atstarojoties no plānās kārtiņas otras virsmas (II), atkal lūzt uz plānās kārtiņas un gaisa slāņa robežvirsmas (zilais stars 2), iznākot atpakaļ gaisā paralēli staram 1;
- interferences rezultāts būs atkarīgs gan no viļņa garuma, gan no plānās kārtiņas biezuma, gan dažādo slāņu laušanas koeficientiem. Lai notiktu atstarošanās no robežvirsmas starp divām vidēm, to gaismas laušanas koeficientiem jābūt atšķirīgiem: \(n_3\neq n_2\neq n_1\).
2. punkts
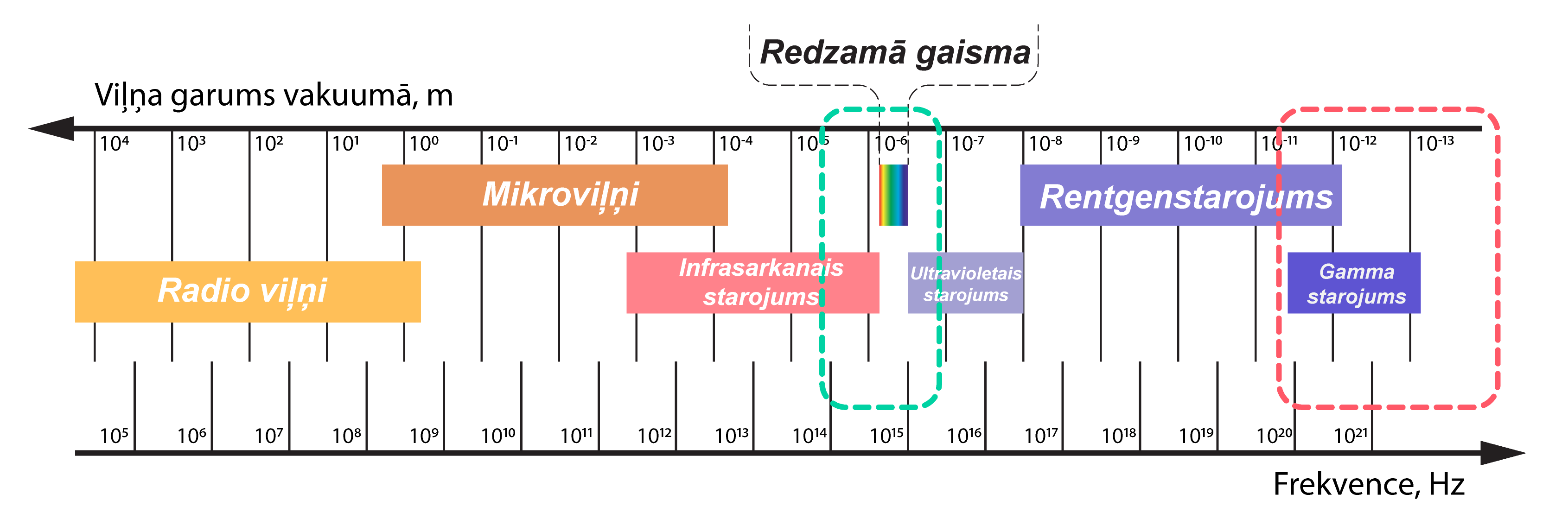
Tā kā šis jautājums ir tikai vienu punktu vērts, tam jābūt vienkāršam. Tas liek domāt, ka ir jāsalīdzina tikai magnija fluorīda optisko logu (\(0{,}110\space\mathrm{\mu{m}}-7{,}5\space\mathrm{\mu{m}}\)) ar gamma starojuma viļņu garuma diapazonu, kas atrodams datu bukletā.
Tomēr atbilde uz jautājumu nav tik vienkārša.
Gamma starojumu veido augstas enerģijas fotoni, un materiāliem, kas efektīvi absorbē gamma starojumu, parasti ir liels atomskaitlis (protonu skaits kodolā) un blīvums. Gamma starojuma ekranēšanai parasti izmanto svinu (Pb, atomskaitlis 82) un volframu (W, atomskaitlis 74), kuriem ir augsts atomskaitlis un blīvums, kas ļauj tiem efektīvi vājināt vai absorbēt gamma starojumu.
Turpretim magnija fluorīdam ir salīdzinoši samērā mazs atomskaitlis (12 magnijam un 9 fluoram) un salīdzinoši mazāks blīvums. Rezultātā tas nav efektīvs gamma starojuma absorbētājs un tas nav piemērots kā gamma starojuma aizsargmateriāls.
Turklāt uzdevumā ir runa par ļoti plānu magnija fluorīda slānīti. Skolēnu zināšanas par radioaktīvo starojumu un tā ekranēšanu varētu būt pietiekamas, lai atbildētu uz jautājumu – magnija fluorīds IR caurspīdīgs gamma starojumam.
Atbilde: magnija fluorīds nav caurspīdīgs gamma starojumam, jo tā caurspīdīguma diapazons (\(0{,}110\space\mathrm{\mu{m}}-7{,}5\space\mathrm{\mu{m}}\)) neatbilst gamma starojuma viļņu garuma diapazonam (\(\lambda<10^{-11}\space\mathrm{m}\)).
3. punkts
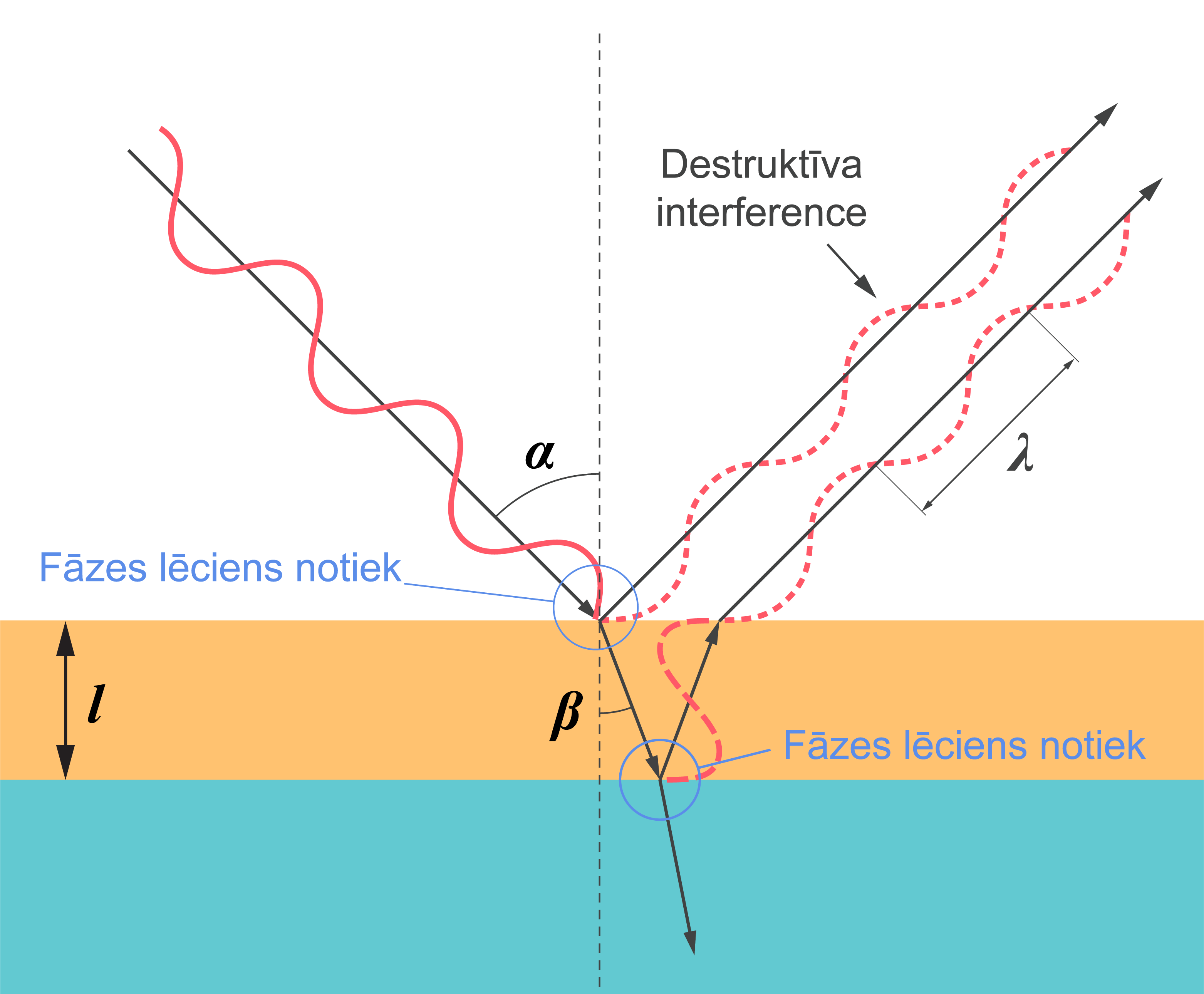
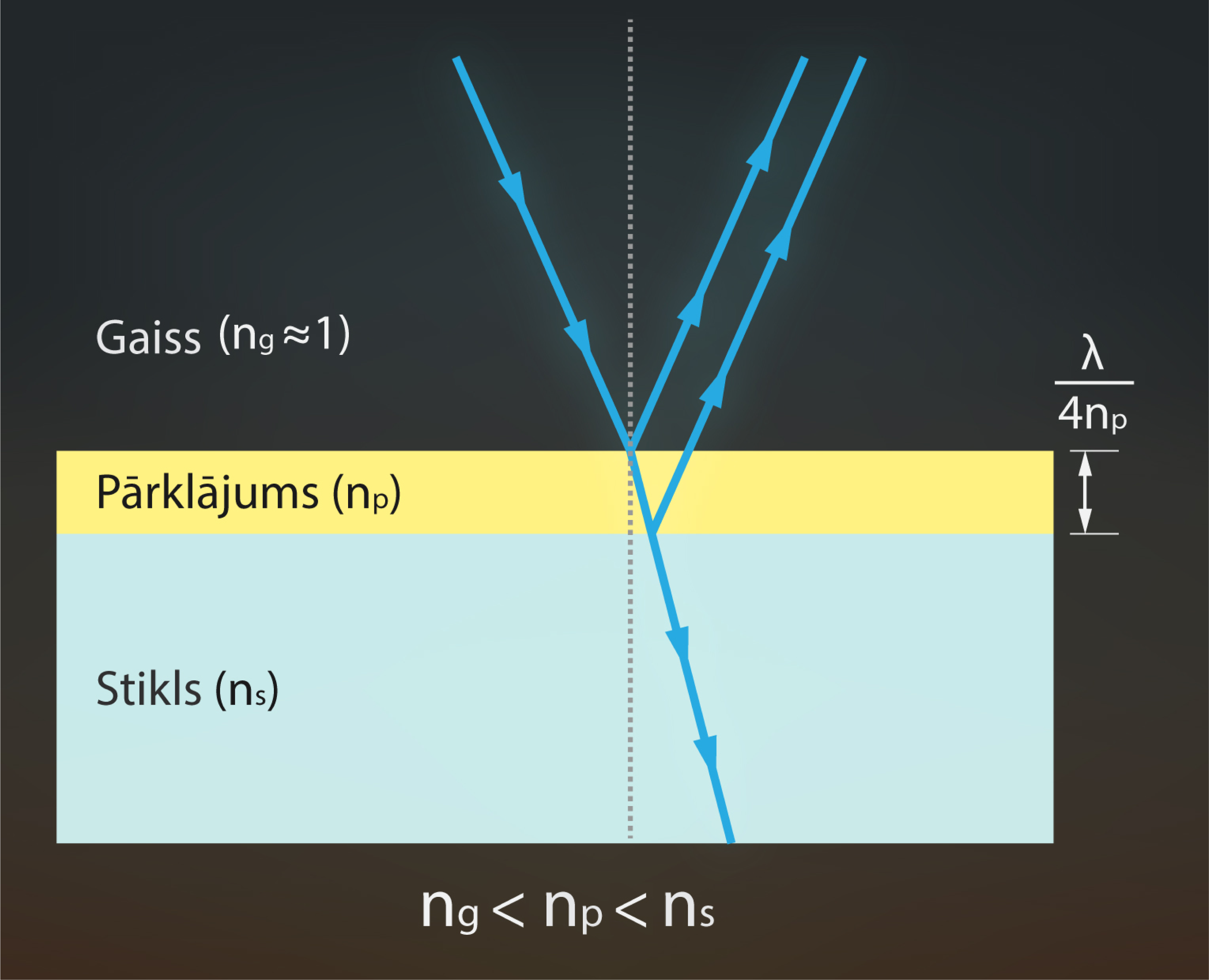Lai nenotiktu atstarošanās, jānotiek destruktīvai staru 1 un 2 interferencei.
Lai iegūtu destruktīvu interferenci (lai gaismas stari dzēstu viens otru), staram 2 ir jāveic par \(\frac{\lambda}{2}\) garāks ceļš nekā staram 1.
Stariem, kas krīt gandrīz perpendikulāri pret virsmu (leņķi \(\alpha\) un \(\beta\) praktiski vienādi ar nulli), gājienu ģeometriskā starpība ir \(2l\), kur \(l\) ir plānās kārtiņas biezums. Tā kā abi stari 1 un 2 atstarojas no optiski blīvākas vides, fāžu lēciens nevienam no tiem nenotiek. Pārējot optiski blīvakajā vidē, viļņa garums samazinās: \(\lambda_\mathrm{kārt}=\frac{\lambda}{n_\mathrm{kārt}}\). Par optikas dzidrināšanu vairāk var lasīt Fizmix portālā Fiztēmās.
Tādā gadījumā
\(2l=\frac{\lambda_\mathrm{kārt}}{2}\)
kur gaismas viļņa garums plānajā kārtiņā \(\lambda_\mathrm{kārt}=\frac{\lambda}{n_\mathrm{kārt}}\).
No kurienes plānās kārtiņas biezums:
\(l=\frac{\lambda}{4n_\mathrm{kārt}}=\frac{550\cdot10^{-9}}{4\cdot1{,}38}=99{,}6\space\mathrm{nm}\).
Atbilde: minimālajam kārtiņas biezumam jābūt \(99{,}6\space\mathrm{nm}\).
4. punkts
Iepriekš iegūta kārtiņas biezuma aprēķina formula: \(l=\frac{\lambda}{4n_\mathrm{kārt}}\).
Sarkanās gaismas viļņu garums ir lielāks nekā \(550\space\mathrm{nm}\), līdz ar to arī uz lēcas būtu jāklāj biezāks plānās kārtiņas slānītis nekā gadījumā, ja ir jāfotografē \(550\space\mathrm{nm}\) gaismā.
\(l=\frac{\lambda}{4n_\mathrm{kārt}}=\frac{700\cdot10^{-9}}{4\cdot1{,}38}=127\space\mathrm{nm}\).
Atbilde: sarkanās gaismas viļņu garums ir lielāks nekā \(550\space\mathrm{nm}\), tātad jāklāj biezāks plānās kārtiņas slānītis.
1. punkts
Uzdevuma izpilde eksāmenā – 26,7%.
Vērtēšanas kritēriji
Uzzīmēts situācijas zīmējums, aprakstīta staru gaita: uz pirmās robežvirsmas daļēji lūzt, daļēji atstarojas – 1 punkts.
Uzzīmēts situācijas zīmējums, aprakstīta staru gaita: uz otrās robežvirsmas notiek gaismas atstarošanās, atstarotais stars lūzt, izejot gaisā – 1 punkts.
Salīdzina, kādam \(n\) vērtībām parādība ir iespējama (\(n_3\neq n_2\neq n_1\)) – 1 punkts. Laušanas koeficientu attiecība var būt pieminēta 3. punktā, tad to jāieskaita šeit; faktu, ka zīmējumā doti ūdens/eļļa, var neievērot, jo uzdevumā jautāts par vispārīgo gadījumu.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 3 punktiem.
2. piemērs: risinājums novērtēts ar 3 punktiem.
3. piemērs: risinājums novērtēts ar 3 punktiem. Redzams, ka gaisma lūst uz otrās virsmas, tātad, skolēns demonstrē izpratni, ka \(n_2\) un \(n_3\) atšķirīgi.
4. piemērs: risinājums novērtēts ar 2 punktiem. Otrais stars neatgriežas gaisā.
5. piemērs: risinājums novērtēts ar 1 punktu. Attēlots tikai atstarotais stars.
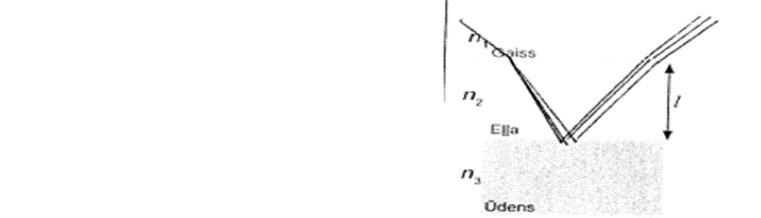
6. piemērs: risinājums novērtēts ar 0 punktu. Nav, kam interferēt.
2. punkts
Uzdevuma izpilde eksāmenā – 73,7%.
Vērtēšanas kritēriji
Atbilde "nē" pamatota ar magnija fluorīda optiskā loga neatbilstību gamma starojuma diapazonam – 1 punkts.
VAI
Atbilde "jā" pamatota ar zināmo par radioaktīvā starojuma ekranēšanu – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 1 punktu.
2. piemērs: risinājums novērtēts ar 1 punktu.
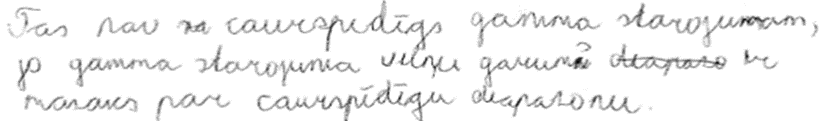
3. piemērs: risinājums novērtēts ar 1 punktu.
4. piemērs: risinājums novērtēts ar 0 punktu. Jautājums nav atbildēts.
5. piemērs: risinājums novērtēts ar 0 punktu. Diapazoni salīdzināti, secinājums nepareizs.
3. punkts
Uzdevuma izpilde eksāmenā – 3,9%.
Vērtēšanas kritēriji
Uzraksta, ka jānotiek destruktīvai interferencei vai ka gājuma starpībai starp atstarotiem viļņiem jābūt \(\frac{\lambda}{2}\) (gājumu starpība \(\Delta x=(2k+1)\frac{\lambda}{2}\)) – 1 punkts.
Sastāda izteiksmi, kas apraksta destruktīvas interferences situāciju gaismas stariem, kas krīt perpendikulāri virsmai, (spriedums par fāžu lēcienu nav obligāts): \(2l=\frac{\lambda_\mathrm{kārt}}{2}\) – 1 punkts.
Izmanto sakarību, kas saista gaismas viļņu garumu plānā kārtiņā ar krītošās gaismas viļņa garumu un gaismas laušanas koeficientu plānajā kārtiņā: \(\lambda_\mathrm{kārt}=\frac{\lambda}{n_\mathrm{kārt}}\) – 1 punkts.
Aprēķina plānās kārtiņas biezumu, norādot atbilstošu mērvienību (zīmīgo ciparu skaitu nevērtē, pieļaujama kļūda aprēķinā) – 1 punkts.
Faktiski var vērtēt līmeņos – ir pieci momenti, kam jābūt:
- jānotiek destruktīvai interferencei
- gājuma starpībai starp atstarotiem viļņiem jābūt \(\frac{\lambda}{2}\)
- gājumu starpība ir \(2l\)
- viļņa garums plānajā kārtiņā samazinās (gājumu starpība pieaug) \(n_\mathrm{kārt}\) reizes
- aprēķins
Lai iegūtu visus četrus punktus, kaut kas viens no pirmajiem diviem var nebūt. Savukārt, ja pirmie četri punkti ir izpildīti korekti, par kļūdu skaitliskajā aprēķinā punkti netiek noņemti.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 4 punktiem. Formulu skolēnam ir tiesības atcerēties, ja optikas dzidrināšana apgūta mācību procesā.
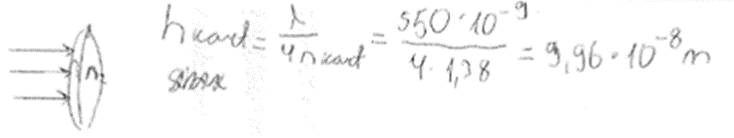
2. piemērs: risinājums novērtēts ar 4 punktiem.
3. piemērs: risinājums novērtēts ar 4 punktiem.
4. piemērs: risinājums novērtēts ar 4 punktiem. Formulā \(n_\mathrm{kārt}\) pareizi, aprēķinā kļūda. Lietot jēdzienu "jāapsorbējas" uzdevuma kontekstā ir nepareizi, bet var to uztvert kā ideju par destruktīvu interferenci.
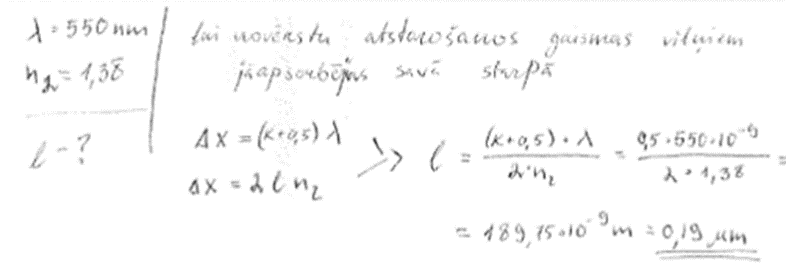
5. piemērs: risinājums novērtēts ar 3 punktiem. Risinājumā tika aplūkota konstruktīvā interference.
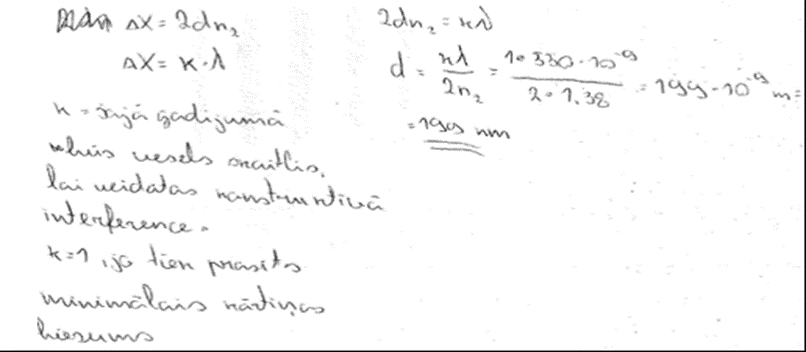
6. piemērs: risinājums novērtēts ar 2 punktiem. Risinājumā ir parādīta izpratne par to, ka jānotiek destruktīvai interferencei un gājuma starpībai starp atstarotiem viļņiem jābūt \(\frac{\lambda}{2}\).
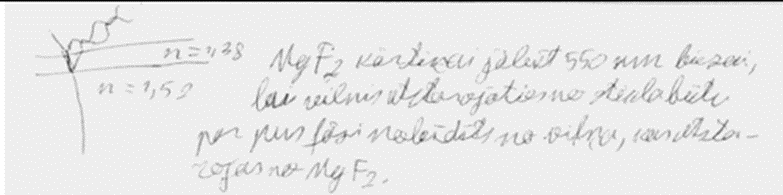
7. piemērs: risinājums novērtēts ar 1 punktu. Risinājumā ir parādīta izpratne par to, ka jānotiek destruktīvai interferencei.
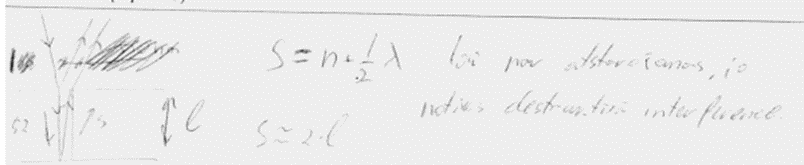
8. piemērs: risinājums novērtēts ar 0 punktu. Risinājums nav par interferenci.
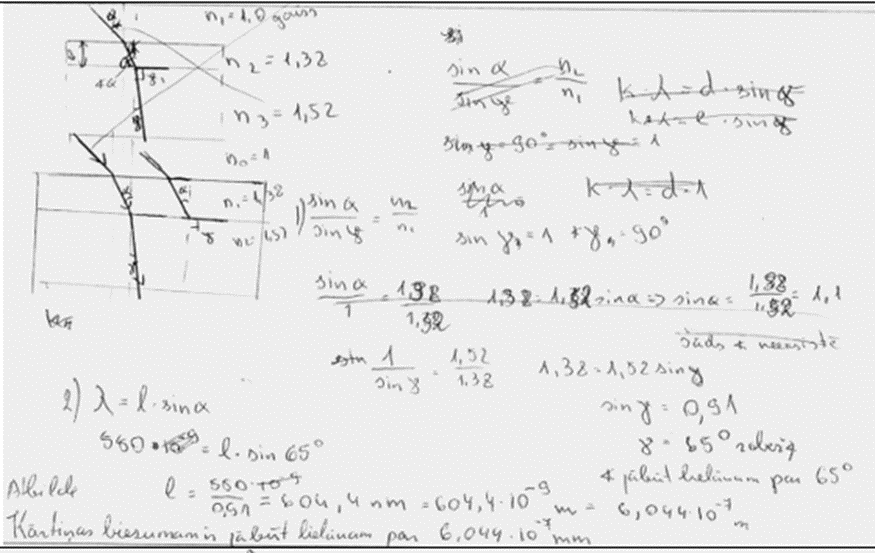
9. piemērs: risinājums novērtēts ar 0 punktu. Risinājumā interference tikai pieminēta.
4. punkts
Uzdevuma izpilde eksāmenā – 34,7%.
Vērtēšanas kritēriji
Salīdzina sarkanās gaismas viļņa garumu ar doto gaismas viļņa garumu \(550\space\mathrm{nm}\) – 1 punkts.
Secina, ka kārtiņas biezumam jābūt biezākam (izmantojot iepriekšējā punktā iegūto sakarību, kam nav jābūt pārrakstītai vai pieminētai). Ja iepriekš iegūta cita, nepareiza slānīša biezuma atkarība no viļņa garuma, šo punktu vērtē atbilstoši tai – 1 punkts.
Ja uzrakstīts vēl kaut kas, nepareizs, to nevērtē.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 2 punktiem.
2. piemērs: risinājums novērtēts ar 2 punktiem.
3. piemērs: risinājums novērtēts ar 1 punktu. Nepareizs secinājums atbilstoši iegūtajai formulai.
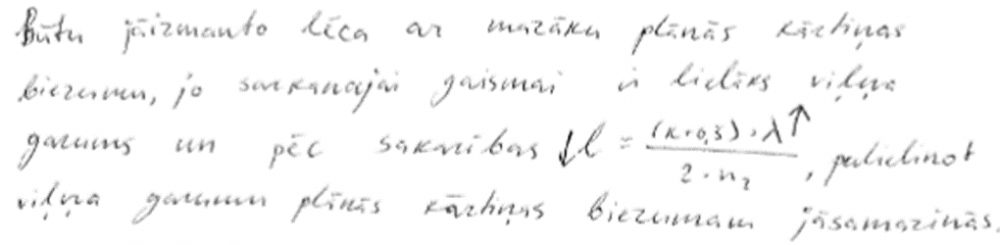
4. piemērs: risinājums novērtēts ar 1 punktu. Salīdzināts sarkanās gaismas viļņa garums ar doto gaismas viļņa garumu.
5. piemērs: risinājums novērtēts ar 0 punktu. Atbilde un pamatojums nav pareizi.
