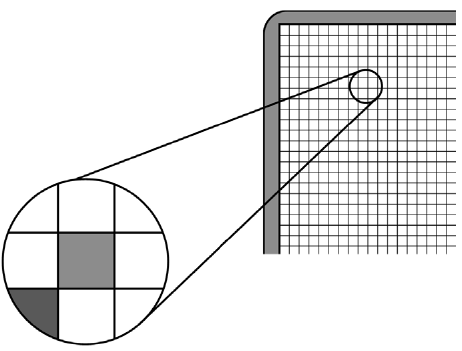
Telefonu displeji ir sadalīti pikseļos. Pikseļu malas veido regulāru režģi. Ja uz telefona ekrānu spīdina lāzera gaismu, tad uz telpas sienas aiz novērotāja veidojas neparasta aina – nevis viens gaišs plankums, bet gan punktu sērija. Stundā skolēni veica eksperimentu, nosakot telefona pikseļu skaitu vienā centimetrā.
1. Ar ko skaidrojama punktiņu parādīšanās atstarotajā gaismā uz ekrāna?
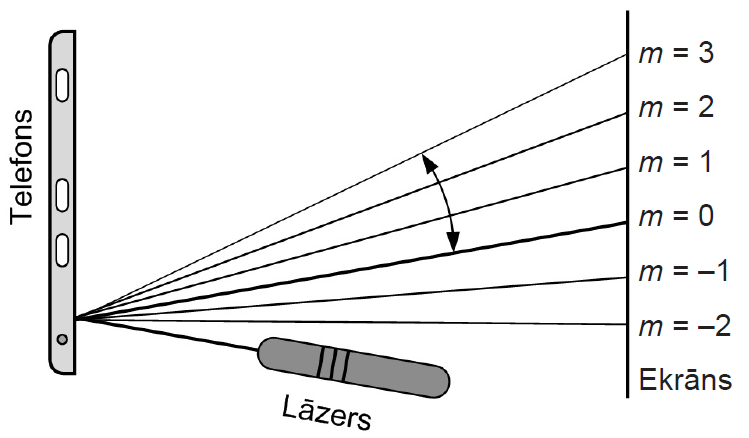
2. Eksperimentā noteica, ka trešais maksimums novērojams \(1,9^{\mathrm o}\) lielā leņķī no centrālā maksimuma. Izmantoja zaļās gaismas lāzeru, kura viļņa garuma \(550\space\mathrm{mm}\). Aprēķini pikseļu skaitu vienā centimetrā!
3. Kā mainītos tādā pašā veidā noteiktais leņķis, ja izmantotu nevis zaļās, bet sarkanās gaismas lāzeru? Pamato savu viedokli!
1. Mobilā telefona ekrānu aplūko, kā divus perpendikulāri novietotus difrakcijas režģus, kas atstaro gaismu. Notiek gaismas difrakcija šaurās spraugās, atstarotie gaismas stari interferē, un uz telpas sienas veidojas difrakcija aina – gaišu punktu sērija.
Atbilde: punktiņu parādīšanās atstarotajā gaismā uz ekrāna skaidrojama ar difrakcijas un interferences parādībām.
2. Pikseļa izmēru pieņem vienādu ar difrakcijas režģa konstanti \(d\). Pielieto difrakcijas režģa formulu \(d\sin\varphi=m\lambda\), kur \(\varphi\) - difrakcijas leņķis, \(m\) – spektra kārta, \(\lambda\) – lāzera starojuma viļņa garums. Difrakcijas režģa konstanti \(d\) nosaka pēc formulas \(d=\frac{l}{N}\), kur \(l\) – nogriežņa garums, kurā atrodas \(N\) spraugas. Uzdevumā \(l=1\space\mathrm{cm}=1\cdot10^{-2}\space\mathrm m\), bet \(N\) ir pikseļu skaits.
No difrakcijas režģa formulas izsaka \(d=\frac{m\lambda}{\sin\varphi}\).
Pēc tam no formulas \(d=\frac{l}{N}\) izsaka \(N=\frac{l}{d}\).
Aprēķini:
\(d=\frac{m\lambda}{\sin\varphi}=\frac{3\cdot550\cdot10^{-9}}{\sin 1,9^{\mathrm o}}\approx5,0\cdot10^{-5}\space\mathrm m\).
\(N=\frac{l}{d}=\frac{1,0\cdot10^{-2}}{5,0\cdot10^{-5}}=200\).
Piezīme: var noteikt pikseļu skaitu vispārīgā veidā \(N=\frac{l}{d}=\frac{l\sin\varphi}{m\lambda}\).
Atbilde: vienā centimetrā ir 200 pikseļi.
3. Sarkanās gaismai viļņa garums \(\lambda_\mathrm s\) ir lielāks nekā zaļās gaismas viļņa garums \(\lambda_\mathrm z\). Pielieto difrakcijas režģa formulu \(d\sin\varphi=m\lambda\) un secina, ka difrakcijas leņķa sinuss ir tieši proporcionāls viļņa garumam: \(\sin\varphi\sim\lambda\). Pirmajā kvadrantā sinusa funkcija ir augoša. Tādēļ lielākam viļņa garumam atbilst lielāks difrakcijas leņķis: \(\lambda_\mathrm s>\lambda_\mathrm z\) un \(\varphi_\mathrm s>\varphi_\mathrm z\).
Atbilde: ja izmantotu nevis zaļās, bet sarkanās gaismas lāzeru, tādā pašā veidā noteiktais leņķis būtu lielāks, jeb difrakcijas aina būtu "platāka".
Vērtēšanas kritēriji
1. Atpazīst gaismas difrakcijas un interferences parādību – 1 punkts.
2. Saista pikseļa izmēru ar režģa konstanti – 1 punkts.
Zina vai atrod formulu lapā difrakcijas režģa formulu un aprēķina difrakcijas režģa konstanti – 1 punkts.
Aprēķina pikseļu skaitu vienā centimetrā – 1 punkts.
3. Izmanto difrakcijas režģa formulu – 1 punkts.
Secina, kā mainās difrakcijas leņķis, ja zaļās gaismas lāzera vietā izmanto sarkanās gaismas lāzeru – 1 punkts.