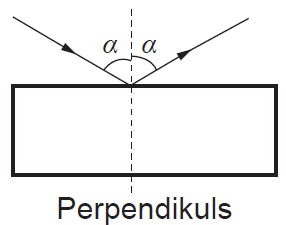
 Šaurs gaismas stars krīt no gaisa uz caurspīdīgu cirkonija plāksnīti. Daļa gaismas tiek atstarota, kā parādīts attēlā, un daļa gaismas tiek lauzta. Leņķis starp atstaroto un lauzto staru ir taisns. Cirkonija laušanas koeficients attiecībā pret gaisu ir 2,15.
Šaurs gaismas stars krīt no gaisa uz caurspīdīgu cirkonija plāksnīti. Daļa gaismas tiek atstarota, kā parādīts attēlā, un daļa gaismas tiek lauzta. Leņķis starp atstaroto un lauzto staru ir taisns. Cirkonija laušanas koeficients attiecībā pret gaisu ir 2,15.
1. Iezīmē lauzto gaismas staru plāksnītē! (1 punkts)
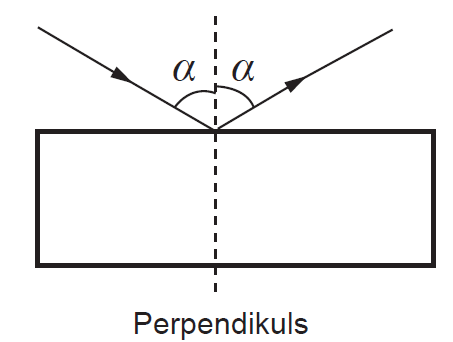
2. Aprēķini gaismas ātrumu cirkonija plāksnē! Pieņem, ka gaismas ātrums gaisā ir \(3\cdot10^8~\mathrm{m/s}\)! (1 punkts)
3. Kā mainās gaismas viļņa garums, staram šķērsojot robežu starp gaisu un cirkoniju? Pamato savu atbildi! (2 punkti)
4. Pamatojoties uz gaismas laušanas likumu, aprēķini stara krišanas leņķi uz plāksnīti! (3 punkti)
5. Aprēķini, cik liels ir pilnīgās iekšējās atstarošanās robežleņķis uz cirkonija un gaisa robežvirsmas! Parādi aprēķinu gaitu! (2 punkti)
6. Kā mainītos leņķis starp atstaroto un lauzto staru, ja cirkonija vietā izmantotu stikla plāksnīti, kuras gaismas laušanas koeficients pret gaisu ir 1,5? (1 punkts)
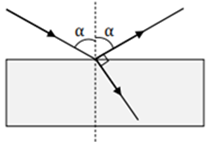 1. Uzdevuma tekstā teikts, ka leņķis starp atstaroto un lauzto staru ir taisns. Tātad – jāiezīmē lauztais stars, kurš pieliecas perpendikulam pret virsmu stara krišanas punktā, un jāparāda, ka leņķis ir taisns. Var izmantot ģeometrijā pieņemto apzīmējumu, vai ierakstīt, ka leņķis ir \(90^\mathrm{o}\). Ja uzdevums izlasīts neuzmanīgi, var aprēķināt laušanas leņķi un, tam atbilstoši, iezīmēt lauzto staru.
1. Uzdevuma tekstā teikts, ka leņķis starp atstaroto un lauzto staru ir taisns. Tātad – jāiezīmē lauztais stars, kurš pieliecas perpendikulam pret virsmu stara krišanas punktā, un jāparāda, ka leņķis ir taisns. Var izmantot ģeometrijā pieņemto apzīmējumu, vai ierakstīt, ka leņķis ir \(90^\mathrm{o}\). Ja uzdevums izlasīts neuzmanīgi, var aprēķināt laušanas leņķi un, tam atbilstoši, iezīmēt lauzto staru.
2. Lai atrisinātu uzdevumu jāzina, ka gaismas laušanas koeficients parāda, cik reizes gaismas ātrums vakuumā ir lielāks nekā gaismas ātrums konkrētā vidē. Tātad gaismas ātrums cirkonijā \(v=\frac{c}{n}=\frac{3\cdot10^8}{2,15}\approx1,4\cdot10^8\space\mathrm{m/s}\).
3. Viļņa garumu var aprēķināt, ja zina vai atrod datu bukletā sakarību \(\lambda=vT\).
Šķērsojot robežu starp divām vidēm, starojuma frekvence nemainās, bet ātrums, kā aprēķināts apakšuzdevumā 2., samazinās.
Secinājums – viļņa garums samazinās.
4. Lai atrisinātu uzdevumu, jāizmanto datu bukletā atrodamo sakarību – Snelliusa likumu \(\frac{\sin\alpha}{\sin\gamma}=\frac{v_1}{v_2}=\frac{n_2}{n_1}=n\),
kā arī uzdevuma tekstā doto informāciju, ka leņķis starp atstaroto un lauzto staru ir taisns, tātad, \(\gamma=\pi/2-\alpha\). Zināms, ka stara krišanas un atstarošanas leņķi ir vienādi. Abas sakarības apvienojot, iegūst izteiksmi leņķa \(\alpha\) tangensa aprēķināšanai:
\(n=\frac{\sin\alpha}{\sin\gamma}=\frac{\sin\alpha}{\sin(\pi/2-\alpha)}=\frac{\sin\alpha}{\cos\alpha}=\mathrm{tg}\alpha\)
\(\alpha=\mathrm{arctg}\space n=\mathrm{arctg}\space 2,15\approx65^\mathrm{o}\)
Atbilde: stara krišanas leņķis uz plāksnīti ir \(65^\mathrm{o}\).
5. Pārejot no vides ar lielāku laušanas koeficientu vidē ar mazāku laušanas koeficientu, lauztais stars atliecas no perpendekiula, kas vilkts pret robežvirsmu stara krišanas punktā – laušanas leņķis ir lielāks par krišanas leņķi. Saprotams, ka laušanas leņķis nevar kļūt lielāks par \(90^\mathrm{o}\), tātad pilnīgās iekšējās atstarošanās robežleņķis \(\alpha_0\) būs krišanas leņķis, pie kura laušanas leņķis \(\gamma\) ir precīzi vienāds ar \(90^\mathrm{o}\).
Izmantojot Snelliusa likumu, faktu, ka \(\sin{90^\mathrm{o}}=1\) un zinot, ka stars pāriet no cirkonija gaisā, kura laušanas koeficients ir 1, iegūstam sakarību:
\(\frac{\sin{\alpha_0}}{1}=\frac{n_2}{n_1}=\frac{1}{2,15}\space\implies\space\sin{\alpha_0}=\frac{1}{2,15}=0,465\)
\(\alpha_0=\mathrm{arcsin}\space0,465\approx27,7^{\mathrm{o}}\)
Atbilde: pilnīgās iekšējās atstarošanās robežleņķis uz cirkonija un gaisa robežvirsmas ir \(27,7^\mathrm{o}\).
6. Stara krišanas un atstarošanas leņķi nemainās. Tā kā stikla laušanas koeficients mazāks nekā cirkonija, tad, saskaņā ar Snelliusa likumu, laušanas leņķis būs lielāks. Līdz ar to leņķis starp atstaroto un lauzto staru būs mazāks.
1. Vērtēšanas kritēriji
1 punkts: iezīmē lauzto staru, parādot taisnu leņķi starp atstaroto un lauzto staru. Atbilde tiek ieskaitīta arī, ja lauztais stars ir iezīmēts, aprēķinot un parādot laušanas leņķi \(\gamma=25^\mathrm{o}\) vai leņķi \(\alpha\) mērot ar transportieri, bet lenķi \(\gamma\)mērot un parādot.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 1 punktu.
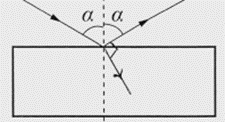
2. piemērs: risinājums novērtēts ar 1 punktu.
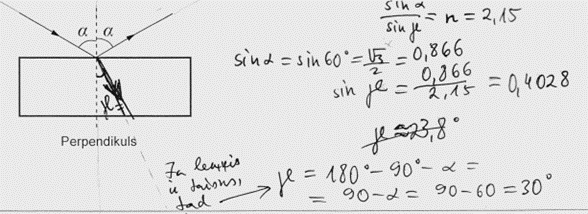
3. piemērs: risinājums novērtēts ar 0 punktu.
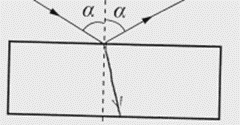
2. Vērtēšanas kritēriji
Aprēķina gaismas ātrumu cirkonijā, parādot risinājuma gaitu, norāda mērvienību – 1 punkts. Zīmīgo ciparu skaitu nevērtē. Risinājums var būt parādīts tikai skaitliski.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 1 punktu.
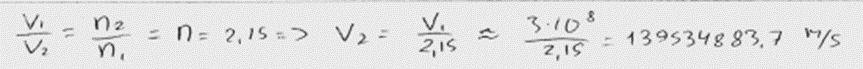
2. piemērs: risinājums novērtēts ar 1 punktu.
![]()
3. piemērs: risinājums novērtēts ar 1 punktu. Izmantota datu bukletā atrodamā formula, rēķināts, izmantojot izmērītu leņķi \(\alpha\).
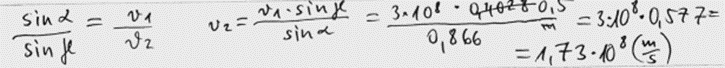
4. piemērs: risinājums novērtēts ar 0 punktu.
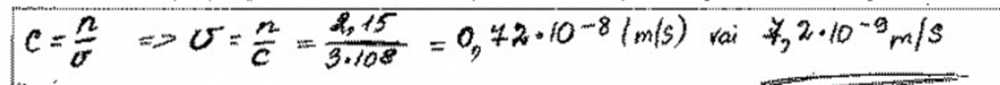
3. Vērtēšanas kritēriji
• Uzraksta sakarību starp viļņa garumu un gaismas ātrumu ar formulu vai skaitliski – 1 punkts.
• Secina, ka viļņa garums samazinās – 1 punkts.
Ja 2. apakšuzdevumā aprēķināts, ka gaismas izplatīšanās ātrums pieaug, un izdarīts atbilstošs secinājums, punktus ieskaita.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 2 punktiem.

2. piemērs: risinājums novērtēts ar 2 punktiem.

3. piemērs: risinājums novērtēts ar 1 punktu. Nepilnīgs pamatojums.
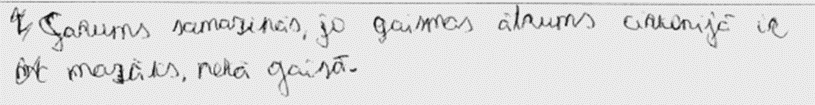
4. piemērs: risinājums novērtēts ar 0 punktu.

4. Vērtēšanas kritēriji
• Uzraksta sakarības (vienādojumu sistēmu) leņķa \(\alpha\) aprēķināšanai – 1 punkts.
• Izsaka no sakarībām \(\mathrm{tg}\space\alpha\) – 1 punkts.
• Aprēķina leņķi skaitliski, norāda mērvienību – 1 punkts.
Ja aprēķināts laušanas leņķis – 2 punkti.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 3 punktiem.
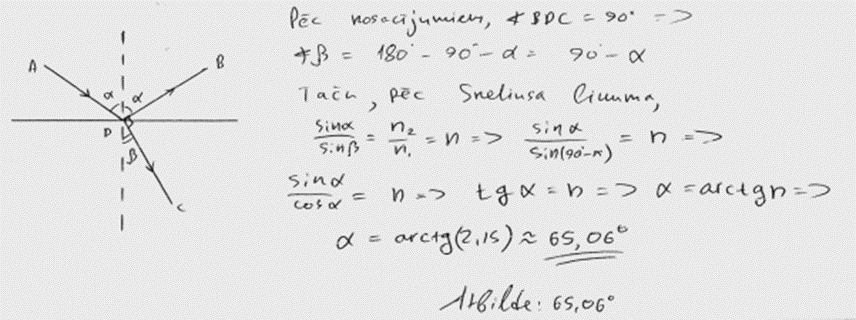
2. piemērs: risinājums novērtēts ar 2 punktiem. Nepareizi aprēķināts skaitliski.
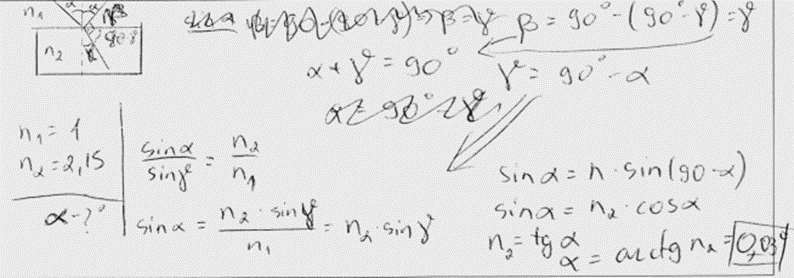
3. piemērs: risinājums novērtēts ar 2 punktiem. Aprēķināts laušanas leņķis.
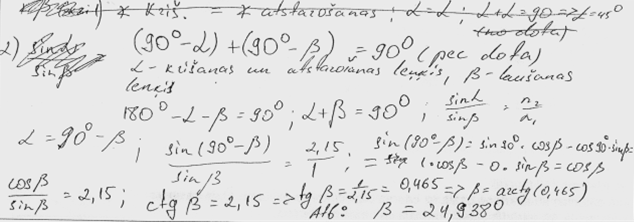
4. piemērs: risinājums novērtēts ar 1 punktu. Tikai 1. punkts no vērtēšanas kritērijiem.
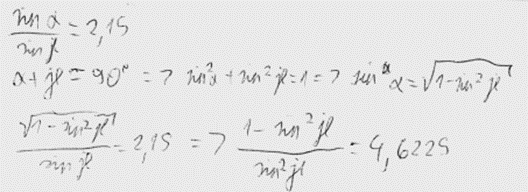
5. piemērs: risinājums novērtēts ar 0 punktu. Absurds risinājums. Rakstīts, ka krišanas leņķis ir izmērīts, pēc tam, pamatojoties uz izmērīto vērtību, tas tiek aprēķināts.
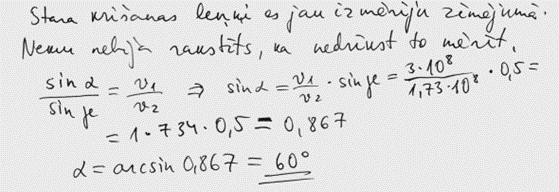
5. Vērtēšanas kritēriji
• Aprēķina robežleņķa sinusa vērtību, parādot risinājuma gaitu – 1 punkts.
• Aprēķina leņķi, izmantojot leņķa sinusa vērtību – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 2 punktiem.
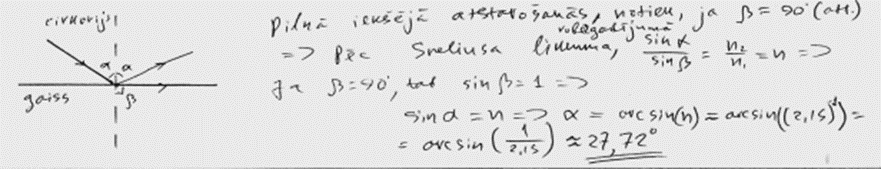
2. piemērs: risinājums novērtēts ar 2 punktiem.
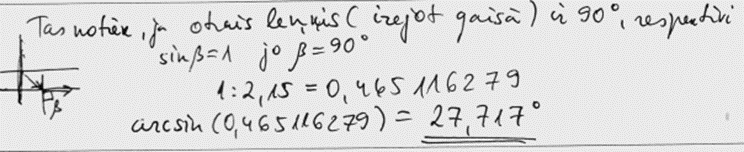
3. piemērs: risinājums novērtēts ar 1 punktu. Risinājums nepilnīgs un pieraksts nekorekts.
![]()
4. piemērs: risinājums novērtēts ar 1 punktu. Nepareizi sarēķināts skaitliski.

5. piemērs: risinājums novērtēts ar 0 punktu.
![]()
6. Vērtēšanas kritēriji
Pamato, ka leņķis būs mazāks – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 1 punktu.

2. piemērs: risinājums novērtēts ar 1 punktu.

3. piemērs: risinājums novērtēts ar 0 punktu. Trūkst jebkāda pamatojuma.
![]()