Gaismas stars krīt uz 1. spoguli punktā x.
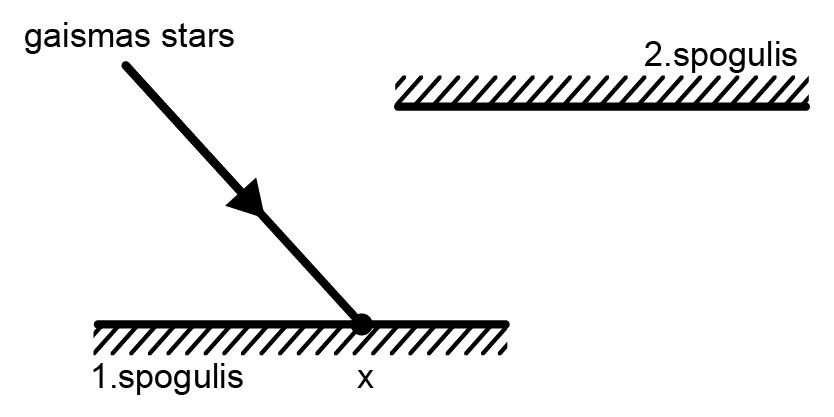
Uzzīmē no 1. spoguļa atstaroto staru! Norādi zīmējumā krišanas leņķi \(\alpha\) un atstarošanās leņķi \(\beta\)! 2. spogulis novietots paralēli pirmajam.
No 1. spoguļa atstarotais stars krīt uz otro spoguli un atstarojas no tā. Uzzīmē no 2. spoguļa atstaroto staru!
Salīdzini uz 1. spoguli krītošā stara un no 2. spoguļa atstarotā stara virzienu!
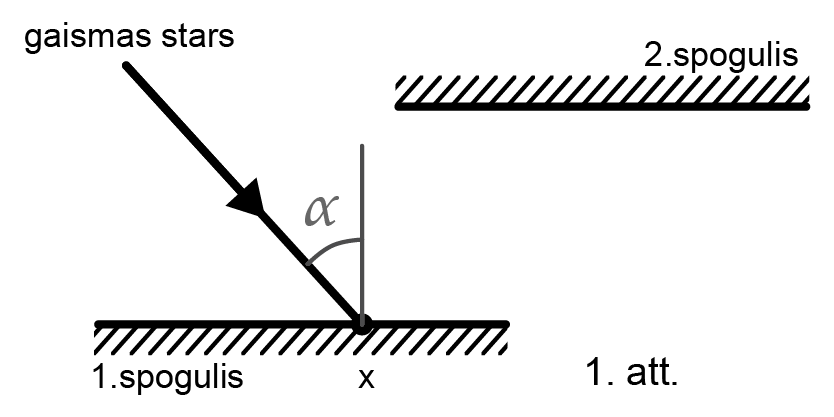
Gaismas stara krišanas punktā x uzzīmē perpendikulu pret 1. spoguļa virsmu. Leņķis starp krītošo staru un perpendikulu ir krišanas leņķis \(\alpha\) (skatīt 1. attēlu).
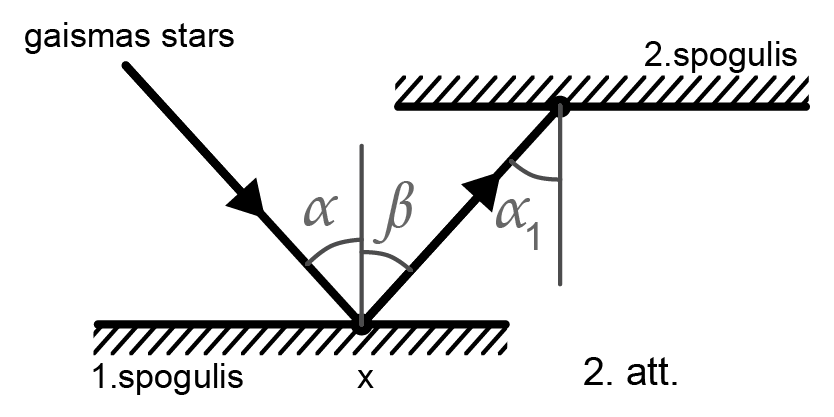
Konstruē atstaroto staru tā, lai atstarošanas leņķis \(\beta\) (leņķis starp atstaroto staru un perpendikulu) būtu vienāds ar krišanas leņķi \(\alpha\) (skatīt 2. attēlu). Atstarotajam staram norāda virzienu.
Tālāk stars krīt uz 2. spoguļa virsmu. Gaismas stara krišanas punktā novelk perpendikulu pret 2. spoguļa virsmu, atzīmē gaismas stara krišanas leņķi \(\alpha_1\), konstruē atstaroto staru atbilstoši gaismas atstarošanas likumam (atstarošanas leņķis \(\beta_1\) ir vienāds ar krišanas \(\alpha_1\) (skatīt 3. attēlu). Atstarotajam staram norāda virzienu.
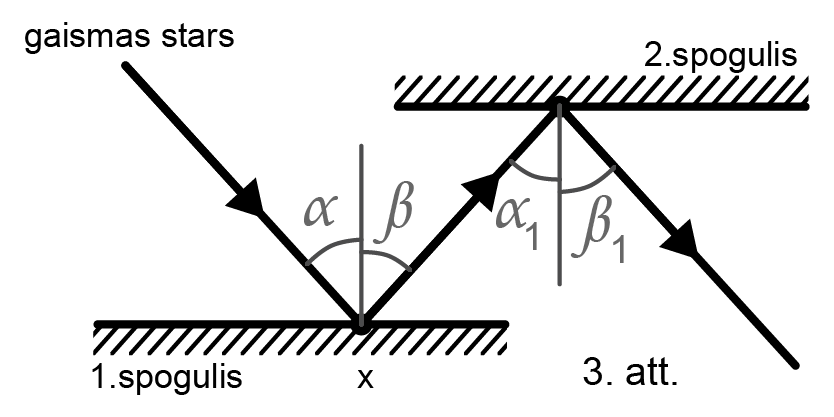
Spoguļi ir novietoti paralēli, tāpēc krišanas punktos novilktie perpendikuli ir savā starpā paralēli. Tas nozīmē, ka atstarošanas leņķis \(\beta\) no 1. spoguļa ir vienāds ar krišanas leņķi \(\alpha\) uz 2. spoguli. Var redzēt, ka visi leņķi \(\alpha\), \(\beta\), \(\alpha_1\) un \(\beta_1\) ir savstarpēji vienādi. Tas nozīmē, ka, par cik lielu leņķi 1. spogulis “staru pagriež”, par tik pat lielu leņķi 2.spogulis to atkal “pagriež atpakaļ”.
Uz 1. spoguļi punktā x krītošais stars ir paralēls no 2. spoguļa virsmas atstarotajām staram.
Vērtēšanas kritēriji
Konstruē perpendikulu pret spoguļa virsmu stara krišanas punktā x, zīmē atstaroto staru un norāda tā virzienu, zīmējumā norāda krišanas un atstarošanas leņķus – 1 punkts.
Salīdzina uz 1. spoguli krītošā stara un no 2. spoguļa atstarotā stara virzienus. Pamato spriedumu gaitu – 1 punkts.