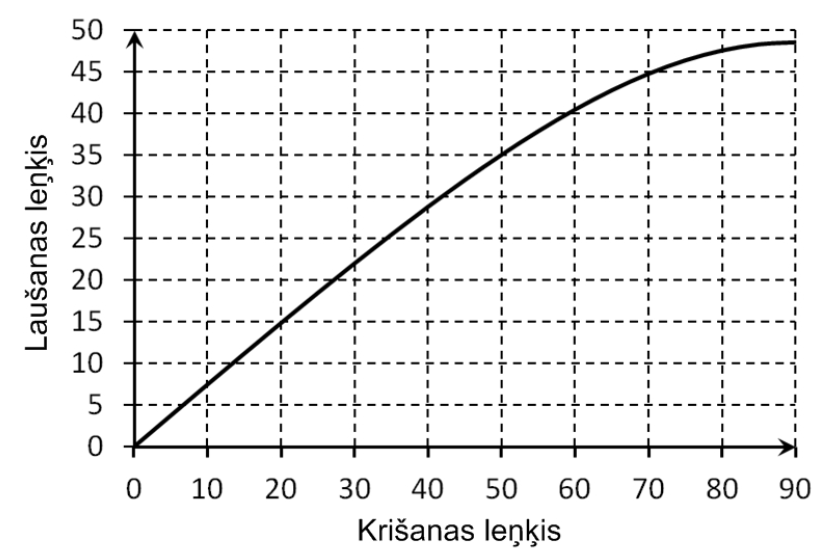
Grafikā ir parādīta gaismas laušanas leņķa atkarība no gaismas krišanas leņķa uz robežvirsmas starp gaisu un kādu nezināmu vidi. Leņķi ir doti grādos. Gaismas laušanas koeficients gaisam ir 1. Izmantojot doto grafiku, nosaki gaismas laušanas koeficientu nezināmajai videi! Parādi aprēķinu gaitu!
Gaismas laušanas koeficienta noteikšanai izmantosim gaismas laušanas likumu (Snelliusa likumu):
\(\frac{\sin\alpha}{\sin\gamma}=\frac{n_2}{n_1}\), kur \(\alpha\) – krišanas leņķis, \(\gamma\) – laušanas leņķis, \(n_1\) – pirmās vides absolūtais gaismas laušanas koeficients (uzdevumā – gaiss), \(n_2\) – otrās vides absolūtais gaismas laušanas koeficients (uzdevumā – nezināmā vide). Ir zināms, ka gaisa absolūtais laušanas koeficients ir aptuveni vienāds ar 1. Apzīmēsim nezināmās vides absolūto laušanas koeficientu \(n_2\) ar \(n\). Tad gaismas laušanas likuma formulu pieraksta šādi: \(\frac{\sin\alpha}{\sin\gamma}=n\)
Ērtāk izvēlēties krišanas leņķa un laušanas leņķa skaitliskās vērtības punktos, kur grafika līkne šķērso rūtiņu krustpunktus. Attēlā ir iezīmēti divi tādi punkti, A un B:
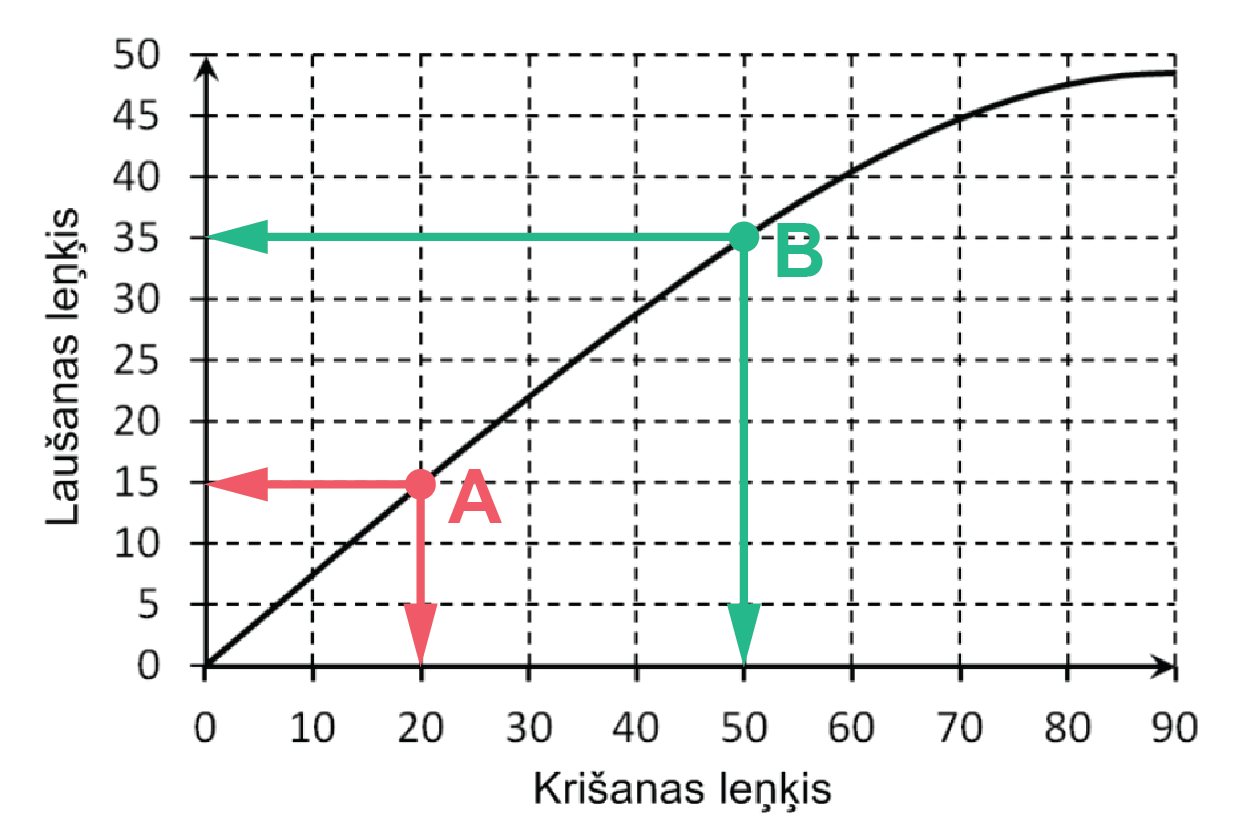
Punktam A atbilst krišanas leņķis \(\alpha=20^{\mathrm{o}}\), laušanas leņķis \(\gamma=15^{\mathrm{o}}\), \(n=\frac{\sin\alpha}{\sin\gamma}=\frac{\sin{20^{\mathrm{o}}}}{\sin{15^{\mathrm{o}}}}\approx1,3\)
Punktam B atbilst krišanas leņķis \(\alpha=50^{\mathrm{o}}\), laušanas leņķis \(\gamma=35^{\mathrm{o}}\), \(n=\frac{\sin\alpha}{\sin\gamma}=\frac{\sin{50^{\mathrm{o}}}}{\sin{35^{\mathrm{o}}}}\approx1,3\)
Atbilde: nezināmās vides gaismas laušanas koeficients ir \(1,3\).
Vērtēšanas kritēriji
Zina vai atrod formulu lapā gaismas laušanas likuma formulu – 1 punkts.
Nolasa no grafika krišanas un laušanas leņķu vērtības – 1 punkts.
Aprēķina laušanas koeficientu nezināmajai videi – 1 punkts.