Studenti, izmēģinot jaunu gumijlēkšanas trosi, tajā nostiprina akmeni, kura masa \(m\) = 60,0 kg. Akmeni palaiž vaļā bez sākuma ātruma no gaisa trošu vagoniņa, kas atrodas \(h\) = 42,0 m augstumā virs upes.
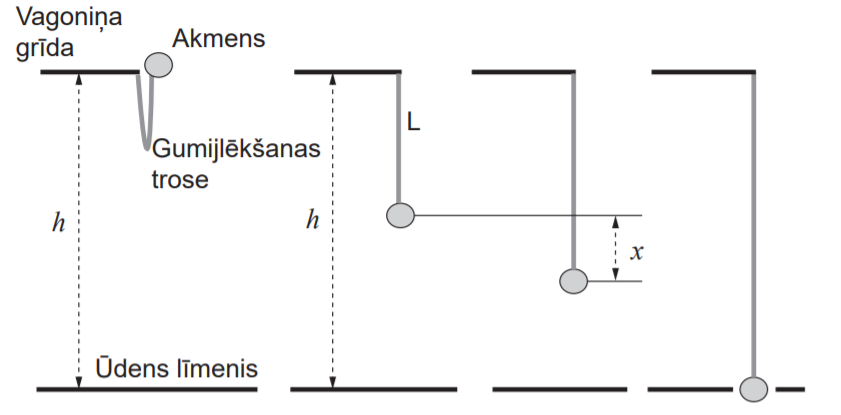
Kritiena viszemākajā punktā akmens pieskaras ūdens virsmai. Troses garums ir \(L\) = 21,0 m, un tā deformējas atbilstoši Huka likumam. Akmens izmērus, gaisa pretestību un troses masu var neievērot. Maksimālo ātrumu akmens sasniedz brīdī, kad trose ir izstiepusies par \(x\) = 5,25 m. Aprēķini, cik lielu maksimālo ātrumu sasniedz akmens! Parādi risinājuma gaitu! \(g\) = 10 m/s2 .
Uzdevumu atrisinājums pieejams video formātā un rakstiski.
\(m=40\space \mathrm{kg}\\ v_{0}=0\space \mathrm{m/s}\\ h=42\space \mathrm{m}\\L=21\space \mathrm{m}\\x=5,25\space \mathrm{m}\\g=10\space \mathrm{m/s^2}\\ v_{\mathrm{max}}-?\)
Kamēr trose nav sastiepta, akmens kustība ir brīvā krišana - kustība tikai smaguma spēka ietekmē. Kad akmens veic attālumu \(L\), uz to sāk iedarboties troses sastiepuma spēks, kas ir atkarīgs no troses stinguma koeficienta un troses pagarinājuma.
Kad trose sasniedz maksimālo kustības ātrumu? Kamēr smaguma spēks un troses elastības spēka radītais rezultējošais paātrinājums ir vērsts uz leju (jeb tā virziens sakrīt ar ātruma virzienu), ātrums turpina pieaugt. Ātrums sāks samazināties, kad sastiepuma spēks pārsniegs smaguma spēku. Tātad, maksimālais ātrums tiks sasniegts brīdī, kad smaguma spēks tiek līdzsvarots ar elastības spēku: \(F_{\mathrm{sm}}=F_{\mathrm{el}}\\ mg=kx\space \implies\space k=\frac{mg}{x}\)
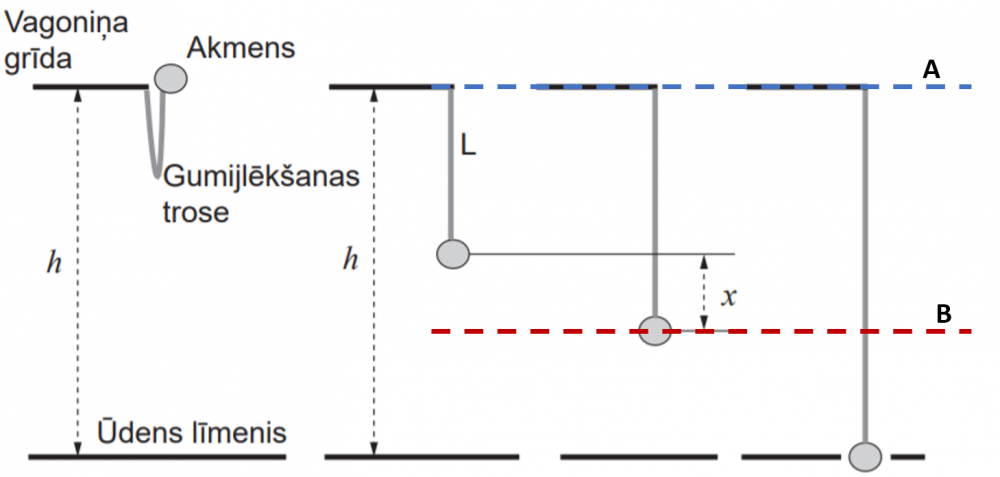
Lai noteiktu akmens ātrumu punktā B, izmantosim pilnās mehāniskās enerģijas nezūdamības likumu. Punktā A akmenim piemīt potenciālā enerģija attiecībā pret punktu B \(mg(L+x)\), kas, akmenim krītot, pārvēršas kinētiskajā un elastīgi deformētas troses potenciālajā enerģijā:
\(mg(L+x)=\frac{mv^2_{\mathrm{max}}}{2}+\frac{kx^2}{2} \space\)
ievietojot \(k=\frac{mg}{x}\), iegūst:
\(mg(L+x)=\frac{mv^2_{\mathrm{max}}}{2}+\frac{mgx}{2}\space / :m\space/ \cdot2\)
\(2gL+2gx=v^2_{\mathrm{max}}+gx\)
\(v^2_{\mathrm{max}}=g(2L+x)\\ v_{\mathrm{max}}=\sqrt{g(2L+x)}=\sqrt{10\cdot(2\cdot21+5,25)}\approx21,7 \space \mathrm{m/s}\)
Atbilde: akmens sasniegs maksimālo ātrumu \( 21,7\space \mathrm{m/s}\)
Piezīme 1.: skolēni drīkstēja arī veikt aprēķinus pa soļiem, neiegūstot augstāk piedāvātā risinājuma vispārīgo izteiksmi maksimālā ātruma noteikšanai, Tādā gadījumā būtu jāizmanto uzdevumā doto akmens masas vērtību:
\(mg=kx \space\implies k=\frac{mg}{x}=\frac{60\cdot10}{5,25}\approx114\space \mathrm{N/m}\)
Un tad ievietot iegūto stinguma koeficienta vērtību izteiksmē maksimālā ātruma noteikšanai:
\(mg(L+x)=\frac{mv^2_{\mathrm{max}}}{2}+\frac{kx^2}{2}\\ v_{\mathrm{max}}=\sqrt{\frac{2mg(L+x)-kx^2}{m}}=\sqrt{2g(L+x)-\frac{k}{m}x^2}=\sqrt{2\cdot10\cdot(21+5,25)-\frac{114}{60}\cdot 5,25^2}\approx21,7\space \mathrm{ m/s^2}\)
Piezīme 2.: Troses stinguma koeficienta noteikšanai varēja izmantot arī pilnās mehāniskās enerģijas nezūdamības likumu, pieņemot, ka akmens kustības zemākajā punktā (kad notiek pieskaršanās ūdens virsmai) tā ātrums ir nulle:
\(mgh=\frac{k(h-L)^2}{2}\space \implies \space k=\frac{2mgh}{(h-L)^2}=\frac{2\cdot 60\cdot 10\cdot 42}{(42-21)^2}\approx114\space \mathrm{N/m}\)
Uzdevuma izpilde eksāmenā - 12%.
Vērtēšanas kritēriji
par troses stinguma koeficienta izteikšanu no spēku līdzsvara nosacījuma vai enerģijas nezūdamības likuma - 2 punkti
par korekti sastādītu enerģijas nezūdamības likuma izteiksmi maksimālā kustības ātruma noteikšanai - 2 punkti
par maksimālā akmens kustības ātruma izteiksmes iegūšanu un maksimālā ātruma vērtības aprēķināšanu - 1 punkts
Piezīme: Daži skolēni piedāvāja atšķirīgus risinājumus (piemēram, izmantojot svārstības vai mainīgā spēka darbu), kas tika vērtēti atbilstoši to korektumam no fizikas skatupunkta.
Skolēnu risinājumu un to vērtējumu piemērī
1. piemērs: risinājums novērtēts ar 5 punktiem. Skolēna risinājuma otrā daļa atšķiras no eksāmena autoru piedāvāta risinājuma, bet ir fizikāli korekta (otrajā kustības posmā tiek izmantots vidējā paātrinājuma jēdziens).

2. piemērs: risinājums novērtēts ar 5 punktiem.

3. piemērs: risinājums novērtēts ar 5 punktiem. Skolēna risinājums atšķiras no eksāmena autoru piedāvāta risinājuma, bet ir fizikāli korekts (maksimālā ātruma noteikšanai tiek izmatoti harmonisko svārstību vienādojumi).

4. piemērs: risinājums novērtēts ar 5 punktiem. Skolēna risinājums atšķiras no eksāmena autoru piedāvāta risinājuma, bet ir fizikāli korekts.
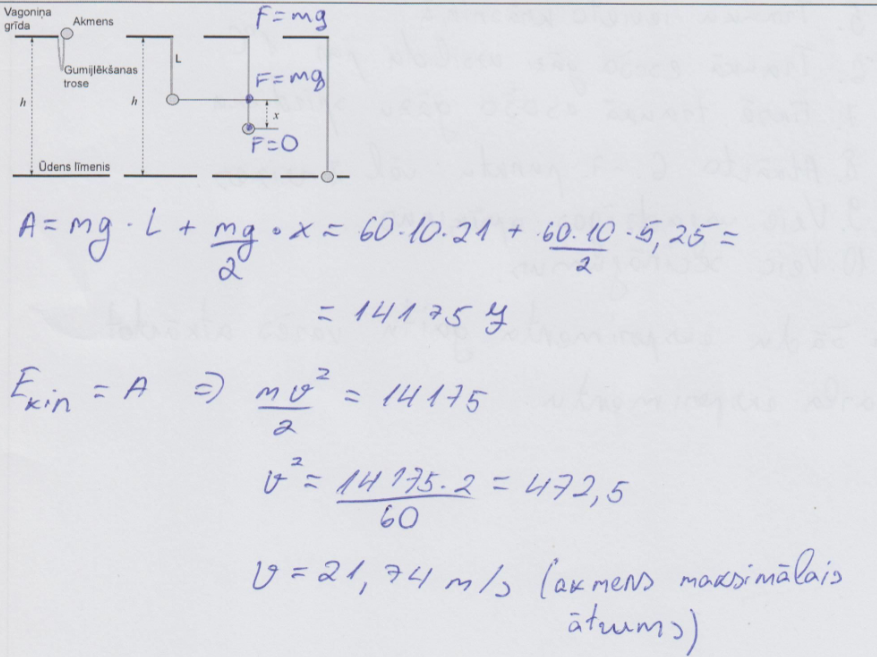
5. piemērs: risinājums novērtēts ar 2 punktiem (par enerģijas nezūdamības likuma izteiksmes sastādīšanu).

6. piemērs: risinājums novērtēts ar 0 punktiem (aprakstītajā situācijā kustība nav vienmērīgi paātrināta).
