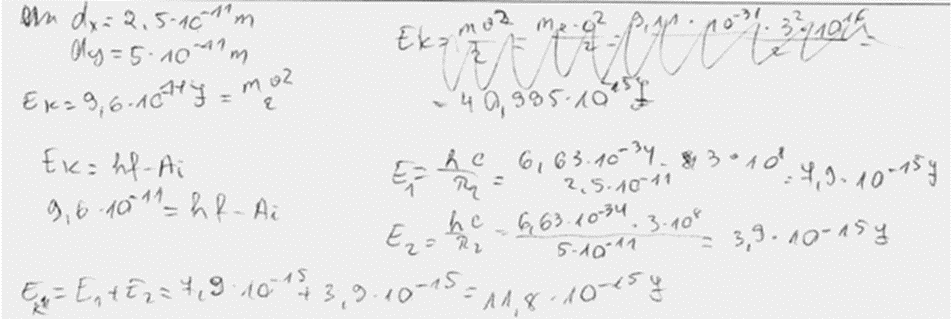Ričards Feinmans 1965. gadā ierosināja veikt dubultspraugas eksperimentu, lai pārbaudītu de Brojī ideju, ka viļņu–daļiņu duālismu var attiecināt uz visām vielas daļiņām, un izpētītu elektronu viļņu īpašības.
Eksperimenta shēma ir parādīta 1. attēlā.
Elektronu paātrināja elektriskajā laukā. Pēc tam elektronu virzīja uz barjeru ar divām spraugām. Detektors reģistrēja vietas, kur elektrons nokļuva pēc tam, kad tas bija izgājis cauri spraugām. Rezultātā tika iegūta 2. attēlā redzamā interferences aina. Melnie punkti apzīmē vietas, kur nokļuva elektrons. Josla, kurā elektrons nenokļuva, ir apzīmēta ar X. Josla, kur elektrons nokļuva, ir apzīmēta ar Y.
1. Pamato, kādēļ šis eksperiments pierāda, ka uz elektroniem var attiecināt de Brojī ideju par viļņu–daļiņu duālismu!
2. Voltmetrs 1. attēlā rāda 3,5 kV. Aprēķini, cik lielu enerģiju iegūst elektrons, paātrinoties homogēnā elektriskajā laukā, ja lauka potenciālu starpība atbilst voltmetra rādījumam!
3. Veikto attālumu starpība elektroniem, kas no atsevišķām spraugām nonāk joslā X, bija 2,5∙10–11 m. Elektroniem, kas nonāk Y joslā, veikto attālumu atšķirība bija 5,0∙10–11 m. Pierādi, ka šāda aina tiek novērota gadījumā, ja elektronu kinētiskā enerģija ir 9,6∙10–17 J (šī vērtība var atšķirties no 2. uzdevumā aprēķinātās)! Elektroni pārvietojas nerelatīvistiskā ātrumā.
1. punkts
Uzdevumā ir runa par interferenci – viļņu pārklāšanos. Pārklājoties diviem vai vairākiem viļņiem, summējas to svārstību amplitūdas. Kopējā svārstību amplitūda var būt gan mazāka, gan arī lielāka par atsevišķo viļņu svārstību amplitūdu. Mazākas amplitūdas gadījuma interferenci sauc par destruktīvu, bet lielākas amplitūdas gadījumā – par konstruktīvu.
Lai, pārklājoties gaismas viļņiem, veidotos interferences aina, šiem viļņiem ir jābūt koherentiem. Viļņi ir koherenti tad, ja ir spēkā īpaši nosacījumi. Pirmkārt, viļņu svārstību frekvencēm ir jāsakrīt, tātad viļņiem ir jābūt monohromatiskiem. Otrkārt, viļņu svārstību fāzei ir jābūt nemainīgai. Treškārt, abiem viļņiem ir jābūt vienādiem elektriskā lauka svārstību virzieniem telpā, tātad arī magnētiskā lauka svārstību virzieniem telpā.
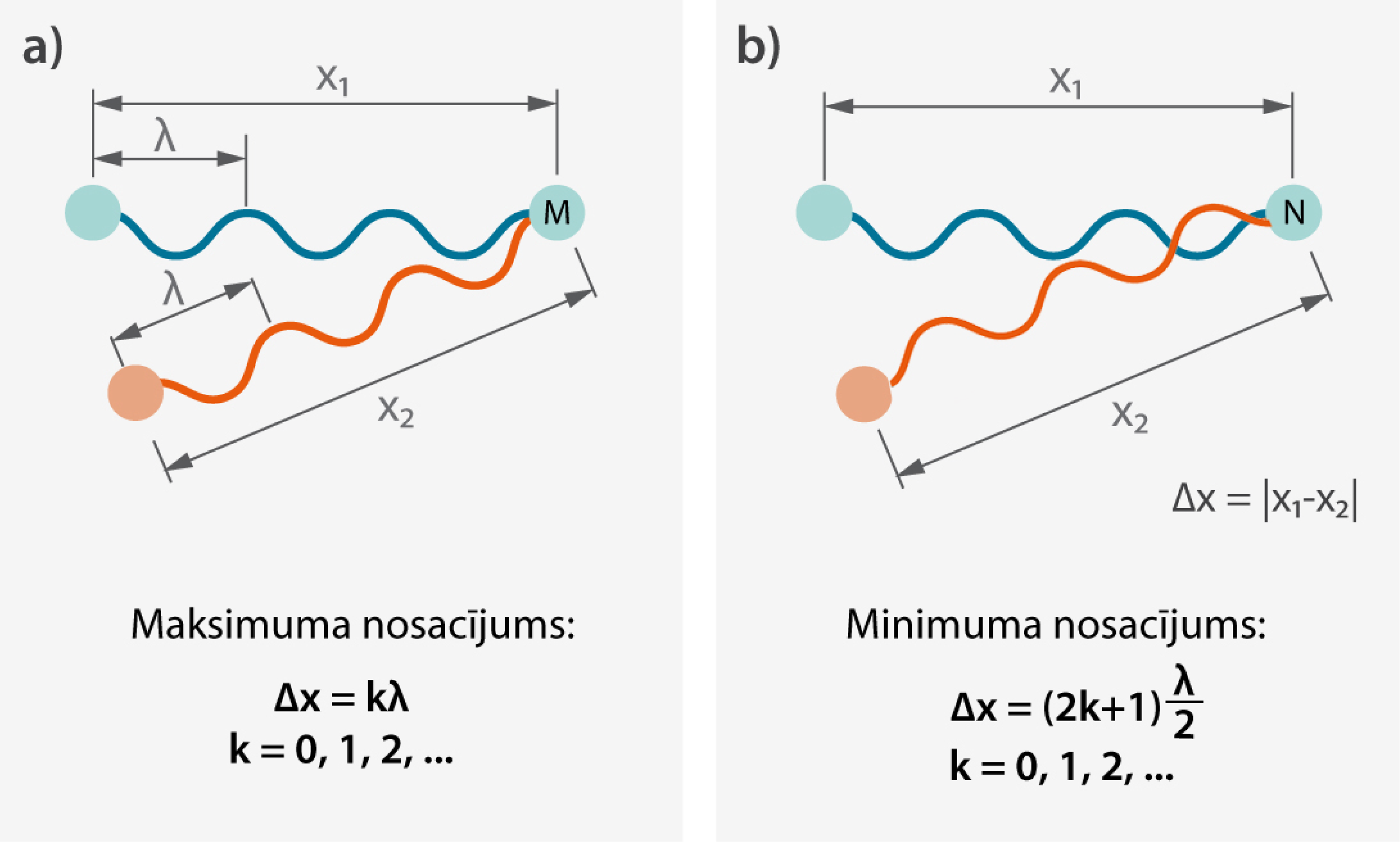
Interferences maksimums veidojas (notiek konstruktīva interference), ja viļņi sakrīt fāzē (to gājumu starpība vienāda ar veselu skaitu viļņu garumu: \(\Delta x=k\lambda\)), bet minimums (destruktīva interference) – ja viļņi nobīdīti viens attiecībā pret otru par pusvilni (to gājumu starpība ir pusviļņa garuma daudzkārtnis: \(\Delta x=(2k+1)\frac{\lambda}{2}\)).
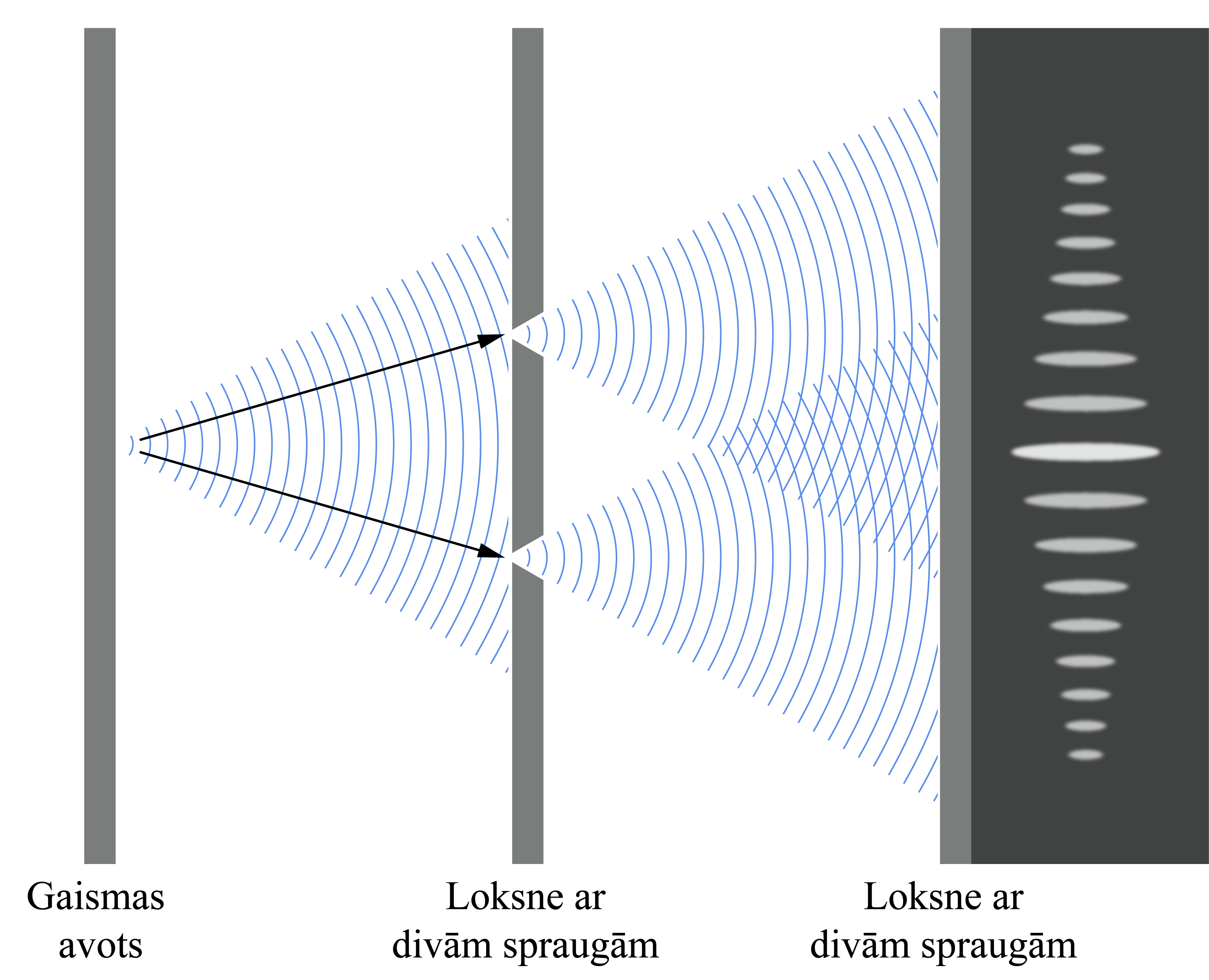
Aplūkosim interferences ainas veidošanos dubultspraugā gaismas viļņu gadījumā. Lai iegūtu interferences ainu, ir jāiegūst koherentas gaismas stari. No spuldzītes nākoši gaismas stari nav koherenti, jo tā gaismas viļņus izstaro haotiski. Tomēr no spuldzītes ir iespējams iegūt koherentus gaismas starus. Saskaņā ar Heigensa principu katru jau esošas viļņu frontes punktu var uzskatīt par jaunu punktveida viļņu avotu un šie viļņu avoti ir koherenti. Tātad, ja gaismas ceļā novieto šķērsli ar spraugu, iegūstot punktveida gaismas avotu, un tālāk novieto šķērsli ar divām tuvu esošām spraugām, tad šīs spraugas kļūst par koherentu viļņu avotiem un šo avotu radītie viļņi pārklājoties veido interferences minimuma un maksimuma nosacījumus. Šādas spraugas sauc par Janga dubultspraugām – izmantojot šādu iekārtu, interferences parādības demonstrējumu un skaidrojumu 19. gs. sākumā sniedza angļu zinātnieks Tomass Jangs (Thomas Young).
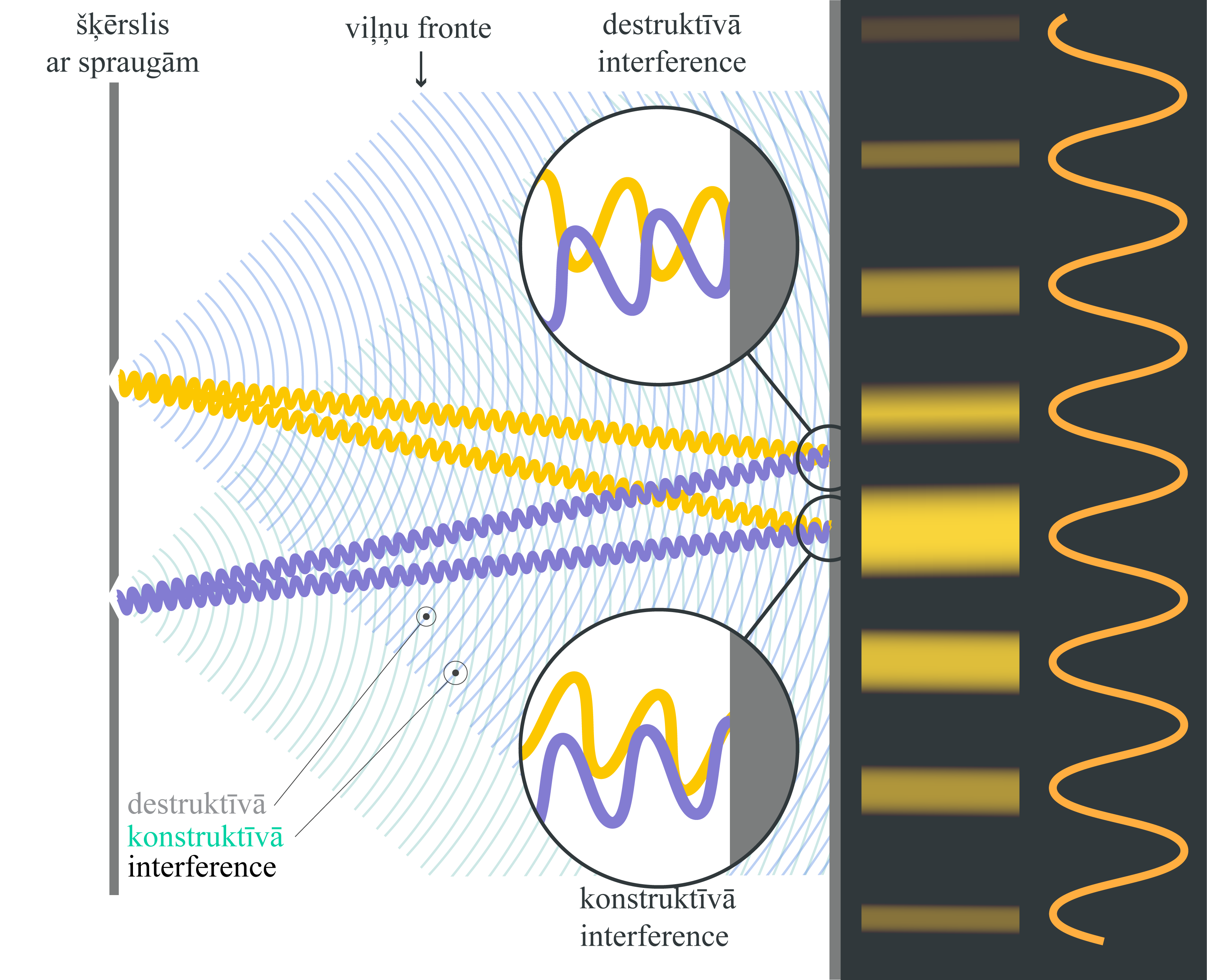
Vairāk par interferences ainas veidošanos var izlasīt Fizmix portālā Fiztēmās.
Dubultspraugas eksperimentu, lai novērotu gaismas interferenci, katrs var veikt arī pats – Fizmix portālā atrodams šāda eksperimenta apraksts.
Nozīmīga šā eksperimenta variācija saistās ar dubultspraugas apstarošanu ar daļiņām, nevis gaismas viļņiem. Ja dubultspraugu apstaro ar daļiņām, piemēram, elektroniem, sūtot tās atsevišķi pa vienai, tad tās izturas tieši tā, kā sagaidāms – kā daļiņas: piemēram, katrs elektrons uz ekrāna nonāk tieši vienā punktā. Bet vienlaikus šie elektroni izturas arī kā viļņi: laikam ejot un elektronu "trāpījumu" veidotajai ainai uz ekrāna uzkrājoties, veidojas koherentu viļņu veidotajai interferences ainai līdzīga aina. Tas parāda viļņu un daļiņu dualitāti, kas nosaka, ka visai vielai piemīt gan viļņu, gan daļiņu īpašības vienlaikus – var uzskatīt, ka elektrons ir interferējis pats ar sevi, tomēr nokļuvis uz ekrāna konkrētā punktā. Kvantu mehānikā šo viļņu – daļiņu duālismu aprakstīt ļauj viļņu funkcija (to vidusskolas skolas kursā neaplūko). Ir pierādīts, ka šī parādība notiek ar fotoniem, elektroniem, atomiem un pat dažām molekulām.
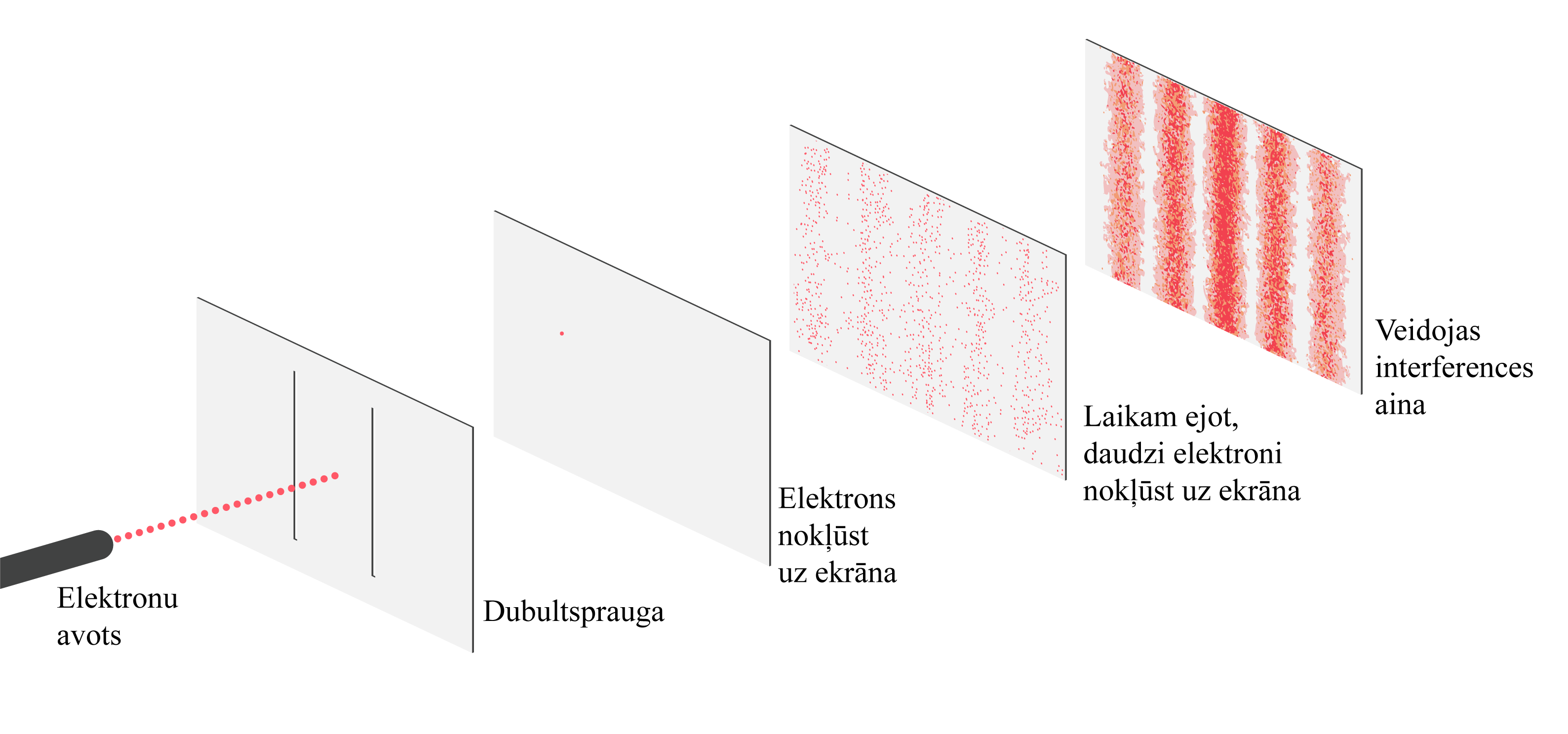
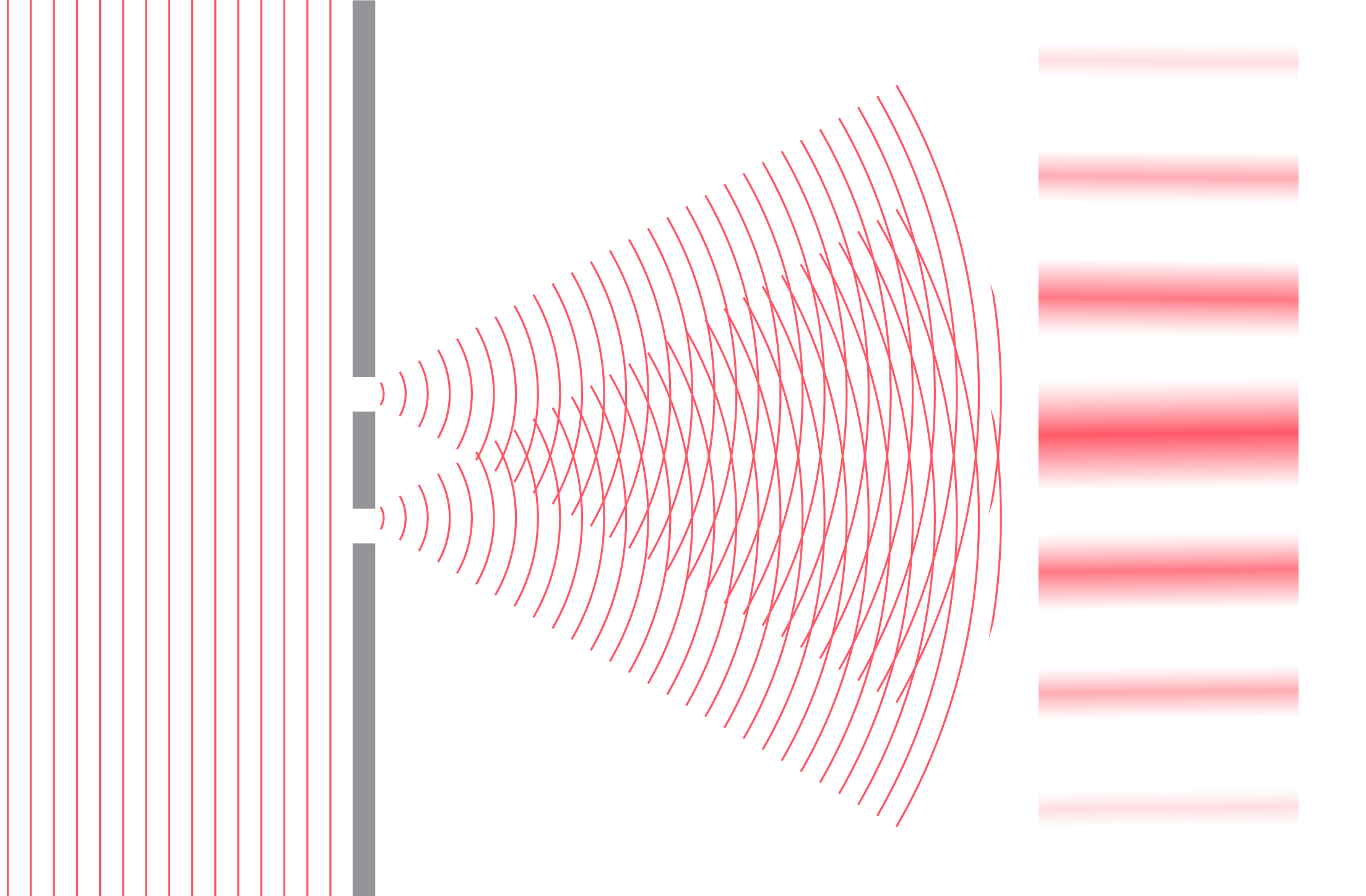
Vairāk par dubultspraugas eksperimentu daļiņām var lasīt šeit vai arī noskatīties Ričarda Feinmana lekciju video.
Atbilde:
- katram elektronam atbilst viens melnais punkts, tātad ir skaidri zināms, kur tas nokļuvis…
- tātad, elektrons ir daļiņa.
- veidojas interferences aina, kas raksturīga viļņiem, tātad, elektrons izpaužas kā vilnis.
2. punkts
Lai atrisinātu uzdevumu jāzina, ka lādēta daļiņa elektriskajā laukā iegūs enerģiju uz elektriskā lauka padarītā darba rēķina, daļiņu pārvietojot starp diviem lauka punktiem.
Datu bukletā atrodama sakarība \(U=\frac{A}{q}\) - elektriskā lauka sprieguma definīcija. Tātad \(A=qU\) vai, šajā gadījumā, \(A=eU\), kur \(e\) – datu bukletā atrodamais elektrona lādiņš \(e=1{,}60\cdot10^{-19}\space\mathrm{C}\).
Ja rodas šaubas, datu bukletā atrodama arī sakarība, kas saista spriegumu ar elektriskā lauka potenciāla izmaiņu: \(U=-\Delta\varphi\),
Kā arī elektriskā lauka potenciāla definīcija: \(\varphi=\frac{W_\mathrm p}{q}\).
Vienkāršoti šo situāciju var salīdzināt ar brīvo kritienu, kurā ķermenis iegūst kinētisko enerģiju, zaudējot savu potenciālo enerģiju gravitācijas laukā – gravitācijas (smaguma) spēks dara darbu.
Tā, šajā gadījumā, elektrons iegūst kinētisko enerģiju potenciālās enerģijas rēķina, kas tam piemīt elektriskajā laukā – darbu dara elektriskais lauks.
Saskaņā ar enerģijas saglabāšanās likumu, elektrona enerģijas izmaiņa \(\Delta W_\mathrm{k}\) (elektrona iegūtā enerģija) ir vienāda ar šo darbu.
Tātad, aplūkojot absolūtās vērtības:
\(A=\Delta W_\mathrm{k}=e\Delta\varphi=eU=1{,}60\cdot10^{-19}\cdot3500=5{,}6\cdot10^{-16}\space\mathrm{J}\space(3500\space\mathrm{eV})\)
Atbilde: elektrons, paātrinoties homogēnā elektriskajā laukā, iegūst \(5{,}6\cdot10^{-16}\space\mathrm{J}\space\) jeb \(3500\space\mathrm{eV}\) lielu enerģiju.
3. punkts
Uzdevumā dotajā attēlā parādīta elektronu interferences aina. Josla Y, kur nonākuši daudzi elektroni, atbilst interferences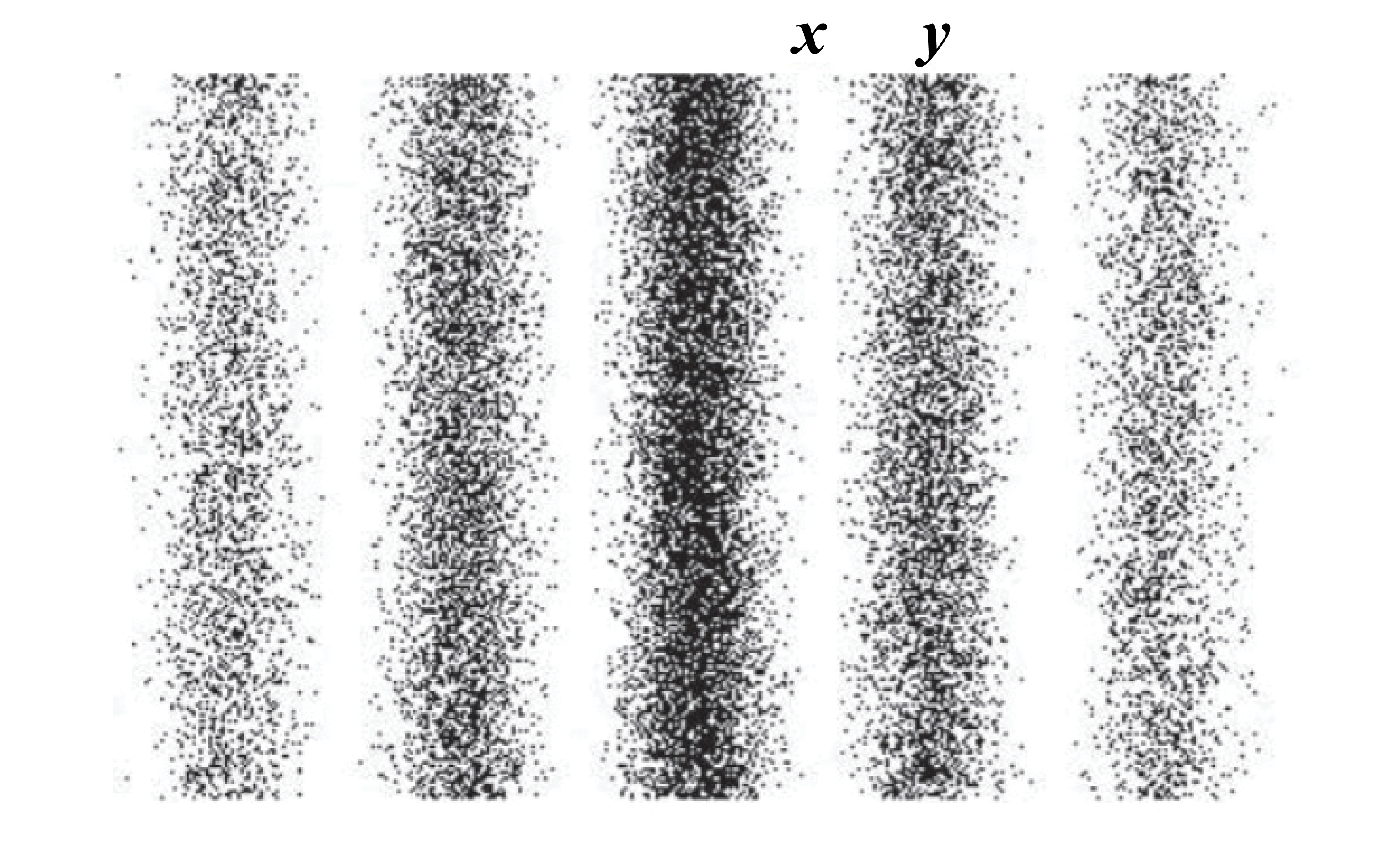 
maksimumam, bet josla X, kur elektroni praktiski nav nonākuši – interferences minimumam.
Lai pierādītu, ka attēlā redzamā elektronu interferences aina veidojas atbilstoši uzdevuma nosacījumiem, ir jāaprēķina elektronam, kam piemīt dotā kinētiskā enerģija \(W_\mathrm{k}\), atbilstošā de Brojī viļņa garums \(\lambda\) un jāsalīdzina šo viļņa garumu ar gājumu starpību interferences maksimuma situācijā: \(\Delta x=5{,}0\cdot10^{-11}\space \mathrm{m}\) (vai pusi šā viļņa garuma jāsalīdzina ar gājumu starpību interferences minimuma situācijā: \(\Delta x=2{,}5\cdot10^{-11}\space \mathrm{m}\)).
Maksimuma nosacījumam (josla Y) gājumu starpība vienāda ar viļņa garuma \(\lambda\) daudzkārtni. Tātad viļņa garumam \(\lambda\) jābūt: \(\lambda=5{,}0\cdot10^{-11}\space \mathrm{m}\) (vai tā daudzkārtnim).
Aprēķina elektrona kinētiskajai enerģijai atbilstošā de Brojī viļņa garumu: \(p=\sqrt{2mW_\mathrm{k}}\), \(\lambda=\frac{h}{p}\)
\(p=\sqrt{2\cdot9{,}11\cdot10^{-31}\cdot9{,}6\cdot10^{-17}}\approx1{,}32\cdot10^{-23}\space\mathrm{\frac{kg\cdot m}{s}}\)
\(\lambda=\frac{h}{p}=\frac{6{,}63\cdot10^{-34}}{1{,}32\cdot10^{-23}}\approx5{,}0\cdot10^{-11}\space\mathrm{m}\)
Iegūtais viļņa garums \(\lambda\) atbilst interferences maksimuma nosacījumam \(\Delta x=5{,}0\cdot10^{-11}\space \mathrm{m}\).
Citi risinājuma varianti:
Var rēķināt elektronu kinētisko enerģiju \(W_\mathrm{k}\) atkarībā no viļņa garuma \(\lambda\) un salīdzināt ar doto vērtību.
Var rēķināt impulsu \(p\) atkarībā no viļņa garuma \(\lambda\) un impulsu \(p\) atkarībā no elektronu kinētiskās enerģijas \(W_\mathrm{k}\), iegūstot vienādas vērtības – der visi iespējamie spriešanas varianti.
1. punkts
Uzdevuma izpilde eksāmenā – 30%.
Jāpamato viļņu-daļiņu DUĀLISMS, ne tikai elektrona viļņa daba.
Vērtē līmeņos
3 punkti:
- pamato elektrona korpuskulāro dabu ar vismaz vienu no:
- katram elektronam atbilstošu vienu punktu uz ekrāna;
- faktu, ka elektronam piemīt masa un/vai lādiņš;
- faktu, ka elektronu paātrināja;
- faktu, ka interferences aina veidojas, laižot elektronus "pa vienam";
- spriedumu, ka, ja elektrons būtu "tikai" daļiņa, tad būtu tikai divas līnijas;
- pamato viļņu dabu ar:
- difrakcijas/interferences ainu, kas veidojas (var būt nosaukta/pieminēta difrakcijas režģa formula, kas ir pieļaujami, aplūkojot dubultspraugu kā "īsu" difrakcijas režģi).
2 punkti:
Pamatojumā ir dažas nepilnības, parādās pretruna skaidrojumā, papildus pareizi nosauktiem argumentiem ir arī pilnīgi aplami spriedumi.
VAI
Fakts, ka elektrons ir daļiņa, pieminēts kā pašsaprotams.
1 punkts:
Pamatojums tikai vienai elektrona dabas izpausmei, otra nav pat pieminēta
VAI
Pieminēta tikai de Brojī formula.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 3 punktiem.
2. piemērs: risinājums novērtēts ar 3 punktiem.
3. piemērs: risinājums novērtēts ar 3 punktiem.
4. piemērs: risinājums novērtēts ar 3 punktiem.
5. piemērs: risinājums novērtēts ar 2 punktiem. Daļiņas daba bez pamatojuma, minēta kā pašsaprotama.
6. piemērs: risinājums novērtēts ar 2 punktiem. Nav pamatojuma, ka elektrons ir daļiņa (nav saprasts arī, ka elektrons interferē pats ar sevi).
7. piemērs: risinājums novērtēts ar 2 punktiem. Nav pamatojuma, ka elektrons ir daļiņa.
8. piemērs: risinājums novērtēts ar 2 punktiem. Atsauce uz gaismas duālo dabu.
9. piemērs: risinājums novērtēts ar 1 punktu. Pamatota tikai viļņa daba, daļiņas daba nav pat pieminēta.
10. piemērs: risinājums novērtēts ar 0 punktu. Nav saprasts, par kādu parādību ir runa.
11. piemērs: risinājums novērtēts ar 0 punktu. Pamatojums nav par elektrona dabu.
2. punkts
Uzdevuma izpilde eksāmenā – 26,1%.
Vērtēšanas kritēriji
Ir uzrakstīta formula vai tai atbilstošs skaitlisks risinājums – 1 punkts. Ja \(\Delta\varphi\) vietā ir \(\varphi\), punktu neatņem.
Sameklēti un formulā ielikti skaitļi. Pareizi aprēķins ar mērvienību (der atbilde džoulos vai elektronvoltos) – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 2 punktiem.
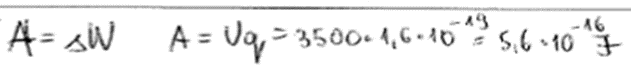
2. piemērs: risinājums novērtēts ar 2 punktiem.
3. piemērs: risinājums novērtēts ar 2 punktiem.
4. piemērs: risinājums novērtēts ar 2 punktiem.
5. piemērs: risinājums novērtēts ar 1 punktu. Ir enerģijas formula.
6. piemērs: risinājums novērtēts ar 0 punktu.
3. punkts
Uzdevuma izpilde eksāmenā – 4%.
Vērtēšanas kritēriji
Ir spriedums: elektrona viļņi punktā X ir pretfāzē (minimuma nosacījums) un/vai elektrona viļņi punktā Y ir vienā fāzē (maksimuma nosacījums). VAI: gājienu starpība punktā X ir \(\lambda/2\); (un/vai punktā Y ir \(\lambda\)) – interferences minimuma un maksimuma nosacījumi. Pieļaujams lietot vārdu "difrakcija" – 1 punkts.
Atrod un izmanto formulu \(\lambda=\frac{h}{p}\) (\(\lambda=\frac{h}{mv}\)) – 1 punkts.
Atrod un izmanto formulu \(W_\mathrm{k}=\frac{mv^2}{2}\) (\(W_\mathrm{k}=\frac{p^2}{2m}\)). Formula var nebūt uzrakstīta, bet ieraugāma risinājumā – 1 punkts.
Atrod un izmanto formulu \(p=mv\). Formula var nebūt uzrakstīta, bet ieraugāma risinājumā – 1 punkts.
Veic aprēķinus, lielumus \(W_\mathrm{k}\) vai \(\lambda\) salīdzina (vai arī salīdzina \(p\), izsakot no \(\lambda\) un \(p\), izsakot no \(W_\mathrm{k}\)). Pieļaujama kļūda aprēķinā, ja skaitliskās vērtības ievietotas pareizi – 1 punkts.
Skolēnu risinājumu un to vērtējumu piemēri
1. piemērs: risinājums novērtēts ar 5 punktiem.
2. piemērs: risinājums novērtēts ar 5 punktiem.
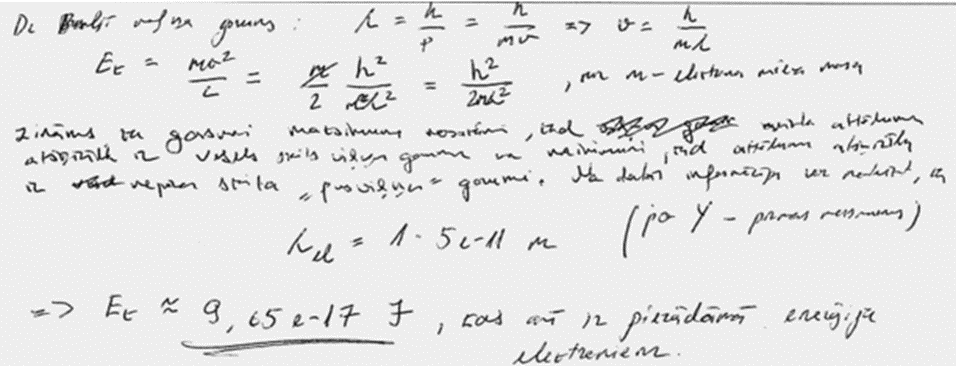
3. piemērs: risinājums novērtēts ar 5 punktiem.
4. piemērs: risinājums novērtēts ar 5 punktiem. Tikai viena neuzmanības kļūda – Planka konstantei kārtu pārskatījies.
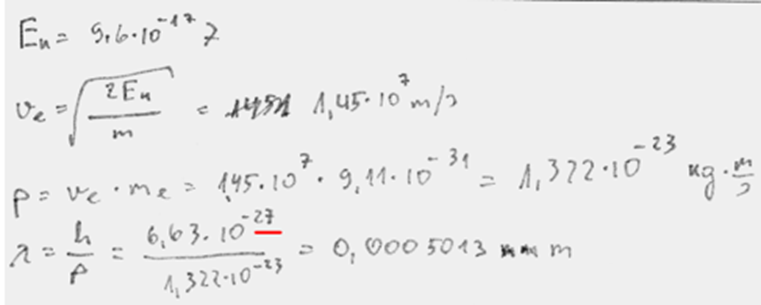
5. piemērs: risinājums novērtēts ar 4 punktiem. Faktiski trūkst tikai maksimuma nosacījums, tātad, nav salīdzināts ar doto viļņa garumu.
6. piemērs: risinājums novērtēts ar 3 punktiem. Ir ideja, ka jāsalīdzina, ir interferences minimuma nosacījums, ir kinētiskās enerģijas formula. De Brojī formulas vietā Planka formula ar haotiskiem pārveidojumiem, sarēķināts nekas nav.
7. piemērs: risinājums novērtēts ar 2 punktiem. Ir ideja salīdzināt viļņa garumu un interference.
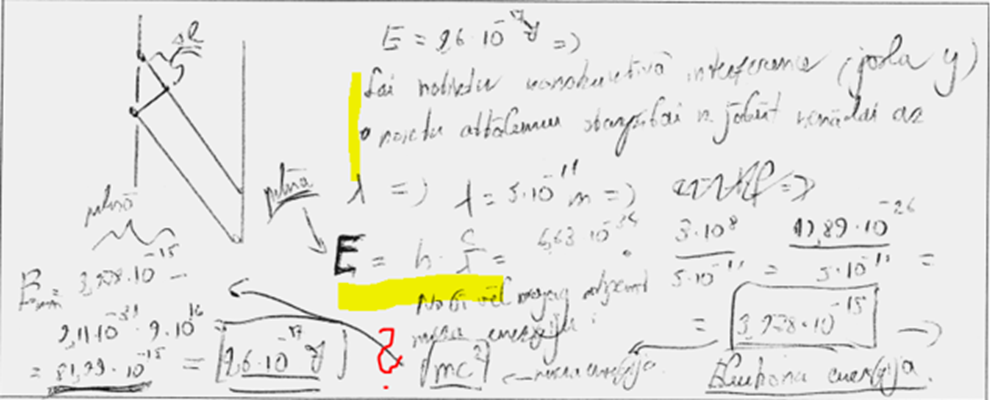
8. piemērs: risinājums novērtēts ar 1 punktu. Ir tikai interferences maksimuma nosacījumi, kas ieraugāmi attēlā.
9. piemērs: risinājums novērtēts ar 1 punktu. Ir kinētiskās enerģijas formula un doma, ka ar to kaut ko jādara tālāk.
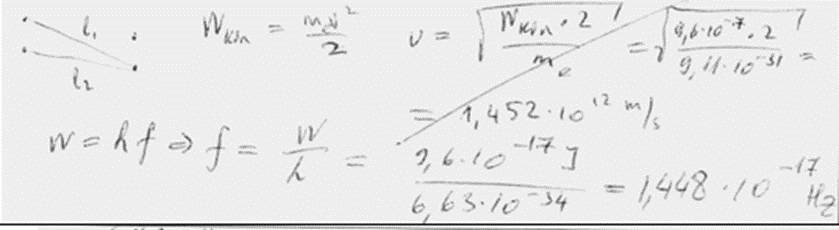
10. piemērs: risinājums novērtēts ar 0 punktu. Ne par šo uzdevumu sarakstīts.
