Cietām vielām ir raksturīgs noteikts daļiņu izkārtojums, turklāt tās nevar pārvietoties cita attiecībā pret citu, kas nodrošina cietām vielām noteiktu formu un spēju to saglabāt, iekams uz to neiedarbojas pietiekami ārējie faktori. Cietas vielas iedala kristāliskās un amorfās vielās, savukārt kristāliskās vielas tālāk iedalās monokristālos un polikristālos (1. att.).
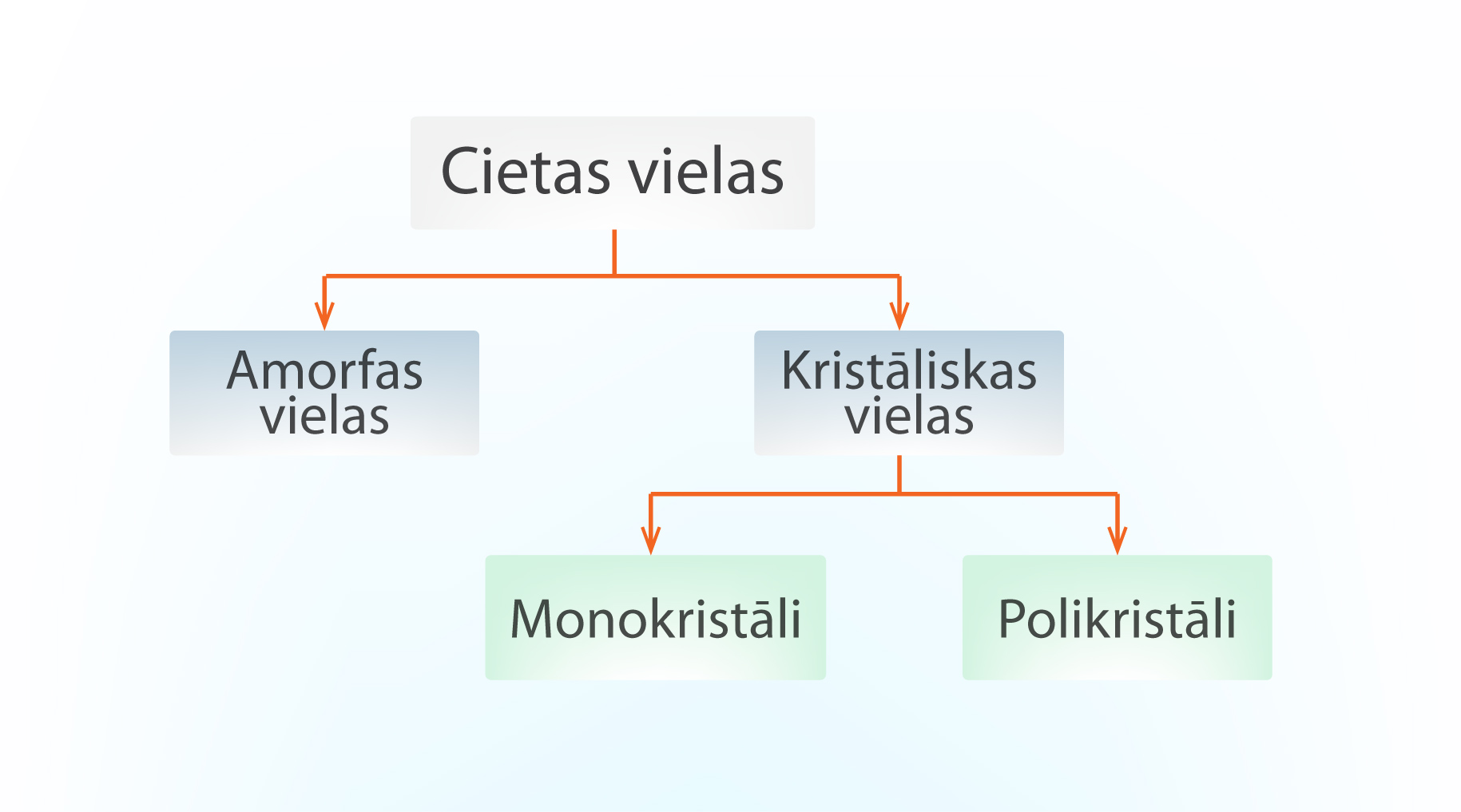
1.att. Cieto vielu iedalījums pēc to uzbūves
Daļiņu sakārtojums kristāliskās vielās, piemēram, vārāmajā sālī, kvarcā un silīcijā, ir regulārs pat lielā attālumā (2. att. a). Šo kārtību sauc par tālo kārtību. Atšķirībā no kristālisku vielu tālās kārtības amorfās vielās ir sastopama tuvā kārtība (2. att. b), tādēļ amorfām vielām īpašības ir izotropas (atkarīgas no virziena). Amorfas vielas ir, piemēram, stikls, karamele, māls, vasks, medus un cements. Kristāliskām vielām ir noteikta kušanas temperatūra, bet amorfām vielām nav. Amorfu vielu kušanas temperatūru raksturo temperatūru diapazons, kurā kušana var notikt. Jebkurai amorfai vielai, piemēram, arī stiklam piemīt plūstamība. Senās pilīs izmērot vitrāžu stikla biezumu, tas lejas daļā ir lielāks, jo stikls vairākos gadu simtos ir notecējis uz leju!
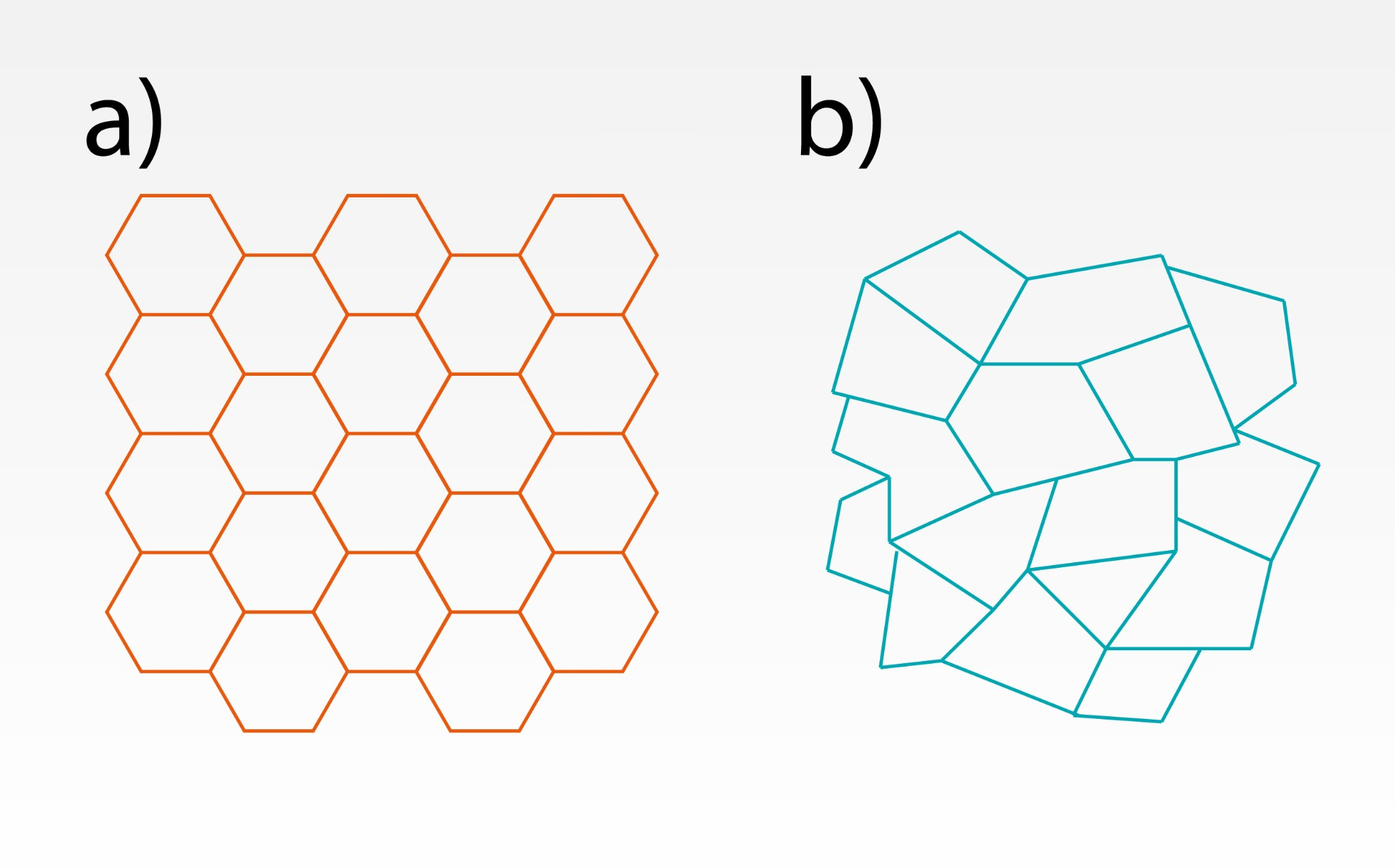
2.att. Kristāliskas un amorfas vielas struktūra
Kristāliskas vielas iedalās monokristālos un polikristālos. Monokristālos daļiņas ir regulāri sakārtotas visā ķermeņa tilpumā (3. att. a), bet polikristāliskas vielas sastāv no kopā saaugušiem haotiski izkārtotiem monokristāliem (3. att. b). Gan monokristāliskas, gan polikristāliskas vielas uz Zemes ir veidojušās dabiskā ceļā, bet, piemēram, tādu monokristālisku vielu kā silīciju (Si) mūsdienās iegūst rūpnieciskā ceļā un pēc tam izmanto mikroelektronikā.

3.att. Monokristāla un polikristāla struktūra
Ja no cietas vielas veidotu stieni vienā galā nostiprina, bet uz otru galu iedarbojas ar spēkuF, tad stienī rodas elastības spēks Fe, kas darbojas pretī pieliktajam spēkam (4. att.). Rezultātā stieņa izmērs mainās par Δ l, jo stienis ir pakļauts deformācijai. Stieņa deformācija materiālā rada mehānisko spriegumu σ. Tas norāda ārējā spēka F lielumu, kas darbojas uz stieņa šķērsgriezuma laukumu S jeb σ = F : S. Ja pēc ārējā spēka noņemšanas ķermenis atgūst savu iepriekšējo formu, tad deformāciju sauc par elastīgu, bet ja neatgūst, tad par plastisku deformāciju.
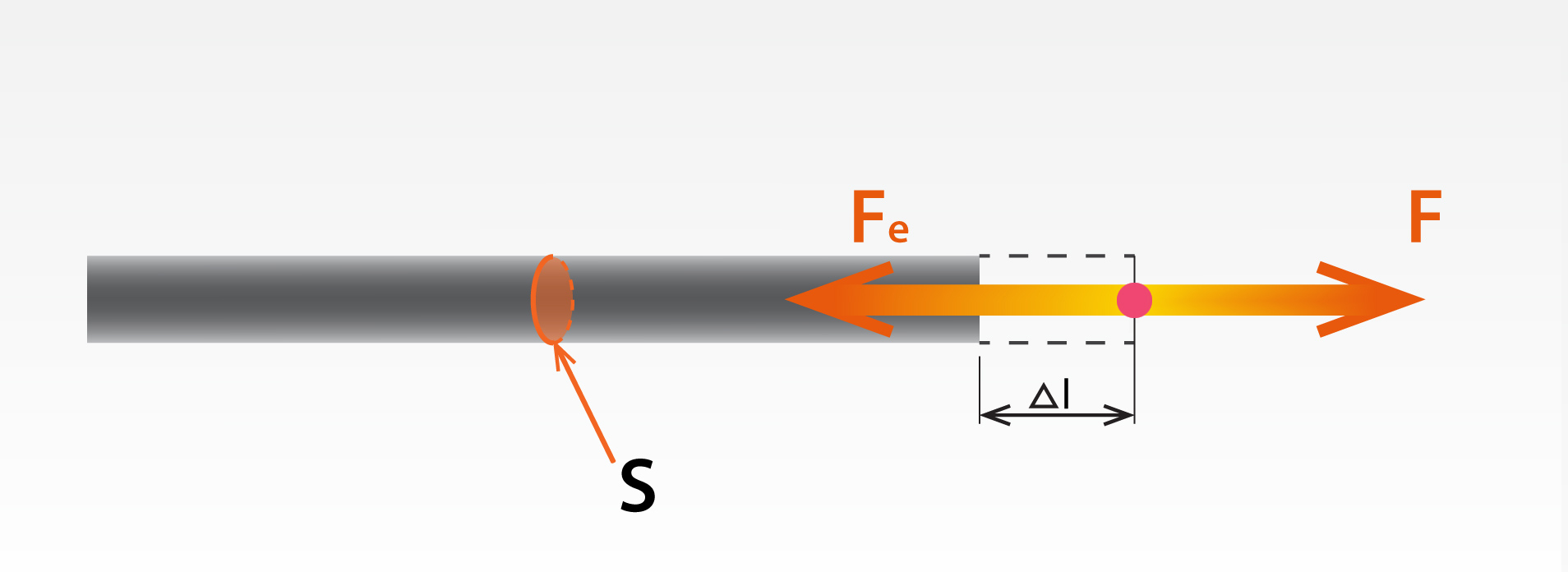
4.att. Stienis, kas pakļauts deformācijai
Cieti ķermeņi maina izmērus ne tikai ārēju spēka ietekmē, bet arī temperatūras maiņas dēļ. Ja pie temperatūras t1stienim ir garumsL0, tad, temperatūrai pieaugot līdz t2, stienis pagarinās parΔL (5. att.). Ķermeņa pagarinājums ir atkarīgs no ķermeņa sākotnēja garuma L0un lineārās izplešanās koeficienta α. Ja pagarinājumu ΔL izdala ar sākotnējo garumu L0, tad iegūst relatīvo pagarinājumu, kuru var izteikt kā ΔL : L0 = α(t2 - t1).
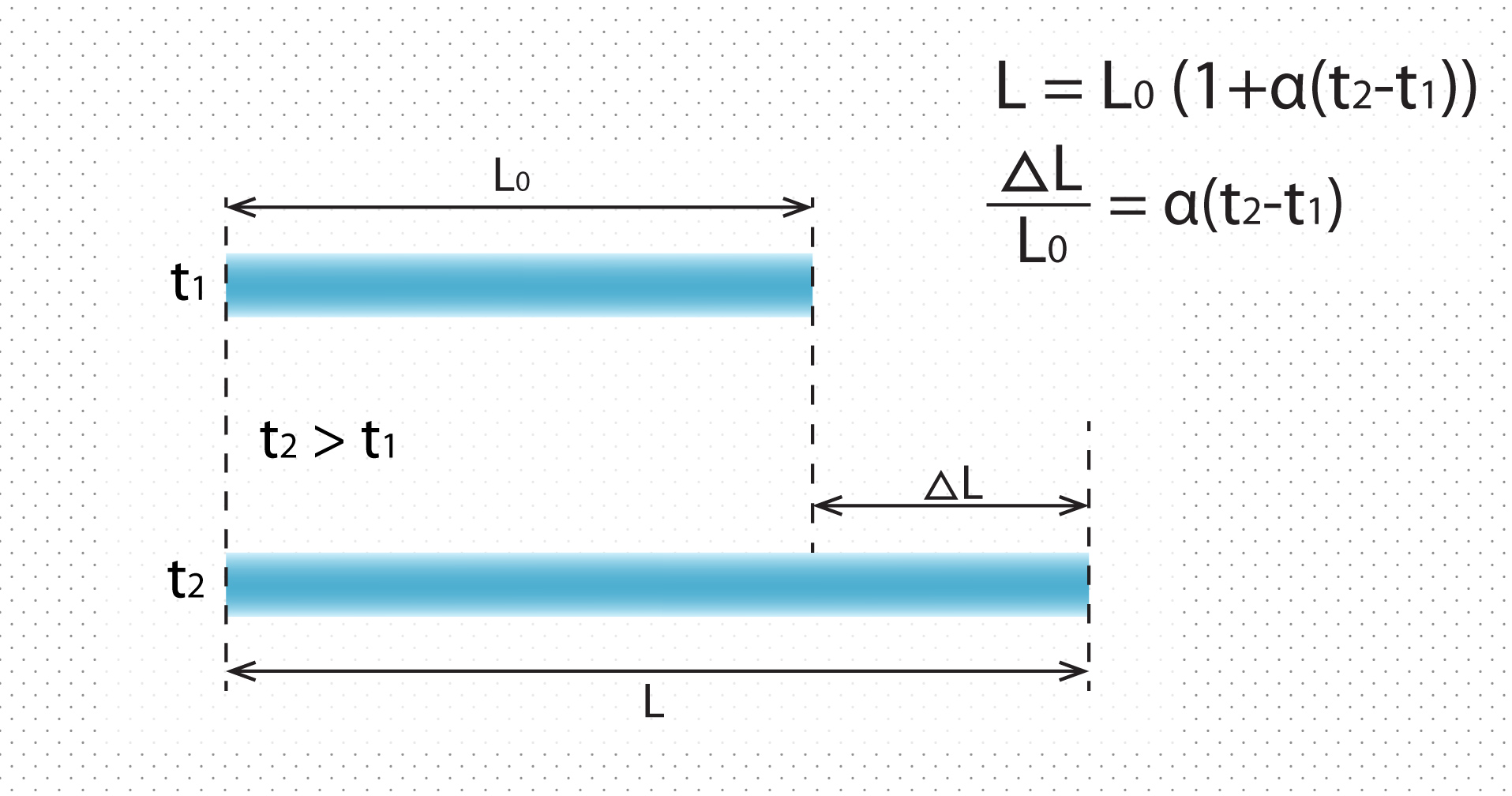
5.att. Cietu vielu termiskā izplešanās
Lineārās izplešanās koeficients α dažādām vielām ir atšķirīgs (6. att.). Būtībā šis koeficients parāda to, par cik metriem palielināsies 1 m garš stienis, ja tā temperatūra pieaugs par 1 Celsija vai Kelvina grādu (6. att.). Ar cietu ķermeņu izplešanos ir jārēķinās, piemēram, dzelzceļa, tiltu un torņu būvniecībā. To apliecina fakts, ka Zaķusalas televīzijas tornis temperatūras svārstību ietekmē augstumu maina pat par vairākiem metriem.
Apskaties DZM materiālu par cietām vielām.
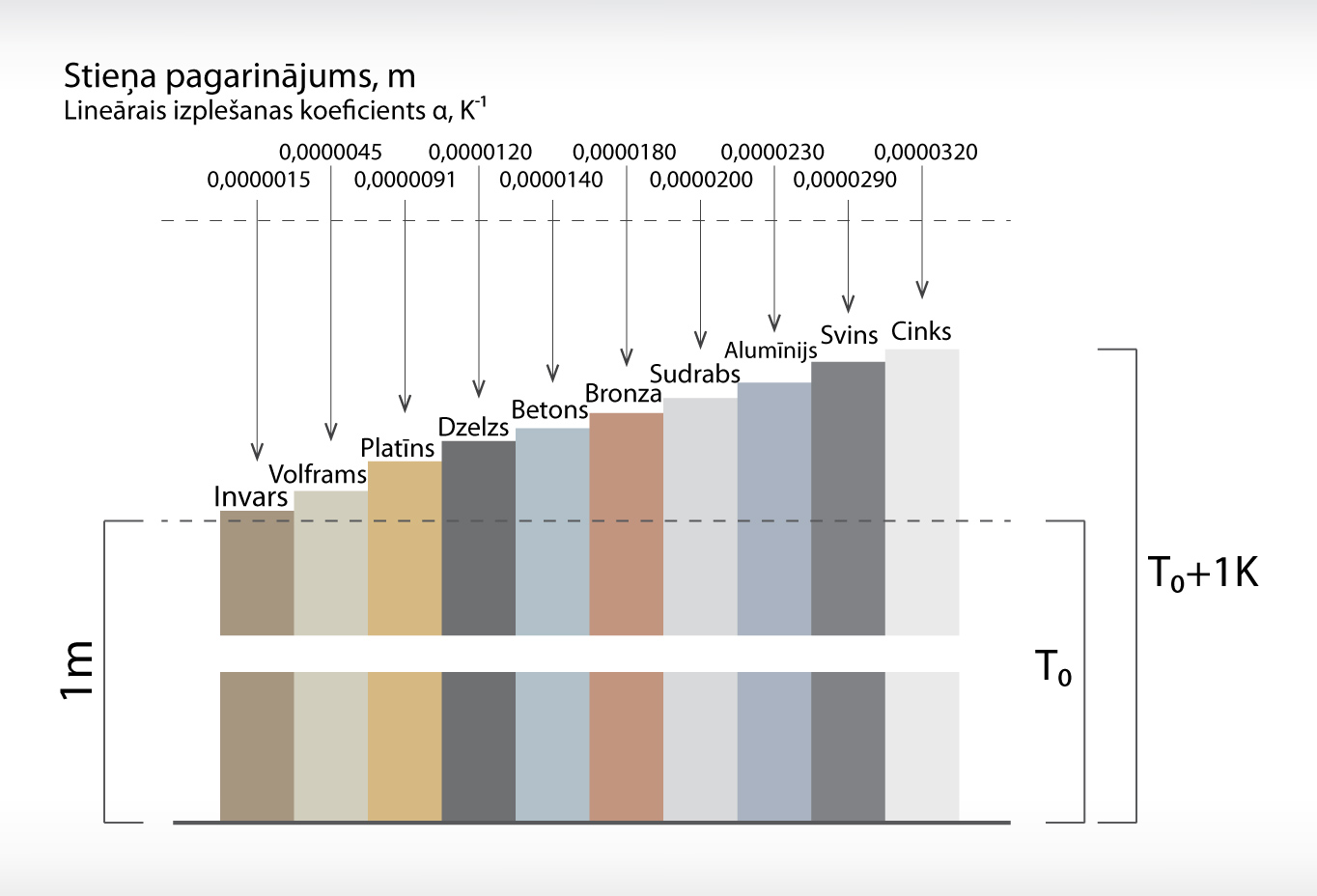
6.att. Dažādu materiālu stieņu lineārā izplešanās
Tādam ķermenim kā stienis garums krietni pārsniedz pārējos izmērus, tādēļ izplešanās temperatūras ietekme tiek apskatīta tikai uz tā garumu. Patiesībā ķermeņu izmēri temperatūras ietekmē mainās visos virzienos, tādēļ tiek apskatīta arī ķermeņu tilpuma izplešanās. Ja ķermeņa sākotnējais tilpums ir V0, tad, palielinot temperatūru par ΔT, ķermeņa tilpums izplešanās beigās ir V = V0(1 + βΔT), kur β ir tilpuma izplešanās termiskais koeficients (1. att.). Ja ķermenis ir veidots no viena materiāla, tad var uzskatīt, ka β ≈ 3α. Ja ķermenis ir veidots no dažādiem materiāliem, tad jārēķinās, ka katrs no tiem temperatūras ietekmē izplešas citādāk, kas var negatīvi ietekmēt ķermeņa izturību. Tādēļ, piemēram, dzelzsbetonā izmanto materiālus, kuru termiskās izplešanās koeficienti ir līdzīgi.
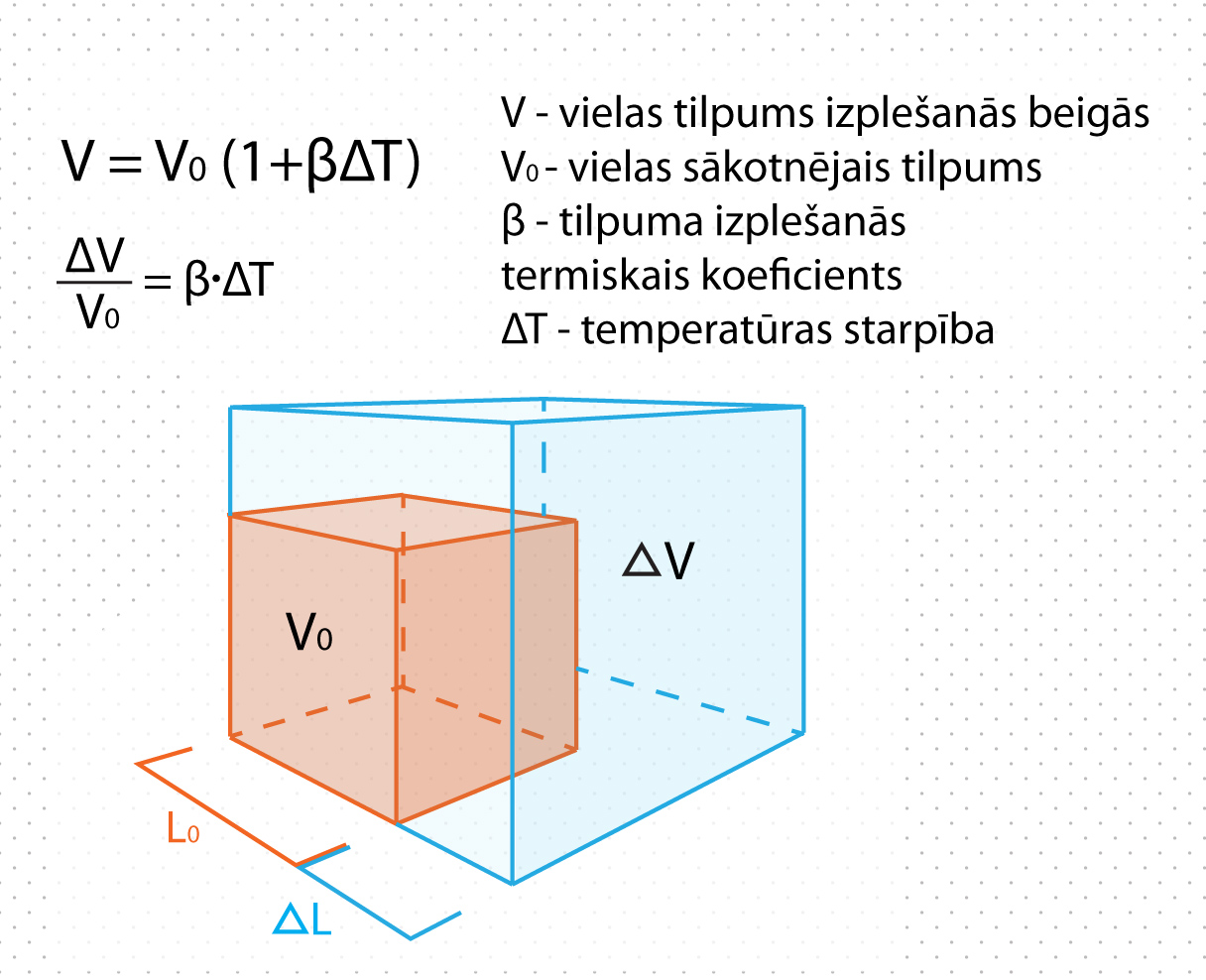
1.att. Cietu ķermeņu tilpuma izplešanās
Ja ķermenis ir pakļauts ārēja spēka deformācijai, tad to, vai deformācija ir elastīga vai plastiska, var noteikt, izmantojot sadaļā par Darbu apskatīto Huka likumu. Ja deformācija ir elastīga, tad ķermeņa pagarinājums pakļaujas Huka likumam, bet ja ne, tad deformācija ir plastiska. Ja uzzīmē grafiku pieliktā spēka atkarībai no ķermeņa pagarinājuma, tad Huka likumam atbilst grafika lineārā daļa (2. att.). Grafikā redzams: ja ķermeni, šajā gadījumā atsperi, no sākotnēja stāvokļa (2. att. a) izstiepj par lielumu ΔL, tad ir jāpieliek spēks F (3. att. b), bet, lai atsperi elastīgajā deformācijā pagarinātu vēl par tādu pašu lielumu (2. att. c), ir jāpieliek tikpat daudz spēka, tātad kopējais spēka apjoms ir 2 F. Taču brīdī, kad tiek sasniegta elastības robeža un ir pielikts spēks Fx (2. att. d), tad turpmāka papildu spēka pielikšana jau rezultēsies plastiskā deformācijā (2. att. e).
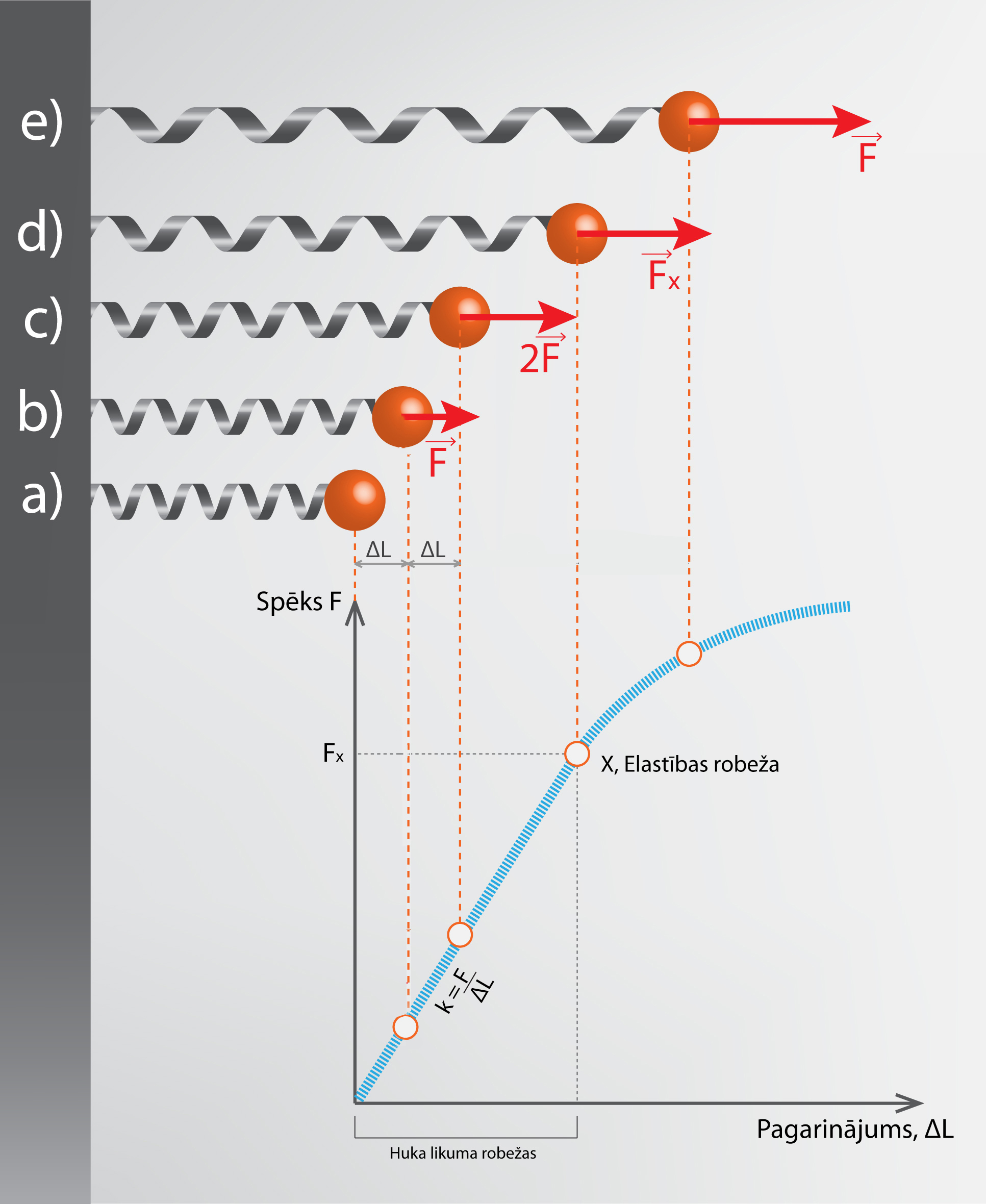
2.att. Huka likums ķermeņa deformācijā
Stiepšana ir tikai viens no ķermeņa deformācijas veidiem. Kopumā ķermeni (3. att. a) var pakļaut šādām deformācijām:
stiepe,
spiede,
liece,
bīde,
vērpe.
Stiepei (3. att. b) ir pakļautas dažādas virves, troses, auklas, ķēdes, bet spiedei (3. att. c) ir pakļauti, piemēram, ēku pamati, grīda, kauli, krēsli un krūzes osiņa, kad tā tiek turēta rokās. Liecē (3. att. d) apvienojas gan stiepe, gan spiede. Šādam deformācijas veidam ir pakļautas sijas, plaukti un mūzikas instrumentu stīgas. Ja dažādi ķermeņa slāņi ir pakļauti kustībai citam pret citu, tad tā ir bīdes deformācija (3. att. e), kas darbojas, piemēram, uz ēdienu mielošanās procesā vai uz kādu materiālu, kas tiek griezts ar nazi vai šķērēm. Visbeidzot ir arī tāda deformācija kā vērpe (3. att. f), kam ir pakļautas dažādas skrūves un rotējošu instrumentu detaļas.Deformējot ķermeni, ir svarīgi zināt, līdz kādam slodzes līmenim tas deformējas elastīgi, tādēļ ar materiāliem tiek veikti dažādu veidu eksperimenti, lai noteiktu šo elastības robežu. Piemēram, dzelzs izturība stiepē ir 290 MPa.
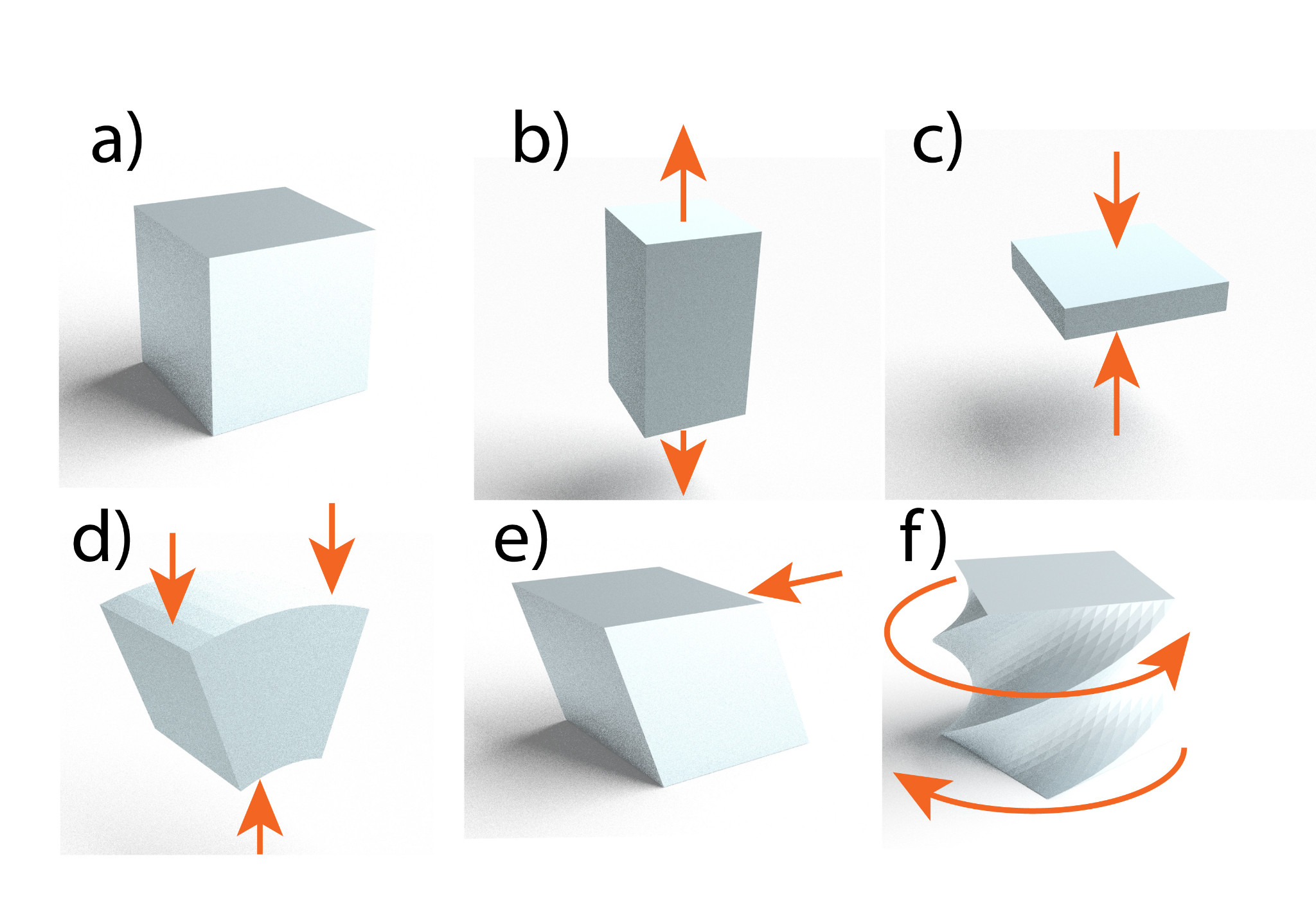
3.att. Deformāciju veidi
To, vai cietā viela ir amorfa vai kristāliska, nosaka daļiņu izkārtojums. Ja daļiņu sakārtojums nav regulārs un to izvietojums ir paredzams tikai tik daudz, ka blakus noteikta veida daļiņām atrodas noteikts skaits cita veida daļiņu (4. att. a), tad vielā pastāv tuvā kārtība un viela ir amorfa. Savukārt ja daļiņu izkārtojumā ir redzama telpiska struktūras atkārtošanās lielākos attālumos nekā attālums starp daļiņām (4. att. b), tad šādās vielās pastāv tālā kārtība un tās ir kristāliskas.
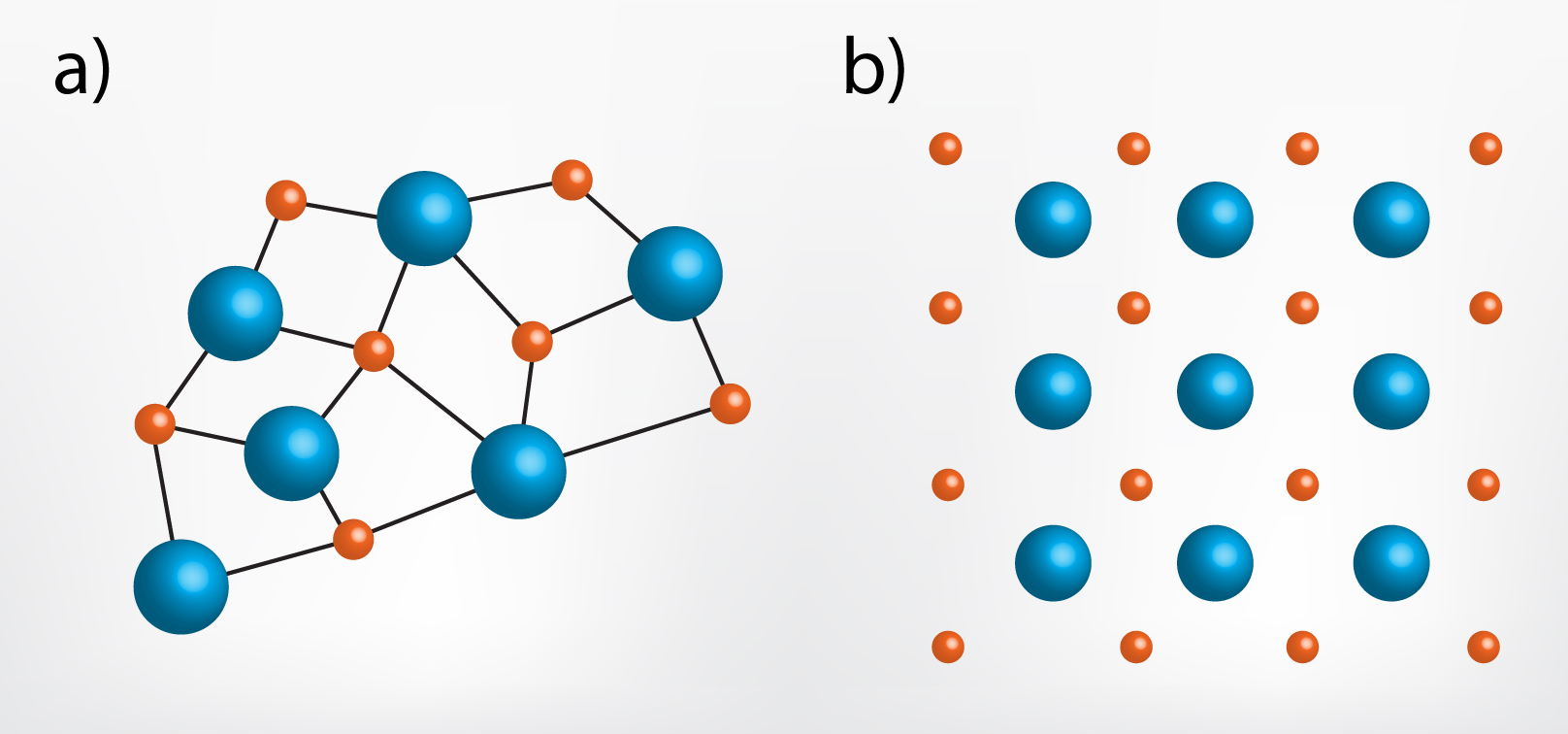
4.att. Cieto vielu tuvā (a) un tālā (b) kārtība
Parasti tālā kārtība ir novērojama tikai cietām vielām, bet šķidrumiem ir raksturīga tuvā kārtība, tomēr pastāv arī izņēmumi. Šķidrajos kristālos pastāv tālā kārtība (5. att.), tomēr tiem ir šķidrumiem raksturīgās īpašības. Šķidrie kristāli ir, piemēram, parafīni un fenilbenzonāti.
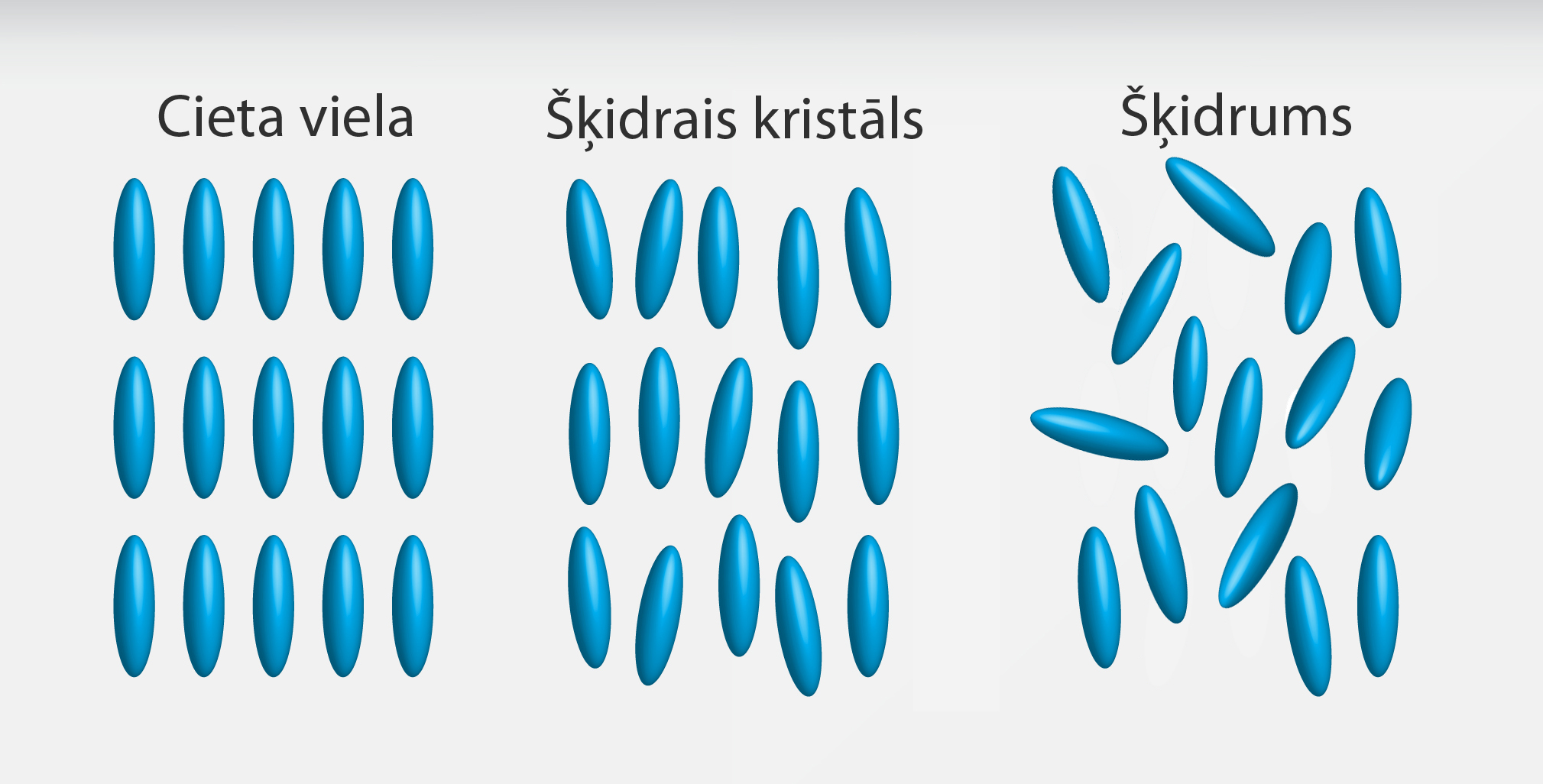
5.att. Daļiņu izkārtojums cietā vielā, šķidrajos kristālos un šķidrumā
Ja šķidrā kristāla šūnai elektriskajā laukā pieslēdz spriegumu, tad tā vairs neatstaro gaismu. Šo efektu izmanto LCD displejos (6. att.), jo tāds risinājums ir energoefektīvs, turklāt displejus var uztaisīt ļoti kompaktus.
6.att. LCD monitors
Reālos kristālos ir vērojamas atkāpes no regulāras struktūras, ko sauc par kristāla defektiem. Pastāv iespēja, ka starp kristālisko vielu veidojošajām daļiņām ir ielavījusies kāda lieka daļiņa (1. att. a, b) vai arī kāda daļiņa iztrūkst (1. att. c, d). Kristāla defekti var negatīvi ietekmēt materiāla fizikālās īpašības, piemēram, izturību pret pielikto slodzi, bet nav ļaunuma bez labuma. Kristāla defektus izmanto, piemēram, pusvadītājmateriālu ražošanā. Ar kristālu defektiem var panākt arī citas vēlamas fizikālās īpašības, piemēram, kušanas temperatūru vai optiskās īpašības, kas kristāliem bez defektiem nav novērojamas.
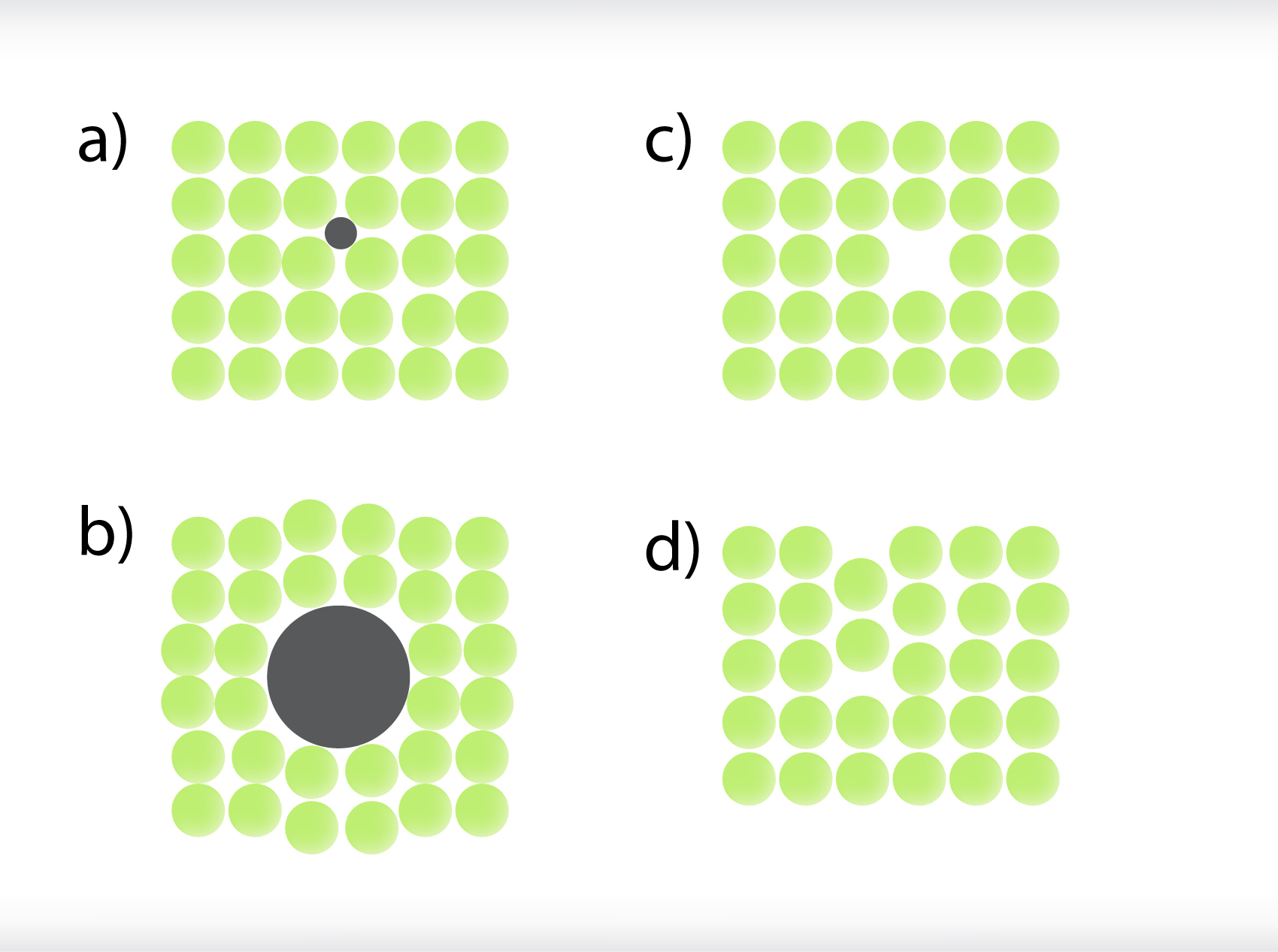
1.att. Defekti kristāliskās vielās
Tomēr, ja kristāliska viela ir monokristāliska un bez defektiem, tad šādās vielās ir vērojama interesanta parādība, kas sauc par fizikālo īpašību anizotropiju. Tas nozīmē, ka dažādas fizikālās īpašības (siltumvadīšana, elektriskā pretestība, laušanas koeficients) dažādos virzienos ir atšķirīgas.
Fizikālo īpašību anizotropiju var mēģināt saprast, ja apskata kādas monokristāliskas vielas kristālrežģi (2. att.). Šajā kritālrežģī ir iezīmēti trīs atšķirīgi virzieni, un ir skaidri redzams, ka katrā no virzieniem vielu veidojošās daļiņas atrodas atšķirīgos attālumos, kas arī nosaka atšķirīgās fizikālās īpašības. Tas nozīmē: ja no kāda monokristāliska materiāla tiks izslīpēta, piemēram, prizma, tad tās optiskās īpašības būs atkarīgas no tā, kādā leņķī pret kristāliskā režģa virzieniem būs noslīpētas prizmas plaknes.
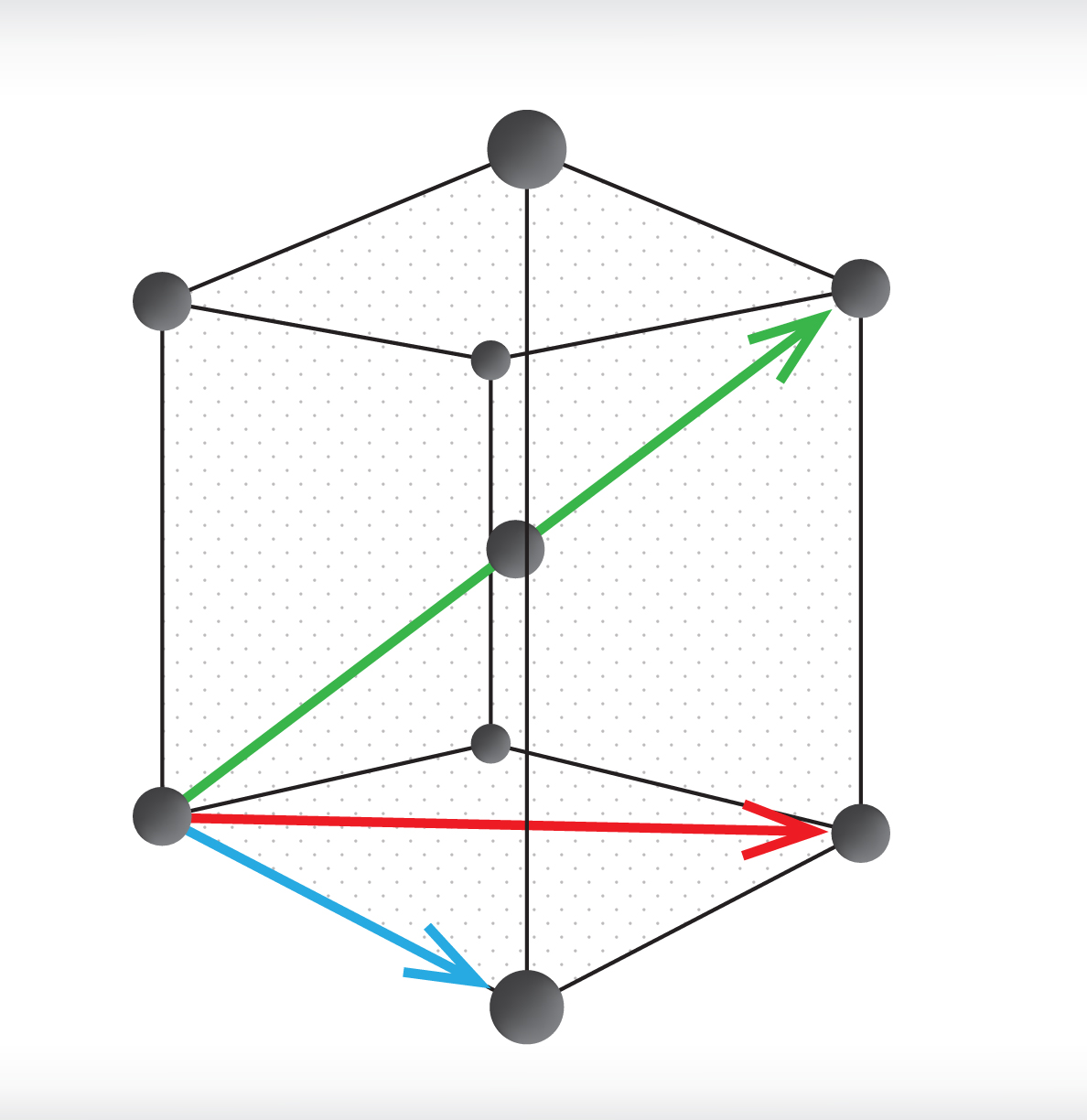
2.att. Fizikālo īpašību anizotropija kristāliskās vielās
Materiāla elastības raksturošanai var lietot Junga moduli E = σ : ε, kur σ ir mehāniskais spriegums, bet ε ir relatīvais pagarinājums, kuru iegūst, ja ķermeņa pagarinājumu ΔL attiecina pret sākotnējo garumu L0jeb ε = ΔL : L (3. att.). Junga moduļa mērvienība ir paskāls (Pa). Jo lielāka ir E vērtība, jo grūtāk ķermeni ir izstiept.
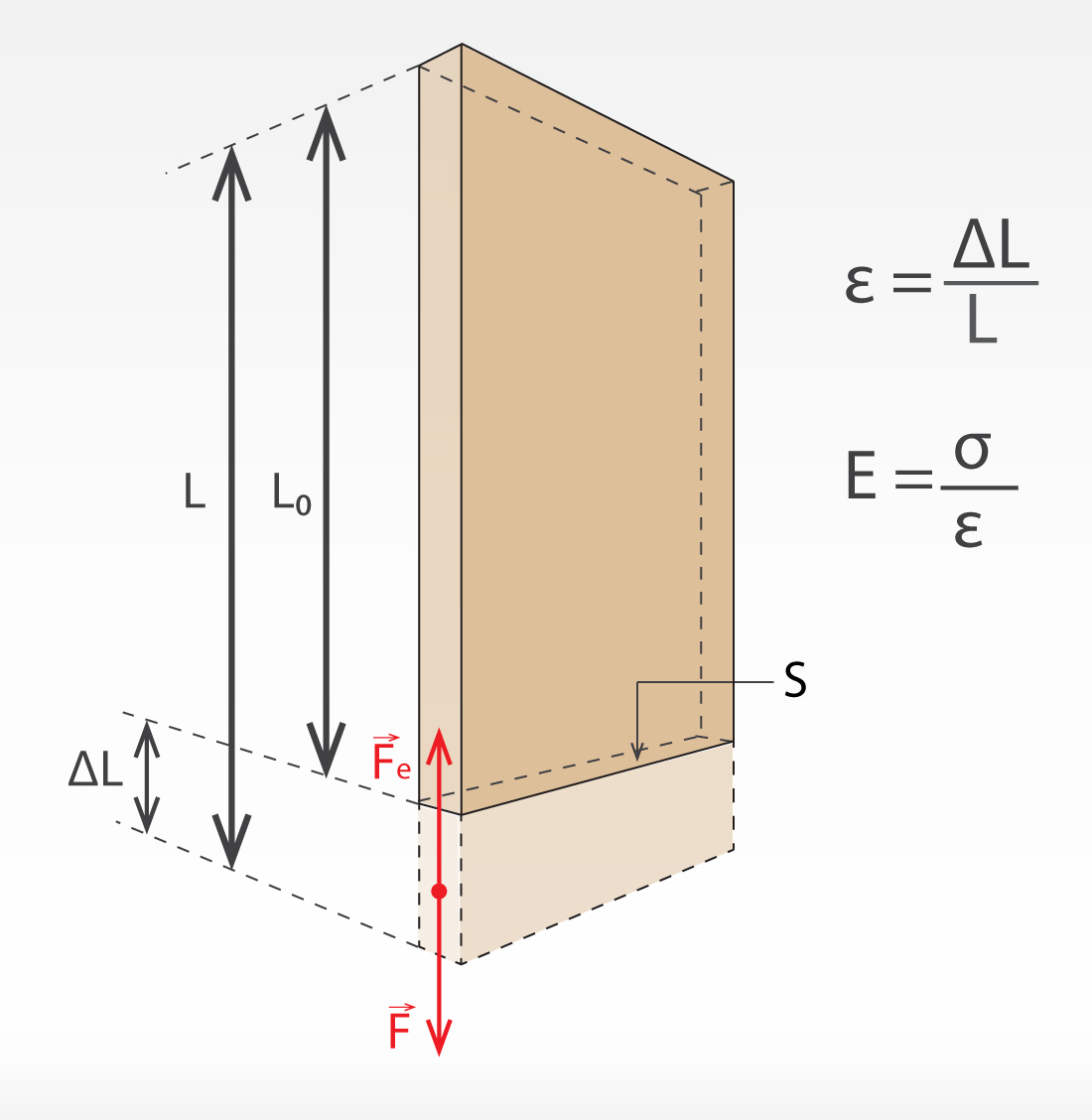
3.att. Junga moduļa noskaidrošana
Piemēram, gumijai Junga modulis ir 7 MPa, tādēļ to izstiep ir viegli, bet dimanta Junga modulis ir 1 140 000 MPa, tādēļ to ir ļoti grūti izstiept. Dažādas Junga moduļa vērtības redzamas 4. attēlā.
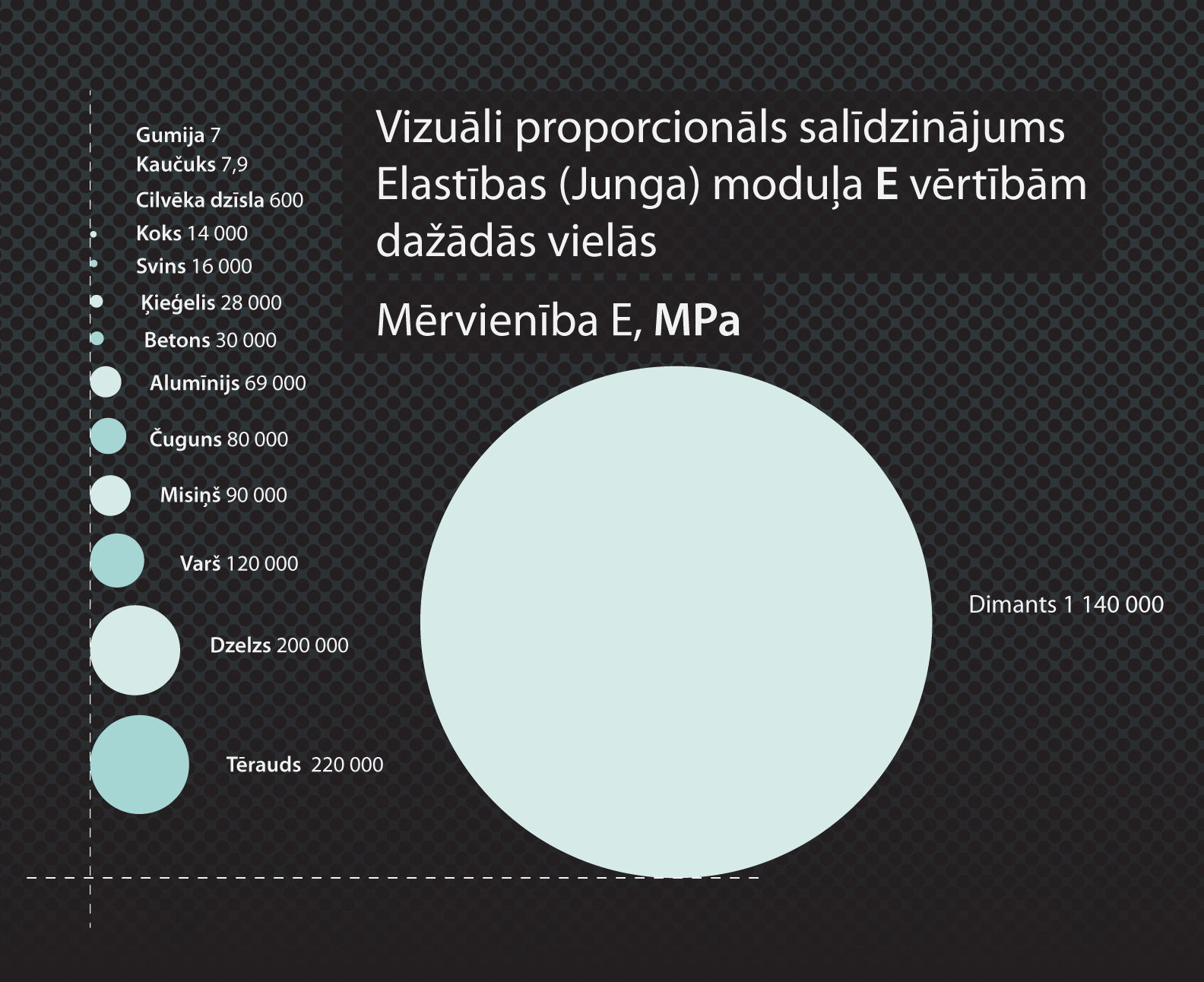
4.att. Dažādas Junga moduļa vērtības
FIZMIX īsfilma par deformācijām: