Daži cilvēki mums liekas pievilcīgi, bet daži ne. Tomēr no fizikas viedokļa izrādās, ka visi cilvēki savā starpā ir pievilcīgi, vismaz gravitācija spēka ietekmē noteikti. Gravitācijas spēks ir cilvēkam vispierastākais no spēkiem, jo ar tā darbību mēs saskaramies ik uz soļa. Mēs skaidri zinām, ka ja mēs kaut ko palaižam vaļā, tad tas krīt virzienā uz Zemi. Ja ābols krīt no ābeles, tad tas krīt taisni lejup. Klīst leģendas, ka tieši krītošs ābols, trāpot Izakam Ņutona pa galvu, lika viņam aizdomāties par to, kādēļ vispār ķermeņi krīt. Gravitācijas spēks darbojas starp jebkuriem ķermeņiem, kuriem piemīt masa. Tādēļ nākošreiz, kad atrodies cilvēku kompānijā, atceries, ka gravitācijas spēka ietekmē Tu pievelcies pie ikviena cilvēka un pie ikviena priekšmeta, kas atrodas Tev apkārt (1. att.). Protams, šie pievilkšanās spēki ir tik mazi, ka nav praktiski sajūtami.

1. att. Gravitācijas spēks starp dažādiem ķermeņiem
Gravitācijas spēku ar kādu pievelkās divi ķermeņi (2. att.) var aprēķināt, izmantojot Ņutona gravitācijas likumu F=G·m1·m2/R2, kur
m1 - viena ķermeņa masa, kg
m2 - otra ķermeņa masa, kg
R - attālums starp ķermeņiem, m
G - gravitācijas konstante, (G=6,67·10-11 N·m2·kg-2)
Gravitācijas likums ir rakstīts punktveida masām, bet pieņemot ķermeņus kā punktveida ķermeņus, varam lietot šo likumu.
Jāatzīmē, ka gravitācijas spēks ir ļoti mazs salīdzinot ar citiem spēkiem, bet tā darbības rādiuss ir bezgalīgs, proti, gravitācijas spēks darbojas gan starp protoniem un neitroniem kāda atoma kodolā, gan arī starp divām zvaigznēm, kas atrodas divās dažādās galaktikās daudzu miljonu gaismas gadu attālumā.
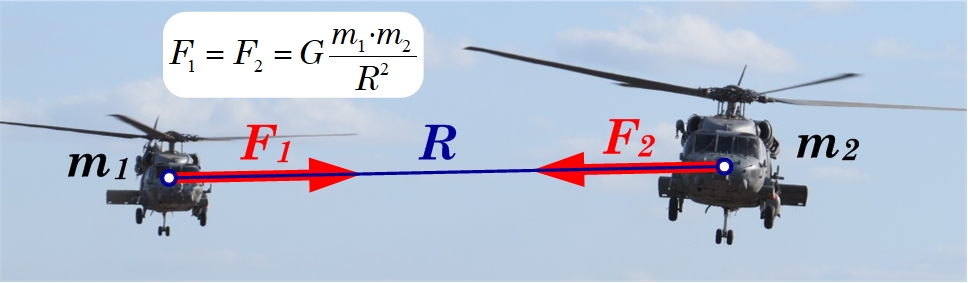
2. att. Gravitācijas spēka aprēķins
Ja mēs apskatām kā Zeme pievelk dažādus ķermeņus, tad no iepriekš minētā seko, ka jo smagāks ir ķermenis, jo spēcīgāk Zeme to pievelk. Šo spēku, ar kādu Zeme pievelk dažādus ķermeņus, sauc par smaguma spēku. Apskatot otro Ņutona likumu, var redzēt, ka, lai masu saistītu ar kādu spēku, ir nepieciešams paātrinājums. Tieši šādu paātrinājumu Zeme katram ķermenim piešķir un to sauc par brīvās krišanas paatrinājumu un apzīmē ar g. Ja ķermenis atrodas netālu no Zemes virsmas, tad g≈9,8 m/s2. Lai gan visiem ķermeņiem Zeme piešķir vienādu paātrinājumu, pēc pieredzes ir zināms, ka A4 lapa un viedtālrunis krīt ar atšķirīgu paātrinājumu. Tas ir tādēļ, ka uz dažādiem objektiem atšķirīgi darbojas gaisa pretestība (3. att. a). Ja objekti brīvi krīt vakuuma (bezgaisa telpā), tad neatkarīgi no ķermeņa masas, tie kritīs ar pilnīgi vienādu paātrinājumu (3. att. b). Lai parādītu, ka divi ķermeņi krīt vienādi, ne vienmēr ir nepieciešams izsūknēt gaisu, jo, piemēram, Zemes pavadonim Mēnesim nav vērā ņemamas atmosfēras, līdz ar to tur nav gaisa, līdz ar to arī gaisa pretestības. “Apollo 15” misijas laikā viens no amerikāņu astronautiem pārbaudīja vai spalva un āmurs uz Mēness krīt vienādi.
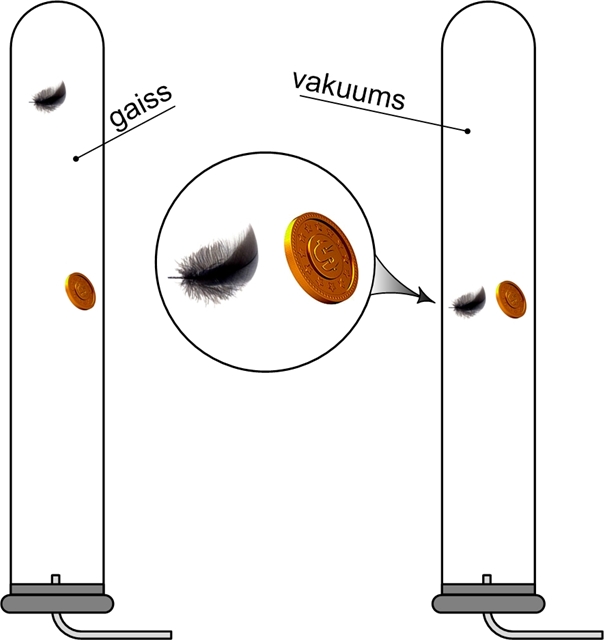
3. att. Dažādu ķermeņu brīvais kritiens gaisā un vakuumā
2013. gadā austrietis Fēlikss Baumgartners veica lēcienu no 39 km augstuma (4. att. a). 39 km augstumā brīvās krišanas paātrinājums ir ievērojami mazāks nekā pie zemes, tomēr, apskatot austrieša ātruma grafiku (4. att. b) lēciena laikā redzams, ka maksimālais ātrums tika sasniegts lēciena 1. minūtes laikā, bet pēc tam ātrums strauji samazinājās, kaut arī brīvās krišanas paātrinājums visu laiku pieaug. Līdzīgi kā 3. att. piemērā, šeit parādās gaisa pretestības ietekmē. 39 km augstumā gaisa pretestības praktiski nav, bet, tuvojoties zemei, atmosfēras blīvums arvien pieaug un gaisa pretestība sāk spēlēt arvien lielāku lomu.
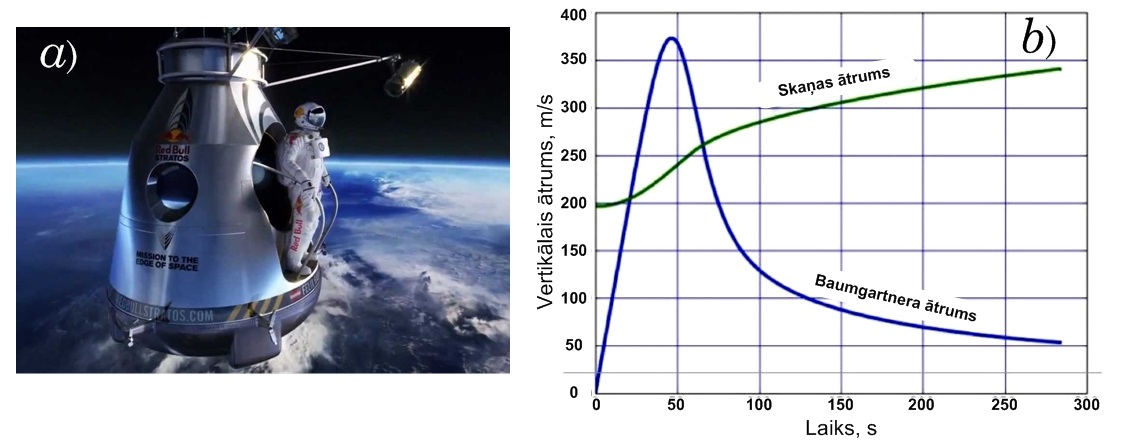
4. att. Baumgartnera leciens
Lai aprēķinātu brīvās krišanas paātrinājumu g, ir jāizmanto gan otrais Ņutona likums F=mg, gan Ņutona gravitācijas likums, jo tie abi izsaka vienu un to pašu spēku. Pielīdzinot šos abus spēkus un neievērojot Zemes rotāciju ap savu asi (Zemes rotācijas dēļ rodas neliels papildus spēks - Koriolisa spēks), iegūst g=GM/(R+h)2, kur
G - gravitācijas konstante, N·m2·kg-2
M - Zemes masa, kg
R - Zemes rādiuss, m
h - augstums virs zemes, m
Uz Zemes virsmas h=0 un brīvās krišanas pāātrinājums ir aptuveni g≈9,8 m/s2.
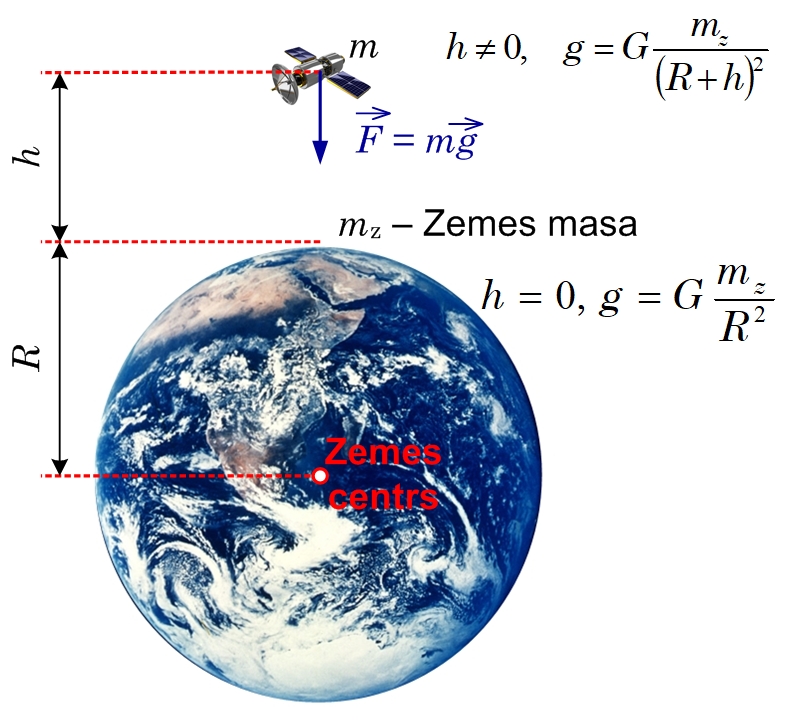
1. att. Brīvās krišanas paātrinājuma aprēķināšana dažādos augstumos virs zemes

2. att. Brīvās krišanas paātrinājuma vērtības atkarībā no atrašanās augstuma virs jūra līmeņa
Lai gan ir pieņemts, ka visapkārt Zemeslodei brīvās krišanas paātrinājuma vērtība ir viena un tā pati, tomēr dažādās vietās uz Zemes tā nedaudz atšķiras, piemēram, Tokijā tas ir 9,79801 m/s2, Berlīnē 9,81280 m/s2, bet Romā 9,80312 m/s2. Brīvās krišanas paātrinājums ir atkarīgs gan no tā cik attiecīgā vieta atrodas augstu virs jūras līmeņa, gan arī kāds ir vidējais zemes blīvums noteiktajā apvidū (jo blīvāka zeme, jo lielāka masa un spēcīgāks gravitācijas spēks). Skaitļi rādā, ka uz Zemes lielas brīvā krišanas paātrinājumu svārstības nevarēs izjust, tādēļ lielas g izmaiņas kārotājiem ir jādodas uz citiem Saules sistēmas ķermeņiem, starp kuriem var atrast tādus, kuriem brīvas krišanas paātrinājums ir gan daudz lielāks, gan arī daudz mazāks nekā Zemei (3. att.).
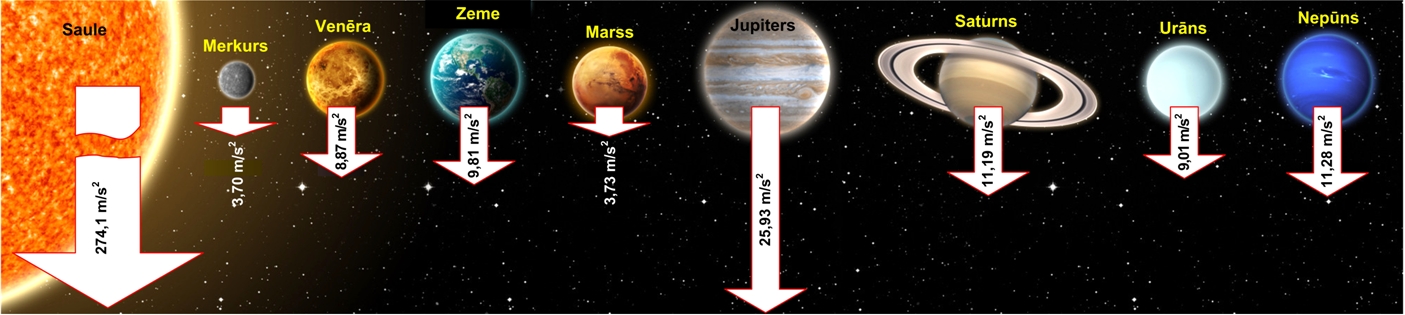
3. att. Brīvās krišanas paātrinājum uz dažādiem Saules sistēmas objektiem
Lielo Saules sistēmas ķermeņu forma, arī Zemes, ir lodveida. Arī tas ir pateicoties gravitācijas spēkam. Zemi un citus debess ķeremeņus veidojošā materiāla daļiņas savstarpēji pievelkas viena pie otras, gala rezultātā izveidojot lodveida formu (4. att.).

4. att. Zemes lodveida forma
Gravitācijas konstantes vērtība parāda ar kādu spēku gravitācijas mijiedarbības dēļ pievilksies divi 1 kg smagi ķermeņi, ja tie atradīsies 1 m attālumā (1. att.). Šīs spēks ir ļoti mazs, tādēļ lai noteiktu gravitācijas konstanti, jāveic ļoti precīzi mērījumi.
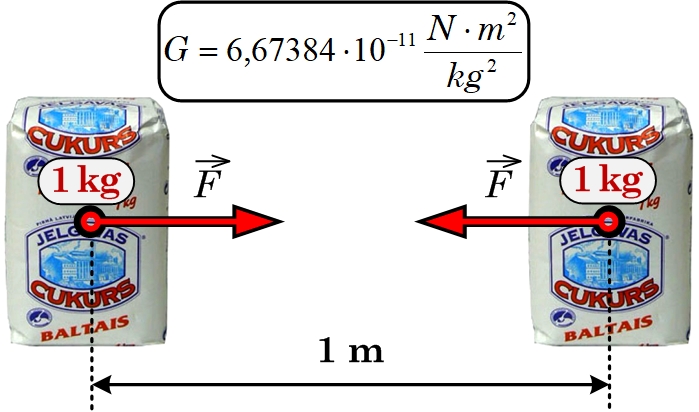
1. att. Gravitācijas konstante
Viens no eksprimentiem, kura tas tika realizēts, ir Kavendiša eksperiments (2. att.). Kavendiša eksperimentā tiek mērīts gravitācijas spēks ar kādu pievelkas svina lodes (2. att. a). Arī Fizikas un matemātikas fakultātē atrodas šāda eksperimentālā iekārta (2. att. b), bet jāteic, ka eksperiments ir ļoti jūtīgs, jo mērījuma rezultāti tiek negatīvi ietekmēti pat tad, kad 200 m attālumā garām pabrauc tramvajs.
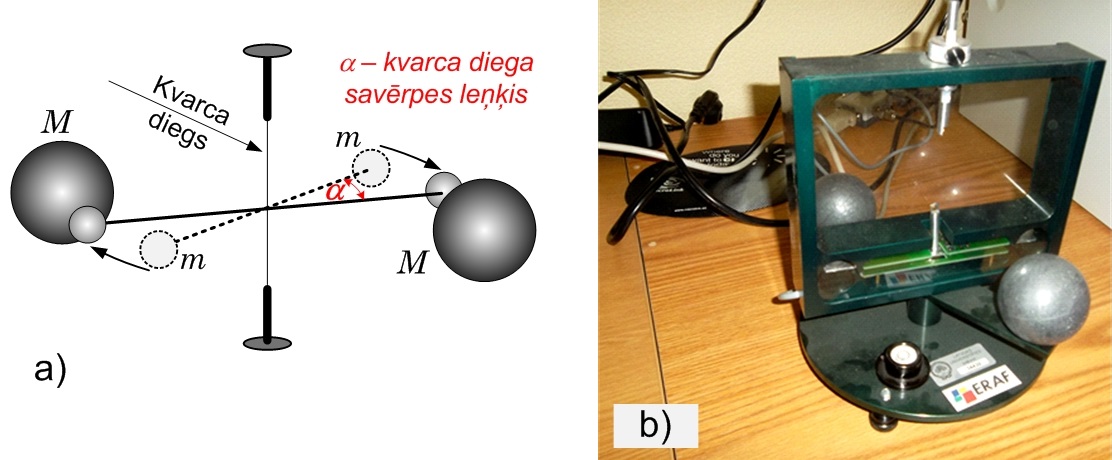
2. att. Kavendiša eksperiments
Gravitācijas konstante ir nemainīgs lielums, tādēļ šīs konstantes mērījumi nevar dot un informāciju par vietu, kurā mērs to mēram, bet brīvās krišanas paātrinājums gan var. Mūsdienās ir izveidoti ļoti precīzi gravitometri, ar kuriem var mērīt smaguma spēku un līdz ar to arī brīvās krišanas paātrinājuma izmaiņas. Šie gravitometri ir tik precīzi, ka var atklāt ļoti nelielas zemes blīvuma izmaiņas kādā apvidū. Šo faktu var izmantot, lai meklētu dažādas derīgo izrakteņu atradnes, kas atrodas zem zemes un kuru blīvums parasti atšķiras no to iekļaujošo zemes masīvu blīvuma. (3.att.). Izmantojot ļoti precīzus gravitometrus, var izmērīt ļoti nelielas brīvā krišana paātrinājuma izmaiņas kāda apvidū, kas var liecināt par pazemē esošu derīgo izrakteņu iegulām.
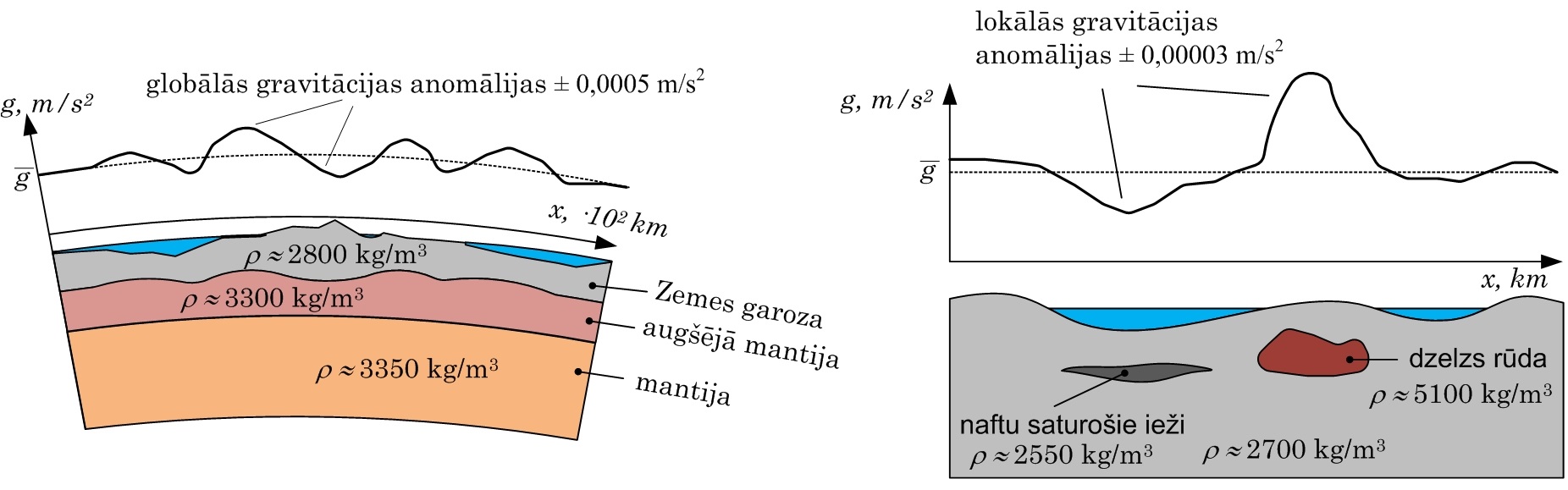
3. att. Gravitācijas anomālija