Procesiem, kas norit dabā, ir noteikta virzība. Izkusis saldējums nekad pats neieņems sākotnējo formu, un apēsts hamburgers vēderā nekad pēkšņi “neizdomās”, ka vēlas atkal savākties kopā vienā veselumā. Izmantojot melnu flomāsteru, uz lapas ir iespējams uzvilkt izteiksmīgas ķēpas (1. att.), bet nekad nebūs tā, ka izlietotā krāsa pēkšņi pati saskries atpakaļ flomāsterā. Šāda lietu virzība ir raksturīga neatgriezeniskiem procesiem, jo neatgriezenisks process pastāvīgi var noritēt tikai vienā virzienā.

1.att. Izlietota flomāstera krāsa pati no sevis vairs neatgriežas atpakaļ flomāsterā
Ja mēs uzkarsējam kāda metāla priekšmeta galu (2. att.), tad temperatūra visā metāla priekšmetā pamazām izlīdzinās. Nav novērota tāda parādība, ka karstākais metāla gals pats no sevis kļūst arvien karstāks un karstāks, bet otrs gals vēsāks. Šādi eksperimentāli fizikas novērojumi noteica 2. termodinamikas likuma (TDL) formulēšanu, proti, siltums nekad pats no sevis neplūst no karstāka ķermeņa uz aukstāku. Šis likums ir spēkā noslēgtām sistēmām.

2.att. Temperatūra uzkarsētā metālā cenšas izlīdzināties
2. TDL ir arī cita veida formulējums, kas saistīts ar kārtību dabā. Tāpat kā siltums pats no sevis neplūst no aukstākas vietas uz karstāku, arī lietas nekad pašas no sevis nesakārtojas. Apskatīsim kādu sakārtotu fizikālu sistēmu, piemēram, divus traukus, kuri ir atdalīti ar aizbāzni (3. att. a). Sākotnēji kreisajā traukā atrodas gāzes daļiņas, bet labais trauks ir tukšs. Tā ir noteikta kārtība. Kad aizbāznis tiek atvērts (3. att. b), gāze sadalās pa abiem traukiem jeb izjūk sākotnējā kārtība. Un atkal nebūs novērojama situācija, ka visas gāzes daļiņas pašas saskries kreisajā traukā. Līdz ar to 2. TDL var formulēt šādi: neatgriezeniskos procesos pieaug noslēgtas sistēmas nekārtības pakāpe.
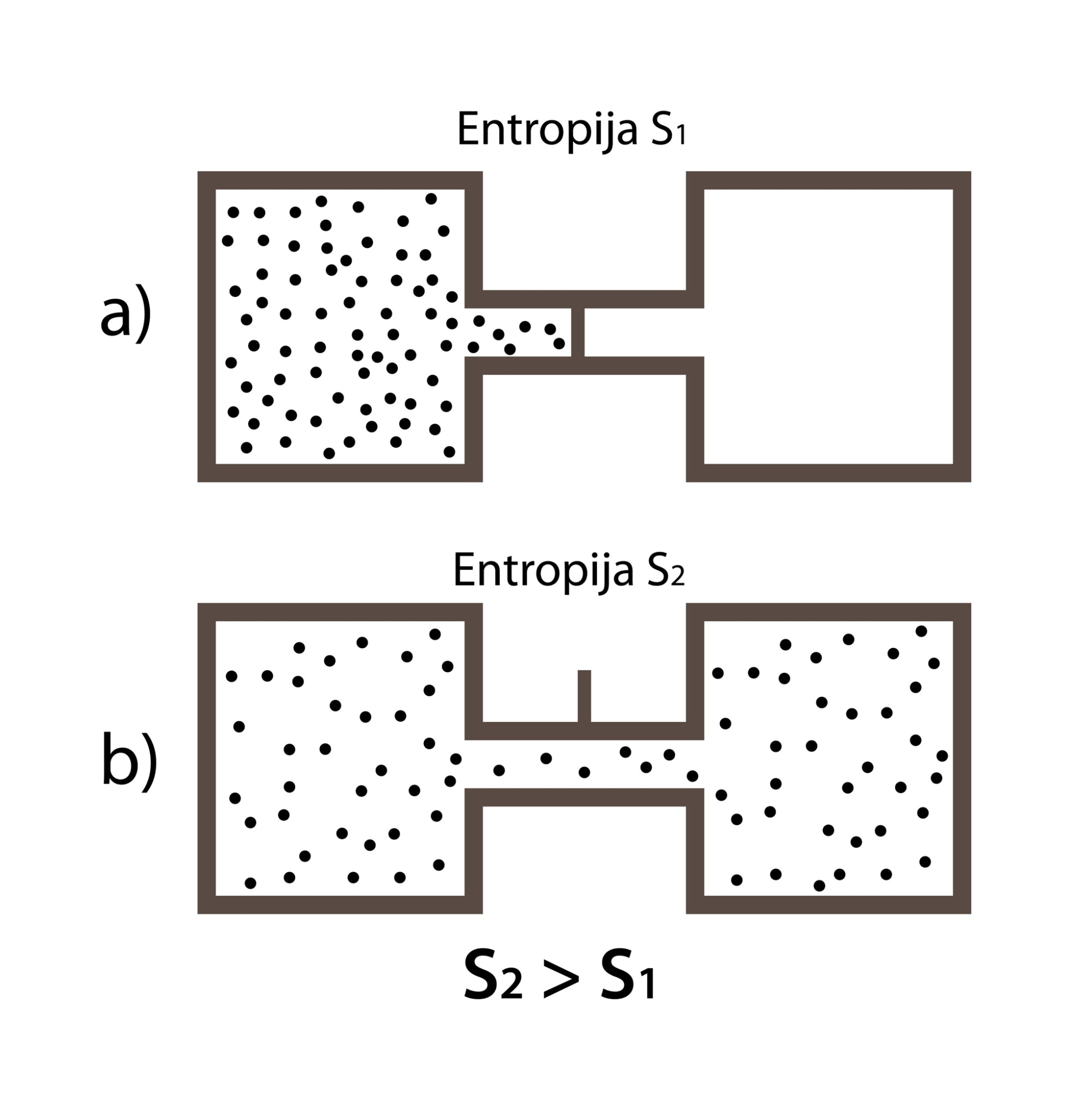
3.att. Kārtība dabā un entropija
Nekārtības pakāpes raksturošanai ir ieviests jēdziens entropija S. Ja iepriekš aplūkotajā piemērā sistēmas sākuma stāvokli (3. att. a) raksturotu entropija ar lielumu S1, bet beigu stāvokli – entropija S2, tad S2 > S1, jo beigu stāvoklī nekārtība ir lielāka (3. att. b). Termodinamiskos procesos ir svarīga entropijas izmaiņa ∆S=∆Q:T, kur ∆Q ir ķermeņa saņemtais siltuma daudzums, bet T ir ķermeņa absolūtā temperatūra. Entropijas mērvienība ir J : K.
Interesantas formas rezultātu var iegūt, ja ūdenī ielej izkausētu parafīnu (4. att.). Ja sakarsēta parafīna temperatūra ir T1, bet ūdens temperatūra T2un T2 1, tad parafīns ūdenim atdod siltuma daudzumu - ∆Q. Pieņemot, ka ūdens temperatūra būtiski nemainās, var uzrakstīt sistēmas entropijas izmaiņu ∆S =∆Q : T2 +∆Q : T1 > 0. Šis rezultāts apliecina, ka situācijās, kad siltums pāriet no karstāka ķermeņa uz aukstāku, entropija palielinās.
Palielini entropiju te uzrakstītam tekstam!

4.att. Izkausēta parafīna liešana ūdenī
Kā iepriekš noskaidrojām, reāli dabā notiekoši procesi ir neatgriezeniski, un neatgriezeniskā procesā pieaug sistēmas entropija. Piemēram, degšana (1. att.) ir neatgriezenisks process, kurā sistēmas entropija pieaug, jo degšana noris vienā virzienā.

1.att. Degšana ir neatgriezenisks process
Arī kušana (2. att.) ir neatgriezenisks process, kurā pieaug sistēmas entropija, jo izkusis ledus gabaliņš vai izkususi kupena pati no sevis neatgūst iepriekšējo formu un konsistenci.

2.att. Kušana ir neatgriezenisks process
Ja kāds centīgs cilvēks ir uzcēlis kāršu namiņu (3. att.), tad šis cilvēks ir ieinteresēts, lai kāršu entropija nepieaug, jo tas nozīmētu kāršu namiņa brukšanu.

3.att. Spēļu kāršu entropijas pieaugums nozīmē namiņa sabrukšanu
Ar entropiju var raksturot arī grāmatu kārtību. Ja grāmatas ir izkaisītas pa visu galdu (4. att. a), tad to entropija ir daudz lielāka nekā tad, ja tās ir glīti sakārtotas plauktā. (4. att. b)

5.att. Jo kārtīgāk sakārtotas grāmatas, jo mazāka to entropija
Sistēmas entropijas pieaugumu var izskaidrot arī ar statistiku. Izveidosim sistēmu, kas sastāv no desmit melnām un desmit baltām bumbiņām (1. att.). Sākotnējā stāvoklī bumbiņas ir izvietotas divos slāņos tā, ka apakšpusē ir melnās bumbiņas, bet augšpusē baltās. Ja mēs šo sistēmu sakratīsim, tad visticamāk sistēmas beigu stāvoklis būs kaut kas līdzīgs 1. attēla lejasdaļā esošajam stāvoklim, proti, ka augšējā slānī un apakšējā slānī balto un melno bumbiņu skaits būs vienāds.

1.att. Sakratot bumbiņas, tās sajaucas
Beigu stāvokļa izskatu var izskaidrot, ja apskata dažādu iespējamo stāvokļu varbūtību. 2. attēlā ir redzama tabula, kurā ir izrēķināta varbūtība tam, ka augšējā slānī ir noteikts balto un melno bumbiņu skaits. Redzams, ka varbūtīgākais ir stāvoklis, kad balto un melno bumbiņu skaits ir vienāds. Tas ir tādēļ, ka piecām baltajām un piecām melnajām bumbiņām ir visvairāk dažādo iespējamo veidu, kā tās var izvietoties vienā slānī. No tā var secināt: jo varbūtīgāku stāvokli ieņem sistēma, jo lielāks ir entropijas pieaugums.

2.att. Lodīšu stāvokļu varbūtību sadalījums