Ja apskatām gāzi kā sastāvošu no atsevišķām daļiņām, tad katrai daļiņai piemīt enerģija. Katru vienatoma gāzes, piemēram, hēlija vai neona daļiņu raksturo vidējā kinētiskā enerģija Ek = 3 : 2kT (1. att.), kur k ir Bolcmaņa konstante, bet T – gāzes temperatūra. Ja vēlas iegūt visas gāzes kinētisko enerģiju, tad vienas daļiņas kinētiskā enerģija jāpareizina ar daļiņu skaitu N. Bet nevienam nav laika un pacietības sēdēt un skaitīt, cik daļiņu dotajā tilpumā ir, tādēļ, izmantojot gāzu likumu sakarības, iegūst, ka vienatoma gāzes daļiņu kopējā kinētiskā enerģija U = 3 : 2m : MRT. Šī kinētiskā enerģija raksturo gāzes stāvokli kādā noteiktā temperatūrā, spiedienā un tilpumā, tādēļ to sauc par gāzes iekšējo enerģiju.
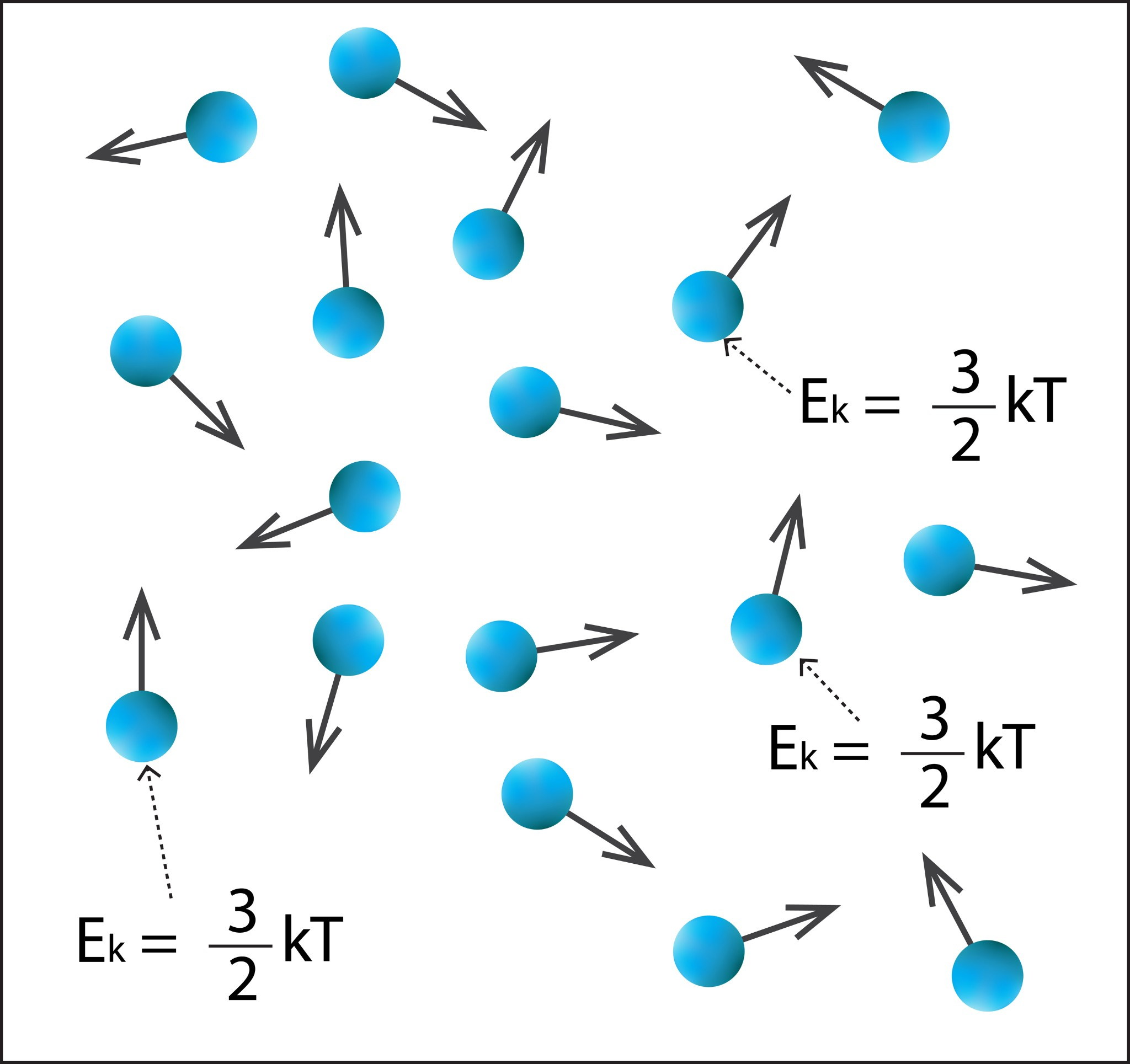
1.att. Katru vienatoma gāzes daļiņu raksturo kinētiskā enerģija
Ja gāze nav ideāla vienatoma gāze, tad papildus kinētiskajai enerģijai klāt nāk molekulu potenciālā enerģija (2. att.), kas veidojas no molekulu savstarpējā mijiedarbības, kā arī atomu mijiedarbības vienas molekulas ietvaros. Līdz ar to par vielas iekšējo enerģiju U sauc par vielā esošo daļiņu kinētiskās un potenciālās enerģijas summu.
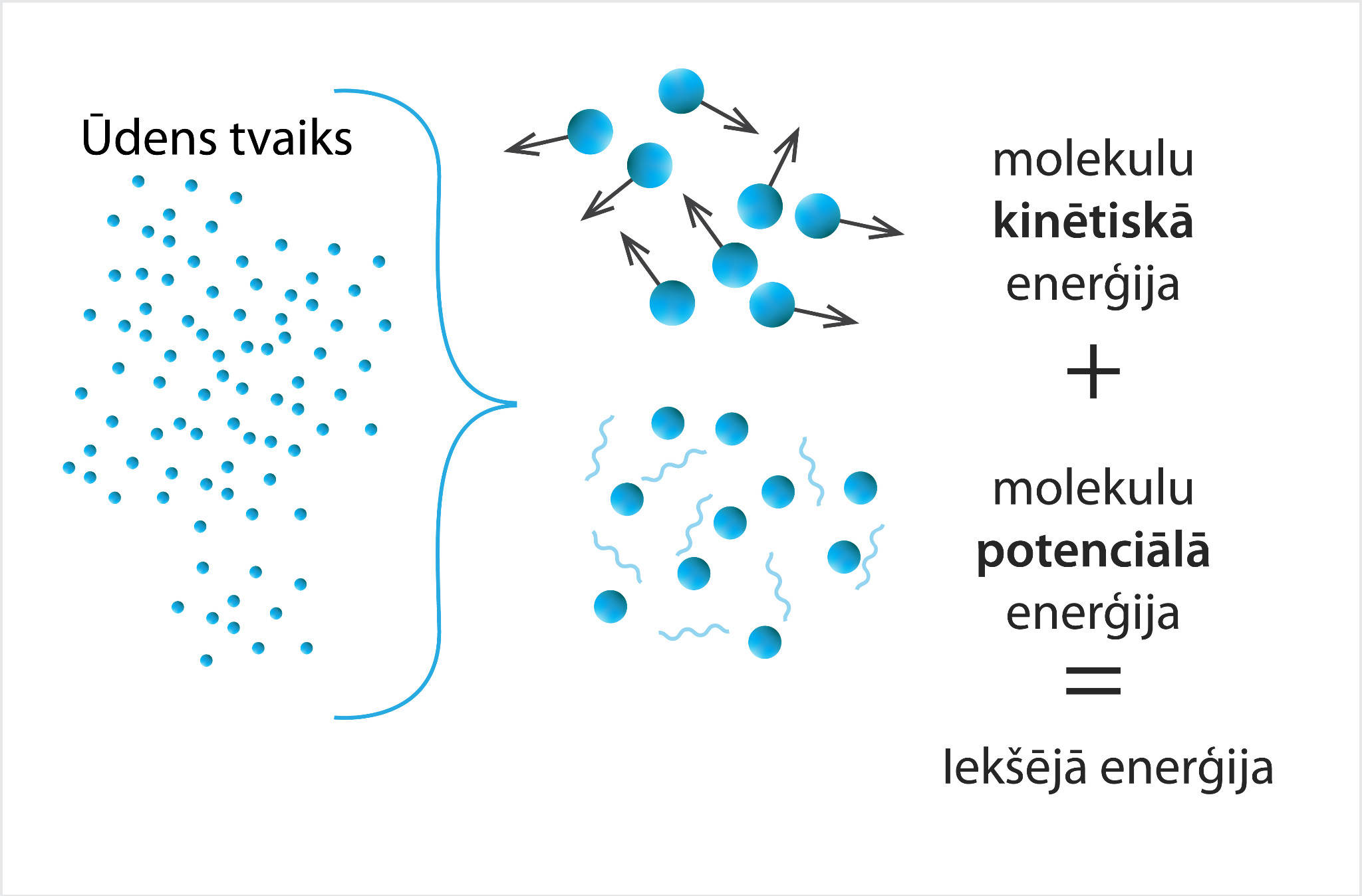
2.att. Ūdens tvaika iekšējā enerģija
3. attēlā apskatīta divu vienādas masas gāzu iekšējā enerģija pie vienas un tās pašas temperatūras. Redzams, ka kinētiskās enerģijas daļa abām gāzēm ir vienāda, jo tā nav atkarīga no gāzes daļiņu veida, bet potenciālās enerģijas daļa ir krasi atšķirīga. Tas ir tādēļ, ka ūdeņradim piemīt krietni lielāka (aptuveni 14 reizes) siltumietilpība, kas nosaka lielo potenciālo enerģiju.
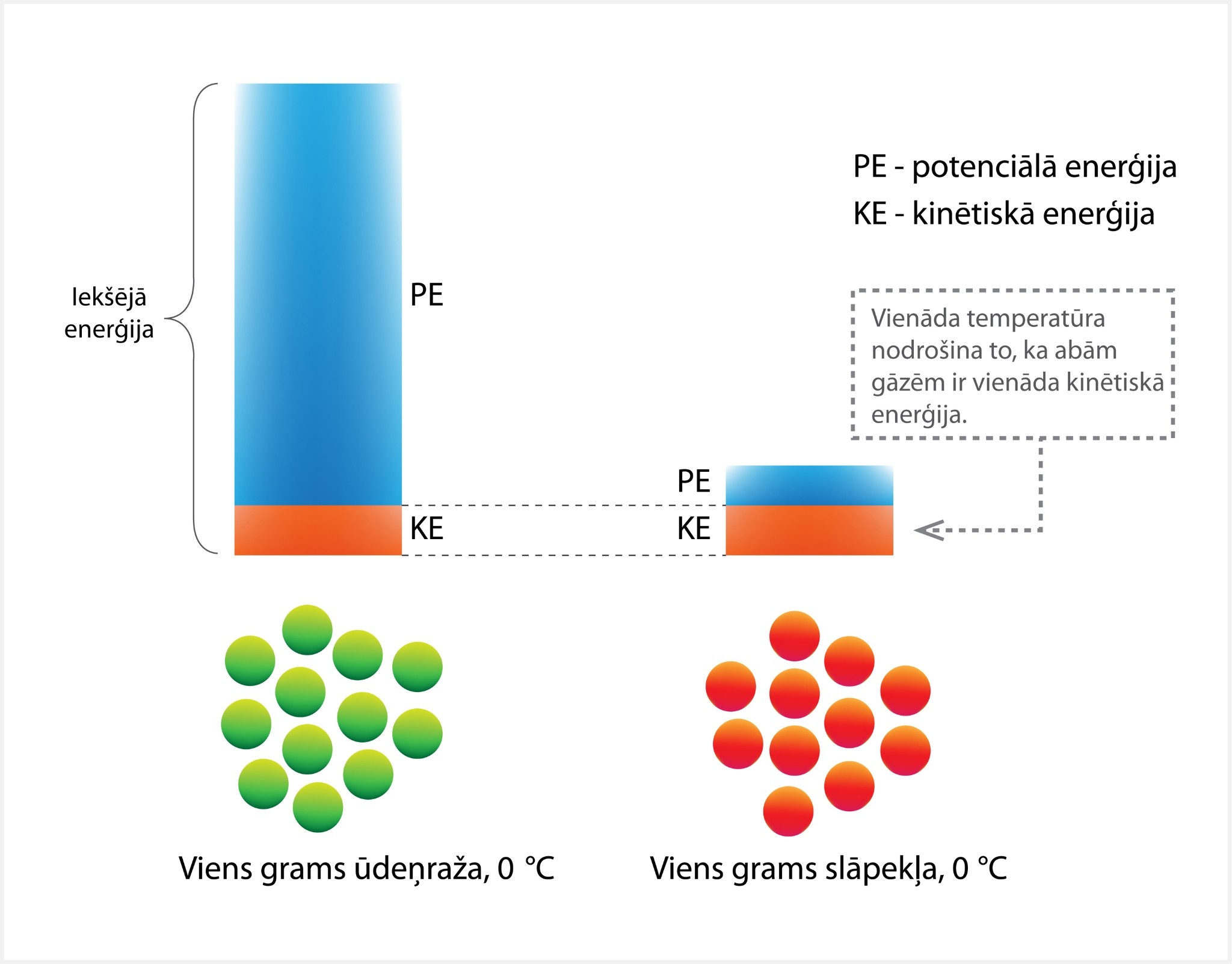
3.att. Divu gāzu iekšējo enerģiju salīdzinājums
Ja vienas gāzes daļiņas kinētiskā enerģija Ek = 3 : 2kT, tad N daļiņām tā būs Ek = N . 3 : 2kT. Lai iegūtu izteiksmi ērtākā formā, izmanto izteiksmi, kas izsaka Bolcmaņa konstanti k = R : NA, kur R ir universālā gāzu konstante, bet NA ir Avogadro skaitlis. Vēl pēdējā izteiksme, kas jāņem talkā, ir daļiņu skaita vienādība N = m : M . NA, kur m ir gāzes masa, bet M – molmasa. Apvienojot iepriekšējās izteiksmes, iegūst U = 3 : 2m : MRT.
Gāzes iekšējās enerģijas noteikšanā liela nozīmē ir brīvības pakāpju skaitam jeb tam, cik dažādos veidos molekula telpā var kustēties. Vienatoma gāzes molekulu var iedomāties kā mazu lodīti. Šai lodītei koordinātu sistēmā (1. att. a) ir trīs neatkarīgi virzieni x, y, z, kuros tā var kustēties, tādēļ brīvības pakāpju skaits vienāds ar 3.
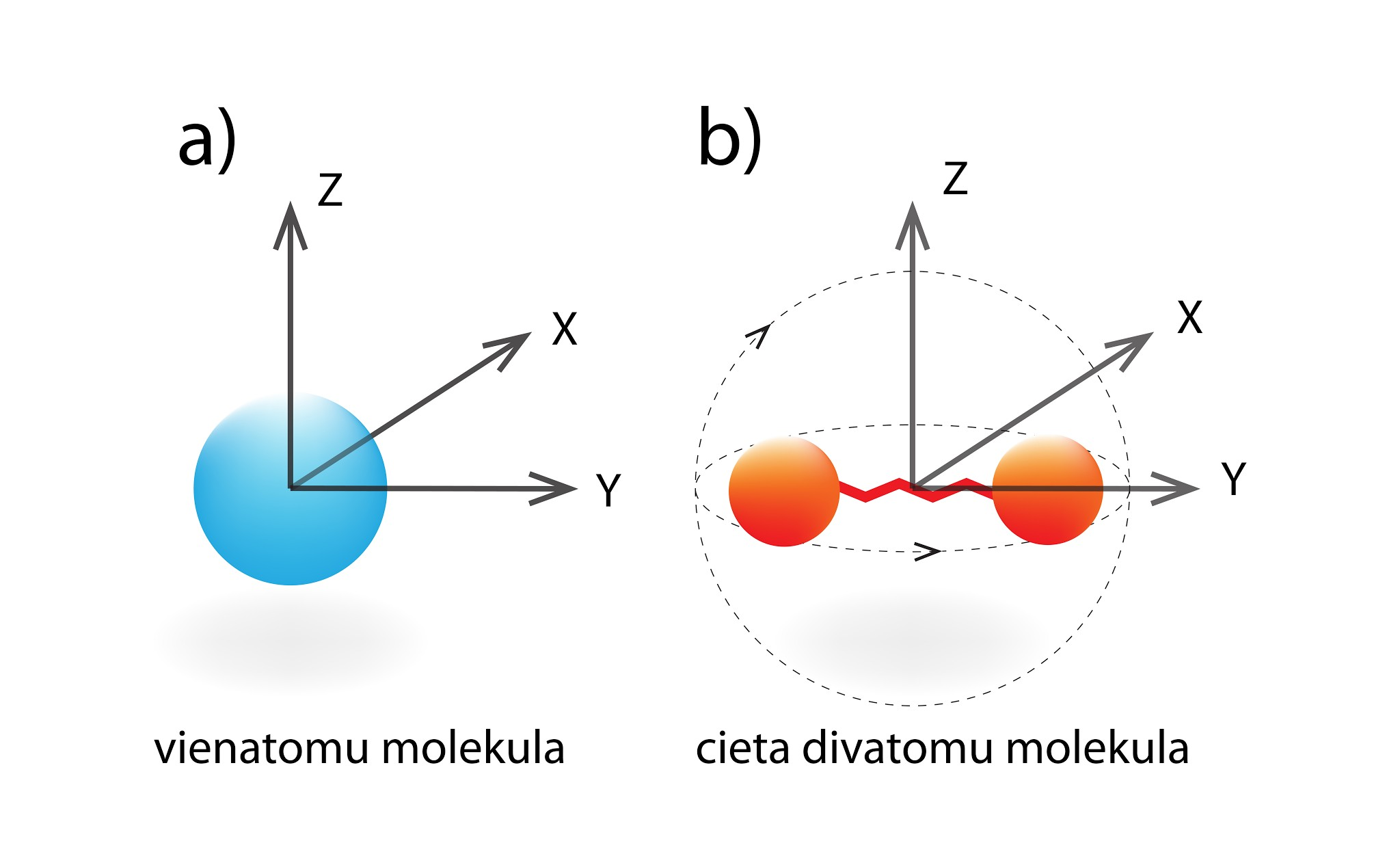
1.att. Brīvības pakāpes vienatoma un divatomu molekulām
Tā kā ideālai vienatoma gāzei 3 brīvības pakāpēm ir iekšējā enerģija U = 3 : 2m : MRT, tad uz katru brīvības pakāpi iznāk 1 : 2m : MRT. Šo lielumu var iedomāties par tādu kā enerģijas porciju vai kūkas gabaliņu (2. att.), kas piemīt vienai brīvības pakāpei. Palielinoties brīvības pakāpju skaitam, vēl aizvien katru brīvības pakāpi raksturos šāds enerģijas daudzums.
Ja apskatām cietas divatomu molekulas modeli (atomi saistīti ar cietu saiti, 1. att. b), tad šeit brīvības pakāpju skaits ir piecas, jo klāt nāk rotācija ap divām asīm. Šādā gadījumā iekšējo enerģiju rēķina U = 5 : 2m : MRT
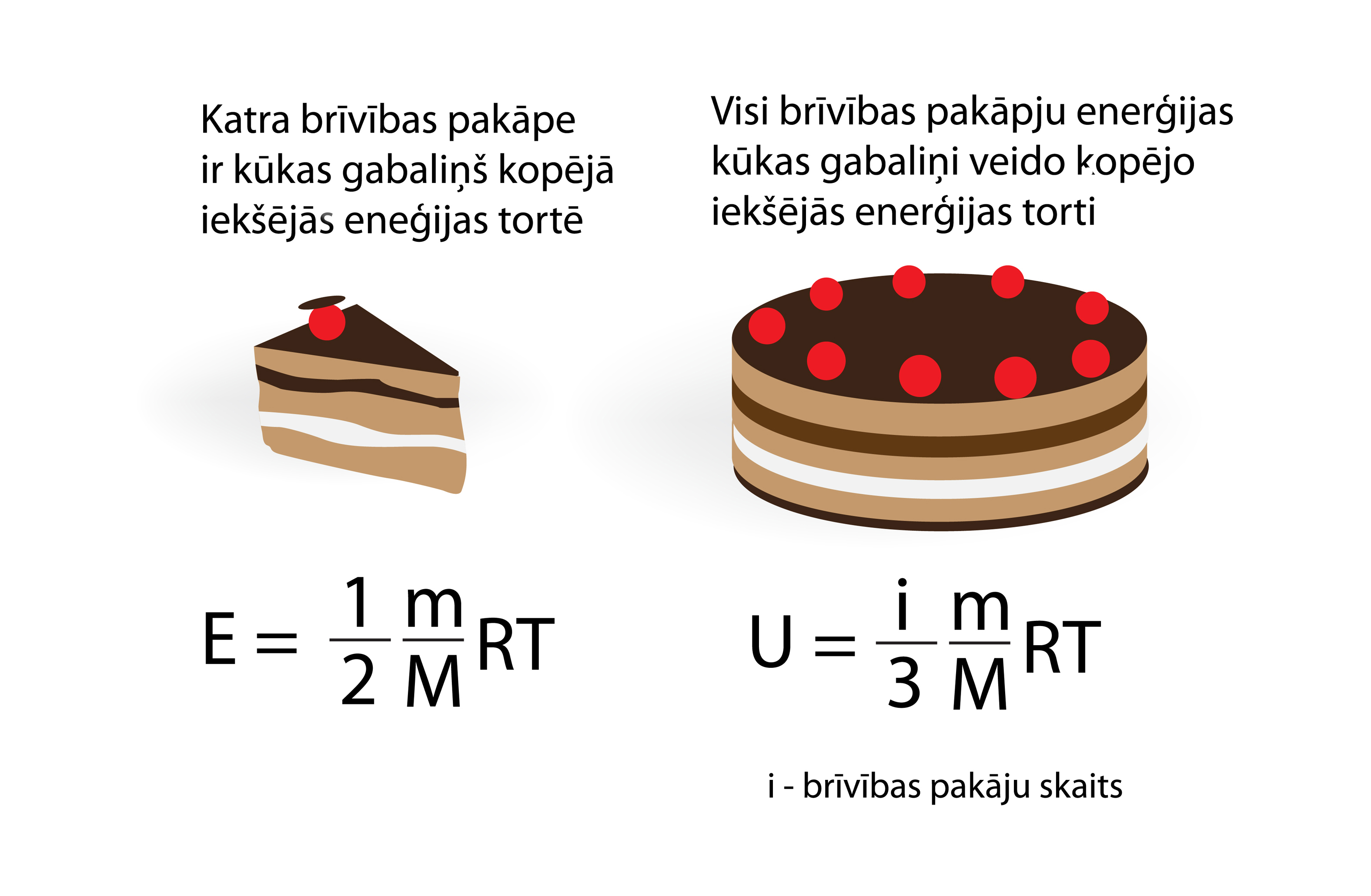
2.att. Iekšējo enerģiju veido visu brīvības pakāpju enerģiju summa
Ja divatomu molekula nav cieta, tad kopējais brīvības pakāpju skaits ir septiņas: kustības x, y, z ass virzienos (3. att. a), rotācija ap divām asīm (3. att. b) un vēl divas brīvības pakāpes no iespējamās svārstību kustības (3. att. c). Attiecīgi šādas gāzes iekšējo enerģiju rēķina, izmantojot izteiksmi U = 7 : 2m : MRT.
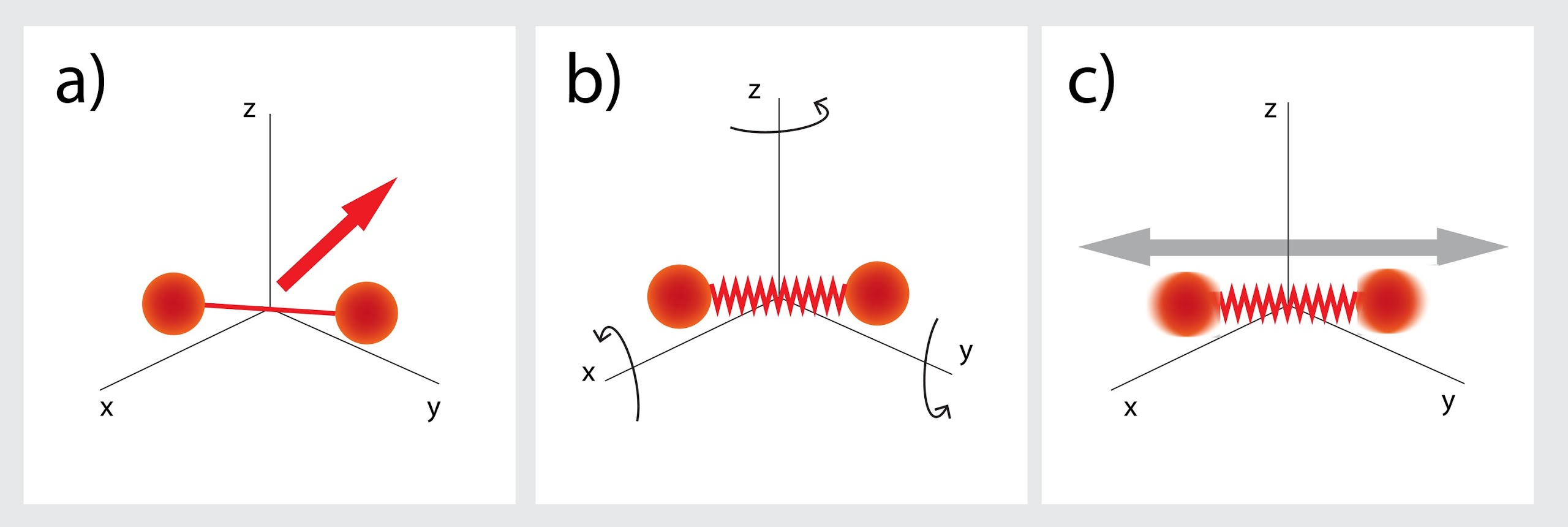
3.att. Septiņas brīvības pakāpes divatomu molekulai
Lai rastos taustāma nojausma par to, cik liela ir gāzu iekšējā enerģija, izrēķināsim gāzu iekšējo enerģiju, kas atrodas tējas krūzē. Krūzes diametrs ir 7 cm, bet dziļums 9 cm. Tas nozīmē, ka krūzes tilpums ir aptuveni 350 cm3, kas ir 3,5 . 10-4 m3. Gaisa sastāvā ir galvenokārt divatomu molekulas N2 un O2. Pieņemot šīs gāzes par ideālām divatomu gāzēm ar 5 brīvības pakāpēm, iekšējā enerģija ir U = 5 : 2m : MRT. Izmantojot Mendeļejeva - Klapeirona vienādojumu, izteiksmi var pārrakstīt U = 5 : 2pV. Spiediens vienāds ar atmosfēras spiedienu p = 1,01 . 105 Pa. Līdz ar to iekšējā enerģija iznāk aptuveni 90 J. Tas ir pietiekami, lai 50 g šokolādes batoniņu paceltu 180 m augstumā (1. att.).
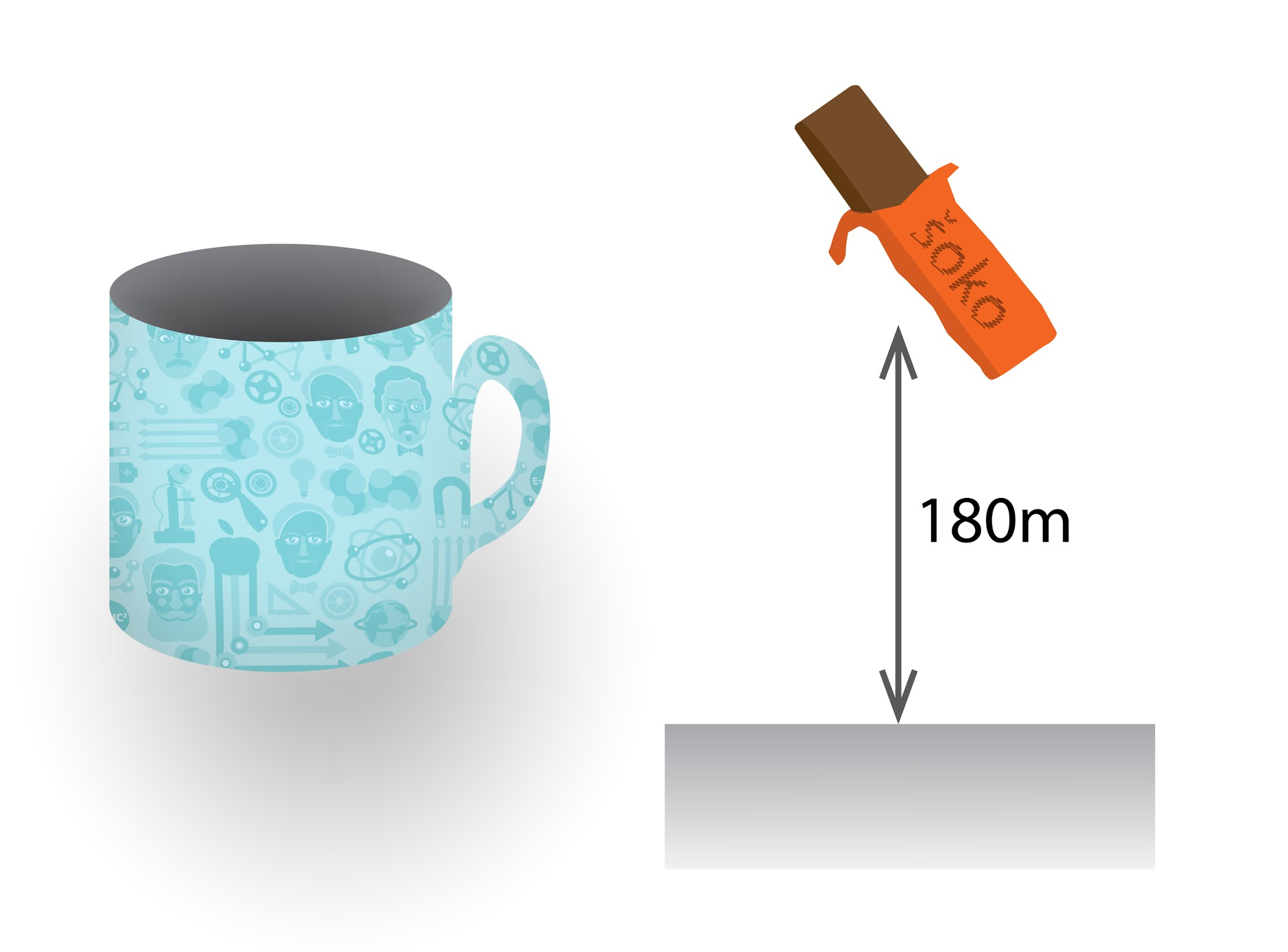
1.att. Krūzē esošā gaisa iekšējā enerģija ir tik liela, lai šokolādes batoniņu paceltu 180 m augstumā
Reālai divatomu gāzei brīvības pakāpju skaits mainās atkarībā no temperatūras (2. att.). Pie zemas temperatūras ir tikai translācijas kustība un trīs brīvības pakāpes, jo nepietiek enerģijas, lai molekulas varētu svārstīties vai rotēt. Pieaugot temperatūrai, kādā brīdī daļa molekulu sāk svārstīties, tad brīvības pakāpju skaits sāk palielināties līdz momentam, kad visas molekulas svārstās un brīvības pakāpju skaits ir vienāds ar 5. Kad temperatūra pieaug vēl, tad kādā brīdī molekulas sāk arī rotēt un pakāpeniski brīvības pakāpju skaits pieaug līdz septiņām.
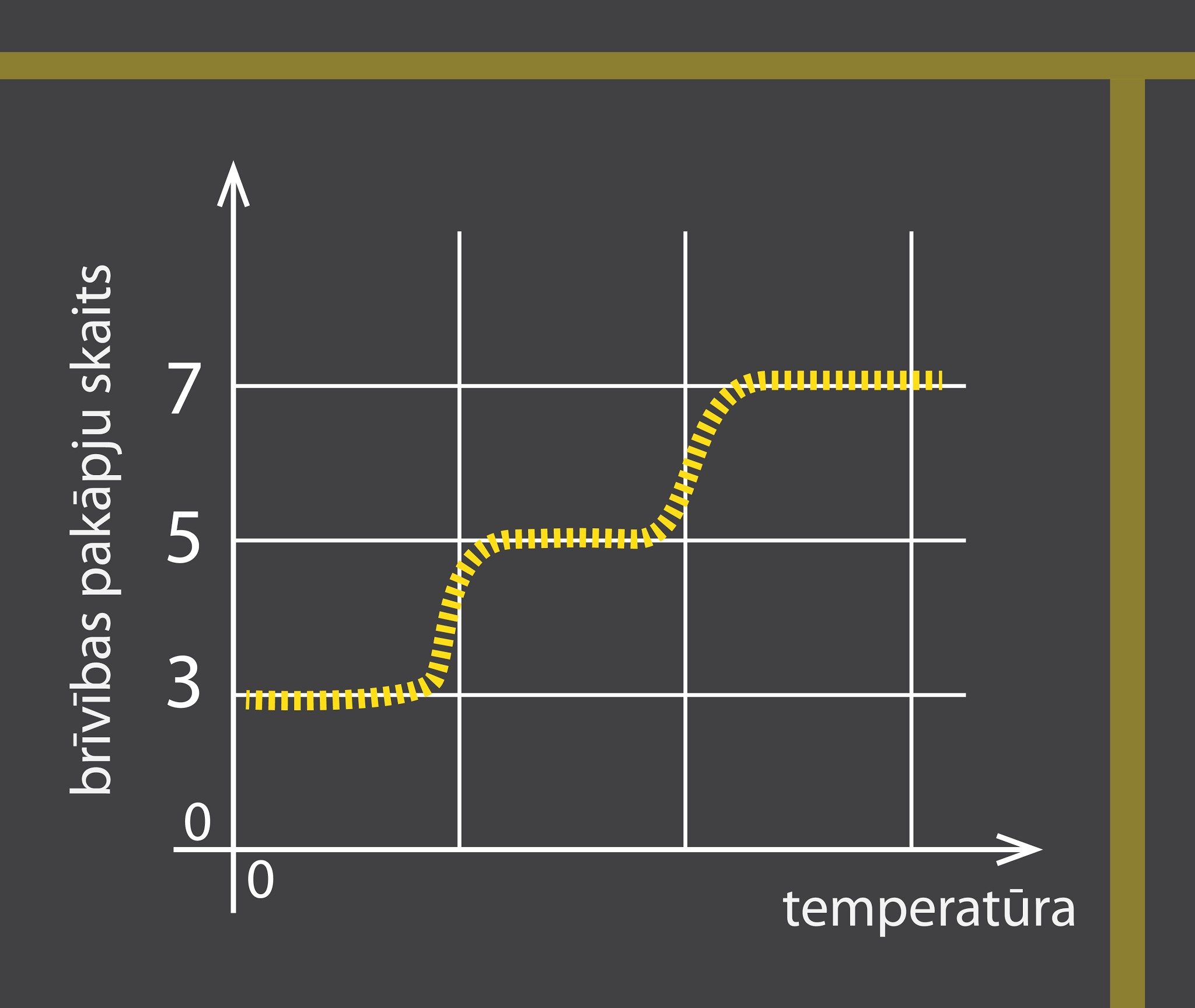
2.att. Brīvības pakāpju skaits reālai divatomu molekulai