Šoreiz, lai būtu mazliet īsāk, sauksim termodinamikas likumu saīsināti - 1TDL!
Sadaļā par iekšējo enerģiju apskatījām, ka gāzei piemīt iekšējā enerģija. Tomēr ikdienas procesos mums ir svarīgi nevis tas, cik liela ir kādas sistēmas iekšējā enerģija, bet gan tās izmaiņas lielums. Gāzes iekšējās enerģijas izmaiņu apraksta 1. termodinamikas likums: ΔU = A + Q, kur ΔU ir iekšējās enerģijas izmaiņa, A ir ārējo spēku veiktais darbs, bet Q - pievadītais siltuma daudzums (1. att.)
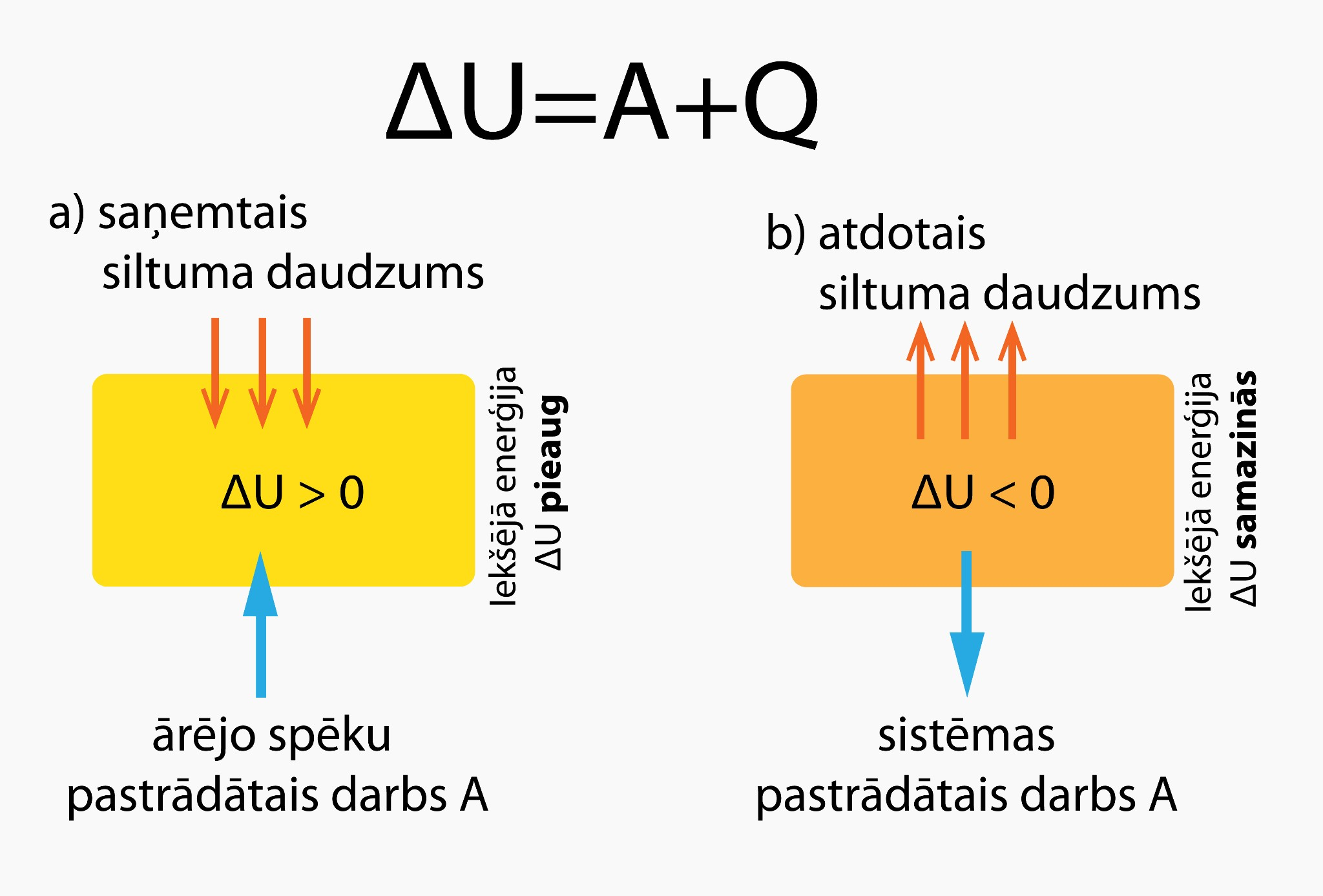
1.att. 1. Termodinamikas likums
Ja sistēma siltuma daudzumu saņem vai apkārtējie spēki pastrādā darbu, tad iekšējā enerģija palielinās (1. att. a), bet, ja sistēma siltuma daudzumu atdod vai pati pastrādā darbu, tad iekšējā enerģija samazinās (1. att b). Piemēram, ja mēs apskatām gaisa balonu (2. att a) un vēlamies tajā esošajai gāzei palielināt iekšējo enerģiju, tad mums ir vai nu jāpastrādā darbs (2. att. b), vai arī jāpievada gaisa balonam siltuma daudzums Q (2. att. c).
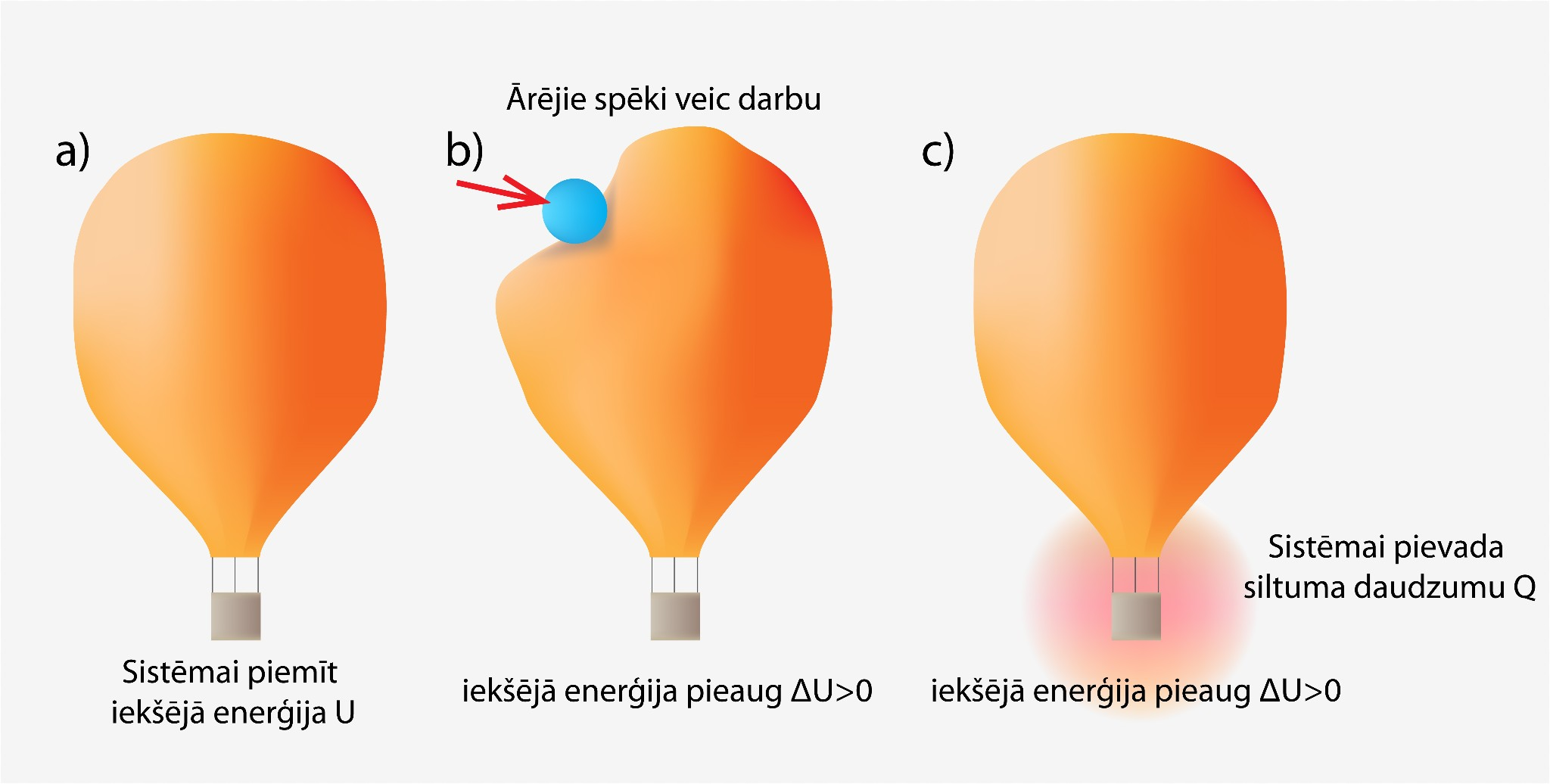
2.att. Sistēmas iekšējo enerģiju var palielināt divos veidos
Ja apskata 1. termodinamikas likumu (TDL) dažādos izoparamteriskos procesos (izobāriskā, izohoriskā, izotermiskā), tad dažos gadījumos šī likuma formula reducējās uz vienkāršāku izteiksmi, jo attiecīgajā izoparametriskajā procesā nav iespējams kāds no iekšējās enerģijas izmaiņas veidiem.
Izobāriskā procesā (3. att. a) 1. TDL ir pilnā formā, jo šajā procesā var mainīties gan gāzes temperatūra, gan tilpums.
Izohoriskā procesā (3. att. b) 1. TDL reducējas uz ∆U = Q, jo sistēma nemaina tilpumu, līdz ar to darbu pastrādāt nav iespējams.
Izotermiska procesa gadījumā (3. att. c) 1. TDL izskatās Q = A. Tas ir tādēļ, ka nemainās gāzes temperatūra, līdz ar to vienīgā iespēja palielināt gāzes iekšējo enerģiju ir pastrādāt darbu.
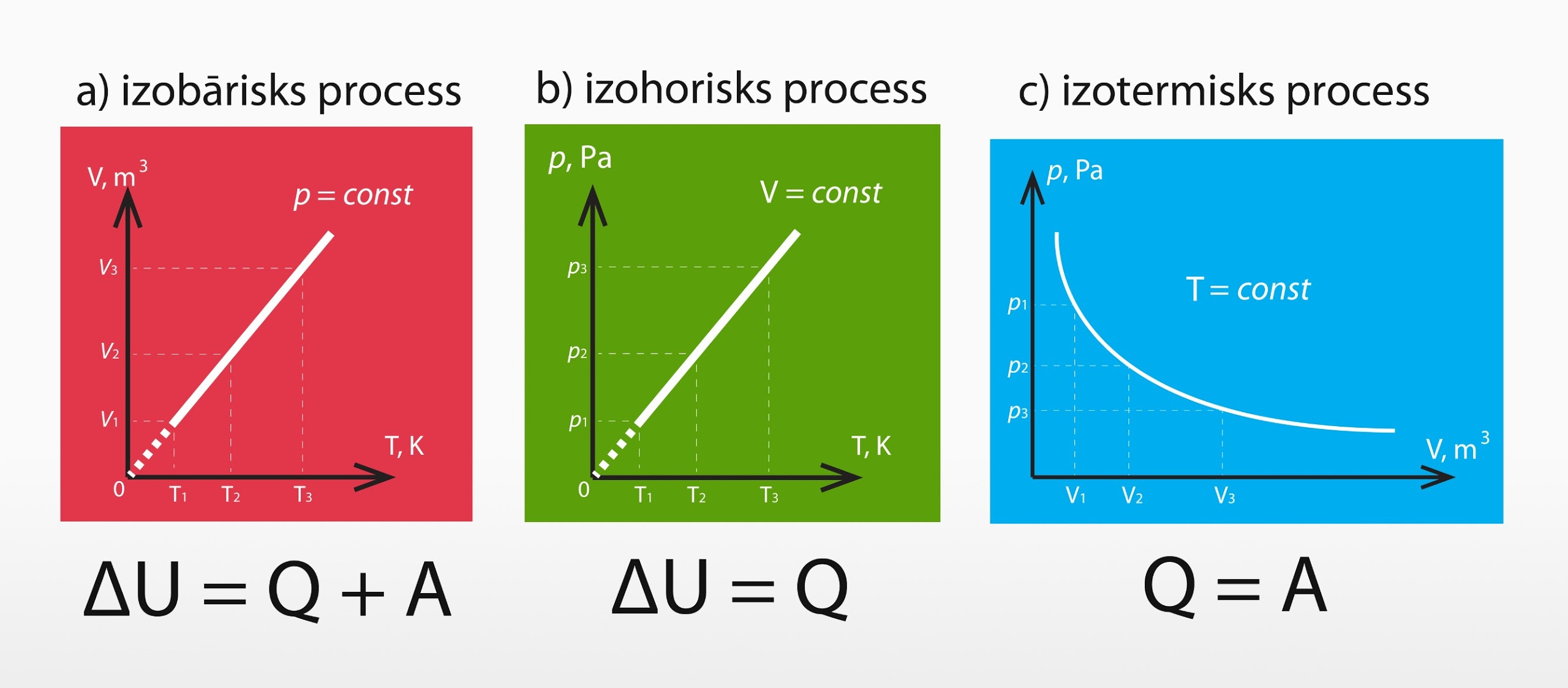
3.att. 1. termodinamikas likums izoparametriskos procesos
Starp dažādiem termodinamiskajiem procesiem izceļ vēl vienu – adiabātisku procesu. Par adiabātisku sauc tādu procesu, kurā nenotiek siltumapmaiņa ar apkārtējo vidi. Atšķirībā no izoparametriskajiem procesiem šajā gadījumā mainās gan temperatūra, gan tilpums, gan arī spiediens. Adiabātiska process grafiskais attēlojums ir līdzīgs izotermiskā procesa attēlojumam (4. att.), atšķirība ir tā, ka, pieaugot tilpumam, adiabātiskā procesā spiediens krīt straujāk.
Tā kā adiabātiskā procesā nenotiek siltuma apmaiņa ar apkārtējo vidi, tad šī procesa laikā sistēmai nevar tikt pievadīts vai aizvadīts siltums, līdz ar to 1. TDL lietojams formā ΔU = A.
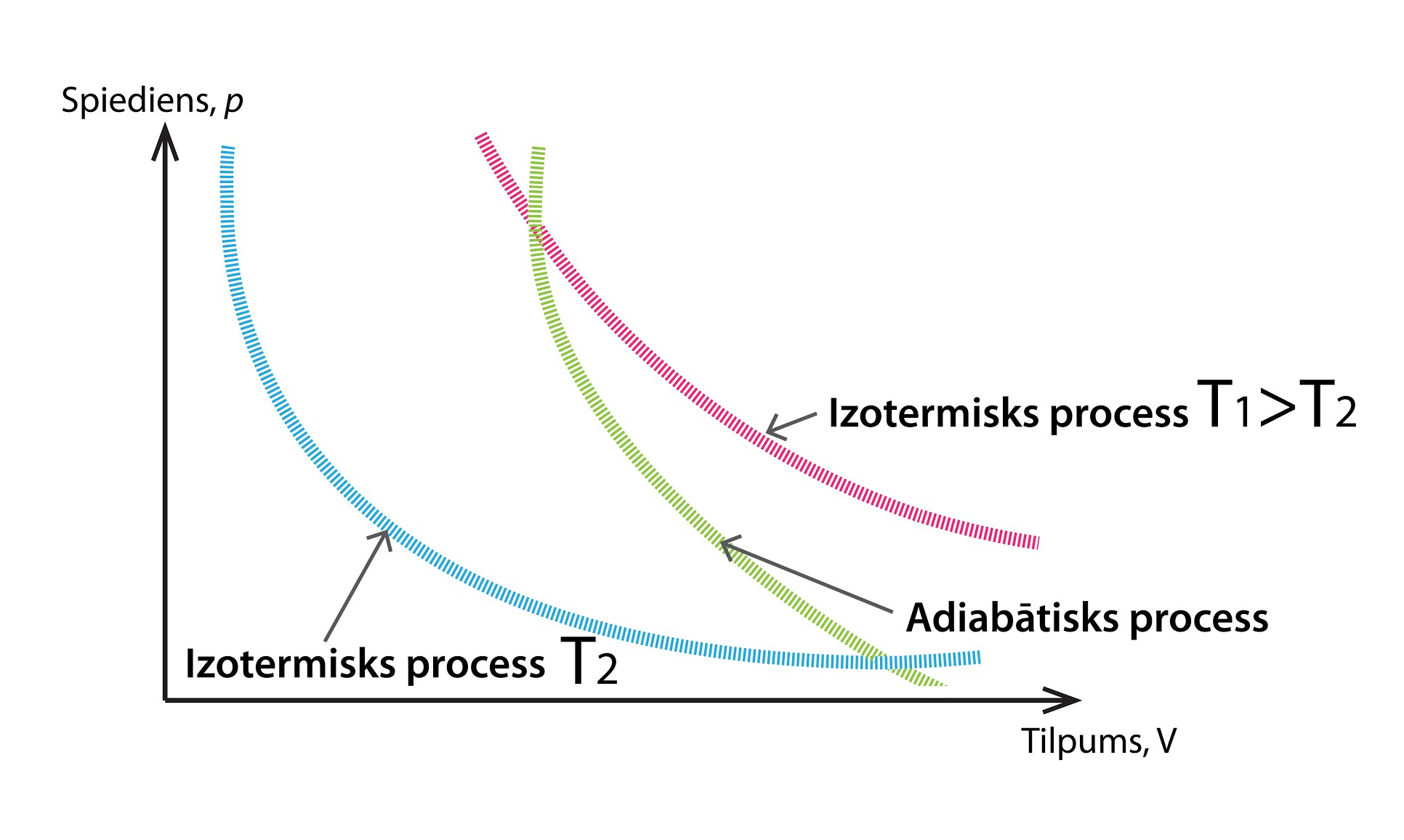
4.att. Adiabātiska procesa grafisks attēlojums
Lai process būtu adiabātisks, tam jānorit ļoti strauji, lai nepaspētu notikt siltumapmaiņa ar ārējo vidi. Šādi procesi ir novērojami, piemēram, dažādos sprādzienos (5. att.), kā arī dažādās tehniskās ierīcēs, piemēram, iekšdedzes dzinējos, pneimatiskajos āmuros un kompresoros.

5.att. Sprādzienos gāzes izplatās adiabātiski
Ideāla gāze siltumu var gan uzņemt, gan atdot. Darbu attiecībā uz gāzi var veikt ārējie spēki vai arī darbu var veikt pati gāze. Minētie faktori palielina vai samazina gāzes iekšējo enerģiju, tādēļ, rēķinot iekšējās enerģijas izmaiņu, ir svarīgi zināt, vai dotais process iekšējo enerģiju palielina vai samazina. Piemēram, apskatīsim izobārisku procesu (1. att.).
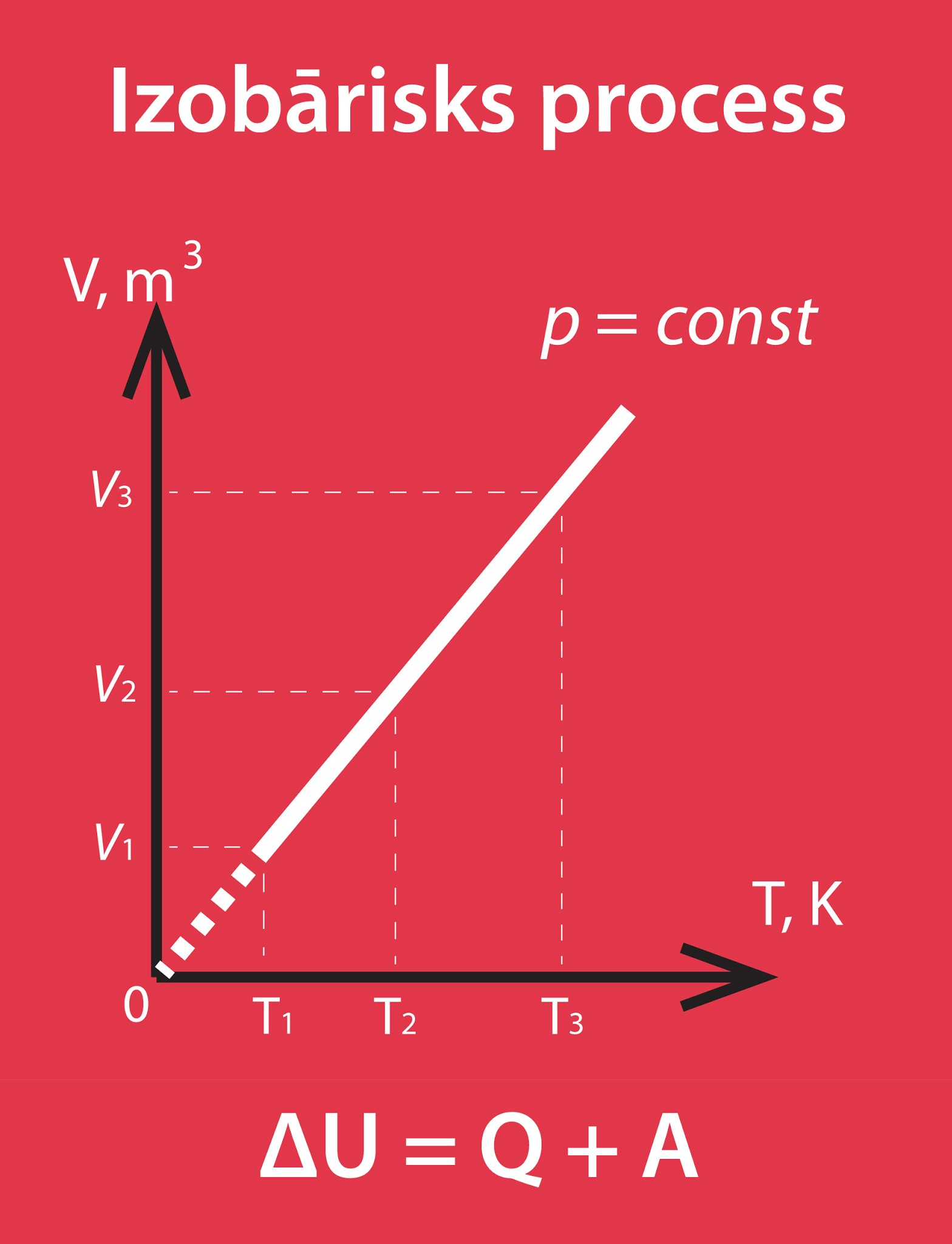
1.att. Izobārisks process
Ja ārējie spēki veic darbu A, tad gāzes iekšējā enerģija uz šī rēķina pieaug. Ja no ārpuses vēl papildus tiek pievadīta enerģija Q, tad arī notiek ieguldījums gāzes iekšējā enerģijā. Tādēļ, ja darbu veic ārējie spēki un vienlaikus no ārpuses tiek pievadīta enerģija (2. att. a), tad gāzes iekšējā enerģija pieaug abu šo faktoru dēļ, un var rakstīt ΔU = Q + A. Pretējs gadījums ir tad, ja gāze pati veic darbu A un atdod apkārtējai videi siltuma daudzumu Q, tad šie abi lielumi samazina gāzes iekšēja enerģiju un līdz ar to gāzes iekšējās enerģijas pieaugums ir ΔU = -Q-A (2. att. b). Redzams, ka šis pieaugums būs negatīvs jeb gāzes iekšējā enerģija samazināsies.
_1.png)
2.att. Iespējamie procesi izobāriskā procesā ideālā gāzē
Izobāriskā procesā var būt arī situācijas, kas ir pa vidu abām iepriekš minētajām. Ja gāzei no ārpuses tiek pievadīts siltuma daudzums Q, bet gāze tajā pašā laikā veic darbu A (3. att. a), tad pievadītais siltuma daudzums gāzes iekšējo enerģiju palielina, bet gāzes veiktais darbs samazina, tādēļ jāraksta ΔU = Q - A. Var būt arī otrādi, proti, ārējie spēki attiecībā pret gāzi veic darbuA, bet gāze apkārtējai videi atdod siltuma daudzumu Q (3. att. b), tad iekšējās enerģijas izmaiņas izteiksme izskatās ΔU = A - Q.
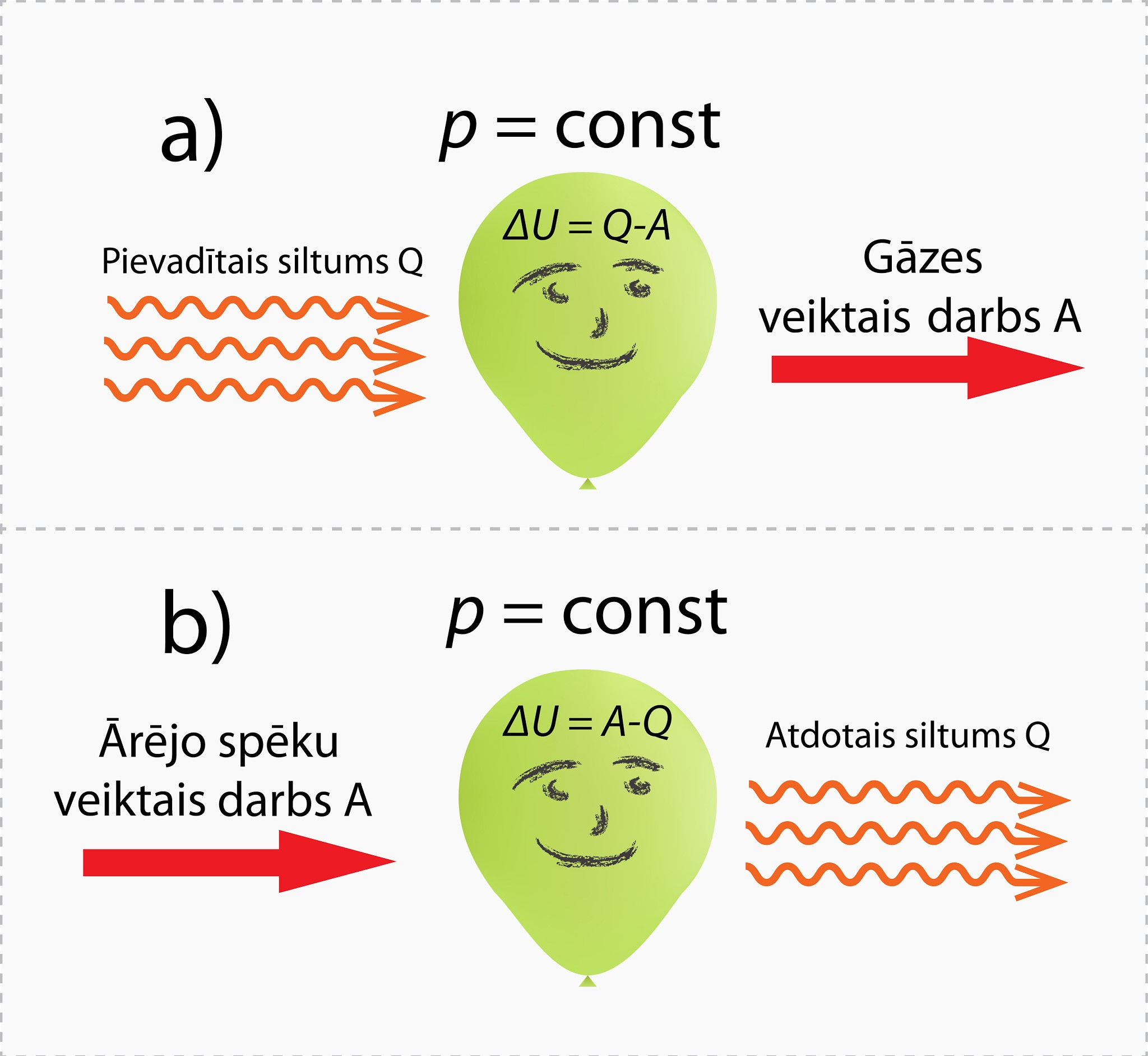
3.att. Ideālas gāzes iekšējās enerģijas izmaiņa izobāriskā procesā
Izohoriskā procesā (nemainās tilpums) situācija ir nedaudz vieglāka, jo šajā gadījumā nemainās sistēmas tilpums (4. att.), līdz ar to ne ārējie spēki, ne pati gāze darbu nevar pastrādāt.
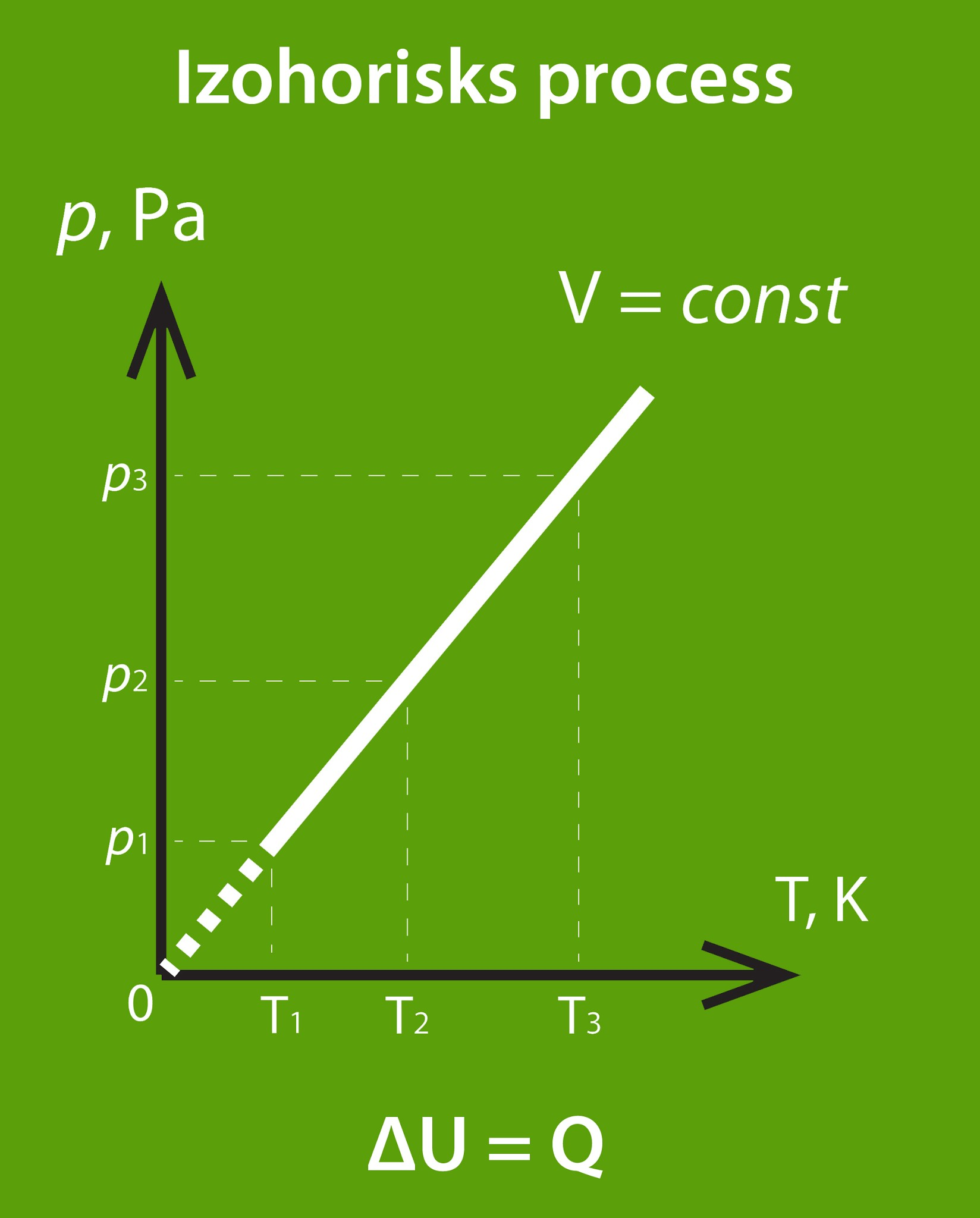
4.att. Izohorisks process
Gadījumā, ja siltuma daudzums Q tiek pievadīts no ārpuses (5. att. a), gāzes iekšējā enerģija pieaug jeb ΔU = Q, bet, ja gāze siltuma daudzumu Q atdod apkārtējai videi (5. att. b), tad iekšējā enerģija samazinās, proti, ΔU = -Q.
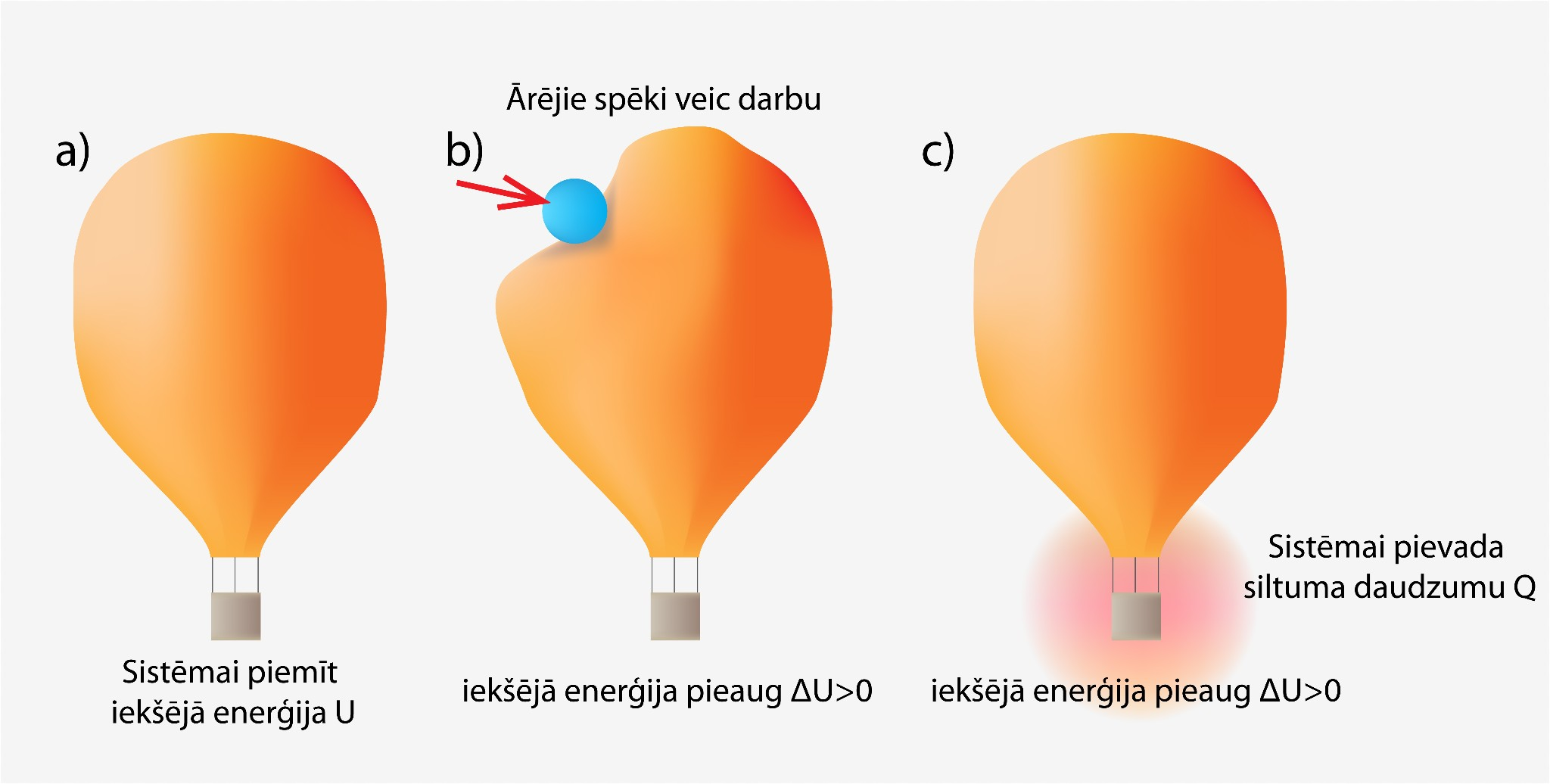
5.att. .Ideālas gāzes iekšējās enerģijas izmaiņa izohoriskā procesā
Ar izohoriska procesa sekām ir jārēķinās, ja saulē ir atstāts kāds noslēgts tukšs trauks, piemēram, tukša metāla muca (6. att.). Saule mucā esošajam gaisam pievada siltuma daudzumu Q, kas palielina tā iekšējo enerģiju (5. att. a). Gaisam pieaug temperatūra un spiediens, līdz kādā brīdī muca padodas spiedienam un nedaudz deformējas. Šādas deformācijas siltās un saulainās dienās var sadzirdēt kā dobju skaņu, kas rodas no metāla konteineriem, piemēram, mucām.

6.att. Metāla mucas var deformēties, ja tās atstāj saulē
Atšķirībā no izobāriska un izohoriska procesa izotermiskā procesā (7. att.) nepieaug sistēmas iekšējā enerģija, jo temperatūra paliek konstanta.
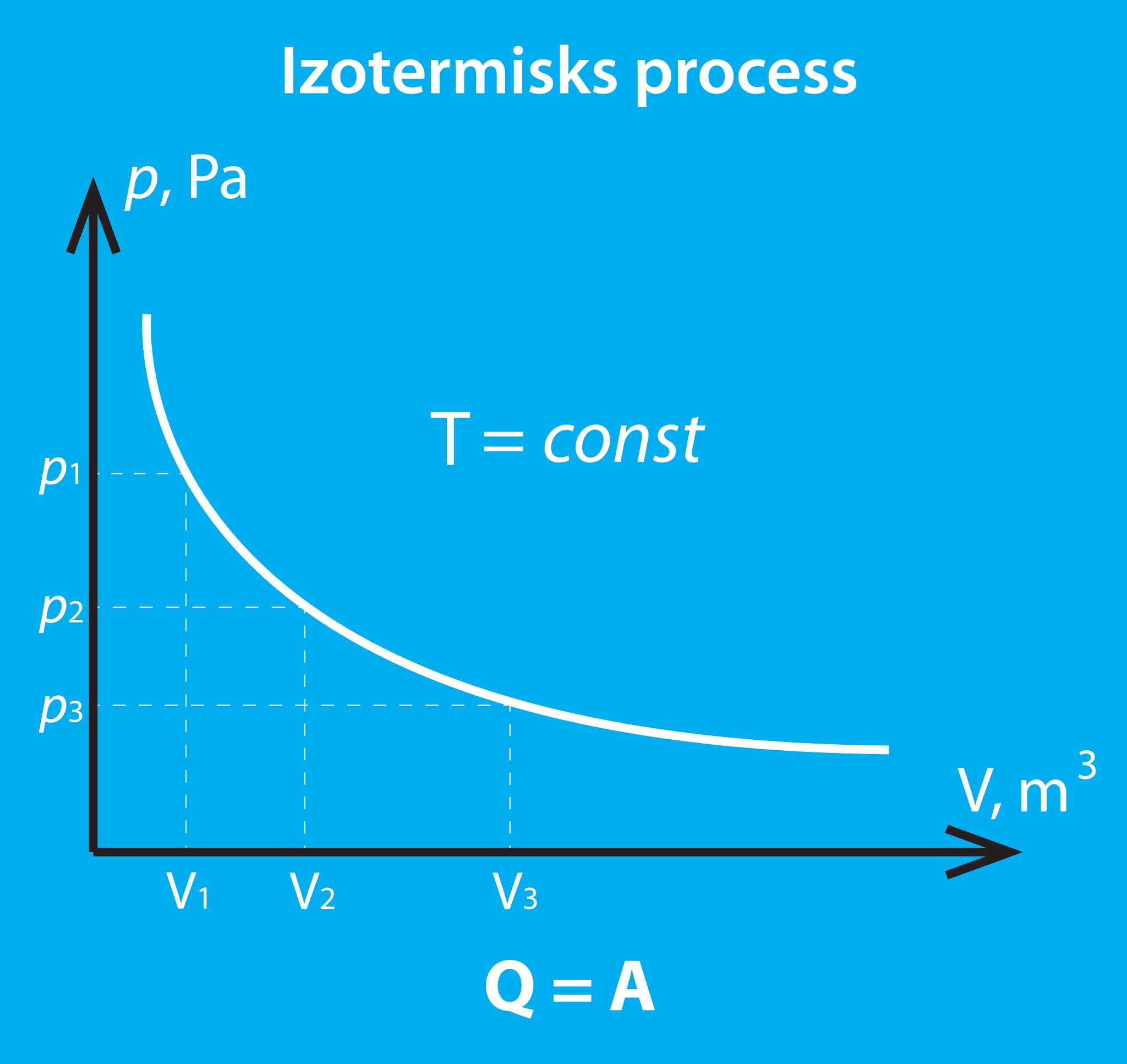
7.att. Izotermisks process
Tādēļ, piemēram, ja gāzei no ārpuses tiek pievadīts siltuma daudzums Q, tad tai ir jāpastrādā tāda paša lieluma darbs A, lai iekšējā enerģija nepieaugtu, līdz ar to Q = A (8. att. a), bet var gadīties, ka ārējie spēki pastrādā darbu A, tad gāzei iegūtā enerģija ir jāatdod kā siltuma daudzums Q apkārtējai videi (8. att. b), un atkal Q = A.
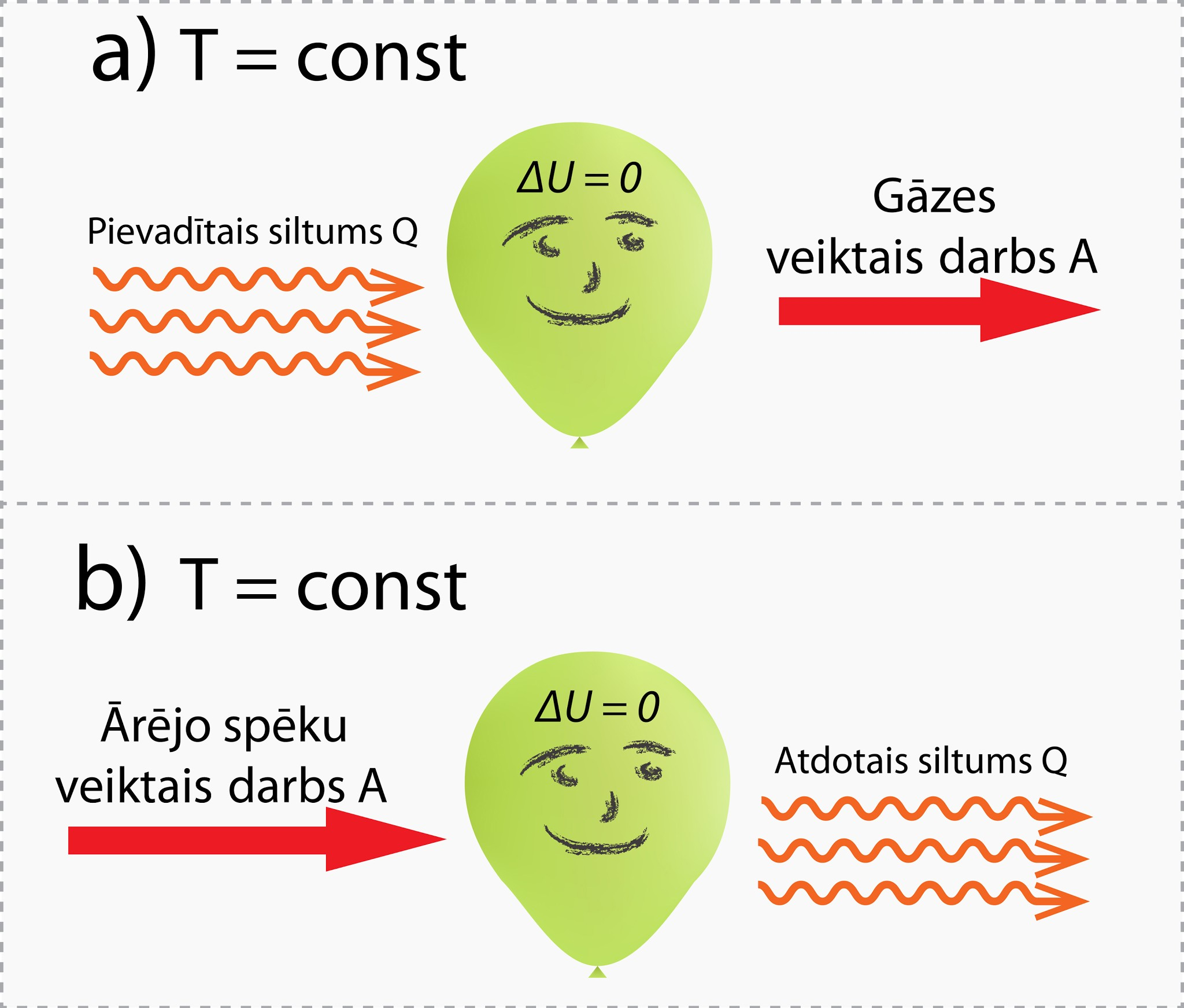
8.att. .Ideālas gāzes uzvedība izotermiskā procesā
Adiabātiskam procesam ir raksturīgs tas, ka nenotiek siltuma apmaiņa ar apkārtējo vidi (9. att), līdz ar to, ja ārējie spēki pastrādā darbu A (9. att. a), tad iekšējā enerģija pieaug par šo lielumu jeb ΔU = A, savukārt, ja gāze paveic darbu A (9. att. b), tad iekšējā enerģija par tādu lielumu samazinās: ΔU = -A.
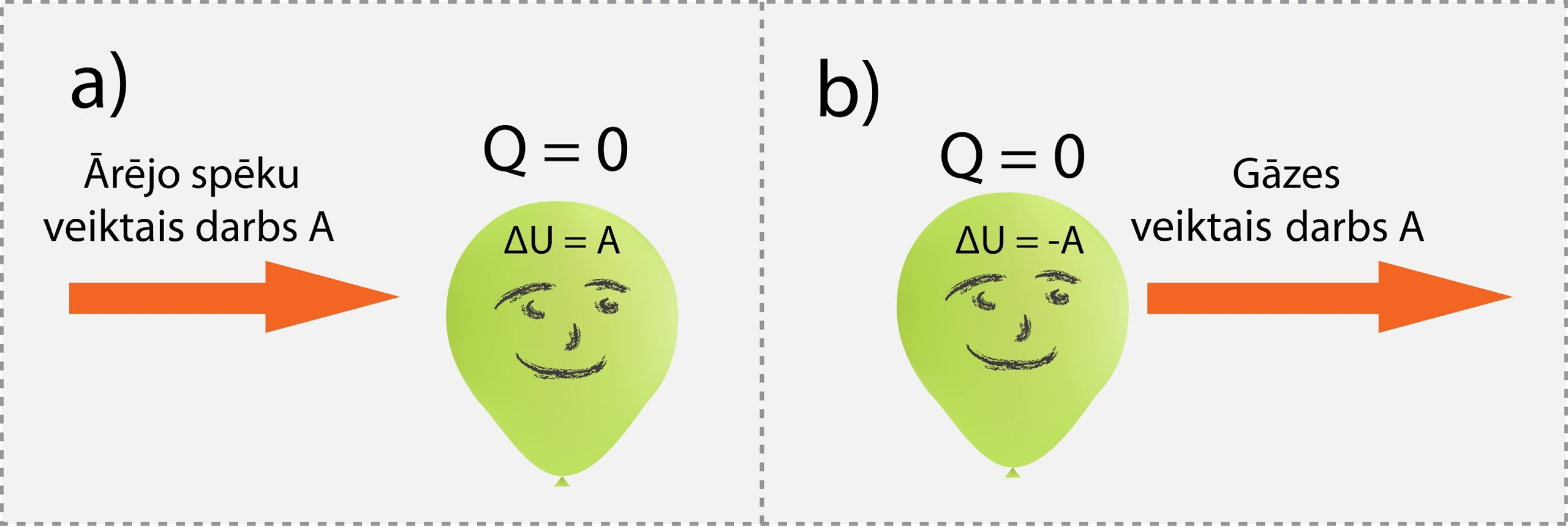
9.att. Ideālas gāzes iekšējās enerģijas izmaiņa adiabātiskā procesā
Ar adiabātisku procesu var saskarties automašīnu dzinējs (10. att.). Tur, saspiestai gāzei strauji uzliesmojot, tā strauji izplešas un padara darba, tādējādi nodrošinot motora darbību.
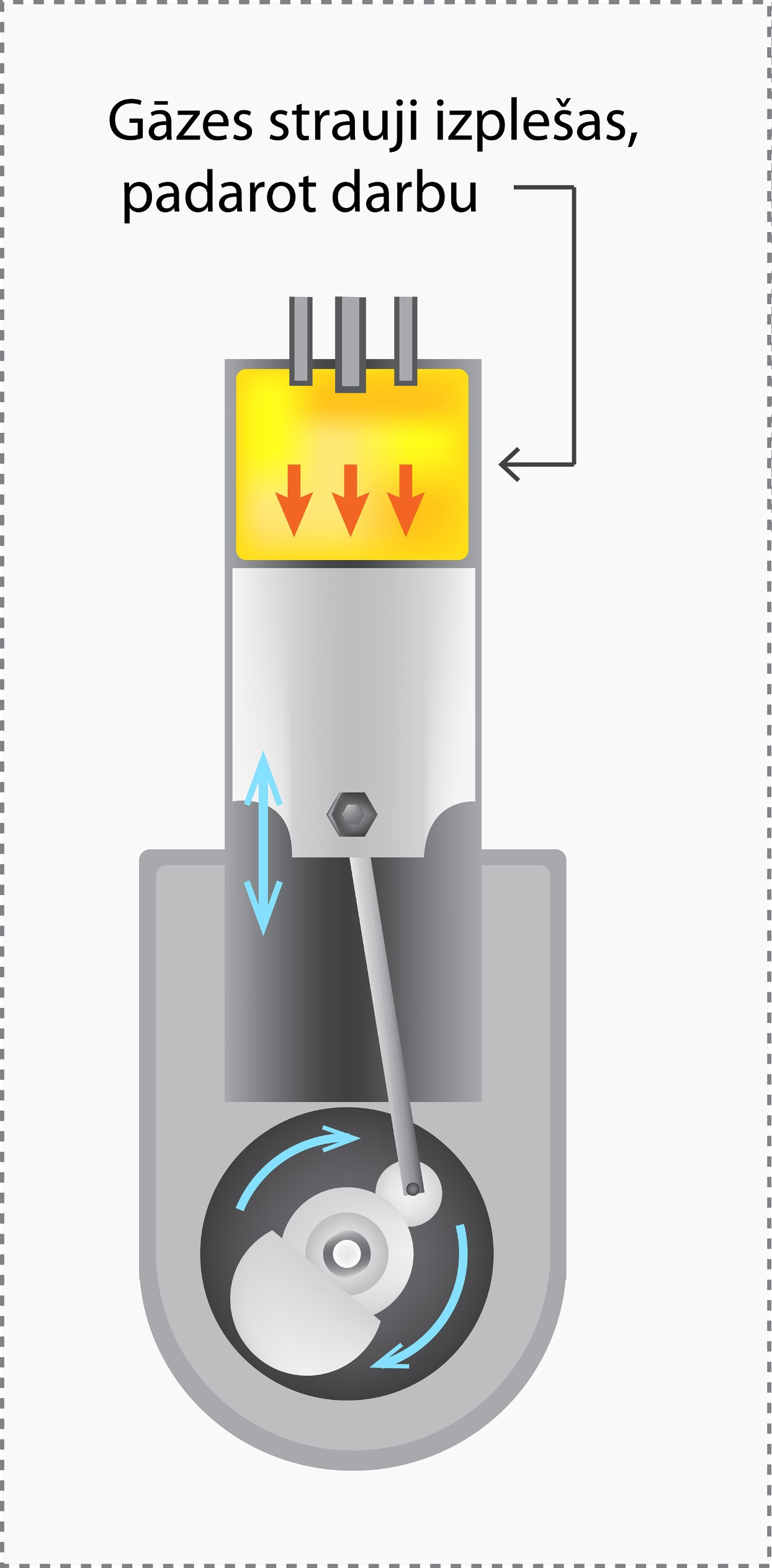
10.att. Adiabātisks process automašīnu dzinējos
Kā jau minēts 1. solī, adiabātiska procesa grafiskais attēlojums (1. att.) ir līdzīgs izotermiska procesa grafikam. Ja izotermiskam procesam nemainīgs ir spiediena un tilpuma reizinājums pV = const, tad adiabātiskā procesa atšķirība ir tā, ka tilpumam ir papildu pakāpes rādītājs k, ko nosaka gāzes siltumietilpību attiecība konstantā spiedienā un konstantā temperatūrā. Adiabātiskā procesā pVk = const.
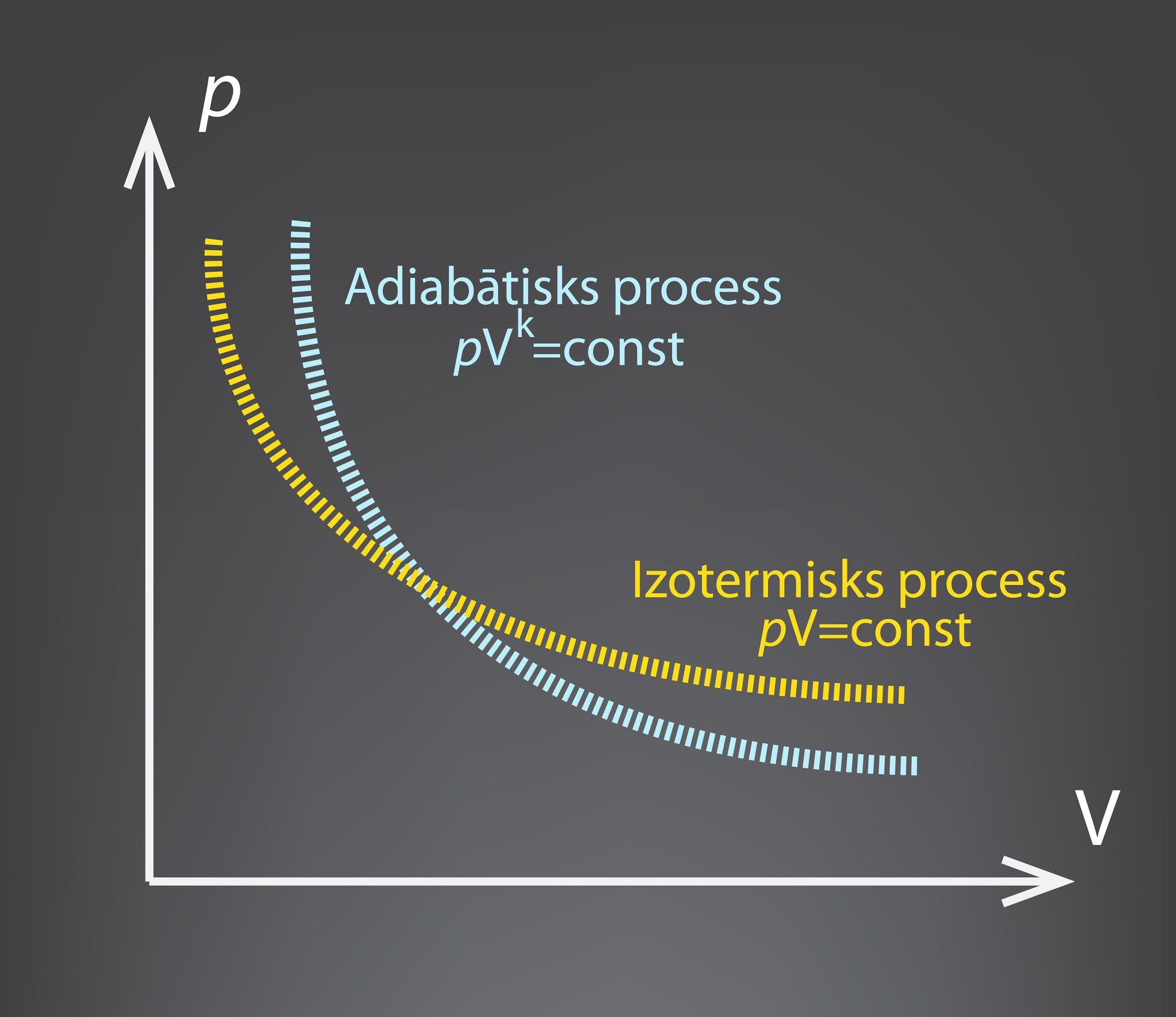
1.att. Adiabātiska un izotermiska procesa grafisks attēlojums
Bez minētajiem adiabātiska procesa piemēriem dažādos sprādzienos un eksplozijās, tai skaitā degmaisījuma eksplozijās, kas norit iekšdedzes dzinējos, adiabātiska gāzes saspiešana un izplešanās sastopama arī daudz vienkāršākos procesos. Piemēram, ja pumpējam automašīnas riepu, tad pumpēšanas procesā mēs veicam regulāru adiabātisku gaisa saspiešanu, pēc kuras tas ieplūst automašīnas riepā (2. att.).

2.att. Automašīnas riepas pumpēšana
Adiabātiski procesi novērojami arī dabā, piemēram, gubu mākoņu (3. att) veidošanās pamatā ir gāzu adiabātiska izplešanās. Konvekcijas rezultātā siltās gaisa masas paceļas augšup un, adiabātiski izplešoties, atdziest. Rezultātā notiek ūdens tvaika kondensācija un veidojas gubu mākoņi.

3.att. Gubu mākoņi
Adiabātiski procesi ir iesaistīti arī skaņas izplatīšanās procesā. Skaņa gaisā pārvietojas kā periodiski gaisa sablīvējumi un retinājumi, kuros ir atšķirīgs gāzes spiediens. Tā kā apkārtējais gaiss nesasilst skaņas viļņu ietekmē, tad var secināt, ka skaņas viļņu izraisītās gaisa spiediena maiņas notiek adiabātiski, bez siltumapmaiņas ar apkārtējo vidi.
vilnis_gaze_1.png)
4.att. Skaņa izplatās, gaisam adiabātiski izplešoties un saraujoties