Ikdienā cilvēkam ir pieradums par skaņu saukt ko tādu, kas ir sadzirdams, tomēr fizikā uz šo lūkojas plašāk un par par skaņu vai skaņu viļņiem sauc elastības spēku ietekmē radušos svārstību izplatīšanos apkārtējā vidē, līdz ar to skaņu viļņi var būt gan viļņi, kas pārvietojas pa gaisu un atļauj mums noklausīties rīta ziņas, kā arī viļņi, kas izplatās tramvaja sliedēs (1.att.).
1. att. Skaņas viļņi dažādās situācijās
Skaņas viļņi ir mehāniskas vides svārstības jeb mehāniskie vilņi un kā jau jebkuras svārstības, arī skaņu raksturo noteiktas frekvences. Pēc šīm frekvencēm skaņas var iedalīt dažādos veidos (2. att.) Piemēram, cilvēka dzirdes orgāni uztver frekvences diapazonā no 16 Hz līdz 20 kHz, tādēļ tās sauc par dzirdamajām skaņam. Skaņas ar zemāku frekvenci sauc par infraskaņām. Tās neizraisa dzirdes sajūtu, toties tās var sajust kā vibrācijas un tās var izraisīt baiļu sajūtu. Ja skaņas frekvence pārsniedz augšējo dzirdamības robežu, tad tās ir vai nu ultraskaņas vai hiperskaņas (2. att.). Pārbaudi kā skan dažādu frekvenču skaņas.
2. att. Skaņas viļņu iedalījums pēc frekvencēm un atbilstošie piemēri
Skaņu raksturo tās izplatīšanās ātrums v, kas ir atkarīgs no vides elastības un inertuma, bet gadījumā, ja skaņas vilnis izplatās gaisā, nav atkarīgs no skaņas frekvences. Gāzēs un šķidrumos skaņa izplatās kā garenvilnis (3. att.). Gāzēs un šķidrumos nenotiek elastīgas bīdes deformācijas. Tas nozīmē, ka starp dažādiem šķidruma un gazes slāņiem nerodas pietiekoši lieli spēki, lai svārstību kustībā viens kustīgs gāzes vai šķidruma slānis “parautu” līdzi citu. Skaņas ātrums gāzēs ir galvenokārt atkarīgs no temperatūras. Ja ir zināma gāzes temperatūra, tad aptuveni skaņas ātrumu var atrast pēc izteiksmes v≈331,4 + 0,6t, kur t ir gāzes temperatūra, kas izteikta Celsija grādos. Skaņas ātrumu šķidrumos var aprēķināt pēc izteiksmes \(v= { \sqrt{k \overρ}}\) , kur k ir šķidruma saspiežamības koeficients, bet ρ - šķidruma blīvums (kg/m3).
3. att. Skaņas viļņi gāzē un šķidrumā
4. attēlā parādītās skaņas ātruma vērtības dažādās vidēs.
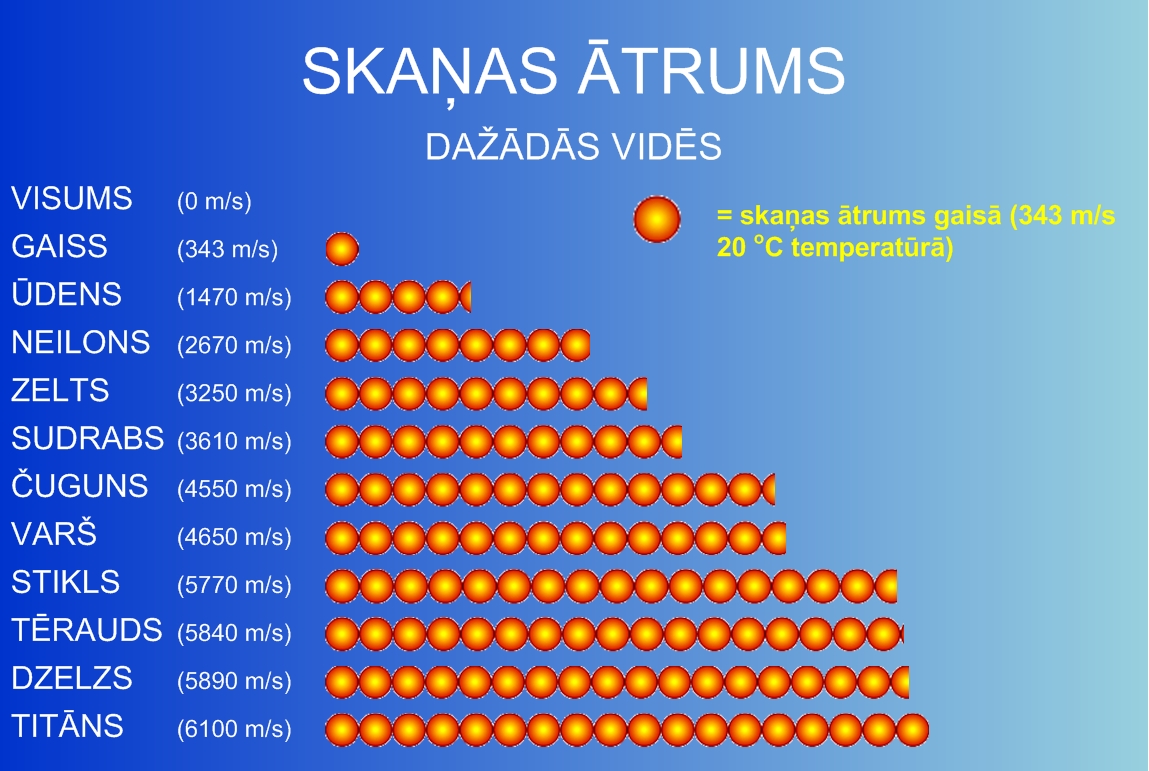
4. att. Skaņas ātruma vērtībā dažādās vidēs
Atšķirībā no šķidruma un gāzes, cietvielā skaņas viļņi var izplatīties gan kā šķērsviļņi, gan kā garenviļņi (1. att.). Šķērsviļņa ātrumu v cietvielā nosaka stiepes-spiedes elastības modulis E un cietvielas blīvums ρ , gala rezultātā \(v= { \sqrt{E \overρ}}\) . Savukārt garenviļņa pārvietošanās ātrumu cietvielā izsaka formula \(v= { \sqrt{G \overρ}}\), kur G - bīdes elastības modulis.
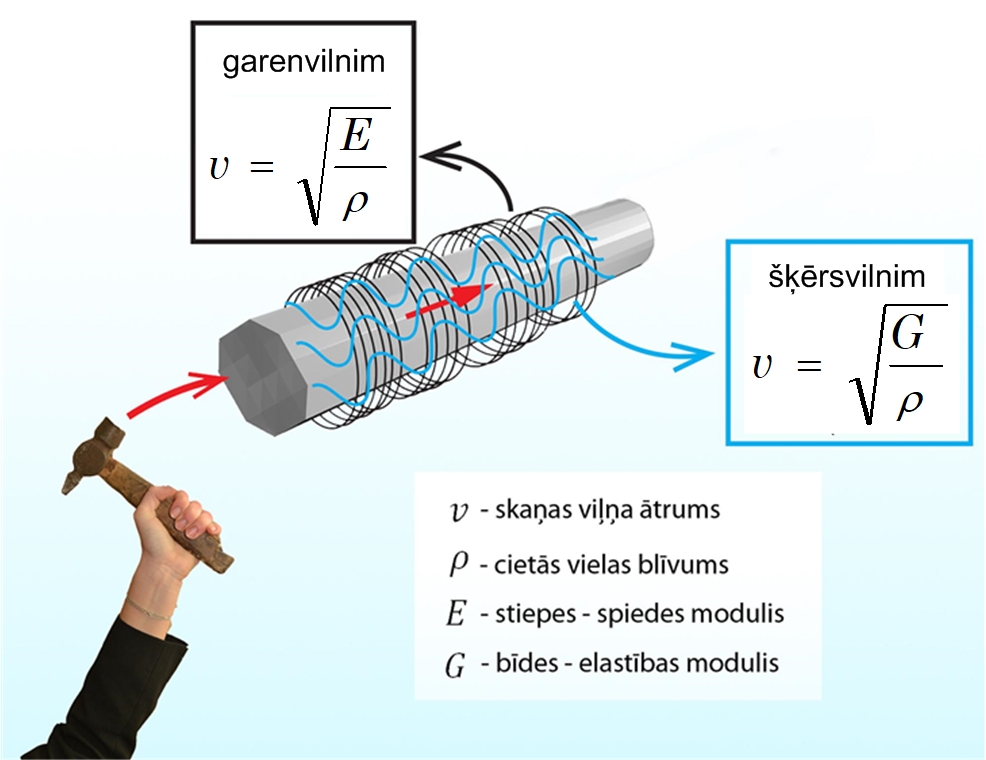
1. att. Skaņas izplatīšanās cietās vielās
Skaņas viļņi var izraisīt logu rūšu trīcēšanu un pat saplīšanu, kā arī citi objekti, piemēram, galds nav pasargāts no trīcēšanas skaļas mūzikas ietekmē. No tā var secināt, ka skaņas viļņiem piemīt arī enerģija. Ja apskata kādu laukumu S, kas atrodas perpendikulāri skaņas izplatīšanās virzienam (2. att.), tad laika momentā t caur šo laukumu izplūst skaņas enerģija E. Tomēr šo enerģijas plūsmu caur virsmu ir praktiski grūti izmērīt. Tādēļ praksē visbiežāk, lai varētu noteikt skaņas ietekmi uz cilvēkiem un apkārtējo vidi, tiek mērīts skaņas spiediens, ko rada skaņa ar spēku F iedarbojoties uz laukumu S (2. att. a).
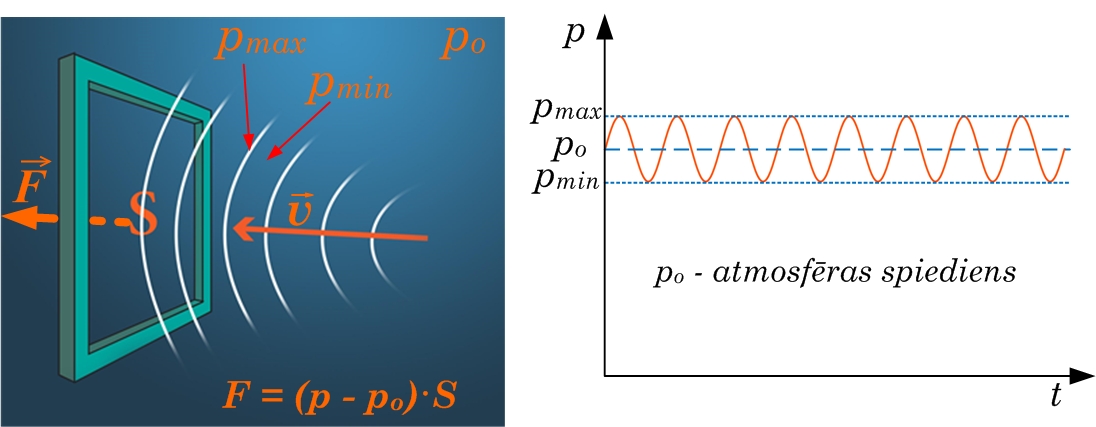
2. att. Skaņas iedarbība uz laukumu S
Mazākā skaņas spiediena vērtības, kas cilvēkam izraisa dzirdes sajūtu, ir aptuveni p0=20·10-6 Pa, savukārt, ja skaņas spiediens pārsniedz 20 Pa, tad cilvēkam rodas sāpju sajūta. Lai būtu ērtāk lietot un vieglāk saprast, cik tad liela ir skaņas spiediens, tiek ieviests skaņas spiediena līmenis L, ko aprēķinā pēc izteiksmes L=20·lg(p/p0), kur p ir skaņas spiediens, bet p0=20·10-6 Pa ir mazākais skaņas spiediens, kas izraisa dzirdes sajūtu. Skaņas intensitātes līmeni mēra decibelos (dB). Šajā skalā cilvēkam uztveramās skaņas ir robežās no 0 dB (pilnīgs klusums) līdz pat 130 dB (sāpju slieksnis). Dažādu skaņu spiedienu līmeņi atrodami 3. attēlā.

3. att. Piemēri dažādām skaņas intensitātes vērtībām
Cilvēka dzirdes orgāni skaņas uzver subjektīvi, līdz ar to ir daudzi faktori, kas ietekmē to, cik skaļi mēs skaņu dzirdam, frekvence ir viens no šie lielumiem. 4. attēlā redzams, ka, lai dzirdētu vienādi skaļi dažādu frekvenču skaņas, tad skaņas intensitātes līmeni var nākties vai nu palielināt, vai samazināt. Cilvēku dzirdes orgāns visjutīgākāk uztver skaņas frekvenču diapazonā no 3000 - 4000 Hz.
4. att. Grafiks cilvēka subjektīvās dzirdes rakstura attēlošanai
Vēl viena viļņiem raksturīga parādība ir stāvviļņa veidošanās. Stāvvilnis veidojās, ja vilnis savā kustībā saskaras ar kādu šķērsli un atstarojas no tā. Stāvviļņa svārstības nosaka krītošā un atstarotā viļņa svārstību summa (1. att.). Stāvviļņa punktus, kuros nenotiek vides daļiņu svārstības, sauc par mezglu punktiem, savukār tie punkti, kas svārstās ar maksimālo amplitūdu, ir blīzuma punkti (1. att.)
1. att. Stāvvilņa veidošanās
Mūzikas instrumentu spēlēšana balstās uz to, ka tajos veidojas stāvviļņi. Kā piemēru aplūkosim kāda mūzikas instrumenta stīgu. Stīgas garums ir L un tā ir nostiprināta abos galos (2. att. a), līdz ar to tai ir vismaz divi mezglu punkti. Starp šiem diviem mezglu punktiem var novietoties vismaz viens blīzuma punkts (2. att. b), kurā stīgas svārstību amplitūda ir maksimālā. Šādā gadījumā stīgas stāvviļņa garums λ0=2L (2. att. b), jo visā stīgas garumā ietilpst viens pusviļņa garums. Šis stāvvilnis ir ar lielāko iespējamo vilņu garumu, kas šajā stīgā ir iespējamas, tādēļ tās sauc par pamattoņa svārstībām. Stīgā var novietoties ne tikai viens pusviļņa garums, bet arī divi (2. att. c), trīs (2. att. d) un vairāk. Šādas svārstības sauc par pirmā virstoņa svārstībām, otrā virstoņa svārstībām utt. Stīgas skanējumu veido gan pamattoņa svārstības, gan virstoņa svārstības kopā.
2. att. Stāvviļņi stīgā
Ja pamattoni un virstoņus apskata frekvenču skalā (3. att.), tad pamattonis ir tonis ar viszemāko frekvenci, ko rada akustiskā sistēma. Tālāk frekvenču skalā atrodami dažādas kārtas virstoņi, turklāt, attālums frekvenču skalā starp dažādiem virstoņiem ir viens un tas pats, kas nozīmē to, ko stīgas blakus esošo virstoņu frekvences atšķiras par vienu un to pašu lielumu.
3. att. Pamattoņa un virstoņu attēlojums frekvenču skalā
Pušamajos instrumentos (4. att. a) nav stīgas, kas varētu svārstīties. Šajos mūzikas instrumentos tiek ierosināti plūstošā gaisa stāvviļņi, kuru viļņu garums, līdzīgi kā stīgām, ir atkarīgs no caurules garuma, kuram cauri gaiss plūst (4. att. b). Arī šajā gadījumā pamattoņa svārstības atbilst viļņa garumam 2L, kur L ir caurules garums, bet katram nākošajam virstonim nāk klāt viens pusviļņa garums.
4. att. Gaisa stāvviļņi, kas veidojas pūšamajos instrumentos