Visbiežāk dabā sastopamās kustības ir nevis taisnlīnijas, bet gan līklīnijas. Piemēram, 1. attēlā, apskatot punkta kustību uz ielu vingrotāja kājas, var redzēt, ka faktiski nevienā trajektorijas daļā taisnlīnijas kustība nav sastopama.

1.att. Ielu vingrotāja kreisās kurpes kustības trajektorija
Viens no līklīnijas kustību veidiem ir kustība pa riņķa līniju jeb rotācija. Ar to var iepazīties arī DZM materiālā.
Rotāciju raksturo periods T, kas parāda, cik ilgā laikā ķermenis veic vienu pilnu apgriezienu. Pulksteņa minūšu un stundu rādītājs piedalās rotācijas kustībā, un to periodi ir attiecīgi viena stunda un 12 stundas (2. att.). Periodam ir laika mērvienība. Periodam T apgrieztais lielums (apgrieztais lielums nozīmē, ka f = 1 : T) ir rotācijas frekvence f, kas parāda, cik pilnus apgriezienus ķermenis veic vienā laika vienībā. Ja laika vienība ir sekunde, tad frekvenci mēra hercos (Hz). Frekvence un periods ir savstarpēji apgriezti lielumi, tādēļ f = 1 : T un T = 1 : f (2. att.). Aprēķinot stundu un minūšu rādītāja rotācijas frekvenci, iegūst aptuveni 0,000023 Hz un 0,00028 Hz (2. att.).

2.att. Pulksteņa rādītāju rotācijas kustība
Periodu un frekvenci var aprēķināt, ja ir zināms apriņķojumu skaits N un laiks, cik ilgi notikusi kustība t (3. att.). Piemēram, 3. attēlā redzams, ka automašīnas tahometrs rāda 1500 apgriezienus minūtē. Tas nozīmē: ja mēs motoru darbinām vienu minūti jeb 60 sekundes, tad kloķvārpsta ir veikusi N = 1500 apgriezienus. Periodu aprēķina T = t : N. Šajā gadījumā T = 60 : 1500 = 0,04 s. Frekvencei ir apgriezta formula f = N : t. 3. attēla gadījumā f = 1500 : 60 = 25 Hz.

3.att. Perioda un frekvences saistība ar apriņķojumu skaitu un laiku
Rotācijas piemērs ir ielu vingrotājs, kas riņķo ap savu asi. Ja apskata viena punkta kustību uz viņa izstiepās rokas plaukstas (4. att.), tad redzam, ka šajā gadījumā notiek rotācijas kustība. Attiecīgais punkts ir pakļauts gan lineārajam ātrumam, gan paātrinājumam.
Lineārais ātrums ir ātrums, ar kādu ķermenis kustas pa riņķa līnijas aploci. Zinot riņķa līnijas rādiusu R un apriņķošanas periodu T, to var aprēķināt, izmantojot formulu v = 2πR : T. Lai gan lineārais ātrums ir nemainīgs, tomēr ātruma vektora virziens visu laiku mainās (4. att.). Šo izmaiņu raksturo centrtieces paātrinājums ac. Šis paātrinājums ir atkarīgs no lineārā ātruma v un riņķa līnijas rādiusa R, rezultātā ac = v2 : R. Līklīnijas kustībai ātruma vektors katrā trajektorijas punktā ir vērsts pa pieskari, kas novilkta attiecīgajā punktā, bet centrtieces paātrinājums katrā punktā ir vērsts uz rotācijas centru (4. att.). Lineārā ātruma un centrtieces paātrinājuma vektori ir perpendikulāri.
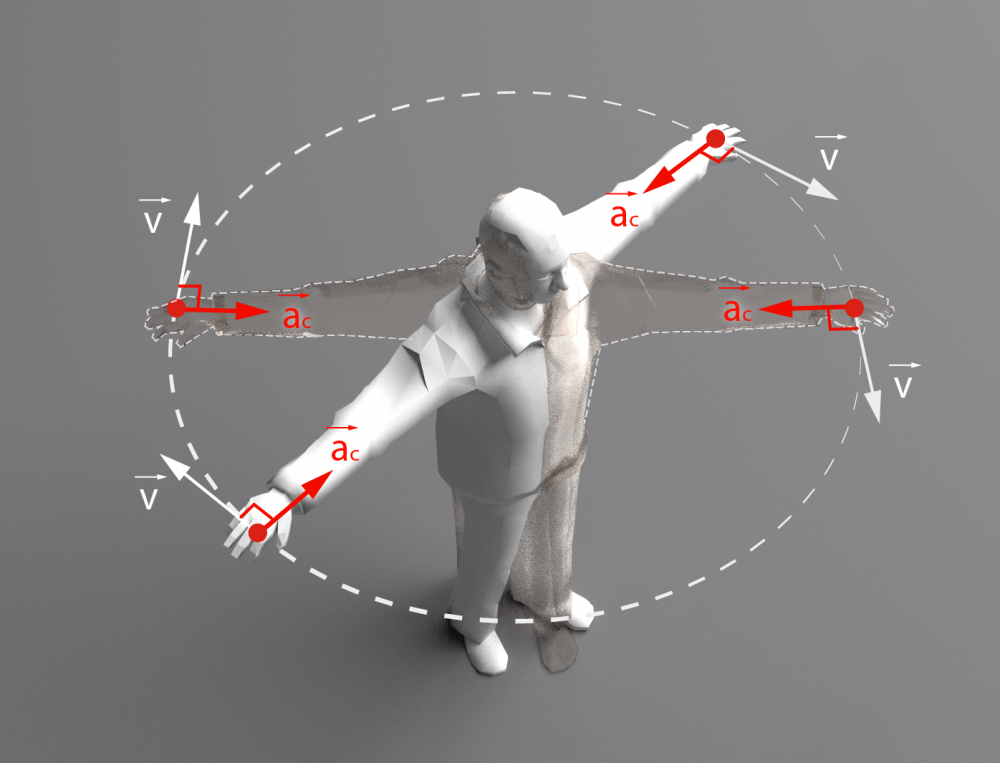
4.att. Lineārais ātrums un centrtieces paātrinājums
Tāpat kā taisnlīnijas kustība, arī kustība pa riņķa līniju var būt vienmērīga un nevienmērīga. Ja ātruma modulis kustībā pa riņķa līniju nemainās, tad to sauc par vienmērīgu kustību pa riņķa līniju, ja mainās, tad par nevienmērīgu kustību pa riņķa līniju. Lineārais ātrums nav vienīgais ātrums, kas raksturo ķermeņa rotācijas kustību. To raksturo arī leņķiskais ātrums, kas parāda, cik ātri ķermenis maina savu pagrieziena leņķi φ. 5. attēlā redzams, kā pagriežas trīs punkti uz ielu vingrotāja rokas. Katrs punkts vienā un tajā pašā laikā ir nogājis atšķirīgus attālumus, līdz ar to lineārais ātrums tiem būs atšķirīgs, bet visi punkti ir nogājuši vienādu leņķi φ. Tātad to leņķiskais ātrums ω, ko aprēķina ω = φ : t, ir visiem punktiem vienāds. Leņķisko ātrumu mēra grādi/s vai rad/s. Centrtieces paātrinājumu ac, lineāro ātrumu v un leņķisko ātrumu ω saista šāda sakarība: ac = v2 : R = ω2R.
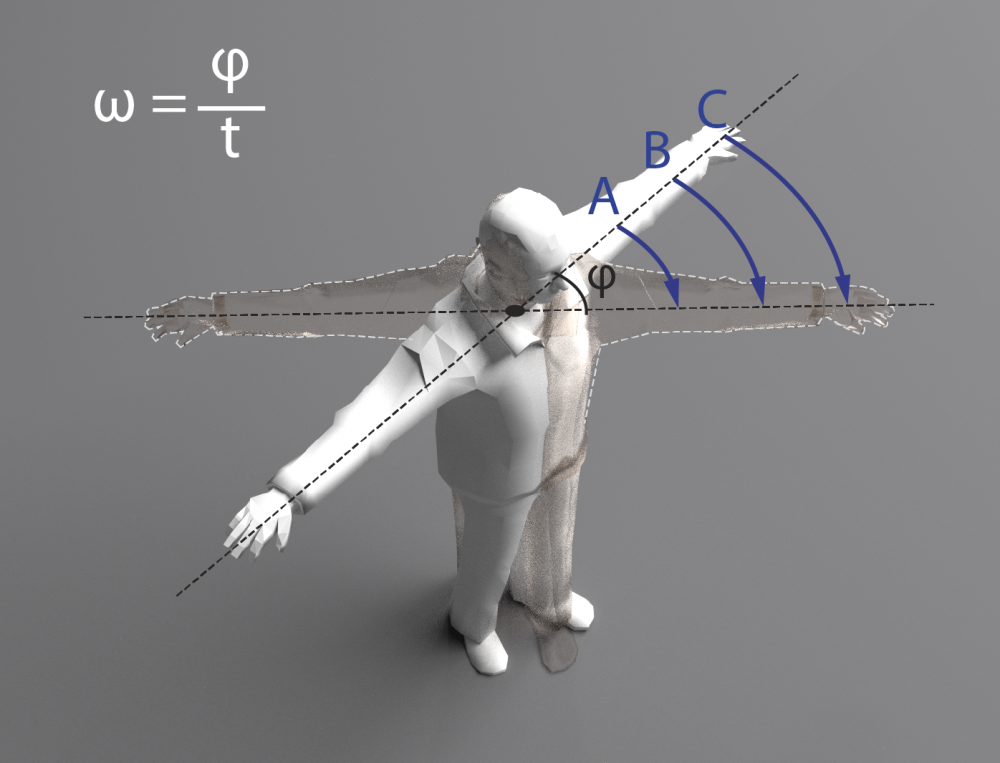
5.att. Leņķiskais ātrums
Rotācijas kustība ir ļoti nozīmīga tehnikā. Riteņa izgudrošana, kas ir ciešā saistība ar rotācijas kustību, revolucionizēja transportēšanas iespējas. Tas ir tādēļ, ka rotācijas kustībā ir jāsaskaras ar daudz mazākiem pretestības spēkiem. Piemēram, ja velk metāla kasti pa metāla virsmu, tad slīdes berzes koeficients var būt μ = 0,20 (1. att. a), bet, ja to pašu kravu velk ratiņos (1. att. b), tad rites berzes koeficients ir ap μ = 0,02. Tas nozīmē, ka pretestības spēki atšķiras aptuveni 10 reizes. Šī atšķirība ir tādēļ, ka kastei ir lielāks saskares laukums ar zemi (1. att. c) nekā ratiņu riteņiem (1. att. d).
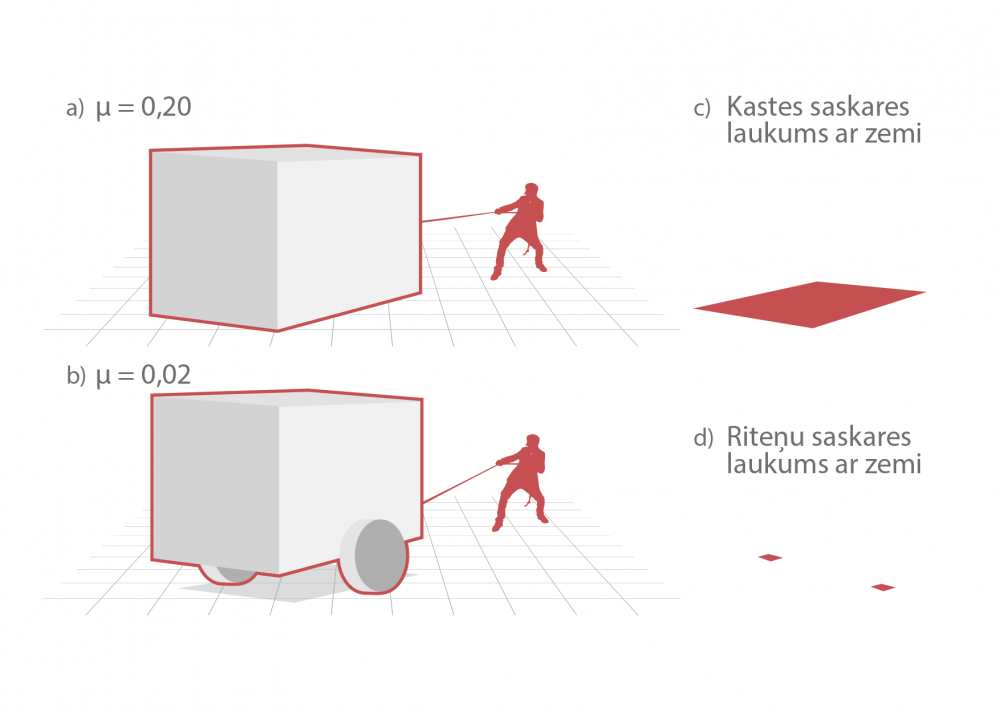
1.att. Slīdes un rites berze
Dažkārt ir jāapvieno taisnvirziena un rotācijas kustība, lai iegūtu labāko efektu. Tas notiek, piemēram, automašīnu dzinējos, kuros automašīnas kustībai nepieciešamā rotācijas kustība rodas virzuļa taisnvirziena kustībā augšup lejup (2. att. a). Šī taisnvirziena kustība tiek pārvērsta rotācijas kustībā, izmantojot īpašu kloķa-klaņa mehānismu. Arī lietojot, piemēram, trīšu mehānismu, krava kustas taisnā virzienā, bet pašā trīsī notiek rotācijas kustība (2. att. b).
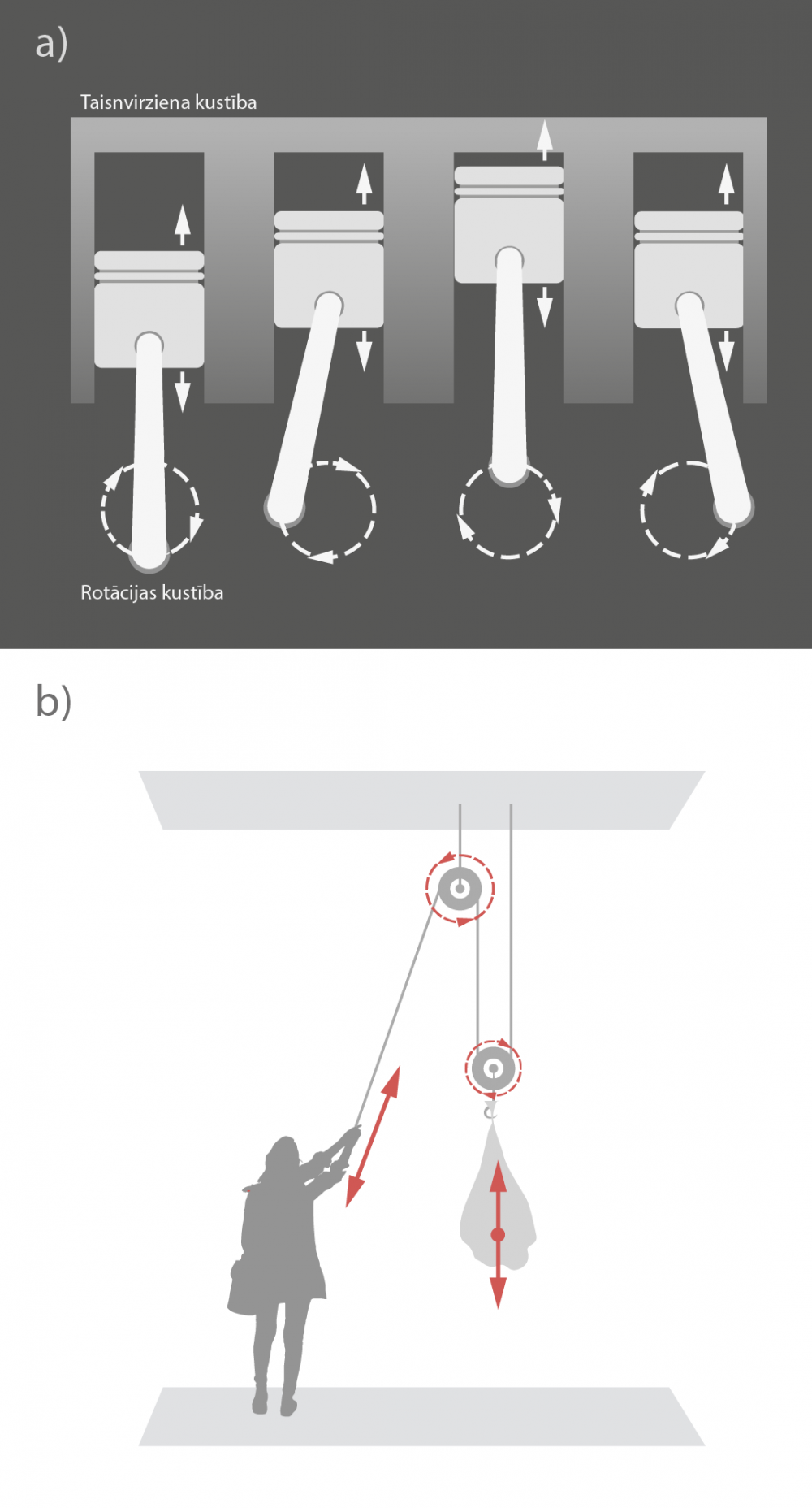
2.att. Taisnvirziena un rotācijas kustība automašīnas dzinējā un trīšu sistēmā
Kloķa-klaņa mehānismā (2. att.) viena mehānisma daļa ir pakļauta taisnvirziena kustībai, bet otra – rotācijas kustībai. Pastāv iespēja, ka viens objekts ir pakļauts šiem abiem kustības veidiem. Ja taisnvirziena kustība notiek perpendikulāri rotācijas plaknei, tad objekts ir pakļauts spirālveida kustībai (3. att. a). Šādi kustas, piemēram, lādētās daļiņas, kas nonākušas Zemes magnētiskā lauka ietekmē (3. att. b). Šīs daļiņas ir tās, kas izraisa ziemeļblāzmas.
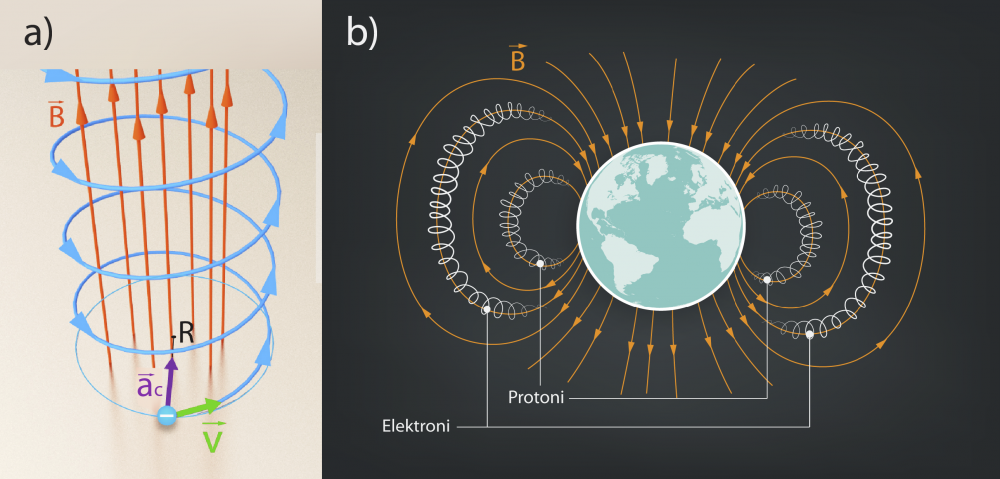
3.att. Spirālveida kustība
Ja taisnvirziena kustība notiek paralēli rotācijas plaknei, tad objekts kustas pa trajektoriju, ko sauc par cikloīdu. Pa šādu trajektoriju kustas, piemēram, punkti uz velosipēda vai automašīnas riteņa ārējās apmales (4. att.).

4.att. Cikloīda velosipēda kustībā
Ja ir nepieciešams mainīt rotācijas ātrumu, tiek lietoti zobratu pārnesumi (5. att. a). Ja starp diviem zobratiem ir saķere un tie griežas, tad zobratu ārējās malas lineārie ātrumi ir vienādi, bet atšķiras to leņķiskie ātrumi (5. att. b). Leņķisko ātrumu attiecība ir apgriezti proporcionāla zobratu rādiusiem. Zobratu pārnesumus izmanto dažādās ātrumkārbās. Arī velosipēdu pārnesumos efektu iegūst ar dažādu izmēru zobratiem, tikai šajā gadījuma zobrati nav tiešā saķerē, bet saķeri nodrošina ķēdē (5. att. c).
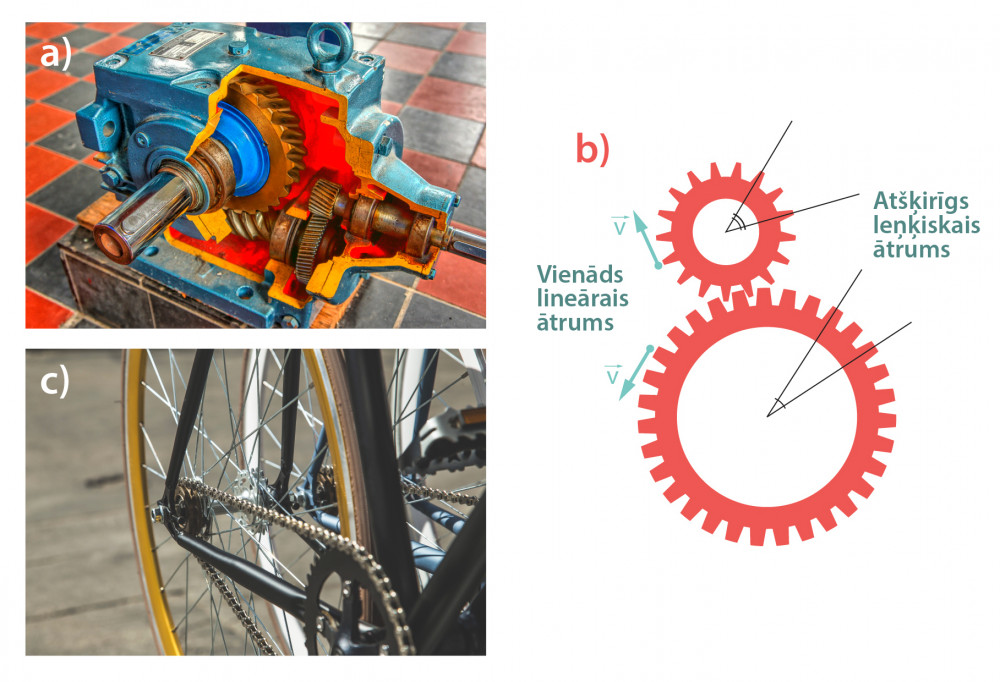
5.att. Zobratu rotācijas kustība
Ja zvaigžņotā naktī pret debesīm pavērš fotoaparātu, kam ir uzlikts liels ekspozīcijas laiks (laiks, cik ilgi tiek uzņemta bilde), tad var iegūt tādas fotogrāfijas, kāda redzama 1. attēlā. Attēls parāda to, ka arī zvaigznes atrodas rotācijas kustībā, turklāt šī rotācija notiek ap centru, kura tuvumā atrodas Polārzvaigzne, tādēļ izskatās, ka visas zvaigznes it kā rotē ap polārzvaigzni.

1.att. Zvaigžņotās debess rotācija
Zvaigžņu rotācija patiesībā ir tikai šķietama, jo tā notiek Zemes rotācijas dēļ. Rotē nevis pašas zvaigznes, bet gan novērotājs. Zemes rotācijas dēļ ir vēl daži interesanti efekti, piemēram, kustošu objektu noliekšanās Koriolisa spēka ietekmē (2. att. a). Koriolisa spēks ir noliecošs spēks, kas rodas rotācijas dēļ. Šī spēka ietekmē ķermeņi ziemeļu un dienvidu puslodēs nolieksies pretējos virzienos (2. att.). Koriolisa spēks ietekmē arī ūdens un gaisa masu kustību. Ja vēja virziens ir perpendikulārs Zemes rotācijas virzienam (2. att. b), tad Koriolisa efekta dēļ atmosfērā veidojas virpuļi (2. att. c).
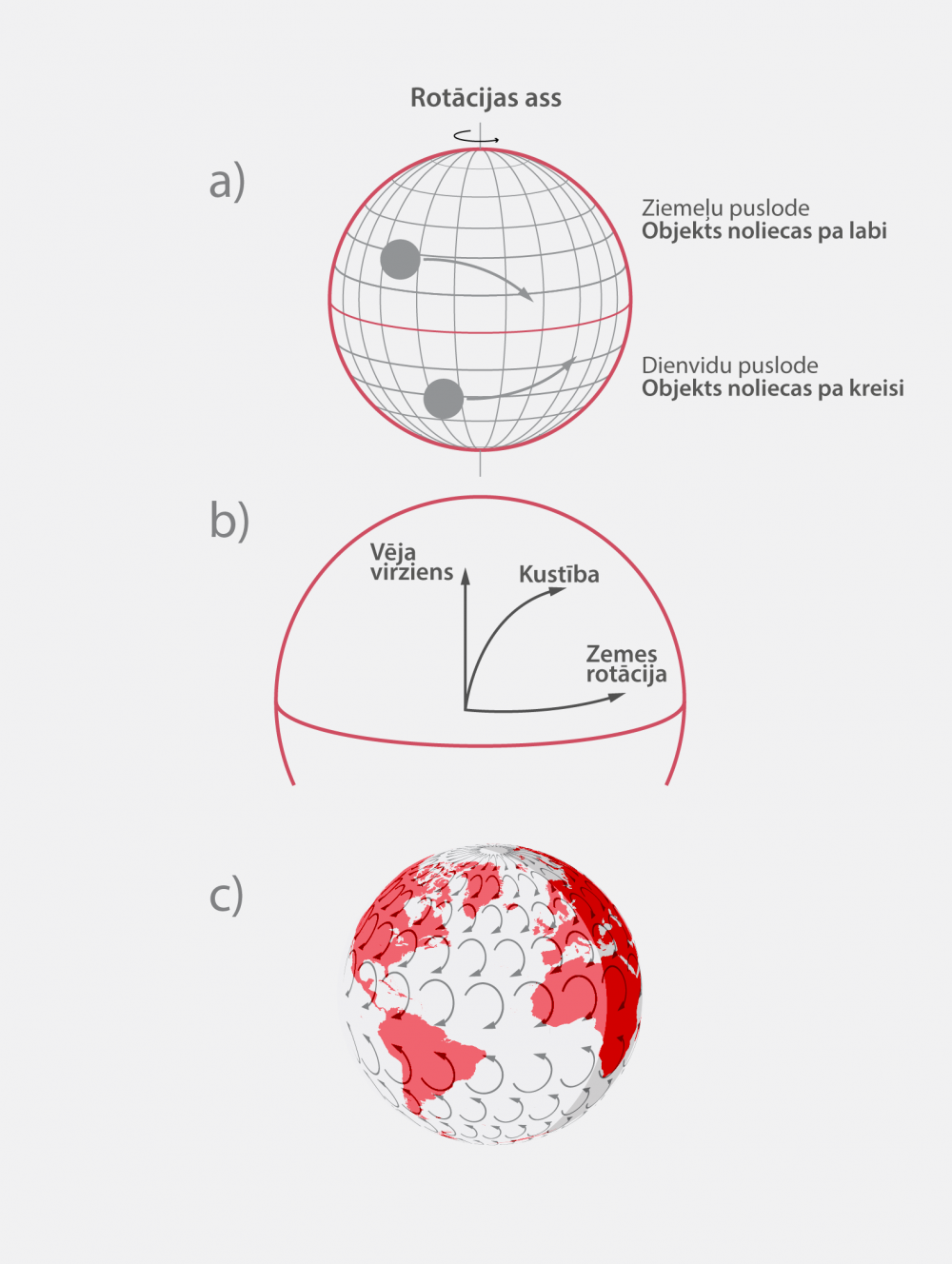
2.att. Koriolisa spēks darbībā
Polārzvaigzni var izmantot, lai orientētos uz Zemes. Tomēr paceļoties augstāk, piemēram, dodoties izplatījumā, orientēšanās iespējas pēc Polārzvaigznes un arī pēc Zemes magnētiskā lauka pazūd. Tad var izmantot rotācijas dinamikā balstītu sistēmu – žiroskopu (3. att.), kas sastāv no trīs savstarpēji perpendikulārām rotācijas asīm, kurās var rotēt disks. Šādā sistēmā iegriezts disks saglabā savu rotācijas pozīciju inerces dēļ, un šo noteikto pozīciju var izmantot kosmosa aparāti, lai orientētos kosmosā.

3.att. Žiroskops