Ja ķermeni paceļ virs zemes un palaiž vaļa, tad vairs nav balsta reakcijas spēks, kas kompensē Zemes pievilkšanās spēka jeb smaguma spēka iedarbību, līdz ar to ķermenis iegūst paātrinājumu, kas vērst Zemes centra virzienā (1. att. a) . To sauc par brīvās krišanas paātrinājumu g. Brīvās krišanas kustību apraksta ar vienmērīgi paātrinātas kustības likumiem (1. att. b), vienīgi veiktais attālums tiek apzīmēts ar h, bet piešķirtais paātrinājums ir brīvās krišanas pāatrinājums g. Brīvās krišanas kustība pa vertikāli pēc kinemātikas ir līdzīga vienmērīgi paātrinātai kustībai pa horizontāli. Ja sākuma ātrums v0=0, tad hmax=gt2/2 (1. att. b). Ja zina ķermeņa krišanas laiku t, tad, izmantojot šo formulu, var aprēķināt no kāda augstuma ķermenis ir kritis. Tā pat spēkā ir arī krišanas ātruma noteikšanas sakarība vk=gt.
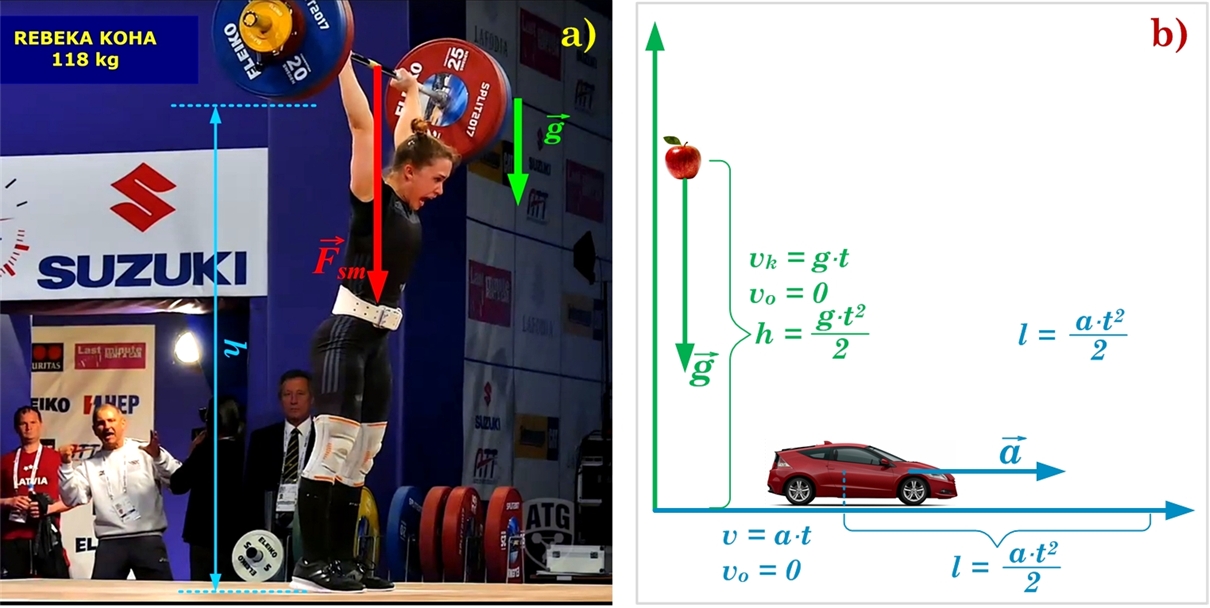
1. att. Ķermeņu brīvā krišana
Ja ķermenim tiek piešķirts vertikāli vērsts ātrums vs, tad gan kustībā augšup, gan lejup darbojas brīvās krišanas paātrinājums g un veiktais attālums abos virzienos ir vienāds. Ja gaisa pretestību var neievērot un tiek fiksēts ķermeņa stāvoklis ik pēc kāda noteikta laika momenta, tad vertikālā sviediena laikā ķermenis augšupceļā un lejupceļā iziet caur vienām un tām pašām pozīcijām (2. att.). Rezultātā kustības laiks abos virzienos būs vienāds līdz ar sākuma un beigu ātrumiem vs un vb. Lai aprēķinātu maksimālo pacelšanās augstumu hmax, ir jālieto tā pati sakarība, kas brīvajam kritienam hmax=gt2/2!
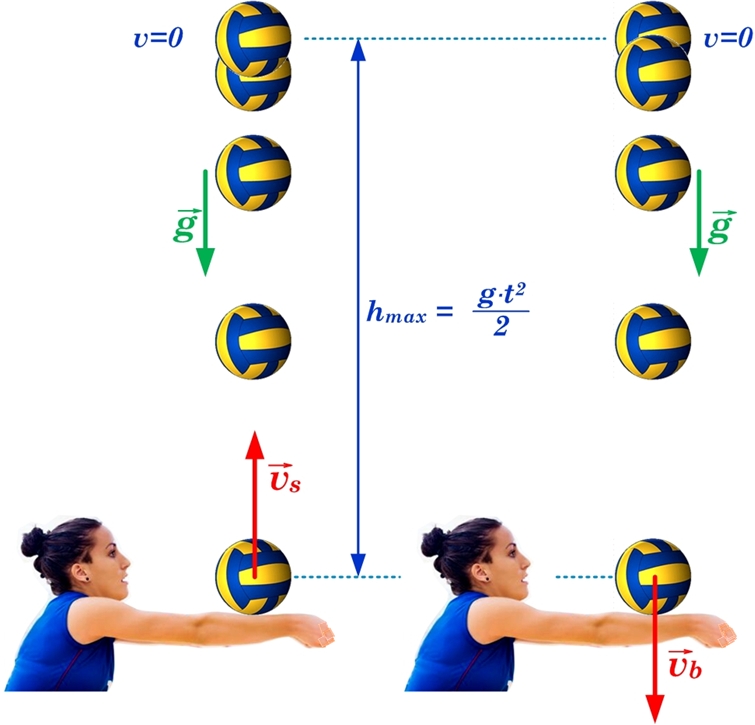
2. att. Vertikālais sviediens
Ja ķermenim, kas atrodas augstumā h, piešķir sākuma ātrumu v0 horizontālā virzienā, tad ķermenis vienlaicīgi tiek pakļauts divām kustībām: iepriekš aprakstītajai brīvajai krišanai vertikālā virzienā un vienmērīgajai horizontālajai kustība ar ātrumu v0 (3. att.). Fiksējot ķermeņu pozīciju horizontālajā un vertikālajā virzienā ik pēc noteikta laika redzams, ka horizontālajā virzienā vienā un tajā pašā laika mometnā tiek veikts vienāds attālums x, bet vertikālajā virzienā veiktais attālums y ar katru brīdi pieaug. Saskaitot horizontālās un vertikālās ķermeņa pozīcijas ik pēc noteikta laika, iegūst kopējo ķermeņa pozīciju horizontālajā sviedienā (3. att.)!
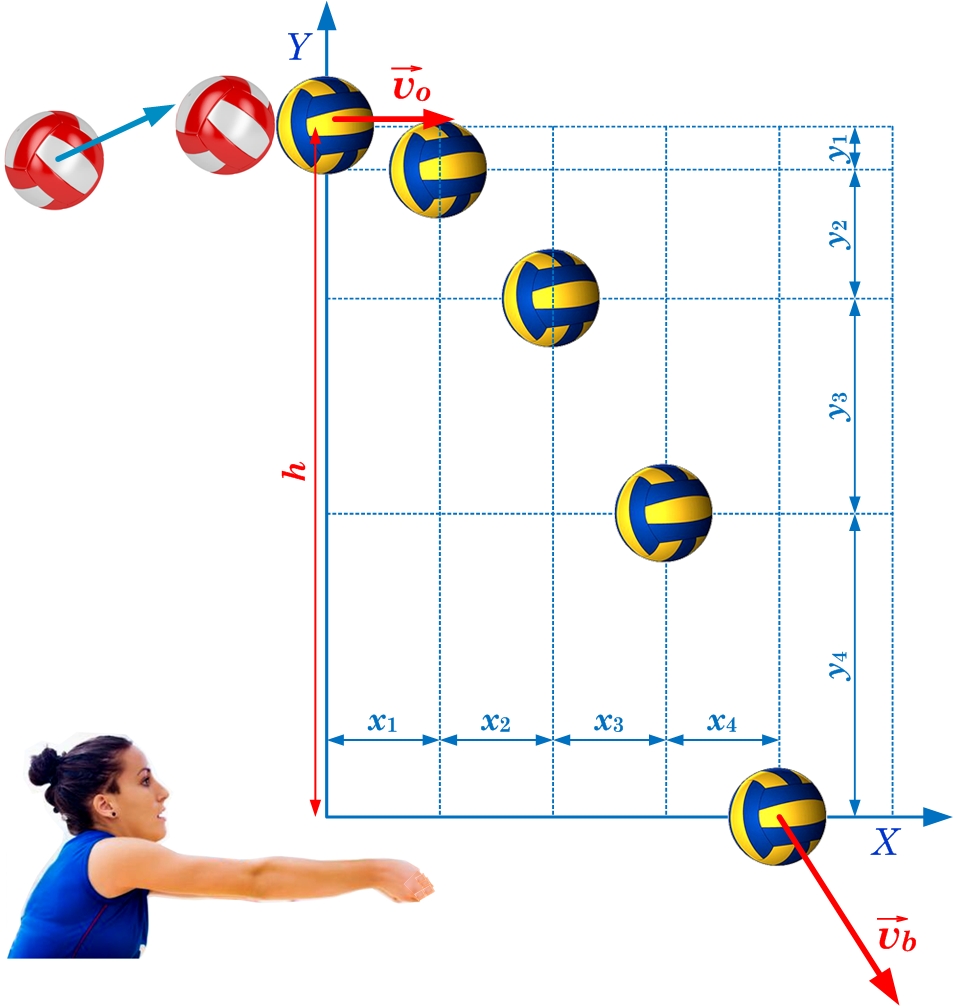
3. att. Horizontālā sviediena sadalīšana divās kustībās
Tā kā horizontālā sviediena kustības ilgums ir atkarīgs tieši no vertikālās kustības, proti, līdz ķermenis sasniedz zemi, izsviešanas augstumu var aprēķināt tādā pašā veidā kā brīvā kritiena gadījumā: h=gt2/2 .Visu krišanas laiku ķermenis pārvietojas arī horizontālā virzienā. To, cik lielu attālums šajā virzienā tiek veikts, var aprēķināt pēc vienmērīgas kustības ceļa aprēķina formulas l=v0t (4. att.). Horizontālais sviediens sastāv divām savstarpēji neatkarīgām kustībām, tādēļ arī kopēja ātruma vektoram v ir divas komponentes: horizontālā (v0) un vērtikālā (vk) (4. att.). Horiznotālā komponente visas kustības laikā paliek nemainīga, savukārt vertikāla komponente pieaug. Kopējā ātruma vektoru iegūst, ja saskaita horizontālā ātruma vektoru ar vertikālā ātruma vektoru.
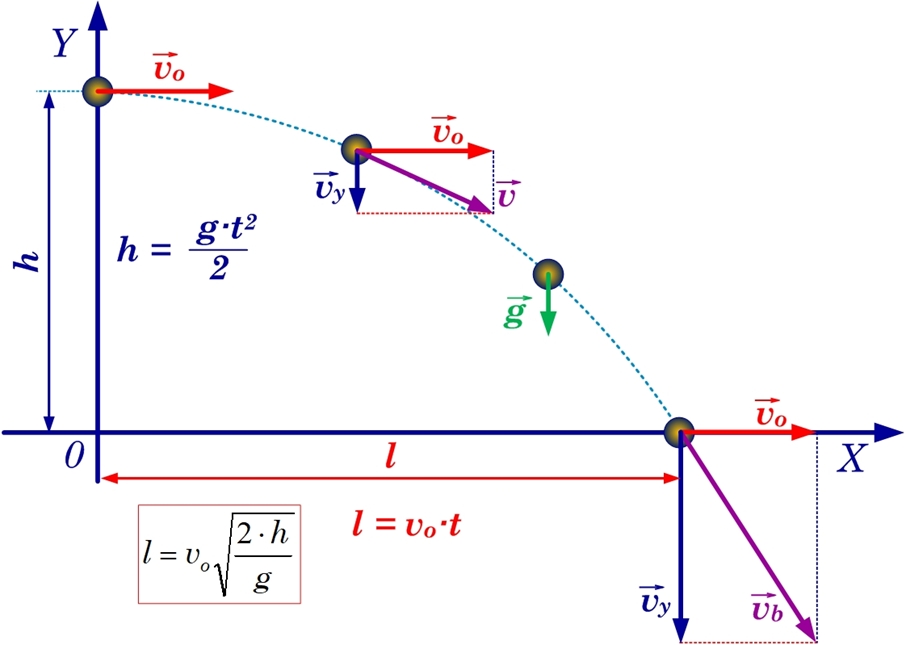
4. att. Fizikālie lielumi horizontālajā sviedienā
Lielākoties sviedieni nav ne horizontāli, ne vertikāli, parasti tiek notiek kādā noteiktā leņķī pret horizontu (5. att.).Šādu kustību raksturo šādi galvenie lielumi:
1) Sākuma ātrums v0;
2) Sākuma ātruma leņķis pret horizontu α;
3) Maksimālais pacelšanās augstums h;
4) Attālums l, ko paveic izsviestais ķermenis;
5) Kustības laikas t.
Šī kustība sevī apvieno vertikālo un horizontālo sviedienu. Visas kustības laikā horizontālais ātrums vx paliek nemainīgs, un to var aprēķināt pēc trigonometriskas sakarības, ja ir zināms sākuma ātrums v un leņķis, kādā ķermenis izsviests: vx=v·cosα.
Vertikālais ātrums kustības laikā mainās. Vertikālā ātruma sākotnējo vertību arī var izrēķināt pēc trigonometriskām sakarībām: vy=v·sinα. Vertikālais ātrums sākuma momentā ir maksimālais iespējamais un vērst vertikāl augšup. Tad, kad tiek sasniegts maksimālais augstums h, tad vy=0. Savukārt, kustības beigās vertikālā ātruma vērtība atkal sasniedz maksimumu, tikai šoreiz tas ir vērts uz leju (5. att.).
DZM materiāls
Var izspēlēties un nomodelēt visus sviedienus
Slīps sviediens kurā ik pa laikam novelk pārvietojuma vektoru
Medniekš šauj pa kokosriekstu
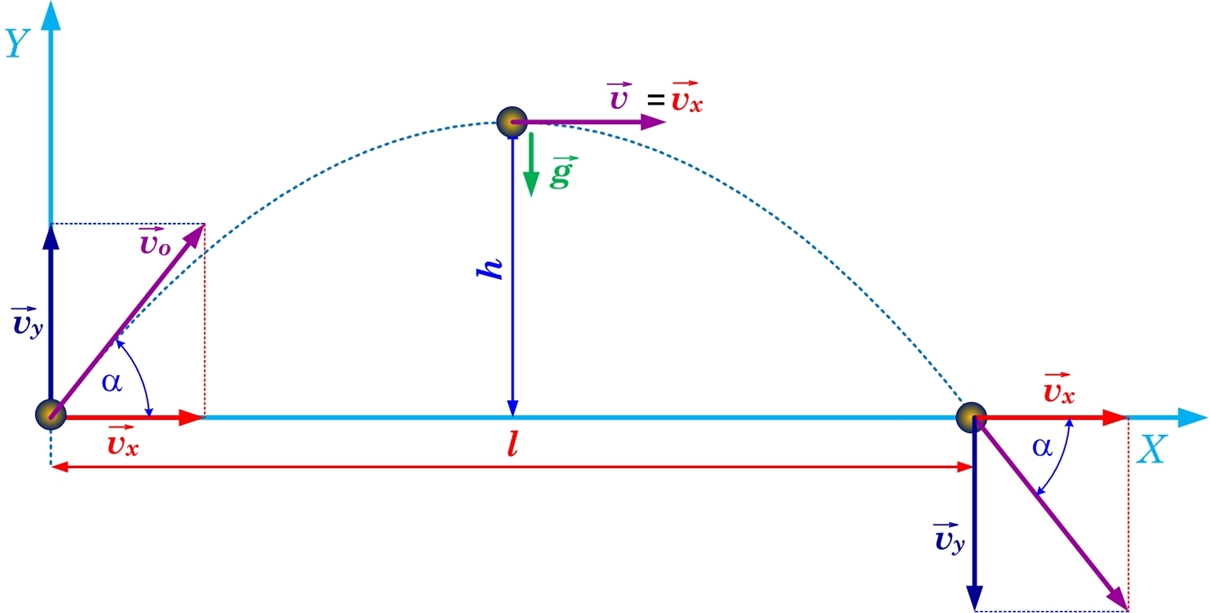
5. att. Slīpais sviediens
Apskatot divu atšķirīgu masu un formu ķermeņu brīvo krišanu tilpumā, no kura ir izsūknēts gaiss (1. att. a), šie ķermeņi kristu pilnīgi vienādi, līdz ar to var secināt, ka brīvās krišanas paātrinājums g visiem ķermeņiem ir vienāds. Ikdienā gan novērojam, ka smagāki ķermeņi nereti sasniedz Zemi ātrāk nekā vieglāki gaisa pretestības dēļ. Krītoši ķermeņi uz Zemes sastopas ar gaisa pretestību, kas darbojas pretēji kustības virzienam. Gaisa pretestības spēka lielums ir atkarīgs no ķermeņa kustības ātruma: jo lielāks ātrums, jo lielāka gaisa pretestība. Līdz ar to ir brīdis, kad gaisa pretestības spēks sasniedz smaguma spēka lielumu, un ķermeņa ātrums vairs nepieaug. Pēc izpletņlēcēja ātruma grafika (1. att. b) redzams, ka kustības laikā divas reizes tiek sasniegts nemanīgs ātrums, jo, pieaugot gaisa pretestības spēkam, tas pilnībā kompensē smaguma spēku.
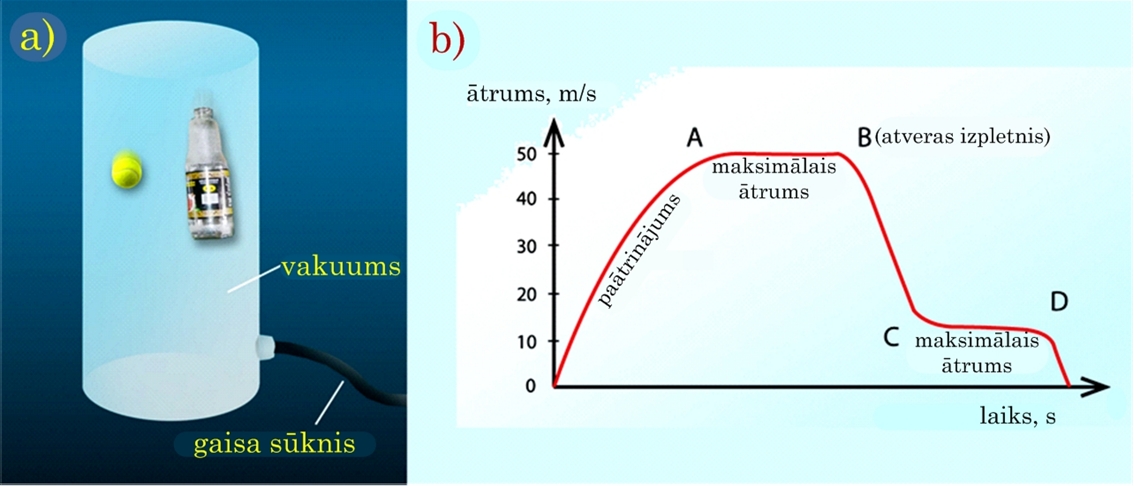
1. att. Brīvā krišana gaisa un bezgaisa telpā
Vertikālajā sviedienā ķermeņa kustība ir vienmērīgi palelināta vai paātrināta atkarībā no tā kurā virzienā ķermenis kustas. Uzzīmējot vertikālā sviediena ātruma grafiku atkarībā no laika redzams, ka ātrums vienmērīgi samazinās līdz 0, kad ķermenis atrodas augstākajā punktā, bet pēc tam vienmērīgi palielinās līdz sasniedz sākotnējo ātrumu (2. att. a). Augsta līmeņa basketbolistiem ir intuitīvi jāpārzina sava un bumbas vertikālā kustība, jo spēles laikā, kad tiesnesis starp diviem vienāda garuma spēlētājiem vertikāli augšup izmet bumbu, to parasti iegūst tas sportists, kas visprecīzāk izvēlas atspēriena momentu, lai vertikālā leciena maksimālo augstumu sasniegtu tajā laika momentā, kad bumba, krītot lejā, ir sasniegusi to vietu, līdz kurai maksimāli sportists var uzlēkt (2.att. b).
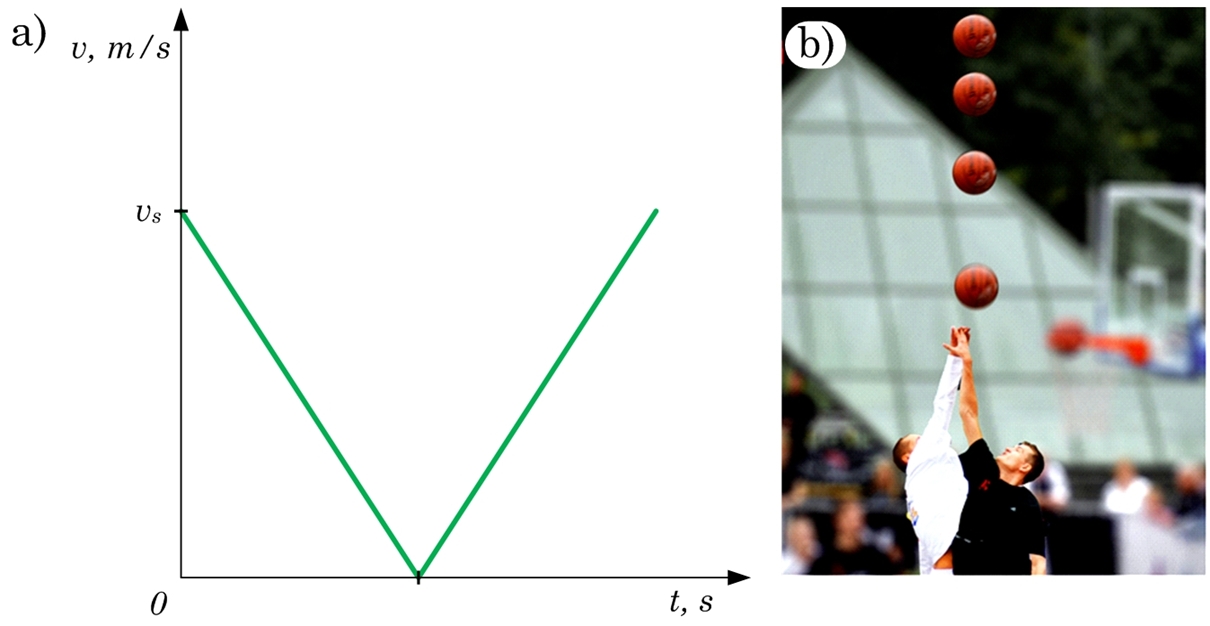
2. att. Vertikālā sviediena ātruma grafiks un pielietojums
Dažados dabā sastopamos procesos ir novērojams vertikālais sviediens. Piemēram, vulkānā izvirdumā centrālā izsviestā masas kustība atbilst vertikālajam sviedienam. Vēl ļoti līdzīgi ir geizeru izvirdumi, kad vertikāli augšup tiek izsviestas ūdens masas. Līdzīgu efektu geizeri var panākt, ja pagriež dušas klausuli tā, lai ūdens sļāktos vertikāli augšup. Tad pēc ūdens strūklas augstuma var mēģināt aptuveni novērtēt ātrumu ar kādu ūdens izšļācās no dušas klausules (3. att).

3. att. Vertikālais sviediens dušā
Horizontālā sviediens parādās ieroču lietojumā, jo nereti lode tiek izšauta horizontālā virzienā (4. att. a). Lodes sākuma ātrums ir tik liels, ka ir grūti pamanīt tās vertikālo kustību, tomēr ja mērķis atrodas ļoti tālu, tad ir jārēķinās, ka lodei vertikālais ātrums pieaugs. To ņem vērā dažāda veida tēmekļos (4. att. b).

4. att. Horizontālais sviediens ieroču lietojumā
Un ja ar dušas klausules palīdzību varēja pētīt ūdens vertikālo sviedienu, tad, pagriežot klausu horizontālā virzienā, ir iespējams skatīties kā ūdens uzvedas horizontālajā sviedienā (5. att.). Arī šajā gadījumā var pētīt ātrumu ar kādu ūdens izšaujas no klausules un salīdzināt vai tas sakrīt ar to ātrumu, kas iegūts pēc vertikālā sviediena aprēķiniem.
Horizontālā un vertikālā sviediena salīdzināšana

5. att. Horizontālais sviediens dušā
6. attēlā redzams, ka mainoties izsviešanas leņķim pret horizontu, mainās gan maksimālais pacelšanās augstum h, gan arī lidojuma tālums l, atšķirība tikai tā, ka samazinoties leņķim, samazinās maksimālai pacelšanās augstums, bet lidojuma tālums līdz noteiktam leņķim palielinās, un tikai pēc tam sāk samazināties. Vistālākais sviediens ir, ja ķermeni met 45 grādu leņķi pret horizontu (6. att.).
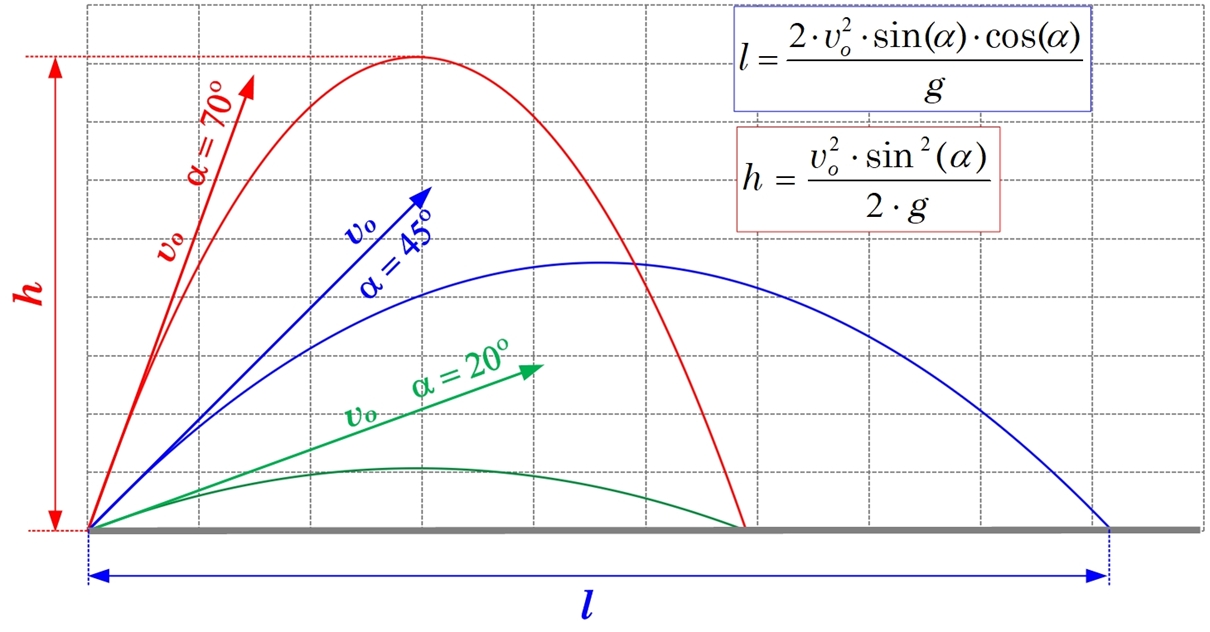
6. att. Maksimālais pacelšanās augstums un lidojuma tālums ir atkarīgs no ķermeņa izsviešanas leņķa pret horizontu
Maksiālo pacelšanās augstumu var aprēķināt līdzīgi kā vertikālajā sviedienā hmax=gt2/2, kur t ir visas kustības laiks. Zinot sākuma ātruma horizontālo komponenti vx un kustības laiku, pēc vienmērīgas kustības vienādojuma var aprēķināt ķermeņa veikto attālumu l=vxt. Slīpos sviedienus ļoti bieži sastop sportā, piemēram, lodes grūdēji vai šķēpmetēji (7. att. a). Arī jau vairākas reizes pieminētajā dušā var novērot slīpo sviedienu (7. att. b).

7. att. Slīpā sviediena pielietojums
Lai iegūtu sakarības dažādiem fizikālajiem lielumiem vertikālajā sviedienā jāatceras, ka šajā gadījumā darbojās vienmērīgi paātrinātas kustības likumi.
Vienmērīgi paātrinātā kustība nobraukto ceļu aprēķina l=v0t+at2/2, kur
v0 - sākuma ātrums, m/s
t - kustības laiks, s
a - paātrinājums, m/s2
Ņemot vērā, ka vertikālajā sviedienā paātrinājums ir brīvās krišanas paātrinājums g, turklāt ar negatīvu zīmi, jo kustība tiek palenināta, un veikto attālumu apzīmējot ar y, iegūst sakarību y=v0t-gt2/2 (1. att.).
Ātruma v maiņas vienādojums vienmērīgi paātrinātā kustība ir v=v0+at! Atkal ņemot vērā darbojošos paātrinājumu, vertikālajā sviedienā ātruma maiņas vienādojums ir v=v0-gt.
Ja zināms laiks tp pēc kura ķermenis sasniedz maksimālo augstumu, tad, izmanotojot sakarību y=v0t-gt2/2,var izteikt sakarību maksimālā augstuma hmax aprēķināšanai. Izteiksme hmax=v0tp-gtp2/2. Katru kustības sekundi kustības ātrums samazinās par g, tādēļ kustībai līdz maksiālās pacelšanās augstumam ir spēkā v0=gt. Ievietojot šo izteiksmi sākotnējā hmax izteiksmē, iegūst
hmax=v0t-gt2/2=gt2-gt2/2=gt2/2!
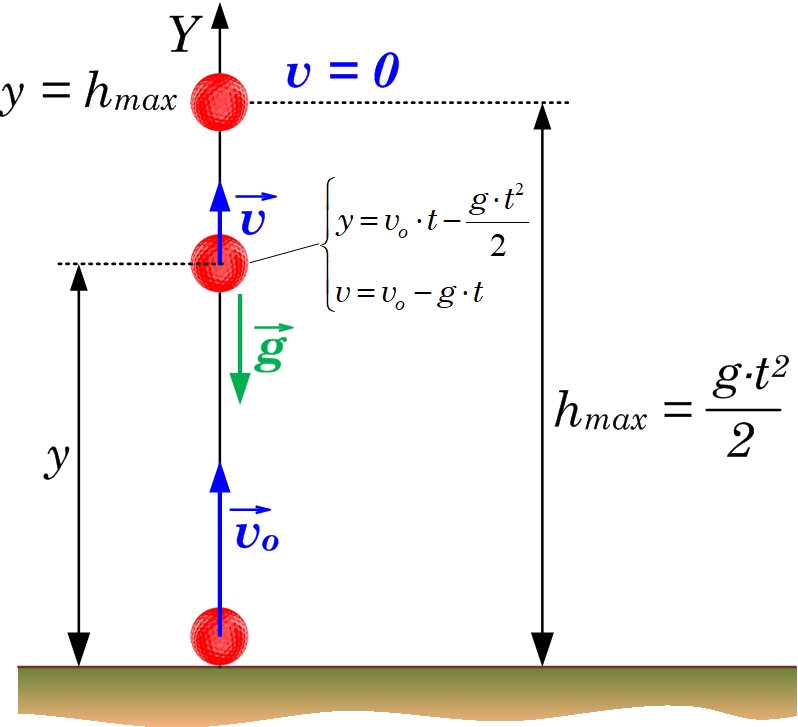
1. att. Fizikālo lielumu sakarības vertikālajā sviedienā
Arī likumus, kas apraksta ķermeni vertikālajā kritienā, iespējams iegūt no vienmērīgi paātrinātas kustības sakarībām ņemot vērā to, ka ķermeņa sākuma atrums v0=0 un kustības sākas no augstuma h ar paātrinājumu g.
Vertikālaja kritienā svarīgs lielums ir atlikušais attālums līdz zemei. Lai to iegūtu tā izteiksmi, jāizmanto koordinātes vienādojums vienmērīgi paātrinātas kustībā x=x0+v0t+at2/2,
x0 - sākuma koordināte, m
v0 - sākuma ātrums, m/s
t - kustības laiks, s
a - paātrinājums, m/s2
Ņemot vērā, ka vertikālajā kritienā sākuma ātrums v0=0 un sākuma koordināte ir h, iegūst sakarību y=h-gt2/2 (2. att.). No ši vienādojuma iespējams arī izteikt krišanas laiku tk (2. att.). Ātruma v maiņas vienādojums vertikālajā kritienā v=gt, jo sākuma ātrums ir 0.
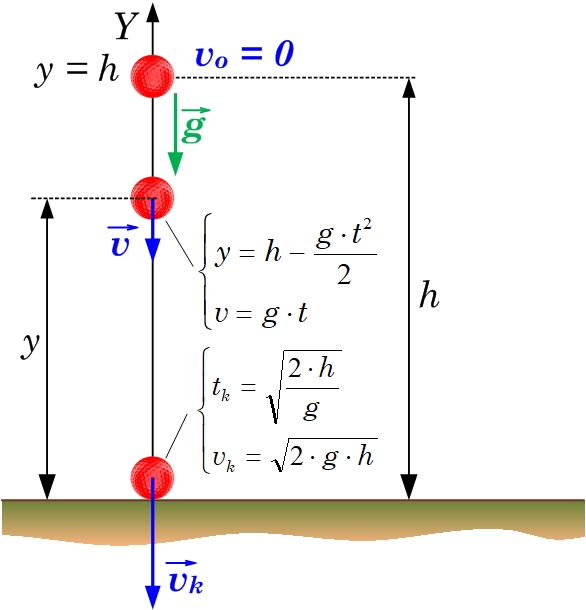
2. att. Fizikālo lielumu sakarības vertikālajā kritienā
Lai pārbuadītu, vai pacelšanās laiks vertikālajā sviedienā ir vienāds ar krišanas laiku, var veikt šādu eksperimentu. Bumbiņu sviež vertikāli augšup un izsviešanas brīdi palaiž hronometru. Kad bumbiņa sasniedz maksimālo augstumu, hronometra pogu nospiež pirmo reizi, lai reģistrētu pacelšanās laiku. Vēlāk, kad bumbiņa nokrīt uz zemes, hronometrs tiek nospiests otrreiz, lai varētu noteikt krišanas laiku. Šādā eksperimentā krišanas laiks visticamāk būtu lielāks un to var ietekmēt vairāki faktori:
1) Nevarēja precīzi noteikt momentu, kad bumbiņa sasniedz maksimālo augstumu;
2) Atšķirību radīja eksperimenta veicēja reakcijas laiks, attiecīgajā momentā nospiežot hronometra pogu;
3) Bumbiņai kustībā augšup bija jāveic mazāks ceļš nekā krītot lejā;
Skatoties no bumbiņas izmešanas vietas ir ļoti grūti noteikt kurā brīdī bumbiņa sasniedz maksiālo augstumu, turklāt katram cilvēkam ir noteikt reakcijas laiks, kas paiet no brīža, kad saproti, ka sānospiež hronometra poga līdz brīdim, kad tā reāli tiek nospiest. Turklāt reakcijas laiks var katrā brīdī būt nedaudz atšķirīgs. Jāatceras arī tas, ja beigu laiku uzņem brīdī, kad bumbiņa atsitas pret zemi, tad lejupceļa bumbiņai ir jāveic garāks ceļš (3. att.). Kādēļ? Pamēģini izmest bumbiņu tā, lai tā kustību sāktu tieši no Zemes virsmas, vienmēr ir vajadzīgs neliels gabals, kura uzsākt sviediena kustību.
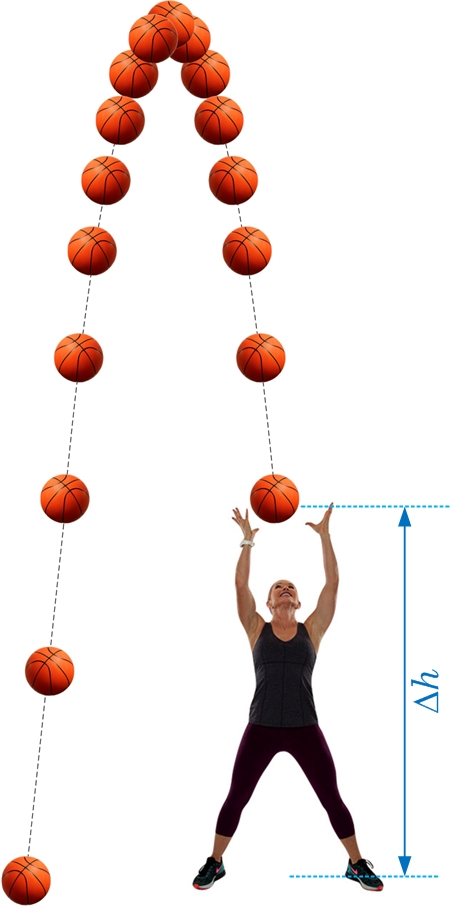
3. att. Pacelšanās un krišanas laika pārbaude
Horizontālā sviediena gadījumā var apvienot iepriekš iegūtā sakarības. Piemēram, lai iegūtu attālumu, ko veic ķermenis pirms piezemēšanās, jālieto formula l=v0t, bet, ieliekot t vietā krišanas laiku tk, kas arī ir laiks, ko ķermenis pavada lidojumā, iegūst 4. att. redzamo izteiksmi!
Attāluma noteikšanai līdz zemei var lietot to pašu iegūto sakarību vertikālā kritiena gadījumā: y=h-gt2/2.
Ja nepieciešams aprēķināt ātruma momentāno vērtību kāda laika momnentā, tad jāizmanto taisnleņķa trīstūra sakarību - Pitagora teorēmu (4. att.).
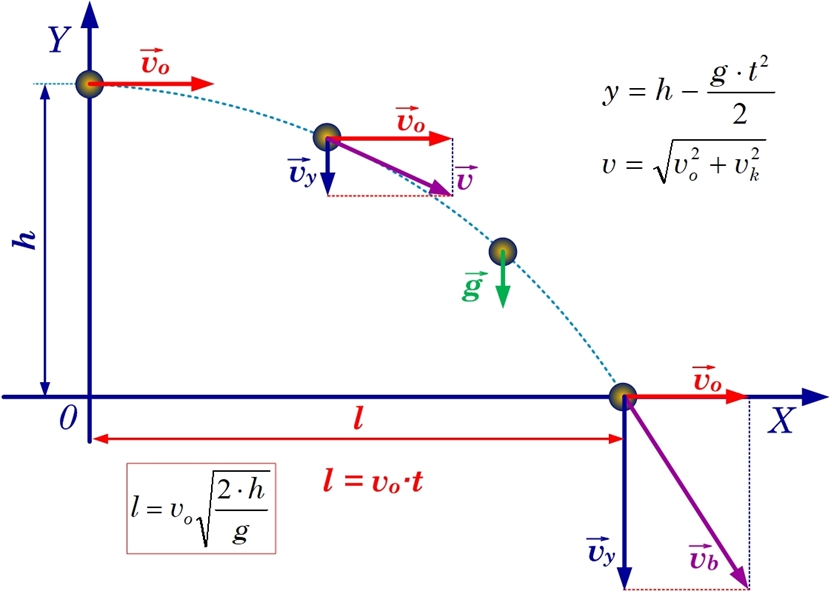
4. att. Fizikālo lielumu sakarības horizontālajā sviedienā
Slīpajā sviedienā liela nozīmē ir ķermeņa sākuma ātrumam v0 un leņķim α kādu tas veido ar X asi. Lai šajā gadījumā varētu pielietot iepriekš iegūtās sakarības, jāiegūst ātruma projekcijas uz X un Y asīm:
vx=v0cosα;
vy=v0sinα.
Tālāk, lai iegūtu pacelšanās augstuma izteiksmi, jāizmanto iepriekš iegūtā izteiksme hmax=gt2/2. Pacelšanās laiku t iegūst, izmantojot vertikālo ātrumu t=vy/g=v0sinα/g. Ievietojot šo laiku augstuma izteiksmē, iegūst hmax=v02/2g·sin2α.
Nolidotā attālums l=vx·t. Ieliekot aprēķināto ātruma projekciju pa X asi un iegūto pacelšanās laiku, iegūst l=v0cosα·v0sinα/g=v02/g·cosα·sinα. Ņemot vērā, ka sinα·cosα=sin2α, iegūst l=v02/g·sin2α (5. att.).
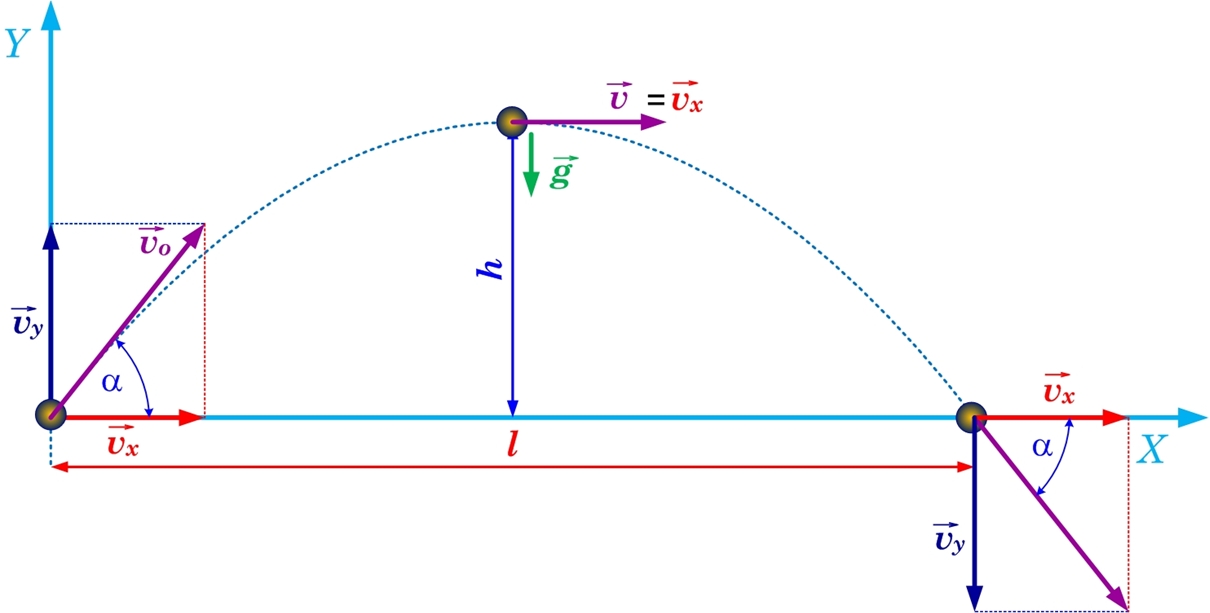
5. att. Fizikālo lielumu sakarības slīpajā sviedienā
Jāatceras, ka iegūtās sakarības ir spēkā, ja gaisa pretestību var neņemt vērā. Ja gaisa pretstības spēks ir ievērojams, tad lidojuma trajektorija mainās (6. att.).
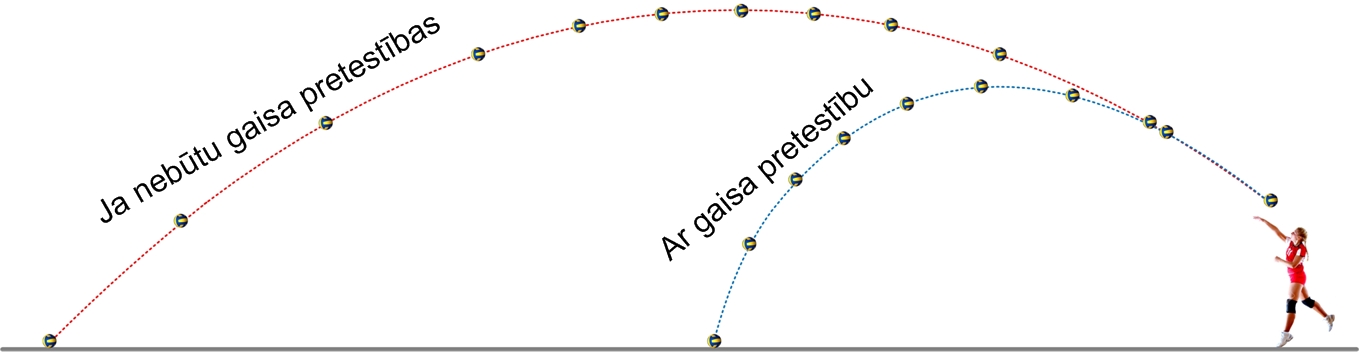
6. att. Slīpais sviediens ievērojot un neievērojot gaisa pretestību