Ja vadītājā plūst strāva, tad elektriskie lādiņi tajā pārvietojas spēka F ietekmē, ko rada elektriskais lauks E (1. att.). Lai pārvietotu lādiņu, nepieciešams padarīt darbu A, ko šajā gadījumā veic strāva, tādēļ to sauc par strāvas darbu. Sadaļā par elektriskā lauka potenciālu noskaidrojām, ka lādiņa pārvietošanai elektriskajā laukā jāveic darbs A = q · U, kur
q – pārvietojamā lādiņa lielums (C),
U– potenciālu starpība (V).
Sadaļā par elektriskās strāvas stiprumu tika apskatīta strāvas stipruma I definīcijaI = q : t, no kuras, no formulas izsakot lādiņu, iegūst q = I · t, kur t ir laiks. Apvienojot sākotnējo un pēdējo sakarību, iegūst A = I · U · t.
Mehāniska darba veikšanas ātrumu raksturo jauda, līdzīgi ir ar strāvas darbu. Elektriskā jauda P ir vienāda ar laika vienībā veikto darbu: P = A : t = I · U. Jaudas mērvienība ir vats (W).
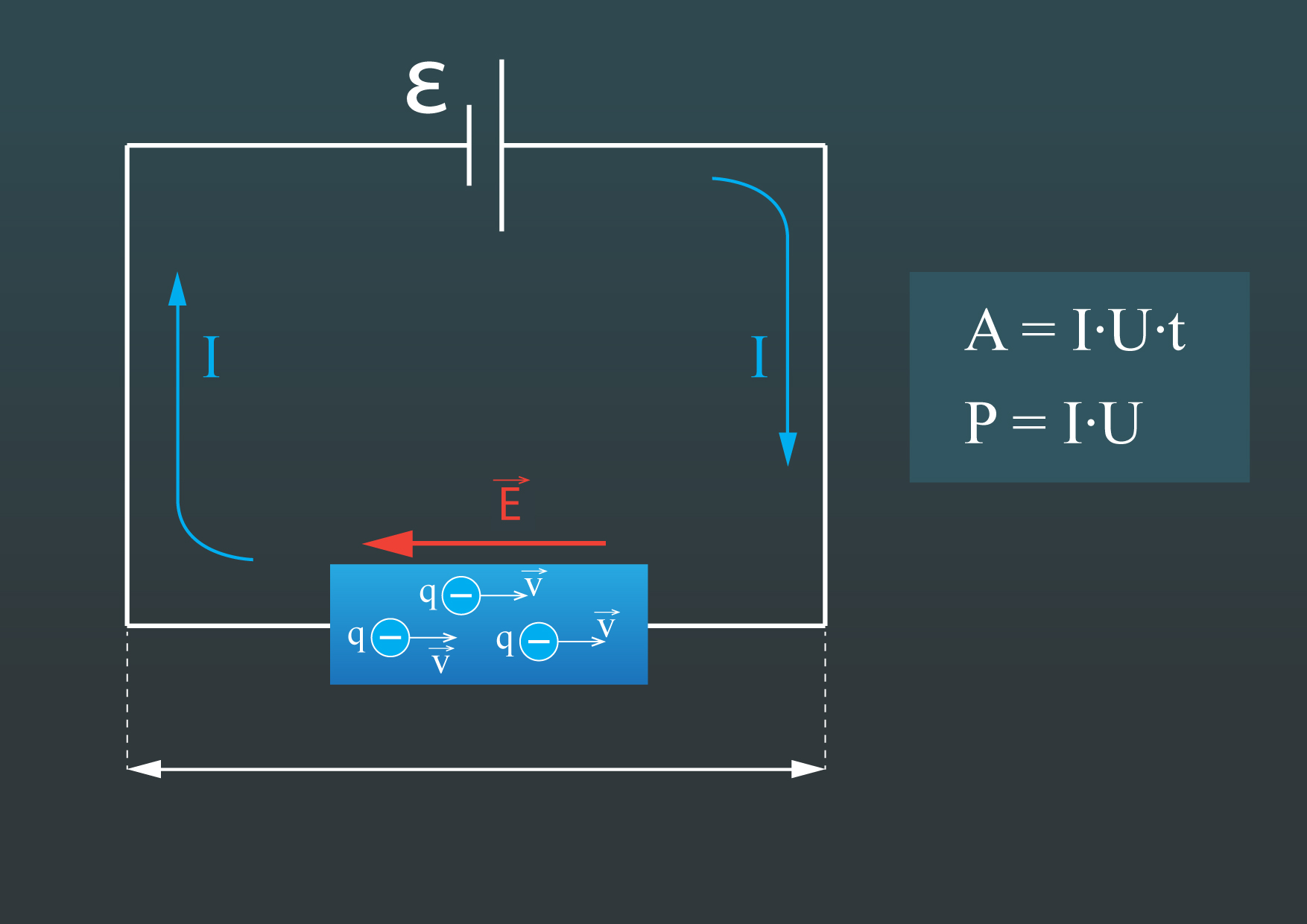
1.att. Elektriskās strāvas darbs un jauda
Strāvas stiprumu I, spriegumu U, jaudu P un elektrisko pretestību R savstarpēji saista dažādas sakarības, no kurām iespējams izveidot elektrisko sakarību apli (2. att.). Šajā aplī iespējams izvēlēties vienu no fizikālajiem lielumiem un apskatīt, kā to var izteikt, izmantojot pārējos lielumus.
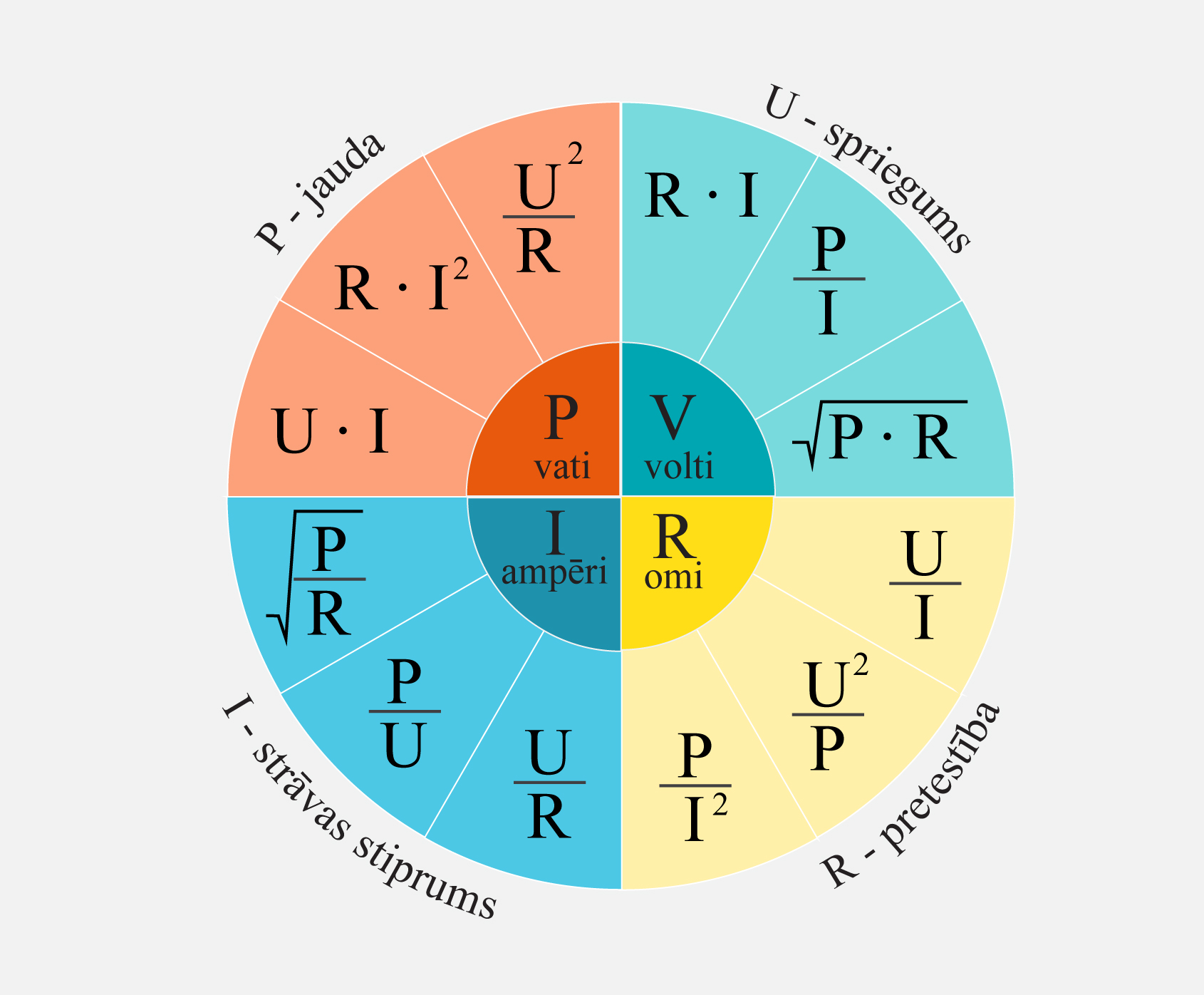
2.att. Elektrisko sakarību aplis
Lādiņnesēji, plūstot cauri vadītājam, ik pa laikam saduras ar to veidojošajām daļiņām, tādējādi piešķirot tām daļu savas enerģijas, un tā rezultātā vadītājs uzsilst. Vadītājam uzsilstot, tas apkārtnei atdod siltuma daudzumu Q (3. att.), kas ir vienāds ar strāvas padarīto darbu: Q = IUt. No Oma likuma izsakot U = IR un ievietojot to siltuma izteiksmē, iegūst Q = I2Rt, kur
I – strāvas stiprums (A),
R – elektriskā pretestība (Ω),
t – strāvas plūšanas ilgums (s).
Šo sakarību sauc par Džoula – Lenca likumu.
Apskaties DZM materiālu!
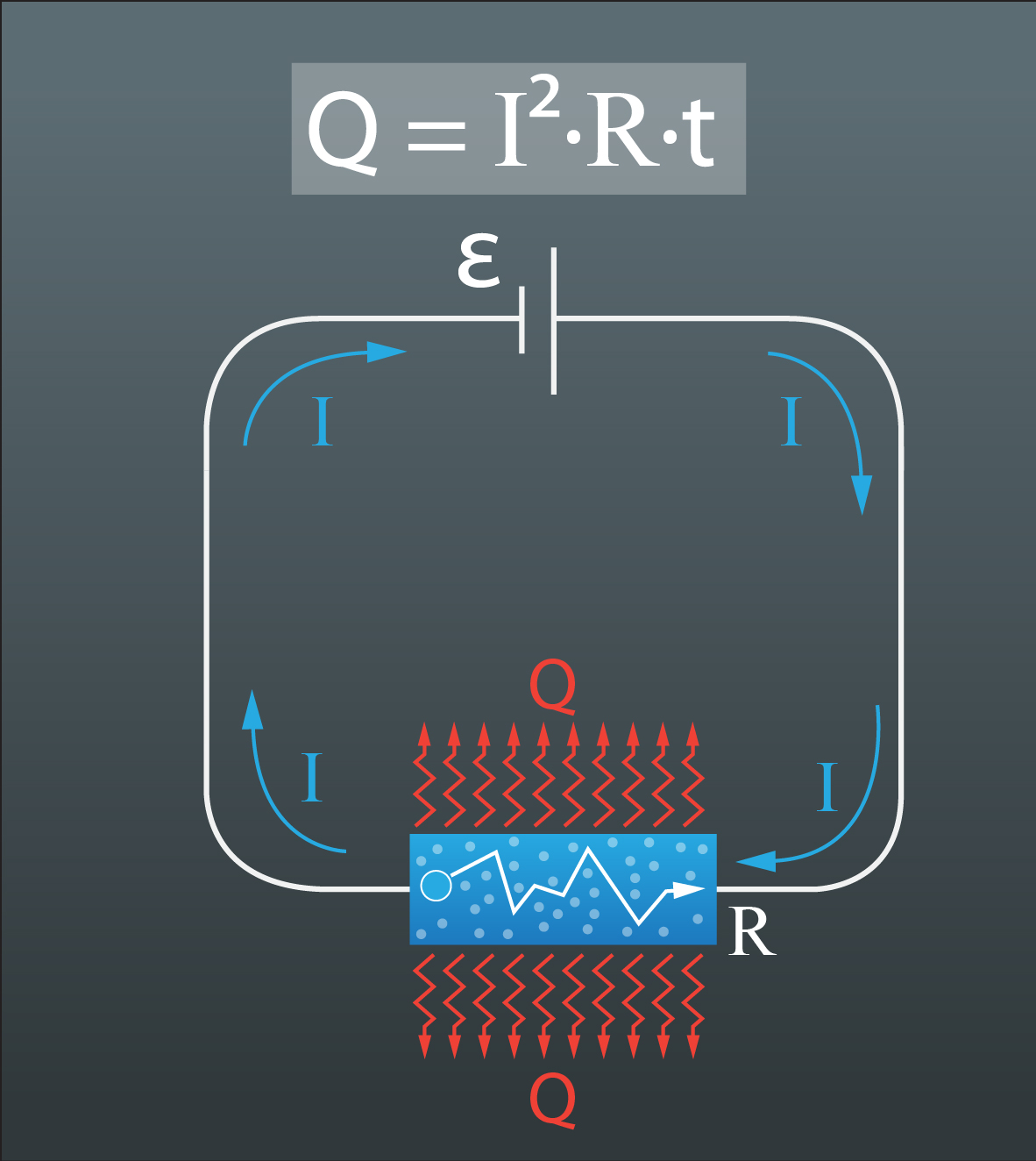
3.att. Džoula-Lenca likums
Uz lādiņu q elektriskajā laukā ar intensitāti E darbojas spēks F = qE. Pārvietojot lādiņu attālumā Δl, tas veic darbu A = F · Δl = qE · Δl (1. att.). Elektriskā lauka intensitāte izsakāma kā E = U : Δl, no kā izsakām E · Δl = U. Ievietojot šo darba izteiksmē: A = qU. Lādiņu q var izteikt no strāvas stipruma definīcijas I = q : t ⇒ q = I · t. Tagad strāvas padarīto darbu var uzrakstīt kā A = IUt.
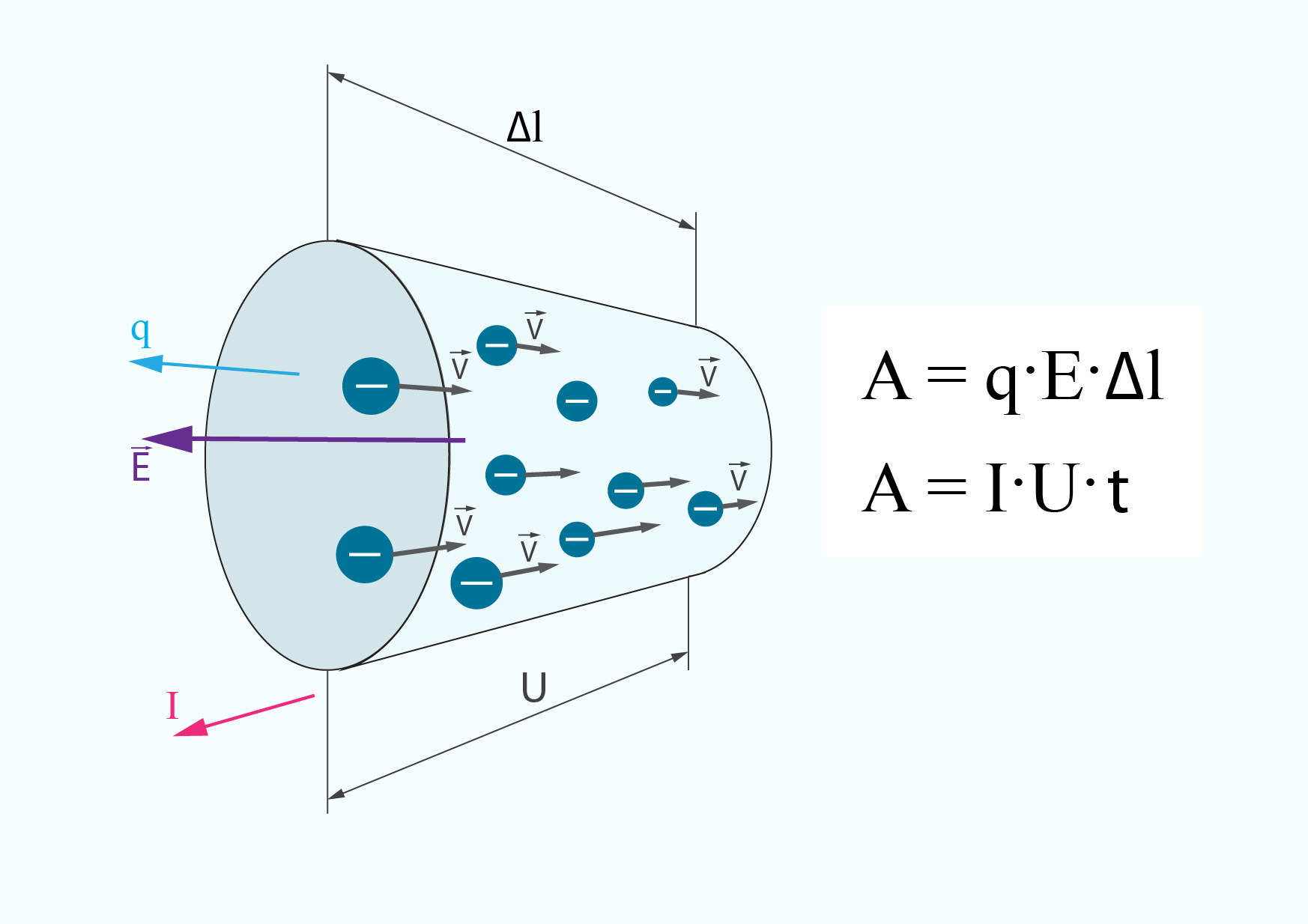
1.att. Strāvas padarītais darbs A
Elektrība darbina dažādas elektriskās ierīces, kas vairāk vai mazāk atvieglo mūsu ikdienas dzīvi. Katrai ierīcei ir sava elektriskā jauda P, kas norāda to, cik daudz elektroenerģijas laika vienībā nepieciešams, lai šo ierīci darbinātu. Jo lielāka ir iekārtas jauda, jo vairāk elektroenerģijas tā patērē. Pieņemot, ka mums ir dots noteikts elektrības daudzums, var salīdzināt cik ilgi katra iekārta būs spējīga darboties ar atvēlēto elektrības daudzumu (2. att.). Jaudas izteikšanai lieto arī mērvienību daudzkārtņus, piemēram, 1 kW = 1000 W vai 1 MW = 1000 000 W.
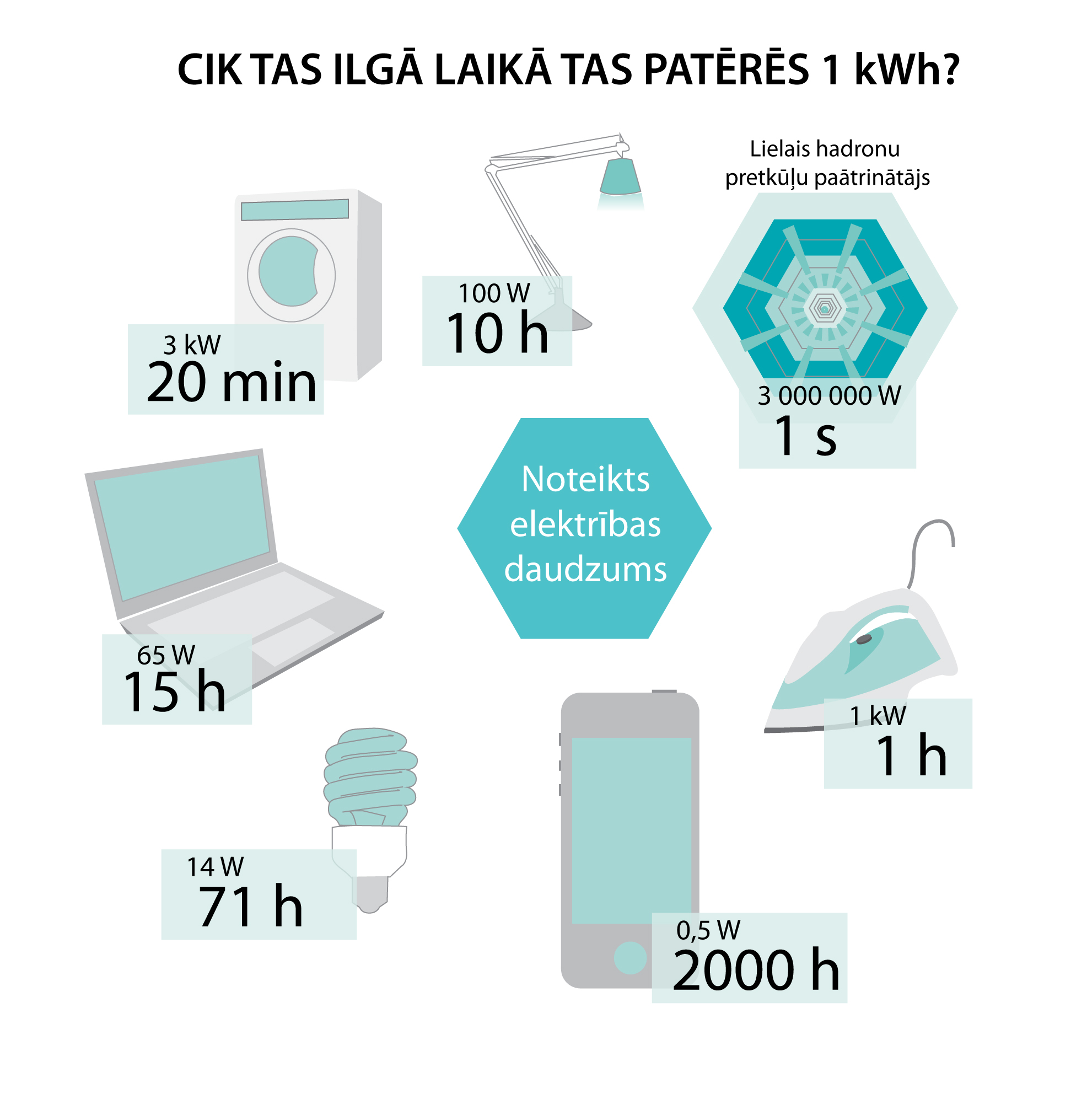
2.att. Dažādu iekārtu strāvas patēriņš
Neviens šajā pasaulē nestrādā par velti, arī elektrība. Par elektrības padarīto darbu ir jāmaksā, tādēļ katra elektrības lietotāja patērētais elektrības daudzums tiek uzskaitīts, izmantojot elektroenerģijas skaitītāju (3. att.). Elektroenerģijas uzskaites mērvienība ir kilovatstunda (kWh). Patērēto kilovatstundu skaitu aprēķina, jaudu P (kilovatos) pareizinot ar laiku t (stundās) (3. att.). Ja elektroenerģijas patērētāja jauda ir 1000 W jeb 1 kW, tad tas stundas laikā patērē 1 kWh.

3.att. Elektroenerģijas skaitītājs
Sadzīvē tiek lietotas arī pie tīkla nepieslēgtas elektriskās ierīces, kurām ir noteikta jauda. Ar dažādu ierīču jaudām iespējams iepazīties 4. attēlā.

4.att. Dažādu elektrības patērētāju jaudas
Dažādās ierīcēs un elektriskos slēgumos mēdz notikt kļūmes. Piemēram, ja enerģijas avotam ir pieslēgts patērētājs ar elektrisko pretestību R, tad ķēdē plūst strāva, kuras stiprums nosakāms pēc Oma likuma pilnai ķēdei: I = E : (R+r), kur E ir avota EDS, bet r – avota iekšējā pretestība (5. att. a). Ja kāda faktora ietekmē notiek īsslēgums jeb ķēde noslēdzas pirms patērētāja (trieciena, ļaunprātīgas darbības, neuzmanības vai kā cita rezultātā), tad strāva labprātāk plūst cauri īsslēgumam (5. att. b), jo tam ir daudz mazāka pretestība Rv(vadu pretestība). Īsslēguma laikā dramatiski pieaug strāvas stiprums, jo patērētāja pretestība Rvir niecīga, līdz ar to I = E : r. No Džoula – Lenca likuma Q = I2Rt izriet, ka ķēdē sāk pastiprināti izdalīties liels siltums, kas var rezultēties kā enerģijas avota vai iekārtas bojājums vai pat avārija. Šī iemesla dēļ elektriskajā ķēdē ieslēdz drošinātāju (5. att. c), kas, sasniedzot noteiktu strāvas stiprumu, izraisa ķēdē strāvas pārtraukumu. Sadzīvē plaši lieto automātiskos drošinātājus (5. att. d), kas nodrošina strāvas atslēgšanu īsslēguma vai tīkla pārslodzes gadījumos.
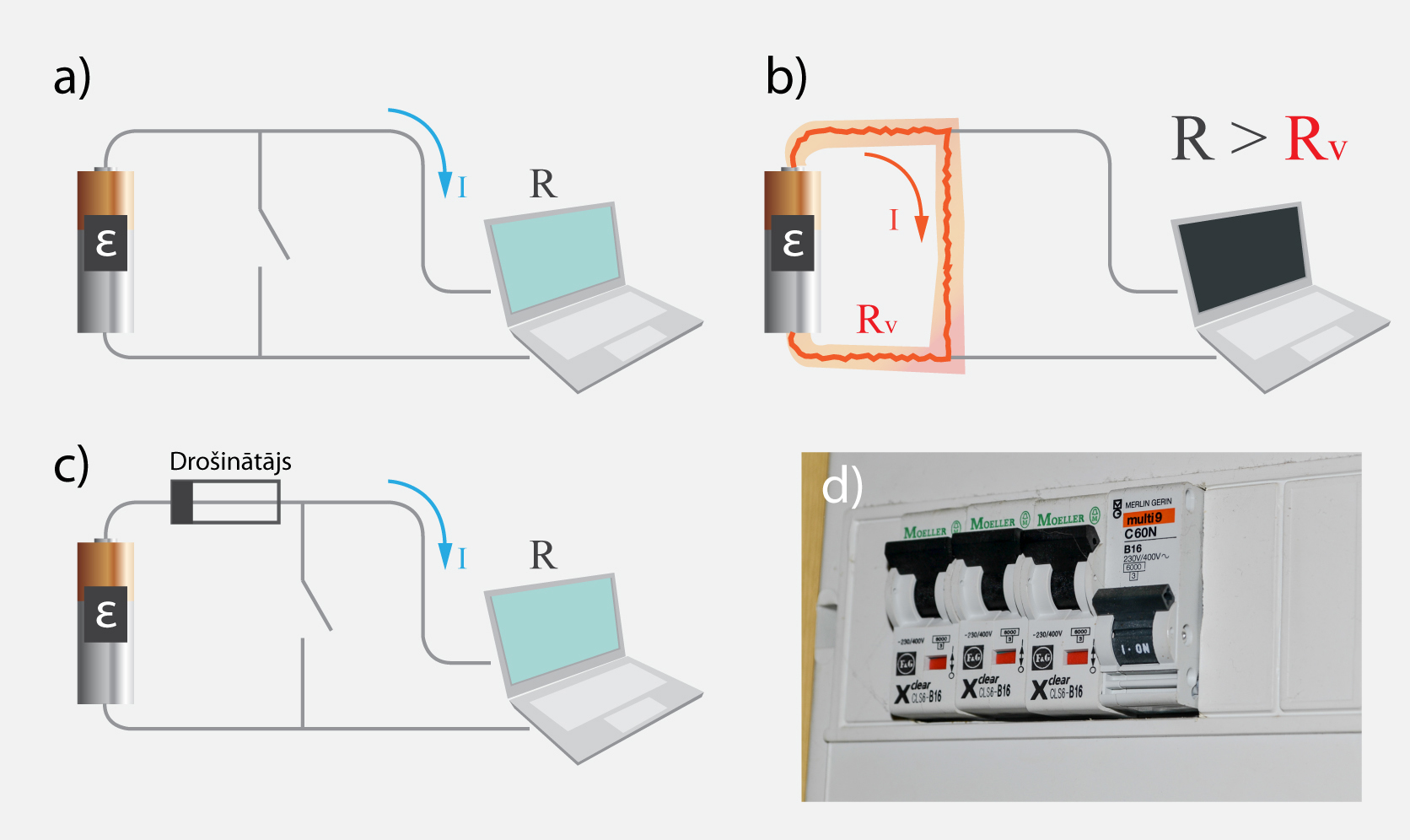
5.att. Elektriskā ķēde un drošinātājs
Lai varētu paredzēt kādas iekārtas elektroenerģijas patēriņu, mums ir jāzina tās jauda. Sadzīvē mēs lietojam vairākas iekārtas reizē, kuras ir saslēgtas dažādos slēgumos un pieslēgtas pie viena elektroenerģijas avota, piemēram, vienam pagarinātājam pieslēgta lampa, dators un radio ir saslēgti paralēli un pieslēgti elektrotīklam (avots). Lai aprēķinātu šādas sistēmas patērēto enerģiju, ir jāzina slēguma kopēja jauda. Ja paralēlajā slēgumā saslēgti trīs patērētāji ar pretestībām R1, R2un R3un pieslēgti elektrības avotam ar spriegumu U, tad katrs patērētājs ir pakļauts spriegumam U, kura rezultātā caur to plūst attiecīgi I1, I2un I3stipra strāva, ko noteic patērētāja pretestība (1. att.). Katra atsevišķā avota jauda ir šāda: P1 = I1U, P2 = I2U, P3 = I3U. Kopējā jauda P = IU. Tā kā paralēlajam slēguma I = I1 + I2 + I3, tad P = IU = (I1 + I2 + I3)U = I1U + I2U + I3U = P1 + P2 + P3. Redzams, ka slēguma kopējā pretestība ir vienāda ar atsevišķo patērētāju jaudas summu.
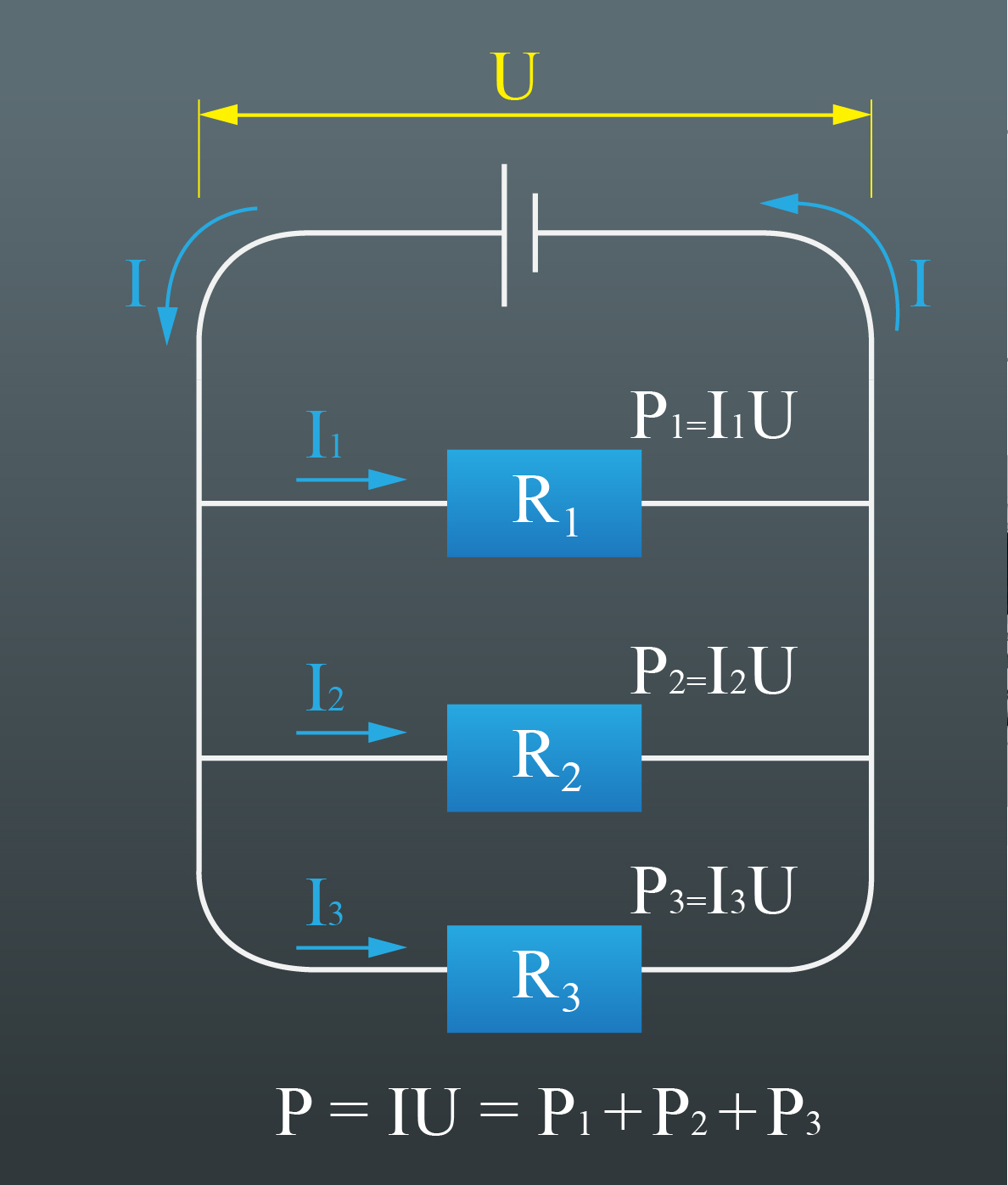
1.att. Jauda paralēlajā slēgumā
Ja trīs pretestības R1, R2un R3saslēdz virknē un pieslēdz vienam un tam pašam avotam, tad katram patērētājam raksturīgs savs sprieguma kritums U1, U2un U3, taču strāvas stiprums caur visiem patērētājiem ir viens un tas pats – I (2. att.). Katra patērētāja jauda ir šāda: P1 = IU1, P2 = IU2un P3 = IU3. Arī šajā gadījumā kopējā jauda P = IU. Ņemot vērā, ka virknes slēgumam U = U1 + U2 + U3, redzam, ka P = IU = I(U1 + U2 + U3) = IU1 + IU2 + IU3 = P1 + P2 + P3. Tas nozīmē, ka arī virknes slēguma kopējā jauda ir vienāda ar visu patērētāju jaudas summu.
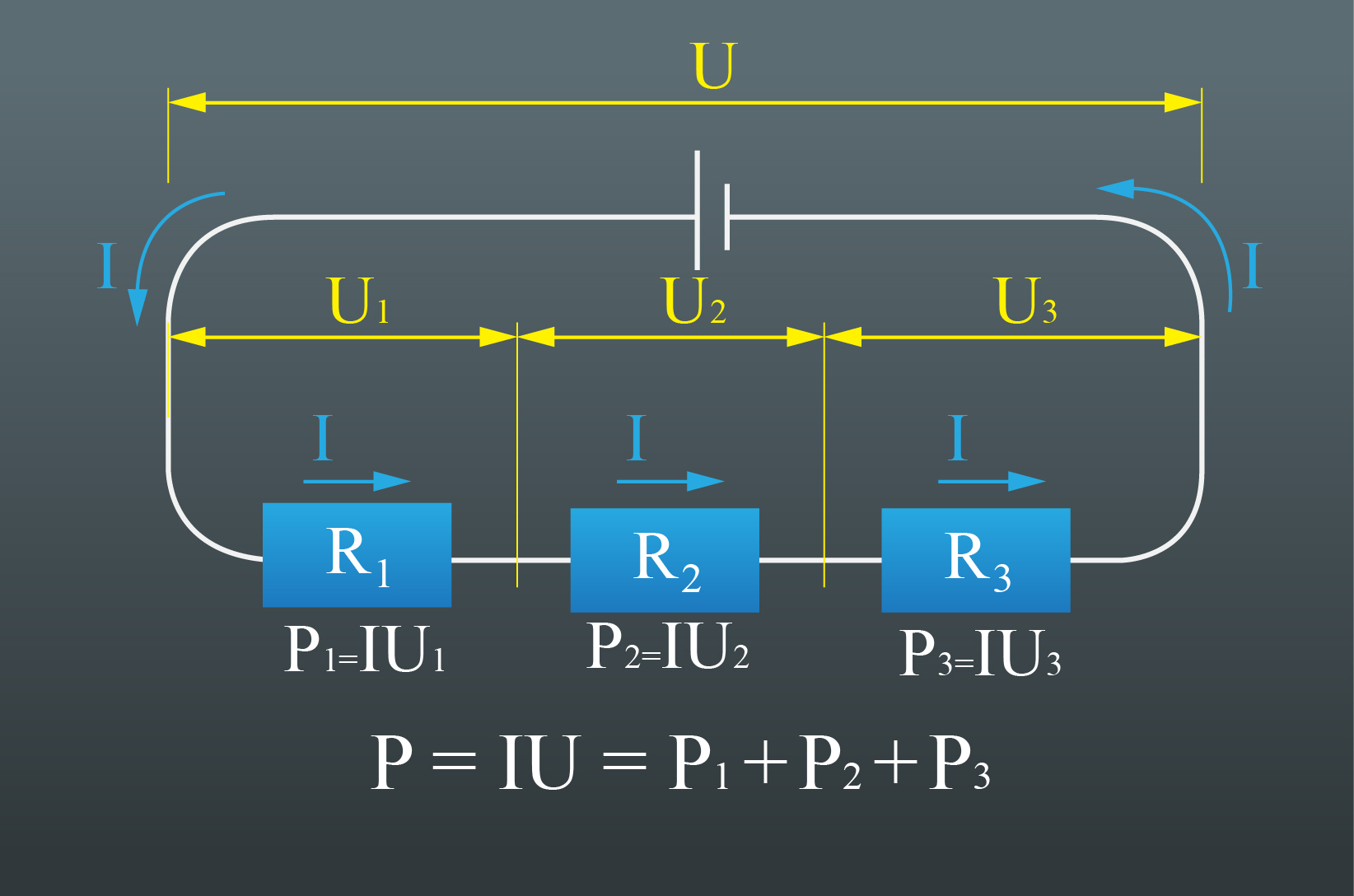
2.att. Jauda virknes slēgumā
Līdztekus patērētāju jaudām dažādos slēgumos svarīgi arī, kāds siltuma daudzums izdalās no katra patērētāja. Ja ierastās trīs pretestības R1, R2un R3saslēgtas virknē un pieslēgtas spriegumam U (3. att. a), tad pēc virknes slēguma likumiem cauri patērētājiem plūst strāva I. Pēc Džoula–Lenca likuma, siltuma daudzums, kas izdalās no katra vadītāja, ir Q1 = I2R1t, Q2 = I2R2tun Q3 = I2R3t. Redzams: jo lielāka ir patērētāja pretestība, jo lielāks siltums no tā izdalās.
Ja pieminētās pretestības saslēdz paralēli un pieslēdz spriegumam U (3. att. b), tad caur katru patērētāju plūst citāda stipruma strāva atkarība no pretestības lieluma, un lietot Džoula–Lenca likumu ierastajā formā nebūs uzskatāmi, jo mainās gan I, gan R. Tādēļ izmantosim U, kas paralēlajā slēguma nemainās. Pēc Oma likuma I = U : R, līdz ar to Džoula–Lenca likumu var pārrakstīt kā Q = U2t : R. Šādā gadījumā no katras pretestības izdalītais siltuma daudzums ir šāds: Q1 = U2t : R1, Q2 = U2t : R2un Q3 = U2t : R3. Tādēļ izriet, ka paralēlajā slēgumā atšķirībā no virknes slēguma visvairāk siltuma izdalās no tā patērētāja, kuram ir mazākā pretestība.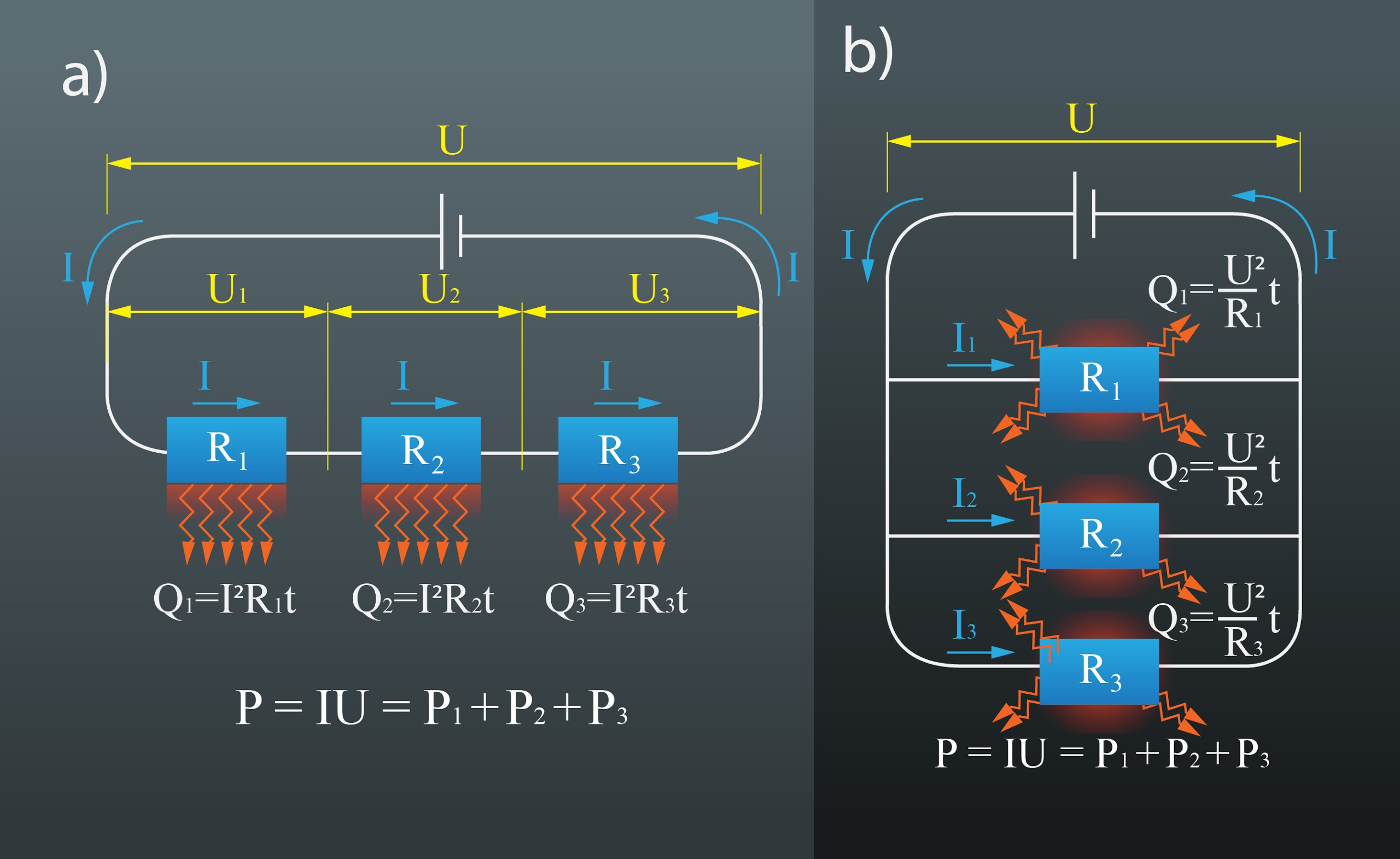
3.att. Siltuma izdalīšanās virknes un paralēlajā slēgumā
Jauda P = IU, ko no elektroenerģijas avota saņem patērētājs, nav visa jauda, ko elektroenerģijas avots var dot, tā ir tikai lietderīgā jauda. Avota iekšējās pretestības r un caur to plūstošās strāvas I dēļ, tam arī piemīt jauda Pr = IU = I2r. Līdz ar to slēguma kopējā jauda Pp = P + I2r (4. att. a). Tā kā elektroenerģijas patērētājam nozīmīga ir lietderīgā jauda, tad ir jāatrod tādi slēguma parametri, kad lietderīgā jauda P ir vislielākā. Ja pie nemainīgas kopējās jaudas tiek variēta patērētāja pretestība un apskatīts, kāda ir lietderīgā jauda (4. att. b), tad var redzēt, ka maksimālā lietderīgā jauda Pmax ir tad, kad patērētāja pretestība R sakrīt ar avota iekšējo pretestību r.
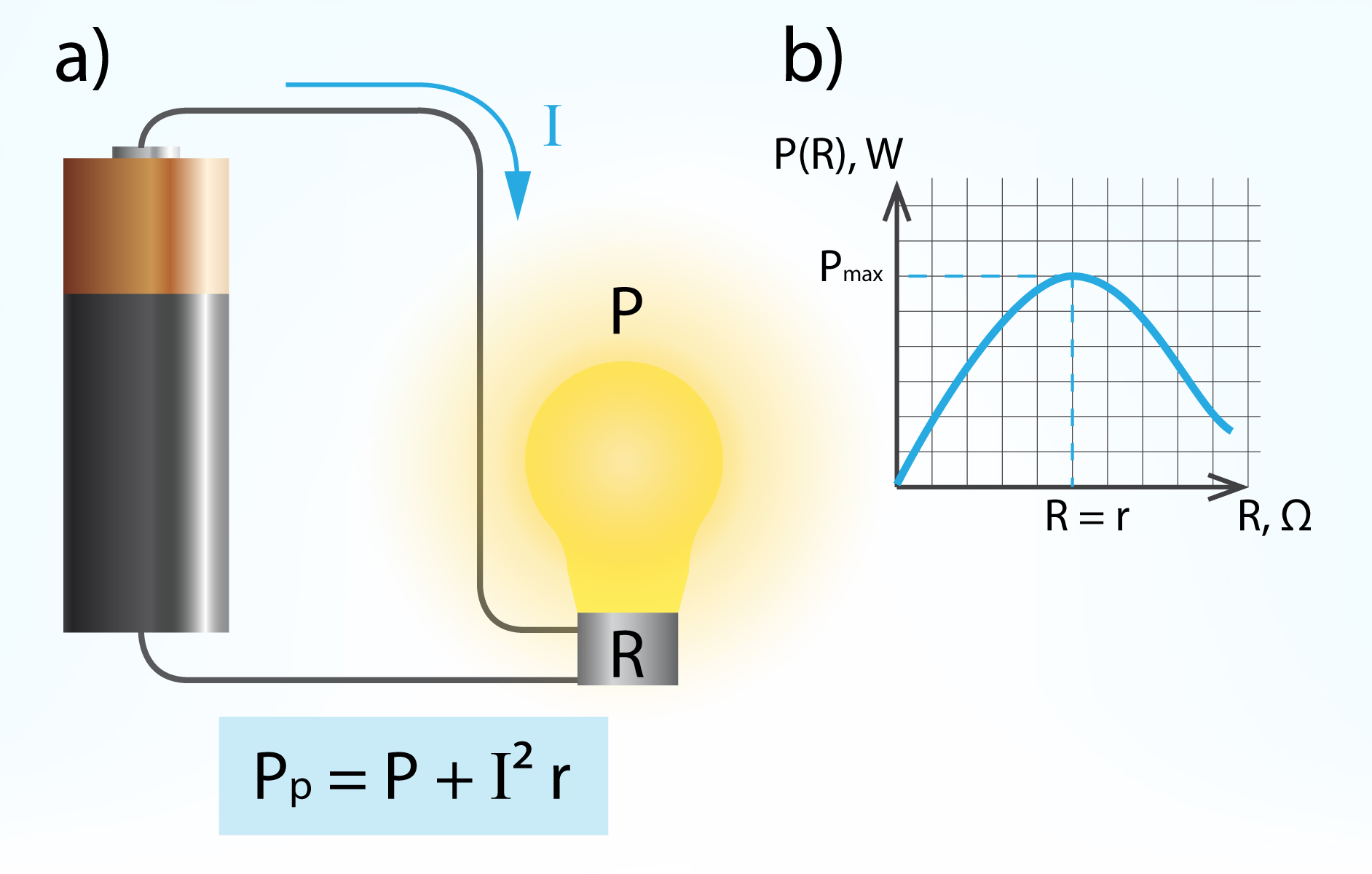
4.att. Lietderīgā jauda P
Elektroenerģijas avotu raksturo lietderības koeficientu η, kas norāda lietderīgās jaudas attiecību pret avota kopējo jaudu: η = P : Pp, kur
P – lietderīgā jauda,
Pp– avota pilnā jauda.
Ja pie nemainīgas kopējās jaudas P slēgumā tiek mainīta patērētāja pretestība R (5. att.), tad ir manāma tendence – jo lielākā ir patērētāja pretestība, jo augstāks lietderības koeficients strāvas avotam. 5. attēlā redzams, ka brīdī, kad patērētāja pretestība vienāda ar avota iekšējo pretestību, lietderības koeficients ir tikai 0,5 jeb 50 %. Līdz ar to elektriskajā slēgumā ir jāizvēlas, vai ir vēlme iegūt maksimāli lielu jaudu (ārējo pretestību salāgot ar avota iekšējo pretestību, 4. att. b), vai arī pēc iespējas lietderīgāk izmantot strāvas avotu. Elektroenerģijas pārvadē izvēlas lietderīgāko variantu, bet, piemēram, skaņas pastiprināšanas ierīcēs nozīmīga ir pēc iespējas lielāka jauda.
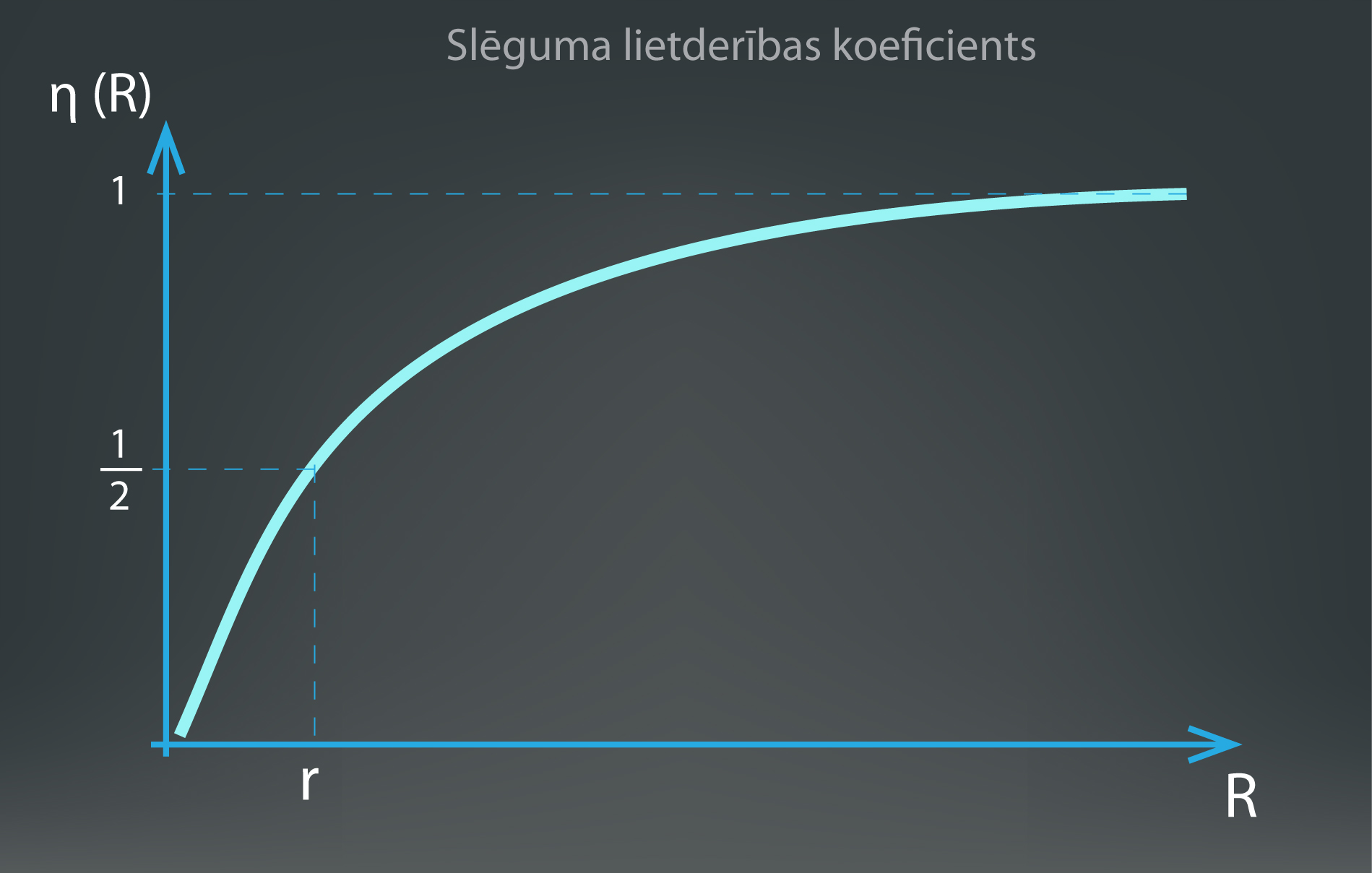
5.att. Slēguma lietderības koeficients
Elektriskie lādiņi elektriskajā ķēdē pārnes enerģiju, kas vienāda ar E = Pt = IUt. No strāvas stipruma definīcijasI = q : t, tādēļ E = qU. Ja 1 C liels lādiņš pārvar 12 V spriegumu (6. att. a), tad tas ir pārnesis E = 1·12 = 12 J enerģijas. Ja 1 C liels lādiņš iziet caur vadītāju, kura spriegumu starpība ir 220 V (6. att. b), tad šādā gadījumā kulons jau ir pārnesis E = 1 · 220 = 220 J enerģijas. Tas nozīmē: jo lielāks ir spriegums, jo lielāku enerģijas daudzumu pārnes viens un tas pats lādiņa lielums.
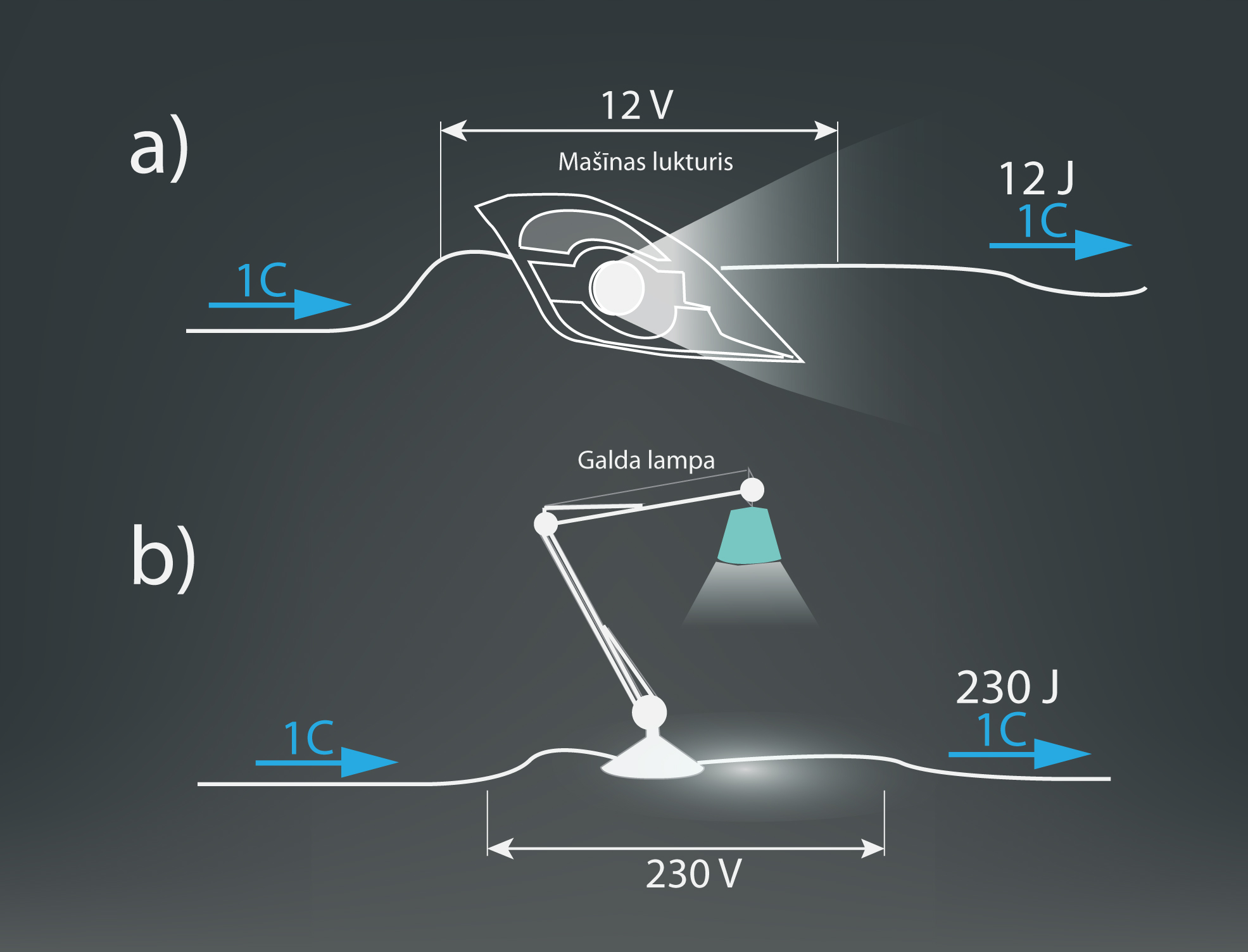
6.att. Kulona enerģija dažādiem spriegumiem
Šis ir iemesls, kādēļ, apskatot, piemēram, automašīnas elektriskās sistēmas drošinātājus (7. att. a), tur figurē drošinātāji, kas iztur pat 30 A strāvu, taču, ielūkojoties dzīvokļa vai mājas drošinātāju klāstā (7. att. b), tur atrodami daudz mazākām strāvas stipruma vērtībām domāti drošinātāji, piemēram, 3 vai 5 A. 220 V sistēmā viens kulons lādiņa pārnes lielāku enerģiju, tādēļ strāvas stipruma vērtībām nav jābūt tik lielām kā, piemēram, automašīnas 12 V sistēmā.

7.att. Drošinātāji 12 V un 220 V elektriskajām sistēmām