Klapeirona – Mendeļejeva vienādojums, ko dēvē par ideālas gāzes stāvokļa vienādojumu, apraksta sakarību starp gāzes parametriem (1. att.)

1.att. Klapeirona – Mendeļejeva vienādojums jeb ideālas gāzes stāvokļa vienādojums
Dabā un tehnikā norisinās procesi, kuros kāds no gāzes parametriem – spiediens, tilpums vai temperatūra – nemainās. Šādus procesus, ja gāzes masa paliek nemainīga, sauc par izoparamteriskiem procesiem (2. att.). Apskata trīs izoparametriskus procesus:
1) izotermisks (nemainās temperatūra T);
2) izobārisks (nemainās spiediens p);
3) izohorisks (nemainās tilpums V).
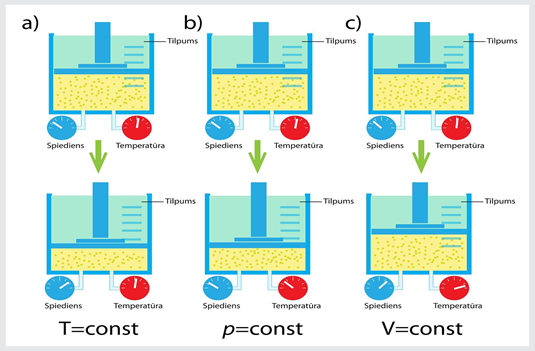
2.att. a) izotermisks, b) izobārisks un c) izohorisks process
Ja kāda procesa laikā nemainās temperatūra, tad to sauc par izotermisku procesu. Šādā procesā reizinājums pV ir konstants. Tas nozīmē: ja palielinās spiediens, tad samazinās tilpums, un otrādi. Šo procesu apraksta Boila – Mariota likums. Tā grafiskais attēlojums p-V koordinātās redzams 3. att.
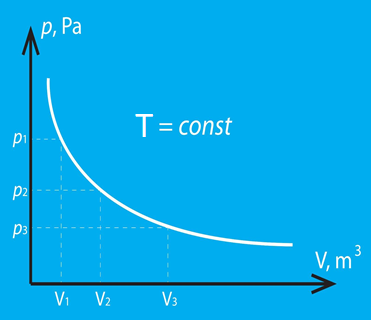
3.att. Izotermiska procesa grafisks attēlojums p-V koordinātās
Par izobārisku sauc procesu, kurā nemainās sistēmas spiediens. Šādā procesā tilpums ir tieši proporcionāls temperatūrai, kas redzams arī procesa grafiskajā attēlojumā (4. att.). Šo likumu sauc arī par Gē Lisaka likumu.
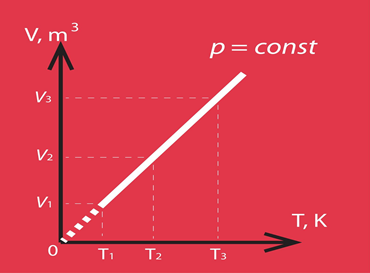
4.att. Izobāriska procesa grafisks attēlojums V-T koordinātu sistēmā
Ja procesa laikā nemainās tilpums, tad šo procesu dēvē par izohorisku. To apraksta Šarla likums, kas nosaka: ja V = const, arī attiecība p : T ir konstanta, līdz ar to iegūstama sakarība, kas skatāma 5. att.
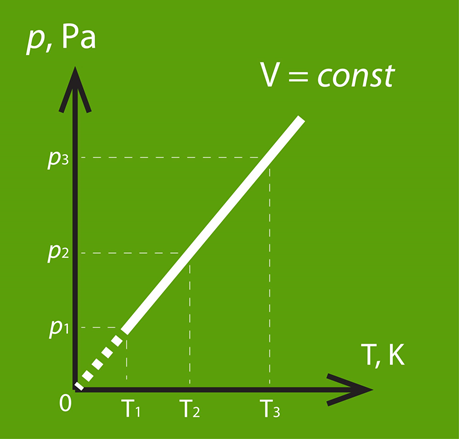
5.att. Izohoriska procesa grafisks attēlojums p - T koordinātu sistēmās
Klapeirona – Mendeļejeva likums tapa divos piegājienos. Vispirms 1834. gadā fiziķis Benuā Klapeirons atklāja: ja ideāla gāze atrodas noslēgtā sistēmā (gāzei paliek nemainīga masa, nenotiek siltumapmaiņa ar ārpusi), tad šie parametri ir savā starpā saistīti tā, ka spiediena un tilpuma reizinājuma attiecība pret temperatūru ir nemainīgs lielums jeb p . V : T = const (1. att.). To pazīst kā Klapeirona vienādojumu. 1874. gadā fiziķis Dmitrijs Mendeļejevs papildināja Klapeirona vienādojumu. Viņa papildinājums noteica, ka konstanto lielumu Klapeirona vienādojumā var izteikt, ja zina gāzes masu un molmasu. Tā tapa Klapeirona – Mendeļejeva vienādojums pV = m : M . R . T
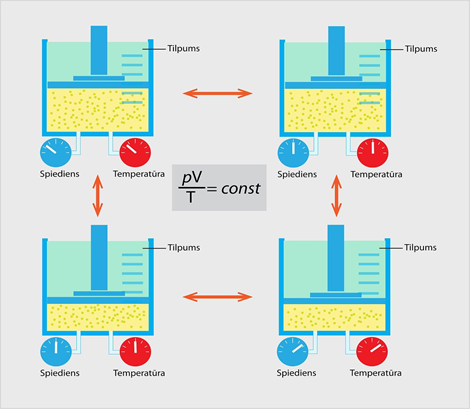
1.att. Noslēgtā sistēmā darbojas Klapeirona vienādojums
Ja apskata Klapeirona – Mendeļejeva vienādojumu pV = m : M . R . T izotermiska procesa gadījumā, var secināt: ja T = const, tad reizinājumam pV arī jābūt konstantam, no kā arī izriet Boila – Mariota likums. Procesa grafiks ir atkarīgs gan no tā, kādus parametrus izvēlas uz asīm, gan arī no nemainīgā gāzes parametra lieluma (2. att.).
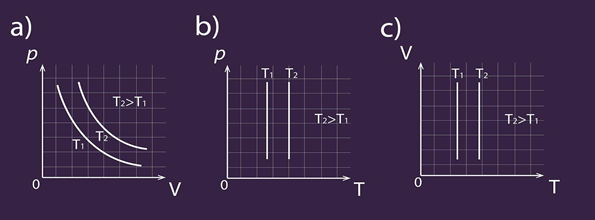
2.att. Izotermiska procesa grafisks attēlojums dažādās koordinātu sistēmās
Ar Boila – Mariota likumu saskaramies tad, kad samazinām kādas noslēgtas sistēmas tilpumu, piemēram, paņemam plastmasas maisiņu, aizspiežam tam atveri un strauji pa to uzsitam, samazinot tā tilpumu. To izdarot, strauji pieaug spiediens, kas var izvērsties par skaļu blīkšķi, jo maisiņš var pārsprāgt. Boila – Mariota likums nosaka arī to, ka gāzes burbulīšu tilpums, kādā ūdens tilpumā, ceļoties augšup palielinās (3. att.). Tas ir tādēļ, ka dziļumā ir lielāks ūdens spiediens, līdz ar to tilpums tur attiecīgi ir mazāks.

3.att. Boila – Mariota likuma izpausme dabā
Izobāriska procesa gadījumā no transformēta Klapeirona – Mendeļejeva vienādojuma V = m : M . R . T : p, ja p = const, izriet, ka tilpums ir tieši proporcionāls temperatūrai. Šā Gē Lisaka likuma grafiskais attēlojums redzams 4. att., kur arī atklājas – jo lielāks ir sistēmas spiediens, jo straujāk mainās tilpums atkarībā no temperatūras.
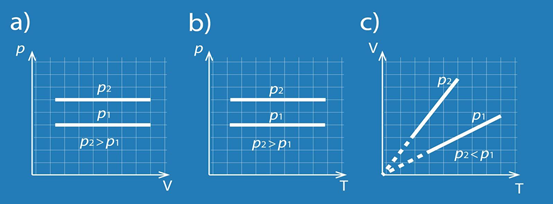
4.att. Izobāriska procesa grafisks attēlojums dažādās koordinātu sistēmās
Ar Gē Lisaka likumu nākas sastapties situācijās, kad ievērojami mainās sistēmas temperatūra, kas izraisa sistēmas tilpuma izmaiņu, piemēram, ziemā automašīnas riepas pie tā paša spiediena ir „mīkstākas”, ieliekot uzsilušu un aizskrūvētu ūdens pudeli ledusskapī, tā, samazinoties temperatūrai, saraujas. Gē Lisaka likums izpaužas arī gaisa balonos (5. att.):
ja balonā spiediens ir nemainīgs, tad, samazinot vai palielinot tajā esošā gaisa temperatūru, attiecīgi samazinās vai palielinās balona tilpums.

5.att. Lidojot ar gaisa balonu, jārēķinās ar Gē Lisaka likumu
Arī izohoriska procesa gadījumā var apskatīt modificētu Klapeirona – Mendeļejeva vienādojumu p = m : M . R . T : V, no kura pie V = const izriet, ka spiediens ir tieši proporcionāls temperatūrai. 6. att. redzami procesa attēlojumi dažādās koordinātu sistēmās. 6. att b redzams: jo lielāks V, jo straujāk mainās p atkarībā no T.
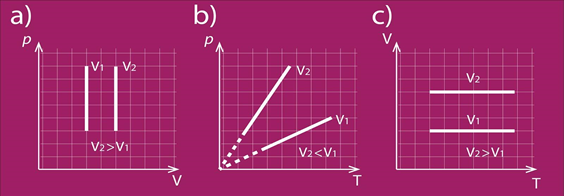
6.att. Izohoriska procesa grafisks attēlojums dažādās koordinātu sistēmās
Ar Šarla likumu dažkārt nākas saskarties nepatīkamā gaisotnē, jo tieši šis likums nosaka dažādu sistēmu uzsprāgšanu. Ja kāds trauks ir noslēgts un tajā pieaug temperatūra T, tad līdz ar T pieaug arī spiediens, kas pēc zināmu vērtību sasniegšanas var izraisīt pat avāriju. Ja katlam, kurā vāra ūdeni, vākā nav atveres spiediena samazināšanai, tad pēc tam, kad sācis vārīties ūdens, katla vāciņš lēkā tieši Šarla likuma dēļ (7. att.).

7.att. Šarla likums uz elektriskās plīts
No izohoriska procesa grafika ideālai gāzei ir iespējams noteikt absolūtās nulles vērtību. Ja p – T grafika taisni turpina, tad tā krusto T asi pie absolūtās nulles vērtības (1. att.)
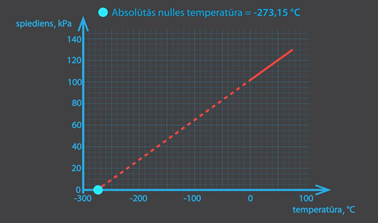
1.att. Ideālas gāzes spiediens, mainoties temperatūrai
Tomēr šāda grafiskā sakarība var būt tikai ideālai gāzei, jo reālas gāzes līkne (2. att.) nesasniedz absolūto nulli. To galvenokārt nosaka molekulu savstarpējā mijiedarbība, ko ideālas gāzes modelī neņem vērā.

2.att. Reālas gāzes līkne atšķiras no ideālas gāzes līknes