Gāzu sastāvā ir ļoti daudz molekulu, turklāt tās ļoti ātri kustas un mijiedarbojas gan savā starpā, gan ar dažādiem šķēršļiem, piemēram, trauka sieniņām. Ja mēģinātu gāzes uzvedību aprakstīt, ņemot vērā visas mijiedarbības, tad būtu nepieciešamas garas un sarežģītas formulas, kas pat vienkāršākajos gadījumos prasītu milzīgus aprēķinus. Tādēļ tiek lietots vienkāršots gāzes modelis – ideālā gāze, kas atvieglo gāzē notiekošo procesu aprakstu (1. att.).
Ideālās gāzes modelī pieņemts, ka
- - molekulu lineārie izmēri ir mazi, salīdzinot ar attālumu starp tām;
- - molekulas ir masas punkti, starp kuriem nedarbojas mijiedarbības spēki, izņemot īsus brīžus molekulu sadursmes laikā;
- - molekulu sadursmes ar trauka sienām ir elastīgas.
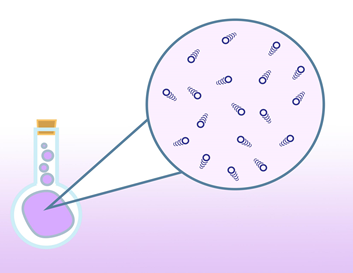
1. att. Ideālās gāzes modelī molekulas uzskata par ļoti mazām, elastīgām lodītēm, starp kurām nedarbojas mijiedarbības spēki
Izmantojot ideālās gāzes modeli, gāzē notiekošo procesu aprakstam lieto vienkāršotas sakarības, tomēr tās adekvāti atspoguļo ikdienas situācijas, kurās iesaistīta gāze, piemēram, procesus ar atmosfērā esošo gāzu vai ūdens tvaika līdzdalību. Arī, piemēram, uzpumpējot ūdens raķeti (2. att.), tā veidojošās gāzes uzvedas kā ideāla gāze: straujš tilpuma samazinājums izraisa strauju spiediena pieaugumu, kas uzpumpē ūdens raķeti.

2.att. Ūdens raķetes uzpumpēšanu var aprakstīt, izmantojot ideālās gāzes modeli
Ideālas gāzes stāvokļa raksturošanai var izmantot vairākus lielumus (3. att.), ko sauc par gāzes parametriem. Galvenie no tiem ir:
1) tilpums,
2) masa,
3) spiediens,
4) temperatūra.
Šie parametri savā starpā ir cieši saistīti, līdz ar to viena parametra izmaiņa izraisa citu gāzi raksturojošu parametru maiņu.
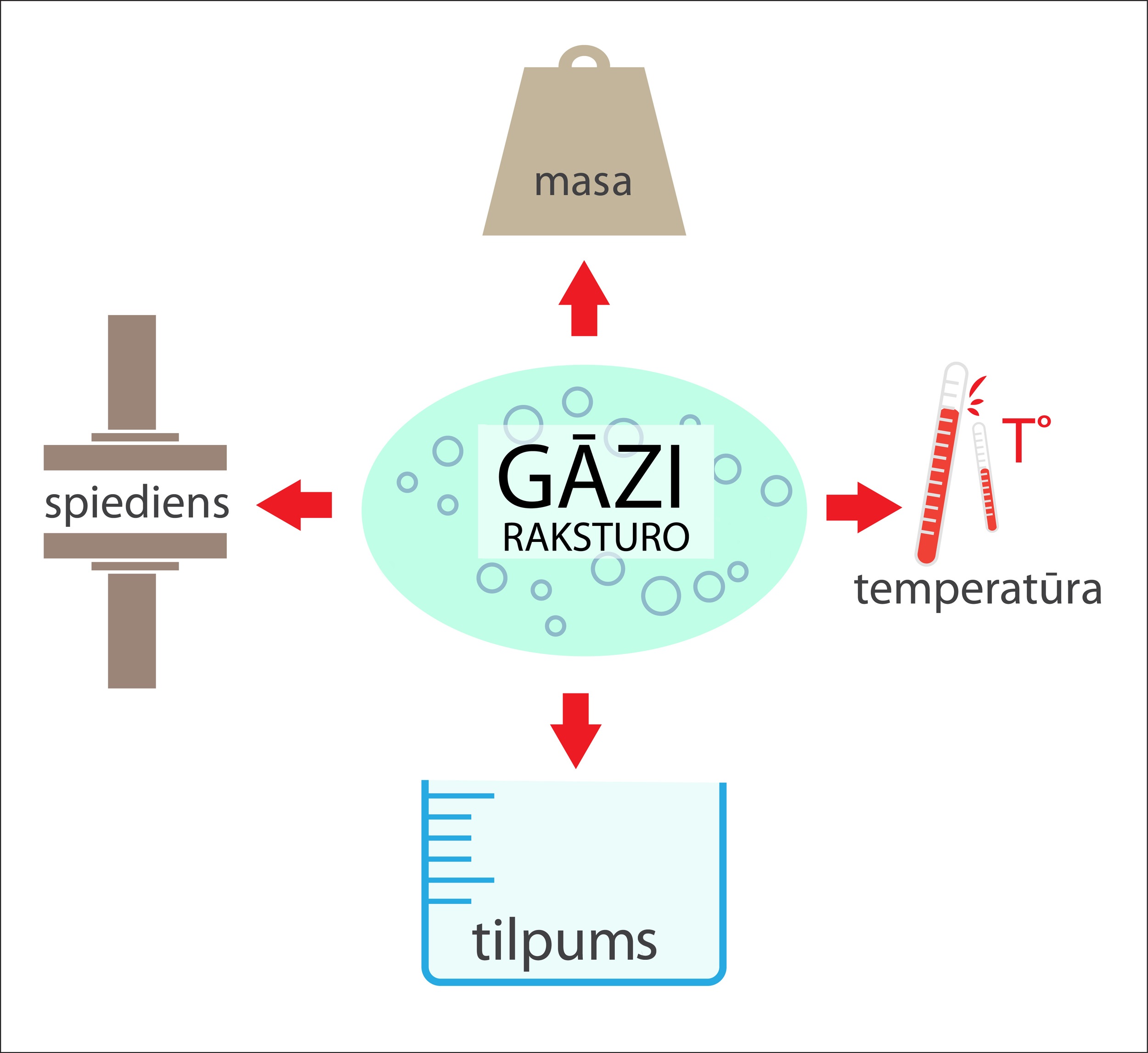
3.att. Gāzi var raksturot ar tilpumu, spiedienu, temperatūru un masu
Gāze izplešas pa visu telpu, kas tai ir dota, tādēļ lietot gāzes tilpumu jēdzienu, ja gāze nav ieslēgta kādā traukā, nav jēgas. Par gāzes tilpumu V sauc tilpumu, kurā gāze ir ieslēgta un pa kuru notiek gāzes daļiņu siltumkustība. Katras atsevišķās tilpumā kustošās gāzes daļiņas masa ir niecīga, tomēr gāzes masu veido visu daļiņu masu summa (4. att.). Tā kā daļiņu skaits gāzē ir liels, tad arī gāzes masa ir ievērojams skaitlis. Sadaļā par vielas uzbūvi un molekulu siltumkustību tika apskatīts molmasas jēdziens, to lieto arī gāzēm. Ja ir N gāzes daļiņas un gāzes molmasa ir M, tad gāzes masa m= N : NA .M, jo Avogadro skaitlis NAnosaka, cik daudz daļiņu atrodas vienā molā gāzes. Apskati animācijas par gāzes likumiem: animācijas.
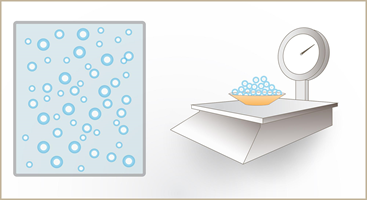
4.att. Gāzes masu veido visu to veidojošo daļiņu kopējā masa
Kādā tilpumā ieslēgtas gāzes daļiņas saduras ne tikai savā starpā, bet arī ar trauka sieniņām. Triecoties pret sienu, gāzes daļiņas rada spiedienu (5. att.). Gāzes spiediens p rodas, daudzām gāzes daļiņām vienlaicīgi nonākot kontaktā ar trauka sienu. Gāzes spiedienu var aprēķināt, lietojot formulup = 1 : 3.m0 .N : V .v2, kur
m0- vienas daļiņas masa,
N - daļiņu skaits,
V – tilpums,
v - daļiņu kustības vidējais ātrums.
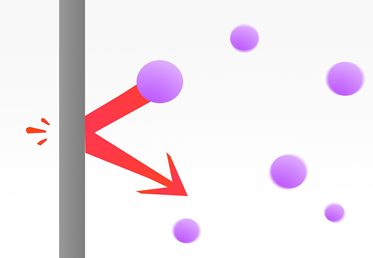
5.att. Gāzes spiedienu rada molekulas, kas triecas pret trauka sienām
Tā kā daļiņu kustības ātrumu raksturo arī enerģija, tad spiediena aprēķināšanas izteiksmi var pārrakstīt kā p = 2 : 3N : V .Wvid, kur Wvidir daļiņu kustības vidējā kinētiskā enerģija, kuru nosaka vēl viens gāzes raksturlielums – temperatūra T. Daļiņu kustības vidējo kinētisko enerģiju un temperatūru saista sakarība Wvid = 3 : 2kT, kur Bolcmaņa konstante k = 1,38 .10-23 J/K. Izteiksme parāda: jo augstāka ir temperatūra, jo lielāka ir daļiņu enerģija un līdz ar to kustības ātrums (6. att.)
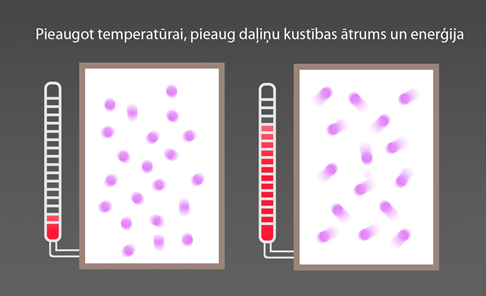
6.att. Pieaugot temperatūrai, ir pieaudzis daļiņu kustības ātrums un enerģija
Temperatūras un spiediena atkarību attēlojot grafiski (7. att.), redz: ja pagarinātu iegūto taisni, tā pie kādas noteiktas temperatūras krustotu x asi, turklāt šī temperatūra nav atkarīga no gāzes sastāva. Šo temperatūru sauc par absolūto nulli, un tās vērtība Celsija skalā ir T0 = -273 0C.
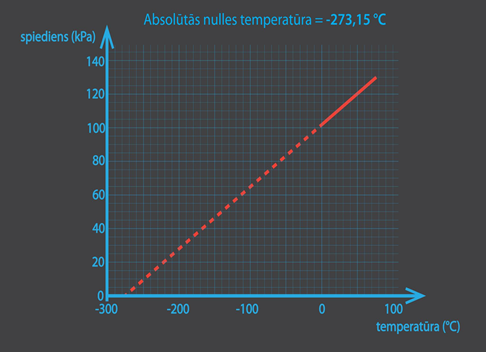
7.att. Absolūtā nulle ir zemākā iespējamā temperatūra dabā