Fizmix sadaļā "Mehāniskās svārstības un viļņi" kopā ar citām viļņu īpašībām tika apskatīta difrakcija, kas piemīt arī gaismas viļņiem. Atšķirība vien tā, ka gaismas viļņiem ir krietni mazāks viļņa garums. Ja gaismas vilni apskatītu kā daļiņu plūsmu, tad šķēršļu ietekmē nekādas novirzes no taisnvirziena kustības nenotiktu, gaisma tiktu “nogriezta” līdz ar barjeras malu (1. att. a). Tomēr tā nenotiek, un gaisma apliecas ap šķēršļiem, kas ir viens no pierādījumiem gaismas viļņveida dabai (1. att. b).
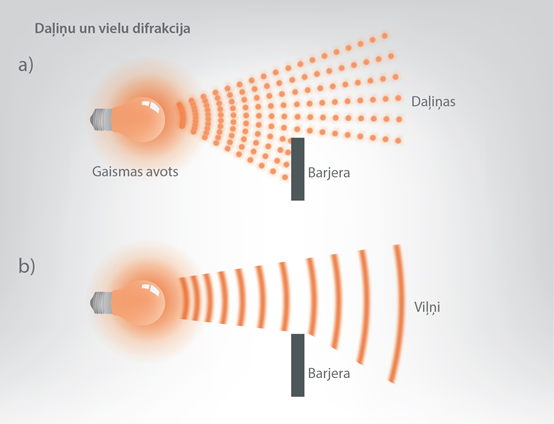
1.att. Daļiņu un viļņu difrakcija
Ja monohromatiska (vienas krāsas) gaisma virzās cauri vienai mazai spraugai, kuras izmēri salīdzināmi ar gaismas viļņu garumu, tad, novietojot aiz spraugas lēcu un ekrānu, var ieraudzīt vienu intensīvi gaišu centrālo maksimumu, kuram blakus rotājas mazāki gaismas intensitātes maksimumi (2. att. a). Šajā gadījumā notiek gaismas difrakcija vienā spraugā. Centrālais maksimums veidojas no stariem, kas iziet cauri spraugai nenoliecoties, bet blakus maksimumi veidojas, interferējot stariem, kas, izejot cauri spraugai, noliecas (2. att. a). Laižot spraugā monohromatisku gaismu, uz ekrāna veidojas interferences aina attiecīgajā gaismas krāsā (2. att. b), bet, ja uz spraugu laiž balto gaismu, tad difrakcijas rezultātā šī gaisma sadalās spektrā (2. att. c).
Izmēģini sīklietotni par difrakciju vienā spraugā!
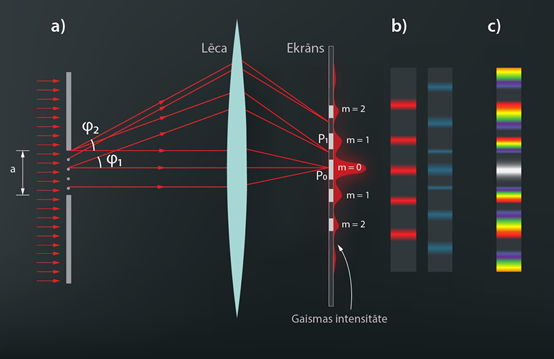
2.att. Gaismas difrakcija vienā spraugā
Tātad papildus tam, ka balto gaismu spektrā var sadalīt, izmantojot stikla prizmu, kurā baltā gaisma sadalās gaismas dispersijas rezultātā (Gaismas izplatīšanās) (3. att. a), pilnu spektru var iegūt arī difrakcijā, kas rodas, gaismai izejot cauri vienai mazai (šaurai) spraugai (3. att. b).
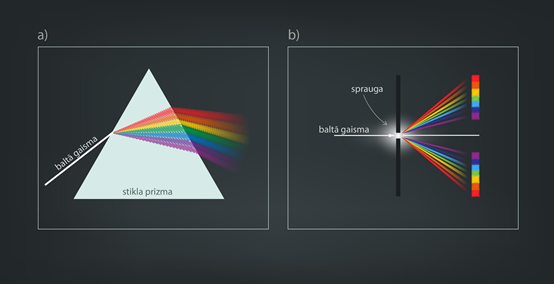
3.att. Baltās gaismas sadalīšanās spektrā
Ar vienu šauro spraugu iegūtais spektrs ir ar mazu izšķirtspēju un vāju apgaismojumu. Lai šos parametrus uzlabotu, var lietot vairākas pēc kārtas vienādos attālumos novietotas šaurās spraugas, tādā veidā iegūstot difrakcijas režģi (4. att.). Ja attālums starp šaurajām spraugām ir d, tad difrakcijas režģi apraksta formula dsinφ=mλ, kur
φ - difrakcijas leņķis, grādos
m - difrakcijas spektra kārta
λ - gaismas viļņa garums, m
Attālumu d sauc par režģa konstanti. Ar difrakcijas režģi iegūtajā ainā ir vairākas spektra kārtas, no kurām centrālai kārtai m = 0, bet pārējās kārtas katram gaismas viļņa garumam tiek numurētas pieaugošā vai dilstošā secībā atkarībā no tā, kurā centrālā maksimuma pusē kārta atrodas (4. att.). Jo tuvāk difrakcijas režģa spraugas atrodas viena otrai, jo vairāk spektra kārtu var saskatīt uz ekrāna.
Aplūko citu materiālu par difrakciju!
Ja netīk lasīt, vari noskatīties mācību video no macibuvideo.lv par difrakciju!
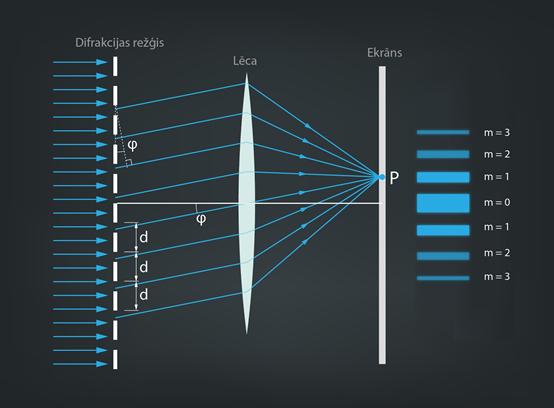
4.att. Gaismas difrakcija režģī
Tā kā difrakcijas režģis sadala balto gaismu spektrā, tad to var izmantot spektrālo aparātu būvē. Viens no šādiem spektrālajiem aparātiem nereti sastopams arī skolas fizikas kabineta aprīkojumā (5. att.). Ar spektrālajiem aparātiem var iegūt gaismas avota izstarotās gaismas spektrālo sastāvu un, veicot tālāku analīzi, var uzzināt, no kādiem elementiem sastāv gaismas avots, kā arī fizikālos apstākļus (temperatūra, spiediens, elektriskais un magnētiskais lauks), kādos tas atrodas.

5.att. Difrakcijas režģa spektrālais aparāts
Ja klasē skolotājs noslēpjas aiz galda un uzrunā skolēnus, tad skolēni skolotāju dzird, bet neredz. Tas nozīmē, ka skolotāja izraisītie skaņas viļņi difrakcijas rezultātā apliecas ap galdu un nonāk līdz skolēniem, bet no skolotāja atstarotie gaismas viļņi nenonāk. Difrakcijas parādība var izpausties abu veidu viļņiem, jo difrakcija var notikt tad, kad šķēršļa izmēri ir salīdzināmi ar viļņa garumu. Skaņas viļņa garums var būt pat līdz vairākiem metriem, kas atbilst galda izmēriem, bet gaismas viļņa garums nesasniedz pat milimetra tūkstošo daļu, tādēļ gaismas difrakciju (apliekšanos) ap galdu nenovēro. Šī iemesla dēļ ir svarīgs spraugas platums, ja vēlamies novērot difrakciju vienā spraugā. Ja spraugas platums būs daudz lielāks par gaismas viļņa garumu, tad gaisma, ejot caur šo spraugu, turpinās pārvietoties taisnā virzienā un nenolieksies (1. att. a), bet, ja spraugas platuma izmērs ir salīdzināms ar gaismas viļņa garumu, tad gaismas viļņi, šķērsojot spraugu, nolieksies (1. att. b).
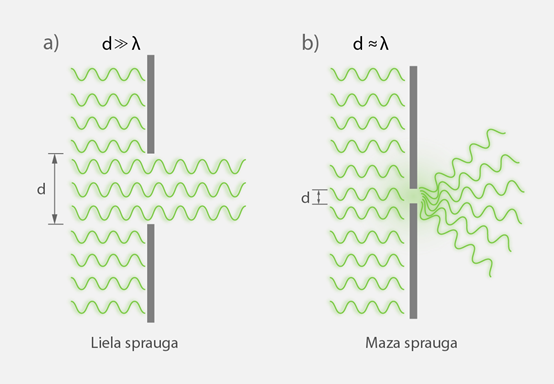
1.att. Gaismas viļņu kustība, atkarībā no spraugas platuma
Fiztēmā par gaismas izplatīšanos 3. solī tika apskatīts Heigensa princips, kuru var izmantot gaismas izplatīšanās skaidrojumā. Heigensa princips noteic: katru jau esošas viļņu frontes punktu var uzskatīt par jaunu punktveida viļņu avotu. Punktveida gaismas avotam viļņu fronte ir sfēriska (2. att. a), un pēc Heigensa principa katra nākamā viļņu fronte arī ir sfēriska. Ja punktveida gaismas avotu aplūko lielā attālumā, tad sfēras liekums ir tik liels, ka viļņu fronti jau var uzskatīt par plakanu (2. att. b). Ja šāda plakana viļņu fronte krīt uz šauro spraugu, tad šaurā sprauga atkal kļūst par punktveida avotam līdzīgu viļņu avotu un aiz spraugas izplatās atkal sfēriski viļņi (2. att. c).
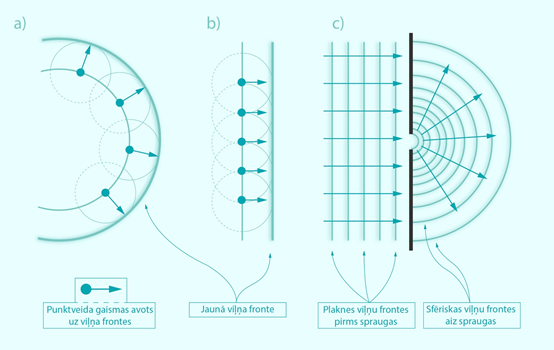
2.att. Heigensa princips difrakcijā
Izejot cauri šaurajai spraugai, katras krāsas gaismas viļņi tiek novirzīti uz visām pusēm (2. att. c) (punktveida gaismas avots staro visos virzienos vienādi), tādēļ uz ekrāna var veidoties vairāki intensitātes maksimumi. Ja tiek lietots difrakcijas režģis, tad katra režģa svītra darbojas kā viena šaura sprauga (3. att.). Lai difrakcijas režģa gadījumā uz ekrāna veidotos intensitātes maksimumi, no dažādiem spraugā nākušiem gaismas viļņiem uz ekrāna jāizpildās konstruktīvās interferences nosacījumam, jo tieši interference ir atbildīga par to, ka uz ekrāna šīs intensīvās joslas veidojas.
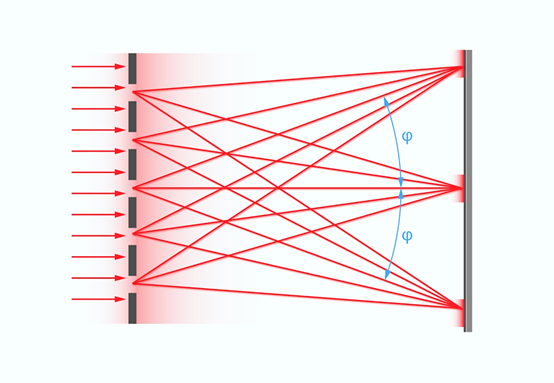
3.att. Vairāku intensitātes maksimumu veidošanās difrakcijā
Apskatīsim gaismu ar viļņu garumu λ, kas ir krīt uz difrakcijas režģi, kam režģa konstante ir d. Gaismas stari, kas pēc iziešanas caur spraugu noliecas vienādā leņķī φ, uz ekrāna nonāk vienā punktā P (4. att.). Lai šajā punktā būtu difrakcijas intensitātes maksimums, starp punktā nonākošajiem gaismas stariem ir jāizpildās konstruktīvās interferences nosacījumam jeb gājienu starpībai ir jābūt vienādai ar mλ, kur m = ±1, ±2, ±3… Gājienu starpība blakus stariem ir vienāda ar dsinφ (4. att.), līdz ar to dsinφ = mλ, kas arī ir difrakcijas režģa formula.
Noskaties mācību video no macibuvideo.lv, kurā parādīts kā iegūst difrakcijas re''zģa formulu!
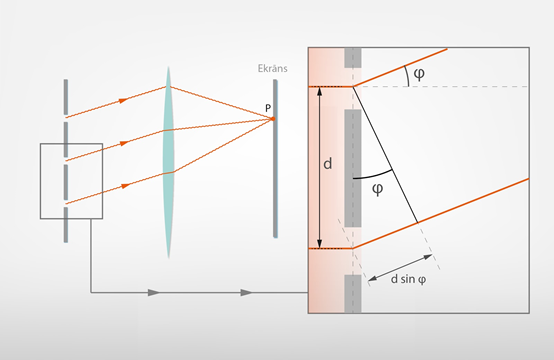
4.att. Difrakcijas režģa formulas iegūšana
Dažādas krāsas gaismas viļņiem ir atšķirīgs viļņa garums, tas var atšķirties pat līdz divām reizēm (sarkanai gaismai ap 800 nm, zilai gaismai – ap 400 nm). Tādēļ sarkanajai gaismai ir vajadzīga lielāka gājiena diference, lai iegūtu difrakcijas maksimumu. Lielāka gājiena diference nozīmē arī lielāku nolieces leņķi, tādēļ sarkanajai gaismai (5. att. a) intensitātes maksimumi atrodas lielākā leņķī no centrālā maksimuma nekā zilajai gaismai (5. att. b). Apmeklē sīklietotni par dažādu krāsu gaismas difrakciju!
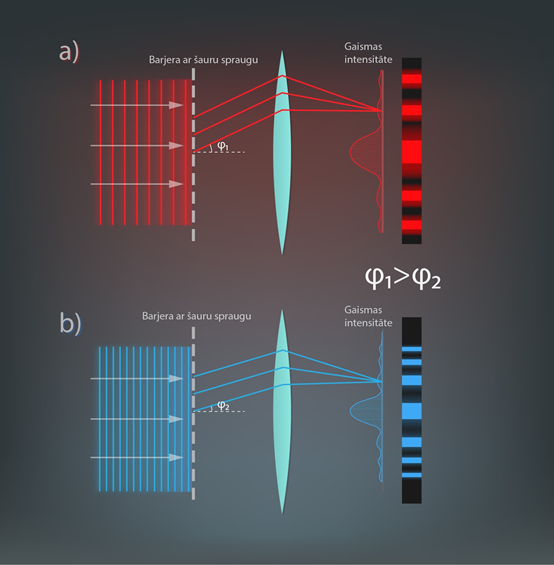
5.att. Sarkanās un zilās gaismas difrakcija
Līdz šim pieminētajos difrakcijas režģos gaisma noliecās, izejot cauri difrakcijas režģa šaurajām spraugām. To sauc par difrakciju caurizgājušā gaismā. Lai šādu difrakcijas režģi izveidotu, ir nepieciešams caurspīdīgs materiāls. Difrakciju var novērot arī atstarotajā gaismā. Ja uz kādu virsmu krīt baltās gaismas stars, tad, pēc atstarošanās likumiem, stara krišanas leņķis būs vienāds ar atstarošanās leņķi (6. att.). Tomēr, ja uz virsmas pietiekoši tuvu cita citai ir savilktas šauras strīpiņas, tad atstarotā gaisma difrakcijas rezultātā sadalās spektrā. To sauc par difrakciju atstarotajā gaismā, un šādā gadījumā difrakcijas režģis var būt veidots no necaurspīdīga materiāla.
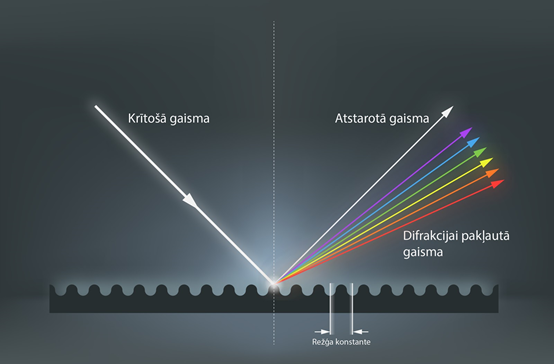
6.att. Difrakcija atstarotajā gaismā
Difrakciju atstarotajā gaismā var novērot, ja pret kādu gaismas avotu aplūko CD vai DVD disku. Šo disku ieraksta celiņi atrodas tik tuvu cits citam (ap 1 μm), ka ieraksta virsma darbojas kā difrakcijas režģis. Apskatot disku pret kādu gaismas avotu, tā virsma zaigo visās varavīksnes krāsās (7. att.).

7.att. Kompaktdisks kā difrakcijas režģis
Tā kā difrakcijas režģis sadala gaismu spektrā, tad to ir iespējams izmantot spektrālo aparātu izveidē. Spektrālie aparāti ir ierīces, ar kurām pēta kāda objekta izstarotās gaismas sastāvu. Vienā no Jauno fiziķu skolas nodarbībām skolēni veidoja sērkociņu kastītes spektrometrus (8. att.). Šāds spektrometrs sastāv no sērkociņu kastītes, kurai augšpusē izgriezts caurums un kurā ievietots gabaliņš no kompaktdiska. Ja sērkociņu kastīti nedaudz paver un pa šo atveri ielaiž gaismu, tad, skatoties noteiktā leņķī pret izgriezto caurumiņu, var redzēt ielaistās gaismas spektru. Attēlā redzamajā spektrometrā ir ielaista Saules gaisma un ir redzams pilns varavīksnes spektrs (8. att.).
Apskaties FIZMIX eksperimentā, kā pašam izveidot savu spektroskopu!

8.att. Jauno fiziķu skolā veidotie sērkociņu kastītes spektrometri
Interference un difrakcija ir ļoti saistītas gaismas īpašības, tādēļ var būt situācijas, kad ir grūti atšķirt, vai runa ir par interferences vai difrakcijas parādību. 1. attēlā ir uzskaitītas dažādas interferences un difrakcijas atšķirības, lai dažādas situācijās šīs parādības būtu vieglāk nodalīt.
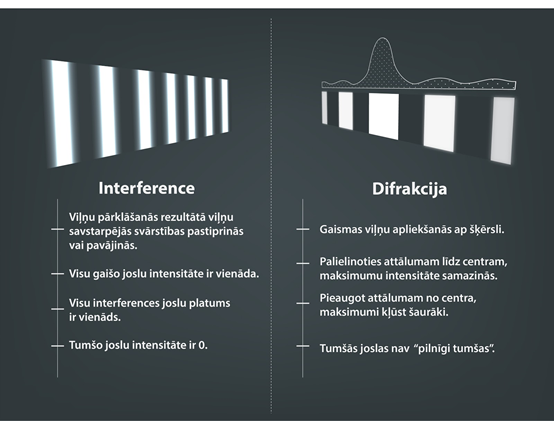
1.att. Atšķirība starp interferenci un difrakciju
Difrakcijas aina ir atkarīga ne tikai no attāluma starp spraugām jeb difrakcijas režģa konstantes d, bet arī no tā, cik platas ir pašas spraugas. 2. attēlā redzams salīdzinājums divām difrakcijas ainām, kurām spraugas platums a atšķiras divas reizes. Vienas spraugas platums ir vienāds ar gaismas viļņa garumu λ, bet otras spraugas platums – ar diviem viļņu garumiem (2. att.). Attēlā redzams, ka plašākai spraugai atbilst asāks difrakcijas centrālais maksimums.
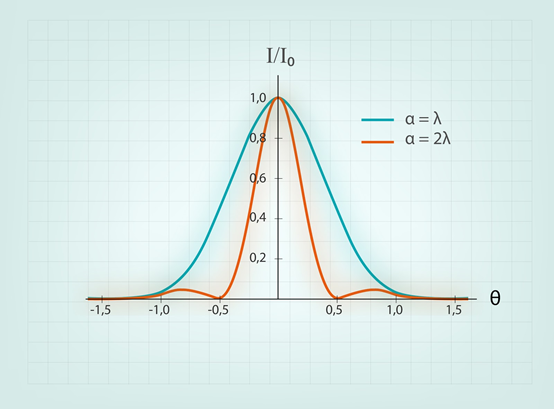
2.att. Difrakcijas aina pie dažādu spraugu platuma
Ja caur vienāda izmēra spraugām laiž sarkano un zilo gaismu, tad difrakcijas ainas centrālo maksimumu platumi atšķiras, un tas ir tieši iepriekš minētā iemesla dēļ, jo sarkanā gaisma (3. att. a) “redz” spraugu divas reizes šaurāku attiecībā pret savu viļņa garumu nekā zilā gaisma (3. att. b).
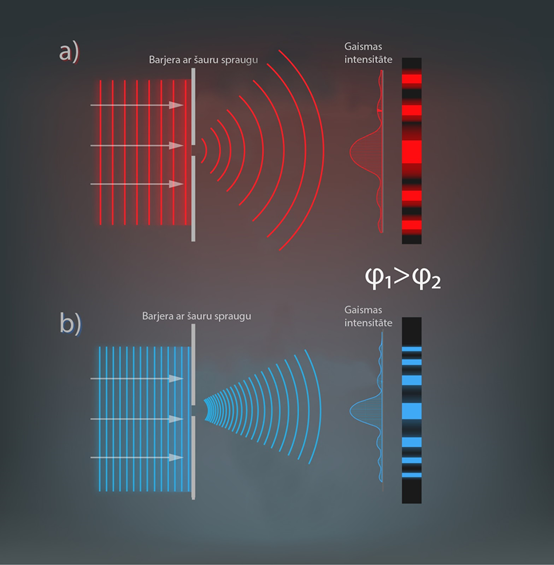
3.att. Sarkanās un zilās gaismas difrakcija vienā spraugā
Ja caur kādu optisko iekārtu tiek apstatīti nelieli objekti, piemēram, tālas zvaigznes, kas izskatās kā spīdoši punkti, tad difrakcijai ir liela nozīme attēla izšķirtspējā jeb tajā, vai šos objektus būs iespējams atšķirt citu no cita. Optiskā aparāta objektīva lēca ir sprauga, kurā notiek gaismas difrakcija, līdz ar to divi spīdoši punkti ir kā divas difrakcijas ainas (4. att. a). Ja difrakcijas ainu maksimumi ir tālu viens no otra, tad punkti ir viegli izšķirami (4. att. a). Ja šie punkti ir pietuvojušies tik tuvu, ka vienas difrakcijas ainas maksimums atrodas otras difrakcijas ainas minimumā, tad punkti ir tik tikko izšķirami (4. att. b), bet ja punkti pietuvojas vēl tuvāk, tad tie vairs nav izšķirami (4. att. c).
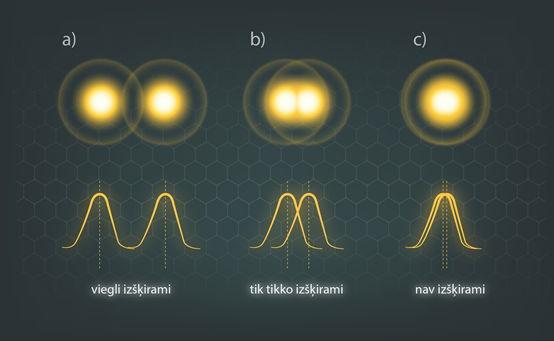
4.att. Divu punktveida attēlu izšķiršana
Difrakcijai pakļaujas ne tikai redzama gaisma, bet arī EM starojums citos viļņu garuma diapazonos. Piemēram, ir iespējams novērot arī rentgena staru difrakciju. Rentgena stariem viļņa garums (zem 1 nm) ir daudz mazāks par gaismas viļņa garumu (vidēji ap 550 nm). Tas nozīmē, ka difrakcijas režģim jābūt ar daudz mazāku režģa konstanti d. Šādus difrakcijas režģus ir tehniski ļoti grūti izveidot, bet, par laimi, daba ir parūpējusies par dabiskas izcelsmes difrakcijas režģiem. Izrādās, ka kristāliskām vielām (Fiztēma par cietām vielām) attālumi starp kristalogrāfiskajām plāksnēm (5. att. a) ir pietiekoši mazi, lai varētu notikt rentgena staru difrakcija (5. att. b). Rentgena staru difrakciju kristālos izmanto šo kristālu uzbūves pētīšanā. Rentgenstaru difrakcija ir nozīmīga metode, ko izmanto ģeologi, lai atšķirtu dažādu veidu minerālus, tāpat rentgena staru difrakciju izmanto, piemēram, stikla ražošanā, lai identificētu kristāliskus apgabalus, kas var izraisīt nelielus defektus stikla materiālā.
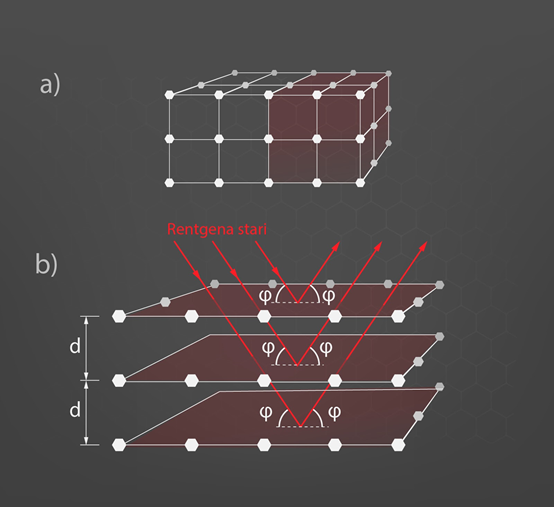
5.att. Rentgena staru difrakcija