Gaismas viļņi, līdzīgi kā iepriekš plašāk apskatītie radioviļņi (EM viļņu īpašības un to izmantošana), ir EM viļņi, līdz ar to šajos viļņos notiek elektriskā lauka intensitātes E un magnētiskā lauka indukcijas B svārstības perpendikulārās plaknēs (1. att. a). Gaismas izplatīšanās ātrums vakuumā ir lielākais dabā iespējamais ātrums c≈3·108m/s. (skaties vēl vienu materiālu par gaismas ātrumu). Lai gan intuitīvi par gaismas viļņiem gribētos saukt redzamo gaismu, tomēr šis jēdziens ir plašāks. Pie gaismas viļņiem pieskaita ne tikai redzamo gaismu, kuras viļņu garums gaisā ir no 760 nm līdz 380 nm (1. att. b), bet arī infrasarkano un ultravioleto starojumu, kuri attiecīgi ir ar lielāku un mazāku viļņu garumu nekā redzamā gaisma (1. att. b).
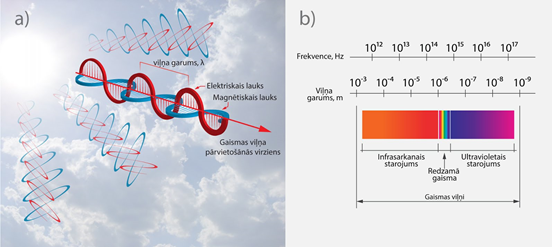
1.att. Gaisma kā EM vilnis
Dažkārt, kad Saule atrodas mākoņu aizsegā, pa mākoņu starpām var manīt izlaužamies Saules starus (2. att. a), un lai arī gaisma neizplatās staru veidā, tomēr gaismas stars ir labs modelis, lai vienkāršotu gaismas izplatīšanās parādību aprakstu. Viena no EM viļņu īpašībām, kas līdz ar to piemīt arī gaismai, ir atstarošanās. Ja gaismas stars krīt uz kādu virsmu, tad daļa no krītošās gaismas atstarojas (2. att. b). Ja pret virsmu novelk perpendikulu, tad leņķi starp šo perpendikulu un krītošos staru sauc par krišanas leņķi α, bet leņķi starp atstaroto staru un perpendikulu – par atstarošanās leņķi β (2. att. b). Turklāt šie abi leņķi ir vienādi: α=β. Gaismas atstarošanās parādība ir līdzīga bumbiņas atlēkšanai no virsmas (2. att. c).
Aplūko papildus materiālu par gaismas atstarošanu!
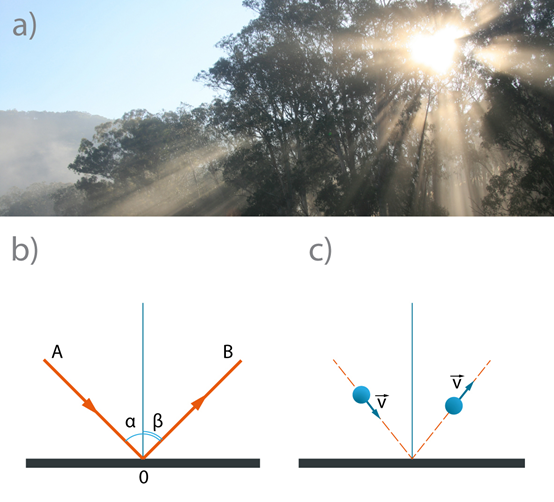
2.att. Saules stari un to atstarošanās
Ja uz robežvirsmu starp divām vidēm krīt gaisma, tad ne vienmēr visa gaisma atstarojas, daļa gaismas var pāriet no vienas vides uz otru (3. att.). Dažādās vielās var būt dažāds gaismas izplatīšanās ātrums. Ja gaisma pāriet vidē, kurā gaismas izplatīšanās ātrums ir atšķirīgs, tad gaisma maina izplatīšanās virzienu. To sauc par gaismas lūšanu. Ja gaismas stara krišanas leņķis ir α, bet laušanas leņķis γ, tad sinα:sinγ=n2:n1, kur n1 un n2 ir vielas absolūtie gaismas laušanas koeficienti, kas ir apgriezti proporcionāli gaismas ātrumam attiecīgajā vielā: n1:n2=v2:v1(3. att.). Vielas ar lielāku absolūto gaismas laušanas koeficientu sauc par optiski blīvākām.
Aplūko vēl vienu materiālu par gaismas laušanu!
Un te būs sīklietotne par gaismas laušanu.

3.att. Gaismas laušanas parādība
Ja gaisma pāriet no optiski blīvākas vides uz optiski mazāk blīvāku vidi (n21), tad laušanas leņķis ir lielāks par stara krišanas leņķi (4. att. a). Palielinot stara krišanas leņķi, pienāk brīdis, kad laušanas leņķis sasniedz 90° (4. att. b). Krišanas leņķi α0, pie kura laušanas leņķis ir 90°, sauc par pilnīgās iekšējās atstarošanās robežleņķi, jo turpmāk palielinot krišanas leņķi, gaisma vairs nepāriet no vienas vides otrā (nelūst), bet pilnībā atstarojas uz robežvirsmas (4. att. c). Šo parādību sauc par pilnīgu iekšējo atstarošanos. Robežleņķi α0 var noteikt, izmantojot izteiksmi sinα0=n2:n1. Gaismas pilnīgu iekšējo atstarošanos var novērot, piemēram, traukā ar ūdeni (4. att. d).
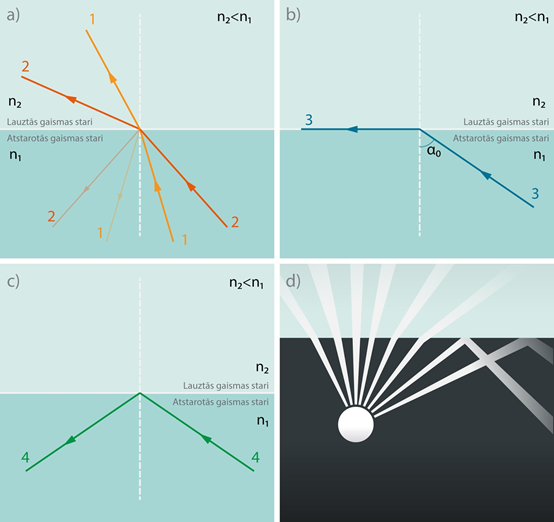
4.att. Gaismas pilnīga iekšējā atstarošanās
Vides absolūtais laušanas koeficients n ir atkarīgs no gaismas viļņu garuma. Piemēram, stikla prizmā visvairāk tiek lauzti zilās gaismas stari (lielāks n), bet vismazāk laušanai pakļaujas sarkanā gaisma (mazāks n). Šī iemesla dēļ uz prizmu laista baltā gaisma, izejot cauri prizmai, sadalās spektrā (5. att.). Šo gaismas sadalīšanos pa dažādām krāsām izraisa gaismas dispersija jeb vides absolūtā gaismas laušanas koeficienta atkarība no gaismas viļņu garuma.
Apskaties citu materiālu par gaismas dispersiju!
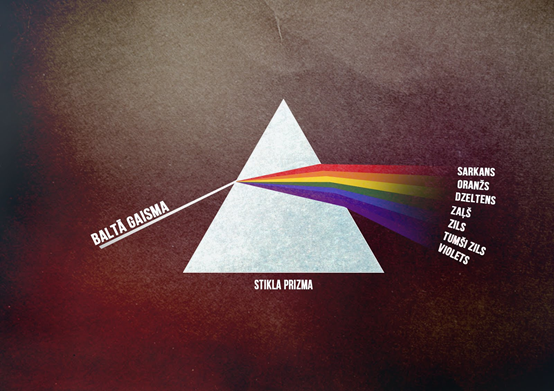
5.att. Gaismas dispersija
Papildus tam, ka stara krišanas un atstarošanās leņķi ir vienādi, un tam, ka krišanas un laušanas leņķu sinusu attiecība ir vienāda ar gaismas laušanas koeficientu attiecību abās vidēs, šie visi trīs stari arī atrodas vienā plaknē (1. att.). Šajā pašā plaknē atrodas arī perpendikuls, kas vilkts pret virsmu stara lūšanas punktā (1. att.).
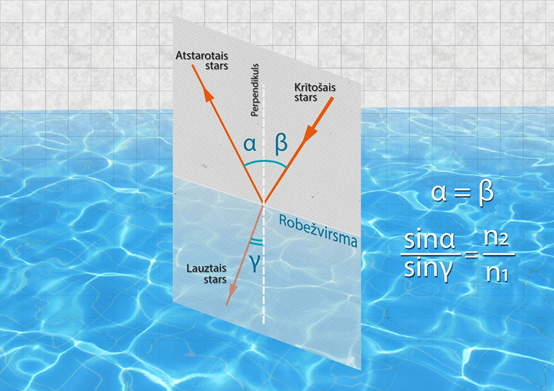
1.att. Krītošā, atstarotā un lauztā stara ģeometriskais novietojums
Gaismas laušanas parādībā ir svarīgi, kāda ir starpība starp absolūtajiem gaismas laušanas koeficientiem tām vidēm, uz kuru robežvirsmas gaismas stars lūst. Ja gaisma pāriet no vides ar mazāku laušanas koeficientu uz vidi, kur tas ir lielāks, jeb, citiem vārdiem sakot, gaismas stars pāriet no vides ar mazāku optisko blīvumu uz optiski blīvāku vidi, tad laušanas leņķis γ ir mazāks par krišanas leņķi α. Tas nozīmē, ka stars lūstot piekļaujas tuvāk perpendikulam (γα), kas vilkts pret robežvirsmu lūšanas punktā (2. att. a). Savukārt, ja gaismas stars pāriet no optiski blīvākas vides uz optiski mazāk blīvāku vidi, tad laušanas leņķis γ ir lielāks par krišanas leņķi α, un līdz ar to gaismas stars noliecas vairāk prom no perpendikula, kas vilkts pret robežvirsmu lūšanas punktā (2. att. b).
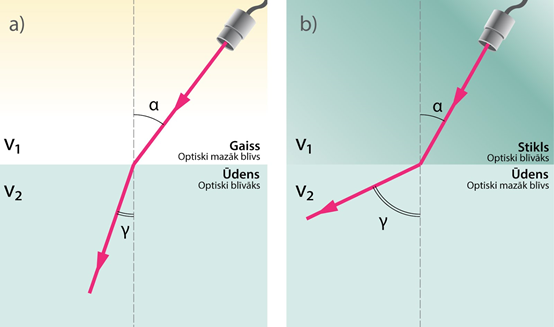
2.att. Gaismas stara lūšana dažādos gadījumos
Ja kāds priekšmets atrodas vienlaicīgi divās vidēs ar atšķirīgu optisko blīvumu, tad mums šis priekšmets izskatās salūzis (3. att. a). Tas ir tādēļ, ka vidē, kurā atrodas mūsu acis, priekšmeta atstarotie gaismas stari nonāk līdz mūsu acīm nelūstot, un mēs redzam šajā vidē esošo priekšmeta daļu tur, kur tā patiesībā atrodas, bet no vides, kurā mūsu acs neatrodas, stari no priekšmeta līdz mūsu acīm ir nonākuši pēc lūšanas, līdz ar to šajā vidē esošā priekšmeta daļa mums parādās ne tajā vietā, kurā tā patiesībā atrodas (3. att. b).
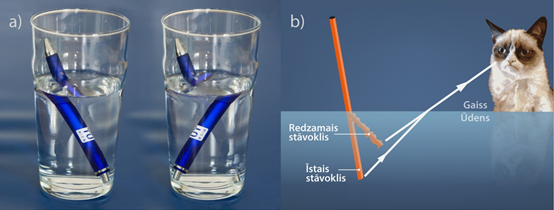
3.att. Gaismas laušanas izraisīts acu apmāns
Iepriekš noskaidrojām, ka tas, cik spēcīgi gaisma lūst, ir atkarīgs no absolūtajiem gaismas laušanas koeficientiem vidēm, starp kurām gaisma pārvietojas. Tādēļ, lai varētu paredzēt gaismas uzvedību, pārvietojoties caur šīm vidēm, ir jāzina vielu absolūtie gaismas laušanas koeficienti. 4. attēlā ir redzams dažādu vielu absolūto gaismas laušanas koeficientu salīdzinājums.
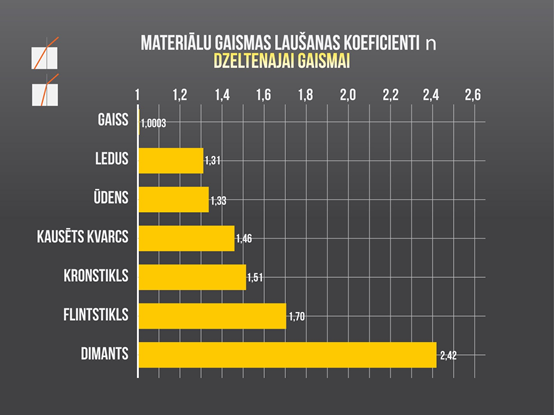
4.att. Materiālu gaismas laušanas koeficienti dzeltenajai gaismai
Laušanas koeficients šķidrumam ir atkarīgs, piemēram, no šķidruma blīvuma vai piemaisījumu daudzuma. Dažādās rūpniecības nozarēs, piemēram, alus ražošanā, ir svarīgi zināt raudzējamā šķidruma īpašības. Tās var noteikt, izmērot šķidruma laušanas koeficientu. Laušanas koeficienta mērīšanai var izmantot refraktometru, kas sastāv no divām trīsstūrveida šūnām (5. att.). Vienā šūnā ir iepildīts atskaites šķidrums jeb šķidrums, kuram ir zināms laušanas koeficients, bet otrā šūnā iepilda pārbaudāmo šķidrumu (5. att.). Ja abiem šķidrumiem laušanas koeficienti ir vienādi, tad gaismas stars caur abām šūnām iziet nenoliecoties (5. att.), savukārt, ja laušanas koeficienti ir atšķirīgi, tad gaismas stars noliecas. Izmērot gaismas stara nolieci, var aprēķināt nezināmo šķidruma laušanas koeficientu.
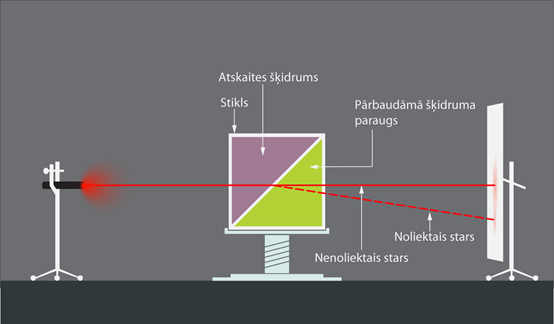
5.att. Gaismas laušanas koeficienta izmantošana šķidruma īpašību pārbaudē
Ja dažādām vielām ir vienāds gaismas laušanas koeficients, tad gaismai robežvirsma nepastāv un tāpārvietojas nelūstot. Šo īpašību var izmantot, piemēram, lai vārglāzē paslēptu nūjiņu. Ja mēs ieliekam nūjiņu vārglāzē, tad tā ir labi redzama. Tas ir tādēļ, ka starp abiem priekšmetiem atrodas gaiss. Gaisam, vārglāzes stiklam un nūjiņai ir atšķirīgi gaismas laušanas koeficienti, līdz ar to gaisma lūst un nūjiņa paveras mūsu skatam. Ja starp abiem priekšmetiem ielej parasto cepamo eļļu, tad nūjiņa skatam pazūd tiktāl, cik tā ir iegremdēta eļļā (6. att.). Šāds acu apmāns rodas tādēļ, ka cepamajai eļļai, vārglāzes stiklam un nūjiņas materiālam ir vienādi laušanas koeficienti, līdz ar to gaisma pa vārglāzes stiklu un eļļu pārvietojas kā pa vienu vielu un nelūst, līdz ar to mūsu acis arī to uztver kā vienu objektu.

6.att. Gaismas laušanas koeficientu sakritība var likt priekšmetiem pazust
Starp divām vidēm ar atšķirīgiem gaismas laušanas koeficientiem varēja iegūt arī pilnīgu iekšējo atstarošanos, ja gaismas stars ceļo no vides ar lielāku optisko blīvumu uz vidi ar mazāku optisko blīvumu (1. solis 4. att.). Pilnīgo iekšējo atstarošanos izmanto, piemēram, optisko signālu pārvadē, izmantojot optiskos kabeļus. Optiskais kabelis sastāv no augstas kvalitātes kvarca šķiedrām, kuras aptver plāns apvalks ar mazāku laušanas koeficientu nekā pašai šķiedrai (7. att. a). Šādā sistēmā izplatās gaismas stars, atstarojoties no sieniņām un neizejot laukā no paša kabeļa. Tomēr optisko kabeļu ātruma priekšrocība neslēpjas faktā, ka gaismas signāls vadā pārvietotos ātrāk par elektrisko signālu. Optiskajam signālam ir tā priekšrocība, ka pa to pašu kanālu var pārraidīt vairākus signālus vienlaicīgi, līdz ar to pieaug datu apjoms, ko vienā reizē var pārsūtīt. Arī Latvijā interneta un TV piegādātāji izmanto optiskos kabeļus (7. att. b) un to piedāvātās priekšrocības.

7.att. Pilnīgās iekšējās atstarošanās izmantošana signālu pārvadē un optiskais kabelis
Optiskajā kabelī (7. att. b) signālu pārraidošā daļa aizņem tikai mazu daļiņu no visa kabeļa diametra (dzeltenais vads 8. att a). Pārējā daļa ir aizsargmateriāls, kas pasargā šķiedras no ārējas mehāniskas iedarbības. Caur vienu šādu optisko kabeli reizē tiek pievadīts gan ātrs internets, gan arī TV signāls, atliek tikai šo kabeli pieslēgt modēmam un dekoderim, kas signālu padara datoram un TV saprotamu (8. att. b).
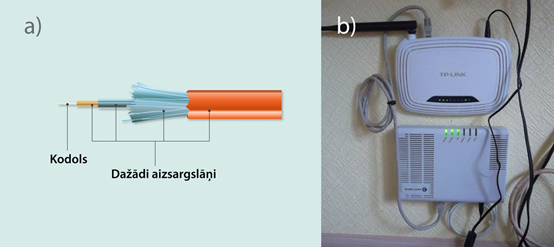
8.att. Optiskais kabelis un tā izmantošana interneta un TV piegādē
Atkarībā no gaismas viļņa garuma materiāla gaismas laušanas koeficients mainās. To sauc par gaismas dispersiju. Piemēram, ledus gaismas laušanas koeficients mainās tā, kā redzams 9. attēlā. Arī citiem materiāliem, piemēram, ūdenim, šī laušanas koeficienta līkne ir ar līdzīgu raksturu, tādēļ, apgaismojot ūdeni, noteiktos apstākļos ir iespējams iegūt varavīksni.
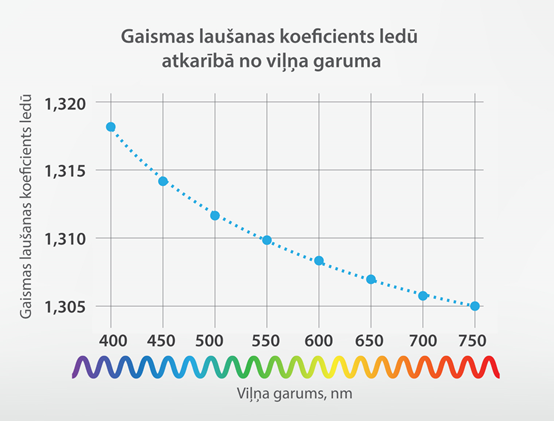
9.att. Ledus gaismas laušanas koeficients atkarībā no viļņu garuma
Viens no veidiem, kā mākslīgi iegūt varavīksni, ir apskatīts FIZMIX eksperimentu sadaļā (10. att.)

10.att. Varavīksnes iegūšana mākslīgā veidā
Par varavīksnes burvību šad un tad parūpējas arī daba, kad novērotājam aiz muguras spīd Saule, bet priekšā līst lietus (11. att. a). Tad baltās gaismas stari lūst ūdens pilieniņos un sadalās spektrā, veidojot varavīksni (11. att. b).
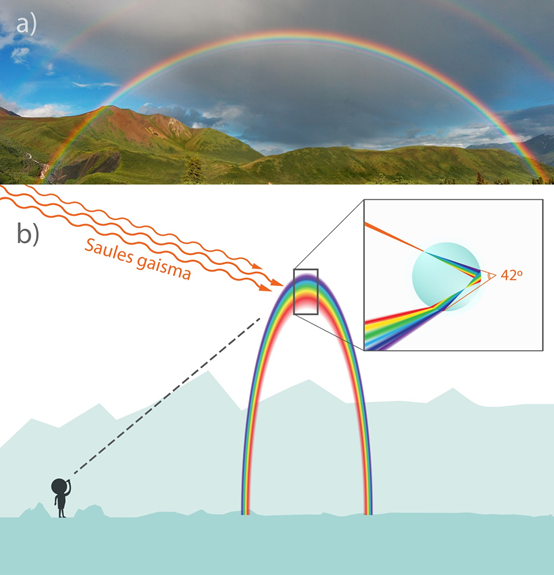
11.att. Varavīksne dabā un tās veidošanās mehānisms
Gaismas atstarošanās un laušanas parādībās savā labā izmanto arī juvelieri. Izdzirdot vārdu “dimants”, parasti nāk prātā dārgakmens, kas zaigo pilnā spožumā visos iespējamos krāsas toņos un ar savu spožumu var apžilbināt katru, kas uz to paskatās. Tomēr tikko pēc dimanta atrašanas raktuvēs, tas ne tuvu neizskatās tik pievilcīgs. Dimanta skaistums rodas pēc speciālas pieslīpēšanas, kad tas iegūst noteiktu ģeometrisku formu un kļūst par briljantu (1. att. a). Šī ģeometriskā forma kopā ar to, ka dimantam ir ļoti liels absolūtais gaismas laušanas koeficients (n=2.42), nodrošina dimanta spēju gan atstarot balto gaismu, nesadalot to spektrā (1. att. b), gan arī sašķelt gaismu visās varavīksnes krāsās (1. att. c).
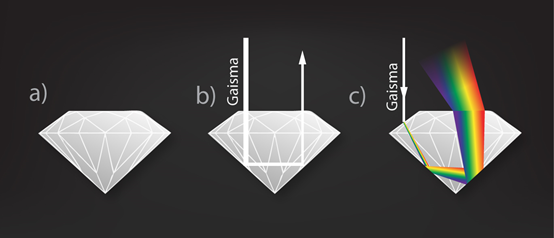
1.att. Noslīpēts dimants un gaismas izplatīšanās tajā
Gaismas avotus ar ļoti maziem ģeometriskajiem izmēriem sauc par punktveida gaismas avotiem. Par punktveida gaismas avotu var kalpot, piemēram, spuldzīte (2. att. a). Gaismas viļņiem, ko izstaro punktveida gaismas avots, ir līdzība ar mehāniskajiem viļņiem, ko uz ūdens virsmas rada iemests akmens (2. att. b).
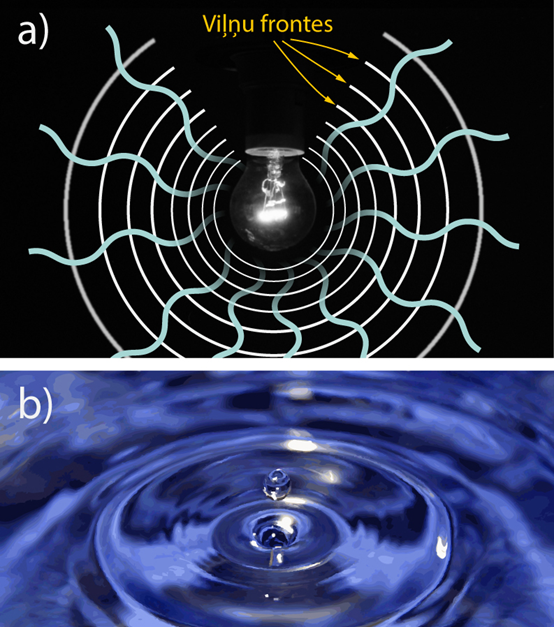
2.att. Gaismas un ūdens viļņu izplatīšanās telpā
Līdzība starp gaismas viļņu izplatīšanās vizualizāciju un mehāniskajiem viļņiem uz ūdens virsmas ir tā, ka to izplatīšanos var novērot, ja seko līdzi tam kā kustas viļņu frontes. Viļņu fronte ir virsma, uz kuras svārstības ir vienā fāzē (3. att.). Viļņiem izplatoties telpā, izplatās arī viļņu frontes. Attēlos, kuros redzama gaismas izplatība ap kādu gaismas avotu, parasti iezīmē viļņu frontes, kas atbilst vienādām svārstību fāzēm (2. att. a).
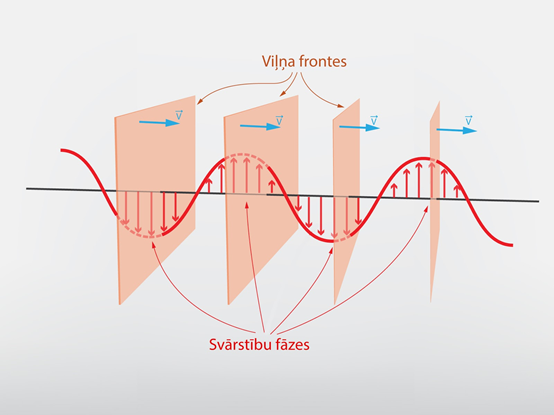
3.att. Viļņu frontes izplatības telpā
Lai izsekotu viļņu frontes kustībai, var izmantot Heigensa principu. Balstoties uz Heigensa principu, katru jau esošas viļņu frontes punktu var uzskatīt par jaunu punktveida viļņu avotu (4. att. a). Tas nozīmē, ka mēs uz viļņu frontes varam izvēlēties vairākus punktus un uzskatīt, ka šie punkti darbojas kā sekundārie viļņu avoti. Pēc tam, apvelkot apliecēju ap šīm sekundārajām viļņu frontēm, mēs iegūstam jauno fronti. Piemēram, 4. attēlā b gadījumā sekundārās viļņu frontes vispirms ir iezīmētās sarkanas un to aplicēja ir jaunā fronte ar numuru “1”. Pēc tam uz šīs jaunās frontes atkal ir daudz sekundārie viļņu avoti, kuru frontes iezīmētās oranžas. To apliecēja ir jaunā fronte ar numuru “2”, uz kuras savukārt atkal ir sekundārie viļņu avoti ar dzeltenām frontēm, kuru apliecēja ir jaunā fronte ar numuru “3”. Tādā veidā pēc Heigensa principa viļņu frontes izplatās telpā.
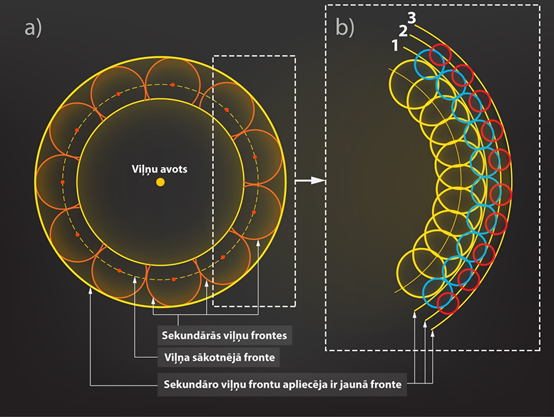
4.att. Heigensa princips
Apstiprinājumu Heigensa principam var iegūt, atrodoties uz tiltiņa, kas ved pāri upei. Ja mēs tiltiņa labajā pusē iemetīsim akmeni, tad pēc brītiņa tiltiņa kreisajā pusē varēs redzēt viļņus, kas atnākuši no viļņu izraisīšanas vietas (5. att. a). Ja pēc tam kā viļņu avots tiks izmantota, piemēram, apaļa konservu bundža, kura piestiprināta kāta galā, tad atkal pēc mirkļa kreisajā tilta pusē varēs novērot viļņus, turklāt šie viļņi būs tādi paši kā gadījumā ar iemestu akmeni (5. att. b). Tas nozīmē – ja kāds skatās tikai no tilta pa kreisi un ierauga viļņus, tad viņš nevar zināt, vai tos izraisīja akmens vai liela apaļa konservu bundža. Tas pierāda faktu, ka katrs viļņu frontes punkts ir sekundāru viļņu avots.
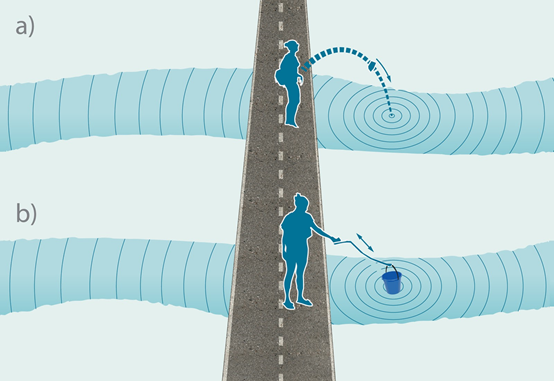
5.att. Heigensa principa apstiprinājums
Pirmajā solī tika minēts, ka “gaisma neizplatās staru veidā, tomēr gaismas stars ir labs modelis, lai vienkāršotu gaismas izplatīšanās parādību aprakstu.” Tomēr gaismas stars nav vienkārši uz labu laimi novilkts nogrieznis, kas aptuveni vērsts gaismas izplatīšanas virzienā. Gaismas stars ir cieši saistīts ar to, kā izplatās viļņu frontes, jeb gaismas stari ir perpendikulāri viļņu frontēm (6. att.)
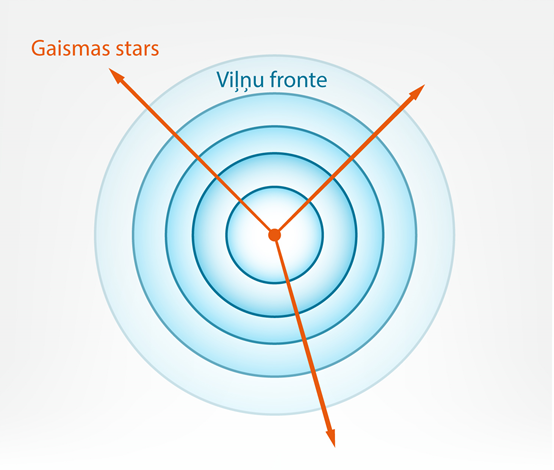
6.att. Gaismas staru saistība ar viļņu frontēm
Tas nozīme, ja viļņi rodas no punktveida gaismas avota, tad viļņu frontes ir koncentriski riņķi ap šo avotu un gaismas stari ir radiāli, izejoši no paša gaismas avota (7. att.). Savukārt, ja viļņu frontes ir plakanas (plakanviļņi), tad gaismas stari ir paralēli viens otram (7. att. b).
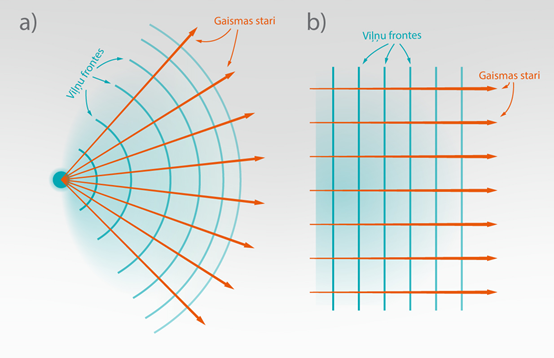
7.att. . Dažādas viļņu frontes un atbilstošie gaismas stari
Gaismas viļņu frontes var izmantot, lai ilustrētu gaismas atstarošanos. Tādā gadījumā uz robežvirsmu krīt nevis gaismas stari, bet gaismas viļņu frontes (8. att.).
Skaties vēl vienu materiālu par Heigensa pricnipu!