Staru gaitas izmainīšanai var lietot arī lēcas. Lēca ir caurspīdīgs ķermenis ar liektām virsmām (1. att.). Plaši tiek lietotas lēcas ar sfēriskām virsmām. 1. attēlā redzama lēca, kuras vienu virsmu veido sfēras segments ar rādiusu R1, bet otru virsmu sfēras segments ar rādiusu R2. Ar lēcu ir saistīti vairāki svarīgi jēdzieni:
1) par lēcas optisko centru sauc nogriežņa AB viduspunktu (1. att.);
2) taisni O1O2sauc par lēcas galveno optisko asi un tā iet caur lēcas virsmu liekuma centriem, šķērsojot optisko centru (1. att.);
3) citas taisnes, kas šķērso optisko centru, sauc par optiskām blakusasīm.
Ja attālums AB ir mazs, salīdzinot ar R1un R2, tad lēcu sauc par plānu lēcu. Turpmāk tiks apskatītas tikai plānās lēcas.
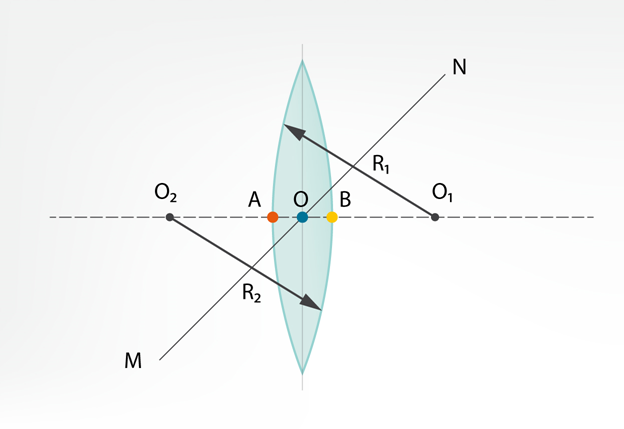
1.att. Plāna lēca ar sfēriskām virsmām
Par savācējlēcām sauc tādas lēcas, uz kurām krītošs paralēls staru kūlis lūst, un pēc tam lauztie stari krustojas vienā punktā (2. att.). Ja uz savācējlēcu no vienas puses krīt stari, kas paralēli galvenajai optiskai asij, tad pēc lūšanas stari krustojas lēcas fokusā (2. att. a). Lēcai ir divi fokusi – ja paralēlais staru kūlis krīt uz lēcu no otras puses, bet vēl aizvien paralēli galvenajai optiskajai asij, tad lauztie stari krustojas otrā fokusā (2. att. b). Attālums līdz lēcas optiskajam centram abiem fokusiem var nebūt vienāds, tas ir atkarīgs no tā, vai vienāds ir abu lēcas virsmu liekuma rādiuss. Savācējlēcu optiskajās konstrukcijās apzīmē tā, kā redzams 2. attēla c gadījumā.
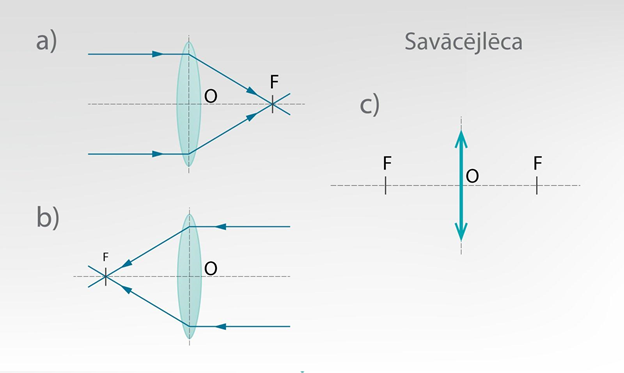
2.att. Savācējlēcas fokusi un apzīmējums
Iepriekš noskaidrojām – ja stars krīt uz savācējlēcu paralēli tās optiskajai asij, tad pēc lūšanas stars iet caur lēcas fokusu (3. att. a). Spēkā ir arī apgrieztais princips: ja stars uz savācējlēcu krīt caur fokusu, tad pēc lūšanas tas virzās paralēli lēcas galvenajai optiskajai asij (3. att. b). Pastāv iespēja, ka krītošais stars lēcā nelūst. Tas ir tādā gadījumā, ja stars iet caur lēcas optisko centru (3. att. c). Ja uz savācējlēcu krīt stars, kas paralēls kādai lēcas optiskajai blakusasij, tad pēc lūšanas stars iet caur punktu, kas veidojas, krustojoties optiskajai blakusasij un līnijai, kas vilkta perpendikulāri galvenajai optiskajai asij caur lēcas fokusu (3. att. d). Saka, ka stars pēc lūšanas krusto fokālo plakni, kas ir fokusu saturoša plakne, perpendikulāra galvenajai optiskajai asij.
Apskaties materiālu par attēlu veidošanos savācējlēcā!
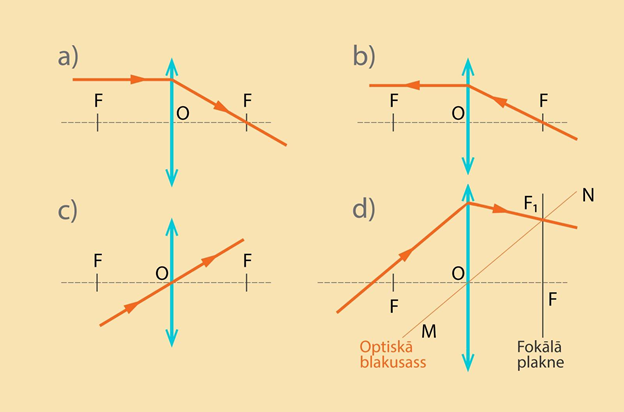
3.att. Dažādu staru gaitas savācējlēcā
Ja paralēls staru kūlis krīt uz izkliedētājlēcu, tad stari pēc lūšanas nekrustojas vienā punktā, līdz ar to reālu fokusu šādām lēcām nav (4. att.). Tomēr, ja lauztie stari tiek pavilkti garāki pretēji to izplatīšanās virzienam, tad redzams, ka šīs pagarinātās līnijas krustojas vienā punktā, ko sauc par izkliedētājlēcas šķietamo fokusu (4. att. a). Līdzīgi kā savācējlēcai, arī izkliedētājlēcai ir divi fokusi, kuru attālums līdz optiskajam centram ir atkarīgs no virsmu liekuma rādiusa (4. att. a,b). Izkliedētājlēcu optiskajās konstrukcijās apzīmē tā, kā redzams 4. attēla c gadījumā.
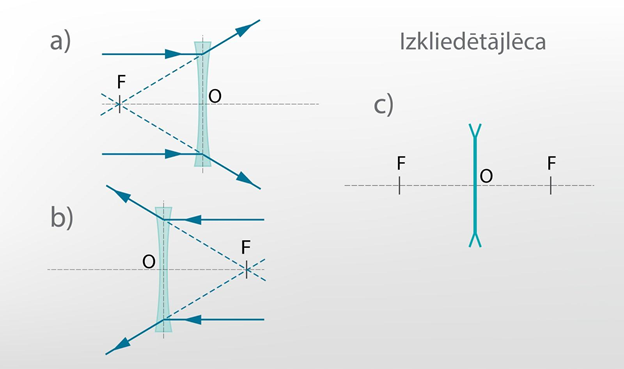
4.att. Izkliedētājlēcas šķietamie fokusi un apzīmējums
Tātad, ja stars krīt uz izkliedētājlēcu paralēli tās optiskajai asij, tad lauztā stara pagarinājums iet caur lēcas šķietamo fokusu (5. att. a). Arī šeit ir spēkā apgrieztā sakarība, proti, ja uz izkliedētājlēcu krītošā stara pagarinājums iet caur lēcas šķietamo fokusu, tad lauztais stars virzās paralēli lēcas galvenajai optiskajai asij (5. att. b). Līdzīgi kā savācējlēcai, arī izkliedētājlēcas gadījumā stars netiek lauzts, ja tas iet caur lēcas optisko centru (5. att. c). Un visbeidzot, ja stars uz savācējlēcu krīt paralēli kādai no optiskajām blakusasīm, tad lauztā stara pagarinājums iet caur punktu, kas atrodas fokālas plaknes un optiskās blakusass krustošanās punktā (5. att. d).

5.att. Dažādu staru gaitas savācējlēcā
Ja lēcas vienā pusē atrodas priekšmets AB, tad lēcas ietekmē veidojas priekšmeta attēls A1B1(6. att.). Priekšmets atrodas no lēcas attālumā d, bet tā attēls attālumā f (6. att.). Attēla attālums f ir atkarīgs gan no d, gan no lēcas fokusa attāluma F. Šos trīs lielumus saista sakarība 1:F=1:d+1:f, kur
F – lēcas fokusa attālums, m
d – attālums no lēcas līdz priekšmetam, m
f – attālums no lēcas līdz attēlam, m
Reāliem attēliem f>0, bet šķietamiem ff ar d, tad iegūst lēcas lineāro palielinājumu Г=f:d. Šis skaitlis norāda to, cik reizes priekšmeta attēls ir lielāks par pašu priekšmetu. Lēcu raksturo arī optiskais stiprums D=1:F, kur F ir lēcas fokusa attālums metros. Optisko stiprumu mēra dioptrijās.
Skaties DZM materiālu par gaismas laušanas parādību!
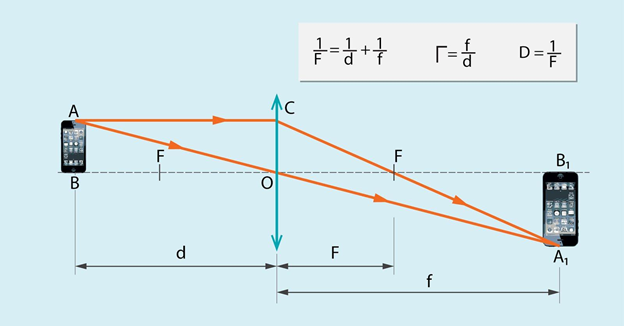
6.att. Dažādas ar lēcām saistītas sakarības
Lēcas formulu iespējams iegūt no trijstūru līdzības sakarībām (apskaties informāciju par līdzīgiem trijstūriem). Uzkonstruējot priekšmeta attēlu, kas veidojas lēcas ietekmē, ir iespējams atrast vairākus līdzīgu trijstūru pārus (1. att.). Pirmkārt, līdzīgi ir trijstūri ABO un A1B1O, jo abi ir taisnleņķa trijstūri, turklāt leņķi AOB un B1OA1ir vienādi, jo tie ir šķērsleņķi. Līdz ar to no vienādu trijstūru pazīmes seko: A1B1:AB=f:d, jo OB1=fun BO=d.
Līdzīgi ir arī trijstūri FOC un FB1A1. No šo trijstūru līdzības izriet tas, ka A1B1:OC=FB1:OF. Attēlā var redzēt (1. att.), ka OC=AB un FB1=f-F. Ieliekot šīs pēdējās divas sakarības izteiksmē, ko ieguva no otrās trijstūru līdzības, iegūst A1B1:AB=(f-F):F, jo OF=f (1. att.). Izmantojot pirmās trijstūru līdzības rezultātu, iegūst f:d=(f-F):F. Izdalot abas vienādojuma puses ar f, iegūst 1:d=(1-F:f):F. Labajā vienādojuma pusē, izdalot skaitītāju ar saucēju, kopumā iegūst 1:d=1:F-1:f. Pārnesot 1:f otrā vienādības pusē, iegūst kāroto formulu: 1:F=1:d+1:F.
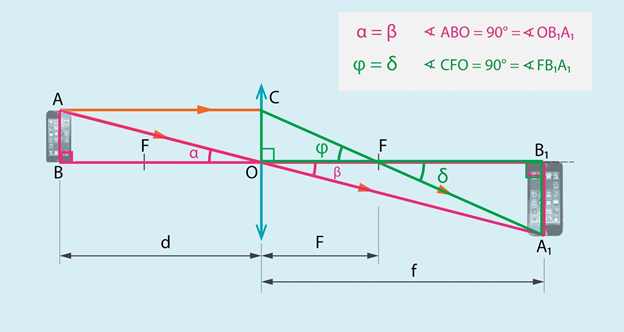
1.att. Lēcas formulas iegūšana no trijstūru līdzības
Sadaļā par attēliem spoguļos noskaidrojām, ka spoguļa veidotā attēla raksturlielumi ir atkarīgi no tā, cik tālu priekšmets atrodas no paša spoguļa. Ar lēcām ir līdzīgi – lai noteiktu attēla parametrus, ir jānoskaidro priekšmeta attālums no lēcas. Ja priekšmets atrodas no lēcas tālāk nekā divu fokusu attālumā, tad priekšmeta attēls ir reāls, apgriezts un samazināts (2. att. a). Šāds gadījums realizējas fotoaparātos, piemēram, telefonā iebūvētajā kamerā. Fotografētā priekšmeta attēls veidojas uz gaismjūtīgas matricas, kuras signāls tālāk tiek pārvērsts attēlā, kuru jau redzam tiešu, nevis apgrieztu (2. att. b).
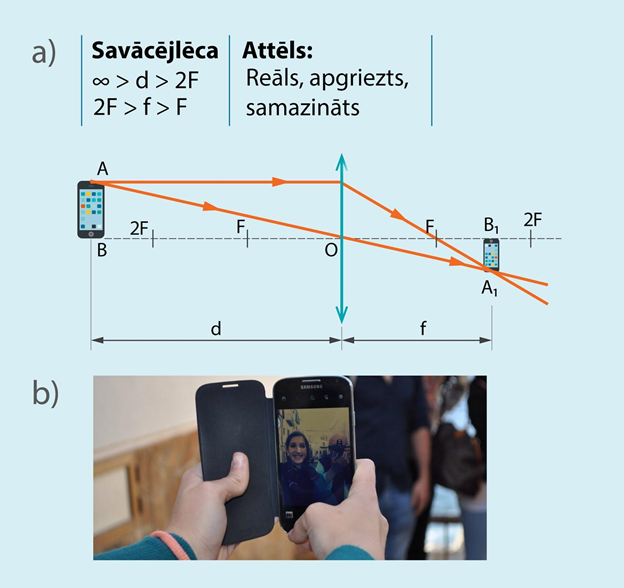
2.att. Attēla iegūšana ar savācējlēcu, ja priekšmets atrodas tālāk nekā divu fokusu attālumā no lēcas
Ja priekšmets atrodas tieši divu fokusu attālumā no lēcas, tad lēca veido reālu un apgrieztu attēlu, kas ir tādā pašā lielumā kā priekšmets (3. att. a). Arī šādi gadījumi var realizēties fotoaparātos (3. att. b). Jāatceras, ka digitālo fotoaparātu gaismas jutīgā matrica ir salīdzinoši maziņa ar objektiem, kas parasti tiek fotografēti. Tādēļ, lai attēls, kas veidojas uz gaismjutīgas matricas, būtu vienādi liels ar priekšmetu, priekšmetam ir jābūt maziņam un jāatrodas tuvu fotoaparātam. Visticamāk, ka šādai fotografēšanai ir nepieciešami speciāli objektīvi (lēcas), kas paredzētas sīku priekšmetu fotografēšanai.
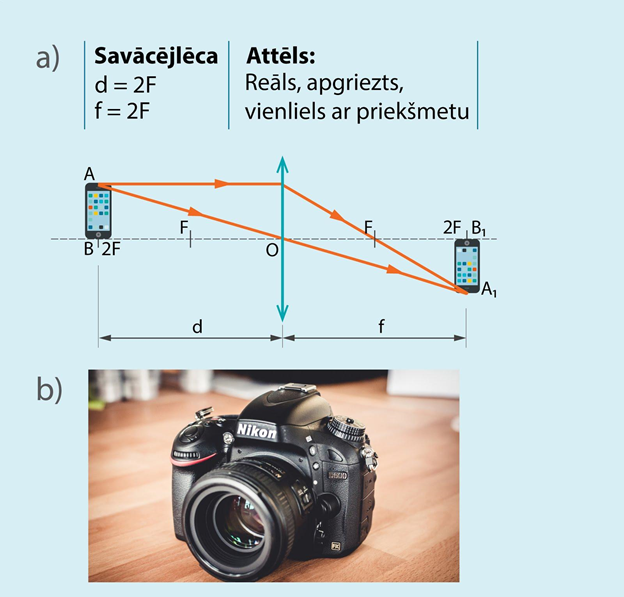
3.att. Attēla iegūšana ar savācējlēcu, ja priekšmets atrodas divu fokusu attālumā no lēcas
Ar datora projektoriem (4. att. b) tiek iegūts palielināts attēls. Lai tas notiktu, projicējamajam elementam ir jāatrodas attālumu intervālā starp F un 2F no izmantotās lēcas (4. att. a). Šādā konfigurācijā gan tiek iegūts apgriezts attēls, taču tas tiek kompensēts ar to, ka attēlu veidojošais elements tiek apgriezts otrādi pašā projektorā. Jāatceras, ka šajā gadījumā ar palielinātu attēlu ir domāts tas, ka tiek palielināts attēls, kas projektorā atrodas uz attēlu veidojošā elementa, nevis palielināts tiek bildē redzamais objekts.
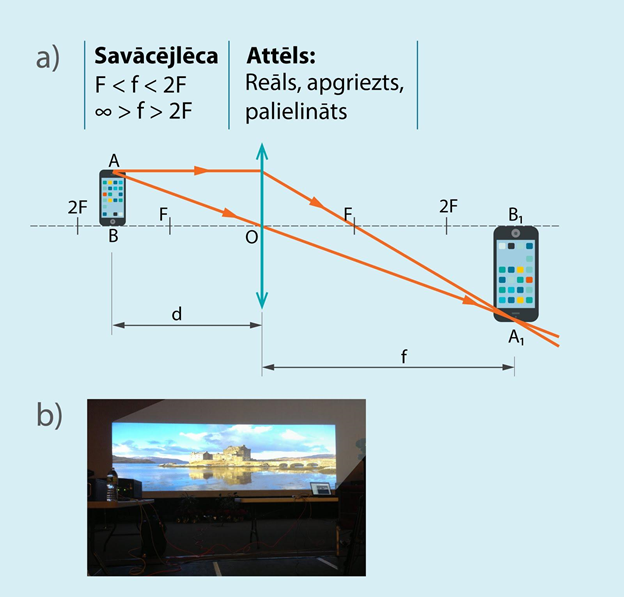
4.att. Palielināta attēla iegūšana ar projekcijas aparātiem
Arī savācējlēcai, līdzīgi kā izliektam spogulim, ir iespējams gadījums, kad attēls neveidojas (5. att. b).Tas notiek situācijā, kad priekšmets atrodas savācējlēcas fokusā (5. att. a).
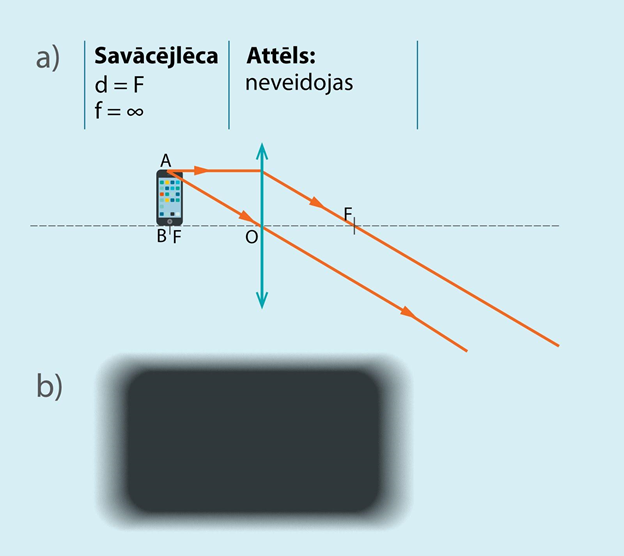
5.att. Priekšmeta novietojums gadījumā, kad attēls neveidojas
Ja savācējlēcas gadījumā priekšmets atrodas tuvāk lēcai nekā fokusa attālums, tad iegūtais priekšmeta attēls ir šķietams, tiešs un palielināts (6. att. a). Pēc šāda principa darbojas lupa (6. att. b). Lupas gadījumā, lai apskatītu šķietamo attēlu, ir jāskatās pašā lupā, jo nav iespējas attēlu projicēt uz kāda ekrāna, kā tas bija iepriekšējos savācējlēcas gadījumos. Interesanti, vai Šerloks Holmss zināja, ka, lūkojoties lupā, viņš redz tikai šķietamu attēlu?
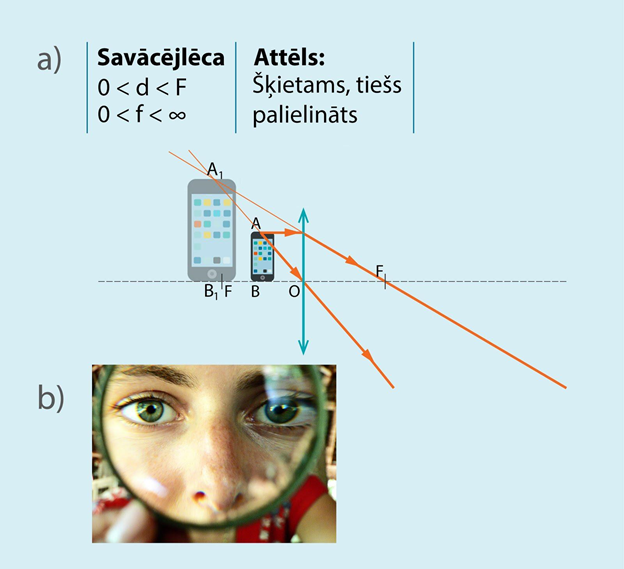
6.att. Ar savācējlēcu iegūstams arī šķietams attēls
Vēl viens lēcu veids ir izkliedētājlēcas. Tā kā izkliedētājlēcas gadījumā stari izklīst nevis sakopojas, tad ar šo lēcu iespējams iegūt itkā šķietamu attēlu, turklāt tas ir samazināts jebkurā attālumā, kādā priekšmets var atrasties no lēcas (7. att. a). Izkliedētājlēcas lieto brillēs, lai koriģētu tuvredzību (7. att. b).
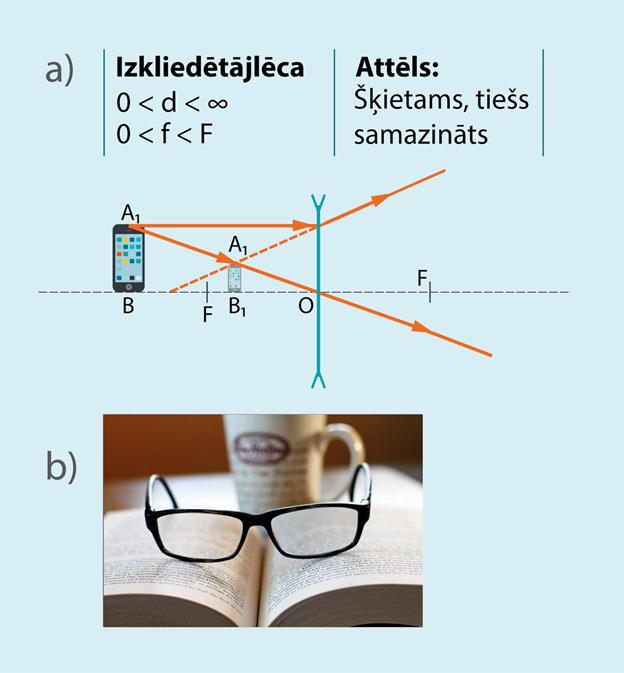
7.att. Izkliedētājlēcas izmantošana
Kā sava veida lēca darbojas jebkurš caurspīdīgs ķermenis, kam ir kāda liekta virsma (8. att.). Šī iemesla dēļ ir bīstami mežā atstāt stikla pudeles, jo saulainā dienā pudele var nostrādāt kā saules starus sakopojoša lēca un izraisīt meža ugunsgrēku.

8.att. Sfērisks ķermenis darbojas kā savācējlēca
Cilvēka acs ir ļoti sarežģīts optiskais instruments, kas sastāv no ļoti daudz sastāvdaļām (1. att.). Dažas no acs sastāvdaļām un raksturlielumiem:
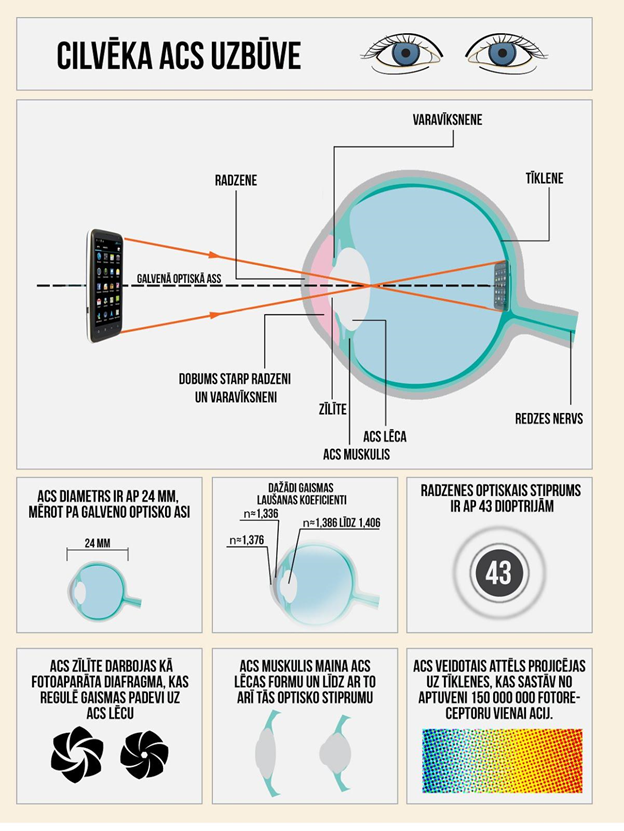
1.att. Cilvēka acs uzbūve
Acs muskulis pieregulē lēcas formu atkarībā no tā, cik tālu atrodas saskatāmais priekšmets. Ja priekšmets atrodas tālu, tad acs muskulis nesaspringst un acs lēcas optiskais stiprums ir vismazākais (2. att. a). Bet, ja aplūkojamais priekšmets atrodas tuvu, tad acs muskulim ir jānodrošina tas, ka lēca spēcīgāk lauž starus, tādēļ muskulis saspringst un lēcas optiskais stiprums pieaug (2. att. b).
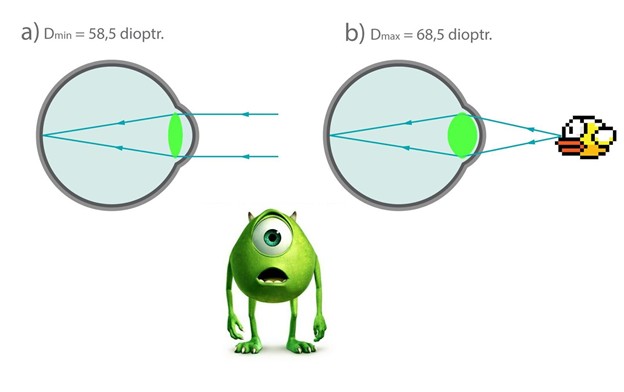
2.att. Cilvēka acs skatoties uz tālu (a) un tuvu (b) priekšmetu
Ja cilvēkam ir normāla redze, tad acī ienākošie gaismas stari fokusējas uz tīklenes un cilvēks redz skaidru attēlu (2. att.). Taču nereti cilvēki piedzīvo redzes defektus, no kuriem divi pazīstamākie ir tuvredzība un tālredzība. Ja cilvēkam piemīt tālredzība, tad acī iekļuvušie gaismas stari vairs nefokusējas uz tīklenes, bet aiz tās (3. att. a). Šādu redzes defektu var koriģēt ar savācējlēcu, kas koncentrē starus uz tīklenes un cilvēks atkal var redzēt skaidru attēlu (3. att. b).
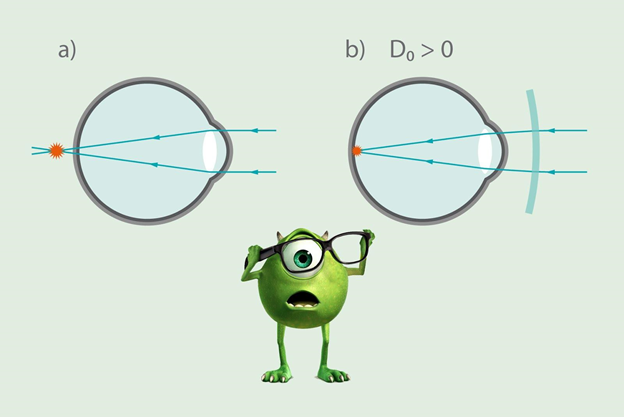
3.att. Tālredzības izpausme acī un tās korekcija ar savācējlēcu
Ja stari fokusējas pirms tīklenes (4. att. a) un cilvēks atkal redz miglainu attēlu. Šādu redzes defektu koriģē ar izkliedētājlēcu, kas izvērš krītošos starus tā, ka tie koncentrējas uz tīklenes, lai iegūtu skaidru attēlu (4. att. b).
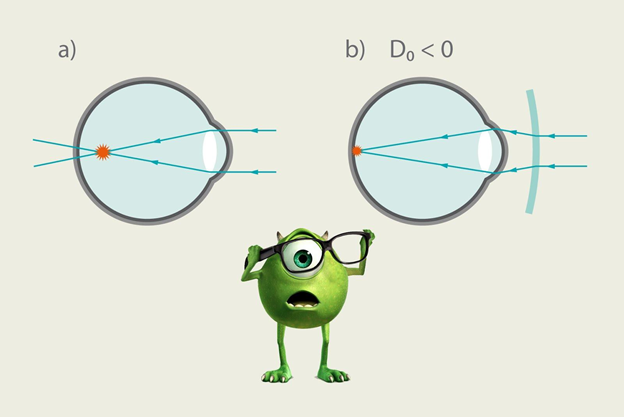
4.att. Tuvredzība un tās korekcija ar izkliedētājlēcu
Ja cilvēks lieto brilles, tad redze tiek nodrošināta, izmantojot vairākas lēcas (briļļu lēca un acs lēca). Šīs lēcu sistēmas kopējais optiskais stiprums veidojas, ja saskaita atsevišķo lēcu optiskos stiprumus. Šis likums attiecas arī uz lēcu sistēmām, kas sastāv no vairāk nekā divām lēcām (5. att.). Saskaitot optiskos stiprumus, jāatceras, ka savācējlēcām optiskais stiprums ir pozitīvs lielums, bet izkliedētājlēcām tas ir negatīvs. 5. attēlā redzamās lēcu sistēmas kopējais optiskais stiprums D=D1+D2+D3+D4, kur D1, D2, D3un D4ir atsevišķo lēcu optiskie stiprumi. Šādas lēcu sistēmas izmanto dažādos optiskajos aparātos, piemēram, projektoros, kuros nepieciešama iespēja regulēt attēla veidošanās attālumu. 5. attēlā redzamajā lēcu sistēmā, pārbīdot izkliedētājlēcu, ir iespēja šo attālumu regulēt.
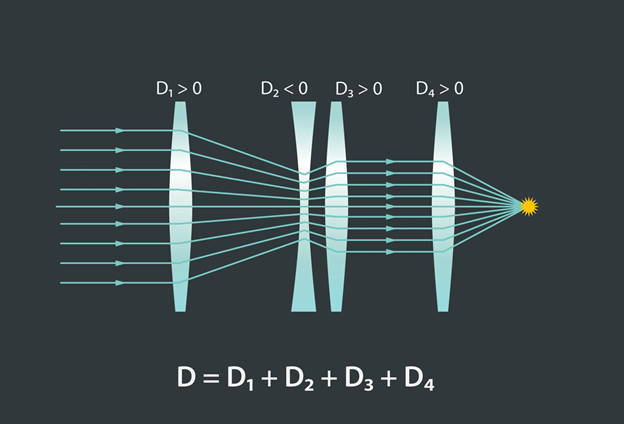
5.att. Lēcu sistēmas kopējais optiskais stiprums
Tādā optiskajā instrumentā kā mikroskopā tiek izmantota divu lēcu sistēma (6. att.). Stari no apskatāmā priekšmeta vispirms iet caur objektīva lēcu, un izveidojas objektīva attēls, kas ir starpattēls (6. att.). Tālāk stari no objektīva attēla iet caur okulāru un nonāk cilvēka acī, līdz ar to cilvēks ierauga palielinātu priekšmeta attēlu. Ar šādu lēcu sistēmu iegūst priekšmeta palielinājumu, ko var aprēķināt pēc formulas Г=DobDokd·L, kur
Г – optiskais palielinājums;
Dob–objektīva optiskais stiprums, dioptrijās;
Dok –okulāra optiskais stiprums, dioptrijās;
d –attālums no priekšmeta līdz objektīvam;
L –attālums starp objektīva un okulāra fokusiem, m.
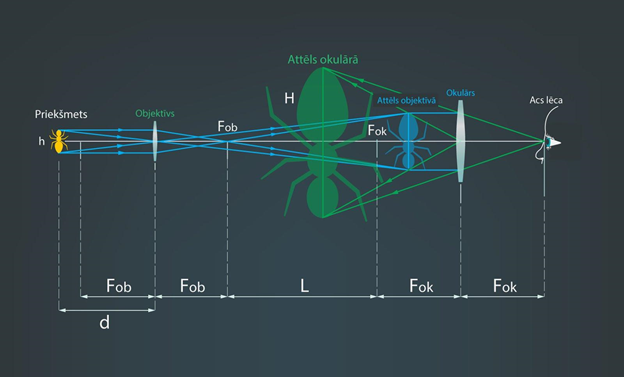
6.att. Staru gaita optiskajā mikroskopā
Arī tālskatim (7. att. a) optiskā sistēma sastāv no divām lēcām: objektīva un okulāra (7. att. b). Atšķirība no mikroskopa ir tā, ka paralēls staru kūlis, kas ieiet objektīvā, saglabā paralēlo novietojumu arī izejot no okulāra (7. att. b). Tas tiek panākts, savietojot objektīva un okulāra vienus no fokusiem. Ja ir zināmi objektīva un okulāra fokusa attālumi Fob(m) un Fok(m), tad ir iespējams aprēķināt tālskata optisko palielinājumu Г=Fob:Fok.
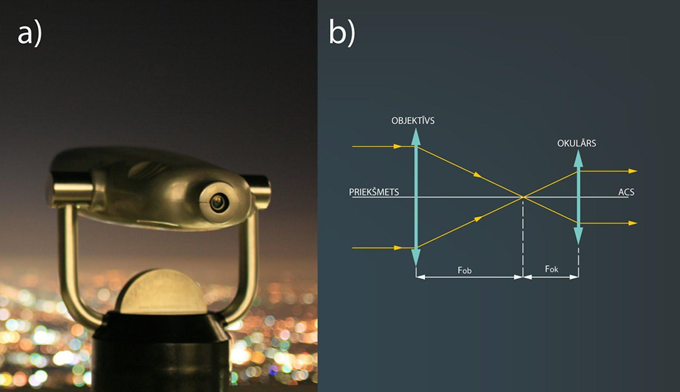
7.att. Teleskops un staru gaita tā optiskajā sistēmā
Līdz šim apskatītās attēlu konstrukcijas lēcām ir idealizēts gadījums, reāli ar šādām optiskajām sistēmām iegūtiem attēliem piemīt dažādas nepilnības, ko sauc par lēcu kļūdām. Vienu no lēcu kļūdām sauc par hromatisko aberāciju, kuras pastāvēšanas iemesls ir gaismas laušanas koeficienta atšķirības dažāda viļņu garuma gaismai (Fiztēma par gaismas izplatīšanos). Sfērisko lēcu materiāla gaismas laušanas koeficients ir lielāks zilajai gaismai nekā sarkanajai, līdz ar to, ja uz lēcu krīt baltā gaisma, tad tās sastāvā esošā zilā gaisma fokusējas tuvāk lēcai nekā sarkanā gaisma (8. att. a). Hromatiskā aberācija izpaužas kā varavīksnes krāsu ieskauta attēla kontūra. Otra minētā lēcu kļūda ir sfēriskā aberācija, kas rodas tāpēc, ka stari, kas lēcā ienāk tālāk no optiskā centra, lūst vairāk (8. att. b). Šīs kļūdas rezultātā var veidoties neass attēls.
Skaties DZM materiālu par optiskajiem instrumentiem!
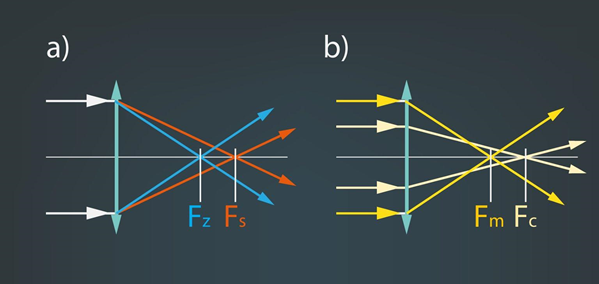
8.att. Lēcu hromatiskā (a) un sfēriskā (b) aberācija
Agrāk hromatisko aberāciju (9. att. a) novērsa, lietojot lēcas ar pēc iespējas lielāku fokusa attālumu. Bet to nevarēja realizēt visos optiskajos instrumentos, jo lielāks fokusa attālums nozīmē arī lielākus instrumenta izmērus (17. gadsimta teleskops: http://en.wikipedia.org/wiki/Aerial_telescope). Mūsdienīgāks risinājums ir izmantot papildu lēcas, kurām ir citādi laušanas koeficienti nekā pamata lēcai. Tādā veidā iespējams samazināt hromatiskās aberācijas ietekmi (9. att. b,c).
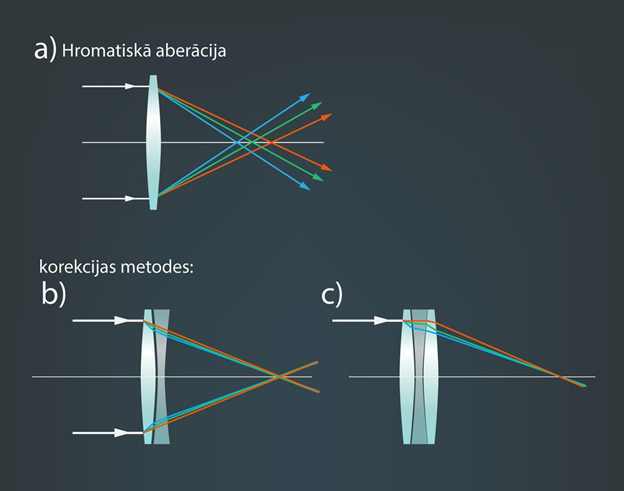
9.att. Lēcu hromatiskā aberācija un tās korekcijas metodes