Lai izlasītu šo fiztēmu, ir jāpaveic darbs, bet lai paveiktu darbu, ir vajadzīga enerģija! Arī, piemēram, pirms ejam uz skolu vai darbu mēs kaut ko iekožam/ieēdam. Tātad, enerģiju var definēt kā fizikālas sistēmas spēju veikt darbu. Padarītais darbs ir vienāds ar enerģijas izmaiņu, kas nepieciešama darba veikšanai, tādēļ gan darbam, gan enerģijai ir viena un tā pati mērvienība - džouls (J). Piemēram, ja 1 N lielu spēku pārvieto kasti par 1 m, tad ir padarīt 1 J liels darbs un līdz ar to patērēta 1 J liela enerģija (1.att.).
Enerģija var izpausties divās formās:
1) Kinētiskā enerģija;
2) Potenciālā enerģija.
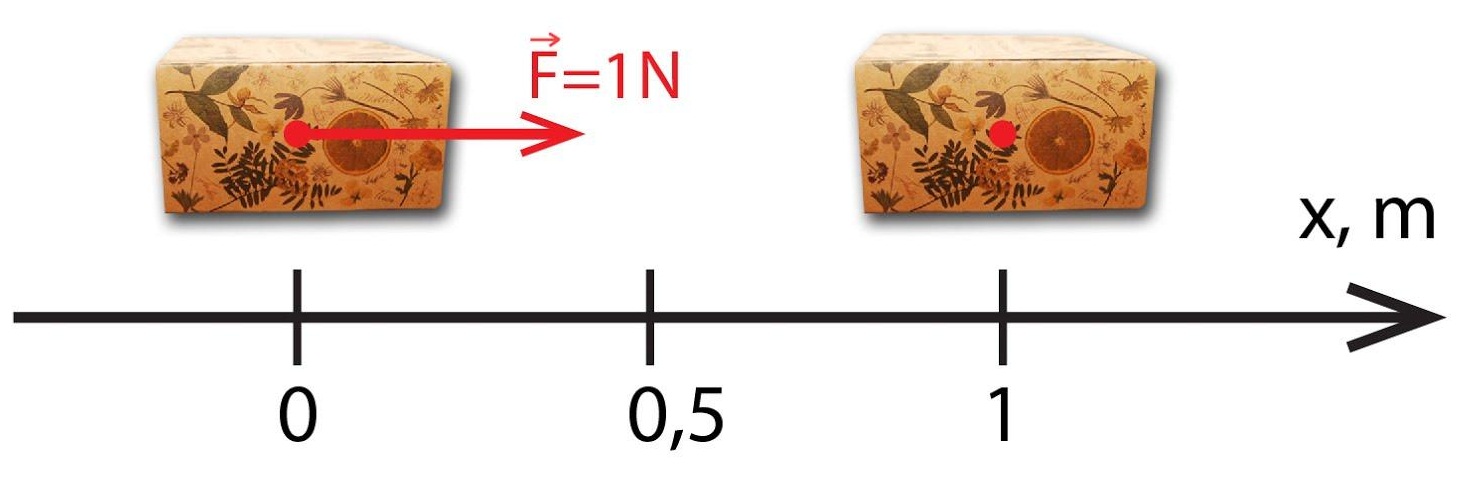
1. att. Vienu džoulu liela darba padarīšana izmantojot 1 J enerģijas
Kinētiskā enerģija jeb kustības enerģija piemīt kustībā esošam ķermenim, piemēram, braucošai automašīnai (2. att). Kinētisko enerģiju aprēķina, izmantojot izteiksmi Ek=mv2/2, kur
m - ķermeņa masa, kg
v - kustības ātrums, m/s

2. att. Braucošai automašīnai piemīt kinētiskā enerģija
Fiztēmā par darbu (saite uz fiztēmu) noskaidrojām, ka, palaižot vaļā virs zemes paceltu ķermeni, smaguma spēks veic darbu, lai ķermenis kristu zemes virzienā. Līdz ar to var secināt, ka arī paceltam ķermenim piemīt spēja veikt darbu, kaut gan tas sākotnēji neatrodas kustībā. Šādā gadījumā saka, ka ķermenim ir potenciālā enerģija Ep, ko aprēķina Ep=mgh, kur
m - ķermeņa masa, kg
g - brīvās krišanas paātrinājums, m/s2
h - augstums virs zemes, m
Svarīgi ir tas, ka nosakot potenciālo enerģiju ir jāpieņem nulles līmenis, piemēram, zemes virsmu vai grīdu. Lai arī cilvēks ir aizmidzis krēslā un daudz nekustas (3. att.), tā masas centrs atrodas noteiktā augstumā virs zemes un tam piemīt potenciālā enerģija.

3. att. Sēdoša cilvēka potenciālā enerģija
Ja tiek deformēts kāds elastīgs ķermenis, piemērma, atspere, tad šādā gadījumā arī tiek uzkrāta enerģija, jo, pārtraucot deformāciju, ķermenis ir spējīgs veikt darbu. Līdzīgi kā brīvās krišanas un smaguma spēka gadījumā, arī deformētas atsperes veiktais darbs ir vienāds ar potenciālās enerģijas izmaiņu. Ja par potenciālās enerģijas nulles līmeni pieņem atsperes nedeformēto stāvokli (4. att. a), tad deformētas atsperes (4. att. b) potenciālā enerģija vienāda ar Ep=k(∆x)2/2, kur
k - atsperes stinguma koeficients, N/m
∆x - deformācijas lielums, m
Ja atsperes uzbūve to atļauj, tad potenciālo enerģiju var iegūt gan atsperi izstiepjot, gan saspiežot.
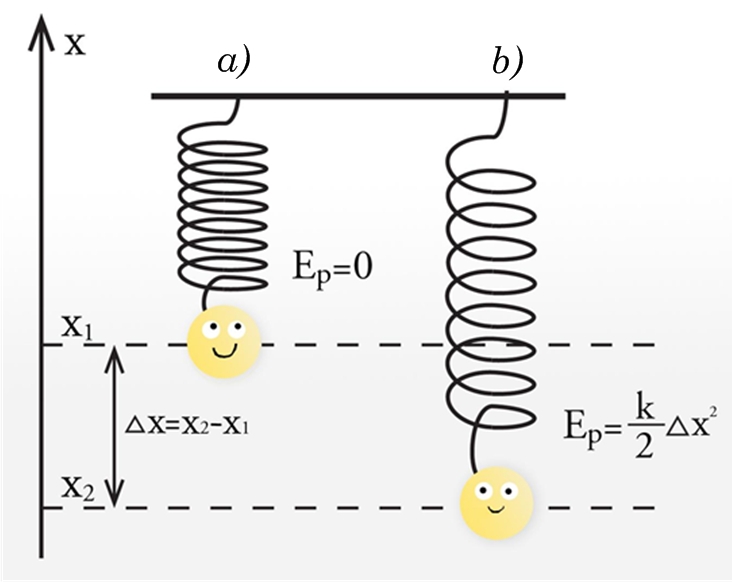
4. att. Atsperē uzkrātā potenciālā enerģija
Ķermenim reizē varbūt gan kinētiskā, gan potenciālā enerģija, līdz ar to ķermeni stāvokli var raksturot, ja izmanto abus šos enerģijas veidus. Potenciālas Ep un kinētiskās enerģijas Ek summu sauc par pilno mehānisko enerģiju E (5. att.). Ja aplūkotais ķermenis neatrodas mijiedarbībā ar citiem ķermeņiem, tad pilnā mehāniskā enerģija paliek nemainīgs lielums, tas ir viens no universālajiem fizikas likumiem - enerģijas nezūdamības likums -, kas nosaka to, ka enerģija nezūd un nerodas no jauna, bet tikai maina savu formu. Tāpēc, ja palielinās vai samazinās kinētiskā enerģija, tad attiecīgi palielinās vai samazinās potenciālā enerģija.

5. att. Lidmašīnas pilnā mehāniskā enerģija
Kinētiskās enerģijas aprēķina izteiksme Ek=mv2/2 parāda, ka visvairāk kinētisko enerģiju ietekmē ātrums, jo kinētiskā enerģijas atkarība no ātruma ir kvadrātiska. Tādēļ arī tiek uzsvērta ātruma lielā nozīmē ceļu satiksmes drošībā, jo, palielinot ātrumu 2 reizes, transporta līdzekļa kinētiskā enerģija pieaug 4 reizes un lai automašīnu apturētu, kādam spēkam ir jāpastrādā darbs šīs kinētiskaš enerģijas apmērā. Ja 1 t smaga automašīna pilsētā apstājusies pie luksofora (1. att. a), tad tās kinētiskā enerģija ir 0. Sasniedzot pilsētā atļauto ātrumu 50 km/h, kinētiskā enerģija ir pieaugusi aptuveni līdz 10 kJ (1. att. b). Grafiski attēlojot kinētiskās enerģijas atkarību no ātruma, iegūst uzskatāmu kvadrātiskā pieauguma grafiku (1. att. c).
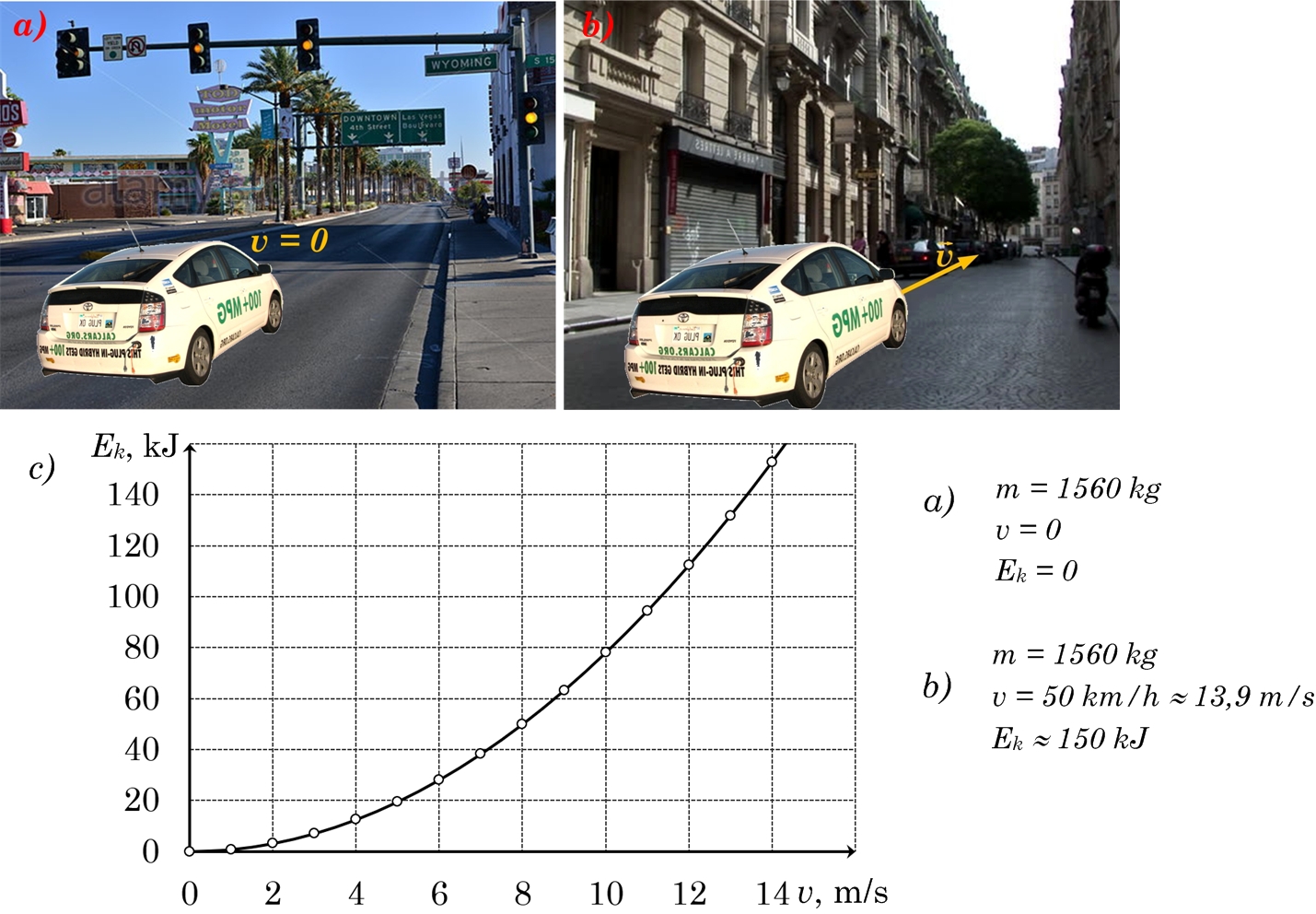
1. att. Automašīnās kinētiskās enerģijas izmaiņa pilsētā
Līdz ar ātruma lielo ietekmi uz kinētisko enerģiju, nav jābrīnās, ja viegli ķermeņi sasniedz masīvu ķermeņu kinētisko enerģiju, tiem tikai jākustās pietiekoši ātri! Latviešu tenisista Ernesta Gulbja maksimālais serves ātrums ar 57 g smagu bumbiņu ir 240 km/h. Šādai bumbiņai kinētiskā enerģija ir 127 J. Ja pēc spēles Gulbis izbrac nelielu līkumu ar motociklu (kopējā masa 250 kg), tad braucot ar ātrumu 1 m/s, tiktu sasniegta tieši tā pati kinētiskā enerģija (2. att.).

2. att. Dažādas masas ķermeņi ar vienādu kinētisko enerģiju
Arī potenciālo enerģiju ietekmē vairāki lielumi. Ja ķermenis kāda spēka ietekmē maina savu augstumu, tad mainās tā potenciālā enerģija. Piemēram, ja ķermenis ir pakļauts kādam no sviediena veidiem, tad tā vertikālo kustību ietekmē smaguma spēks. Ja apskata potenciālo enerģiju divās ķermeņa pozīcijās ar augstumiem h1 un h2, tad potenciālās enerģijas starpība vienāda ∆Ep=mgh1-mgh2=mg(h1-h2). Šis lielums arī ir vienāds ar smaguma spēka veikto darbu (3. att.).
3. att. Potencionālās enerģijas maiņa
«Monster Truck» šova laikā iespaidīgie automobiļi veic galvu reibinošus trikus (4. att. a), kuros tiem jārēķinās ar uz automobili darbojošos smaguma spēku. Tomēr smaguma spēks nav vienīgais, kas ietekē mūsu vertikālās kustības dinamiku. Izmantojot, piemēram, liftu vai eskalatoru (4. att. b) elektromotori veic darbu, lai pārvietotu mūs noteiktā augstumā un izmainītu mūsu potenciālo enerģiju.
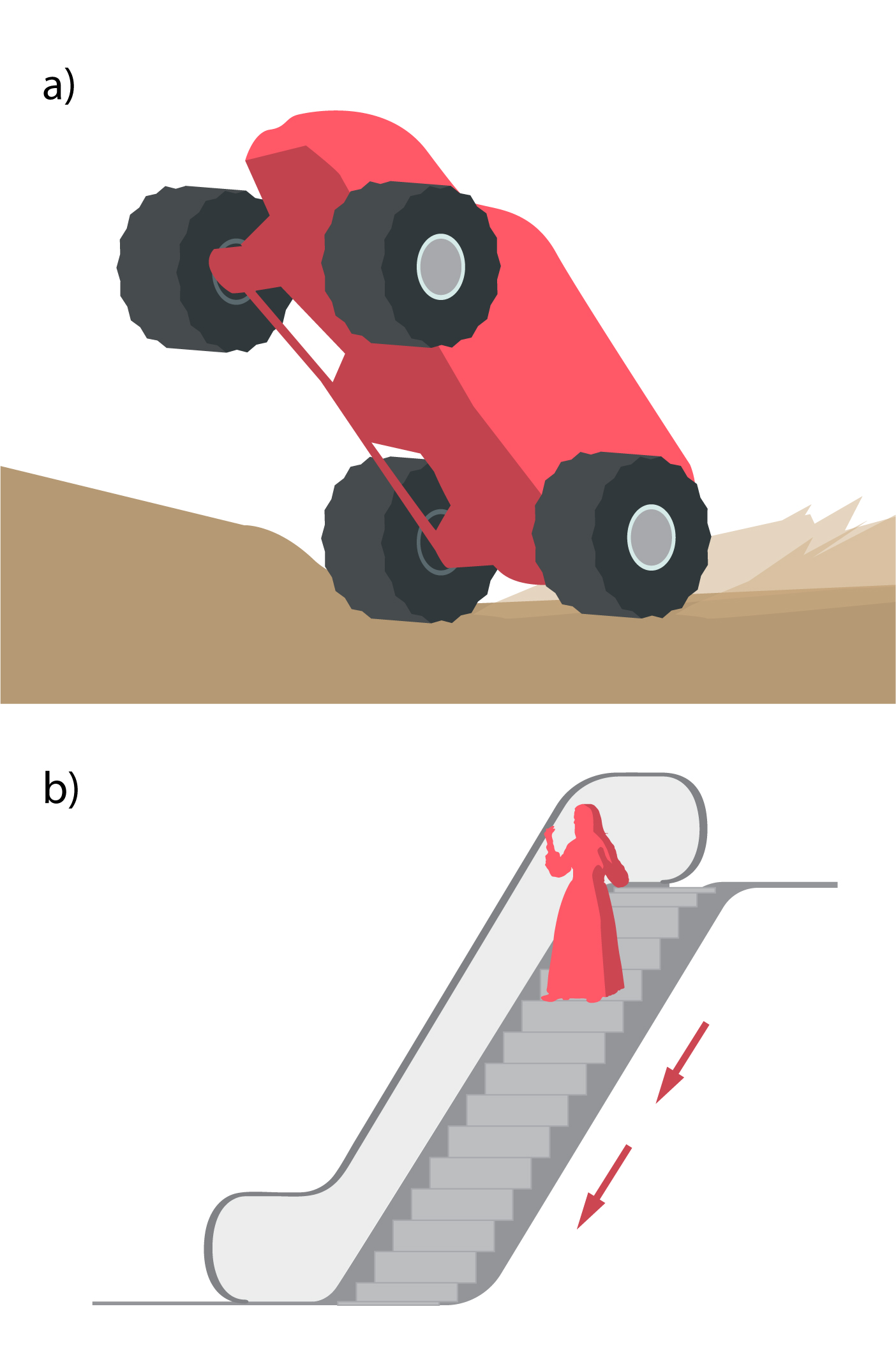
4. att. Potenciālās enerģijas izmaiņa «Monster Truck» šovā un uz eskalatora
Ja tiek deformēts kāds elastīgs ķermenis, tad šādā gadījumā arī tiek uzkrāta enerģija, jo pārtraucot deformāciju, ķermenis ir spējīgs veikt darbu. Piemēram, ja tiek nospiesta poga uz tālvadības pults (5. att.), tad pēc pogas atlaišanas tā atgriežas sākotnēja stāvoklī, veicot darbu uz uzkrātās potenciālās enerģijas rēķina.
5. att. Pogas darbībā
Ja pogai ir jāpadara lielāks mehāniskais darbs nekā tas ir, piemēram, 5. att. redzamajai pultij, tad pogas mehānismā tiek iebūvēta atspere, kas uzkrāj potenciālo enerģiju un veic nepieciešamo darbu pogas atgriešanai sākuma stāvoklī. Drošības noteikumu ietvaros, Lielā Hadronu paātrinātāja (LHC) darbības apturēšanai vadības panelī (6. att. a) ir ierīkota liela, sarkana poga (6. att. b), kuras mehānismā ir atspere, kas pogas lietošanas gadījumā to atgriež sākotnējā stāvoklī.

6. att. Vadības panelis LHC
Iepriekš kinētiskā enerģija tika pieminēta, ja objekts pārvietojās, tomēr tas nav obligāti nepieciešams. Arī rotējošiem ķermeņiem ir noteiks kinētiskās enerģijas daudzums (7. att. a), ko aprēkiņa, izmantojot izteiksmi Ek=Iω2/2, kur
I - ķermeņa inerces moments, kg·m2
ω - rotācijas leņķiskais ātrums, rad/s
Datora cietais disks parasti nemēdz kustēties prom no datora korpusa, tomēr šīs datora komponentes iekšpusē notiek atmiņas elementa rotācijas kustība (7. att. b), kas piešķir tam kinētisko enerģiju.
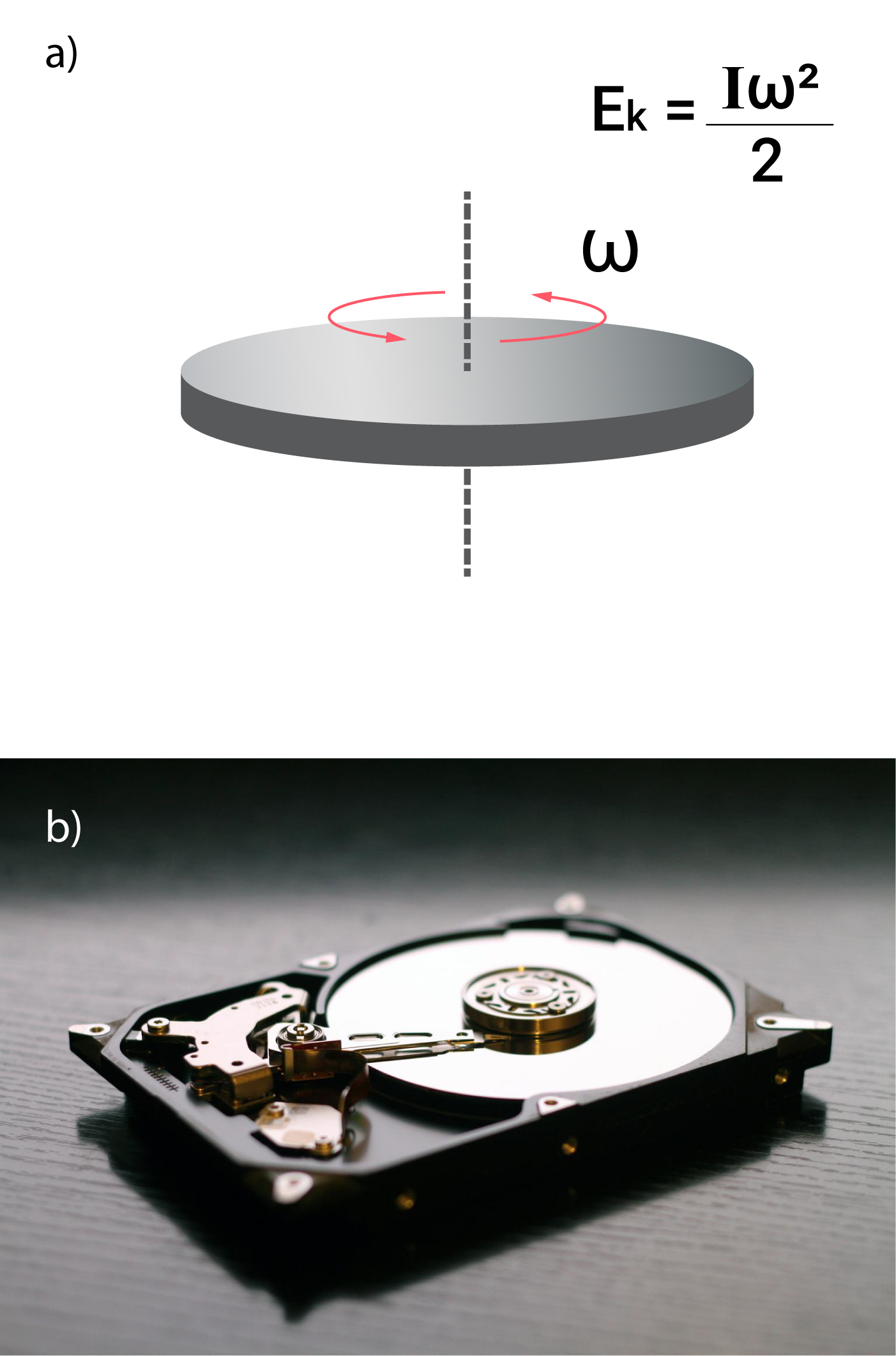
7. att. Kinētiskā enerģija rotācijas kustībā
Zinot, ka ķermenim tiek piešķita enerģija uz pastrādātā darba rēķina, iespējams iegūt enerģijas arpēķina izteiksmes, izmantojot līdz šim apskatītās darba, spēka un kustības izteiksmes. Lai iegūtu kinētiskās enerģijas izteiksmi, piemēram, lidmašīnai, kas ar nemainīga vilcējspēka F palīdzību vienmērīgi paātrinātā kustībā palielina ātrumu no v0 līdz v (1. att.), jāizmanto trīs sakarības:
1) Paveiktā darba izteiksme A=Fs;
2) Spēku un paātrinājumu saistošā izteiksme F=ma;
3) Izteiksme, kas saista sākuma un beigu ātrumus ar pārvietojumu un paātrinājumu v2-v02=2as;
Kur
A - paveiktais darbs, J
F - spēks, N
s - pārvietojums, m
m - ķermeņa masa, kg
a - paātrinājums, m/s2
v - beigu ātrums, m/s
v0 - sākuma ātrums, m/s
Vispirms 1. solī darba A izteiksmē (1) spēks jaaizstāj ar (2) izteiksmē izteikto spēku un no (3) izteiksmes jāizsaka pārvietojums s (1. att.).
2. solī iegūtajā darba izteiksmē jāievieto s vietā iegūta izteiksme no (3).
Gala rezultātā iegūst, ka A=mv2/2-mv02/2. Ja sākuma ātrums ir 0, tad iegūstam kinētiskās enerģijas izteiksmi A=Ek=mv2/2
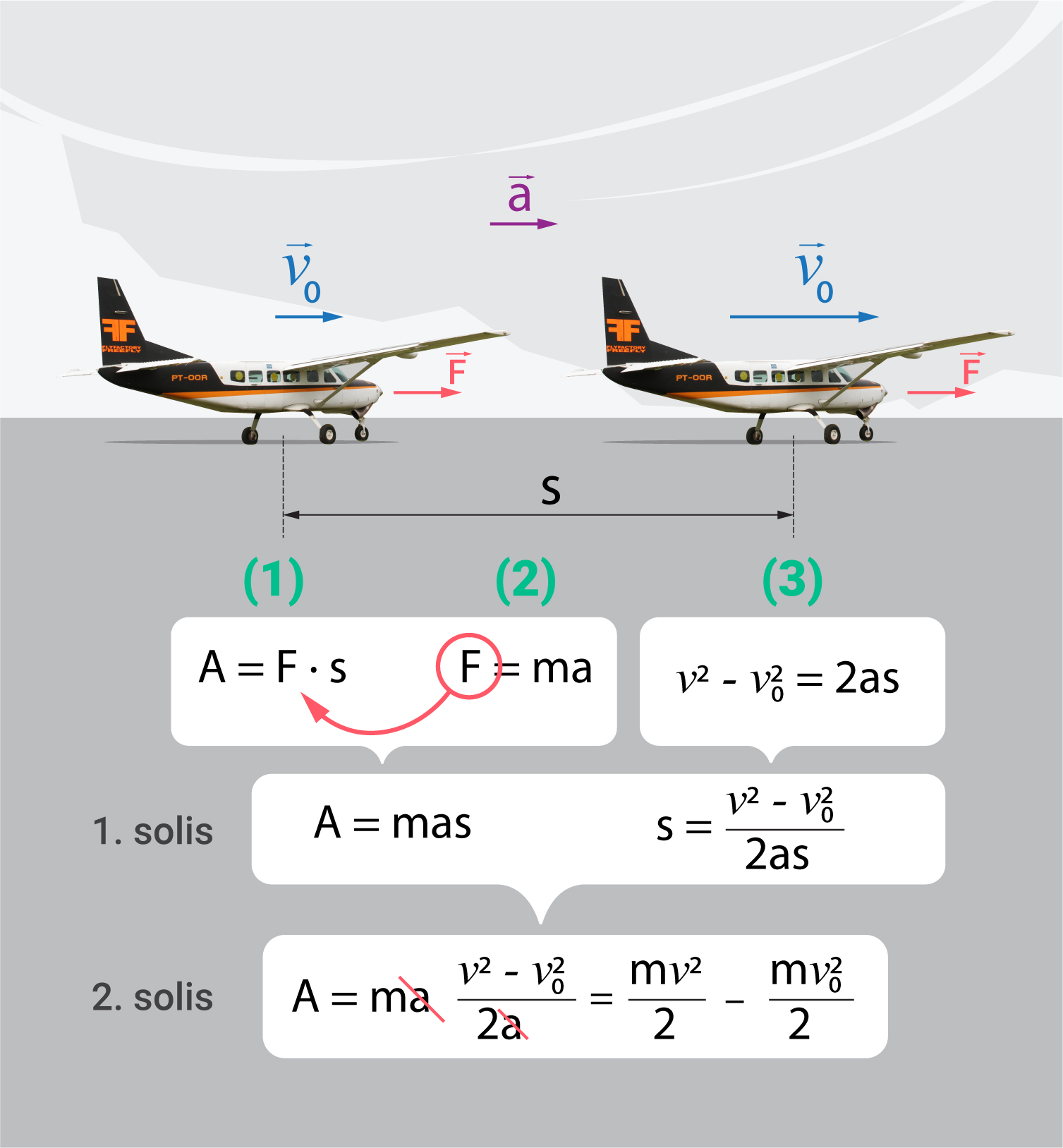
1. att. Kinētiskās enerģijas izteiksmes iegūšana
Lai iegūtu virs zemes pacelta ķermeņa potenciālas enerģijas Ep izteiksmi, apskatīsim gadījumu, kad karogs ar masu m tiek vienmērīgi pacelts no zemes līdz augstumam h (2. att.). Ja ātrums ir nemainīgs (v=const), tad vilcējspējs FV, kas veic darbu karoga pacelšanā, ir vienāds ar smaguma spēku FG. Pārvietojums s šajā gadījumā būs augstums h (2. att.). Paveiktā darba izteiksmē A=Fs=Fvh ietvietojot smaguma spēka lielums FG=mg (jo FV=FG), iegūst A=Ep=mgh.
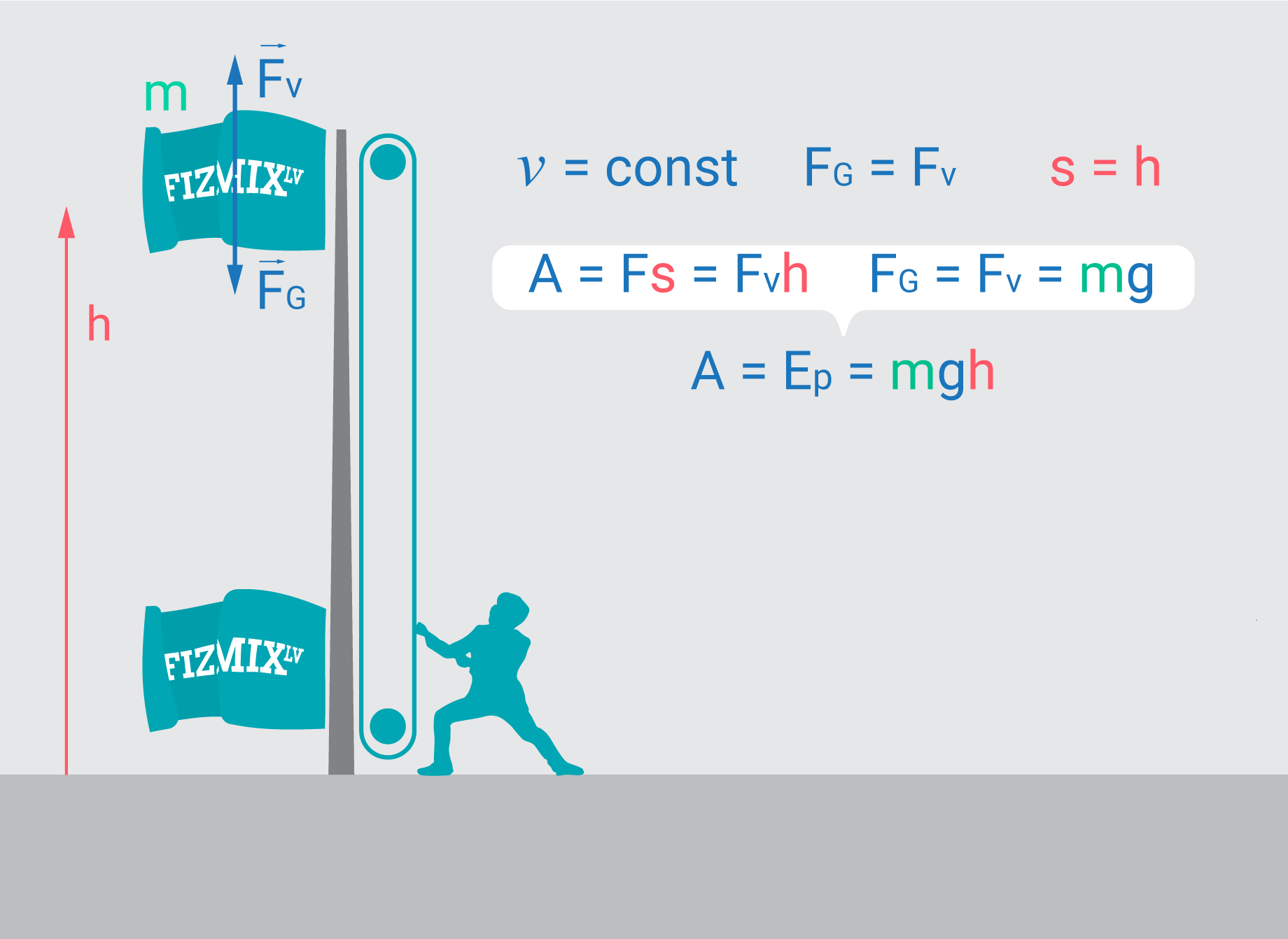
2. att. Virs zemes pacelta ķermeņa potenciālās enerģijas izteiksmes iegūšana
Arī elastīgos ķermeņos, piemēram, atsperē var uzkrāt potenciālo enerģiju. Šādā gadījumā pārvietojums s darba izteiksmē A=Fs ir atsperes pagarinājums ∆x. Šoreiz spēks, kas nodrošina potenciālās enerģijas uzkrāšanos, ir elastības spēks Fe, tomēr pēc Huka likuma Fe=k∆x seko, ka elastības spēks visu deformācijas laiku mainās, bet darba izteiksme paredzēta nemainīgam spēkam. Šī iemesla dēļ darba izteiksmē tiek ņemta elastības spēka vidējā vērtība, kuras izteiksmi iegūst kā pagarinājumu pieņemot vidējo atsperes pagarinājumu ∆xvid=∆x/2 (3. att.). Šādi var darīt, jo elastības spēks pieaug lineāri atkarība no deformācijas lieluma. Gala rezultātā paveiktais darbs A ir vienāds ar uzkrāto potenciālo enerģiju A=Ep=k∆x2/2, kur
k - atsperes stinguma (elastības) koeficients, N/m
∆x - pagarinājums, m
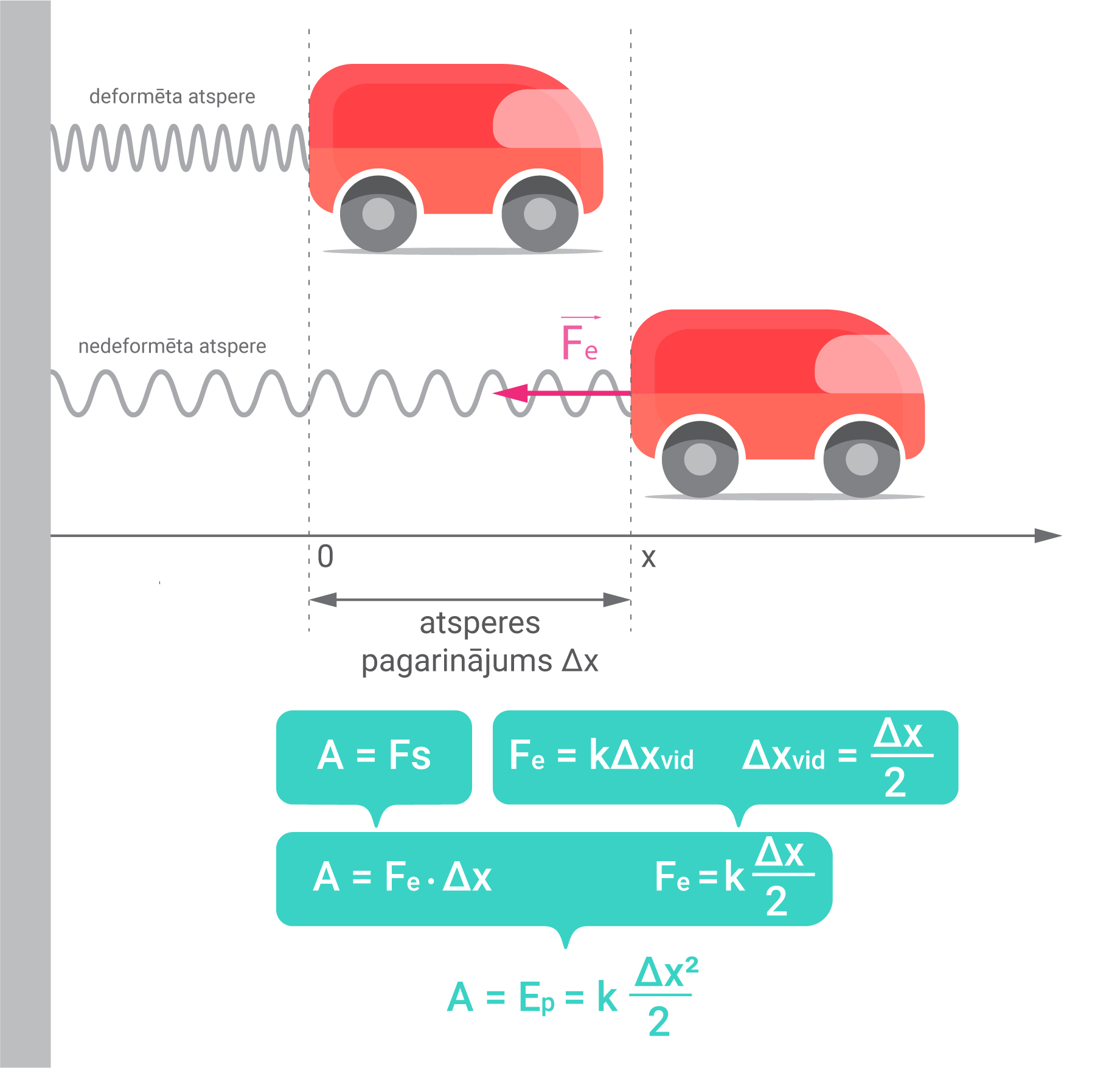
3. att. Atsperē uzkrātās potenciālās enerģijas izteiksmes iegūšana