Ja ķermenis spēka ietekmē pārvietojas, tad spēks pastrādā darbu. Par nemainīga spēka darbu A sauc pārvietojuma moduļa un spēka, kas iedarbojas kustības virzienā, reizinājumu (1. att. a) jeb A=F·s, kur
F - spēks, N
s - pārvietojums, m
Darba mērvienība ir N·m, ko sauc par džoulu J. Spēka darbs mēra, cik daudz šis konkrētais spēks pārvietojuma laikā ir "ieguldījis" ķermeņa kustībā. Spēks, kas strādā pozitīvu darbu, cenšas ķermeni pāatrināt, bet negatīvu darbu strādājošs spēks - nobremzēt. Arī dzīvē ir piemēri, kad viens cilvēks ceļ māju, bet cits strādā par graustu noārdītāju.
Ja kustību izraisošais spēks F nav vērsts kustības virzienā, bet leņķī α, tad spēka veikto darbu aprēķina, izmantojot izteiksmi A=F·s·cosα. Līdz ar to spēks var būt gan pozitīvs, gan negatīvs, gan arī vienāds ar nulli (1.att. b).
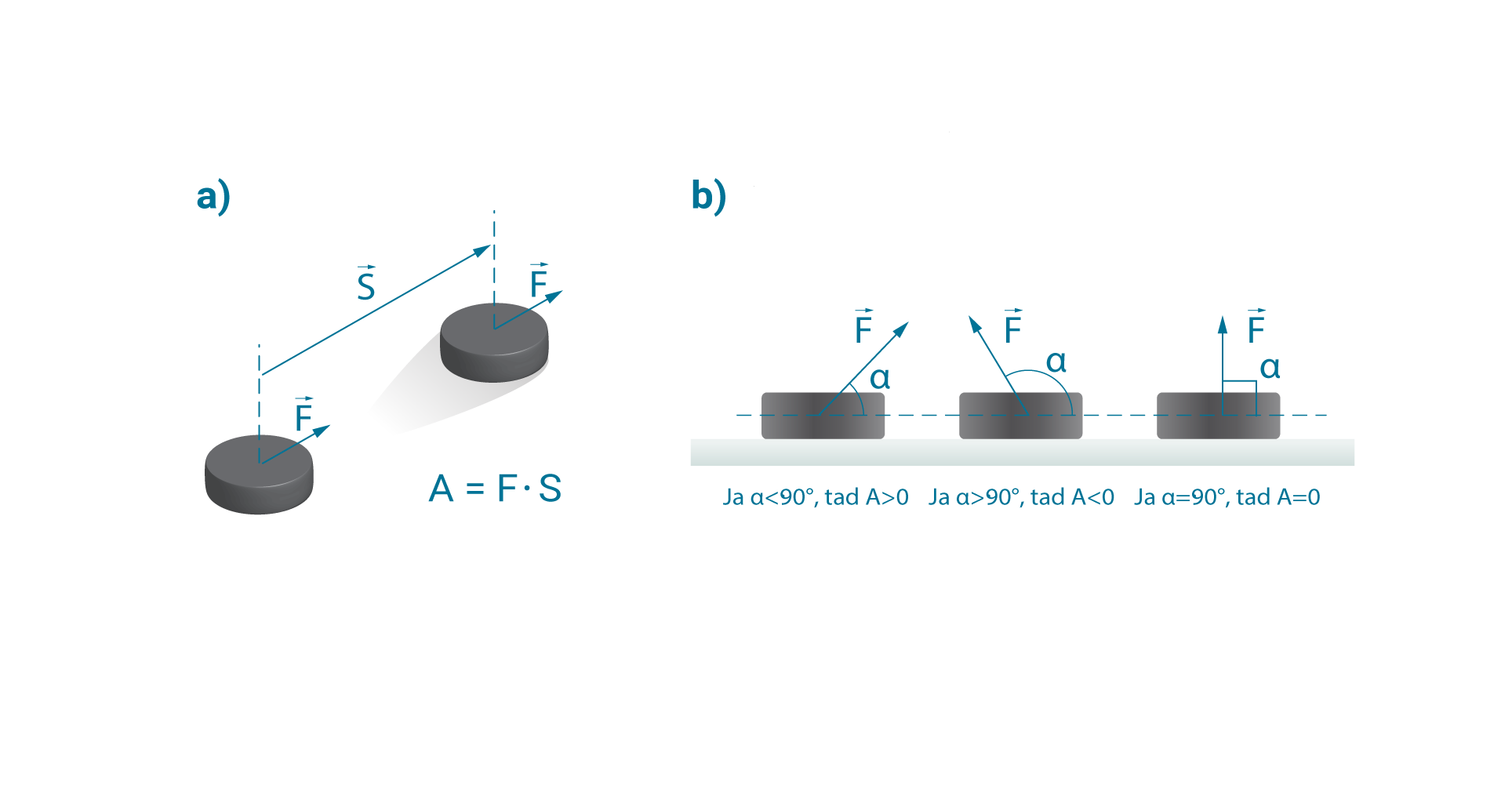
1. att. Spēka veiktais darbs
Pozitīvu darbu, piemēram, veic spēks ar kādu cilvēks velk kādu kravu (2. att. a). Savukārt piemērs spēkam, kas veic negatīvu darbu, ir berzes spēks Fb, kas ir vērsts pretēji ķermeņa ātruma vektoram (2. att. b). Berzes spēka gadījumā α=180o, līdz ar to iepriekš apskatīta izteiksme, lai aprēķinātu spēka veikto darbu, kļūst par A=Fb·s·cos180o=-Fb·s. Velkot ar pirkstu pa planšeti, berzes spēks visu laiku darbojas pretī kustībai un veic negatīvu darbu (2. att. b).
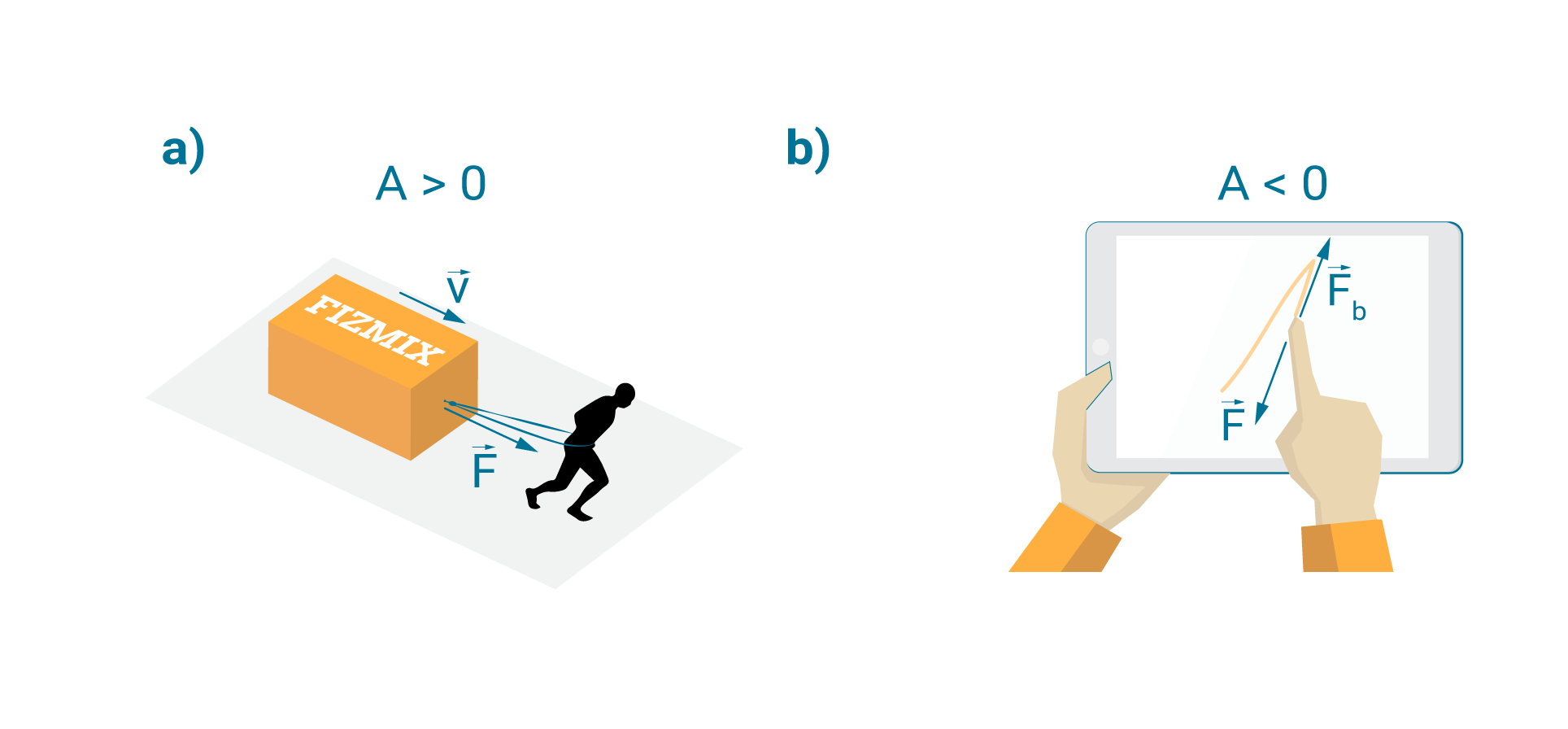
2. att. Pozitīvs un negatīvs spēka darbs
Arī smaguma spēks var veikt darbu. Ja kādu ķermeni paceļ augstumā h (3. att.) un palaiž vaļā, tad tas smaguma spēka ietekmē nokrīt līdz zemei. Līdz ar to veiktais attālums ir h, no kā seko, ka smaguma spēka veiktais darbs A=F·h=m·g·h, kur
m - ķermeņa masa, kg
g - brīvās krišanas paātrinājums, m/s2
h - krišanas augstums, m
Smaguma spēka veiktais darbs, brīvi krītoša ķermeņa gadījumā, vienāds ar smaguma spēka moduļa reizinājumu ar krišanas augstumu h.
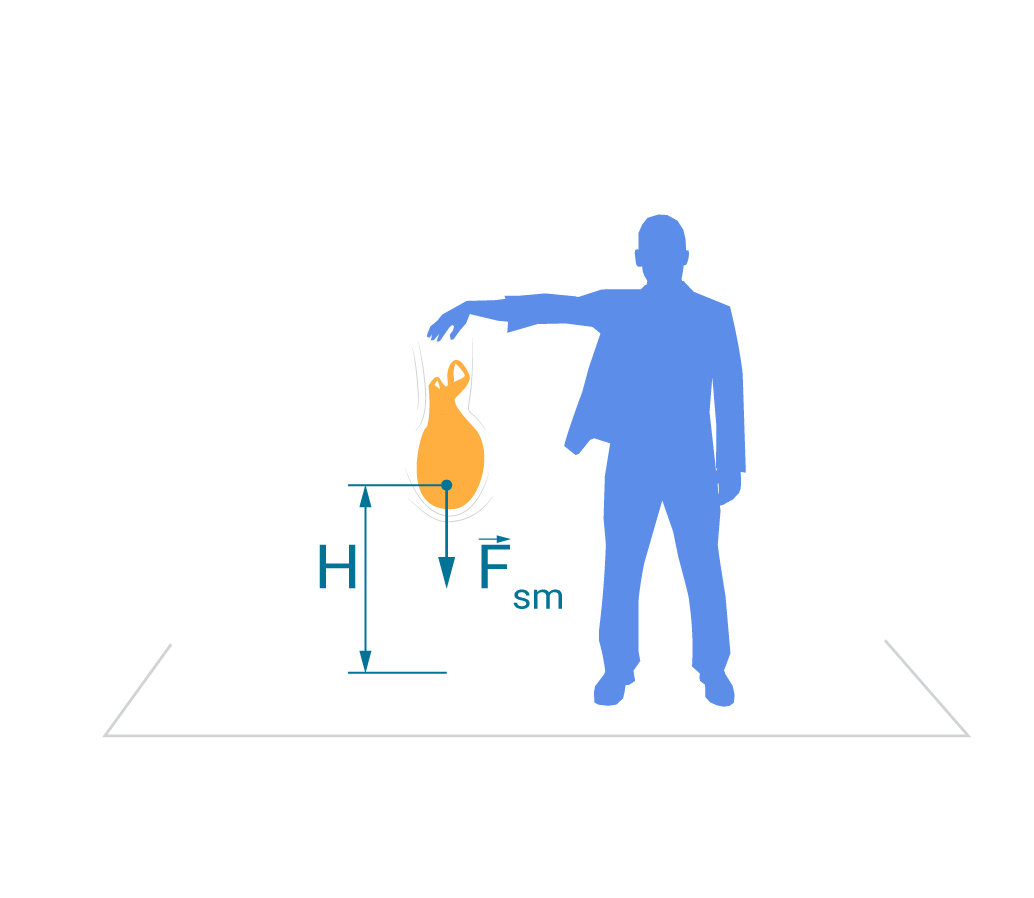
3. att. Smaguma spēka veiktais darbs
Mūsdienu skrejošajā dzīves ritmā ir svarīgi ne tikai tas, ka mehānisks darbs tiek padarīts, bet arī ātrums, kādā tas notiek. Mehāniska darba veikšanas ātrumu raksturo jauda N (4. att.). Ja laika momentā t tiek vienmērīgi padarīts darbs A, tad jaudu N aprēķina pēc formulas N=A/t, kur
A - padarītais darbs, J
t - laiks, s
Jaudas mērvienība ir vats (W)!
Mūsdienās ar automašīnu sasniegt 100 km/h lielu ātrumu nav nekas īpašs, tomēr ir cilvēki, kas šo ātrumu vēlas sasniegt pēc iespējās ātrāk, tādēļ viņi izvēlās automašīnas ar jaudīgākiem dzinējiem (4. att.).
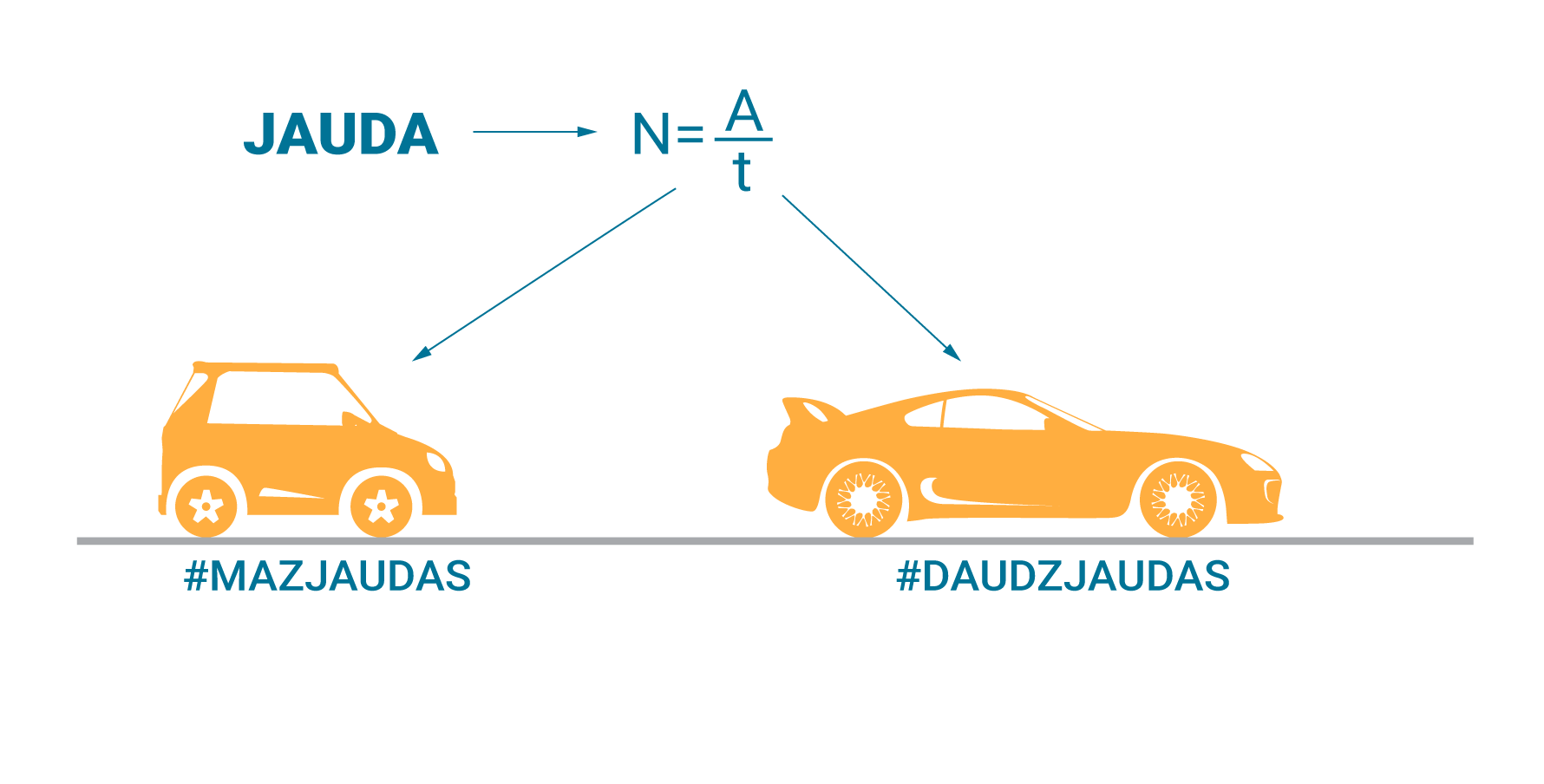
4. att. Jauda
Jebkura ierīce, kas pārvērš viena veida enerģiju citā, spēj noderīgā enerģijā pārvērsti tikai daļu no kopējās enerģijas. Pārēja enerģija pārvēršas iekšējā enerģijā (siltumā). Lai tas būtu iekšdedzes dzinējs vai cilvēka organisms, nevienā no šīm enerģijas pārvēršanas mašīnām nedarbojas bez enerģijas zudumiem, kas izpaužas kā iekšējā siltuma palielināšanās jeb sasilšana. Lai raksturotu enerģijas daudzumu, kas tiek izmantots lietderīgi, lieto lietderības koeficientu η (5. att.), kas ir vienāds ar lietderīgā darba Al jeb lietderīgi pārvērstās enerģijas attiecība pret kopēja darbu A jeb kopējo pārvērsto enerģiju: η=Al/A. Ja lietderības koeficientu pareizina ar 100, tad iegūst lietderības koeficientu procentos (%).
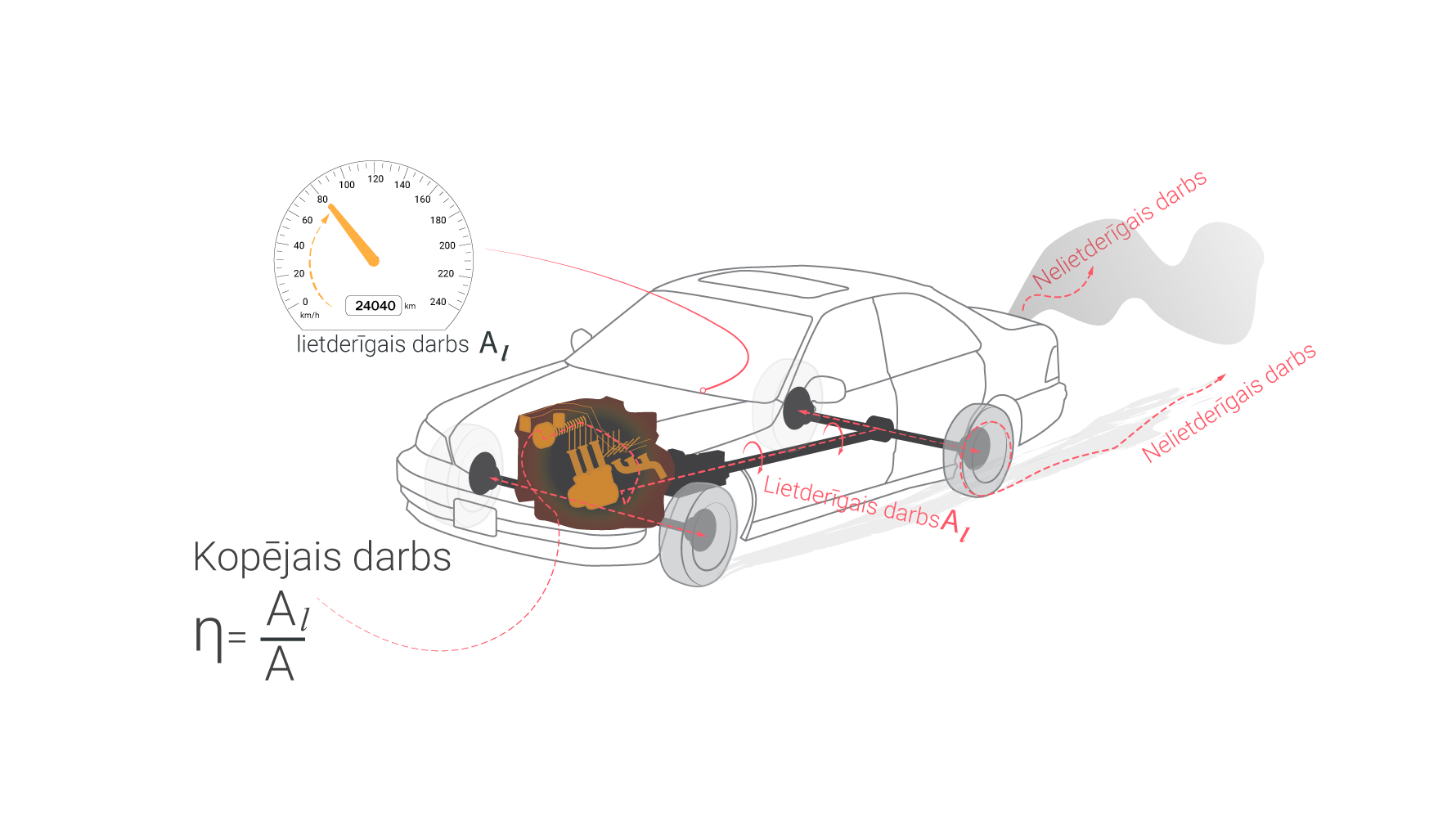
5. att. Lietderības koeficients
Ja uz kustībā esošu ķermeni darbojas tikai berzes spēks, tad pēc noteikta laika momenta kustība apstājas. Tomēr parasti uz ķermeni darbojas arī citi spēki. Lai aprēķinātu, cik lielu kopējo darbu veic spēki, var rēķināt katra spēka veikto darbu atsevišķi, un tad tos sasummēt, bet var arī noteikt kopspēku un tā veikto darbu. Lai aprēķinātu kādu darbu veic automašina attiecībā pret zemi, velkot citu spēkratu, var saskaitīt katra iesaistītā spēka veikto darbu, vai arī aprēķināt kopsēku un tā veikto darbu (1. att.).
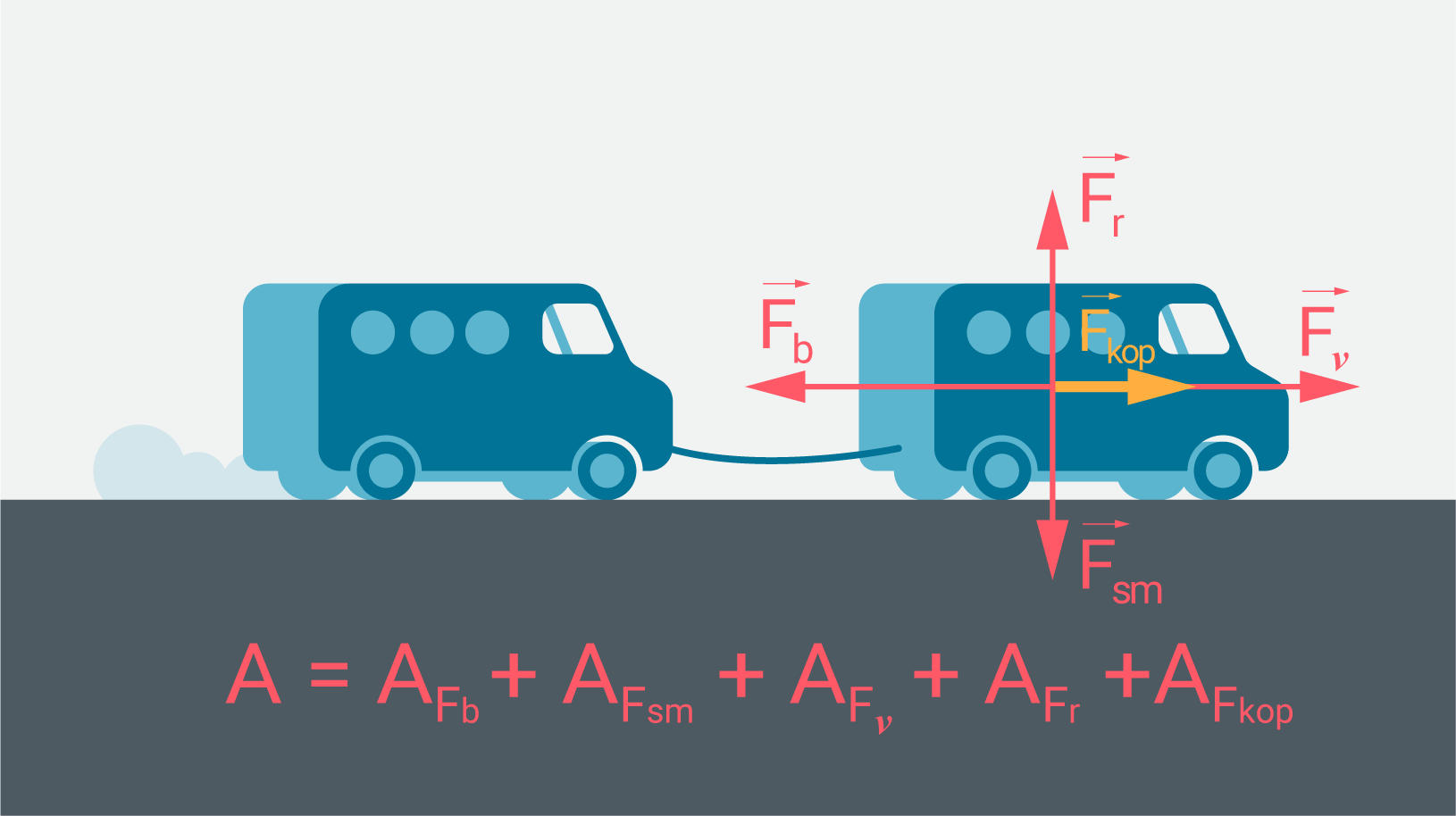
1. att. Darba aprēķins vairāku spēku gadījumā
Līdz šim apskatītie spēki kustības laikā nemainīja savu vērtību, līdz ar to darbu varēja aprēķināt, ņemot vērā nemainīgu spēka vērtību. Tomēr gadās, ka spēks kustības laikā mainās, un tad vairs nevar pielietot līdz šim apskatīto darba aprēķināšanas metodi. Tāds, piemēram, ir elastības spēki un to veiktais darbs. 2. attēlā redzama velosipēda aizmugurēja amortizatora atspere, kurai piemīt noteikts stinguma koeficients k. Pēc Huka likuma elastības spēks vienāds ar Fel=k·∆x. Līdz ar to, jo lielāka atsperes deformācija, jo lielāks elastības spēks darbojās. Šādā gadījumā var lietot divas darba aprēķina metodes.

2. att. Velosipēda amartizatora atspere
Pirmkārt, balstoties uz Huka likumu, elastības spēks pieaug lineāri, atkarībā no deformācijas lieluma, līdz ar to mēs varam viegli noteikt spēka vidējo vērtību, proti, jānosaka kāds elastības spēks darbojas pusceļā pilnai deformācijai. 3. attēlā redzama atspere, kura tiek deformēta sākot no koordinātes x1 līdz koordinātei x2. Vidējais elastības spēks ir vienāds ar elastības spēku koordinātē (x1+x2)/2 jeb kad deformācija lielums sasniedz ∆x/2, un tas ir Fvid=k·∆x/2. Kad ir iegūts vidējais elastība spēks, tad tālāk var lietot iepriekš apskatīto izteiksmi A=F·s, līdz ar to elastības spēka veiktais darbs Ael=k·∆x/2·∆x=k·∆x2/2.
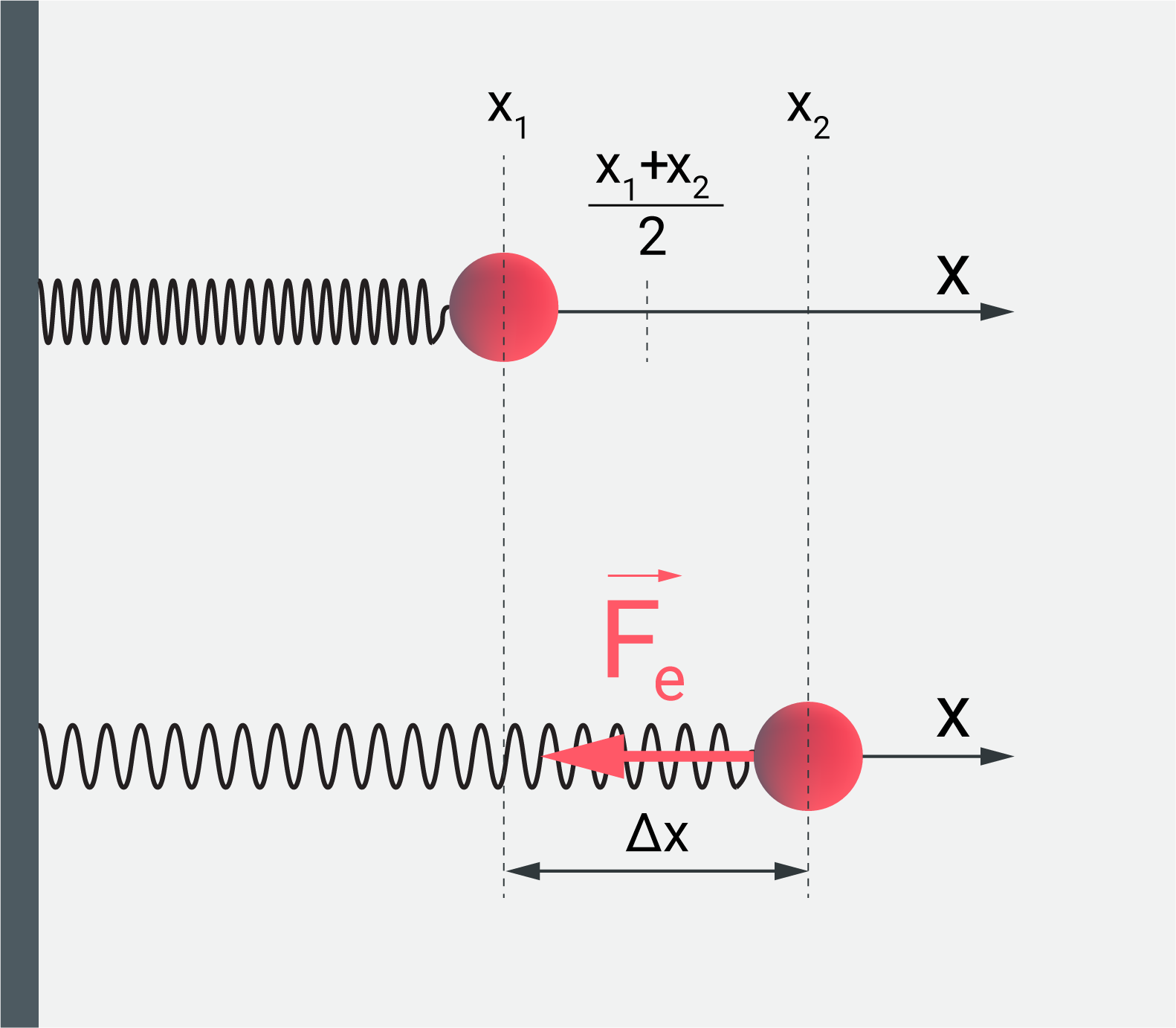
3. att. Elastības spēks veic darbu
Otrs darba aprēķināšanas veids ir grafiskā metode. Ja koordinātu asīs atzīmē grafiku spēka atkarībai no pārvietojuma, tad padarītais darbs ir vienāds ar laukumu zem F-s grafika. Ja spēks ir konstants (4. att. a), tad laukumam zem grafika ir taisnstūra forma un laukuma aprēķinam iegūst sākumā apskatīto darba aprēķināšanas izteiksmi A=F·s. Ja spēks nav konstants (4. att. b un c), tad laukuma aprēķinam jālieto citas izteiksmes.
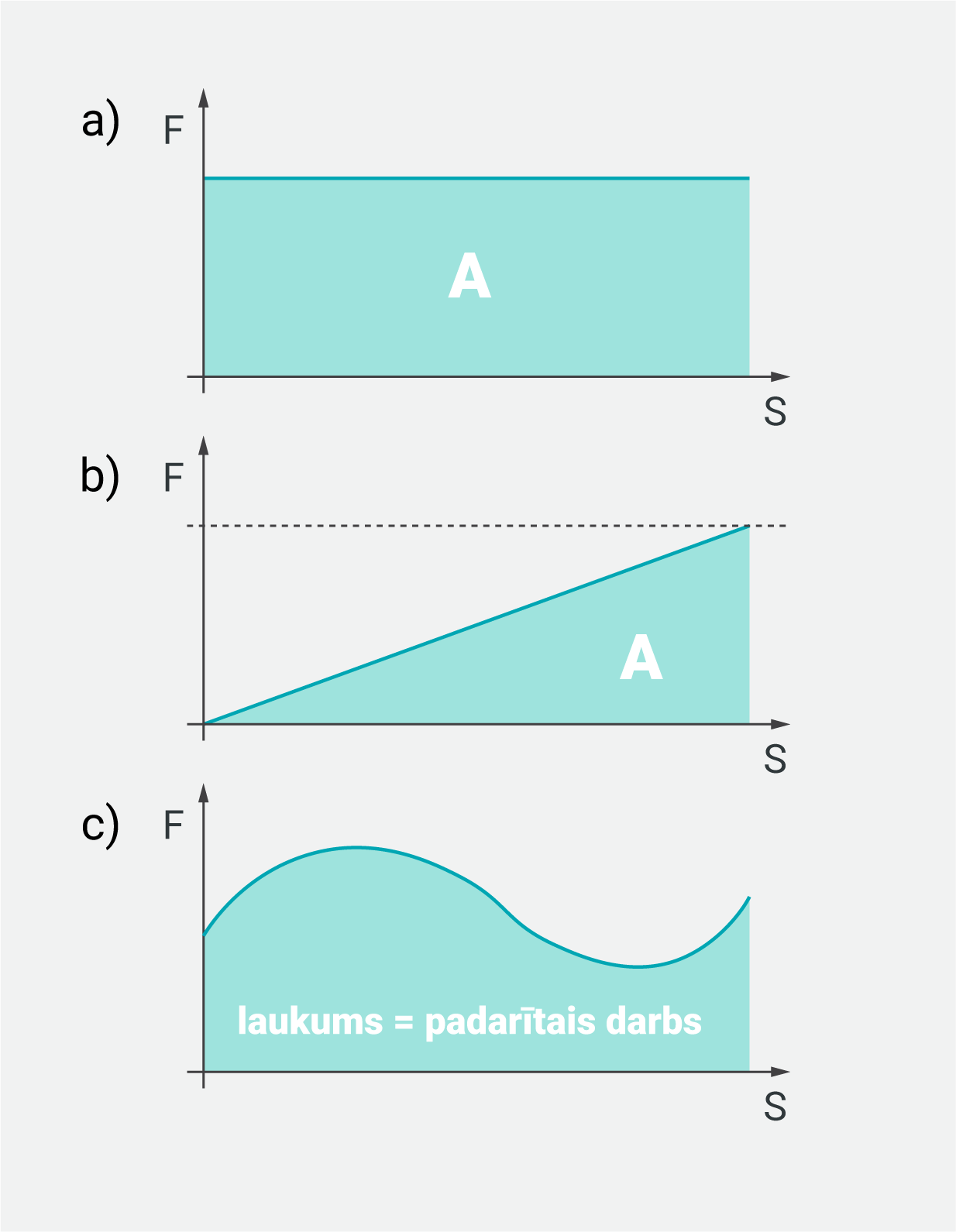
4. att. Darba grafiskā interpretācija
Ja norisinās vienmērīga kustība ar ātrumu v, tad jaudas izteiksmi var pārrakstīt kā N=A/t=F·s/t=F·v, kur
F - vilcējspēks, N
v - kustības ātrums, m/s
No šīs izteiksmes seko, ka jauda ir proporcionāla ātrumam (5. att.). Tieši tādēļ, jo ielāku ātrumu ir nepieciešams attīstīt transporta līdzeklim, jo lielākas jaudas motoru vajag izvēlēties. Braucot ar konstantu ātrumu, transporta līdzekļa vilcējspēks komensē berzes un pretestības spēkus, un ja šie pretestības spēki paliek nemainīgi, tad transporta līdzekļa jauda ir proporcionāla ātrumam (5. att.).
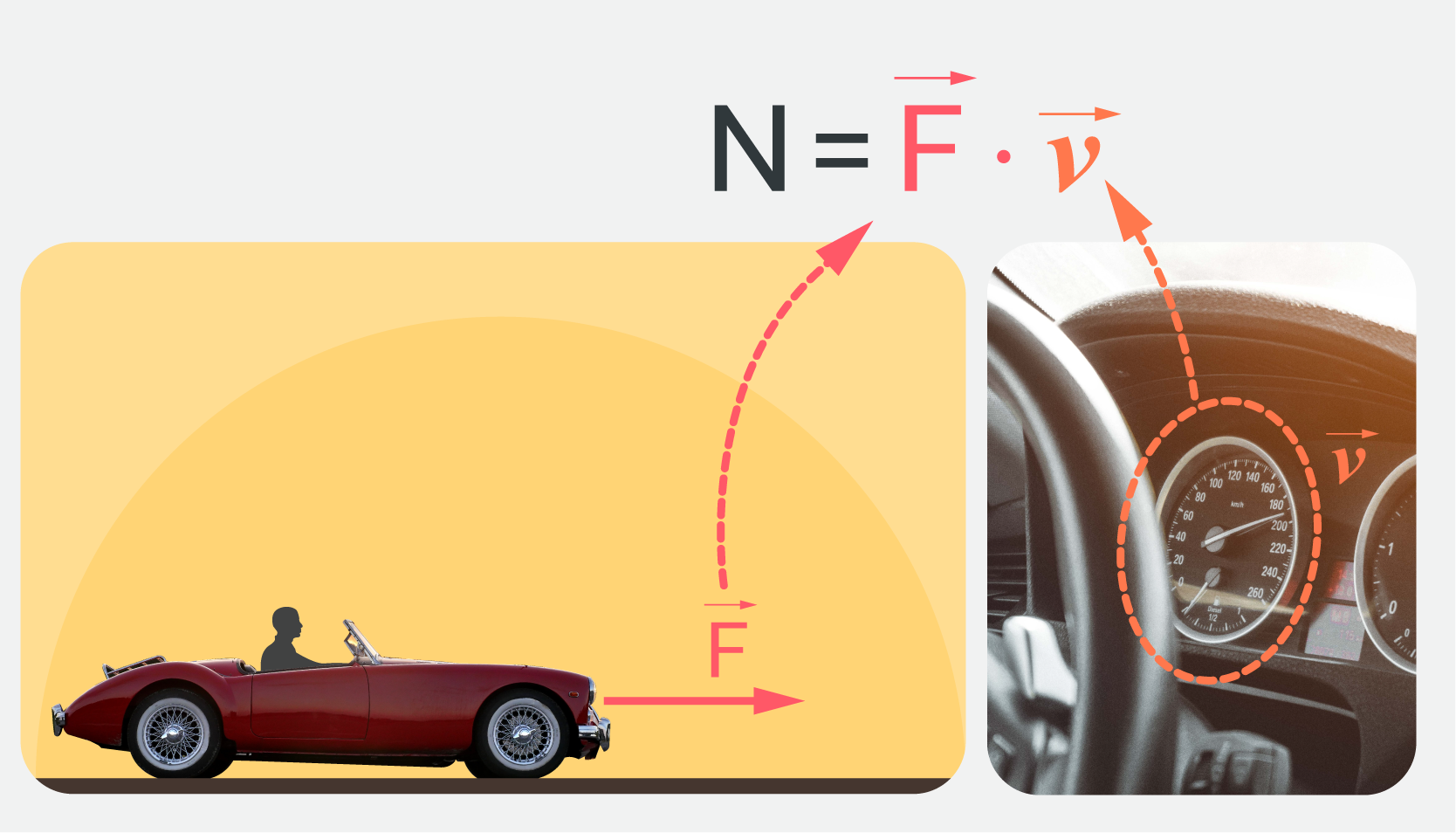
5. att. Jaudas atkarība no kustības ātruma
Praksē ir ļoti grūti noturēt vienmērīgu ātrumu, kā arī, piemēram, agresīvi auto vadītāji arī ir tika cilvēki un viņus dažkārt moka ziņkāre, cik lielu jaudu viņi ir attīstījuši ar savu spēkratu, tādēļ lieto jēdzienu vidēja jauda Nvid, ko iegūst paveikto darbu izdala ar laika momentu, kurā tas veikts Nvid=∆A/∆t, kur
Nvid - vidējā jauda, W
∆A - paveiktais darbs, J
∆t - laiks, s
Ikdienā braucot pa pilsētu, uzturēt vienmērīgu ātrumu ir praktiski neiespējami luksaforu, sastrēgumu un citu fakotoru dēļ. Šādā gadījumā ērti ir aprēķināt automašīnas vidējo jaudu (6. att.).

6. att. Ikdienišķa kustība ar auto pa pilsētu
7.attēlā redzams, ka dažāda veida dzinējiem ir atšķirīgi lietderības koeficienti, jo atšķiras zudumu apmēri. Lai gan dīzeļa dzinējam ir ievērojami augstāks lietderības koeficients nekā benzīna dzinējam, redzams, ka tik un tā iekšdedzes dzinēju lietderības koeficients ir zem 50%.
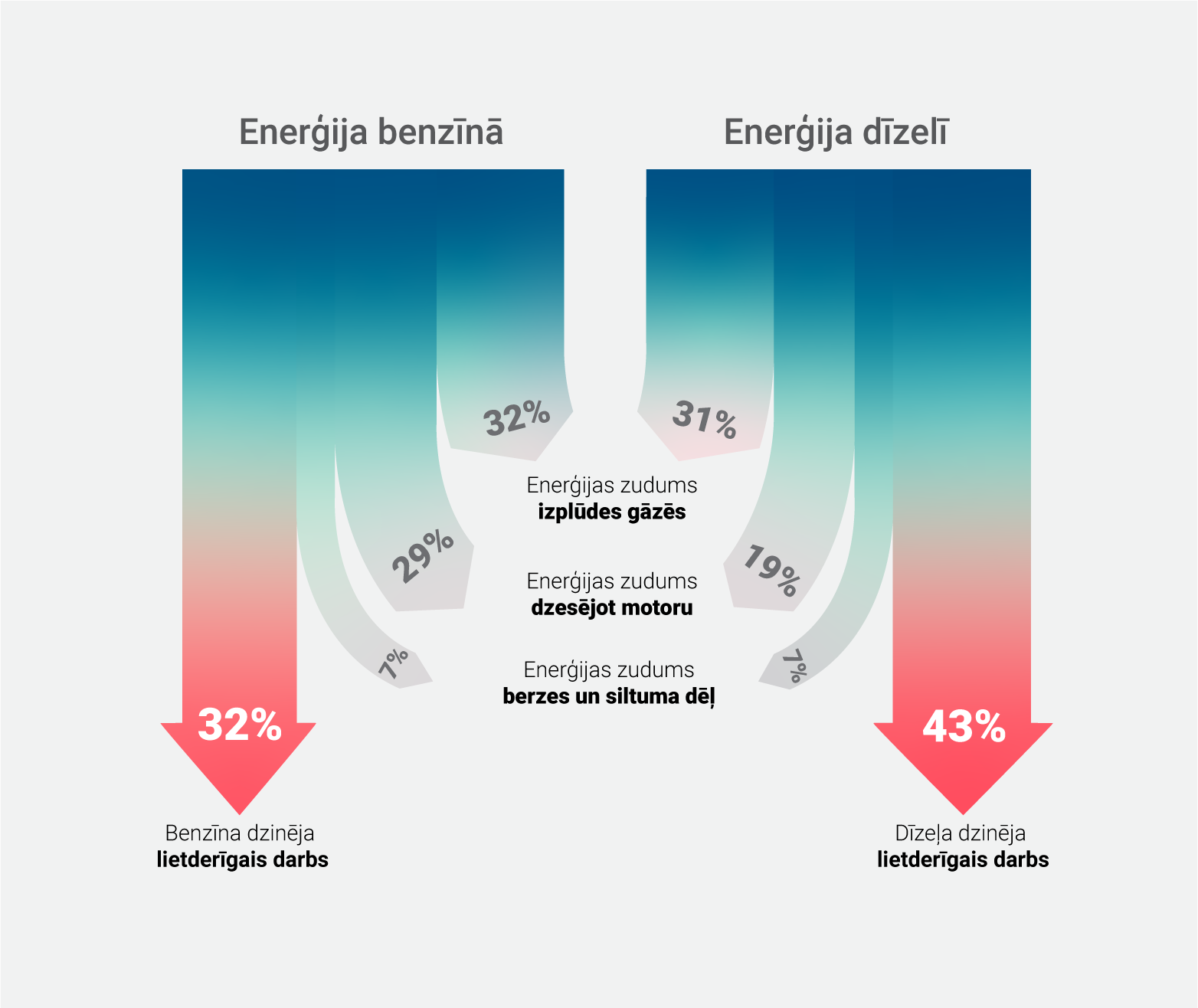
7. att. Dažādu dzinēju lietderības koeficienti
8. attēlā var apskatīt dažādu ierīču lietderības koeficientus. Redzams, ka lietderības koeficients ir atkarīga gan no enerģiju veidiem, starp kuriem notiek pārvēršana, gan arī ierīces izmēriem.
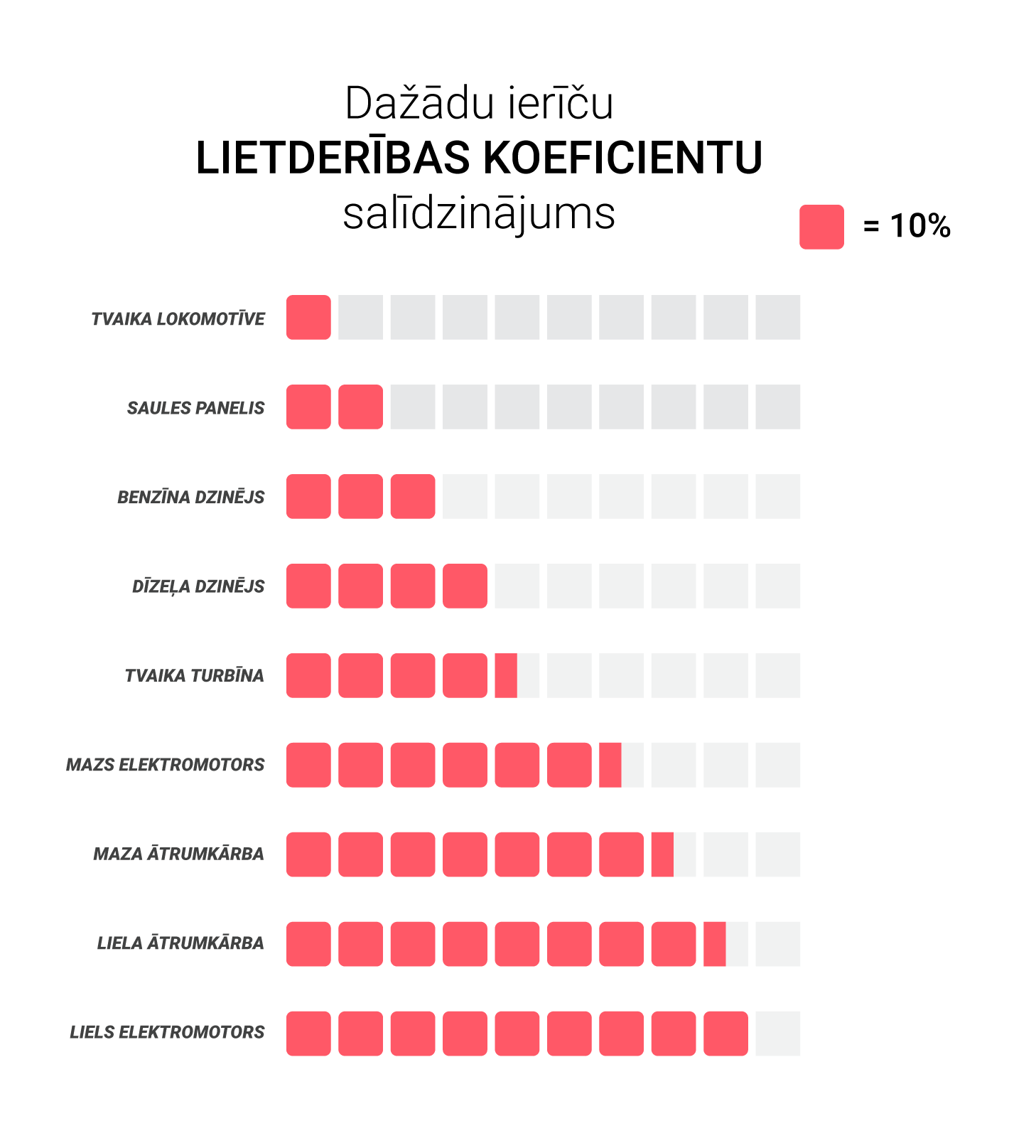
8. att. Dažādu ierīču lietderības koeficienti
Automašīnas jauda ir viens no parametriem, kam tiek pievērsta pastiprināta uzmanība, novērtējot automašīnu. Tomēr jauda pati par sevi sniedz nepilnīgu informāciju par automašīnas kustības dinamikas iespējām. Lai iegūtu plašāku skatu, jāapskata trīs savā sarpā saistīti automašīnas dzinēja parametri: apgriezieni, jauda un griezes moments.
Automašīnas dzinējā vertikāla virzuļa kustība tiek pāvērsta rites kustībā, izmantojot kloķa-klaņa mehānismu. Kloķa klaņa mehānisms sastāv no pie virzuļa piestiprināta klaņa, kas savienots ar kloķvārpstu (1. att. a). Dzinējam darbojoties, tas griežas ar noteiktu leņķisko ātrumu ω, tomēr pierasta dzinēja apgriezienu mērvienība ir apgriezieni minūtē jeb rpm (revolutions per minute), ko mēra tahometrs (1. att. b).
1. solī tika apskatīta jaudas P mērvienība vats (W), tomēr automāšīnas dzinēja jaudu pieņemts izteikt ar senāku mērvienību - zirgspēku (ZS). 1 ZS liela jauda tiek attīstīta, ja 75 kg smaga krava 1 s laikā tiek pacelta par 1 m (1. att. c)! Viens ZS vienāds ar 736 W!
Griezes moments ir īpašs nosaukums iepriekš apskatītajam spēka momentam M (Fiztēma par Spēka momentu un rotāciju). Uz virzuli attīstītais spēks F caur klani tiek novirzīts uz kloķvārpstu, to iegriežot (1. att. a).
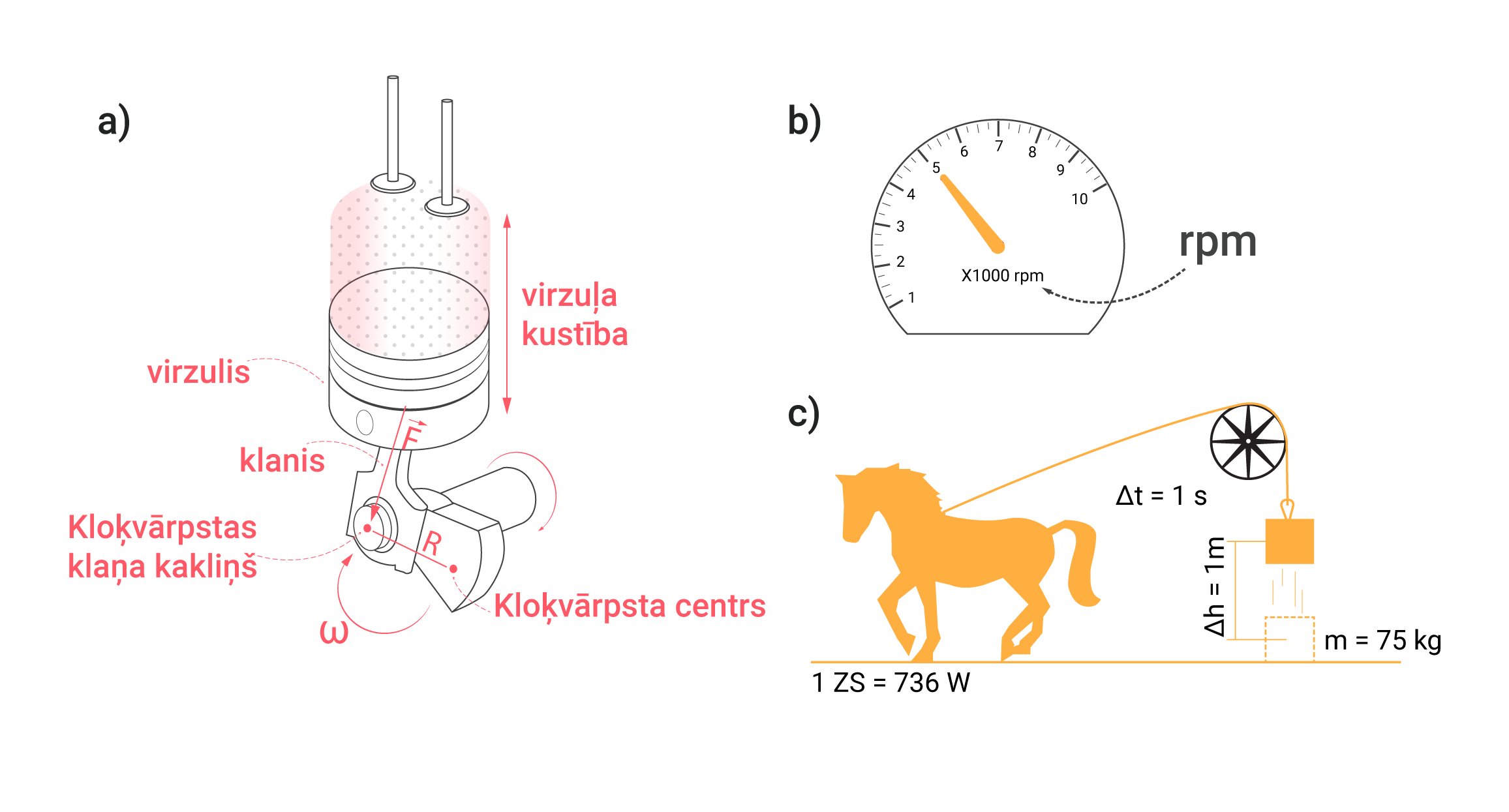
1. att. Automašīnas dzinēja detaļas un parametri
Kā jau tika minēts, dzinēja apgriezieni, jauda un griezes moments ir savstarpēji saistīti lielumi.
(2. att. 1) Sakarību starp šiem lielumiem var iegūt izmantojot 2. solī apskatīto jaudas P formulu!
(2. att. 2) Pārveidojumos ļoti svarīgi sekot līdzi mērvienībām, tādēļ katram fizikālajam lielumam iekavās tiek norādīta mērvienība!
(2. att. 3) Formulā iekļautais ātrums ir lineārais ātrums v (2. att.) ar kādu kustas kloķvārpstas klaņa kakliņš (1. att. a). Šo ātrumu var noteikt, izmantojot formulu v=2πRf, kur
R - attālums starp kloķvārpstas klaņa kakliņu un kloķvārpstas rotācijas centru, m
f - rotācijas frekvence, Hz
(2. att. 4) Spēka F un attāluma R reizinājums veido spēka jeb griezes momentu M!
(2. att. 5) Hercs (Hz) ir apgriezienu skaits sekundē, bet automašīnām ierasts apgriezienu skaitu mērīt minūtē (rpm). Šie lielumi savā starpā ir saistīti šādi: f(Hz)=f(rpm)/60!
(2. att. 6) Lai no vatiem (W) pārietu uz zirgspēkiem (ZS), jāizmanto iepriekš apskatītā sakarība P(W)=P(ZS)·736, bet 2π tiek aizstāts ar 2π=2·3,14=6,28!
(2. att. 7) Tālāk visi konstantie lielumi tiek pārnesti uz labās puses saucēju! Gala rezultātā ir iegūta izteiksme, kas saista jaudu (ZS), griezes momentu (N·m) un dzinēja apgriezienu skaitu (rpm)!
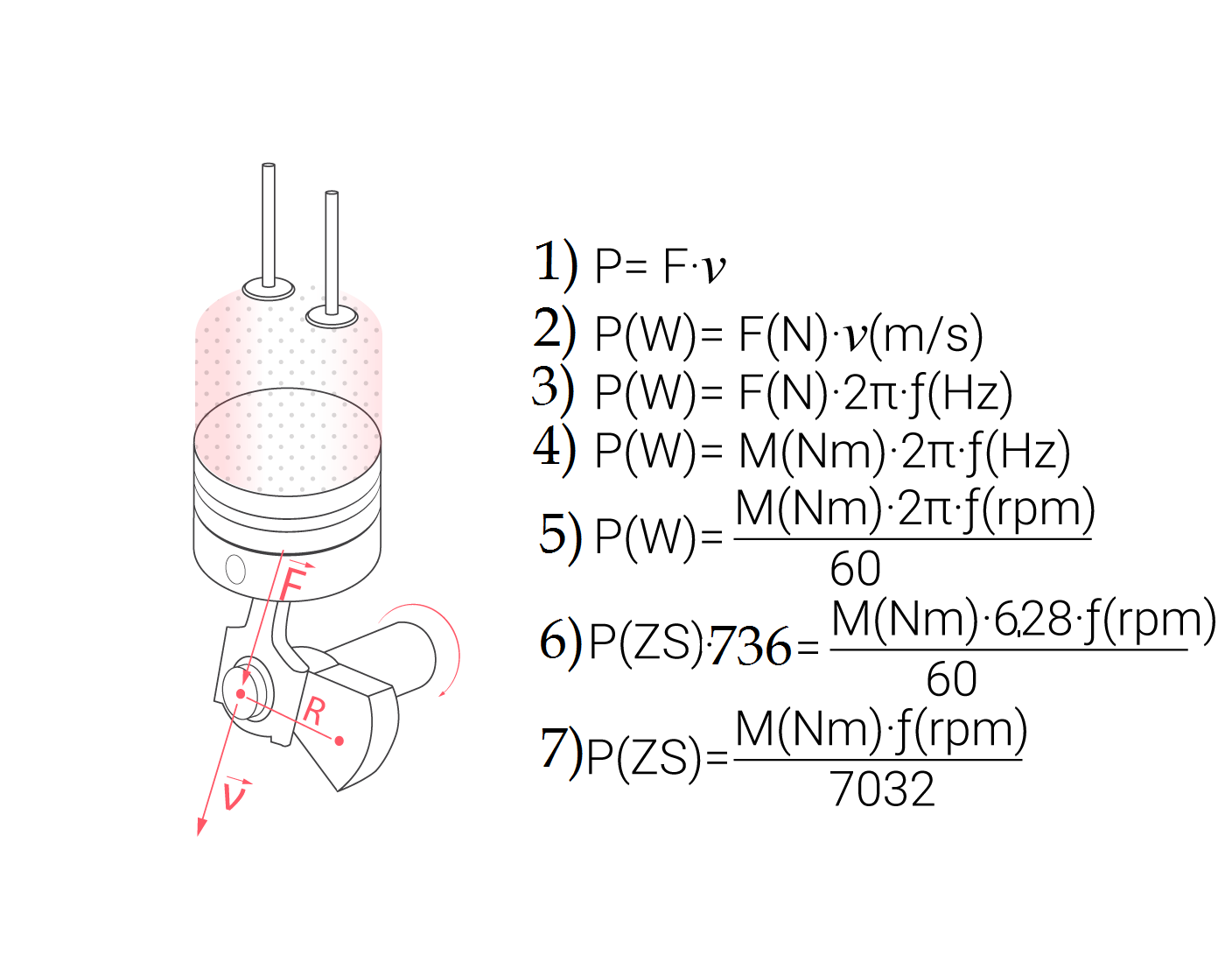
2. att. Jaudas, apgriezienu un griezes momenta saistība
Gan griezes moments, gan dzinēja jauda ir atkarīgi no dzinēja apgriezienu skaita minūtē. Viens piemērs šo fizikālo lielumu aktarībai no dzinēja apgriezienu skaita minūtē redzams 3. att. Abi fizikāliem lielumi pie noteikta apgriezienu skaita minūtē sasniedz maksimālo vērtību, bet, turpinot palielināt dzinēja apgriezienu skaita minūtē, tie sāk kristies. Griezes momenta un jaudas maksimālās vērtības parādās pie dažādiem dzinēja rotācijas ātrumiem. Vispirms maksimumu sasniedz griezes moments. Griezes moments lielāktoies nosaka to, cik liels būs automašīnas paātrinājums. Jo lielāks griezes moments, jo straujāk automašīna uzņem ātrumu. Īpaši nozīmīgs griezes moments ir braucot pret kalnu vai vedot smagu kravu. Jo lielāka krava vai stāvāk ceļš, jo lielāku griezes momentu vajag, lai iekustinātu automašīnu!
Pēc maksimālās vērtības sasniešanas, griezes moments sāk dilt. Tas notiek tādēļ, ka palielinās berze starp dzinēja kustīgajām daļām un dzinējs sāk zaudēt efektivitāti. Toties jauda turpina pieaugt uz apgriezienu skaita pieauguma rēķina, jo jaudas galvenokārt parāda to, cik lielu maksimālo ātrumu varēs sasniegt. Tomēr arī jauda nepalielinās visu laiku dažādu konstrukciju un fizikālo ierobežojumu dēļ, piemēram, degvielas pilnīgai sadegšanai ir nepieciešams noteikt laika un ja dzinējs griežas pārāk ātri, tad degviela vienkārši nepaspēj sadegt.
Liela jauda un mazs griezes moments nozīmē to, ka kustības ātrums ir liels, bet dzinējam jāpieliek lielas pūles, lai šo ātrumu palielinātu.
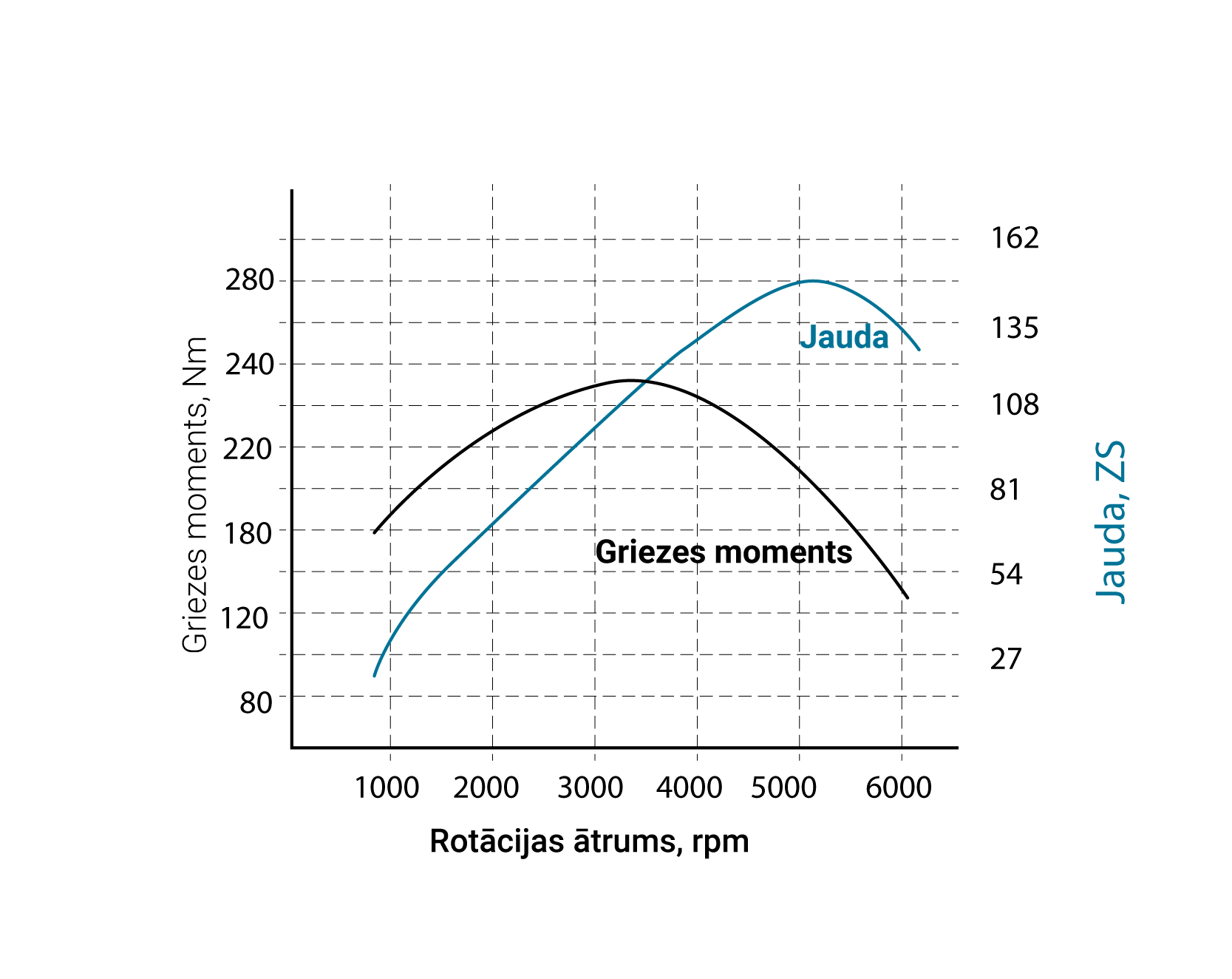
3. att. Griezes momenta un jaudas atkarība no dzinēja rotācijas ātruma
Griezes momenta un jaudas atkarību no dzinēja apgriezienu skaita noska gan, piemēram, dzinēja darba tilpums, cilindru skaits un attālums no kloķvārpstas centra līdz kloķvārpstas klaņa kakliņam, gan arī to kāda veida degviela dzinēja tiek sadedzināta. 4. att. redzams benzīna un dīzeļa dzinēju salīdzinājums. Redzams, ka benzīna dzinējam maksimālais griezes moments ir pie lielāka apgriezienu skaita. 4. att. arī redzama dzinēja degvielas patērīņa atkarība no dzinēja apgriezienu skaita. Jau iepriekš tika minēts, ka jo lielāks griezes moments, jo dzinējs ir efektīvāks jeb patērē mazāk degvielas. Dzinēja apgriezienu diapazonā no maksimālā griezes momenta līdz maksimālajai jaudai, tas strādā ar visaugstāk efektivitāti (4. att.).
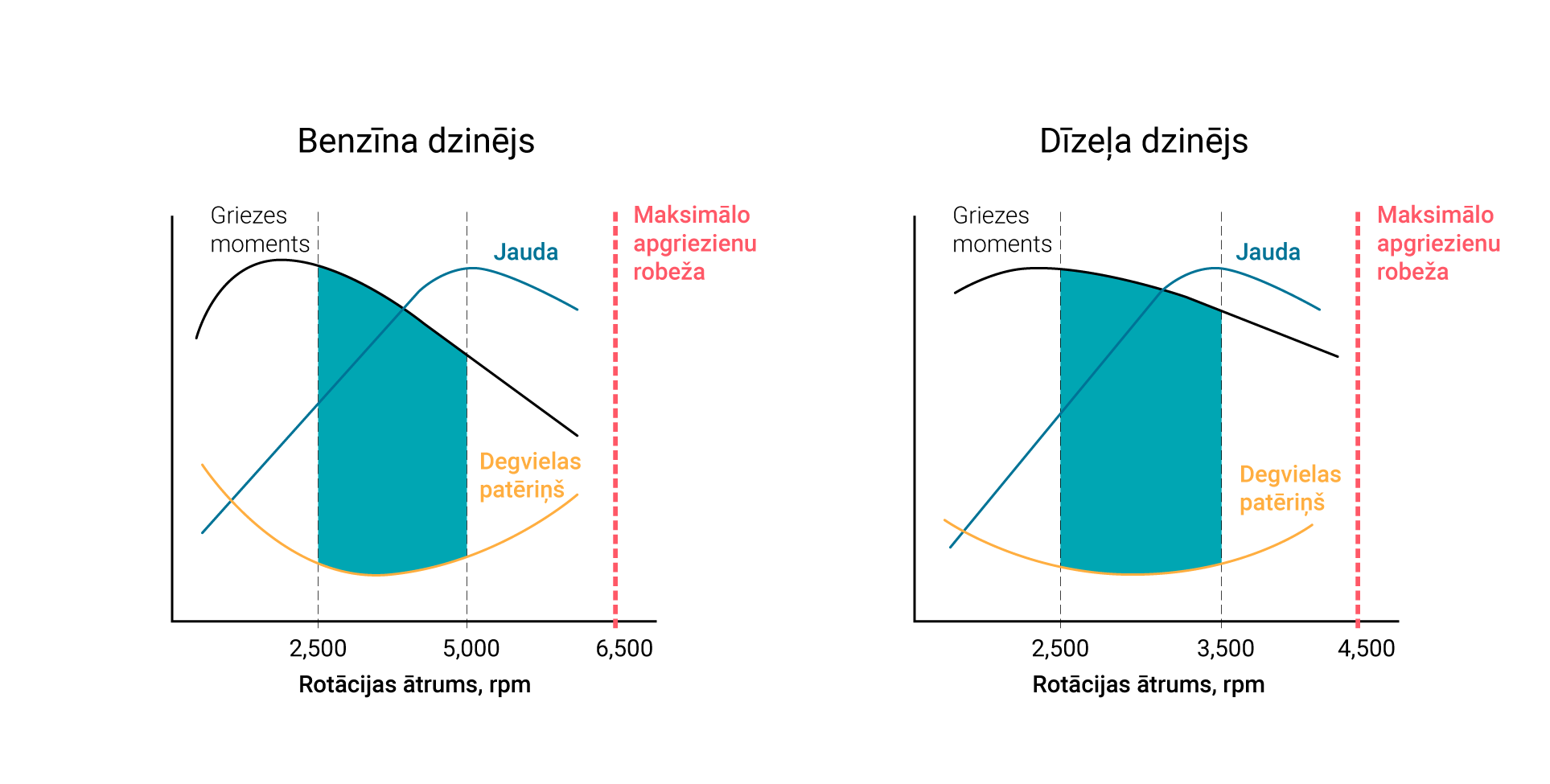
4. att. Griezes momenta, jaudas un patēriņa atkarība no dzinēja tipa
Dzinējs nav pa taisno pievienots pie riteņiem, jo, piemēram, atkarībā no ceļa apstakļiem, braukšanas ātruma un kravas apjoma ir nepieciešams nodrošināt atšķirīgu griezes momentu pie tiem pašiem dzinēja apgriezieniem. Tādēļ tie lietota pārnesumu kārba jeb ātrumkārba, kas sastāv no daudziem dažāda diametra zobratiem, kurus, mainot pārnesumu jeb pārslēdzot “ātrumu”, var savienot dažādās kombinācijās (5. att. a). Savienojot vienu rotējošu zobratu ar otru, kuram ir divas reizes lielāks diametrs (divas reizes vairāk zobu), tā rotācijas ātrums būs divas reizes mazāks nekā pirmajam zobratam, toties griezes moments pieaugs divas reizes. Jo ātrumkārbai ir zemāks pārnesums, jo lielāks griezes moments. Lielāks griezes moments ir nepieciešams, lai automašīna uzsāktu kustību vai kustētos pret kalnu, tādēļ šādos gadījumos tiek izmantoti zemāki pārnesumi. Visefektīvāk pārslēgt uz augstāku pārnesumu ir tad, kad dzinēja apgriezienu skaits minūtē ir starp augstāko griezes momentu un lielāko jaudu (4. att.).
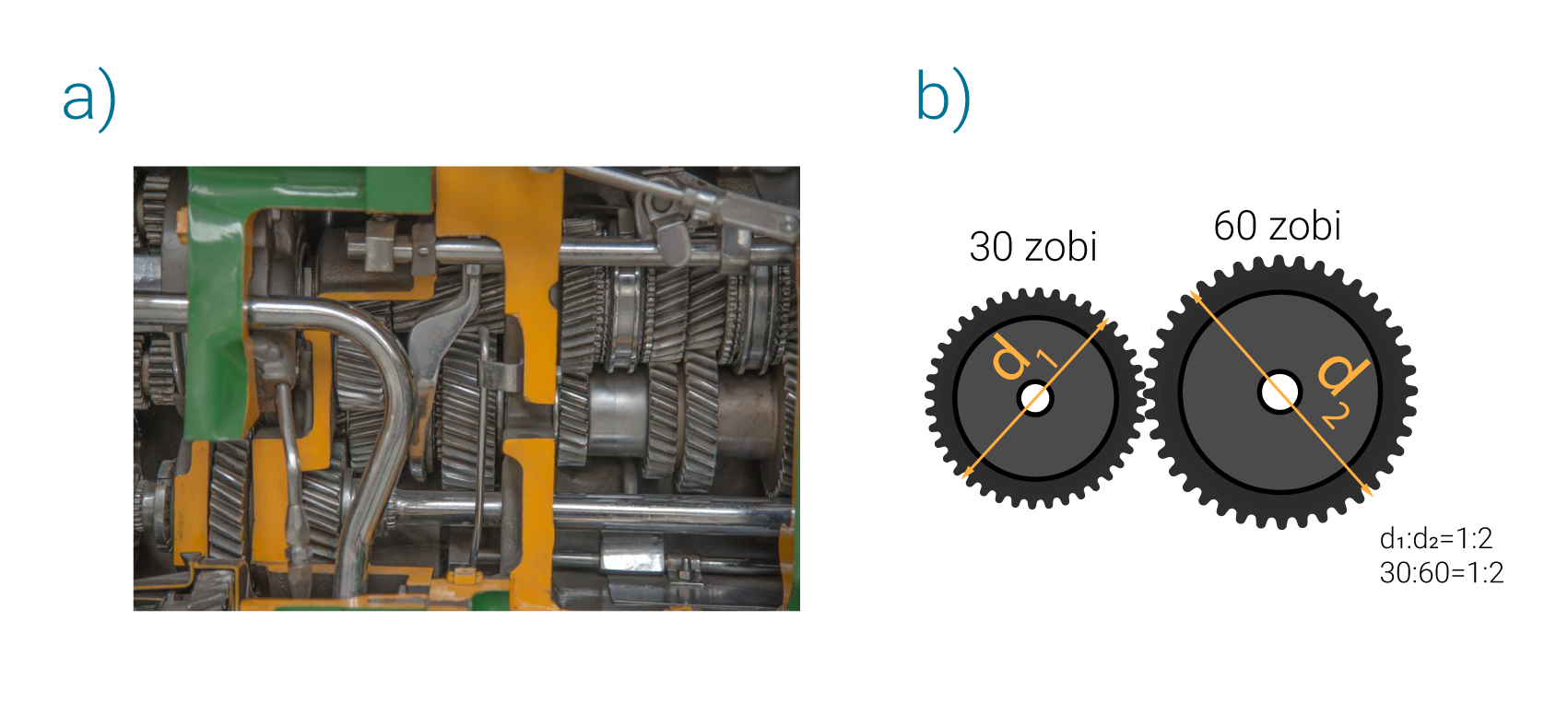
5. att. Automašīnas ātrumkārba un tās darbība
6. att. redzams dažādu transporta līdzekļu maksimāla griezes momenta un maksimālās jaudas salīdzinājums
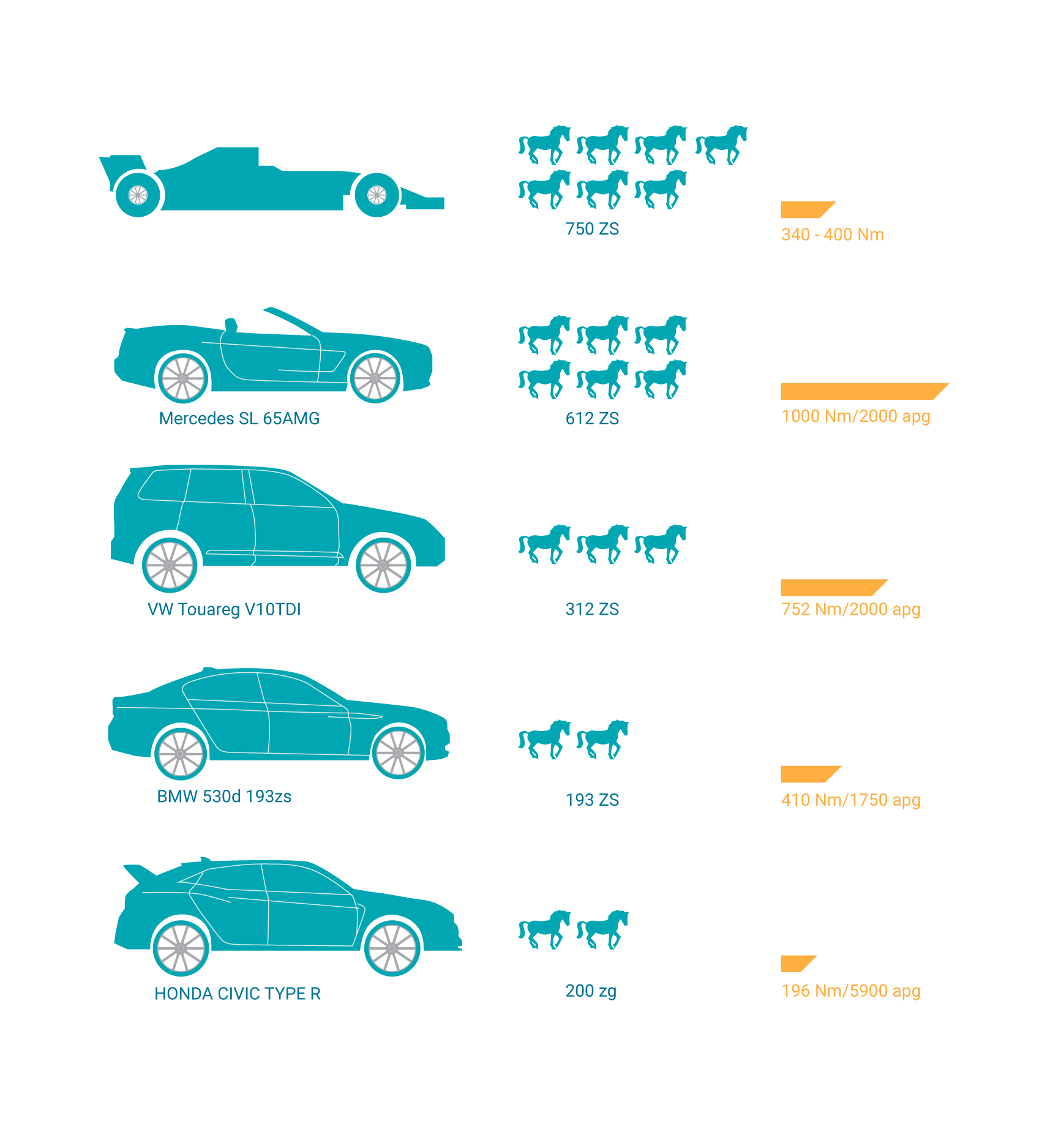
6. att. Dažādu transporta līdzekļu maksimālā griezes momenta un maksimālās jaudas salīdzinājums