Ja kādā vada cilpā vai spolē plūst strāva, tad ap šo vadu vai spoli pastāv magnētiskais lauks (1. att.). Līdz ar magnētisko lauku strāvas kontūru caurvij arī magnētiskā plūsma Φ, kas ir jo lielāka, jo lielāks ir strāvas stiprums I kontūrā. Visiem kontūriem magnētiskās plūsmas atkarība no strāvas stipruma nemainās vienādi, tādēļ strāvas kontūra raksturošanai izmanto strāvas kontūra induktivitāti L un magnētisko plūsmu izsaka kā Φ = LI, kur
L- kontūra induktivitāte, H,
I- strāvas stiprums kontūrā, A.
Induktivitātes mērvienība ir henrijs (H). Kontūra induktivitāte ir atkarīga no kontūra formas un izmēriem, kā arī no kontūru aptverošās vides magnētiskajām īpašībām. Piemēram, spoles induktivitāti (1. att.) var aprēķināt pēc formulas L = μμ0N2S : l, kur
μ- spoles centrā esošās vides relatīvā magnētiskā caurlaidība,
μ0- magnētiskā konstante,
N- spoles vijumu skaits,
S- spoles šķērsgriezuma laukums, m2,
l- spoles garums, m.
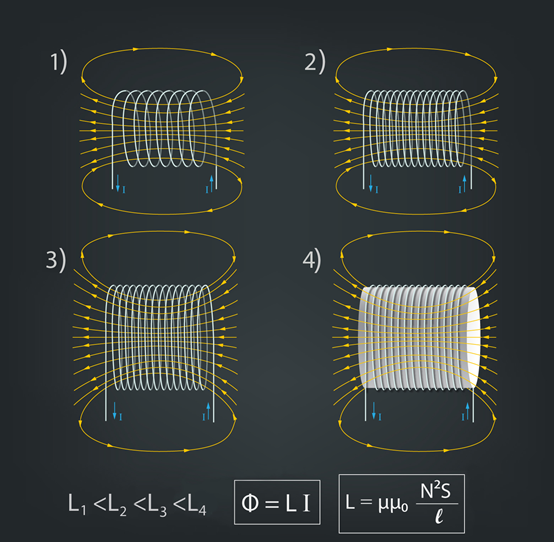
1.att. Magnētiskā plūsma spolē un spoles induktivitāte
Ja kontūrā mainās plūstošās strāvas stiprums I, tad pēc elektromagnētiskās indukcijas likumiem kontūrā inducējas elektrodzinējspēks E (2. att.), kas vērsts pretēji strāvas izmaiņai: E = -L· ΔI : Δt, kur
L- strāvas kontūra induktivitāte, H,
ΔI- strāvas stipruma izmaiņa, A,
Δt- laika moments, kurā notiek strāvas izmaiņa, s.
Ja spole, kurā plūst strāva ar stiprumu I, tiek atvienota no strāvas avota, tad spolē sāk kristies strāvas stiprums. Šādā gadījumā spolē rodas indukcijas EDS, kas cenšas plūstošās strāvas stiprumu saglabāt. Tas nozīmē, ka spolē ir uzkrāta enerģija, uz kuras rēķina iespējams nodrošināt centienus strāvas plūsmu saglabāt. Šī enerģija ir magnētiskā lauka enerģija, kas tiek uzkrāta spolē, un to var aprēķināt, izmantojot izteiksmi W = LI2: 2, kur
W- magnētiskā lauka enerģija, J,
L- spoles induktivitāte, H,
I- strāvas stiprums, A.
Par šo tēmu vari apskatīties DZM materiālu (spied uz iekrāsotā vārda).
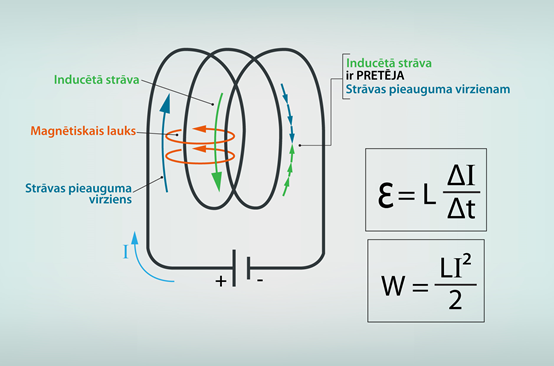
2.att. Spoles pašindukcijas EDS un magnētiskā lauka enerģija
Lai iegūtu izteiksmi spoles induktivitātes atrašanai, jāizmanto sakarība spoles magnētiskā lauka indukcijas noteikšanai: B = μμ0I · N : l, kur
B- spoles magnētiskā lauka indukcija, T,
μ- spoles serdes relatīvā magnētiskā caurlaidība,
μ0- magnētiskā konstante,
I- caur spoli plūstošās strāvas stiprums, A,
N- spoles tinumu skaits,
l- spoles garums, m.
Ja spole sastāv no viena vijuma (1. att. a), tad magnētiskā lauka plūsma caur šo vijumu ir Φ0 = BS, kur S ir spoles šķērsgriezuma laukums (m2). Ja spoles vijumu skaits tiek palielināts (1. att. b), tad palielinās arī magnētiskā plūsma, jo magnētiskais lauks caurvij visus spoles tinumus, līdz ar to izteiksmē Φ = BS kā laukums S ir jāņem visu vijumu kopējais laukums. Ja spolei ir N vijumi, tad kopējais vijumu laukums ir NS un kopējā plūsma Φ = BNS. Ievietojot B vietā spoles magnētiskā lauka indukcijas izteiksmi, iegūst Φ = μμ0I · N2S : l. Izmantojot 1. solī apskatīto formulu Φ = LI, var izteikt induktivitāti L = Φ : I. Aizstājot Φ ar magnētiskā lauka plūsmu caur spoli, iegūst spoles induktivitāti L = μμ0N2S : l.
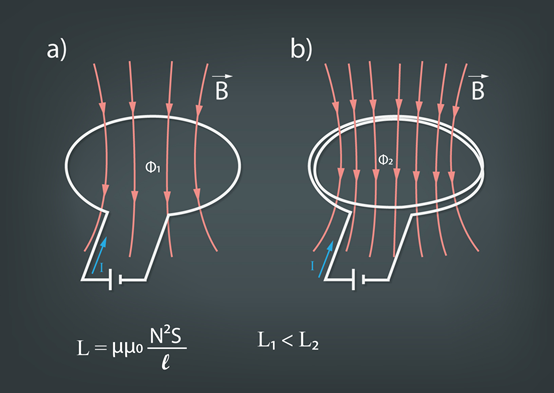
1.att. Spoles induktivitāte
Spoles tinumus var uztīt tā, ka daļa no tinumiem ir vīti vienā virzienā, bet daļa pretējā virzienā. Šādu spoli sauc par bifilāru spoli. Atšķirība no parastās spoles ir tā, ka pretēji vītos tinumos magnētiskā plūsma ir vērsta pretējos virzienos, līdz ar to šīs plūsmas viena otru nodzēš. Tādēļ bifilārai spolei, kurai vienā virzienā tinumu skaits ir N1, bet otrā virzienā N2 (2. att. a), indukcijas aprēķinam jālieto izteiksme L = μμ0(N1-N2)2S : l. Ja N1 = N2, tad spoles induktivitāte ir 0 (2. att. b). Ja kāda strāvas kontūra induktivitāte nav nulle, tad šis kontūrs “pretojas” strāvas izmaiņām. Šī “pretošanās” rada nevēlamus efektus dažādās elektroniskās ierīcēs, tādēļ šādās ierīcēs, piemēram, regulējamos strāvas avotos, ar kuriem var mainīt strāvas spriegumu vai stiprumu, lieto bifilāras spoles, kurām L = 0.
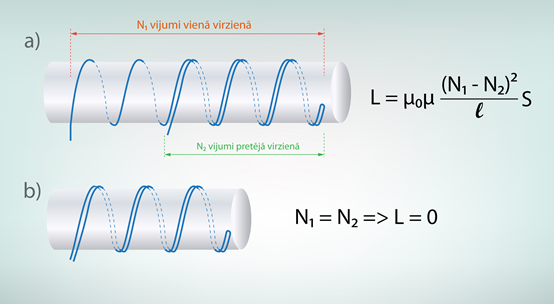
2.att. Spoles induktivitāte
Ja spoli izliec riņķveida formā, tad iegūst toroidālu spoli (3. att.). Šādu spoli ir grūtāk izveidot, bet tai ir daudz priekšrocību. Piemēram, parastajai spolei magnētiskais lauks ir galvenokārt koncentrēts spoles centrālajā daļā, bet spoles galos magnētiskais lauks izkļūst apkārtējā vidē (1. soļa 1. att), bet toroidālai spolei tādu galu īsti nav, tādēļ magnētiskais lauks cirkulē tikai pa toroīda centrālo daļu (3. att.). Tas nozīmē, ka šādas spoles ar savu lauku mazāk ietekmē citas tuvumā esošas elektronikas komponentes. Toroidālas spoles lieto telekomunikācijā, medicīnas iekārtu un audio tehnikā, piemēram, dažādu veidu pastiprinātājos. Toroidālai spoles indukcijas aptuvenu vērtību var iegūt, izmantojot izteiksmi L ≈ μμ0(N)2S : (2πr), kur r ir toroīda rādiuss (3. att.).

3.att. Torodiāla spole
Spoles induktivitātes dēļ, pieslēdzot to līdzstrāvas avotam, strāva spolē pieaug lēnām, nevis uzreiz sasniedz maksimālo vērtību (4. att.). Šo pakāpenisko strāvas pieaugumu nodrošina indukcijas elektrodzinējspēks E, kas darbojas pretēji strāvas izmaiņai. Sadaļā par elektriskā lauka potenciālu tika noskaidrots, ka elektriskā lauka veiktais darbs ir vienāds ar lādiņa un potenciālu starpības reizinājumu. Šajā gadījumā potenciālu starpība ir pašindukcijas EDS E, bet darba darītājs ir strāvas avots. Strāvas palielināšanas procesā strāvas avots pastrādā darbu A = Eq, kur
E- pašindukcijas EDS, V
q- lādiņš, C
No elektriskās strāvas stipruma definīcijas I = q : Δt, var izteikt lādiņu q = IΔt un ievietot strāvas avota padarītā darba izteiksmē A = EIΔt. Izmantojot elektromagnētiskās indukcijas likumu E = ΔΦ : Δt, padarītā darba izteiksmi var pārveidot par A = ΔΦIΔt : Δt = ΔΦI. Ja magnētiskā plūsma pieaug no nulles līdz Φ, tad ΔΦ = Φ. Strāva ir izmainījusies no 0 līdz I, tāpēc kā strāvas vērtību ņemsim vidējo vērtību strāvas izmaiņas procesā, kas ir I : 2. Gala rezultātā strāvas avota padarītais darbs A = ΦI : 2 un tas ir vienāds ar magnētiskā lauka enerģiju W, kas uzkrājas spolē, tādēļ W = ΦI : 2. Tālāk var izmantot magnētiskās plūsmas izteiksmi Φ = LI, lai izteiktu L = Φ : I. Ievietojot šo iegūtajā spoles magnētiskā lauka enerģijas W izteiksmē, iegūst 1. solī apskatīto formulu W = LI2 : 2.
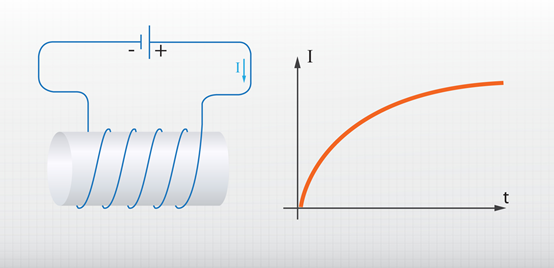
4.att. Strāvas stipruma pieaugums spolē, kas pieslēgta strāvas avotam
Iepriekšējā solī jau saskārāmies ar to, ka strāvas pieaugums spolē ir pakāpenisks. Ja mēs strāvas avotam pieslēgtu vienkāršu patērētāju bez induktivitātes, tad strāvas stiprums teju momentāni sasniedz maksimālo vērtību un paliek laikā nemainīgs lielums (1. att. a). Ja tam pašam strāvas avotam pieslēdz spoli, tad strāvas stiprumam ir nepieciešams zināms laiks, lai sasniegtu maksimālo vērtību (1. att. b)
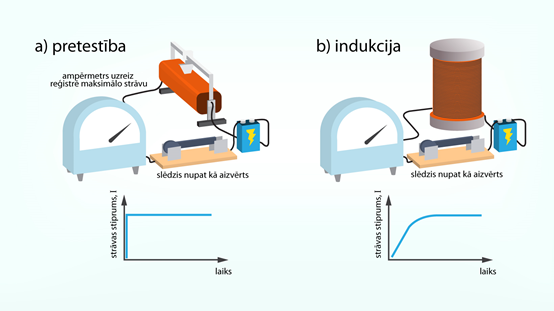
1.att. Pretestības un indukcijas salīdzinājums
Tas nozīmē, ka spoles gadījumā, strāvu ieslēdzot un izslēdzot (tad, kad notiek strāvas stipruma izmaiņas), nav spēkā Oma likums ķēdes posmam, kas paredz ķēdes posmam nemainīgu spriegumu U = IR. Spoles gadījumā ir jāņem vērā indukcijas EDS E = LΔI : Δt. Līdz ar to papildināts Oma likums ķēdes posmam ar spoli (2. att.) izskatās U = IR + LΔI : Δt, kur
U- spriegums ķēdes posmā, V
R- ķēdes posma pretestība, Ω
L- ķēdes posma induktivitāte, H
ΔI- strāvas stipruma izmaiņa, A
Δt- laika moments, kurā notiek strāvas stipruma izmaiņas, s
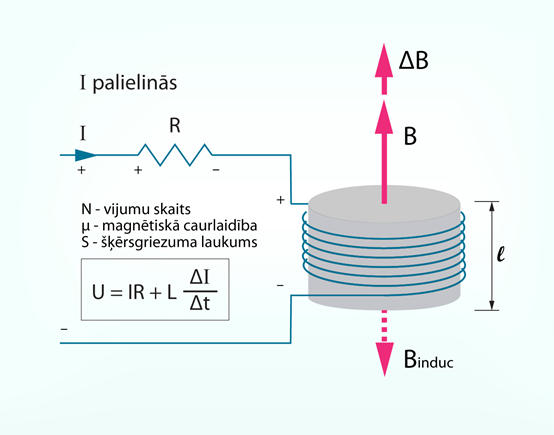
2.att. Oma likuma papildinājums ar pašindukcijas EDS
Ja spoli pieslēdz strāvas avotam, tad strāvas stiprums I aug lēnām un pašindukcijas EDS līdz ar to ir salīdzinoši neliels. Ja strāva ķēdē tiek pārtraukta, tad strāvas stiprums krītas ļoti strauji (3. att. a). Pēc pašindukcijas EDS formulas E = LΔI : Δt seko, ka rodas straujš E pieaugums (3. att. b). Šo parādību sauc par izslēgšanas strāvu, un tās izpausmes ir novērojamas dažādās vietās. Piemēram, izslēgšanas strāvas rezultātā rodas dzirkstele benzīna iekšdedzes dzinēja aizdedzes svecēs. Tomēr izslēgšanas strāvas straujais Epieaugums var radīt arī nevēlamas sekas, kas izpaužas kā elektriskā lokizlāde un dzirksteļošana starp kontaktiem. Tādēļ nedrīkst uzreiz pārtraukt strāvu ķēdē, kurā atrodas daudz patērētāju ar lielu induktivitāti. Šādām ķēdēm ir paredzēti speciāli slēdži, kas strāvas izslēgšanas brīdī strāvas spriegumu samazina pakāpeniski. Izslēgšanas strāva ir atbildīga par to, ka starp trolejbusa un tramvaja kontaktstieni un elektrības pievades vadu šad un tad pārlec dzirksteles (3. att. c). Pašindukcijas E strāvas izslēgšanas brīdī var pat vairākus simtus reižu pārsniegt spriegumu, kas nodrošināja strāvas plūsmu ķēdē.
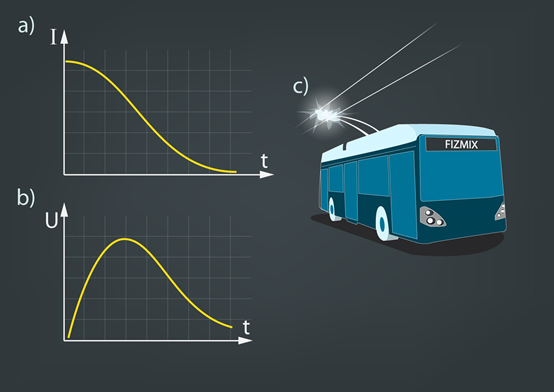
3.att. Izslēgšanas strāva un tās piemērs
Iepriekš elektriskās ķēdes induktivitāte tika saistīta ar liektiem ķēdes posmiem, tomēr induktivitāte piemīt, piemēram, arī taisnai divvadu līnijai (4. att.), un tā ir atkarīga no līnijas garuma l, no attāluma d starp vadiem, vadu diametra R, kā arī no vadus ieverošās vides magnētiskajām īpašībām (4. att.). Piemēram, ja 0,5 km gara divvadu līnija sastāv no vadiem, kuru diametrs ir 0,2 mm un attālums starp vadiem ir 3 mm, tad šādas līnijas induktivitāte ir aptuveni 0,64 μH.
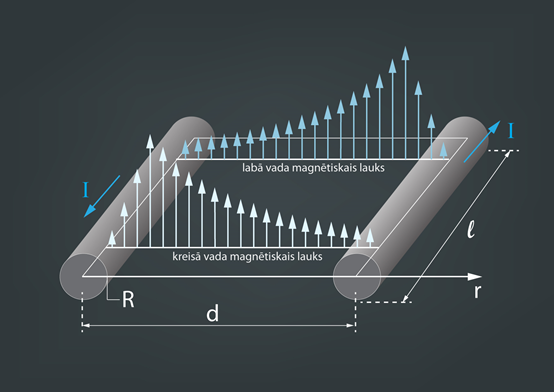
4.att. Divvadu līnijai arī piemīt induktivitāte