Līdz šim ar svārstībām saskārāmies tēmā par mehāniskajām svārstībām un viļņiem. Sadaļā par svārstību raksturojošiem lielumiem tika noskaidrots, ka mehāniskās svārstības var iegūt, piemēram, ja diegā vai atsperē iekārtu objektu (1. att. a, b) novirzām no līdzsvara stāvokļa un palaižam vaļā. Tad nu šīs objekts ir pakļauts mehāniskajām svārstībām ap līdzsvara stāvokli. Elektromagnētiskās (EM) svārstības atšķiras ar to, ka svārstās nevis kāds objekts, bet gan elektriskā lauka intensitāte E un magnētiskā lauka indukcija B, turklāt šo abu fizikālo lielumu izmaiņas ir cieši saistītas viena ar otru, tādēļ tās sauc par elektromagnētiskajām svārstībām. Mehāniskās svārstības tiek apskatītas, izmantojot matemātiskā svārsta (1. att. a) un atsperes svārsta (1. att. b) modeļus (Atsperes un matemātiskais svārsts), bet elektromagnētisko svārstību apskatam izmanto ideālu svārstību kontūru, kas ir noslēgta elektriskā ķēde, sastāvoša no kondensatora ar kapacitāti C un spoles ar induktivitāti L (1. att. c), turklāt šim kontūram nepiemīt elektriskā pretestība R.
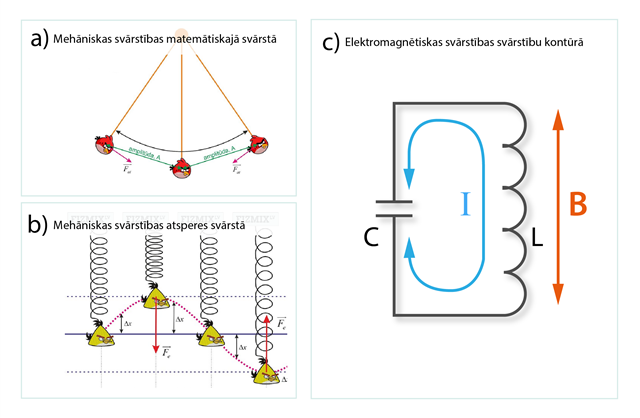
1.att. Mehāniskās un elektromagnētiskās svārstības
Lai iesvārstītu mehānisku svārstu, tam ir jāpiešķir enerģija. Piemēram, ar roku atvelkot diegā iekārtu dusmīgo putnu (piešķirot tam potenciālo enerģiju) un palaižot vaļā (1. att. a). Arī lai ierosinātu EM svārstības, svārstību kontūram ir jāpiešķir enerģija. To var izdarīt, piemēram, izmantojot elektrisko shēmu, kurā caur slēdzi iespējams kondensatoru pieslēgt enerģijas avotam (2. att. a) un pēc tam svārstību kontūram (2. att. b). Pieslēdzot kondensatoru strāvas avotam (2. att. a), ir jāpagaida, līdz tas uzlādējas līdz maksimālajam spriegumam Um,un tad slēdzis jāpārslēdz pozīcijā, kurā kondensators tiek ieslēgts vienā ķēdē ar spoli, kuras induktivitāte L (2. att. b). Tiklīdz uzlādētais kondensators ir pieslēgts spolei, tā kontūrā sāk plūst strāva I un elektromagnētiskās svārstības var sākties (2. att. b).
Apskaties animāciju, kā darbojas svārstību kontūrs!
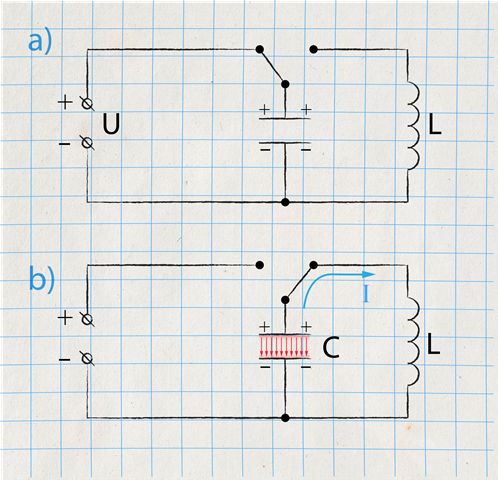
2.att. Enerģijas piešķiršana EM svārstību kontūram
EM svārstībām ir laba analoģija ar mehāniskajām svārstībām, piemēram, matemātisko svārstu (Atsperes un matemātiskais svārsts). Kad matemātisko svārstu novirza no līdzsvara stāvokļa, tam tiek piešķirta potenciālā enerģija Ep = mgh. Svārstību laikā potenciālā enerģija pāriet kinētiskajā enerģijā Ek = mv2 : 2 un atkal atpakaļ potenciālajā (3. att. a). EM svārstam svārstību laikā notiek pāreja starp maksimālo elektriskā lauka enerģiju WE = CUm2 : 2 (Elektriskā kapacitāte un kondensatori) un maksimālo magnētiskā lauka enerģiju WM = LIm2 : 2 (3. att. b) (Induktivitāte un pašindukcija).
Svārstību sākumā kondensatoram ir maksimālā elektriskā lauka enerģija WE, kas ceturtdaļperioda laikā pāriet magnētiskā lauka enerģijā WM(3. att. b). Līdzīgi kā matemātiskais svārsts inerces dēļ turpina kustību pēc tam, kad ir sasniegts līdzsvara stāvoklis (3. att. a), arī EM svārstību kontūrā pēc maksimālās magnētiskā lauka enerģijas sasniegšanas strāvas plūsma turpinās un enerģija sāk plūst uz kondensatoru, līdz visa WMatkal pāriet WE. Pēc pusperioda T : 2 visa elektriskā lauka enerģija ir atgriezusies kondensatorā, vienīgi tas ir uzlādēts otrādi, līdzīgi kā matemātiskais svārsts atgūst visu potenciālo enerģiju, bet tas atrodas pretēja pusē līdzsvara stāvoklim. Nākošajā svārstību pusperiodā kondensators atkal izlādējas caur spoli un perioda beigās kondensators ir atkal pilnībā uzlādēts gluži kā sākumā (3. att.).
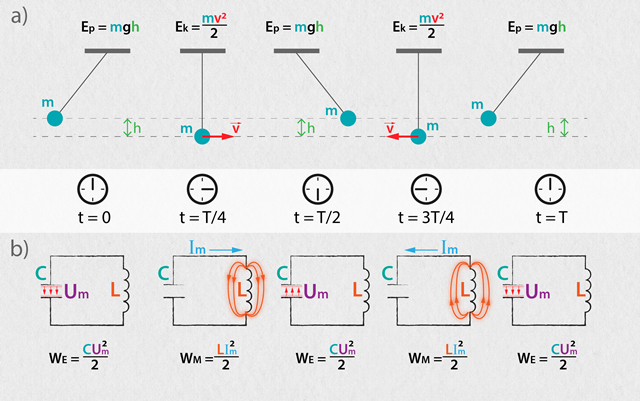
3.att. Elektromagnētisko svārstību analoģija ar matemātisko svārstu
Līdzīgi kā EM svārstībām ir zināma līdzība ar mehāniskajām svārstībām, arī EM vilnim var vilkt paralēles ar mehānisko vilni. Sadaļā Šķērsviļņi un garenviļņi tika apskatīta žurka, kas, priecīgi lēkājot, radīja šķērsvilni optiskajā vadā (4. att. a). Kamēr optiskais vads mierīgi atradās savā vietā, nekāds vilnis neizplatījās, bet, nonākot priecīgas žurkas nagos, optiskā vada gals periodiski mainīja pozīciju, kas izraisīja mehāniskā viļņa izplatīšanos. Līdzīgi notiek ar EM vilni. Nemainīgs elektriskais un magnētiskais lauks EM vilni nerada, turklāt nemainīgs elektriskais lauks var pastāvēt neatkarīgi no nemainīga magnētiskā lauka un otrādi. Toties tiklīdz telpā notiek elektriskā vai magnētiskā lauka izmaiņas, tā uzreiz rodas elektromagnētiskais vilnis, kas izplatās telpā un kurā elektriskā lauka izmaiņas ir cieši saistītas ar magnētiskā lauka izmaiņām. Piemēram, ja tā pati priecīgā žurka noķer negatīvi lādētu dusmīgo putnu un atkal aiz priekiem sāk lēkāt, tad ap dusmīgo putnu sāk mainīties elektriskais lauks. Šī iemesla dēļ rodas EM vilnis, kas izplatās telpā. (4. att. b).

4.att. Žurkas izraisīts mehāniskais un EM vilnis
Tāpat kā mehāniskajam vilnim, arī EM vilnim ir noteikts viļņa garums λ; tas vienāds ar attālumu starp divām blakus esošām EM viļņa daļām, kas svārstās vienādi (4. att. b). EM vilnis vakuumā izplatās ar ātrumu c ≈ 3·108m/s, kas ir vienāds ar gaismas ātrumu šajā vidē. Ātrumu sakritība nav nejauša, jo arī gaisma ir EM vilnis (5. att.). EM viļņi ir šķērsviļņi, kuros elektriskais un magnētiskais lauks svārstās perpendikulāri viļņa izplatīšanās virzienam, turklāt arī elektriskais un magnētiskais lauks svārstās perpendikulārās plaknēs (4. att. b). EM viļņus iedala pēc to viļņu garuma λ vai frekvences f. Viļņa garumu un frekvenci saista sakarība f = c : λ. Redzamā gaisma atrodas frekvenču joslas vidusdaļā (5. att.). Zemāka frekvence nekā redzamajai gaismai ir radioviļņiem, mikroviļņiem un infrasarkanajam starojumam, bet augstāka frekvence – ultravioletajam starojumam, rentgenstarojumam un gamma starojumam (5. att.).
Apskaties DZM materiālu par elektromagnētiskajiem viļņiem!
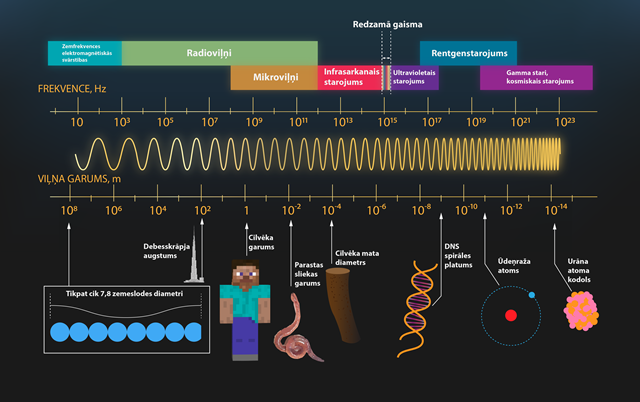
5.att. Elektromagnētisko viļņu skala
Tā kā EM svārstību kontūrā nemitīgi mainās strāvas stiprums un spriegums, tad, lai raksturotu šīs vērtības kādā noteiktā laika momentā, jāizmanto momentānā strāvas stipruma vērtība i (A) un momentānā sprieguma vērtība u (V). Svārstību kontūrā vienu EM svārstību var sadalīt piecos posmos (1. att.):
a) Pašā svārstību sākuma momentā visa enerģija ir koncentrēta kondensatorā, līdz ar to kondensatora spriegums ir vienāds ar maksimālo vērtību u = Umun strāvas stiprums i = 0, jo strāva vēl nav sākusi plūst (1. att. a).
b) Tālāk kondensators sāk izlādēties caur spoli, tādēļ kontūrā sāk pieaugt strāvas stiprums i uz kondensatora sprieguma u samazināšanās rēķina (1. att. b). Strāvas plūsma spolē rada magnētisko lauku un pašindukcijas elektrodzinējspēku (EDS), kas pretojas strāvas pieaugumam. Tā rezultātā pēc laika momenta, kas vienāds ar svārstību ceturtdaļperiodu T : 4, kondensators ir pilnībā izlādējies un tā spriegums u = 0, toties strāvas stiprums ir sasniedzis maksimālo vērtību i = Im. Arī pašindukcijas EDS spolē ir sasniedzis maksimālo vērtību un spole ir pārvērtusies par enerģijas avotu (1. att. b).
c) Nākošā svārstību ceturtdaļperioda laikā spolē uzkrātā magnētiskā lauka enerģija pāriet atpakaļ kondensatorā, līdz kondensatora spriegums atkal sasniedz maksimālo vērtību Um (1. att. c). Atšķirībā no svārstību sākuma momenta (1. att. a) kondensatora klājumi ir uzlādēti pretēji.
d) Tālāk atkal notiek kondensatora izlādēšanās caur spoli, sasniedzot maksimālo strāvas stipumu i = Im (1. att. d).
e)Viens svārstību periods ir noslēdzies tad, kad kondensators atkal ir pilnībā uzlādēts un ar tādu pašu polaritāti kā svārstību sākumā (1. att. e).
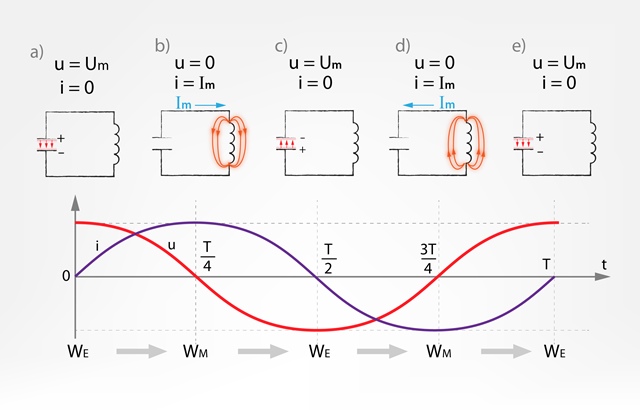
1.att. Elektriskās svārstības ideālā EM svārstību kontūrā
Harmoniskas mehāniskās svārstības apraksta ar kosinusa vai sinusa likumiem (2. att. a) atkarībā no svārsta sākuma pozīcijas (Svārstību veidi, rezonanse). Ideālā svārstību kontūrā EM svārstības notiek harmoniski, un tās arī apraksta ar kosinusa vai sinusa likumiem (2. att. b). EM svārstību sākumā kondensatora lādiņš ir maksimāls, tādēļ lādiņa izmaiņas kondensatorā apraksta vienādojums q = qmcos2πt : T (2. att. b), kur
qm– maksimālais kondensatora lādiņš, C
T – periods, s
t – laika moments, kurā aplūko svārstības, s
Kondensatora lādiņš ir tieši saistīts ar spriegumu U starp kondensatora platēm, tādēļ sprieguma izmaiņu apraksta vienādojums U = Umcos2πt : T (2. att. b), kur
Um– maksimālais spriegums starp kondensatora platēm, V
Tāpat kā lādiņš q ir tieši saistīts ar spriegumu U, tā spriegums U iet roku rokā ar elektriskā lauka intensitāti E, līdz ar to E = Emcos2πt : T (2. att. b), kur
Em– maksimālā elektriskā lauka intensitāte, V/m
Strāvas stiprums kontūra svārstību sākumā ir vienāds ar 0, tādēļ tā izmaiņas tiek aprakstītas ar sinusa likumu: I = Imsin2πt : T (2. att. b), kur
Im– maksimālais strāvas stiprums kontūrā, A
Šajā gadījumā ar strāvas stiprumu roku rokā iet magnētiskā lauka indukcija B, tādēļ B = Bmsin2πt : T (2. att. b), kur
Bm– magnētiskā lauka indukcijas maksimālā vērtība, T
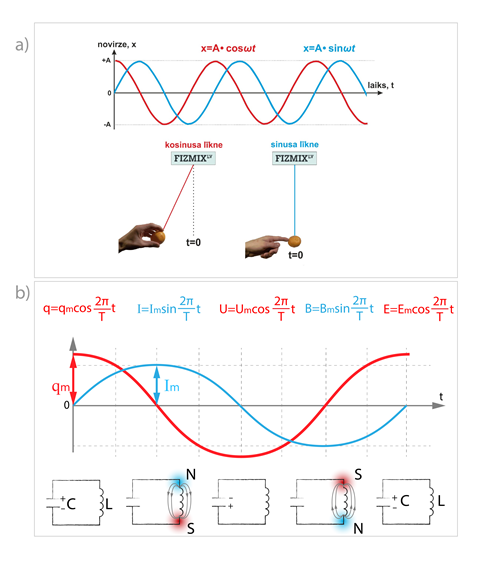
2.att. Svārstošo fizikālo lielumu funkcionālais apraksts
Katrai svārstošai sistēmai ir noteikta īpašfrekvence f0, ar kuru šī sistēma “vislabprātāk” svārstās. Katrai īpašfrekvencei f0ir atbilstošais svārstību periods T, ko aprēķina šādi: T = 1: f0. Matemātiskajam svārstam svārstību periods T = 2π√(l : g) (3. att. a), kur
l – svārsta garums, m
g – brīvās krišanas paātrinājums, m/s2
Atsperes svārstam svārstību periods T = 2π√(m : k) (3. att. b), kur
m – atsvara masa, kg
k – atsperes stinguma koeficients, N/m
Arī EM svārstību kontūram ir sava īpašfrekvence un atbilstošais periods, ko aprēķina pēc formulas T = 2π√(LC) (3. att. c), kur
L – spoles induktivitāte, H
C – kondensatora kapacitāte, F
Šo perioda izteiksmi var iegūt, izmantojot faktu, kas tika apskatīts sadaļā par pretestībām maiņstrāvas ķēdē, proti, ka vismazākā pretestība strāvai maiņstrāvas ķēdē ir tad, kad induktīvā pretestība XL = ωLir vienāda ar kapacitīvo pretestīvu XC = 1 : (ωC). Tādēļ ωL = 1: (ωC), no kā izriet, ka ω2 = 4π2 : T2 = 1: (LC), visbeidzot T = 2π√(LC).
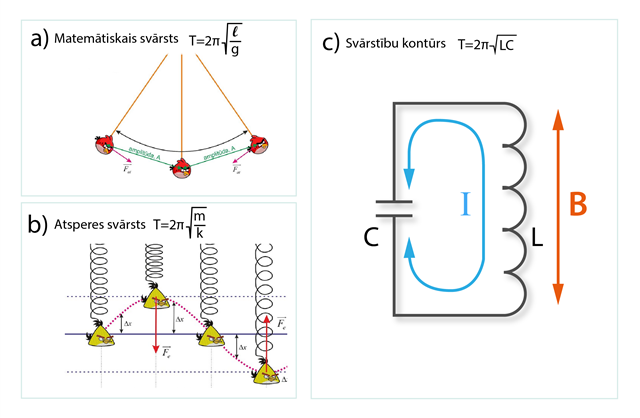
3.att. Dažādu svārstu pašsvārstību frekvences
Ja EM svārstību kontūrā noris svārstības ar kādu frekvenci f, tad varētu gaidīt, ka šis kontūrs izstaros EM viļņus ar atbilstošo frekvenci f, jo kontūrā svārstās elektriskais lādiņš, tādēļ izpildās EM viļņu rašanās priekšnosacījums – ir mainīgs elektriskais lauks. Tomēr realitātē šādi kontūri EM viļņus izstaro ļoti minimāli, varētu teikt, ka faktiski neizstaro. Šo situāciju var izskaidrot, ja apskata kādu mazu apvidu A, kas atrodas attālumā l no svārstību kontūra (4. att. a). Pretējās kontūra malās strāva plūst pretējos virzienos, līdz ar to šo strāvu radītie magnētiskie lauki apvidū A ir pretēji vērsti (ar “·” un “x” ir apzīmēti magnētiskā lauka indukcijas vektori, kas vērsti perpendikulāri laukā no 4. attēla un perpendikulāri 4. attēlā iekšā, 4. att. a). Ja attālums l ir salīdzinoši daudz lielāks par kontūra fiziskajiem izmēriem, tad šie mainīgie magnētiskie lauki viens otru kompensē un EM vilnis nerodas (4. att. a). Līdzīga situācija ir ar spoles vijumiem. Apskatot nelielu apvidu B, kas atrodas ārpus spoles vijuma, redzams, ka spoles vijuma pretējās pusēs plūst pretēja virziena strāvas un šīs strāvas apvidū B rada pretēji vērstus mainīgus magnētiskos laukus, kas viens otru kompensē (4. att. b). No šī var secināt, ka noslēgti kontūri EM viļņus neizstaro.
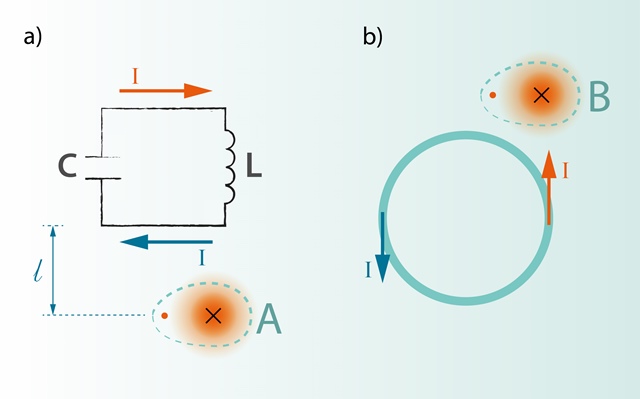
4.att. Kontūra un spoles vijuma magnētisko lauku kompensēšanās
Ja noslēgts kontūrs EM viļņus neizstaro, tad jāpamēģina, kas notiks, ja kontūru atvērs. Ja svārstību kontūru kāda vietā pārrauj, tad svārstības izbeidzas, tomēr, ignorējot daudzus fizikas likumus, iedomāsimies, ka strāva ir tā aizrāvusies ar skriešanu no viena kondensatora klājuma līdz otram, ka nepamana, ka mēs esam kondensatoru pašā viducī pāršķēluši un katru klājumu aizvirzījuši uz savu pusi tik tālu, ka arī spoles tinumi ir iztaisnojušies (5. att.). Šāds iztaisnots svārstību kontūrs nu ir kļuvis par EM viļņu avotu, jo nav vairs pretī plūstošās strāvas, kas atceļ magnētiskā lauka svārstības. Vaļējus kontūrus sauc par antenām. Protams, aplūkotajā piemērā reāli strāvas svārstības un EM izstarošana nenotiks, jo pārrautajā kontūrā strāva neplūdīs, bet, ja šādi izveidotai antenai pievieno svārstību avotu, piemēram, kādu citu noslēgtu kontūru, tad antena reāli sāks uzvesties kā EM viļņu starotājs.
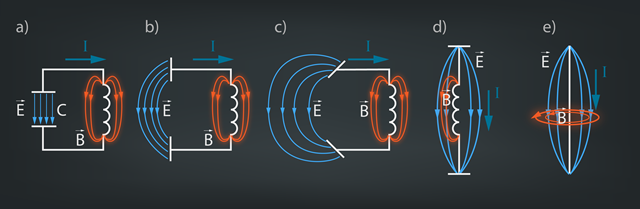
5.att. EM viļņu antenas izveide
EM viļņu diapazons noklāj ļoti plašu frekvenču un viļņu garumu spektru (1. solis 5. att.). Tehnisku ierobežojumu dēļ ar tikko apskatīto antenu ir iespējams radīt tikai salīdzinoši šaura spektra EM viļņus, tādēļ dažādu EM viļņu iegūšanai ir jāizmanto dažādas metodes.
Radioviļņi ir EM viļņi ar zemu frekvenci. Lai gan EM viļņu iedalījumam nav noteiktas robežas, tomēr radioviļņiem piedēvē viļņu garuma diapazonu no 1 mm līdz 100 km (atbilstošās frekvences no 300 GHz līdz 30 kHz). Viens no iespējamajiem radioviļņu avotiem ir apskatītais svārstību kontūrs (6. att. a), tomēr radioviļņiem ir arī daudz dabīgo avotu. Daudzi debess ķermeņi, piemēram, neitronu zvaigznes un pulsāri, izstaro radioviļņus, bet nav vajadzības avotus meklēt tik tālu. Mūsu pašu Saule ir spēcīgs radioviļņu starotājs, un arī uz Zemes zibens spēriena rezultātā rodas radioviļņi (6. att. b).
Mikroviļņi aizņem viļņu garumu joslu no 1 mm līdz 30 cm (300 GHz līdz 1 GHz), jo mikroviļņi būtībā ir īsi radioviļņi. Mākslīgi mikroviļņus iegūst ar vakuuma lampām, piemēram, magnetroniem, kas sastopami mikroviļņu krāsnīs (6. att. c), bet, protams, arī mikroviļņiem ir dabīgie avoti. Pats nozīmīgākais no tiem ir dabīgais starojuma fons kosmosā, ko veido mikroviļņi un kas ir paliekas no, iespējams, kādreiz notikušā Lielā Sprādziena.
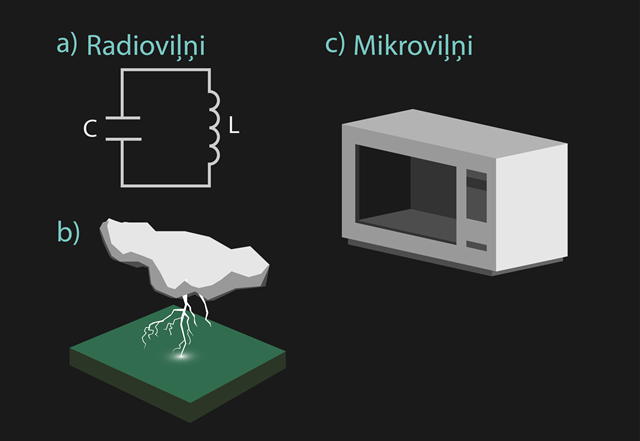
6.att. Radioviļņu un mikroviļņu avoti
EM viļņus ar viļņu garumu no 700 nm līdz 1 mm (4,2·1014Hz līdz 300 GHz) dēvē par infrasarkanajiem viļņiem. Sadaļā Siltumapmaiņas veidi noskaidrojām, ka katrs ķermenis atkarībā no tā temperatūras izstaro noteikta frekvenču sadalījuma EM starojumu. Jo ķermenim ir augstāka temperatūra, jo pieaug izstarojuma intensitāte EM viļņiem, kas atbilst infrasarkanajam starojumam (7. att a). Tātad infrasarkanais starojums ir siltuma starojums un to izstaro visi silti ķermeņi, arī cilvēks (7. att. b). Infrasarkano starojumu iespējams iegūt ne tikai no sakarsētiem ķermeņiem, piemēram, elektronikā izmanto infrasarkano staru diodes, kurās infrasarkanais starojums rodas citu fizikālu procesu rezultātā.
Pasaule mūsu acīm ir krāsu pārpilna, un šo krāsu pārpilnību nodrošina ļoti šaura EM viļņu spektra daļa no aptuveni 380 nm līdz 700 nm (790 THz līdz 430 THz), ko sauc par redzamo gaismu. Cilvēka acs ir pielāgojusies uztvert tieši šo EM viļņu diapazonu, jo mūsu sildītāja un gaismas devēja – Saule – visspēcīgāk staro tieši šajā EM viļņu diapazonā. Redzamās gaismas spektru sadala septiņās krāsās: sarkanā, oranžā, dzeltenā, zaļā, gaiši zilā, zilā un violetā (7. att. c). Bez dabīgā gaismas avota Saules pastāv dažādas veida mākslīgie avoti, piemēram, elektriskās spuldzes, stipri sakarsēti ķermeņi, kā arī redzamā gaisma rodas luminiscences rezultātā. Viena no dabas parādībām, kurā var apskatīt redzamās gaismas spektru, ir varavīksne (7. att. d)
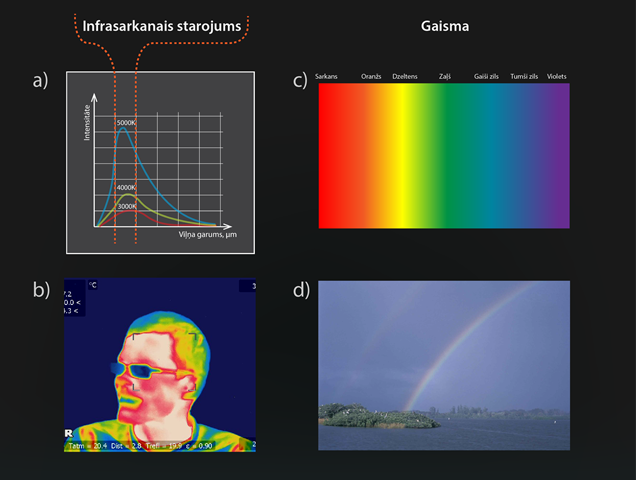
7.att. Infrasarkano viļņu un redzamās gaismas avoti un parādības
EM viļņi ar viļņu garumu no aptuveni 10 nm līdz 400 nm (30 PHz līdz 750 THz) 400 nm tiek saukti par ultravioleto (UV) starojumu, jo frekvenču skalā tie atrodas tieši aiz redzamās gaismas diapazona, kas noslēdzas ar violeto gaismu. Saule ir arī spēcīgs UV starotājs, bet, tā kā UV starojuma enerģija ir lielāka par redzamās gaismas enerģiju, tad no šī starojuma ir jāuzmanās, lai tas saulainā laikā neizraisītu ādas apdegumus. Par laimi, Zemes atmosfēra daļēji šo no Saules nākošo starojumu absorbē un tas līdz Zemes virsmai atceļo tikai daļēji. Par UV starojuma mākslīgajiem avotiem kalpo speciālas UV lampas un LED diodes. Tehniskajos procesos UV starojums rodas, piemēram, metinot, tādēļ šajā procesā ir jālieto speciāli aizsarglīdzekļi (8. att. a)
EM starojuma lielo frekvenču galvgalī atrodas rentgenstarojums ar aptuveniem viļņu garumiem no 1 pm līdz 10 nm (300 EHz līdz 30 PHz) un gamma starojums ar viļņu garumu, kas mazāks par 0,01 nm (vairāk par 30 EHz). Šiem EM viļņiem ir ļoti augsta frekvence un līdz ar to arī liela enerģija, tādēļ to izmantošanā ir jāievēro īpaša piesardzība. Rentgenstarojuma rašanās ir saistīta ar dažādiem procesiem atomā un atoma kodolā. Rentgenstarojumu var izmantot, lai caurskatītu cilvēka acij necaurskatāmus objektus, piemēram, ceļa somas lidostās (8. att. b). Gamma starojuma rašanās parasti ir saistīta ar dažādiem fizikāliem procesiem, kas saistīti ar atoma kodolu, un viens piemērs tam ir kodolsprādziens (8. att. c).

8.att. Ultravioletā, rentgenstarojuma un gamma starojuma avoti
Turpinot meklēt sasaisti starp mehāniskajām un EM svārstībām, ir vērtīgi apskatīt dažādu veidu enerģiju maiņu svārstību procesā. Sadaļā par atsperes un matemātisko svārstu noskaidrojām, ka mehāniskajiem svārstiem svārstību laikā notiek pārēja no potenciālās enerģijas uz kinētisko un otrādi (1. att. a), turklāt viena svārstību perioda laikā potenciālā un kinētiskā enerģija divas reizes sasniedz savas maksimālās vērtības. EM svārstībās potenciālās un kinētiskās enerģijas lomu spēlē elektriskā un magnētiskā lauka enerģija (1. att. b). Kontūra maksimālā enerģija W ir vienāda ar maksimālo elektriskā lauka enerģiju WE = CUm2 : 2vai maksimālo magnētiskā lauka enerģiju WM = LIm2 : 2, jo WE = WM. Ar Umun Imapzīmē kontūra maksimālo spriegumu (V) un strāvas stiprumu (A), bet ar C un L – kontūra kapacitāti (F) un induktivitāti (H). Tāpat kā mehāniskajās svārstībās, arī EM svārstībās elektriskā un magnētiskā lauka enerģijas viena perioda laikā divas reizes sasniedz savas maksimālās vērtības (1. att. b).
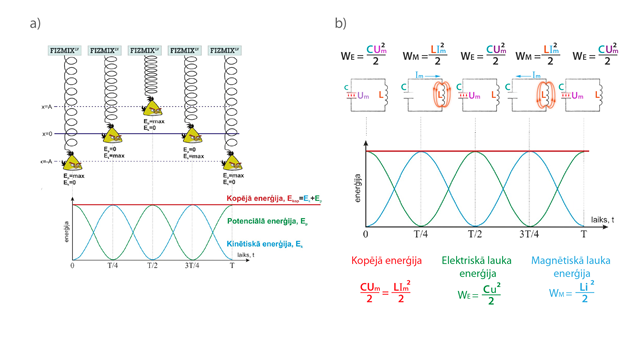
1.att. Enerģijas izmaiņas mehāniskās un EM svārstībās
Kā tika noskaidrots sadaļā par svārstību veidiem un rezonansi, reālām mehāniskajām svārstībām ir jāsastopas ar pretestību, tādēļ svārstību amplitūda laika gaitā samazinās (2. att. a). Līdzīga situācija ir ar EM svārstībām. Reālam svārstību kontūram piemīt aktīva pretestība, tādēļ, ja kontūram netiek pievadīta enerģija, tad laika gaitā samazinās maksimālās vērtības lādiņa lielumam, strāvas stiprumam (2. att. b), spriegumam un no tiem izrietošajām elektriskā lauka intensitātes un magnētiskā lauka indukcijas vērtībām. Pretestību kontūrā rada elektriskās ķēdes un spoles vadi, spoles serdes magnetizācija un kondensatora dielektriķa polarizācija. Lai gan iepriekš tika noskaidrots, ka slēgts svārstību kontūrs faktiski nedarbojas kā EM viļņu antena, realitātē šāds kontūrs tomēr nedaudz izstaro EM viļņus, un arī tas izraisa enerģijas zudumus.
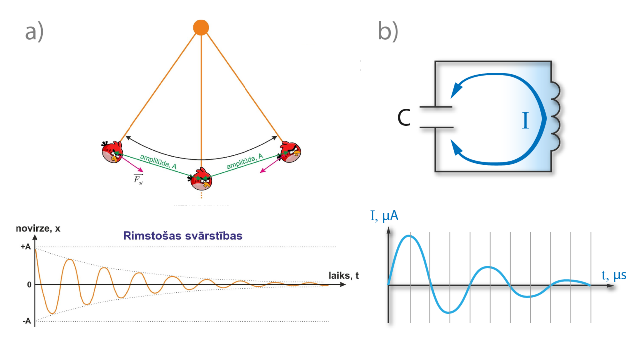
2.att. Mehānisko un EM svārstību rimšana
Lai atjaunotu svārstību amplitūdu mehāniskajām svārstībām, mums ik pa laikam uz svārstu ir jāiedarbojas ar kādu ārēju spēku, lai piešķirtu tam papildu enerģiju, piemēram, ik pa laikam pagrūžot šūpoles. EM svārstību gadījumā, lai nodrošinātu nerimstošas svārstības, kontūram ik pa laikam ir jāpievada elektriskā enerģija no kāda elektroenerģijas avota. Viens elektriskās shēmas piemērs nerimstošu EM svārstību iegūšanai redzams 3. attēla (a) gadījumā. Šajā shēmā strāvas avots kontūram ir pieslēgts caur tranzistoru. Tranzistora darbība tika aplūkota sadaļā par elektrisko strāvu pusvadītājos. Strāvas avota enerģija kontūram pieplūst tādā gadījumā, ja tiek nodrošināta nepieciešamā potenciālu starpība starp tranzistora bāzi (B) un emiteru (E), būtībā bāze darbojas kā elektriskais slēdzis tam, vai strāva plūst caur tranzistoru no emitera uz kolektoru (C) vai neplūst (3. att. a). Tranzistora bāze un emiters ir piesaistīti svārstību kontūram caur induktīvo sasaisti jeb caur spoli. Šīs abas tuvumā esošās spoles darbojas kā transformators (3. att. a). Kontūra svārstības inducē spriegumu gan spolē L, gan arī La, turklāt pusi no svārstību perioda šis spriegums ir pozitīvs, bet pusi – negatīvs. Līdz ar to katru pus periodu tranzistors atveras un kontūram tiek pievadīta enerģija. Šāda periodiska enerģijas pievade nodrošina nerimstošas svārstības (3. att. b).
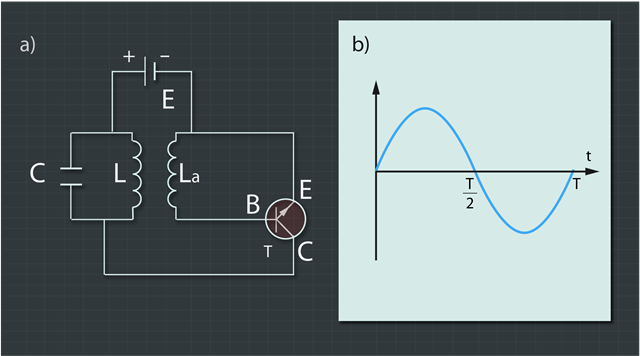
3.att. Elektriskā shēma nerimstošu EM svārstību ģenerēšanai
Uz šo brīdi esam ieguvuši atvērtu svārstību kontūru – antenu, kas var darboties kā EM viļņu starotāja, bet kurā pašā par sevi svārstības nenotiek (2. solis 5. att), kā arī esam ieguvuši svārstību kontūru, kurā ir nerimstošas EM svārstības, bet kurš pats EM viļņus faktiski neizstaro (3. att.). Tagad tikai atliek šīs abas divas komponentes apvienot, un būsim ieguvuši nepārtrauktu EM viļņu starotāju (4. att.). Lai savienotu svārstību kontūru un antenu, var atkal izmantot induktīvo sasaisti (4. att.), kas tika izmantota elektriskajā shēmā, lai iegūtu nerimstošas svārstības (3. att.). Mainīgais magnētiskais lauks spolē L1inducē mainīga virziena strāvu spolē L2,un antena var sākt starot (4. att.). Ir vērts ņemt vērā faktu, ka antenas starošanas jauda P ir atkarīga no svārstību frekvences f ceturtajā pakāpē jeb P ~ f4.
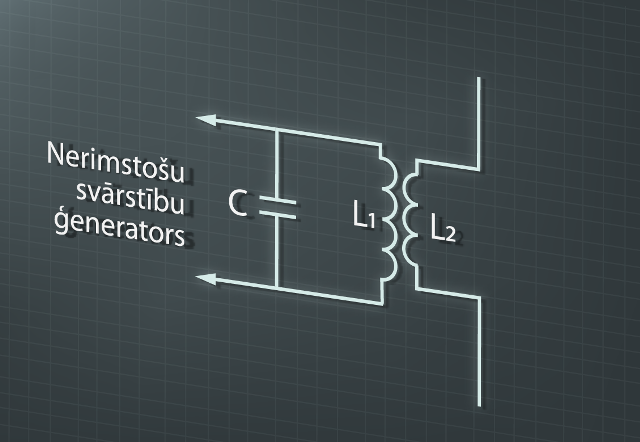
4.att. Nerimstošu svārstību starotājs
Antenā kā starotājā arī notiek EM svārstības, kurās maksimālo vērtību iegūst pārmaiņus spriegums U un strāvas stiprums I (5. att.). Kad spriegums sasniedz maksimālās vērtības, tad ap antenu ir tikai elektriskais lauks, jo strāvas stiprums ir nulle, un līdz ar to magnētiskais lauks uz to brīdi ir atkāpies (5. att. a, c, e). Savukārt, kad strāvas stiprumam ir maksimālās vērtības, tad ap antenu ir magnētiskais lauks, jo elektrisko lauku izraisošais spriegums ir vienāds ar nulli (5. att. b, d).
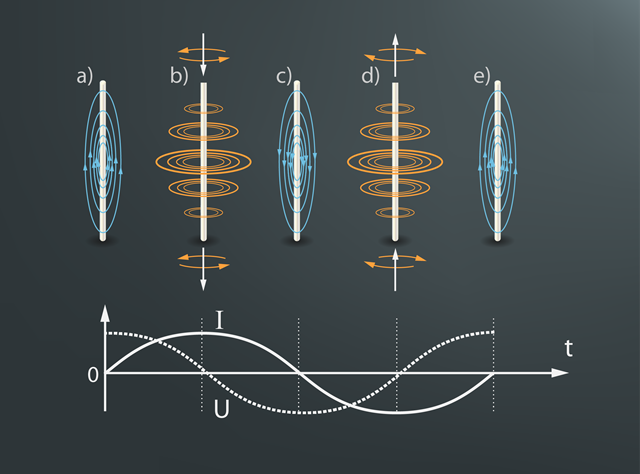
5.att. Nerimstošu svārstību starotājs
Šīs antenas elektriskā un magnētiskā lauka izmaiņas pamazām sāk izplatīties telpā. Tas notiek līdzīgi kā tad, ja mēs ar koku kulstītu ūdeni vienā dīķa malā, bet ūdens viļņi pamazām izplatītos pa visu dīķi. Elektriskā un magnētiskā lauka svārstības notiek perpendikulārās plaknēs, turklāt noslēgto elektriskā lauka līniju cilpu izmērs ir atkarīgs no antenas garuma, tādēļ ap antenu izveidojas ne pārāk vienkāršas formas telpisks EM vilnis, kas pamazām izplatās telpā (6. att.).
Izmēģini simulāciju, kā darbojas antena un uztvērējs!
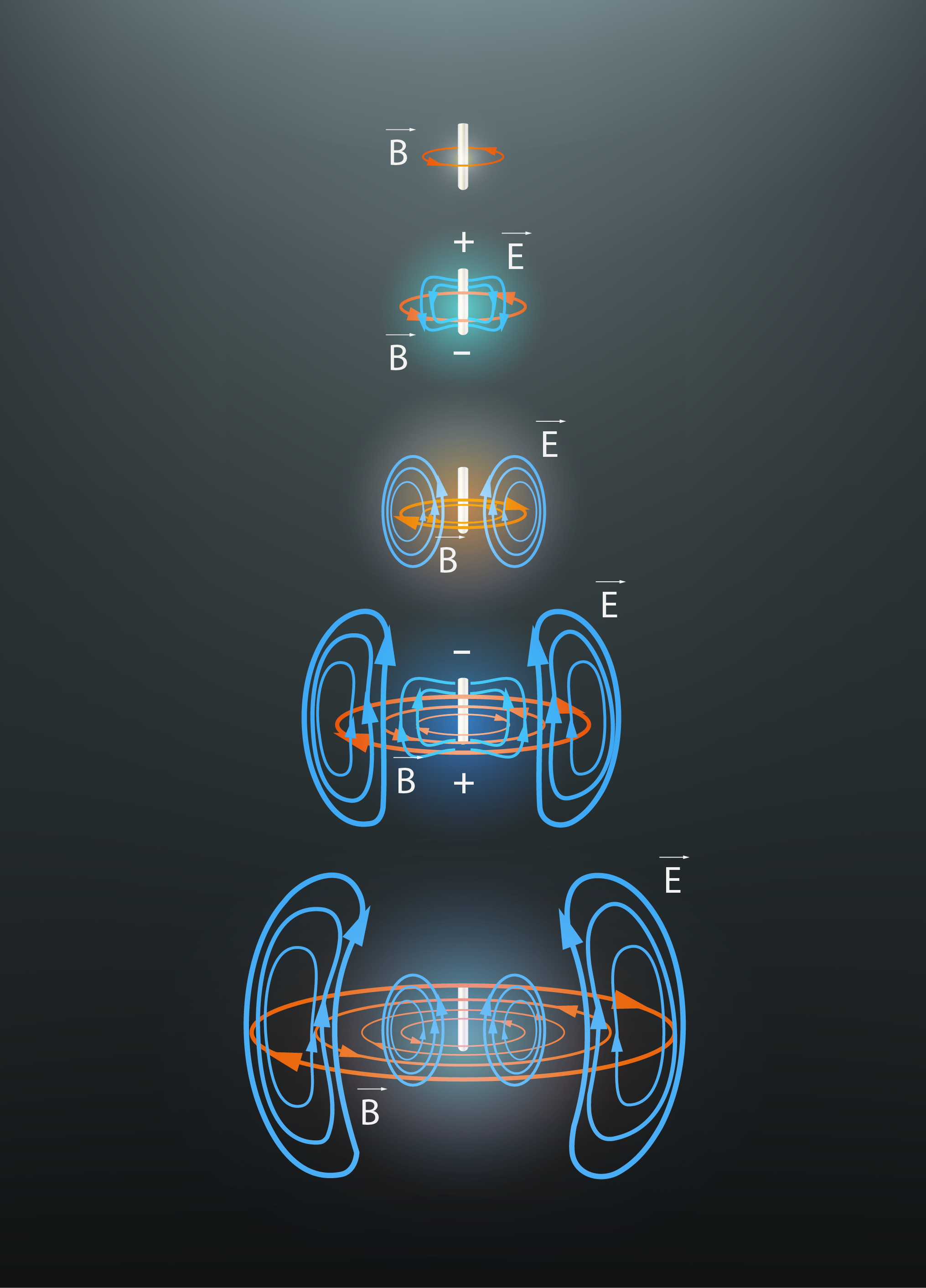
6.att. Antenas radītā EM lauka izplatīšanās telpā