Elektriskie lādiņi pievelkas vai atgrūžas visdažādākajos attālumos cits no cita. Tātad elektromagnētiskā mijiedarbība tiek pārnesta no viena telpas apgabala uz citu. Mēs zinām, ka dzīvē nekas pats no sevis nenotiek, līdz ar to kādam mijiedarbība ir telpā „jāpārnes”. Šajā gadījumā to dara īpašs elektriskās mijiedarbības pārnesējs – elektriskais lauks (1. att.). Elektriskais lauks pastāv ap jebkuru lādētu daļiņu vai ķermeni, bet mēs nevaram to tieši ieraudzīt vai uztvert, varam tikai konstatēt tā klātbūtni. Tomēr, lai varētu paredzēt, kā šis elektriskais lauks ietekmēs citus lādētus ķermeņus, ir jāatrod veidi, kā šo elektrisko lauku aprakstīt un vizualizēt.
1.att. Elektriskais lauks ir elektromagnētiskās mijiedarbības pārnesējs
Pieņemsim, ka mums uzdāvina metāla globusu (2. att.), kura lādiņš ir q0. Parasti jau dāvinātam zirgam zobos neskatās, bet cilvēciska ziņkāre tomēr moka: kāds ir šī globusa elektriskais lauks? Viens veids, kā mēģināt šo lauku aprakstīt, ir ievietot tajā kādu citu lādiņu ar lielumu +q un apskatīties, kādam Kulona spēkam F šis lādiņš tiek pakļauts (2. att. a). Taču, ja mēs ievietotā lādiņa lielumu palielināsim divas reizes līdz +2q, tad divas reizes pieaugs arī Kulona spēks (2. att. b), līdz ar to ar Kulona spēku vien raksturot ķermeņa elektrisko lauku nevar, jo ķermeņa elektriskais lauks ir atkarīgs tikai no paša ķermeņa, nevis no lādiņa, ko šī ķermeņa elektriskajā laukā ievieto. Tādēļ ir jāmeklē fizikāls lielums, kas abos apskatītajos gadījumos nemainās, un tas kā reiz ir Kulona spēka F un ievietotā lādiņa lieluma q attiecība. No šī arī izriet elektriskā lauka raksturojošais lielums – elektriskā lauka intensitāte E –, kuru nosaka izteiksme E = F q, kur
E - elektriskā lauka intensitāte ņutonos uz kulonu (N : C),
F - Kulona spēks ņutonos (N),
q - elektriskais lādiņš kulonos (C),
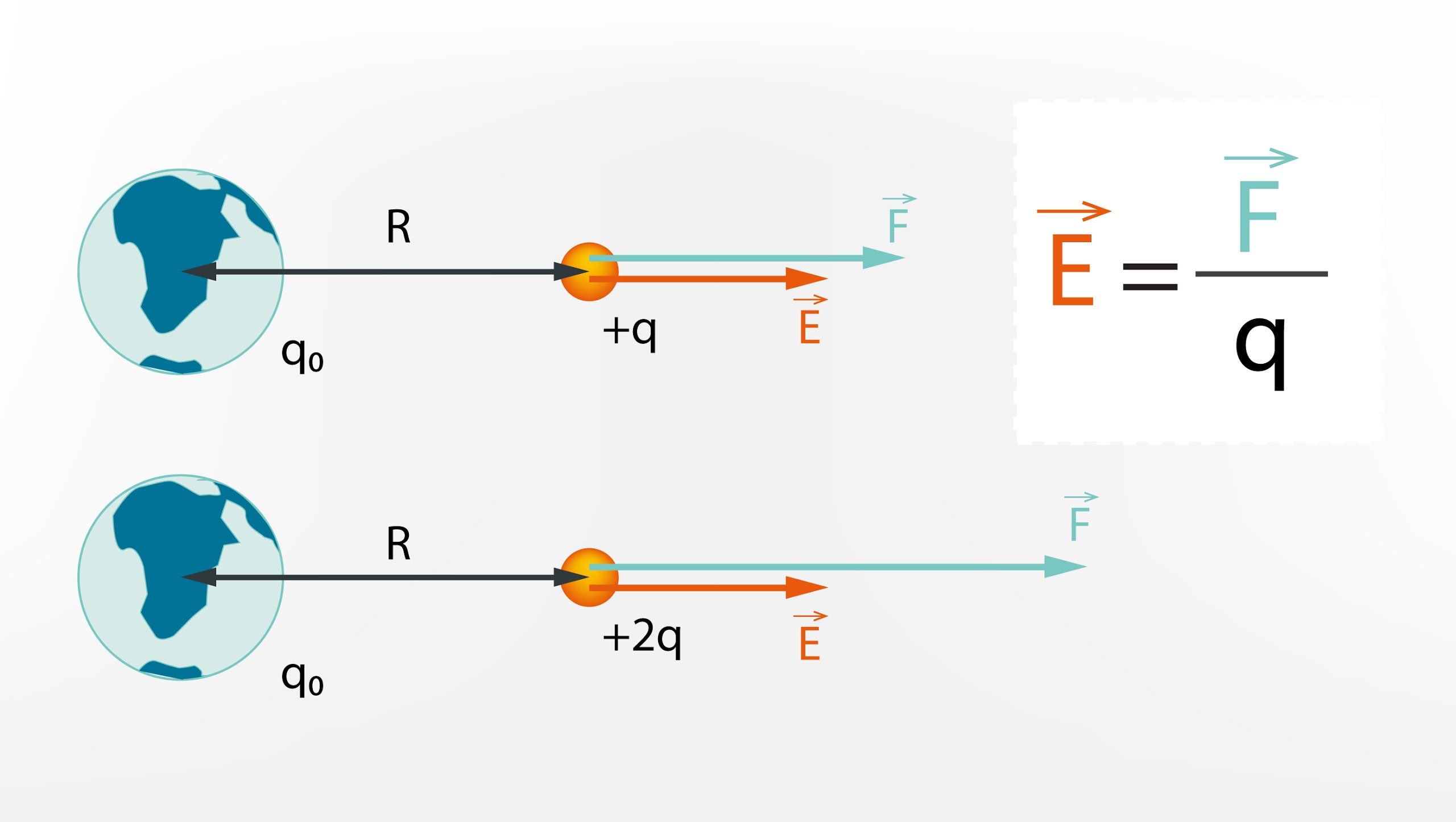
2.att. Elektriskā lauka intensitātes noteikšana
Uzlādētā ķermeņa elektriskā lauka intensitātei noteiktos telpas punktos ir noteikts virziens, kas ir atkarīgs no tā, vai avots ir uzlādēts pozitīvi vai negatīvi. Ja avots ir uzlādēts pozitīvi, tad ir pieņemts, ka elektriskā lauka intensitāte ir vērsta prom no avota (3. att. a). Savukārt ja avotā pārsvarā ir negatīvie lādiņi, tad elektriskā lauka intensitāte ir vērsta uz avotu (3. att. b).
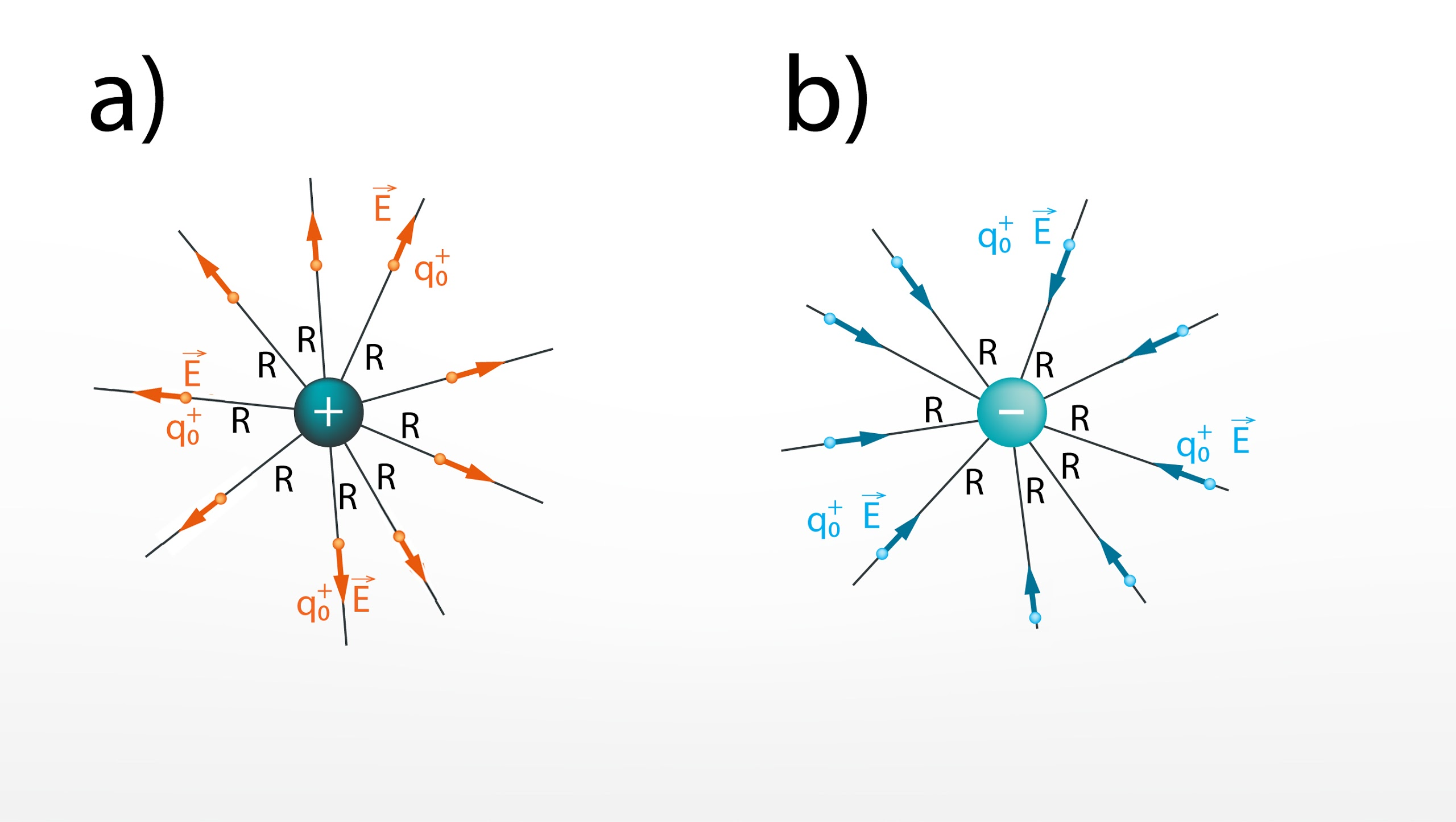
3.att. Elektriskā lauka intensitātes virziens dažādiem avotiem
Elektriskā lauka intensitāte ir vektoriāls lielums, tādēļ to raksturo gan virziens, gan vērtība. Ja lādētā ķermeņa izmēri ir mazi, salīdzinot ar attālumiem, kuros apskata elektrisko lauku, tad tādā gadījumā var lietot punktveida lādiņa modeli un pieņemt, ka elektriskā lauka avots ir koncentrēts vienā telpas punktā. Punktveida lādiņa elektriskā lauka intensitātes moduļa vērtību vakuumā var aprēķināt pēc formulas E = kq0 : R2, kur
k - Kulona spēka konstante (Nm2 : C2),
q0- punktveida lādiņa lielums kulonos (C)
R - attālums līdz punktveida lādiņam metros (m).
Ja ap pozitīvu punktveida lādiņu iezīmē elektriskā lauka intensitātes vektorus (4. att.), tad redzams, ka tie ir vērsti prom no avota un to garums samazinās, attālinoties no avota, jo samazinās elektriskā lauka intensitāte.
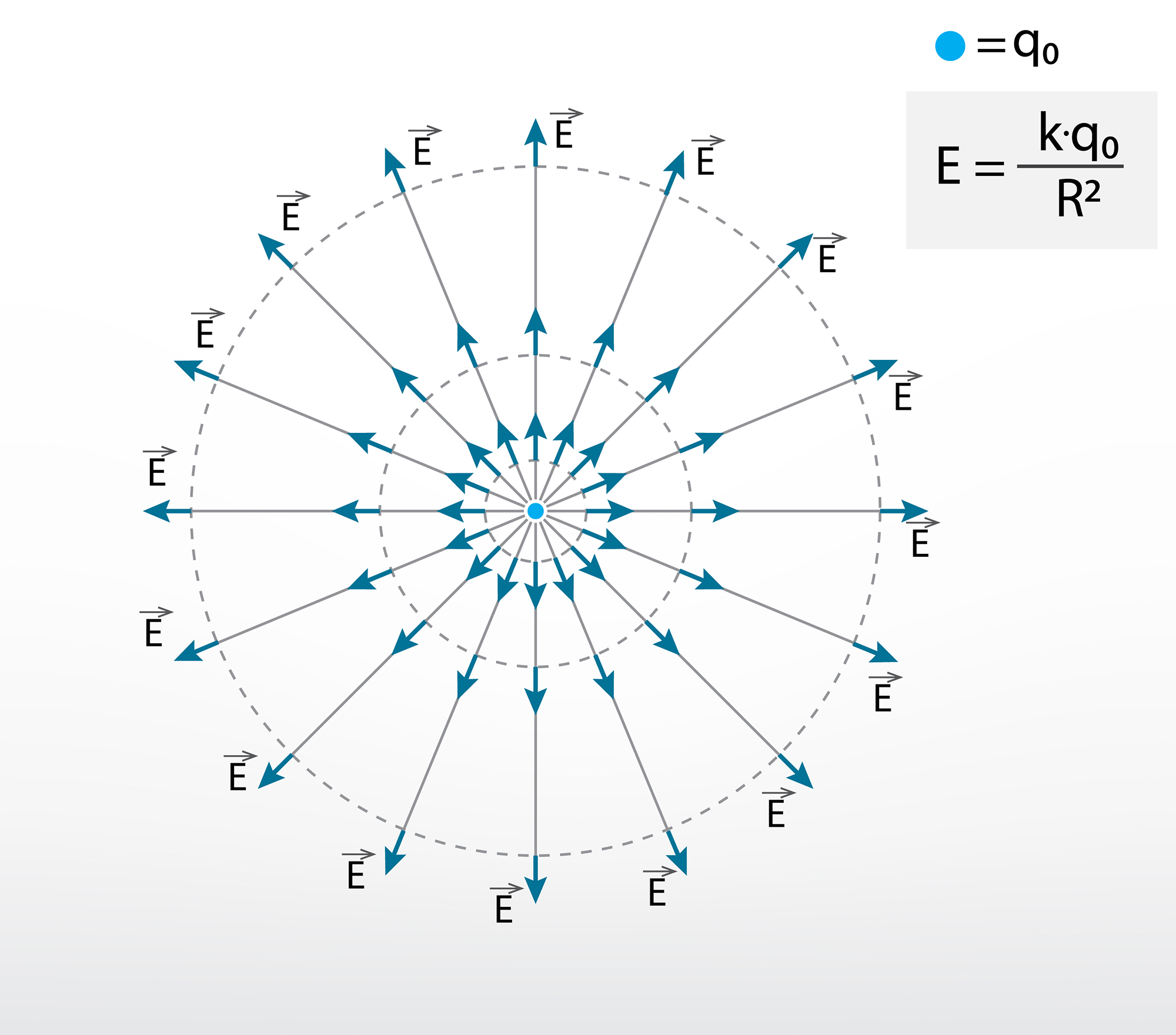
4.att. Pozitīva punktveida lādiņa elektriskais lauks
Bieži telpā elektrisko lauku rada nevis viens, bet vairāki ķermeņi. Tādā gadījumā elektriskā lauka noteikšanai kādā telpas punktā ir jāņem vērā abu avotu radītais elektriskais lauks. Piemēram, ja mums ir pozitīvs lādiņš q1 un negatīvs lādiņš q2 un mēs vēlamies uzzināt elektriskā lauka intensitāti punktā A, kas atrodas abu lādiņu ietekmē (5. att.), tad mums jānoskaidro, kādas elektriskā lauka intensitātes E1 un E2 šajā punktā rada pozitīvais un negatīvais lādiņš, un tad abas šīs intensitātes ģeometriski jāsaskaita, lai iegūtu kopējo intensitāti EA (5. att.).
Spied uz: DZM un uzzini vairāk par vektoru ģeometrisko saskaitīšanu!
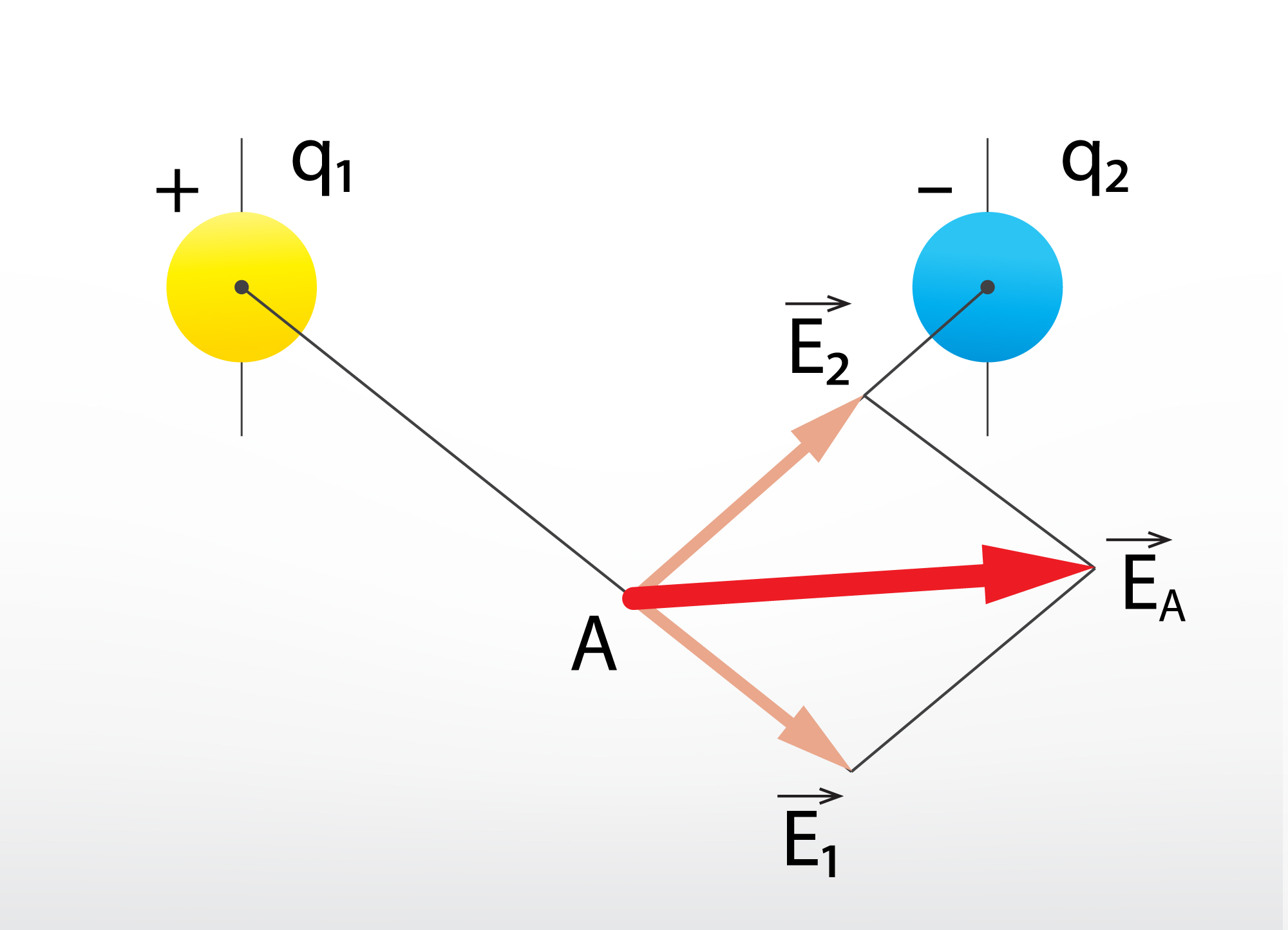
5.att. Pozitīva punktveida lādiņa elektriskais lauks
Ja ir vēlme elektriskā lauka intensitāti attēlot vairākos telpas punktos, tad uzdevums kļūst darbietilpīgs, jo jāattēlo daudz un dažādu vektoru, kam ir daudz un dažādi virzieni un garumi, turklāt tie var sākt klāties cits citam pāri, padarot attēlojumu sarežģītu un grūti uztveramu. Tādēļ elektriskā lauka attēlošanai lieto elektriskā lauka intensitātes līnijas.
Par elektriskā lauka intensitātes līnijām sauc tādas līnijas, kuru pieskares katrā punktā sakrīt ar elektriskā lauka intensitātes vektora virzienu šajā punktā (6. att). Elektriskā lauka līnijas arī ir vērstas no pozitīvā uz negatīvo lādiņu.
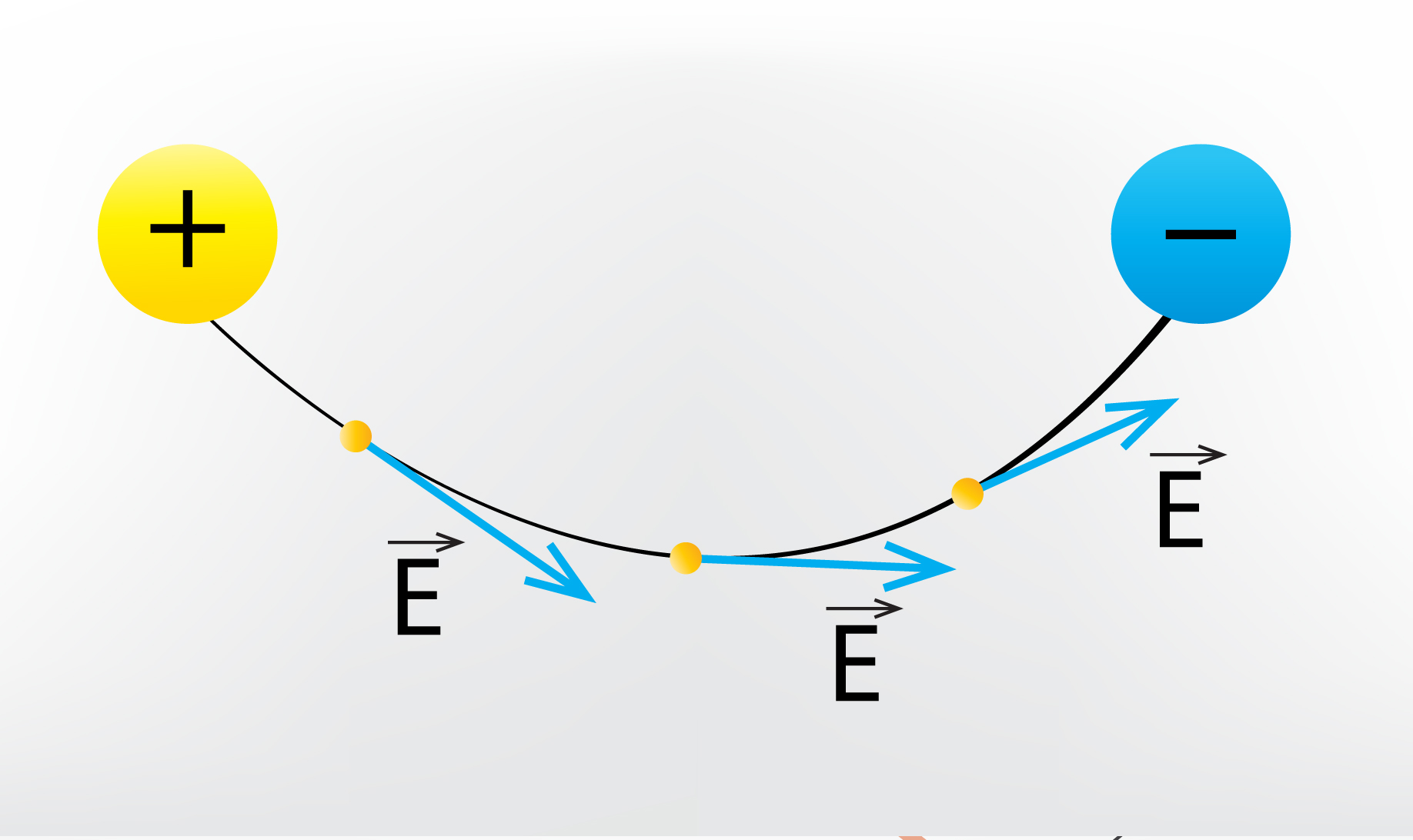
6.att. Elektriskā lauka intensitātes līnija
Izmantojot elektriskā lauka līnijas, var ļoti uzskatāmi attēlot elektrisko lauku divu lādiņu sistēmai gan tad, ja lādiņi ir ar pretējām zīmēm (7. att. a), gan arī vienādas zīmes lādiņiem (7. att. b). Vienādas zīmes lādiņu gadījumā šie lādiņi viens no otra atgrūžas, un līdz ar to atgrūžas arī elektriskā lauka intensitātes līnijas (7. att. b)
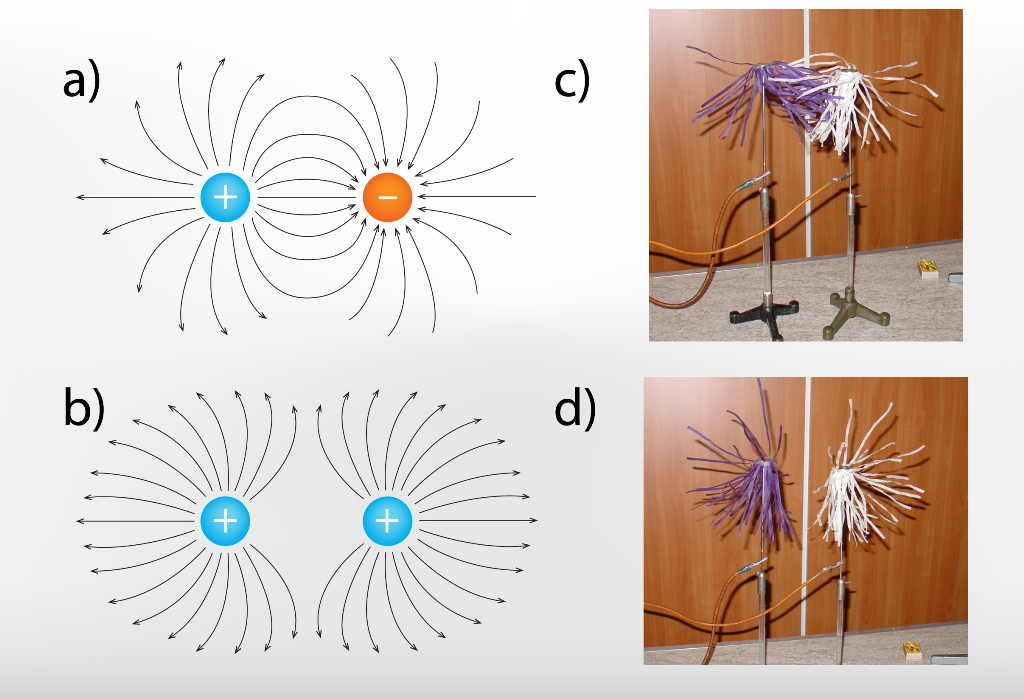
7.att. Elektriskā lauka intensitātes līnijas dažādiem lādiņu komplektiem zīmējumā (a, b) un dabā (c, d)
Lai grafiski attēlotu elektriskā lauka intensitātes lielumu, tiek variēts ar intensitātes līniju biežumu. Ja elektriskais lauks ir mazāks, tad līnijas attēlo retāk (8. att. a), savukārt, ja intensitāte ir lielāka, tad arī intensitātes līnijas tiek zīmētas biežāk (8. att. b).
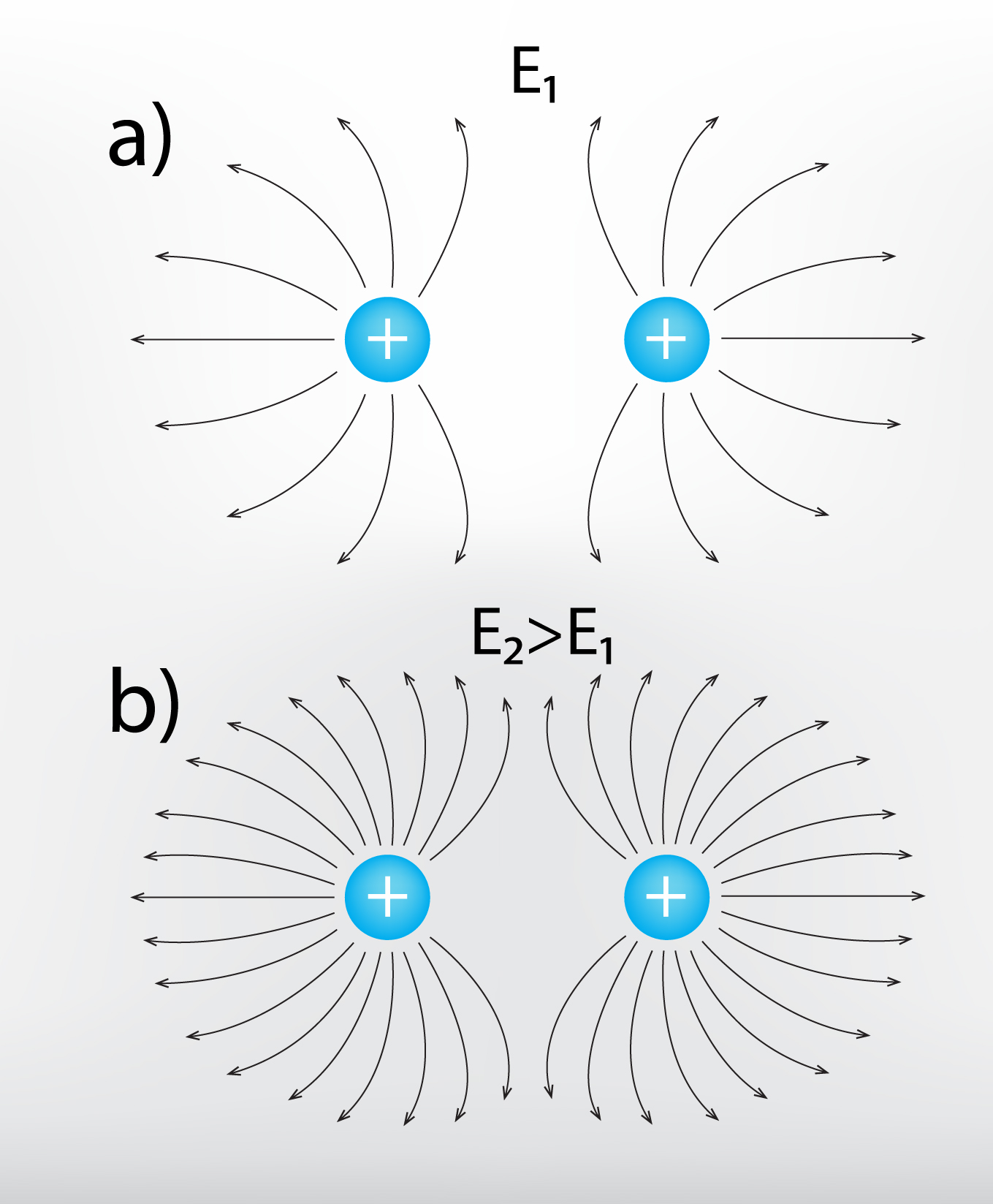
8.att. Elektriskā lauka intensitātes lielums atkarīgs no intensitātes līniju biežuma
Dažādu elektrisko lauku intensitāte apskatāma 9. attēla info grafikā.
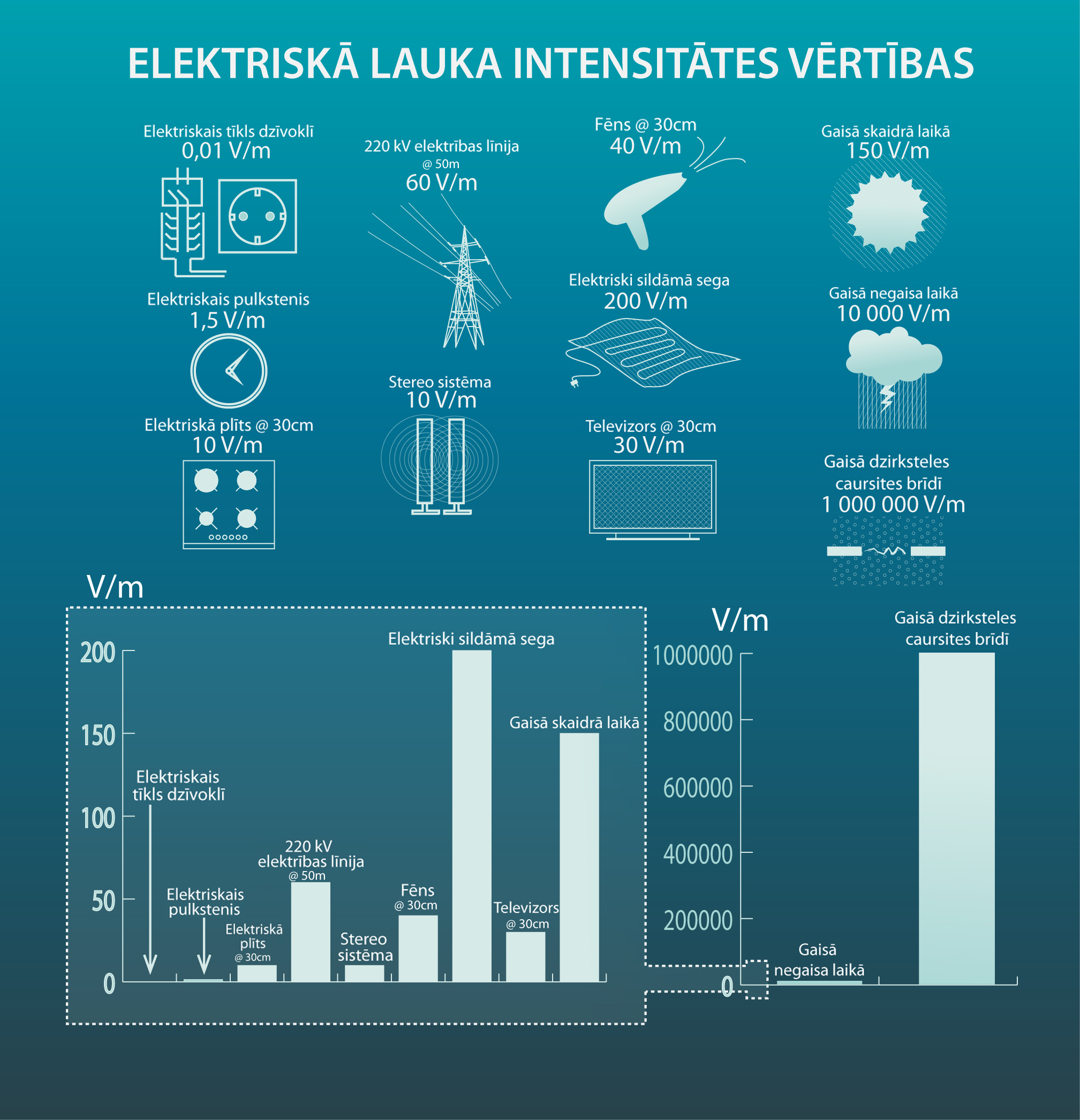
9.att. Elektriskā lauka intensitātes vērtības
Punktveida lādiņa elektriskā lauka intensitāti vakuumā var aprēķināt pēc sakarības E = kq0 : R2. Šo sakarību var iegūt, izmantojot Kulona likumu un elektriskā lauka intensitātes definīciju. Ja lādiņš q0ir elektriskā lauka avots un šajā laukā attālumā R ievieto lādiņu q (1. att.), tad uz ievietoto lādiņu darbojas Kulona spēks F = kq0q : R2. Pēc elektriskā lauka intensitātes definīcijasE = F : q. Ievietojot F vietā Kulona spēka izteiksmi, iegūst E = kq0q : (R2q) = kq0 : R2.
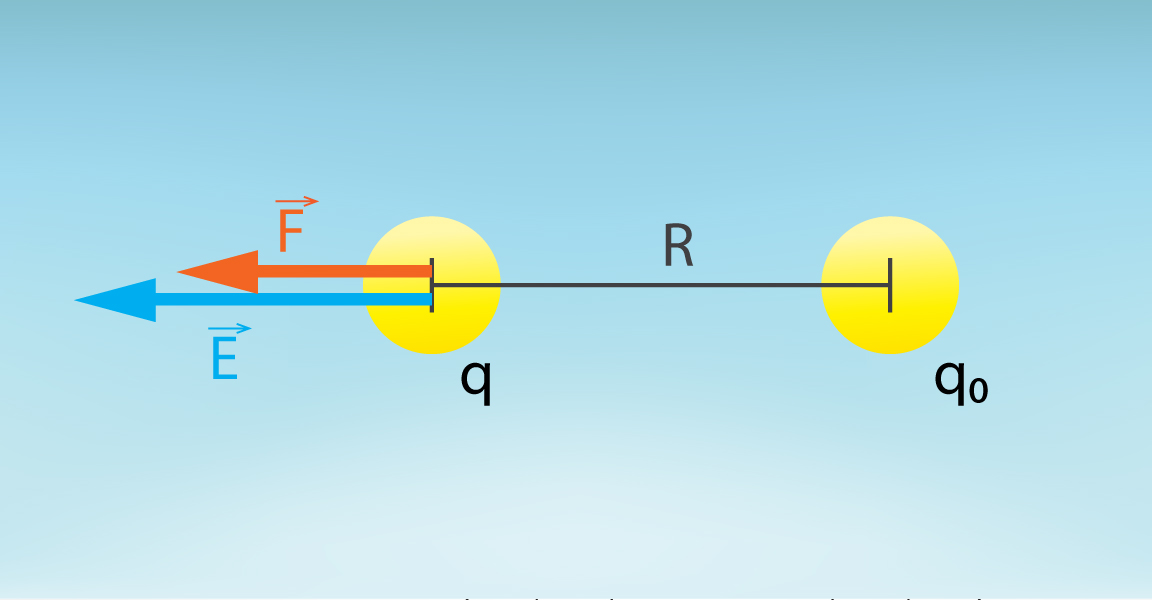
1.att. Punktveida lādiņa elektriskā lauka intensitāte
Ja šo sakarību uzzīmē grafiski (2. att.), tad uzskatāmi parādās tas, ka intensitāte ir apgriezti kvadrātiski atkarīga no attāluma līdz avotam. Tas nozīmē, ka, divas reizes palielinot attālumu, intensitāte samazinās četras reizes. Savukārt četras reizes palielinot attālumu, intensitāte samazinās jau 16 reizes (2. att.).
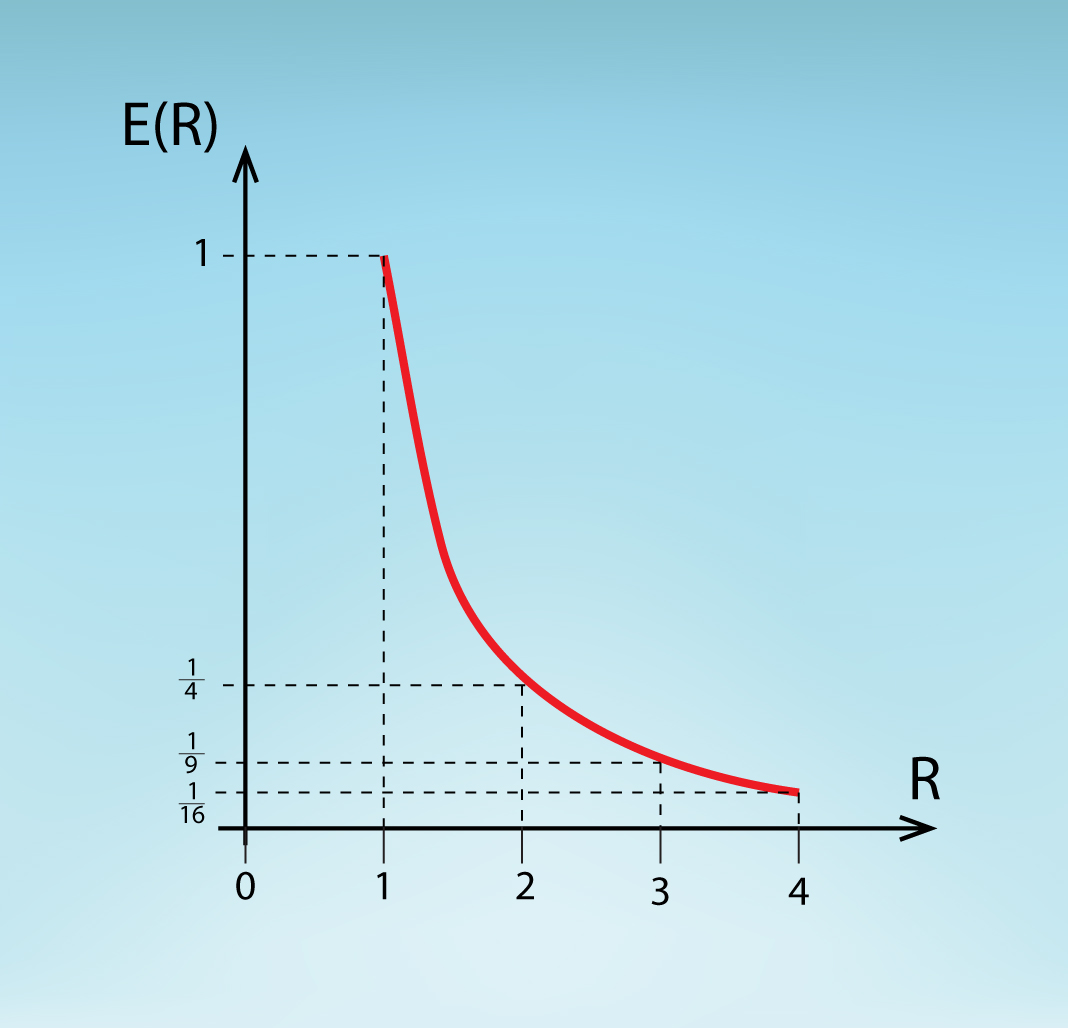
2.att. Punktveida lādiņa elektriskā lauka intensitātes grafisks attēlojums
Ja punktveida avota vietā apskata uzlādētas elektrovadoša materiāla lodes elektrisko lauku, tas izrādās ļoti līdzīgs punktveida avota laukam. Vadītāja lodi raksturo tās rādiuss r (3. att.). Lādiņi šajā lodē var brīvi pārvietoties, un ja to, piemēram, uzlādē pozitīvi, tad lādiņi atgrūžas cits no cita un izvietojas lodes ārmalā (3. att.). Var uzskatīt, ka lodes ārmalu veido ļoti daudz punktveida avotu, un, ja apskata elektrisko lauku attālumā R, kas pārsniedz lodes rādiusu r, tad šo daudzo punktveida lādiņu elektrisko lauku summa veido tādu pašu elektrisko lauku, ja lodes centrā būtu novietots punktveida lādiņš q0. Līdz ar to vadītāja lodes elektriskā lauka intensitāte E = kq0 : R2, jaR>r.
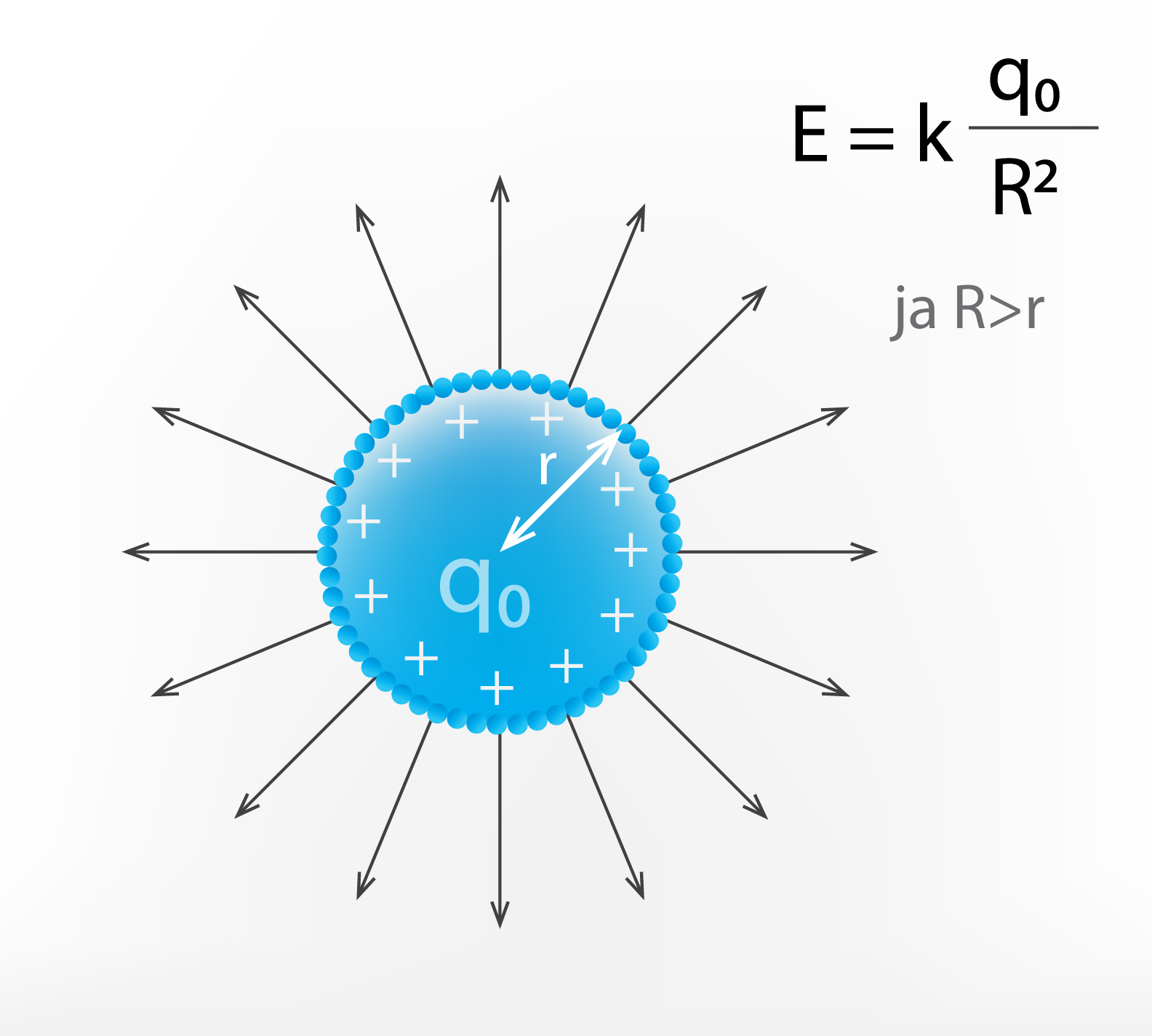
3.att. Vadītāja lodes elektriskais lauks
Elektriskā lauka intensitātes izteiksmes var uzrakstīt arī plakanām virsmām, vienīgi, salīdzinot ar punktveida lādiņu un vadītāja lodi, plakanu virsmu elektrisko lauku nosaka nevis kopējais lādiņš q, bet gan lādiņu blīvums σ. Lādiņu blīvumu iegūst, lādiņa lielumu izdalot ar virsmas laukumu, kurā šīs lādiņš ir koncentrēts. Ja paņemam ar pozitīvu lādiņu q+uzlādētu virsmu ar laukumu S, tad lādiņu blīvums σ = q+ : S (4. att.). Lādiņu blīvumu var iedomāties arī tā: ja uz uzlādētas virsmas tiek ierobežots 1 m2liels laukums, tad tajā ir koncentrēts lādiņš ar lielumu σ (4. att.).
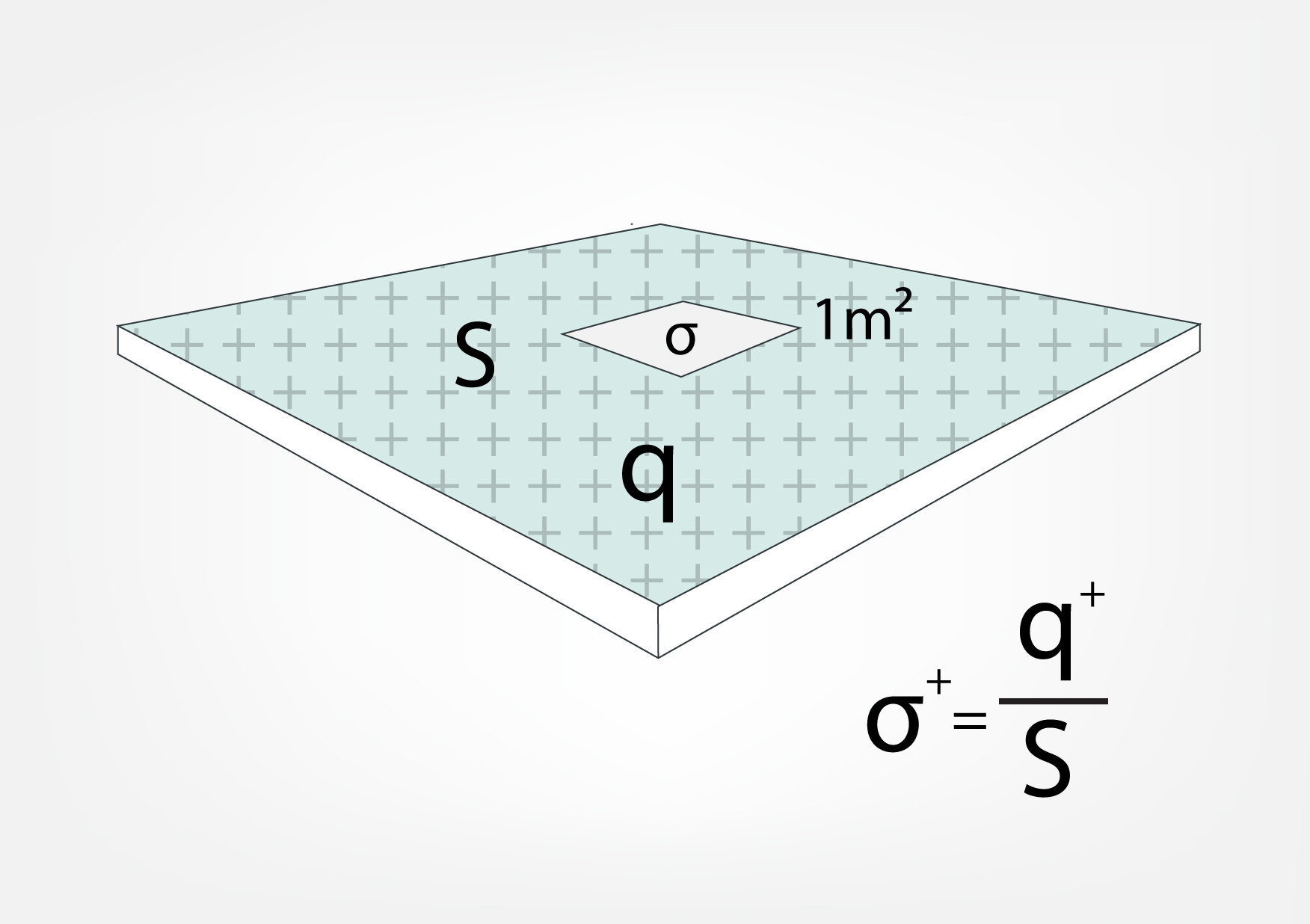
4.att. Uzlādētas virsmas lādiņu blīvums σ
Atrodoties tuvumā bezgalīgai vadītāja plaknei, var konstatēt, ka elektriskā lauka intensitāte visos punktos ir vienāda. Šādu lauku sauc par homogēnu. Atkarībā no tā, vai plakne ir uzlādēta pozitīvi (5. att. a) vai negatīvi (5. att. b), homogēnais elektriskais lauks vai nu izplūst no plaknes, vai ieplūst tajā iekšā. Bezgalīgas plaknes elektriskā lauka intensitātes aprēķiniem vakuumā lieto izteiksmi E = σ : 2ε0, kur
σ - lādiņa virsmas blīvums, kuloni uz kvadrātmetru (C : m2)
ε0- vakuuma elektriskā konstante, kas vienāda ar ε0 = 8,85.10-12F:m
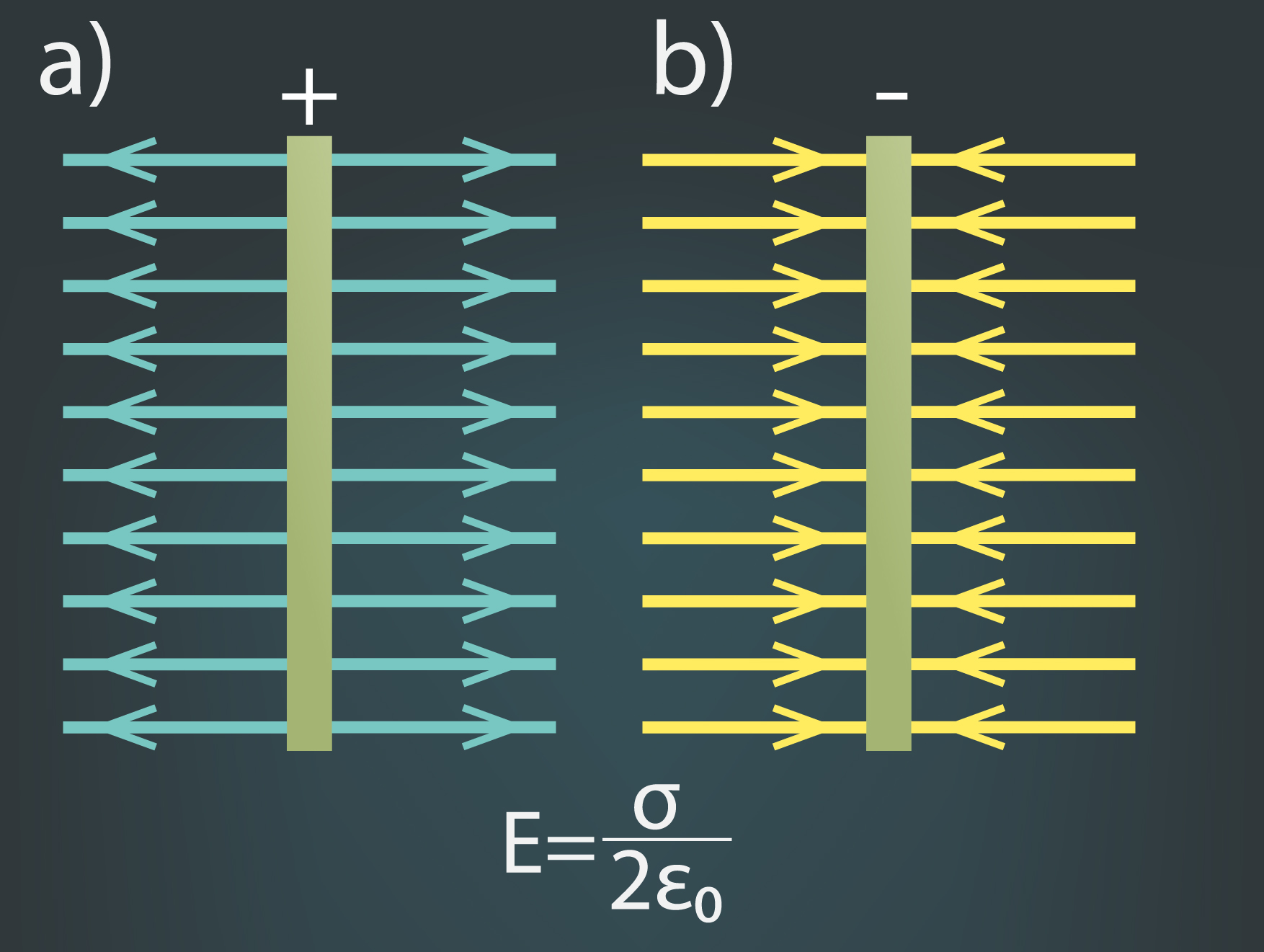
5.att. Uzlādētu plakņu elektriskais lauks
Ja ļoti tuvu novieto divas pretēji lādētas plaknes, kurām lādiņu blīvumi σ ir vienādi, tad elektriskais lauks starp plaknēm summējās un kopēja elektriskā lauka intensitāte izsakāma kā E = σ : ε0(6. att.). Ārpus plaknēm elektriskie lauki viens otru atceļ, tādēļ tur elektriskais lauks ir mazs vai pat vispār nav.
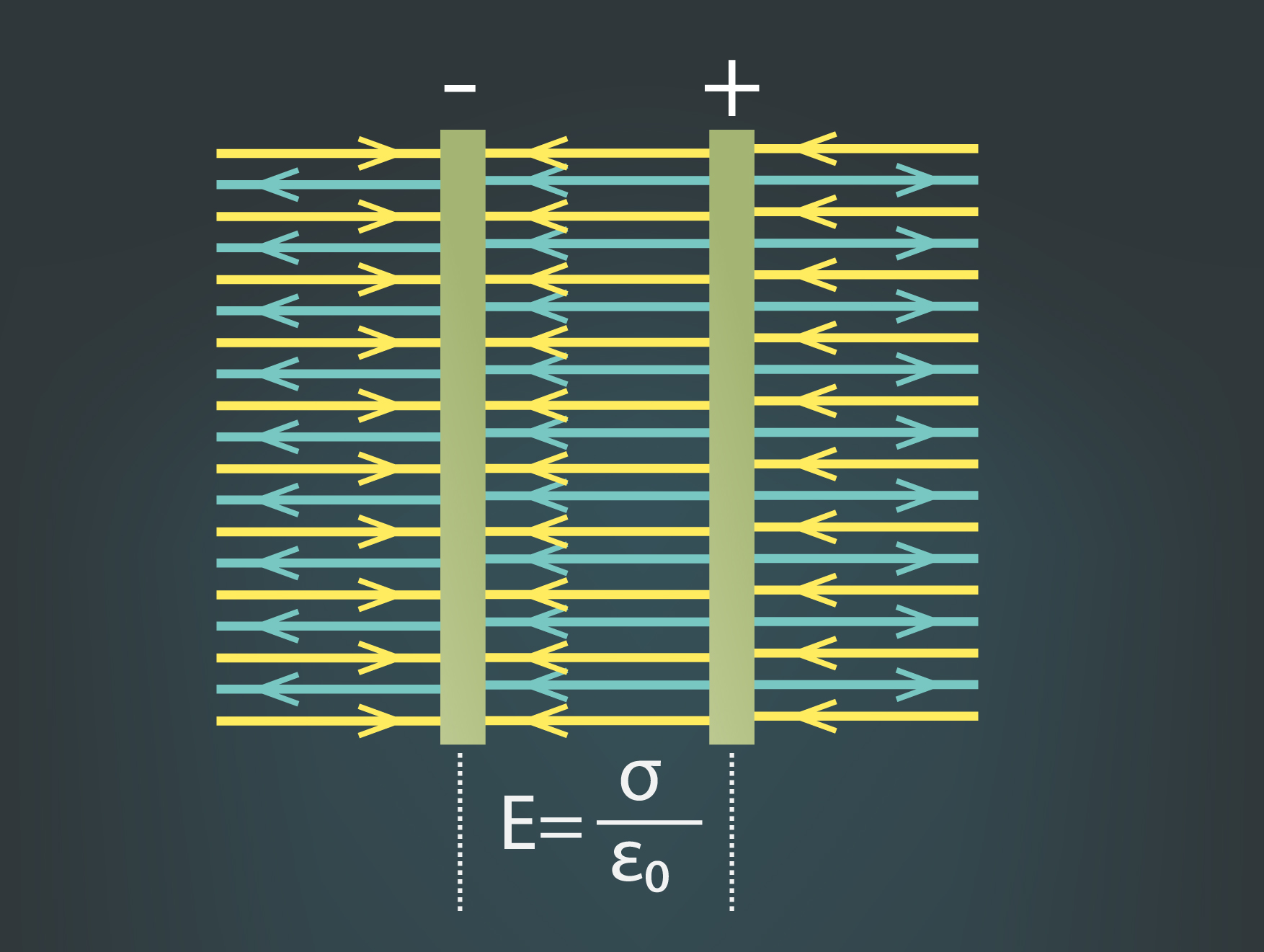
6.att. Divu pretēji uzlādētu plakņu elektriskais lauks
2. solī tika minēts, ka vadītāja lodes elektriskā lauka intensitāte ir aprakstāma ar tādu pašu izteiksmi kā punktveida avota elektriskā lauka intensitāte, ja attālums no lodes centra pārsniedz lodes rādiusu r. Elektriskais lauks pastāv arī lodes iekšpusē. Pašā lodes centrā tas gan ir nulle, bet tālāk, attālinoties no centra, tas lineāri pieaug līdz tā maksimālajai vērtībai uz lodes virsmas (1. att.). Tālāk elektriskā lauka intensitātes izmaiņas raksturs ir tāds, kā jau iepriekš tika apskatīts.

1.att. Vadītāja lodes elektriskā lauka intensitāte
Nedaudz cita situācija ir saistībā ar uzlādētas vadītāja sfēras elektriskā lauka intensitāti. Ārpus sfēras elektriskā lauka intensitāte sakrīt ar lodes elektriskā lauka intensitāti, bet atšķirība no lodes ir tā, ka sfēras iekšpusē elektriskā lauka vispār nav (2. att.).
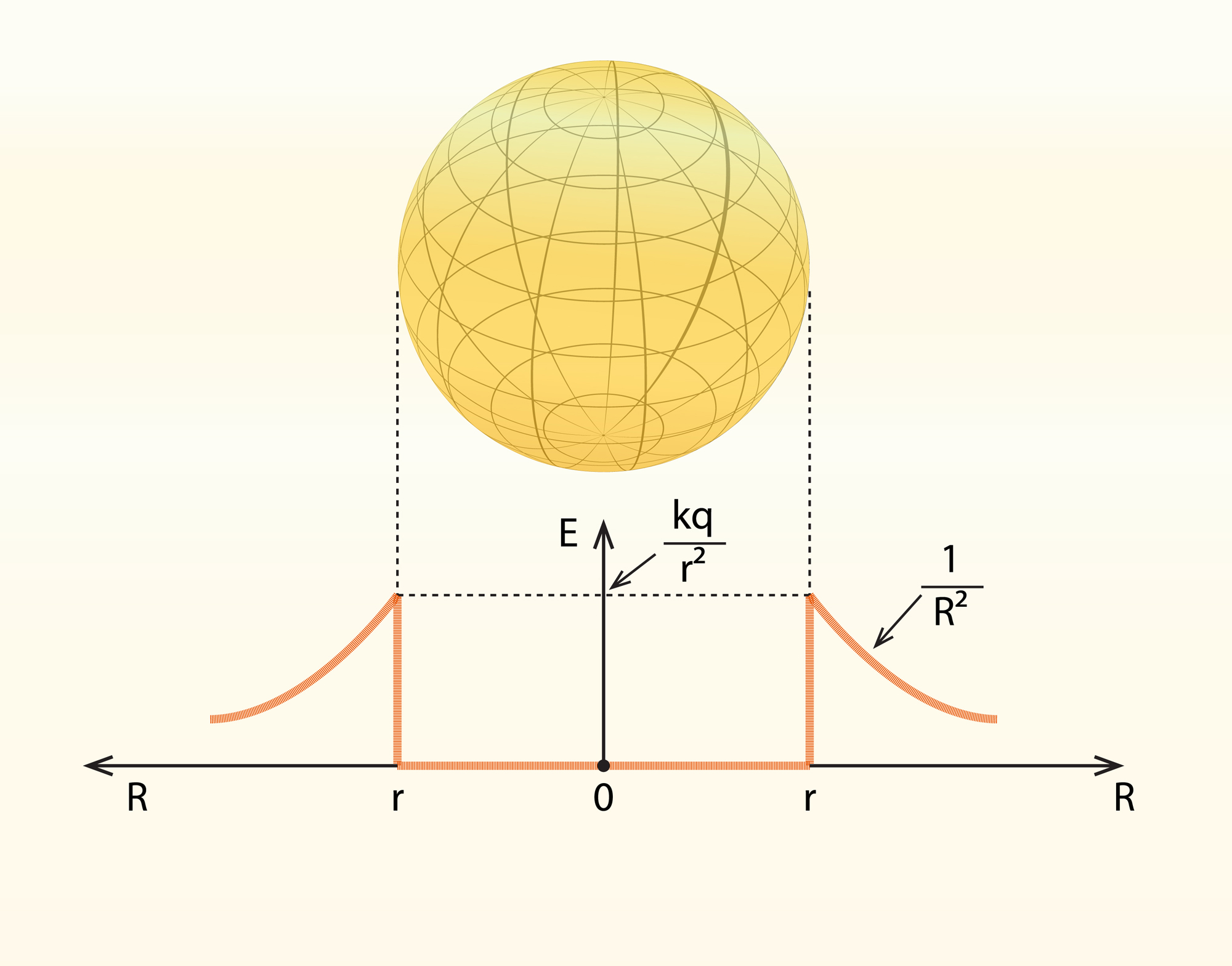
2.att. Vadītāja sfēras elektriskā lauka intensitāte
2. solī tika apskatīts arī bezgalīgu plakņu elektriskais lauks, kas tuvumā plaknēm ir homogēns. Plakņu tuvums pieminēts tādēļ, ka reāli dabā bezgalīgu plakņu nav, katrai uzlādētai plaknei ir galīgs izmērs, un, jo šis izmērs ir lielāks, jo tālāk no plaknes saglabājas homogēns elektriskais lauks. Ja ieskicē elektriskā lauka līnijas divām galīgām plaknēm (3. att.), tad starp plaknēm, kur lauks ir homogēns, elektriskā lauka intensitātes līnijas ir savstarpēji paralēlas, bet ārpusē elektriskā lauka intensitātes līnijas sāk izliekties un vairāk atgādināt divu punktveida avotu elektrisko lauku.
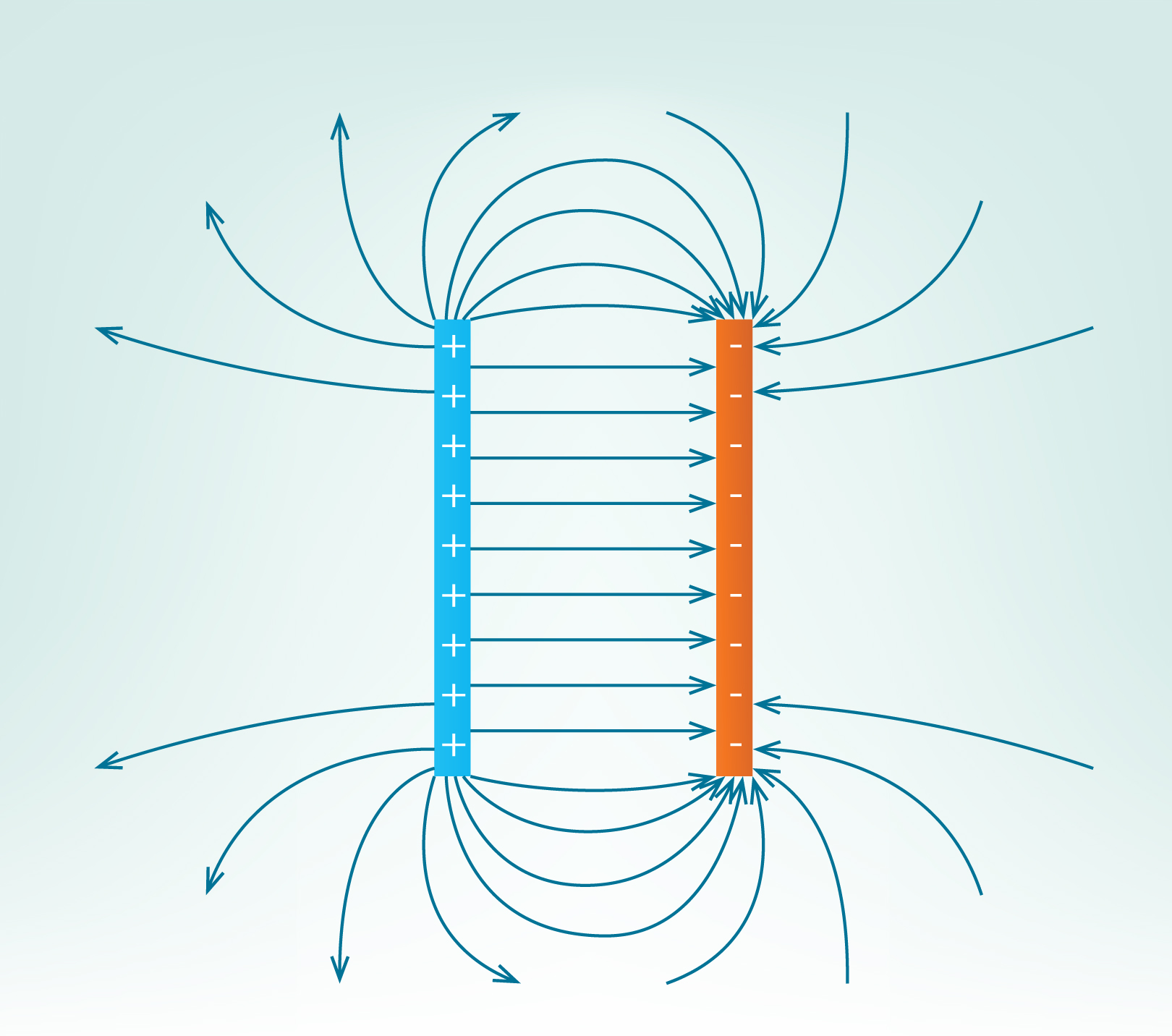
3.att. Divu galīgu plakņu elektriskā lauka intensitātes līnijas
Elektriskā lauka kopainu var veidot arī trīs un vairāk lādiņi. Šie lādiņi var būt gan ar vienādu zīmi (4. att. a), gan arī ar dažādām (4. att. b). Šādām sistēmām elektriskā lauka intensitāšu līniju aprēķinus un vizualizāciju ērti veikt ar dažādām datorprogrammām, ar kurām ātri var veikt pat ļoti komplicētu elektrisko lauku aprēķinus un attēlojumu.

4.att. Vairāku lādiņu elektriskais lauks